樹論
Tree Algorithms
複習一下
樹是什麼樣的圖?
Tree
樹的特點
- 有 \(V\) 個點的圖,有 \(V-1\) 條邊
- 圖上任兩點間皆連通且有唯一的一條路徑
- 圖上不會形成環
樹是從上往下長的
那麼,我們到底要來討論什麼東西呢?
樹直徑
Tree Diameter
不是圓也能有直徑嗎???
回想一下,圓上面的直徑的定義為何?
圓上兩點最遠的距離
那麼樹上的直徑要怎麼定義呢?
沒錯! 樹上兩點最遠距離
樹直徑
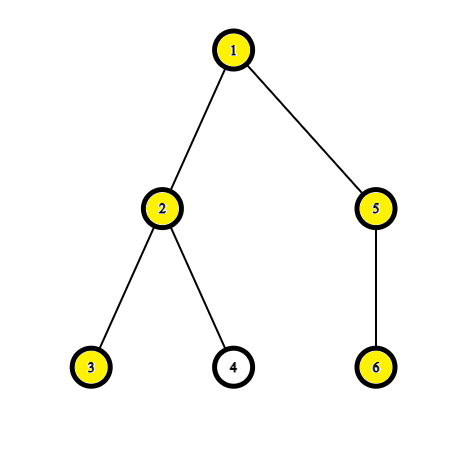
不過,我們要怎麼找到一棵樹的直徑呢?
最常見的方式有兩種
1. BFS/DFS 兩次
2. 樹 DP
我們先來談談第一種作法
樹直徑求法 (DFS)
1. 任意選一個起點 \(a\) 開始,找到離這個起點最遠的點 \(u\)
2. 再去找離 \(u\) 最遠的點 \(v\)
3. \(u,v\) 之間的路徑即為直徑
作法很簡單,而證明的方式也不難
可以自己當作練習證明看看
程式碼
int dis[N], farthest, mxdis;
void dfs(int u, int p){
if(dis[u] > mxdis){
farthest = u;
mxdis = dis[u];
}
for(auto v : adj[u]){
if(v == p) continue;
dis[v] = dis[u] + 1;
dfs(v,u);
}
}
//呼叫以下
dfs(1,-1);
dfs(farthest,-1);
//mxdis is the length of diameter樹直徑求法 (樹 DP)
1. 設 \(dp[u][2]\) 為 \(u\) 往下延伸最長/次長的距離
2. 樹的直徑為 \(\displaystyle max_{u \in G}(dp[u][0]+dp[u][1])\)
兩點的最遠距離一定經過某個點
所以去枚舉點找可以延伸的最長與次長總和
即可得到正確答案
程式碼
int dp[N][2], ans;
void dfs(int u, int p){
for(auto v : adj[u]){
if(v == p) continue;
dfs(v,u);
if(dp[v][0] + 1 > dp[u][0]) dp[u][1] = dp[u][0], dp[u][0] = dp[v][1] + 1;
else if(dp[v][0] + 1 > dp[u][1]) dp[u][1] = dp[v][0] + 1;
}
ans = max(dp[u][0]+dp[u][1]);
}練習題
樹重心
Tree Centroid
大家以前應該都學過三角形的重心吧
三角形的重心為平分三角形面積的點
不過對於樹的重心,我們定義為移除這個點之後
沒有任何一個連通分量有超過 \(\lfloor \frac{V}{2} \rfloor\) 個點
要找樹的重心非常簡單
直接 DFS 去找即可!
找樹重心
void dfs_sz(int u, int p){
sz[u] = 1;
for(auto v : adj[u]){
if(v == p) continue;
dfs_sz(v,u);
sz[u] += sz[v];
}
}
int get_centroid(int u, int p){
for(auto v : adj[u]){
if(v == p) continue;
if(sz[v] > n/2) return get_centroid(v,u);
}
return u;
}樹重心通常會用在 「重心分治」
練習題
最低共同祖先
Lowest Common Ancestor
Lowest Common Ancestor
最低共同祖先
對於一個有根樹上的兩個節點 \(u,v\)
他們的祖先當中共同最低的那個
找法
- 暴力把兩個點往上跳,時間複雜度 \(O(n)\)
- 倍增法,時間複雜度 \(O(\log n)\)
- 樹壓平,時間複雜度 \(O(1)\)
- 樹鍊剖分,時間複雜度 \(O(\log n)\)
但我們今天只會講前三個做法
暴力作法
- 先從根開始 DFS,對每個點紀錄父親與高度
- 在詢問 \(LCA(u,v)\) 時,將矮的點往上跳,直到兩點高度相同
- 將兩點一起往上跳,直到兩點相同
- 直接回傳 \(u\)
暴力 LCA
void dfs(int u, int p){
for(auto v : adj[u]){
if(v == p) continue;
dep[v] = dep[u] + 1;
par[v] = u;
dfs(v, u);
}
}
int lca(int u, int v){
while(dep[u] != dep[v]){
if(dep[u] < dep[v]) swap(u, v);
u = par[u];
}
while(u != v){
u = par[u], v = par[v];
}
return u;
}倍增法
Binary Lifting
倍增法?
我們之前在講 RMQ 時
提過一種使用倍增法時做的資料結構
也就是 Sparse Table
而找 LCA
作法
對於每個點 \(u\) 開一個 \(dp[u][i]\) 的陣列
儲存的資料為 \(u\) 往上跳 \(2^i\) 步時
會跳到哪個節點
(這裡我們用 1-base, 所以如果跳超過根,我們就讓他是 \(0\))
範例
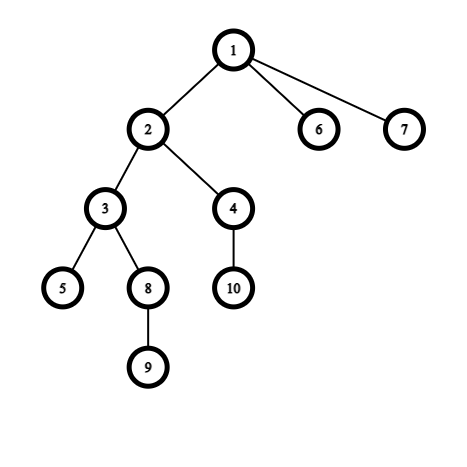
\(dp[5][1] = 2\)
因此,建出倍增表後
我們就可以在很快的時間完成暴力作法的想法了
使用倍增表找 LCA
1. 先將 \(u,v\) 跳到同個高度
2. 如果 \(u = v\),就回傳 \(u\)
3. 否則就兩點繼續往上跳
4. 回傳 \(dp[u][0]\)
倍增法求 LCA
void dfs(int u, int p){
for(auto v : adj[u]){
if(v == p) continue;
dep[v] = dep[u] + 1;
dp[v][0] = u;
dfs(v, u);
}
}
void init(){
for(int i = 1; i <= LOGN; i++){
for(int u = 1; u <= n; u++){
dp[u][i] = dp[dp[u][i-1]][i-1];
}
}
}
int lca(int u, int v){
if(dep[u] < dep[v]) swap(u,v);
for(int i = LOGN; i >= 0; i--){
if((dep[u]-dep[v])&(1<<i))
u = dp[u][i];
}
if(u == v) return u;
for(int i = LOGN; i >= 0; i--){
if(dp[u][i] != dp[v][i])
u = dp[u][i], v = dp[v][i];
}
return dp[u][0];
}練習題
樹壓平
Euler Tour
在之前,我們講了各種區間詢問的資料結構
而這些維護陣列的資料結構,事實上也能使用在樹上
不過,要怎麼把一棵樹轉換成一個序列呢?
Euler TOUR
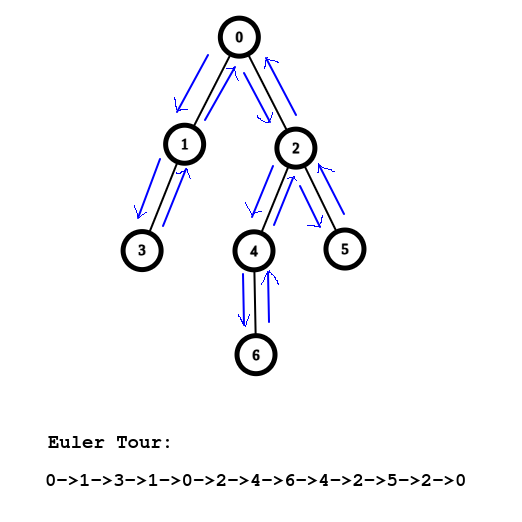
Euler Tour
照節點進入與離開的順序
建出一個樹壓平序列
EULER TOUR

| Euler | 1 | 2 | 3 | 3 | 2 | 6 | 6 | 2 | 4 |
|---|---|---|---|---|---|---|---|---|---|
| Depth | 0 | 1 | 2 | 2 | 1 | 2 | 2 | 1 | 1 |
| 5 | 4 | 1 |
|---|---|---|
| 2 | 1 | 0 |
EULER TOUR

| Euler | 1 | 2 | 3 | 3 | 2 | 6 | 6 | 2 | 4 |
|---|---|---|---|---|---|---|---|---|---|
| Depth | 0 | 1 | 2 | 2 | 1 | 2 | 2 | 1 | 1 |
| 5 | 4 | 1 |
|---|---|---|
| 2 | 1 | 0 |
發現到任兩點的區間的 Depth 的最小值即為 LCA
因為 LCA 通常會有多次詢問
Sparse Table!
Euler Tour
vector<int> euler;
int in[N], out[N];
void dfs(int u, int p){
in[u] = euler.size();
euler.push_back(u);
for(auto v : adj[u]){
if(v == p) continue;
dfs(v, u);
euler.push_back(u);
}
out[u] = euler.size();
}樹壓平處理子樹問題?
CSES - subTree Queries
給你一棵以 \(1\) 為根的樹
每個點皆有各自的權重
每次有兩種詢問與操作
1. 把點 \(u\) 的值改成 \(x\)
2. 計算以點 \(u\) 為根的子樹的點權和
EULER TOUR

| Euler | 1 | 2 | 3 | 3 | 6 | 6 | 2 | 4 | 5 |
|---|
| 5 | 4 | 1 |
|---|
發現到 \(in[u], out[u]\) 之間的節點即為子樹的點
EULER TOUR

| Euler | 1 | 2 | 3 | 3 | 6 | 6 | 2 | 4 | 5 |
|---|
| 5 | 4 | 1 |
|---|
使用線段樹或 BIT 維護答案即可!
練習題
輕重鍊剖分
(Heavy-Light Decomposition)
前面我們提過一種能夠將樹轉成序列的方式
也就是樹壓平
他可以處理 子樹 的問題
不過今天如果是兩點路徑的答案
樹壓平就無法處理了
(例外: 點到根可以處理)
因此,我們這裡要來介紹 HLD 這個方法
Heavy-Light Decomposition
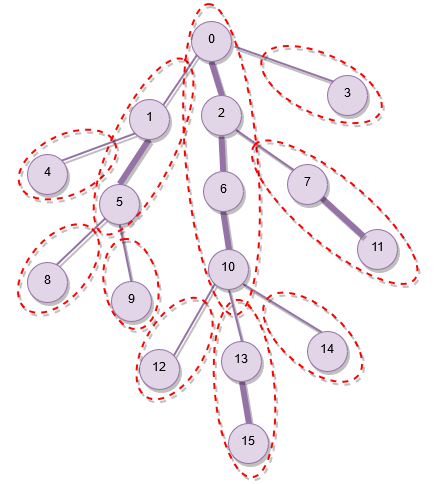
HLD 的原理
- 將一棵樹,拆分成很多條不同的輕重鍊
- 可以對每個節點作編號,以資結維護路徑答案
- 由於拆成輕重鍊,在往上跳時,複雜度最差為 \(O(\log n)\)
HLD
- 對於一個節點 \(v\),若 \(c\) 是 \(v\) 的 child 當中,子樹大小最大的節點,則 \(e=(v,c)\) 是一條重邊
- 重邊所形成的鍊稱作重鍊
- 輕邊所形成的鍊稱作輕鍊
如何找出重邊與輕邊?
DFS!
找重邊、輕邊
int heavy[N], sz[N];
void dfs(int u, int p){
sz[u] = 1;
int mxsz = 0, idx = 0;
for(auto v : adj[u]){
if(v == p) continue;
dfs(v, u);
sz[u] += sz[v];
if(sz[v] > mxsz){
mxsz = sz[v];
idx = v;
}
}
heavy[u] = idx;
}有了這些重邊之後能幹嘛?
HLD Step 2
- 對每條重鍊紀錄最上方的節點
- 並且依序對每個節點標記編號
這步被稱為 Decomposition
也就是剖分!
Decomposition
int head[N], id[N], tmp;
void decompose(int u, int p, int h){
head[u] = h;
id[u] = tmp++; //如果要放到資結上維護路徑答案,才要做這步
if(heavy[u]) decompose(heavy[u], u, h); //延伸重鍊
for(auto v : adj[u]){
if(v == p || v == heavy[u]) continue;
decompose(v, u, v); //如果是輕邊,則 v 的鍊的最上方為 v
}
}所以 HLD 建完之後,能做什麼?
1. LCA,\(O(n)/O(\log n)\)
2. 路徑答案的維護
LCA
使用 HLD 找 LCA 與倍增法的概念類似
同樣都是利用往上跳的方式去尋找答案
LCA

1. u,v 同鍊 => 直接回傳深度較低的!
\(u\)
\(v\)
LCA

2. \(u,v\) 不同鍊,先將鍊的頭深度較深的往上跳
\(u\)
\(v\)
LCA

2. \(u,v\) 不同鍊,先將鍊的頭深度較深的往上跳
\(u\)
\(v\)
直到同鍊
LCA

2. \(u,v\) 不同鍊,先將鍊的頭深度較深的往上跳
\(u\)
\(v\)
LCA

2. \(u,v\) 不同鍊,先將鍊的頭深度較深的往上跳
\(u\)
\(v\)
LCA

2. \(u,v\) 不同鍊,先將鍊的頭深度較深的往上跳
\(u\)
\(v\)
直到同鍊
LCA 程式碼
int lca(int u, int v){
while(head[u] != head[v]){
if(dep[head[u]] < dep[head[v]]) swap(u,v);
u = par[head[u]];
}
if(dep[u] > dep[v]) swap(u,v);
return u;
}詢問路徑答案?
注意到我們在剖分時,對每個節點有紀錄編號!
編號有什麼特殊的地方呢?
HLD 編號

HLD 編號

\(1\)
\(1\)
HLD 編號

\(1\)
\(1\)
\(2\)
HLD 編號

\(1\)
\(1\)
\(2\)
\(3\)
HLD 編號

\(1\)
\(1\)
\(2\)
\(3\)
\(4\)
HLD 編號

\(1\)
\(1\)
\(2\)
\(3\)
\(4\)
\(5\)
HLD 編號

\(1\)
\(1\)
\(2\)
\(3\)
\(4\)
\(5\)
\(5\)
\(6\)
HLD 編號

\(1\)
\(1\)
\(2\)
\(3\)
\(4\)
\(5\)
\(5\)
\(6\)
\(5\)
\(6\)
\(7\)
HLD 編號

\(1\)
\(1\)
\(2\)
\(3\)
\(4\)
\(5\)
\(5\)
\(6\)
\(5\)
\(6\)
\(7\)
\(5\)
\(8\)
HLD 編號

\(1\)
\(1\)
\(2\)
\(3\)
\(4\)
\(5\)
\(5\)
\(6\)
\(5\)
\(6\)
\(7\)
\(5\)
\(8\)
\(5\)
\(6\)
\(7\)
\(8\)
\(9\)
HLD 編號

\(1\)
\(1\)
\(2\)
\(3\)
\(4\)
\(5\)
\(5\)
\(6\)
\(5\)
\(6\)
\(7\)
\(5\)
\(8\)
\(5\)
\(6\)
\(7\)
\(8\)
\(9\)
\(10\)
\(10\)
HLD 編號

\(1\)
\(1\)
\(2\)
\(3\)
\(4\)
\(5\)
\(5\)
\(6\)
\(5\)
\(6\)
\(7\)
\(5\)
\(8\)
\(5\)
\(6\)
\(7\)
\(8\)
\(9\)
\(10\)
\(10\)
\(11\)
HLD 編號

\(1\)
\(1\)
\(2\)
\(3\)
\(4\)
\(5\)
\(5\)
\(6\)
\(5\)
\(6\)
\(7\)
\(5\)
\(8\)
\(5\)
\(6\)
\(7\)
\(8\)
\(9\)
\(10\)
\(10\)
\(11\)
\(12\)
HLD 編號

\(1\)
\(1\)
\(2\)
\(3\)
\(4\)
\(5\)
\(5\)
\(6\)
\(5\)
\(6\)
\(7\)
\(5\)
\(8\)
\(5\)
\(6\)
\(7\)
\(8\)
\(9\)
\(10\)
\(10\)
\(11\)
\(12\)
\(13\)
HLD 編號

\(1\)
\(1\)
\(2\)
\(3\)
\(4\)
\(5\)
\(5\)
\(6\)
\(5\)
\(6\)
\(7\)
\(5\)
\(8\)
\(5\)
\(6\)
\(7\)
\(8\)
\(9\)
\(10\)
\(10\)
\(11\)
\(12\)
\(13\)
\(14\)
HLD 編號

\(1\)
\(1\)
\(2\)
\(3\)
\(4\)
\(5\)
\(5\)
\(6\)
\(5\)
\(6\)
\(7\)
\(5\)
\(8\)
\(5\)
\(6\)
\(7\)
\(8\)
\(9\)
\(10\)
\(10\)
\(11\)
\(12\)
\(13\)
\(14\)
\(15\)
每個鍊上的編號是連續的!
因此,我們可以邊做 LCA 邊詢問路徑!
HLD 維護路徑答案 (點權)
int hld_query(int u, int v){
int res = 0;
while(head[u]!=head[v]){
if(dep[head[u]] < dep[head[v]]) swap(u,v);
res = max(res,query(arr[head[u]],arr[u],1,1,t));
u = par[head[u]];
}
if(dep[u] > dep[v]) swap(u,v);
if(u==v) return res;
res = max(res,query(arr[u],arr[v],1,1,t));
return res;
}
void hld_modify(int u, int v, int val){
if(dep[u] > dep[v]) swap(u,v);
while(head[u]!=head[v]){
if(dep[head[u]] < dep[head[v]]) swap(u,v);
modify(arr[head[u]],arr[u],val,1,1,t);
u = par[head[u]];
}
if(dep[u] > dep[v]) swap(u,v);
modify(arr[u],arr[v],val,1,1,t);
}HLD 維護路徑答案 (邊權)
int hld_query(int u, int v){
int res = 0;
while(head[u]!=head[v]){
if(dep[head[u]] < dep[head[v]]) swap(u,v);
res = max(res,query(arr[head[u]],arr[u],1,1,t));
u = par[head[u]];
}
if(dep[u] > dep[v]) swap(u,v);
if(u==v) return res;
res = max(res,query(arr[u]+1,arr[v],1,1,t));
return res;
}
void hld_modify(int u, int v, int val){
if(dep[u] > dep[v]) swap(u,v);
while(head[u]!=head[v]){
if(dep[head[u]] < dep[head[v]]) swap(u,v);
modify(arr[head[u]],arr[u],val,1,1,t);
u = par[head[u]];
}
if(dep[u] > dep[v]) swap(u,v);
modify(arr[u]+1,arr[v],val,1,1,t);
}練習題
樹 DP
(DP on Tree)
在樹上 DP?
樹 DP 主要會用在一棵有根樹上
而對於一個節點的 \(dp[u]\) 儲存的答案為
在 \(u\) 的子樹中的答案
讓我們來看看例題
這題就是十分經典的樹 DP
設 \(dp[u][0/1]\) 為當 \(u\) 節點被塗成白色/黑色時
以 \(u\) 為根的子樹有幾種塗色方式
轉移式就變得很好思考了!
\(dp[u][0] = \sum_{v \in c[u]} (dp[v][0] + dp[v][1])\)
\(dp[u][1] = \sum_{v \in c[u]} dp[v][0]\)
而這個題目,事實上是在算樹上的「最大獨立集」
最大獨立集:
在一張圖上,找到一個最大的點集,使得點集中任兩點不互相相鄰
在一般圖上找最大獨立集是 NPC 問題
最大匹配:
對於一張圖,找到一個最大的邊集,使得每個點最多連出一條邊
所以同樣的,我們也來想想 DP 式
不過匹配要怎麼做呢?
設 \(dp[u][0]\) 為這個點與他的子節點沒有邊時的最大匹配
\(dp[u][1]\) 為這個點與子節點有邊的最大匹配
轉移式大家可以自己想想看
Codeforces 1528A - Parsa's Humongous Tree
給你一棵樹,樹上的節點的權值可以介於 \(l_u, r_u\) 之間
一棵樹的漂亮程度為所有邊的 \(|a_u-a_v|\) 的總和
問樹的最大的漂亮程度為何?
這題,其實只是把 DP 其中一題經典題放到樹上
而我們都知道,如果點權是一個區間
則最大價值一定會發生在區間的兩個端點
設 \(dp[u][0/1]\) 為 \(u\) 的權重為 \(l_u\) 或 \(r_u\) 時
以 \(u\) 為根的子樹的最大漂亮程度
轉移式大家也可以自己想想
練習題
換根 DP
(Rerooting Technique)
日文: 全方位木 DP
有的時候,題目可能會問你以下兩種可能性
無根樹的最大答案
or
對每個點為根的子樹輸出答案
此時,換根 DP 就可以使用到了
換根 DP 的作法
思考看看如果已經有以某個點為根的答案時
要怎麼樣能計算以他相鄰的點為根的答案
void dfs(int u, int p){
//Tree DP
}
void reroot(int u, int p){
for(auto v : adj[u]){
if(v == p) continue;
//Change root to v
reroot(v, u);
//Change root back to u
}
}不過,換根 DP 主要還是推轉移式
因此還是要好好思考 DP 式
練習題
重心剖分
(Centroid Decomposition)
先來看看幾題例題吧!
你有一棵樹
你想要計算這棵樹有幾條長度為 \(k\) 的路徑
你有一棵樹,你可以做以下兩種事情
1. 將點 \(x\) 塗成紅色
2. 詢問 \(x\) 到最近的紅色點的距離
而這些問題都是重心剖分可以處理的事情
我們先來複習一下什麼是重心
樹的重心
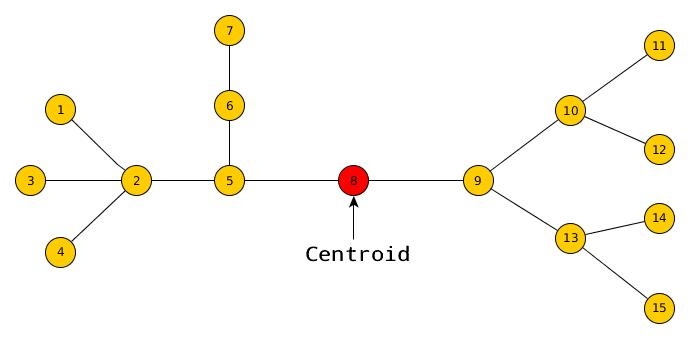
拿掉重心後,不會有大小超過 \(\frac n 2\) 的連通分量
樹的重心
拿掉重心後,不會有大小超過 \(\frac n 2\) 的連通分量
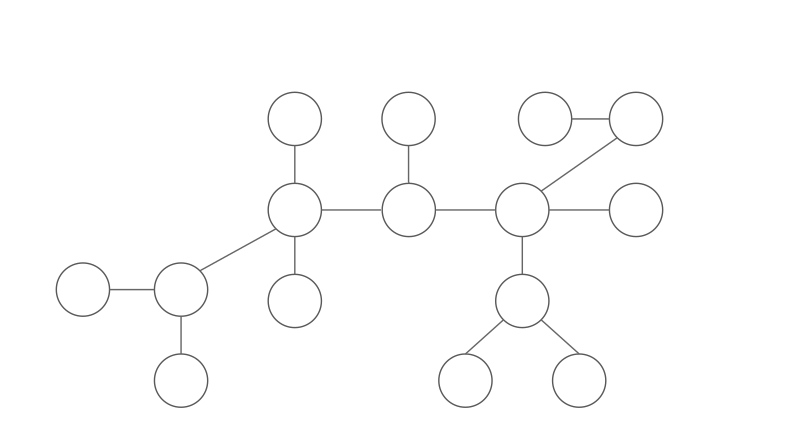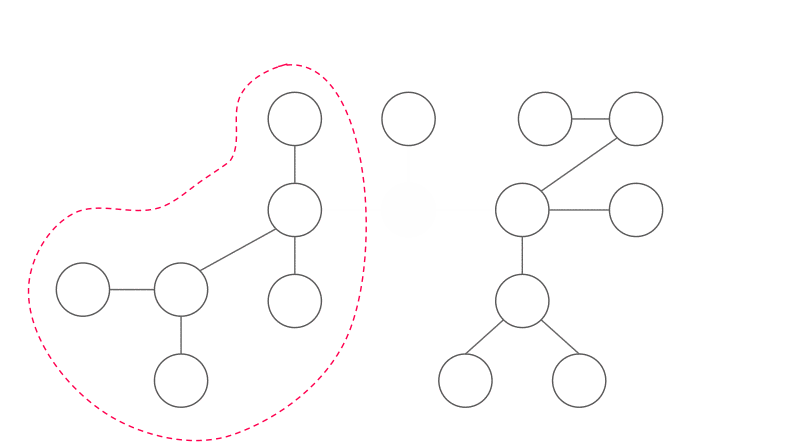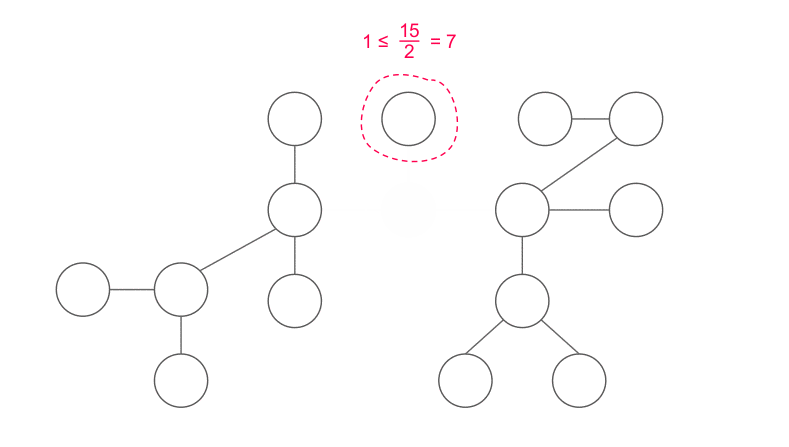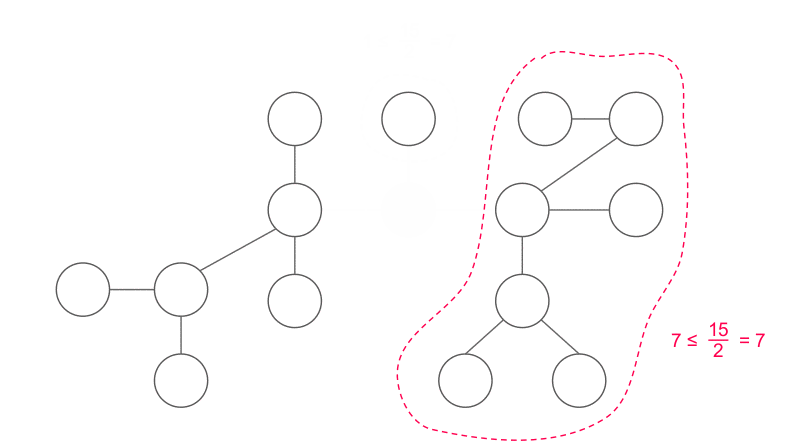
因為這個性質
我們可以如對陣列分治一般
不停地將樹切半
因此重心剖分,也可以想成是在樹上分治
重心剖分
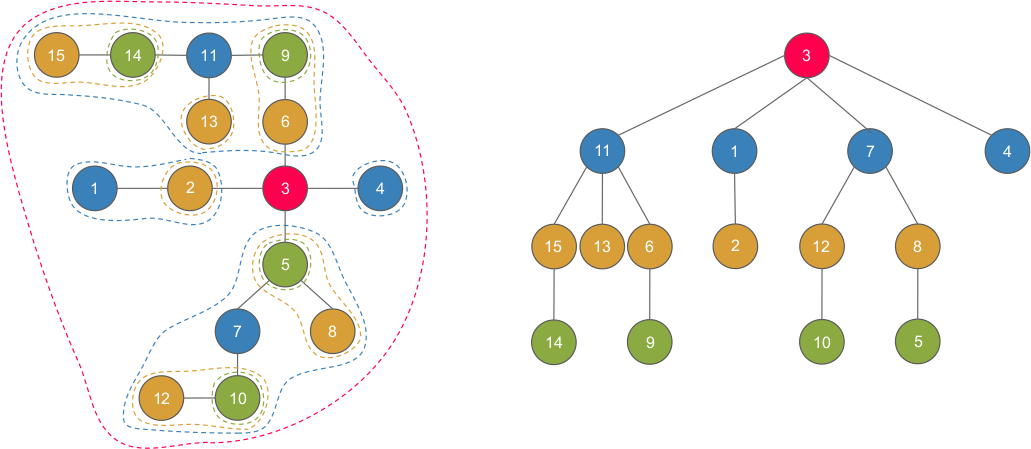
我們會將重心一一找出,建出一棵 重心樹
(重心之間可能沒有邊)
重心剖分

我們會將重心一一找出,建出一棵 重心樹
重心特別的地方在於以重心當根時,任兩個在不同子樹的 \(u,v\) 的路徑會經過這個點
至於要怎麼做到這件事情
這就是我們要來將其寫成程式碼的時候了
重心剖分 (步驟)
- 任意選一個節點當根
- 找到目前這棵樹的重心 (其中一個即可)
- 將重心移除 (或標記走過)
- 往其他連通分量走,並重複 2.~4.
重心剖分
//重心剖分的三個函數
void dfs_sz(int u, int p){
//這個函數預處理子樹大小 => 找重心要用
}
int centroid(int u, int p, int rt){
//這個函數找重心
}
void decompose(int u){
//建出重心樹
}重心剖分
//重心剖分的三個函數
void dfs_sz(int u, int p){
//這個函數預處理子樹大小 => 找重心要用
sz[u] = 1;
for(auto v : adj[u]){
if(v == p || vis[v]) continue;
dfs(v, u);
sz[u] += sz[v];
}
}
int centroid(int u, int p, int rt){
//這個函數找重心
}
void decompose(int u){
//建出重心樹
}重心剖分
//重心剖分的三個函數
void dfs_sz(int u, int p){
//這個函數預處理子樹大小 => 找重心要用
sz[u] = 1;
for(auto v : adj[u]){
if(v == p || vis[v]) continue;
dfs(v, u);
sz[u] += sz[v];
}
}
int centroid(int u, int p, int rt){
//這個函數找重心
for(auto v : adj[u]){
if(v == p || vis[v]) continue;
if(sz[v] >= sz[rt]/2)
return centroid(v, u, rt);
}
return u;
}
void decompose(int u){
//建出重心樹
}重心剖分
//重心剖分的三個函數
void dfs_sz(int u, int p){
//這個函數預處理子樹大小 => 找重心要用
sz[u] = 1;
for(auto v : adj[u]){
if(v == p || vis[v]) continue;
dfs(v, u);
sz[u] += sz[v];
}
}
int centroid(int u, int p, int rt){
//這個函數找重心
for(auto v : adj[u]){
if(v == p || vis[v]) continue;
if(sz[v] >= sz[rt]/2)
return centroid(v, u, rt);
}
return u;
}
void decompose(int u){
//建出重心樹
dfs_sz(u, -1);
int c = centroid(u, -1, u);
vis[c] = 1;
//在這裡通常會處理答案
do_something();
for(auto v : adj[c]){
if(vis[v]) continue;
decompose(v);
}
}分析時間複雜度
每次都將樹從中間切開
建出來的重心樹會高度會是 \(O(\log n)\)
與分治概念很像,我們可以用以下去估
\(T(n) = 2T(n/2) + O(n)\)
根據主定理,時間複雜度為 \(O(n \log n)\)
可能到這裡還不是很了解它在幹嘛
我們實際來解剛剛那個題目看看
你有一棵樹
你想要計算這棵樹有幾條長度為 \(k\) 的路徑
對每個重心去維護往不同子樹的點的路徑長
就可以好好的做到這件事了
程式碼
//重心剖分的三個函數
void dfs_sz(int u, int p){
//這個函數預處理子樹大小 => 找重心要用
sz[u] = 1;
for(auto v : adj[u]){
if(v == p || !vis[v]) continue;
dfs(v, u);
sz[u] += sz[v];
}
}
int centroid(int u, int p, int rt){
//這個函數找重心
for(auto v : adj[u]){
if(v == p || vis[v]) continue;
if(sz[v] >= sz[rt]/2)
return centroid(v, u, rt);
}
return u;
}
void get_dep(int u, int p, int dep){
cnt[dep]++;
for(auto v : adj[u]){
if(v == p || vis[v]) continue;
get_dep(v,u,dep+1);
}
}
void get_ans(int u, int p, int dep){
ans += cnt[k-dep];
for(auto v : adj[u]){
if(v == p || vis[v]) continue;
get_ans(v,u,dep+1);
}
}
void decompose(int u){
//建出重心樹
dfs_sz(u, -1);
int c = centroid(u, -1, u);
vis[c] = 1;
for(auto v : adj[c]){
if(vis[v]) continue;
get_ans(v,c,1); //處理路徑數量
get_dep(v,c,1); //處理點的深度計算
}
fill(cnt,cnt+N,0) //清除深度
for(auto v : adj[c]){
if(vis[v]) continue;
decompose(v);
}
}你有一棵樹,你可以做以下兩種事情
1. 將點 \(x\) 塗成紅色
2. 詢問 \(x\) 到最近的紅色點的距離
這題要利用在重心的不同子樹當中的 \(u,v\)
路徑會經過重心的性質
程式碼
//重心剖分的三個函數
void dfs_sz(int u, int p){
//這個函數預處理子樹大小 => 找重心要用
sz[u] = 1;
for(auto v : adj[u]){
if(v == p || !vis[v]) continue;
dfs(v, u);
sz[u] += sz[v];
}
}
int centroid(int u, int p, int rt){
//這個函數找重心
for(auto v : adj[u]){
if(v == p || vis[v]) continue;
if(sz[v] >= sz[rt]/2)
return centroid(v, u, rt);
}
return u;
}
map<int,int> dis[N];
void get_dis(int u, int p, int rt, int dep){
dis[rt][u] = dep;
for(auto v : adj[u]){
if(v == p || vis[v]) continue;
get_dis(v,u,rt,dep+1);
}
}
void decompose(int u, int p){
//建出重心樹
dfs_sz(u, -1);
int c = centroid(u, -1, u);
vis[c] = 1;
if(p != -1) par[c] = p;
get_dis(u,-1,u,0); //維護重心到點的距離
for(auto v : adj[c]){
if(vis[v]) continue;
decompose(v, c);
}
}
int to[N]; //儲存重心到最近的塗色點的距離
void modify(int u){
//將點塗色
for(int v = u; v != -1; v = par[v]) to[v] = min(to[v], dis[v][u]);
}
int get(int u){
int ans = INF;
for(int v = u; v != -1; v = par[v]) ans = min(ans, to[v] + dis[v][u]);
}