並查集

(Disjoint Set Union)

功能?

維護兩點\((u,v)\)是否連通

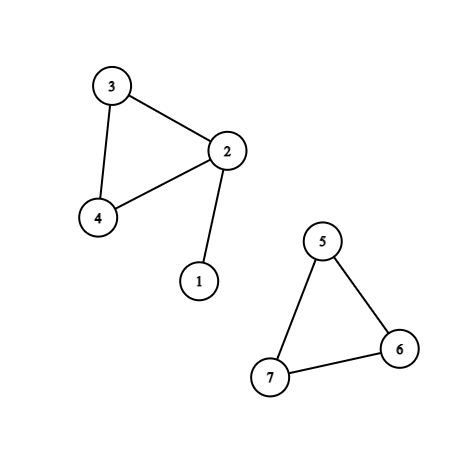
將兩點連接

原理

既然我們想要知道一個點在哪個連通塊中

我們學過! 可以使用 DFS

也就是在 \(O(n)\) 的時間解決

接著我們就能夠在 \(O(1)\) 的時間回答問題了!

但是如果今天一下是詢問，一下是合併呢?

你可能會想，那我們就每次合併完之後再做一次 DFS 阿

 

不過，這樣太慢了!

遇到題目這樣做的話一定會給你 TLE

 

 

因此，我們有個更快的想法

如果我們能夠快速地找到一個點會在哪個連通塊呢?

 

 

這就是 並查集 發揮作用的地方!

 

 

我們假設這些點都有箭頭連結

然後我們試圖去找這些點最終會連到哪個點

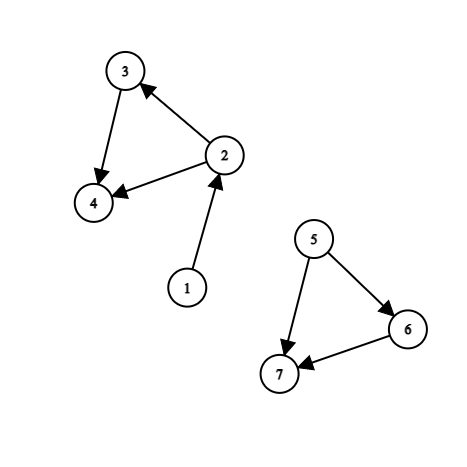
這些節點最終連到的點皆為 4

這些節點最終連到的點皆為 7

 

也因此，我們需要一個可以維護每個人最終會連到誰的一種方式

對於每個點，開一個陣列 \(dsu[u]\)

表示節點 \(u\) 當前在哪一個編號的連通塊

並假設這些點都有箭頭連結

我們會額外搭配一個函數來做這件事情

定義一個函數 \(find(u)\)

他會去找 \(u\) 節點最終會連到誰

而一開始 \(dsu[u]\) 皆為 \(u\) 所指到的節點

(\(u\)若已是最高點，則 \(dsu[u]=u\))

在這張圖中，\(dsu\)陣列為 \([2,3,4,4,6,7,7]\)

而 find(u) 寫法如下

int find(int u){
    if(dsu[u] == u) return u;
    else return find(dsu[u]);
}

可以發現，這樣遞迴下去就可以找到答案了

int find(int u){
    if(dsu[u] == u) return u;
    else return find(dsu[u]);
}

接著，我們已經支援詢問的功能了，那合併呢?

很簡單吧，直接把 \(u\) 連到 \(v\)

或反過來連即可!

Unite

void unite(int u, int v){
    u = find(u), v = find(v);
    if(u == v) return;
    dsu[u] = v;
}

這樣我們就完成這個資料結構了!

整體程式碼

int find(int u){
    if(dsu[u] == u) return u;
    else return find(dsu[u]);
}

void unite(int u, int v){
    u = find(u), v = find(v);
    if(u == v) return;
    dsu[u] = v;
}

分析時間複雜度

\(find(u)\) 最差複雜度會是 \(O(n)\)

(因為走過所有點)

 

而 \(unite(u,v)\)的時間複雜度則是 \(O(1)\)

 

事實上，我們可以在這兩個函數中加入幾行

使得均攤複雜度變成幾乎是常數時間!

 

路徑壓縮

 

int find(int u){
	if(dsu[u] == u) return u;
    else return dsu[u] = find(dsu[u]);
}

//或我們更常寫成

int find(int u){
	return dsu[u]==u ? u : dsu[u] = find(dsu[u]);
}

啟發式合併

void unite(int u, int v){
	u = find(u), v = find(v);
    if(u == v) return;
 	if(sz[u] > sz[v]) swap(u,v);
    dsu[u] = v;
    sz[v] += sz[u];
}

完整程式碼

void init(){
	iota(dsu,dsu+N,0);
    fill(sz,sz+N,1);
}

int find(int u){
	return dsu[u]==u ? u : dsu[u] = find(dsu[u]);
}

void unite(int u, int v){
	u = find(u), v = find(v);
    if(u == v) return;
 	if(sz[u] > sz[v]) swap(u,v);
    dsu[u] = v;
    sz[v] += sz[u];
}

而加入這兩個優化之後的時間複雜度

一個操作的均攤複雜度會變為 \(O(\alpha(n))\)

(\(\alpha (n)\)為反阿克曼函數)

在 \(n = 10^{18}\)以內的數字，幾乎都小於 5

 

證明的話在發明 Disjoint Set 的論文中有

例題

給你一張 \(n\) 個點 \(m\) 條邊的無向圖

接著有 \(q\) 次 query

每次有兩種 query

  1. 將兩點 \((u,v)\) 之間連一條邊
  2. 詢問 \((u,v)\) 是否連通

給你一張 \(n\) 個點 \(m\) 條邊的無向圖

接著有 \(q\) 次 query

每次有兩種 query

  1. 將兩點 \((u,v)\) 之間連一條邊
  2. 詢問 \((u,v)\) 是否連通

這題就是並查集的裸題，直接做即可

給你一張 \(n\) 個點 \(m\) 條邊的無向圖

接著有 \(q\) 次 query

每次有兩種 query

  1. 將兩點 \((u,v)\) 之間的邊拔掉
  2. 詢問 \((u,v)\) 是否連通

給你一張 \(n\) 個點 \(m\) 條邊的無向圖

接著有 \(q\) 次 query

每次有兩種 query

  1. 將兩點 \((u,v)\) 之間的邊拔掉
  2. 詢問 \((u,v)\) 是否連通

既然我們要拔掉邊，那我們把詢問反過來

做時間倒流，拆邊就變成是加邊了

給你一張 \(n\) 個點 \(m\) 條邊的無向圖

接著有 \(q\) 次 query

每次有兩種 query

  1. 將兩點 \((u,v)\) 之間連一條邊
  2. 詢問整張圖是不是二分圖

給你一張 \(n\) 個點 \(m\) 條邊的無向圖

接著有 \(q\) 次 query

每次有兩種 query

  1. 將兩點 \((u,v)\) 之間連一條邊
  2. 詢問整張圖是不是二分圖

這裡我們來想想，要怎麼用並查集看一張圖是不是二分圖

給你一張 \(n\) 個點 \(m\) 條邊的無向圖

接著有 \(q\) 次 query

每次有兩種 query

  1. 將兩點 \((u,v)\) 之間連一條邊
  2. 詢問整張圖是不是二分圖

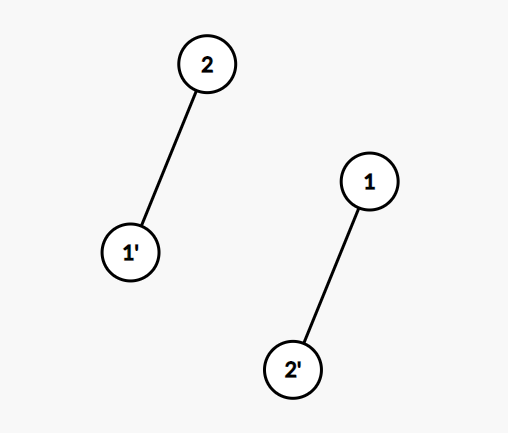
由於要是二分圖

所以兩個相鄰的點不能相同顏色

 

給你一張 \(n\) 個點 \(m\) 條邊的無向圖

接著有 \(q\) 次 query

每次有兩種 query

  1. 將兩點 \((u,v)\) 之間連一條邊
  2. 詢問整張圖是不是二分圖

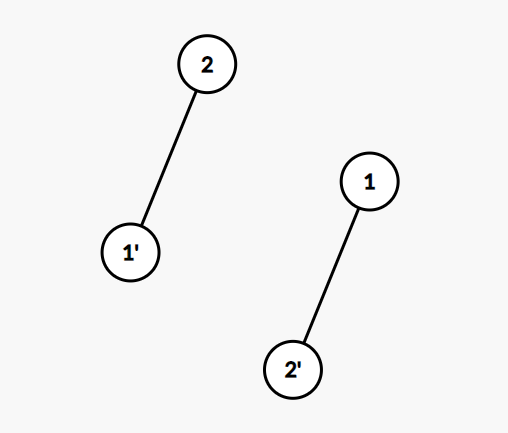
由於要是二分圖

所以兩個相鄰的點不能相同顏色

 

因此我們只要對每個點開兩個顏色

 互相連邊就好 

給你一張 \(n\) 個點 \(m\) 條邊的無向圖

接著有 \(q\) 次 query

每次有兩種 query

  1. 將兩點 \((u,v)\) 之間連一條邊
  2. 詢問整張圖是不是二分圖

由於要是二分圖

所以兩個相鄰的點不能相同顏色

 

給你一張 \(n\) 個點 \(m\) 條邊的無向圖

接著有 \(q\) 次 query

每次有兩種 query

  1. 將兩點 \((u,v)\) 之間連一條邊
  2. 詢問整張圖是不是二分圖
int u, v;
cin >> u >> v;
//在連邊的時候，判斷加入這條邊後是否為二分圖
if(find(u)==find(v)){
	//不是二分圖
}

unite(u,v+n);
unite(v,u+n);

更多練習題

CF EDU - DSU

APCS 2021/11 p4

TIOJ 1420 - 地雷區

(2016 北市賽)

Made with Slides.com