賽局理論
(Game Theory)
賽局 DP
(Game DP)
來看一個超級經典的題目吧
現在,在桌子上有 \(N\) 顆石頭排成一排,每顆石頭上分別都寫著一個數字 \(a_i\)。Alice 和 Bob 在玩一個遊戲,他們只能從最左邊和最右邊的石頭開始拿,兩個人都以最佳的走法去玩遊戲,請問 Alice 最多可以拿到多少石頭?
狀態: 令 \(dp[l][r]\) 表示先手在區間 \([l,r]\) 內所能拿到的最多石頭
轉移式: \(dp[l][r] = \max(sum(l,r) - dp[l+1][r], sum(l,r) - dp[l][r-1])\)
Base Case: \(dp[i][i] = a_i\)
相信大家都已經很熟悉這個做法了!
這種題目特別的點在於,當先手做完操作之後,後手就會變成下一回合的先手。而我們靠著這一點去設計了我們的狀態以及轉移式。
而這題其實也有另外一種狀態的假設方法
令 \(dp[l][r]\) 表示先手與後手在區間 \([l,r]\) 內的分數差
而在這樣的假設方法當中,先手會去最大化分數差,而後手會去最小化分數差
現在有一張 \(H \times W\) 的網格圖,而 Takahashi 和 Aoki 兩個人在玩遊戲。在每一個格子上,都被塗上了紅色與藍色兩種顏色。兩個人輪流移動這個棋子,玩家可以選擇將棋子往右或往下移動,如果將棋子移動到了紅色的格子上,分數就會 \(-1\),否則玩家的分數就會 \(+1\),請問在兩個人皆以最佳策略玩遊戲時,誰會贏?
這題基本上可以滿輕易地列出狀態
令 \(dp[i][j]\) 表示棋子走到 \((i,j)\) 時的分數差
當輪到 Takahashi 時,會是最大分數差
當輪到 Aoki 時,會是最小分數差
轉移式的話應該也算好想到
不過這裏特別的點是,你可能會列出一個
\(dp[i][j]\) 是從 \(dp[i-1][j]\) 與 \(dp[i][j-1]\) 所轉移而來的轉移式
但你仔細想想,會發現我們從前面開始轉移會有很大的問題
你在 \((i,j)\) 時讓自己照著規則這樣去移動的話
真的會是最佳的走法嗎?
組合賽局
(Combinatorial Game Theory)
接下來所提到的所有賽局都會是組合賽局
組合賽局?
說到賽局理論,這個東西其實有很多不同種類
而在競程上,我們主要會討論的
則是所謂的組合賽局
組合賽局
- 由兩人進行對戰,並且輪流進行操作
- 資訊是公開的,兩人都可以知道賽局的完整盤面
- 遊戲不受任何機率所影響,在同個盤面下的操作會有相同結果
- 賽局的結果會是一贏一輸,或者是平手
來看一個經典的小例題吧!
Subtraction Game
Alice 和 Bob 在玩遊戲,現在,在桌子上有 \(n\) 顆石頭,輪到該玩家的回合時,可以選擇拿取 \(1 \sim 3\) 顆石頭,拿不了石頭的人就輸了。Alice 先拿,問你如果雙方都以最佳策略在玩遊戲,Alice 和 Bob 誰會贏?
我們可以來分析一下 \(n\) 很小的 case
- 當 \(n \le 3\) 時,只要先手把石頭都拿完就贏了
- 當 \(n=4\) 呢? 會發現不管怎麼拿,都會導致後手贏!
- 當 \(n=5\) 呢? 只要先手把石頭拿成 \(n=4\) 就會贏了!
我們可以把這個畫成一個表格
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Bob | Alice | Alice | Alice | Bob | Alice | Alice | Alice | Bob | Alice |
在 \(n \bmod 4 = 0\) 的時候,後手贏,否則先手會贏!
遊戲圖
(Game Graph)
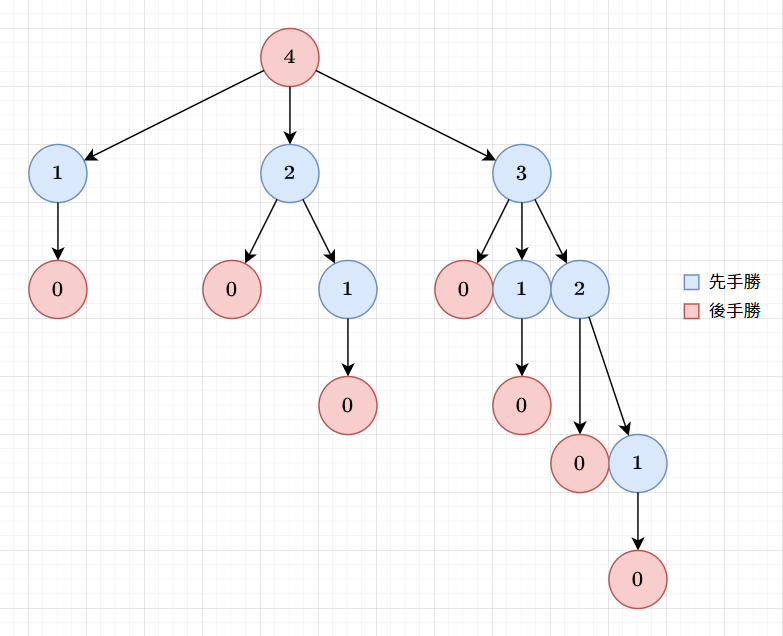
剛剛的 Subtraction Game 的遊戲圖
會發現到
一個狀態是先手勝,倘若可以走到一個後手勝的狀態
一個狀態是後手勝,倘若所有可以走到的狀態皆為先手勝
因此,如果今天遊戲圖是一張 DAG
就可以在上面做拓樸排序 + DP 去找到一個狀態的勝負了!
同時也可以想成是兩個人在一張有向圖上玩遊戲
現在,Takahashi 和 Aoki 在玩三個字母的接龍,而他們可以說 \(n\) 種不同的字串。同一個字可以重複使用,但沒有辦法接下去的人就輸了,請問雙方都以最佳策略下去玩的時候,假設 Takahashi 從第 \(i\) 個字串開始說,誰會贏?
(看原題敘可能會好懂很多)
我們可以將題目轉換一下
其實每個 word 代表的意義可以變成是一條邊
而這條邊是從 前三個字母 \(\rightarrow\) 後三個字母
因此,這個題目就被轉換成了有 \(52^3\) 個狀態與 \(n\) 條邊的遊戲圖了
用拓樸排序就可以計算出每個狀態的答案了!
賽局的分類
對於每一個組合賽局,我們可以將其分類為以下幾種
| 無偏 (Impartial) | 有偏 (Partisan) |
|---|---|
| 無環 (Loopfree) | 有環 (Loopy) |
| 有限 (Finite) | 超限 (Transfinite) |
不過這裡我們只介紹無偏和有偏賽局
無偏 (Impartial):對於同一個盤面,雙方可做的操作皆相同
有偏 (Partisan):對於同一個盤面,雙方可做的操作可不同
簡單來說,例如西洋棋、象棋、圈圈叉叉等都是有偏賽局
而剛剛所介紹的 Subtraction Game 則是無偏賽局
照遊戲決定勝負的方式也被分為以下兩種
標準 (Standard):無法移動的玩家被判輸
匱乏 (Misere):無法移動的玩家被判贏
而我們會講的基本上都是標準無偏賽局
並且這些賽局皆只有輸贏沒有平手
而對於標準無偏賽局,每個賽局有兩種型別
\(N\):先手勝
\(P\):後手勝
也就是當雙方都以最佳策略下去玩的時候
每個賽局只會有這兩種可能性
賽局和
(Disjuntive Sum)
再來要介紹的東西會有點抽象
定義
對於兩個賽局 \(G_1, G_2\),定義他們的賽局和 \(G_1+G_2\) 為將兩個賽局放在同一個盤面上,每一次要選擇 \(G_1,G_2\) 其中一個賽局進行操作所產生的賽局
簡單來說,例如 \(G_1\) 是西洋棋,\(G_2\) 是圍棋
那把西洋棋和圍棋同時擺在桌上就是 \(G_1+G_2\)
定義
對於兩個賽局 \(G_1, G_2\),如果所有賽局 \(H\) 都可以使得 \(G_1+H = G_2 + H\),則我們說兩個賽局等價
這裡可能有點難懂,但可以想成如果我們對兩個盤面做任意相同的操作,都可以使得他們的勝負關係是相同的,那他們就是等價的
而其實後面的很多東西都可以利用這兩點去證明
不過我們接下來會省略證明的部分
主要是想介紹一下名詞
Nim Game
這是整個無偏賽局中最重要的遊戲喔!
在桌上有 \(n\) 堆石頭,每堆分別有 \(a_i\) 顆石頭,有兩個人輪流拿石頭,每次可以選擇一堆,拿取數量非 \(0\) 的石頭,沒有辦法取石頭的人就輸了。請問在雙方都以最佳策略玩遊戲時,先手還是後手必勝?
我們直接來講結論
令 \(X = a_1 \oplus a_2 \oplus \cdots \oplus a_n\)
當 \(X = 0\) 時,後手必勝
當 \(X \ne 0\) 時,先手必勝
(\(\oplus\) 是指 XOR)
至於為什麼是這樣呢?
可以嘗試證明看看以下這兩點
1. 對於 \(X=0\) 的狀態,只能走到 \(X \ne 0\) 的狀態或無法操作
2. 對於 \(X \ne 0\) 的狀態,至少有一個方法可以走到 \(X = 0\)
證明完這兩點,其實概念就跟剛剛講的遊戲圖差不多
而每個盤面,其實都等價於只有一堆 \(X\) 顆石頭的 Nim
然後為了等一下要講的 SG Theorem
這裡我們來看一下一個小小的變化
Nim With Increases
現在桌上有 \(n\) 堆石頭,每次玩家可以選擇一堆石頭拿取或增加石頭 (不可以不做事情),但是當每一堆的石頭數量都是 \(0\) 時,遊戲就結束了,假設遊戲一定會結束。請問先手會贏還是後手會贏。
會發現其實這個跟原本的 Nim 一模一樣
假設當前的玩家將某一堆的石頭增加 \(a\) 顆
那下一位玩家只要把那 \(a\) 顆都拿走就好了
所以其實這個遊戲還是等價於一堆有 \(X\) 顆石頭的 Nim
現在有一個 \(n\) 階的階梯,在每一階上面都放了 \(a_i\) 個石頭
每一次可以選擇任意數量在第 \(k\) 階的石頭 \((k > 0)\)
並將這些石頭移到 \(k-1\) 階
兩個人輪流進行操作,無法移動的人就輸了
請問先手勝還是後手勝
其實這題就是在奇數階的石頭上玩遊戲而已
所以答案就是等價於一堆有 \(a_1 \oplus a_3 \oplus ...\) 的 Nim!
仔細想想,你會發現先手其實不必去碰偶數階梯上的石頭!
因為如果先手將第 \(i\) 階上的石頭移下來
那麼後手一定可以將同樣數量的石頭從 \(i-1\) 階移到 \(i-2\) 階
讓奇數階的石頭數量維持一樣
所以跟 Nim with Increases 的概念一模一樣
而且當奇數階沒有石頭的時候,先手必敗
因為當先手移動偶數階時,後手只要照我們剛剛講的
進行對應的操作
則後手必勝,因此會發現這個遊戲只與奇數階有關
Sprague-Grundy Theorem
任一個無偏賽局都等價於一堆有 \(X\) 顆石頭的 Nim
而這個 \(X\) 我們稱其為這個賽局的 SG Value (或 Grundy Number, Nimber, ...)
Sprague-Grundy Theorem
不過在我們講要怎麼找到一個賽局的 SG Value 之前
我們再來看看另外一個例子吧
Choose Nim
現在有 \(n\) 堆石頭,石頭的數量分別是 \(\{a_1,a_2,\cdots,a_n\}\),先手可以選擇任何一堆,接著兩人就按照 Nim 的規則對那堆石頭玩遊戲。
這個遊戲可能還滿廢的,畢竟只要有任何一堆的石頭數量是 \(0\) 就是先手獲勝,不過,我們這裡想要討論的是,對於這個賽局,他其實等價於一堆數量有 \(X\) 的 Nim With Increases。而我們要怎麼找到這個 \(X\) 呢?
事實上,這個 \(X\) 的值會是
$$\text{mex}(\{a_1,a_2,\cdots,a_n\})$$
而這裡的 mex 指的是這些數字當中,最小沒有出現過的正整數 (Minimum Excluded)
比較好的思考方式是,如果先手選擇了小於 \(X\) 的一堆 \(a\)
那後手一定可以將 \(a\) 增加到 \(X\) 顆
而如果先手選擇了大於 \(X\) 的一堆,後手也可以把它減少回到 \(X\)
因此兩個遊戲其實是等價的
而我們剛剛也看過了,Nim With Increases 其實等價於 Nim
所以這個遊戲等價於 \(X\) 顆石頭的 Nim
因此,根據這個定理,我們會發現
\(SG(A+B) = SG(A) \oplus SG(B)\)
還有
\(SG(A) = \text{mex}(\{SG(C)\}), \forall C \text{ where } A \rightarrow C\)
用遊戲圖來理解 SG Theorem
有了 Sprague-Grundy Theorem 之後
對於每一個無偏賽局的狀態
我們都可以用一個 SG Value 來表示這些狀態
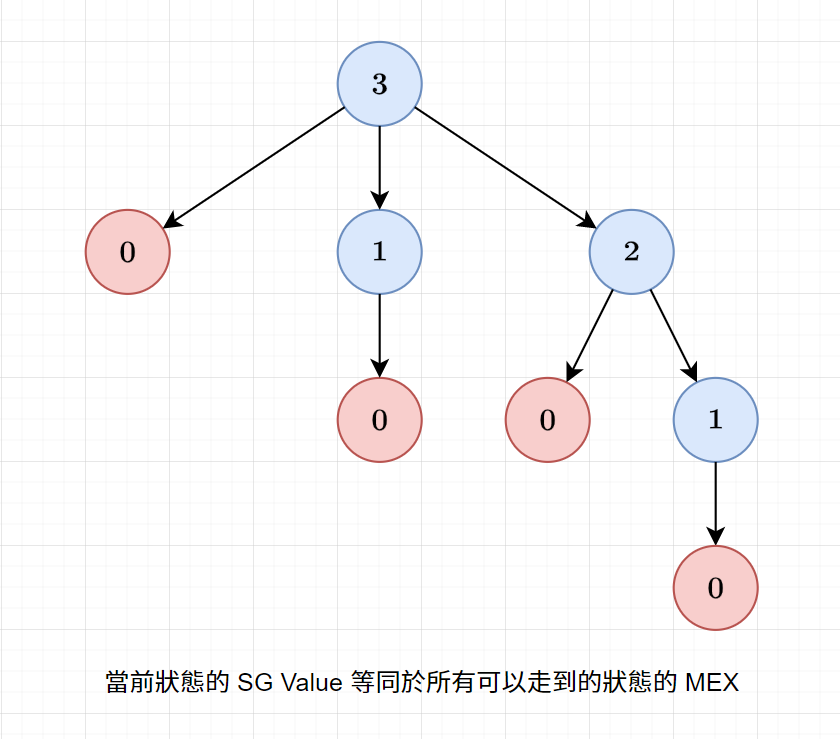
而 \(n\) 堆石頭的 Nim Game
可以把它看成是 \(n\) 個一堆的 Nim 加在一起所得到的遊戲
因此當我們把不同的賽局作賽局和時
其實就只要將他們的 SG Value 給 XOR 起來就可以找到新的 SG 了
感覺很難理解對吧!那我們實際來看看例子吧
我們用前面講過的 Subtraction Game 來作為例子
對於 \(N\) 顆石頭的狀態
\(SG(N) = \text{mex}(SG(N-1),SG(N-2),SG(N-3))\)
而當 \(N=0\) 時,由於後手必勝,\(SG(0) = 0\)
我們可以將圖畫出來,會得到下面這樣的圖
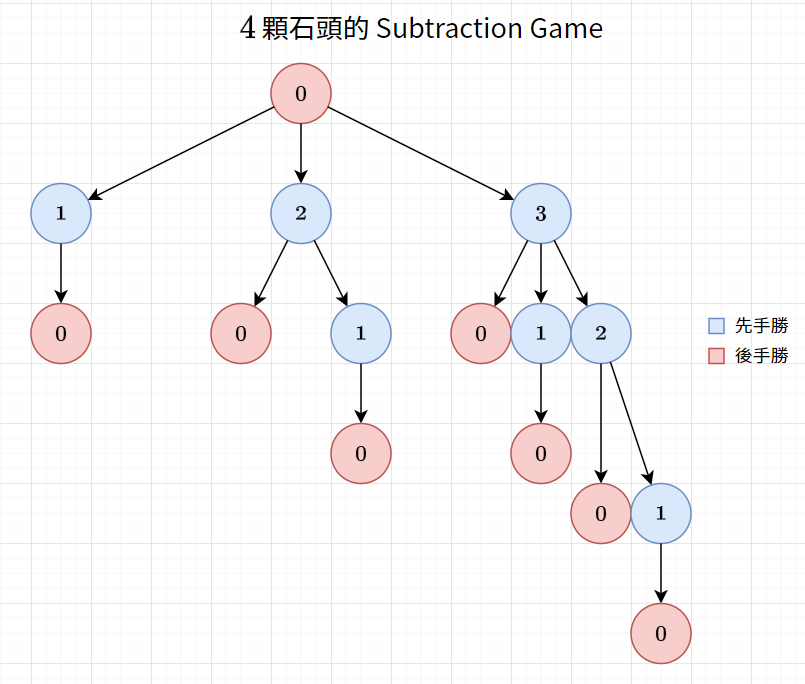
因此,其實會發現,\(SG(X) = X \bmod 4\)
也就是說,有 \(X\) 顆石頭的 Subtraction Game
等價於一堆有 \(X \bmod 4\) 顆石頭的 Nim
Alice 和 Bob 在玩遊戲,現在,在桌子上有 \(n\) 堆石頭,輪到該玩家的回合時,選擇任何一堆拿取 \(1 \sim 3\) 顆石頭,拿不了石頭的人就輸了。Alice 先拿,問你如果雙方都以最佳策略在玩遊戲,Alice 和 Bob 誰會贏?
對於一堆有 \(X\) 顆石頭的 Subtraction Game
我們知道他的 \(SG(X) = X \bmod 4\)
因此對於 \(n\) 堆,其實整個賽局的 SG Value 會是
\((a_1 \bmod 4) \oplus \cdots \oplus (a_n \bmod 4)\)
更多例題
CSES - Grundy's Game
桌上一堆 \(n\) 個硬幣的堆,以及兩個玩家在玩遊戲
兩個玩家輪流進行操作
每次可以選擇一堆,將這堆分成兩堆大小不同的硬幣堆
移動不了的人就輸了
請問先手必勝還是後手必勝
當我們遇到一題賽局時,我們要想辦法算出每個狀態的 SG Value
那現在假設有一堆的石頭數量是 \(x\) 呢
他的 SG Value 會是多少?
我們可以列出下面的轉移式
\(SG(x) = \text{mex}(\{SG(a) \oplus SG(b)\}) , \text{where } a+b = x \text{ and } a \ne b\)
舉例來說,對於 \(5\) 顆石頭,我們有底下幾種分法
\(1+4, 2+3, 3+2, 4+1\)
而分成兩堆之後,這兩堆放在一起的 SG Value 可以 XOR 計算
並且當前狀態的 SG Value 會是所有可以走到的狀態的 MEX
參考程式碼
int mex(vector<int> v){
set<int> s;
for(int i = 0;i < v.size();i++) s.insert(v[i]);
for(int i = 0;i < N;i++) if(s.find(i)==s.end()) return i;
}
void init(){
for(int i = 3;i <= MAXV;i++){
vector<int> v;
for(int j = 1;j < (i+1)/2;j++){
v.push_back(dp[j]^dp[i-j]);
}
dp[i] = mex(v);
}
}不過我們可以來想一下這樣的時間複雜度
對於 \(SG(x)\),可以在 \(O(x^2)\) 的時間內得到所有的狀態的 SG
然後再用 \(O(x)\) 的時間計算出 MEX
因此總共的時間複雜度是 \(O(x^3)\)!
欸? 等等,可是最大的石頭數量可以到 \(10^6\) 欸
實際上,如果實際去跑過這個程式之後
會發現當 \(x\) 超過一定的數字 (一千多) 之後
SG Value 都不會是 \(0\)!
因此,我們可以多判斷這件事
雖然現在有 \(n\) 堆,但是其實我們可以分開來看
先將每一堆各自的 SG Value 計算出來之後
最後再將它們 XOR 起來就好了
照著同樣的概念,我們其實可以很輕易地列出這樣的轉移式
因此只要照著這個轉移式去計算即可!
不過會發現一件事情,\(a_i\) 的數量可以到 \(10^9\) 欸!
因此我們其實可以嘗試將 SG 的表格印出來看看
#include <bits/stdc++.h>
#define int long long
#define fastio ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
using namespace std;
int mex(vector<int> v){
set<int> s;
for(int i = 0;i < v.size();i++) s.insert(v[i]);
for(int i = 0;i < N;i++) if(s.find(i)==s.end()) return i;
}
int k;
int SG(int x){
if(x == 0) return 0;
else if(x % 2 == 1) return mex({SG(x-1)});
else return mex({SG(x-1),SG(x/2)*(k%2)});
}
signed main(){
fastio
int n;
cin >> n;
k = 0;
for(int i = 0; i <= n; i++){
cout << SG(i) << " ";
}
}會發現當 \(k\) 是偶數時,表格長這樣
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| SG(i) | 0 | 1 | 2 | 0 | 1 | 0 | 1 | 0 | 1 |
會發現當 \(i \ge 3\) 的時候
如果 \(i\) 是偶數,\(SG(i) = 1\)
如果 \(i\) 是奇數,\(SG(i) = 0\)
會發現當 \(k\) 是奇數時,表格長這樣
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| SG(i) | 0 | 1 | 0 | 1 | 2 | 0 | 2 | 0 | 1 |
會發現當 \(i > 4\) 的時候
如果 \(i\) 是奇數,答案就是 \(0\)
否則可能是 \(1\) 或 \(2\)
| i | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| SG(i) | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 2 | 0 |
那我們要怎麼知道他是 \(1\) 還是 \(2\) 呢?
我們其實可以直接從轉移式去思考
當 \(k\) 是奇數且 \(X\) 是偶數時,會有
而我們知道當 \(X > 4\) 時,奇數答案都是 \(0\)
所以其實轉移式變成
可以在 \(O(\log x)\) 的時間算完
SG Value 的循環
通常,對於一個賽局,SG Value 常常會出現規律
而最常出現的可能性就是循環!
Kayles
有 \(n\) 堆石頭,每堆有 \(a_i\) 顆石頭
每次可以選擇一堆,並且對他進行以下操作
- 拿取 \(1\) 或 \(2\) 顆
- 將剩下來的石頭分成兩堆 (大小可以是 \(0\) 也可以大小相同)
請問當兩人都以最佳策略在玩的時候,先手還是後手必勝?
同樣的,會發現其實我們可以把 \(n\) 堆看成很多個一堆
因此我們只需要去找出每堆的 SG Value 即可
對於一堆有 \(x\) 顆的石頭,SG Value 可以靠以下轉移式計算
不過如果這個轉移式的複雜度會是 \(O(x^2)\) 欸!
如果石頭的數量很大,就沒辦法用這個方式計算了
所以我們一樣來看看規律!
#include <bits/stdc++.h>
#define int long long
#define fastio ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
using namespace std;
const int N = 1e6+5;
int dp[N];
int mex(vector<int> v){
set<int> s;
for(int i = 0;i < v.size();i++) s.insert(v[i]);
for(int i = 0;;i++) if(s.find(i)==s.end()) return i;
}
int SG(int x){
if(dp[x]) return dp[x];
vector<int> v;
for(int a = 0; a <= x; a++){
int b = x-1-a, b2 = x-2-a;
if(b >= 0) v.push_back(SG(a)^SG(b));
if(b2 >= 0) v.push_back(SG(a)^SG(b2));
}
return dp[x] = mex(v);
}
signed main(){
fastio
int n;
cin >> n;
for(int i = 0; i <= n; i++){
cout << SG(i) << " ";
}
}最後會發現其實當 \(x \ge 72\) 的時候
每 \(12\) 個數字會產生循環!
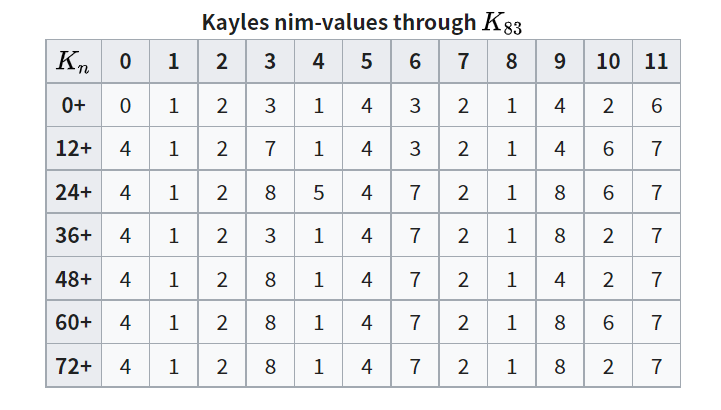
所以其實只要暴力計算出前 \(72\) 個 SG Value
剩下的用規律就可以知道答案了
練習題
CSES Mathematics 所有的 Game
Codeforces 1451F - Nullify the Matrix
Codeforces 1407F - Colouring Game
ABC278G - Generalized Subtraction Game