圖的連通性
(Graph Connectivity)
DFS Tree
提到圖論,大家最熟悉的東西應該就是 DFS 了吧
不論是在處理一般的圖,還是樹上的問題
我們都會使用 DFS 來處理一張圖
DFS Tree?
int visited[N];
void dfs(int u){
visited[u] = 1;
for(int v : adj[u]){
if(visited[v]) continue;
dfs(v);
}
}看看這份 DFS 的 code
如果我們將走過的邊和節點獨立建成一張圖
我們會得到一個生成樹!
DFS Tree
(圖取自 CF)
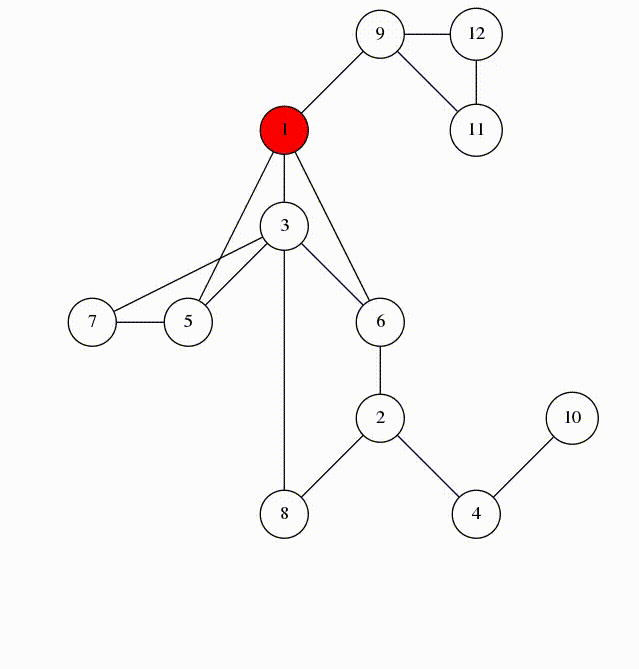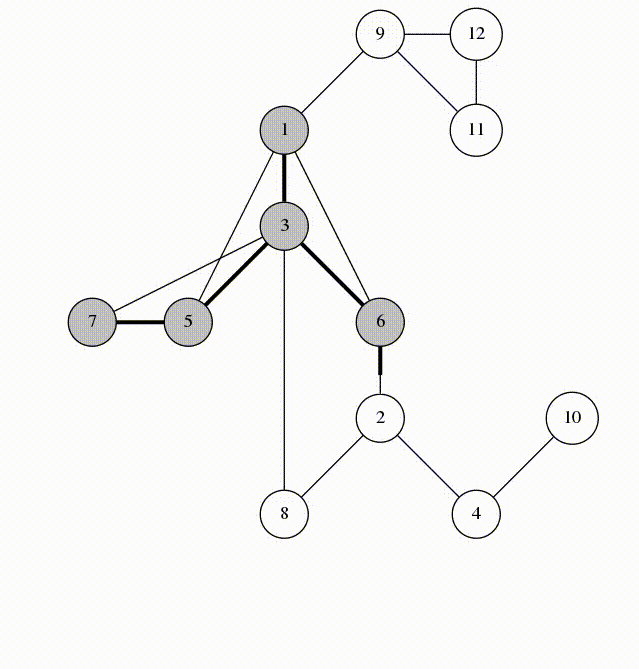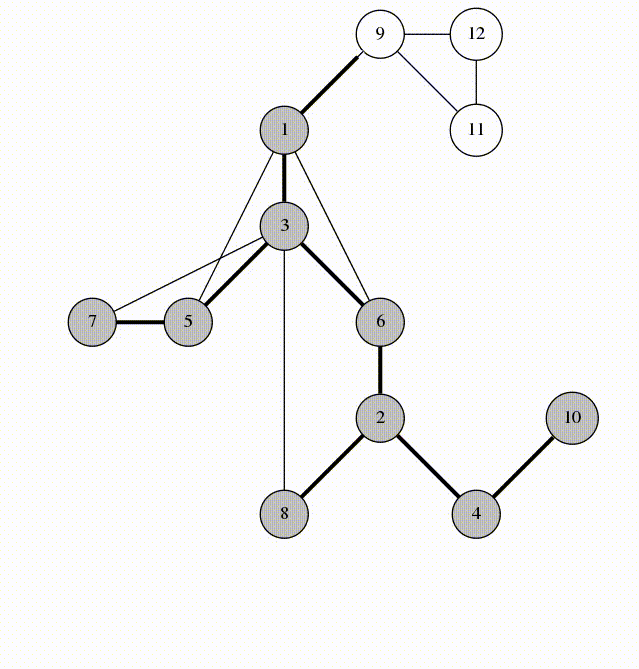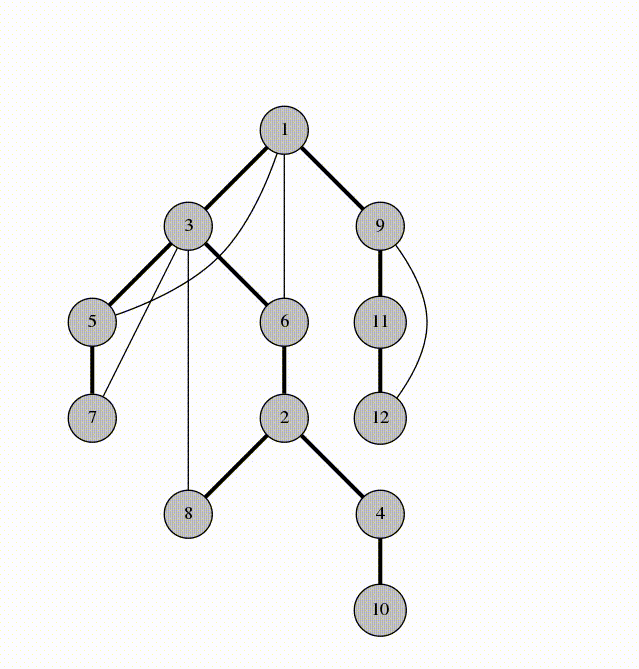
DFS 樹邊的種類
- 樹邊 (Tree Edge): DFS Tree 上的邊
- 回邊 (Back Edge): 往祖先走的邊
- 前邊 (Forward Edge): 往子孫走的邊
- 交錯邊 (Cross Edge): 往非祖先或子孫走的邊
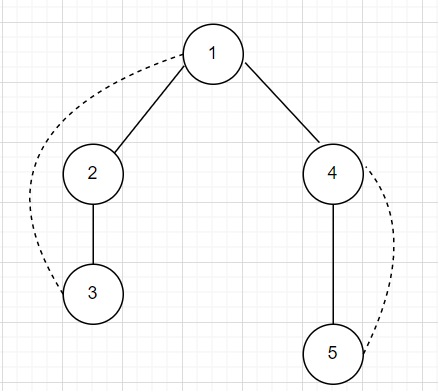
無向圖 DFS Tree
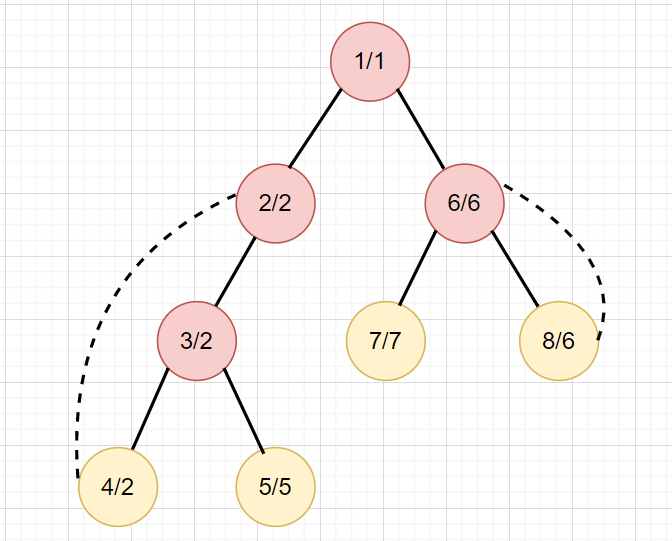
實線為樹邊,虛線為回邊
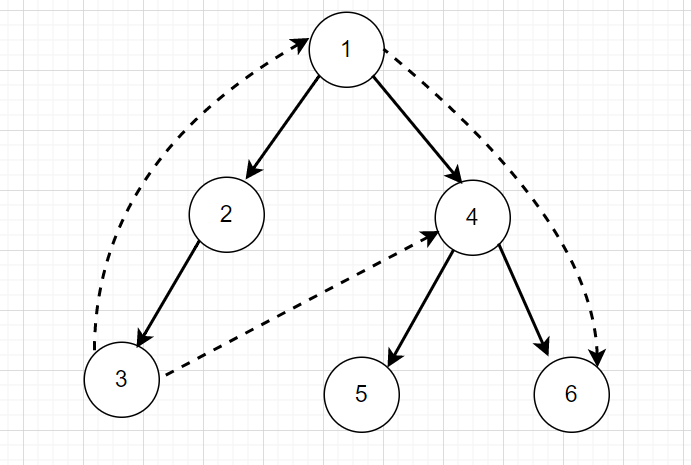
有向圖 DFS Tree
實線為樹邊,\(3 \rightarrow 1\) 是回邊
\(3 \rightarrow 4\) 是交錯邊,\(1 \rightarrow 6\) 是前邊
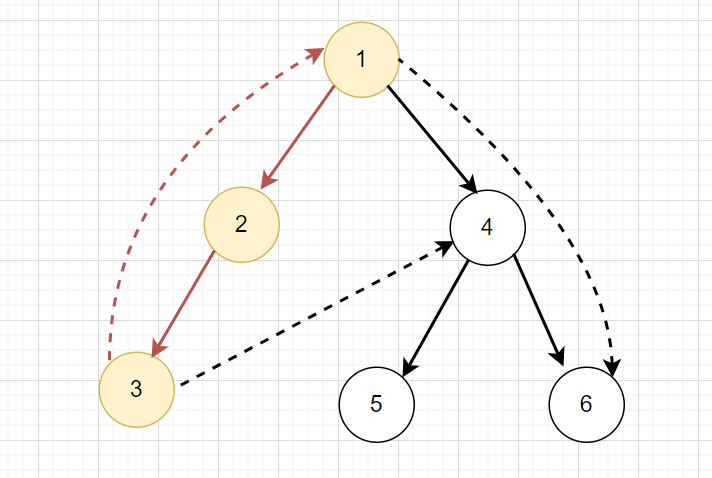
讓我們來看看一些題目
給你一張有 \(n\) 個節點 \(m\) 條邊的有向圖
請找到一個迴路,或回答沒有
對於這個題目,我們可以利用 DFS Tree 的角度來看
圖上有環 \(\iff\) 有一條回邊
之後再回朔答案即可
實作方式如下:
在 DFS 的時候用一個 stack 維護這個點的祖先
當從 \(u \rightarrow v\) 的時候
如果 \(v\) 走過了而且在 stack 內
則 \(u \rightarrow v\) 是一條回邊
這個技巧我們下周講 SCC 的時候會再用到!
參考程式碼:
void dfs(int u){
vis[u] = 1;
st.push(u);
inst[u] = 1;
for(auto v : adj[u]){
if(!vis[v]){
dfs(v);
}else if(inst[v]){
int x;
do{
x = st.top(); st.pop();
ans.push_back(x);
}while(x!=v);
reverse(ans.begin(),ans.end());
ans.push_back(v);
cout << ans.size() << "\n";
for(auto x : ans){
cout << x << " ";
}
exit(0);
}
}
st.pop();
inst[u] = 0;
}給你一棵樹 \(T\),接著有 \(q\) 次操作
每次在圖上加入或刪除一條邊 \(u,v\)
我們稱好的節點滿足
以那些節點為根時,可以找到一棵 DFS 生成樹
使得這棵樹與原本的樹相同
每次操作完要輸出圖上有幾個好的節點
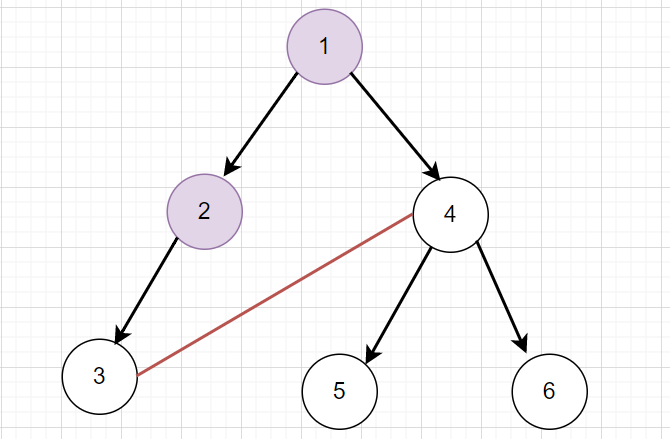
試著列出幾種 case 觀察看看
如果原本的樹長這樣,我們連 \(3,4\)
則 \(1,2\) 會變成不能用的點
試著列出幾種 case 觀察看看
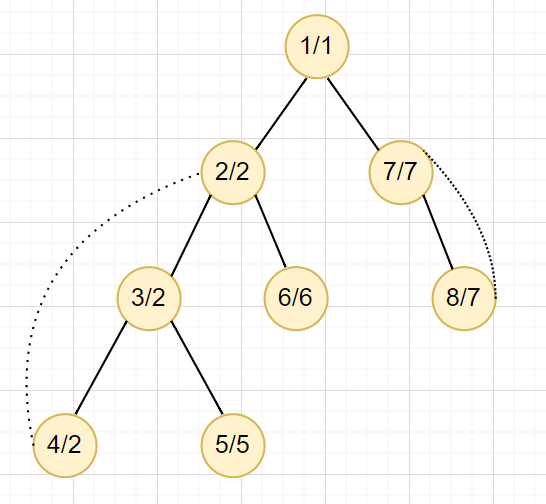
如果原本的樹長這樣,我們連 \(2,7\)
則 \(3\) 會變成不能用的點
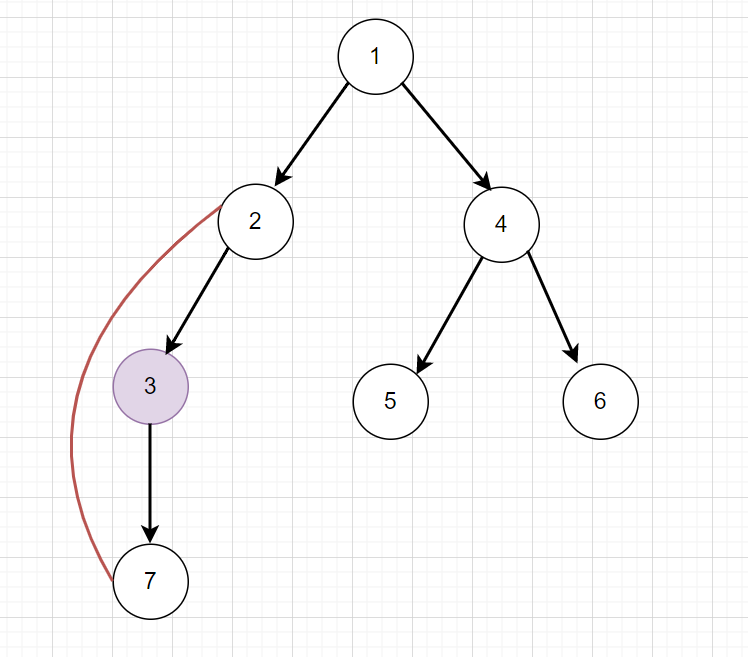
其實就是分成不同鍊與同鍊的回邊去維護答案
有什麼我們學過的東西可以維護這種東西呢?
樹壓平 + 線段樹!


給你一張\(n\)無向圖,請在圖上找到以下兩種其中一種
Path: 找到一個長度 \(\ge \lceil \frac{n}{2} \rceil\) 的簡單路徑
Pairing: 找到包含 \(\ge \lceil \frac{n}{2} \rceil\) 個節點的 Pairs
保證一定存在其中一種
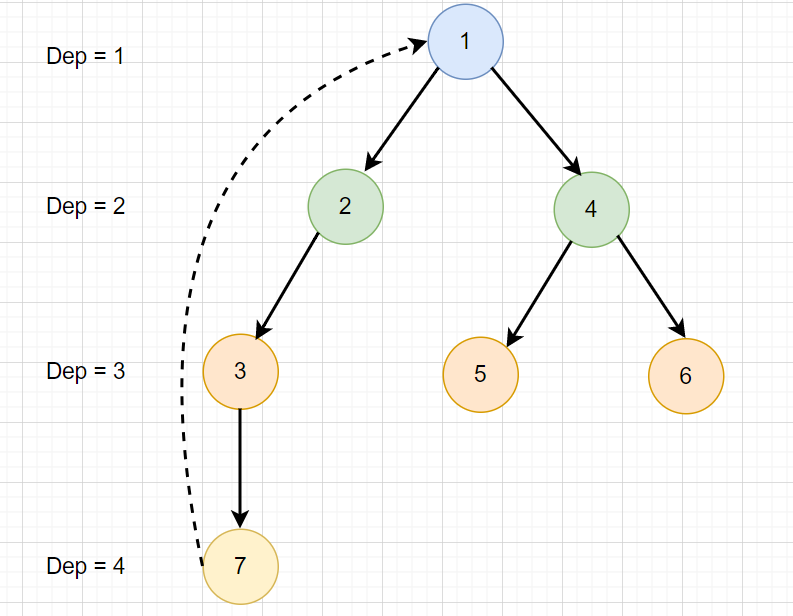
如果有 Path
則存在一個 \(dep[u] \ge \lceil \frac{n}{2} \rceil\)
直接輸出 \(u \rightarrow 1\)
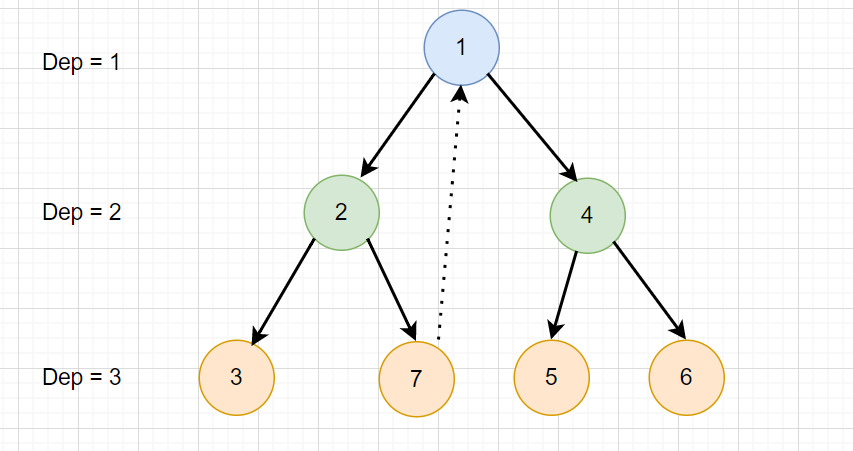
如果沒有 Path
則我們將同樣深度的點 pair 在一起
一定可以找到節點數 \(\ge \lceil \frac{n}{2} \rceil\) 的 pairing
練習題
無向圖的連通性
在這裡,我們要先介紹兩種東西
橋 (Bridge):
一條邊 \(e\) 被稱為橋,若移除 \(e\) 之後
會使圖變得不連通
割點 (Articulation Point):
一個點 \(v\) 被稱為割點,若移除 \(v\) 之後
會使圖變得不連通
橋 (Bridge)
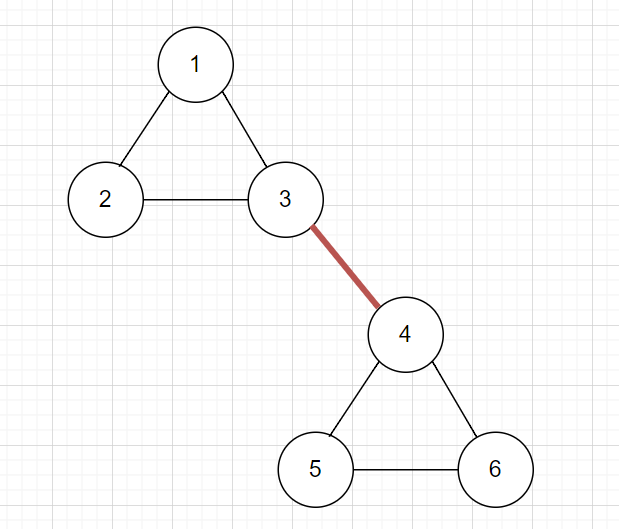
在這張圖中,移除 \((3,4)\) 會使得圖變得不連通
因此 \((3,4)\) 是圖中的橋
割點 (Articulation Point)
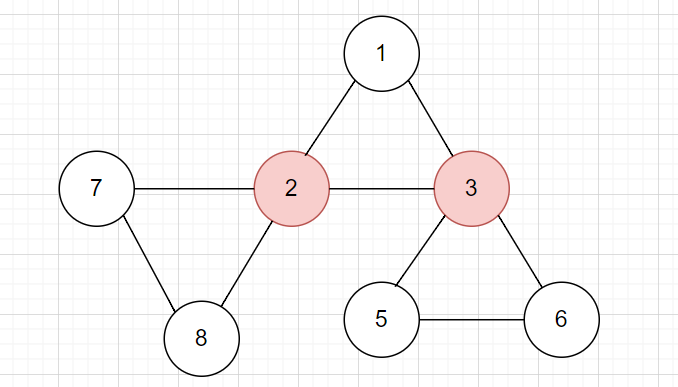
在這張圖中,移除 \(2,3\) 皆會使圖變得不連通
因此 \(2,3\) 皆是圖上的割點
定義一個連通分量
邊雙連通:
對於這張圖,不論移除哪條邊,圖皆會連通
(意即沒有橋)
點雙連通:
對於這張圖,不論移除哪條點,圖皆會連通
(意即沒有割點)
如何找橋 (Bridge)
在這裡,我們會使用 Tarjan's Bridge Finding Algorithm
這裡我們就會用到 DFS Tree 的概念了
Tarjan's Bridge Finding Algorithm
1. 我們會對這張圖建出一棵 DFS Tree
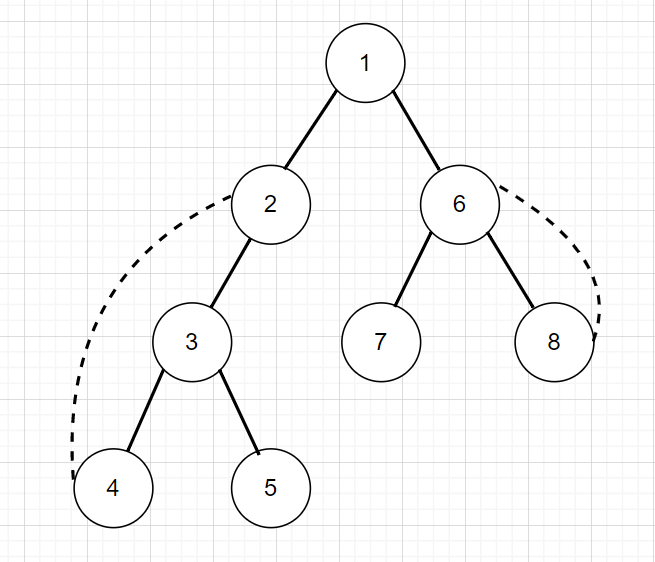
Tarjan's Bridge Finding Algorithm
2. 每個節點 \(u\) 會有兩個值
\(dfn[u]\): 表示這個點的時間戳記
\(low[u]\): 每個點最多經過一條回邊走到的最低時間戳記
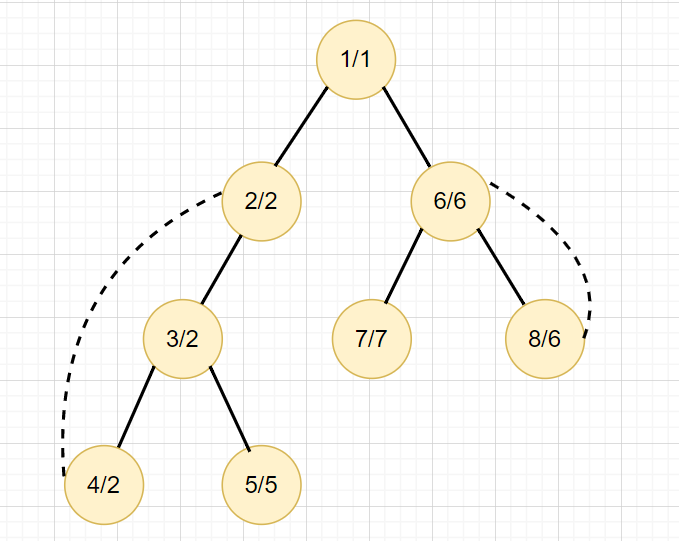
Tarjan's Bridge Finding Algorithm
3. 如果從 \(u\) 到 \(v\) ,\(dfn[u] < low[v]\)
則 \((u,v)\) 是一個橋
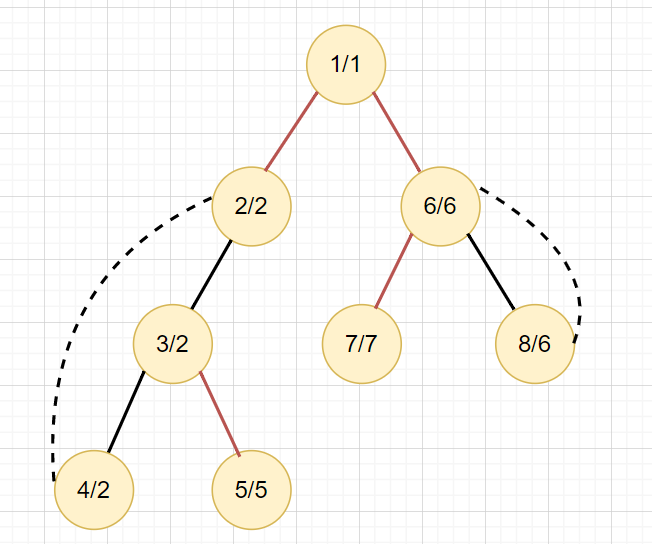
Tarjan's Bridge Finding Algorithm
vector<int> bridges;
int dfn[N], low[N], t;
void dfs(int u, int p){
dfn[u] = low[u] = ++t;
for(int v : adj[u]){
if(v==p) continue;
if(!dfn[v]){
dfs(v,u);
if(dfn[u] < low[v]) bridges.push_back({u,v});
low[u] = min(low[u],low[v]);
}else{
low[u] = min(low[u],dfn[v]);
}
}
}參考程式碼
找割點也是一樣的概念!
Tarjan's AP Finding Algorithm
1. 我們會對這張圖建出一棵 DFS Tree

Tarjan's AP Finding Algorithm
2. 每個節點 \(u\) 會有兩個值
\(dfn[u]\): 表示這個點的時間戳記
\(low[u]\): 每個點最多經過一條回邊走到的最低時間戳記

Tarjan's AP Finding Algorithm
3. 如果從 \(u\) 到 \(v\) 時,\(low[v] \ge dfn[u]\)
則 \(u\) 是一個割點
如果是根要特判度數是否 \(\ge 2\)
Tarjan's AP Finding Algorithm
int dfn[N], low[N], cut[N], t;
void dfs(int u, int p){
dfn[u] = low[u] = ++t;
int cnt = 0;
for(int v : adj[u]){
if(v==p) continue;
if(!dfn[v]){
dfs(v,u);
cnt++;
if(dfn[u] <= low[v]){
cut[u] = 1;
}
low[u] = min(low[u],low[v]);
}else{
low[u] = min(low[u],dfn[v]);
}
}
if(p == -1 && cnt < 2) cut[u] = 0;
}參考程式碼
題目
邊雙連通分量
(Bridge Connected Components)
將圖上的橋變成邊,連通分量變成點?
將圖上的橋變成邊,連通分量變成點?

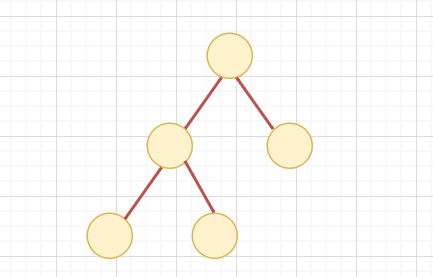
我們會得到一棵樹!
這個動作我們稱為「縮點」
把一張無向圖,藉由這樣的縮點方式
我們就可以得到一棵樹了!
對於一棵樹,問題就變得簡單許多了!
我們可以對他找直徑、重心
樹鍊剖分、重心剖分、樹 DP 等等
如何找出邊 BCC,並縮點?
1. 對原圖建出 DFS Tree,並算出 \(dfn[u]\) 與 \(low[u]\)
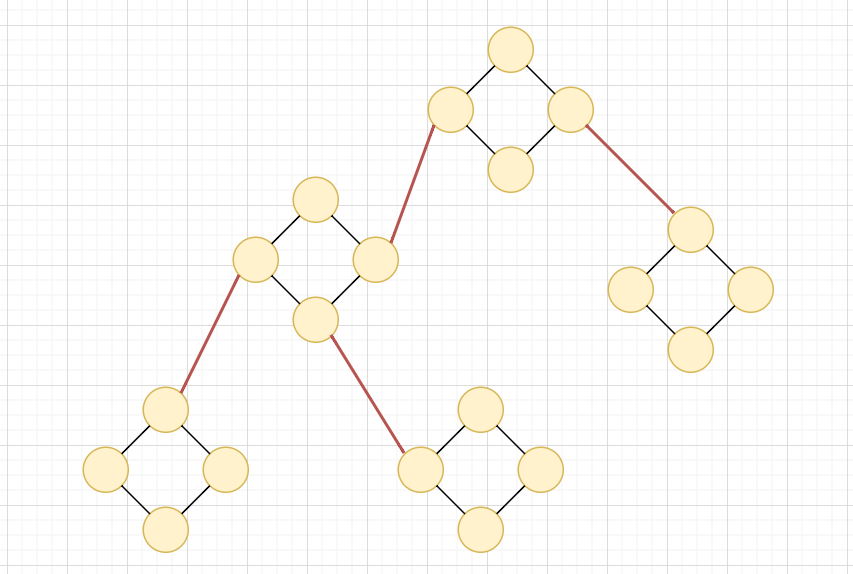
如何找出邊 BCC,並縮點?
2. 使用一個 stack 紀錄 dfs 過的點

如何找出邊 BCC,並縮點?
3. 當 \(dfn[u]==low[u]\) 時,表示我們找到了一個 BCC
將 stack 裡面的點依序 pop 出,標記編號
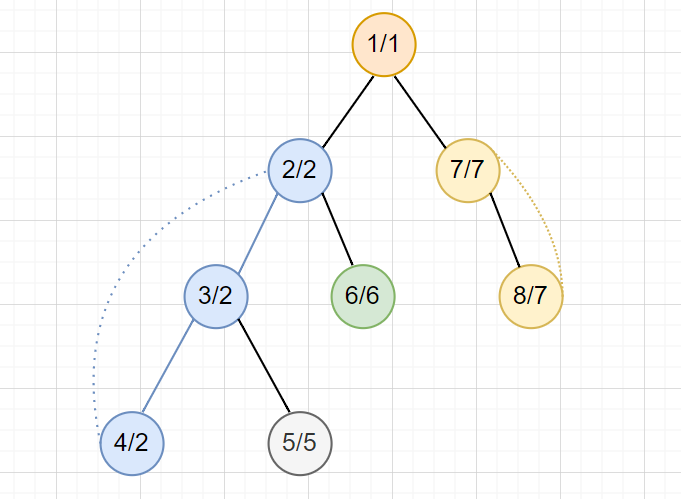
不同顏色表示不同 BCC
如何找出邊 BCC,並縮點?
4. 掃過原本的邊,並將不同 BCC 間的邊建出來

不同顏色表示不同 BCC
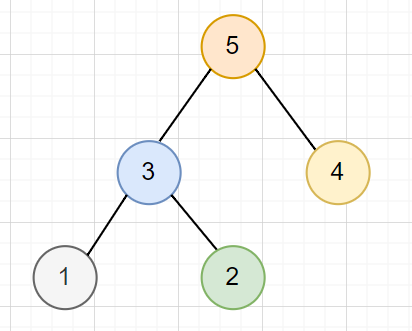
變成一棵樹
如何找出邊 BCC,並縮點?
參考程式碼
int dfn[N], low[N], bcc[N], t, bccid;
stack<int> st;
void dfs(int u, int p){
dfn[u] = low[u] = ++t;
st.push(u);
for(int v : adj[u]){
if(v==p) continue;
if(!dfn[v]){
dfs(v,u);
low[u] = min(low[u],low[v]);
}else{
low[u] = min(low[u],dfn[v]);
}
}
if(dfn[u]==low[u]){
++bccid; //找到一個 bcc 了
int x;
do{
x = st.top(); st.pop();
bcc[x] = bccid; //編號
}while(x!=u);
}
}
void build_bridge_tree(){
for(auto [u,v] : edges){
if(bcc[u]!=bcc[v]){
adj2[bcc[u]].push_back(bcc[v]);
}
}
}例題
Codeforces 1000E - We Need More Bosses
給你一張無向圖,在這張圖上
有個人會從起點 \(s\) 走到終點 \(t\)
而從 \(s\) 走到 \(t\) 的路徑中
有些邊一定會被經過
問對於任意 \(s,t\)
最多有幾條邊一定要經過
對於這張圖,我們對他進行邊 BCC 縮點
我們會得到一棵樹
而既然要最大化一定要走過的邊數
答案其實就是這棵樹的直徑!
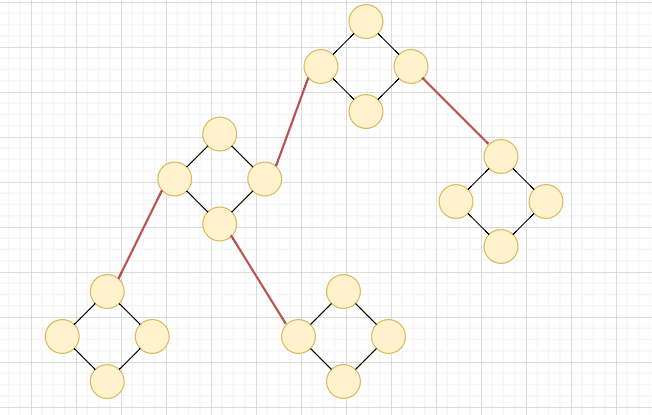
\(s\)
\(t\)
練習題
點雙連通分量
(Biconnected Components)
把割點取出,獨立看做一個點?
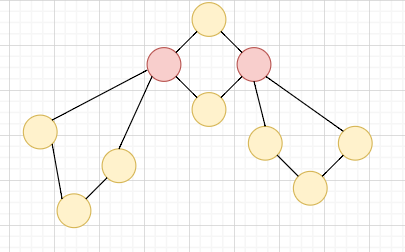
把割點取出,獨立看做一個點?

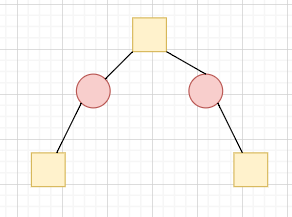
我們也會得到一棵樹,我們叫他「圓方樹」
如何找到點 BCC,並縮點
1. 先建出 DFS Tree,並找到 \(dfn[u]\) 與 \(low[u]\)
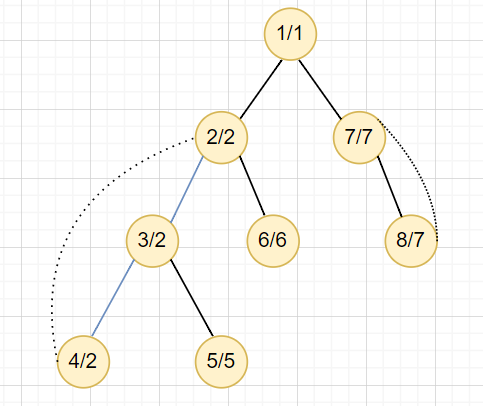
如何找到點 BCC,並縮點
2. 用一個 stack 紀錄走過的點

如何找到點 BCC,並縮點
3. 當我們遇到 \(low[v] \ge dfn[u]\) 時,\(u\) 是割點,而我們也找到了點 BCC
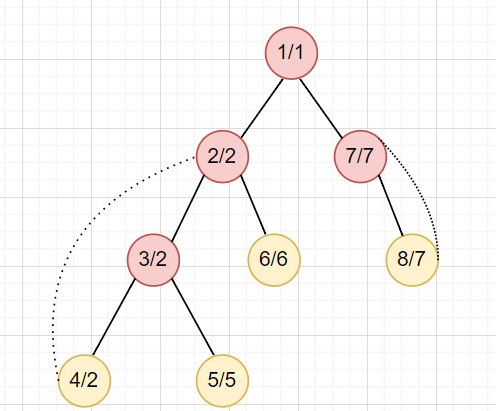
如何找到點 BCC,並縮點
3. 當我們遇到 \(low[v] \ge dfn[u]\) 時,\(u\) 是割點,而我們也找到了點 BCC

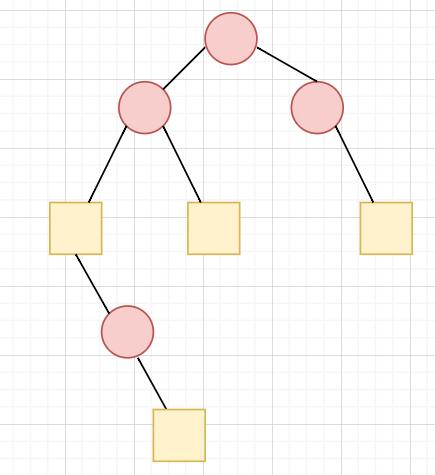
如何找到點 BCC
參考程式碼
const int N = 2e5+5;
vector<int> adj[N], adj2[N], bccids[N];
int low[N], dfn[N], bccid[N], bcccnt;
int cut[N], inst[N], t;
void dfs(int u, int par){
low[u] = dfn[u] = ++t;
int cnt = 0;
st.push(u);
for(auto v : adj[u]){
if(v == par) continue;
if(!dfn[v]){
dfs(v,u); cnt++;
low[u] = min(low[u],low[v]);
if(low[v] >= dfn[u]){
cut[u] = 1;
++bcccnt;
int x;
do{
if(st.empty()) break;
x = st.top(); st.pop();
bccids[x].push_back(bcccnt);
bccid[x] = bcccnt;
}while(x!=v);
bccids[u].push_back(bcccnt);
bccid[u] = bcccnt;
}
}else if(dfn[v] < dfn[u]){
low[u] = min(low[u],dfn[v]);
}
}
if(par==-1&&cnt < 2) cut[u] = 0;
}例題
給你一張 \(n\) 個點的無向圖
接著有 \(q\) 次操作或詢問
1. 把點 \(u\) 的權值改成 \(w\)
2. 詢問從 \(u\) 到 \(v\) 的路徑上可以經過的點的最小權值
圓方樹裸題,建出圓方樹之後
對他做 HLD,套線段樹就結束了
圓方樹的實作細節極多!
有向圖的連通性
強連通 (Strongly Connected)
對於一張圖,若對於任意兩個節點 \(u,v\),都存在一條從 \(u\) 到 \(v\) 的路徑與一條 \(v\) 到 \(u\) 的路徑,則我們稱這張圖強連通
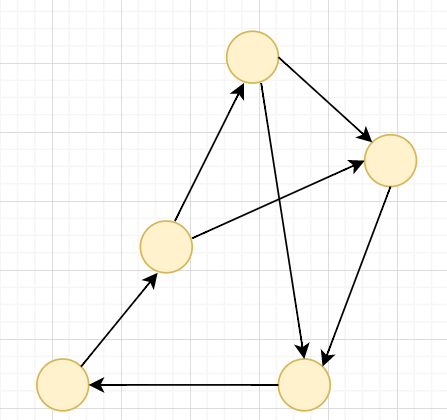
強連通分量 SCC
(Strongly Connected Components)
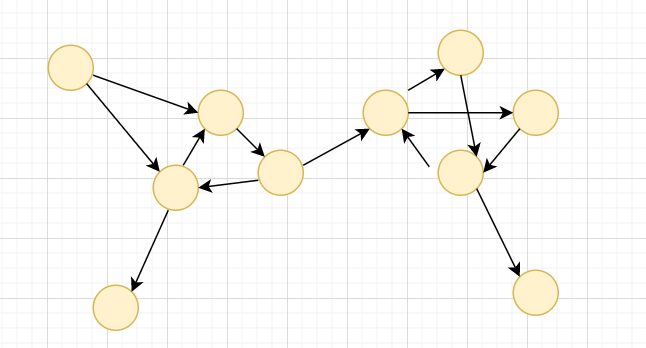
強連通分量 SCC
(Strongly Connected Components)
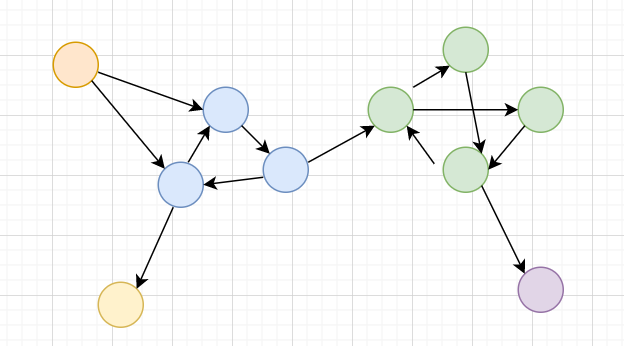
將圖縮點之後! DAG!

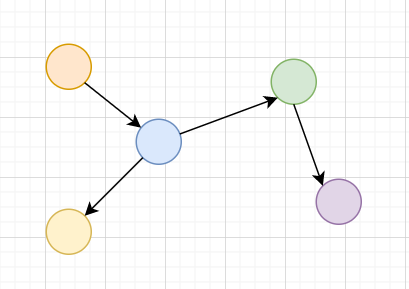
一張無向圖進行 SCC 縮點之後會變成 DAG
找 SCC 有兩個常用的演算法
Tarjan's SCC Algorithm
Kosaraju's Algorithm
Tarjan's SCC Algorithm
1. 對這張圖建出 DFS Tree
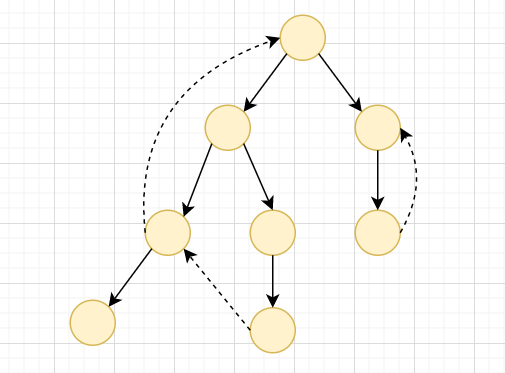
Tarjan's SCC Algorithm
2. 對每個節點找出 \(dfn[u],low[u]\)
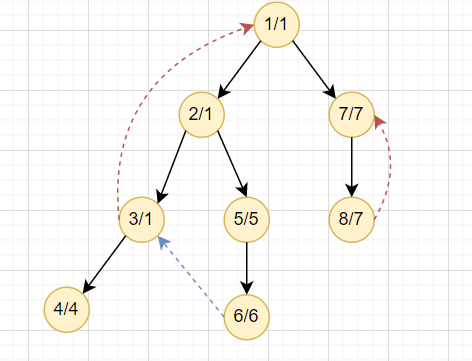
要特別留意,low 只能拉回邊,不能拉交錯邊
Tarjan's SCC Algorithm
3. 如果一個點的子孫都走完了
\(dfn[u]==low[u]\),則我們找到了一個 SCC
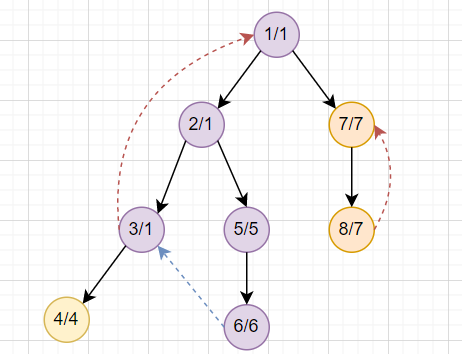
Tarjan's SCC Algorithm
3. 縮點,得到 DAG!

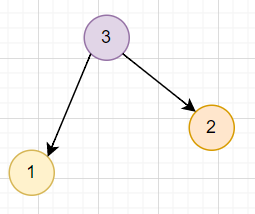
Tarjan 做完之後,得到的編號會是 反的拓樸排序
Tarjan's SCC Algorithm
參考程式碼
const int N = 1e6+5;
vector<int> adj[N];
int dfn[N], low[N], inst[N], scc[N], sccid = 0, cnt = 0;
stack<int> st;
void dfs(int u){
dfn[u] = low[u] = ++cnt;
st.push(u);
inst[u] = 1;
for(auto v : adj[u]){
if(!dfn[v]){
dfs(v);
low[u] = min(low[u],low[v]);
}else if(inst[v]){
low[u] = min(low[u],dfn[v]);
}
}
if(low[u]==dfn[u]){
int x;
do{
x = st.top();
st.pop();
scc[x] = sccid;
inst[x] = 0;
}while(x!=u);
sccid++;
}
}用 stack 維護回邊,類似 Round Trip
Kosaraju's Algorithm
對原圖先 DFS 一次
再用原圖的反 DFS 離開序在反圖上再 DFS 一次
就可以得到 SCC 了
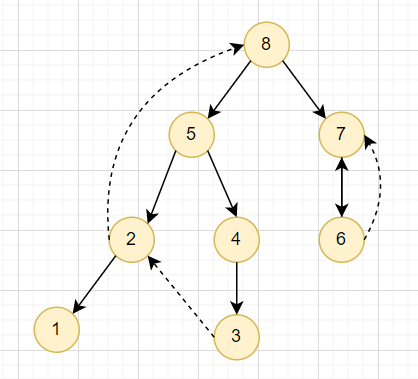
Kosaraju's Algorithm
對原圖先 DFS 一次
再用原圖的反 DFS 離開序在反圖上再 DFS 一次
就可以得到 SCC 了
(Kosaraju 得到的也會是反的拓樸排序)

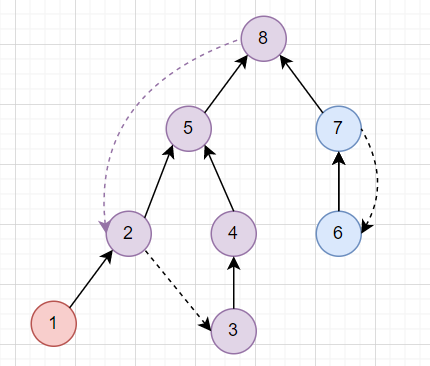
Kosaraju's Algorithm
const int N = 1e6+5;
vector<int> adj[N], adj2[N]; //adj2 是反圖
int vis[N], scc[N], id;
stack<int> st;
void dfs1(int u){
vis[u] = true;
for(auto v : adj[u]){
if(!vis[v]) dfs1(v);
}
st.push(u);
}
void dfs2(int u){
scc[u] = id;
for(auto v : adj2[u]){
if(!scc[v]) dfs2(v);
}
}
void kosaraju(){
for(int i = 1;i <= n;i++){
if(!visited[i])
dfs1(i);
}
while(!st.empty()){
int u = st.top(); st.pop();
if(!scc[u]){
++id;
dfs2(u);
}
}
}
例題
對原圖建出 SCC 縮點完的 DAG
由於同一個 SCC 的點都能互相走到對方
我們可以將縮點完的環權值設為環上點的權值總和
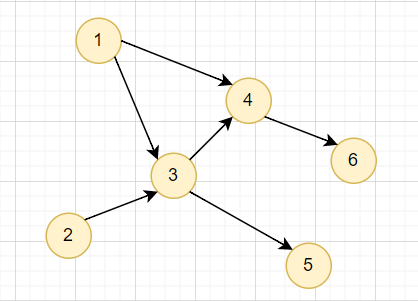
問題就被轉換成 DAG 上 DP 了
例題
Codeforces 1137C - Museum Tour
在一個國家當中
有 \(n\) 個城市,互相由單向的道路連接
經由一條道路所需的時間為一天
每個城市裡面有一間博物館
這個國家一周有 \(d\) 天
而每個博物館會在固定的時段會開放
你可以選擇任意的起點與開始時間
但是不能連續兩天停留在同一個城市
問最多可以看到多少不同博物館的展覽
每個點有時間的限制,不好處理?
建虛點! (\(d \le 50\))
接著,我們將 \(dn\) 個節點的圖,進行 SCC 縮點
就會得到一個 DAG!
在上面做 DAG DP 即可
練習題
2-SAT
(2-satisfiability problem)
2 SAT
形如這樣的 Boolean 運算式
\((x_1 \lor x_2) \land (x_3 \lor x_1) \land \cdots\)
看是否能夠找到一組解
2 SAT
有點難懂?
沒關係,我們直接看例題
例題
我們將每個願望當成一個節點
邊則是當該狀態成立時,會導致另外一個成立
例如: 「有 A,沒 B」
則我們建
沒 A \(\rightarrow\) 沒 B
有 B \(\rightarrow\) 有 A
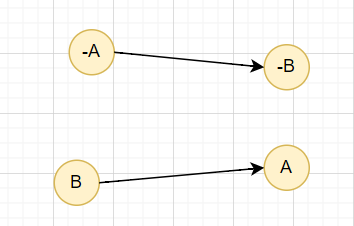
我們將每個願望當成一個節點
邊則是當該狀態成立時,會導致另外一個成立
例如: 「有 A,沒 B」和 「沒 A,沒 B」
則我們建
沒 A \(\rightarrow\) 沒 B
有 B \(\rightarrow\) 有 A
有 A \(\rightarrow\) 沒 B
有 B \(\rightarrow\) 沒 A
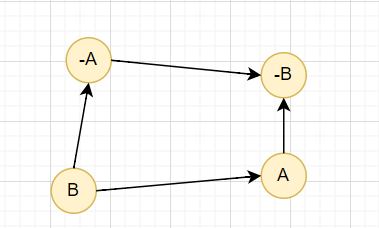
我們將每個願望當成一個節點
邊則是當該狀態成立時,會導致另外一個成立
什麼時候會矛盾?
當 有 \(x\) 和 沒 \(x\) 出現在同一個 SCC 時
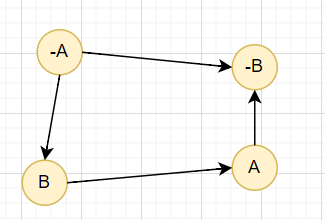
有 \(A\) 會導致要 沒 \(A\)
矛盾!
(回朔的話從依照拓樸排序的順序去給就好)