區間問題合輯
區間問題?
(Range Queries)
給你一個 \(n\) 項的陣列 \(A\)
接下來會有 \(q\) 次 query,而 query 有以下兩種
1. 將某個位置 \(i\) /區間 \([l,r]\) 的值修改/增加 \(x\)
2. 詢問位置 \(i\) 或區間 \([l,r]\) 之間的值
給你一個 \(n\) 項的陣列 \(A\)
接下來會有 \(q\) 次 query,而 query 有以下兩種
1. 將某個位置 \(i\) /區間 \([l,r]\) 的值修改/增加 \(x\)
2. 詢問位置 \(i\) 或區間 \([l,r]\) 之間的值
就這樣講可能有點難理解
因此我把題目在變簡單一點
給你一個 \(n\) 項的陣列 \(A\)
接下來會有 \(q\) 次 query,而 query 有以下兩種
1. 將某個位置 \(i\) 增加 \(x\)
2. 詢問區間 \([l,r]\) 中的最小值
給你一個 \(n\) 項的陣列 \(A\)
接下來會有 \(q\) 次 query,而 query 有以下兩種
1. 將某個位置 \(i\) 增加 \(x\)
2. 詢問區間 \([l,r]\) 中的最小值
這個問題乍看下可以簡單在 \(O(qn)\) 時間做完
但是事實上有方法在 \(O(q \log n)\)
區間問題常用到的技巧、資結
前綴和/前綴最大值/前綴最小值
稀疏表 (Sparse Table)
BIT (Binary Indexed Tree/Fenwick Tree)
線段樹 (Segment Tree)
還有更多...
前綴和
(Prefix Sum)
給你一個 \(n\) 項的陣列 \(A\)
接下來會有 \(q\) 次詢問
對於每次詢問區間 \([l,r]\)
輸出 \(a_l,a_{l+1},\cdots,a_r\) 的總和
\((n \le 10^6, q \le 10^6)\)
給你一個 \(n\) 項的陣列 \(A\)
接下來會有 \(q\) 次詢問
對於每次詢問區間 \([l,r]\)
輸出 \(a_l,a_{l+1},\cdots,a_r\) 的總和
直接回答每次詢問會是 \(O(n)\),整體時間複雜度 \(O(qn)\)
\((n \le 10^6, q \le 10^6)\)
直接回答每次詢問會是 \(O(n)\),整體時間複雜度 \(O(qn)\)
太慢了!
有沒有辦法更快?
如果我們將原本的陣列進行一點小改變
原本陣列是 \(A = \{a_1,a_2,\cdots,a_n\}\)
那我們用另外一個陣列
\(B = \{a_1,a_1+a_2,\cdots, a_1+a_2+\cdots+a_n\}\)
或 \(b_i = \sum_{k \le i} a_k\)
也就是每個位置都存從第一個值加到第 \(i\) 個值的總和
如果我們將原本的陣列進行一點小改變
原本陣列是 \(A = \{a_1,a_2,\cdots,a_n\}\)
那我們用另外一個陣列
\(B = \{a_1,a_1+a_2,\cdots, a_1+a_2+\cdots+a_n\}\)
或 \(b_i = \sum_{k \le i} a_k\)
也就是每個位置都存從第一個值加到第 \(i\) 個值的總和
那要找 \(a_l + a_{l+1} + \cdots + a_r\)
我們其實只需要找 \(b_r - b_{l-1}\)
僅僅是預先對陣列進行加總的處理
我們就可以在 \(O(1)\) 的時間完成一次詢問
這就是前綴和好用的地方!
那如果題目變成這樣呢?
給你一個 \(n\) 項的陣列 \(A\)
接下來會有 \(q\) 次操作
對於每次操作,將區間 \([l,r]\) 的值全都 \(+x\)
接著有 \(k\) 次詢問
對於每次詢問,輸出 \(a_i\) 的值
\((n \le 10^6, q \le 10^6)\)
給你一個 \(n\) 項的陣列 \(A\)
接下來會有 \(q\) 次操作
對於每次操作,將區間 \([l,r]\) 的值全都 \(+x\)
接著有 \(k\) 次詢問
對於每次詢問,輸出 \(a_i\) 的值
\((n \le 10^6, q \le 10^6)\)
同樣的,我們也無法暴力去做這件事
有沒有更好的方法呢?
既然我們今天想要增加區間中每個位置的值
有沒有像 前綴和 那樣快速的方法可以在 \(O(1)\) 做完呢?
觀察到,假設今天我們有個陣列 \(A\)
他的元素為 \(A = \{a_1,a_2,\cdots,a_n\}\)
那當我們將 \(a_l, a_{l+1}, \cdots, a_r\) 都加值時
什麼性質不會改變?
觀察到,假設今天我們有個陣列 \(A\)
他的元素為 \(A = \{a_1,a_2,\cdots,a_n\}\)
那當我們將 \(a_l, a_{l+1}, \cdots, a_r\) 都加值時
什麼性質不會改變?
兩兩元素之間的差距!
只有 \(a_l-a_{l-1}\) 與 \(a_{r+1}-a_r\) 會改變
如果我們將原本的陣列進行一點小改變
原本陣列是 \(A = \{a_1,a_2,\cdots,a_n\}\)
那我們用另外一個陣列
\(B = \{a_1,a_2-a_1,\cdots, a_n-a_{n-1}\}\)
或 \(b_i = a_i - a_{i-1}\)
也就是每個位置都存從第 \(i\) 個值與前一個值的差
那要對 \(a_l,a_{l+1},\cdots,a_r\) 加 \(x\)
我們其實只需要對 \(b_l = b_l - x, b_{r+1} = b_{r+1} - x\)
變回原陣列?
同樣,對修改完的陣列做前綴和
那麼第 \(i\) 個位置就能在 \(O(1)\) 詢問完了!
這個技巧通常會在 DP 時使用
作為一種加速方式
不只有加法可以用?
運算如下皆可以用前綴和的概念
\(+ \Rightarrow -\)
\(* \Rightarrow /\)
\(XOR \Rightarrow XOR\)
練習題
稀疏表
(Sparse Table)
給你一個 \(n\) 項的陣列 \(A\)
接下來會有 \(q\) 次詢問
對於每次詢問區間 \([l,r]\)
輸出 \(a_l,a_{l+1},\cdots,a_r\) 的最小值
\((n \le 10^6, q \le 10^6)\)
給你一個 \(n\) 項的陣列 \(A\)
接下來會有 \(q\) 次詢問
對於每次詢問區間 \([l,r]\)
輸出 \(a_l,a_{l+1},\cdots,a_r\) 的最小值
\((n \le 10^6, q \le 10^6)\)
我們稱這問題為 RMQ 問題
(Range Minimum Queries)
給你一個 \(n\) 項的陣列 \(A\)
接下來會有 \(q\) 次詢問
對於每次詢問區間 \([l,r]\)
輸出 \(a_l,a_{l+1},\cdots,a_r\) 的最小值
\((n \le 10^6, q \le 10^6)\)
最小值不像加法、XOR一樣可以簡單的轉換
那要怎麼處理呢?
我們這裡介紹一種新的概念
倍增法
對於陣列 \(A\) 的每個元素
我們另外開一個陣列 \(B[i][j]\)
維護 \(min(a_i, a_{i+1}, \cdots, a_{i+2^j-1})\)
也就是從第 \(i\)個位置往後延伸 \(2^j\) 個數字
對於陣列 \(A\) 的每個元素
我們另外開一個陣列 \(B[i][j]\)
維護 \(min(a_i, a_{i+1}, \cdots, a_{i+2^j-1})\)
也就是從第 \(i\)個位置往後延伸 \(2^j\) 個數字

對於陣列 \(A\) 的每個元素
我們另外開一個陣列 \(B[i][j]\)
維護 \(min(a_i, a_{i+1}, \cdots, a_{i+2^j-1})\)
也就是從第 \(i\)個位置往後延伸 \(2^j\) 個數字
接著我們就可以在 \(O(\log n)\) 的時間詢問 \([l,r]\)的最小值了
一直往後跳即可!
對於陣列 \(A\) 的每個元素
我們另外開一個陣列 \(B[i][j]\)
維護 \(min(a_i, a_{i+1}, \cdots, a_{i+2^j-1})\)
也就是從第 \(i\)個位置往後延伸 \(2^j\) 個數字
接著我們就可以在 \(O(\log n)\) 的時間詢問 \([l,r]\)的最小值了
一直往後跳即可!
太慢了!
對於陣列 \(A\) 的每個元素
我們另外開一個陣列 \(B[i][j]\)
維護 \(min(a_i, a_{i+1}, \cdots, a_{i+2^j-1})\)
也就是從第 \(i\)個位置往後延伸 \(2^j\) 個數字
接著我們只要詢問
\(min(B[l][\log(r-l)], B[r-\log(r-l)][\log(r-l)])\) 即可
就能在 \(O(1)\) 時間解決了!
對於陣列 \(A\) 的每個元素
我們另外開一個陣列 \(B[i][j]\)
維護 \(min(a_i, a_{i+1}, \cdots, a_{i+2^j-1})\)
也就是從第 \(i\)個位置往後延伸 \(2^j\) 個數字
在建表時
\(B[i][j] = min(B[i][j-1], B[i+2^{j-1}][j-1])\)
程式碼
int dp[N][20], lg[N];
void init(){
for(int i = 0;i < n;i++){
dp[i][0] = arr[i];
}
for(int j = 1;j < 20;j++){
for(int i = 0;i < n;i++){
dp[i][j] = min(dp[i][j-1],dp[i+(1<<j-1)][j-1]);
}
}
//這裡我們會預處理 log
lg[1] = 0;
for(int i = 2;i < N;i++){
lg[i] = lg[i/2]+1;
}
}
int query(int l, int r){
int k = lg[r-l+1];
return min(dp[l][k],dp[l-(1<<k)+1][k]);
}
練習題
要記得這些資結只是解題的工具
可能會在題目中需要用到 RMQ 等等的
可以使用這些資結來協助解題
動態區間操作
複習一下
前綴和: 靜態,\(O(n)\) 預處理,\(O(1)\)詢問
前綴和 + 差分: 詢問與修改不交錯出現,\(O(n)\)預處理,\(O(1)\)修改
稀疏表(ST): 靜態,\(O(n \log n)\) 預處理,\(O(1)\) 詢問
複習一下
前綴和: 靜態,\(O(n)\) 預處理,\(O(1)\)詢問
前綴和 + 差分: 詢問與修改不交錯出現,\(O(n)\)預處理,\(O(1)\)修改
稀疏表(ST): 靜態,\(O(n \log n)\) 預處理,\(O(1)\) 詢問
全是靜態!
如果有同時有修改與詢問呢?
給你一個 \(n\) 項的陣列 \(A\)
接下來會有 \(q\) 次 Query,可能為以下兩種
1. 修改 \(a_i = x\)
2. 每次詢問 \(a_l,a_{l+1},\cdots,a_r\) 的總和
\((n \le 10^6, q \le 10^6)\)
給你一個 \(n\) 項的陣列 \(A\)
接下來會有 \(q\) 次 Query,可能為以下兩種
1. 修改 \(a_i = x\)
2. 每次詢問 \(a_l,a_{l+1},\cdots,a_r\) 的總和
\((n \le 10^6, q \le 10^6)\)
前綴和?
發現到
因為我們想要總和
發現到
因為我們想要總和
前綴和?
\(O(1)\) 詢問但
\(O(n)\) 修改??
發現到
因為我們想要總和
前綴和?
\(O(1)\) 詢問但
\(O(n)\) 修改??
不夠快!
前綴和?
\(O(1)\) 詢問但
\(O(n)\) 修改??
能不能犧牲其中一個 \(O(1)\)
讓其中一種操作變慢
但平均複雜度變好呢?
能不能犧牲其中一個 \(O(1)\)
讓其中一種操作變慢
但平均複雜度變好呢?
BIT
線段樹
\(O(\log n)\) 修改
\(O(\log n)\) 詢問
正因如此,如果只有修改或詢問
前綴和與 ST 皆較快
BIT
(Binary Indexed Tree)
在此之前,我們要先學一種運算
lowbit
Lowbit?
定義為 「數字轉成二進位後,最後一個 1 的數值」
Lowbit?
定義為 「數字轉成二進位後,最後一個 1 的數值」
但我們要怎麼找這個值呢?
但我們要怎麼找這個值呢?
位元運算!
找一個數字的 lowbit
在此直接給結論,\(\text{lowbit}(x) = x\) & \(-x\)
找一個數字的 lowbit
在此直接給結論,\(\text{lowbit}(x) = x\) & \(-x\)
\(-x\) 在二進位的定義為 NOT \(x + 1\)
也就是將 \(x\) 的 \(0/1\) 反轉之後,加 \(1\)
找一個數字的 lowbit
在此直接給結論,\(\text{lowbit}(x) = x\) & \(-x\)
\(-x\) 在二進位的定義為 NOT \(x + 1\)
也就是將 \(x\) 的 \(0/1\) 反轉之後,加 \(1\)
找一個數字的 lowbit
在此直接給結論,\(\text{lowbit}(x) = x\) & \(-x\)
\(-x\) 在二進位的定義為 NOT \(x + 1\)
也就是將 \(x\) 的 \(0/1\) 反轉之後,加 \(1\)
長相
長相
我們用一個 BIT 陣列存這些值
\(\text{BIT}[i] = \text{sum}(i-\text{lowbit}(i)+1,i)\)
根據 lowbit 的性質,我們可以輕易做到以下
單點修改 \(O(\log n)\)
詢問前綴和 \(O(\log n)\)
前綴詢問
int bit[MAXN]; //存BIT節點的陣列
int query(int i){
int res = 0;
while(i){ //當i不等於零時,去找答案
res += bit[i]; //更新答案
i -= i&(-i); //減掉lowbit,繼續找答案
}
return res;
}前綴詢問
int bit[MAXN]; //存BIT節點的陣列
int query(int i){
int res = 0;
while(i){ //當i不等於零時,去找答案
res += bit[i]; //更新答案
i -= i&(-i); //減掉lowbit,繼續找答案
}
return res;
}想要區間總和就 \(query(r)-query(l-1)\) 即可!
單點修改
觀察到一下性質
單點修改
觀察到一下性質
如果我們要修改 \(arr[2]\)
則我們會發現 \(BIT[2], BIT[4], BIT[8]\) 皆有包含 \(arr[2]\)
單點修改
如果我們要修改 \(arr[2]\)
則我們會發現 \(BIT[2], BIT[4], BIT[8]\) 皆有包含 \(arr[2]\)
規律呢?
\(2 + \text{lowbit}(2) = 4\)
\(4 + \text{lowbit}(4) = 8 \)
不停往上加 lowbit(x) 即可!
單點修改
void update(int i, int val){
while(i < MAXN){ //當i小於陣列大小時,去更新答案
bit[i] += val; //更新答案
i += i&(-i); //加上lowbit,繼續更新答案
}
}最多加 \(\log n\) 次! 時間複雜度 \(O(\log n)\)
要記得 BIT 其實就是前綴和
不過支援修改而已
BIT 的應用
逆序數對
在一個陣列 \(A\) 當中
滿足 \(i < j\) 且 \(a_i > a_j\) 的數對數量
逆序數對
在一個陣列 \(A\) 當中
滿足 \(i < j\) 且 \(a_i > a_j\) 的數對數量
之前我們說過可以用 Merge Sort
但我們也可以直接使用 BIT
逆序數對
在一個陣列 \(A\) 當中
滿足 \(i < j\) 且 \(a_i > a_j\) 的數對數量
讓 \(arr[i]\) 存數字 \(i\) 的出現頻率
則 \(pref[i]\) = \(arr[1]+arr[2]+\cdots+arr[i]\)
為小於等於 \(i\) 的數字出現次數
逆序數對
在一個陣列 \(A\) 當中
滿足 \(i < j\) 且 \(a_i > a_j\) 的數對數量
讓 \(arr[i]\) 存數字 \(i\) 的出現頻率
則 \(pref[i]\) = \(arr[1]+arr[2]+\cdots+arr[i]\)
為小於等於 \(i\) 的數字出現次數
逆序數對
int ans = 0;
for(int i = 0; i < n; i++){
//在答案增加在這個元素前有幾個更大的數字
ans += query(MAXN-1)-query(arr[i]);
//更新樹上的資料
update(arr[i],1);
}從前面開始做,要詢問比 \(arr[i]\) 大的值數量
或者
逆序數對
int ans = 0;
for(int i = n-1; i >= 0; i--){
//在答案增加在這個元素後面有幾個更小的數字
ans += query(arr[i]-1);
//更新樹上的資料
update(arr[i],1);
}從後面開始做,要詢問比 \(arr[i]\) 小的值數量
最長遞增子序列 (LIS)
給你一個陣列 \(A\)
問你最長的遞增子序列長度為何?
最長遞增子序列 (LIS)
給你一個陣列 \(A\)
問你最長的遞增子序列長度為何?
之前也教過二分搜的做法
但由於較難想像,我們這裡也用 BIT 來看看
最長遞增子序列 (LIS)
給你一個陣列 \(A\)
問你最長的遞增子序列長度為何?
設 \(arr[i]\) 存的是以數字 \(i\) 結尾的最長LIS
則 \(pref[i]\) 存的是以小於等於 \(i\) 結尾的最長LIS
最長遞增子序列 (LIS)
int query(int i){
int res = 0;
while(i){ //當i不等於零時,去找答案
res = max(res, bit[i]); //更新答案
i -= i&(-i); //減掉lowbit,繼續找答案
}
return res;
}
void update(int i, int val){
while(i < MAXN){
bit[i] = max(bit[i], val);
i += i&(-i);
}
}
int dp[n];
for(int i = 0; i < n; i++){
//找前面比自己小的數字最長的子序列長度+1
dp[i] = max(query(arr[i])+1, dp[i]);
update(arr[i], dp[i]); //更新答案
}BIT上二分搜
今天,你想要一個資料結構
可以維護動態加點,並詢問第 \(k\) 大的元素
BIT上二分搜
今天,你想要一個資料結構
可以維護動態加點,並詢問第 \(k\) 大的元素
設 \(arr[i]\) 存的是數字 \(i\) 的出現頻率
則 \(pref[i]\) 為小於等於數字 \(i\) 時的出現頻率
BIT上二分搜
//正常二分搜
int find(int k){
int l = 0, r = n;
while(l < r){
int m = (l+r)/2;
if(query(m) >= k) r = m;
else l = m+1;
}
}
//l即為第k大的元素\(O(n \log^2 n)\)
BIT上二分搜
//正常二分搜
int find(int k){
int l = 0, r = n;
while(l < r){
int m = (l+r)/2;
if(query(m) >= k) r = m;
else l = m+1;
}
}
//l即為第k大的元素倍增! \(O(n \log n)\)
值域太大怎麼辦?
把數字變成他們的排名
離散化!
//把要離散化的值推進 v
sort(v.begin(), v.end());
v.resize(unique(v.begin(), v.end()) - v.begin());
for(int i = 0;i < n;i++){
arr[i] = lower_bound(v.begin(), v.end(), arr[i]) - v.begin();
}練習題
線段樹
(Segment Tree)
複習一下
稀疏表: \(O(n \log n)\) 預處理,\(O(1)\) RMQ
如果我們想要支援修改的找 RMQ 要怎麼做?
複習一下
稀疏表: \(O(n \log n)\) 預處理,\(O(1)\) RMQ
如果我們想要支援修改的找 RMQ 要怎麼做?
線段樹!
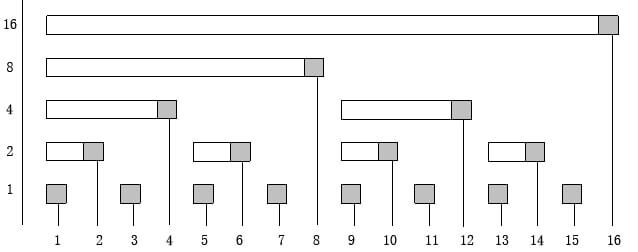
長相
3
4
2
5
3
2
2
每個節點的值都是下面兩個節點值的最小值
長相
[1,1]
[2,2]
[3,3]
[4,4]
[1,2]
[3,4]
[1,4]
每個節點存的都是一個區間的最小值
區間詢問
[1,1]
[2,2]
[3,3]
[4,4]
[1,2]
[3,4]
[1,4]
假設我們想要詢問 [1,3] 的最小值
區間詢問
[1,1]
[2,2]
[3,3]
[4,4]
[1,2]
[3,4]
[1,4]
假設我們想要詢問 [1,3] 的最小值
區間詢問
[1,1]
[2,2]
[3,3]
[4,4]
[1,2]
[3,4]
[1,4]
假設我們想要詢問 [1,4] 的最小值
區間詢問
[1,1]
[2,2]
[3,3]
[4,4]
[1,2]
[3,4]
[1,4]
會發現到我們不會詢問到區間長度個節點那麼多
單點修改
[1,1]
[2,2]
[3,3]
[4,4]
[1,2]
[3,4]
[1,4]
假設我們要修改 [1,1] 的值,會影響到
單點修改
[1,1]
[2,2]
[3,3]
[4,4]
[1,2]
[3,4]
[1,4]
修改一個節點,只會用到樹的高度個節點
建立線段樹
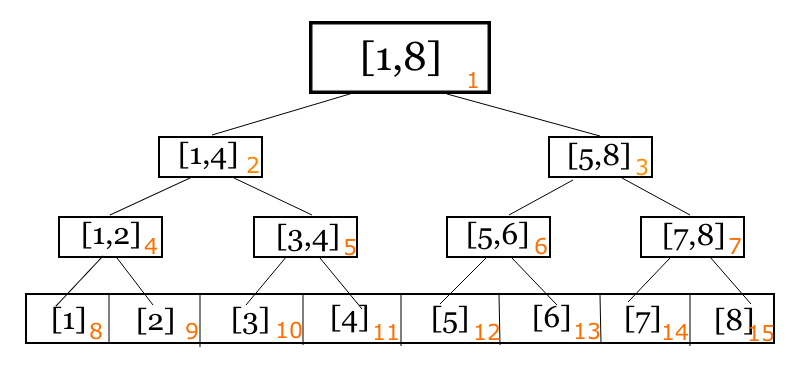
我們會希望能將這棵樹建成完美二元樹
因為這樣我們可以使用陣列來實作 (也有指標的做法)
完美二元樹: 每個節點的 child 為 \(2 \times idx\), \(2 \times idx + 1\)
建立線段樹

也就是點的數量要是 \(2^k-1\)
而葉節點的數量有 \(2^{k-1}\) 個
建立線段樹

如果今天陣列長度為 \(7\) 那怎麼辦呢?
\(\Rightarrow\) 就讓他是空的就好了!
樹的節點數量?
因為要用陣列存,我們要知道我們會用到多少空間!
設目前節點數量為 \(n\)
1. 若 \(n = 2^k\),則節點數量為 \(2n-1\)
2. 若 \(2^k < n < 2^{k+1}\),那我們將其補到 \(2^{k+1}\)
則線段樹的大小為 \(2 \times 2^{k+1} -1 \le 4n -1\)
因此我們只要開 \(4n\) 的陣列大小即可
建立線段樹
步驟:
1. 從節點 \(1\) (包覆整個陣列的節點) 往下遞迴
2. 如果節點的區間 \([l,r]\) 遇到 \(l=r\),則將節點的值設為 \(arr[l]\)
3. 對於每個節點,將他兩個 child 的資料合併
建立線段樹
const int MAXN = 1e5+5;
ll tr[MAXN*4], arr[MAXN]; //線段樹的節點數量一般會開成 4n
void build(int idx, int l, int r){
if(l==r){
//在建立線段樹時,若 l,r 相同,此節點的值為 arr[l]
tr[idx] = arr[l];
}else{
//在建立線段樹時,會從中間分兩邊去建立
int m = (l+r)/2;
build(idx*2,l,m); //一個節點的左子樹一般會用 idx*2 表示
build(idx*2+1,m+1,r); //一個節點的左子樹一般會用 idx*2+1 表示
tr[idx] = combine(tr[idx*2],tr[idx*2+1]); //將左右子樹的資料合併
}
}
//呼叫時會呼叫 build(1,1,n) 或 build(1,0,n-1)區間詢問
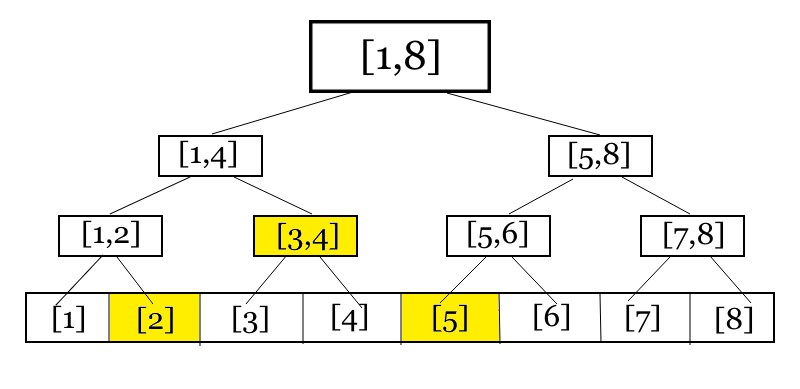
會發現我們在詢問某個區間 (如上圖 [2,5])
其實會將整個區間拆成 \(C \log_2(n)\) 個節點
區間詢問
int query(int ql, int qr, int idx, int l, int r){
//l,r為這個節點的儲存區間的左右界
if(ql <= l && r <= qr){
//若這個區間被詢問完全包住,直接回傳答案
return tr[idx];
}
int m = (l+r)/2;
if(ql > m){
//若詢問的區間完全在右邊,我們只須往右找答案
return query(ql, qr, idx*2+1, m+1, r);
}
if(qr <= m){
//若詢問的區間完全在左邊,我們只須往左找答案
return query(ql, qr, idx*2, l, m);
}
//往左右都尋找答案,並回傳合併後的答案
return combine(query(ql, qr, idx*2, l, m), query(ql, qr, idx*2+1, m+1, r));
}單點修改
[1,1]
[2,2]
[3,3]
[4,4]
[1,2]
[3,4]
[1,4]
修改一個節點,只會用到樹的高度個節點
單點修改
void update(int pos, int val, int idx, int l, int r){
if(l==r){
tr[idx] = val;
return;
}
int m = (l+r)/2;
//依據要更新的位置去更新左或右子樹的資訊
if(pos <= m) update(pos, val, idx*2, l, m);
else update(pos, val, idx*2+1, m+1, r);
tr[idx] = combine(tr[idx*2],tr[idx*2+1]); //將左右子樹的資料合併
}只會修改 \(\log_2(n)\) 個節點
時間複雜度: \(O(\log n)\)
整份單點修改線段樹的code
const int MAXN = 1e5+5;
ll tr[MAXN*4], arr[MAXN];
ll combine(ll a, ll b){
return min(a,b);
}
void build(int idx, int l, int r){
if(l==r){
tr[idx] = arr[l];
}else{
int m = (l+r)/2;
build(idx*2,l,m);
build(idx*2+1,m+1,r);
tr[idx] = combine(tr[idx*2],tr[idx*2+1]);
}
}
void update(int pos, int val, int idx, int l, int r){
if(l==r){
tr[idx] = val;
return;
}
int m = (l+r)/2;
if(pos <= m) update(pos, val, idx*2, l, m);
else update(pos, val, idx*2+1, m+1, r);
tr[idx] = combine(tr[idx*2],tr[idx*2+1]);
}
ll query(int ql, int qr, int idx, int l, int r){
if(ql <= l && r <= qr){
return tr[idx];
}
int m = (l+r)/2;
if(ql > m){
return query(ql, qr, idx*2+1, m+1, r);
}
if(qr <= m){
return query(ql, qr, idx*2, l, m);
}
return combine(query(ql, qr, idx*2, l, m), query(ql, qr, idx*2+1, m+1, r));
}練習看看吧!
線段樹的應用
線段樹上二分搜
昨天,我們談過 BIT 上二分搜 的作法
而線段樹也能做到一樣的事情
線段樹上二分搜
給你一個 \(n\) 項的由 0/1 組成的陣列
問你第一個 1 出現的位置
例題
線段樹上二分搜
給你一個 \(n\) 項的陣列
問你第一個 \(>x\) 的值出現的位置
例題
二分搜!
線段樹上二分搜
給你一個 \(n\) 項的陣列
問你第一個 \(>x\) 的值出現的位置
例題
既然你想要 \(>x\) 的值,那我們先建立一棵
區間最大值 的線段樹
線段樹上二分搜
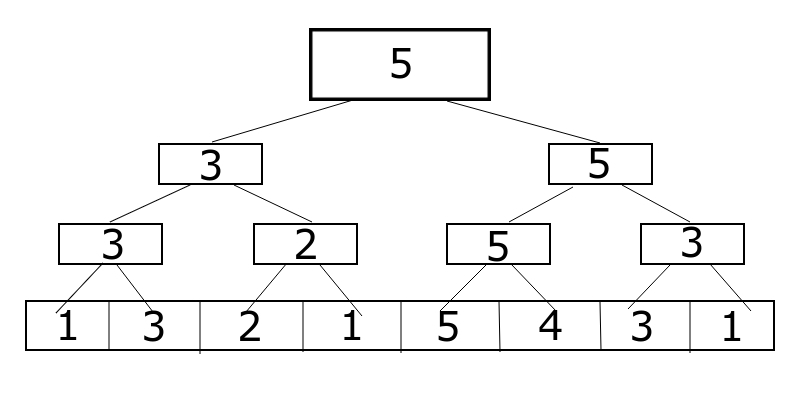
區間最大值的線段樹
線段樹上二分搜
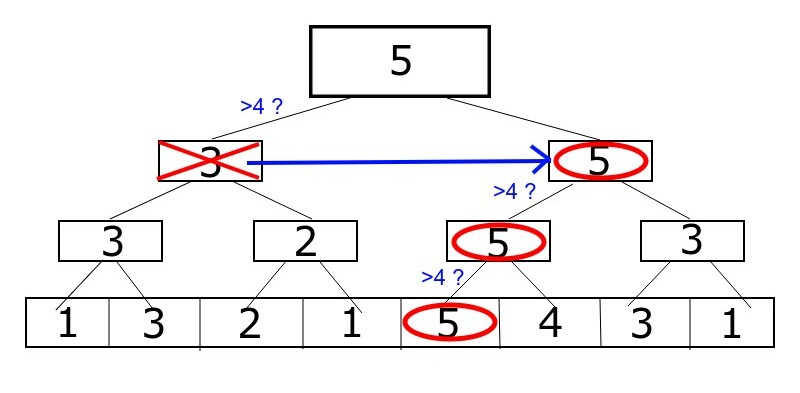
在區間最大值的線段樹上二分搜
線段樹上二分搜
int find(int x, int idx, int l, int r){
if(l==r) return l; //找到了就回傳
int m = (l+r)/2;
//往兩邊找,如果左邊的最大值>x,往左繼續找
//否則往右找
if(tr[idx*2] > x) return find(x, idx*2, l, m);
else return find(x, idx*2+1, m+1, r);
}練習題
線段樹維護 DP
給你一個 \(n\) 項陣列
你每次可以修改某個位置的值
請輸出陣列中的最大連續和
例題
線段樹維護 DP
給你一個 \(n\) 項陣列
你每次可以修改某個位置的值
請輸出陣列中的最大連續和
例題
最大連續和怎麼做?
\(O(n)\) 掃過去?
線段樹維護 DP
給你一個 \(n\) 項陣列
你每次可以修改某個位置的值
請輸出陣列中的最大連續和
例題
事實上,最大連續和也可以使用分治去做
而在線段樹中,我們就是要使用這個做法
線段樹維護 DP
給你一個 \(n\) 項陣列
你每次可以修改某個位置的值
請輸出陣列中的最大連續和
例題
對於每個樹上的節點,我們存四種資料
1. 區間中的最大連續和 \(ans\)
2. 從左開始的最大連續和 \(l\)
3.從右開始的最大連續和 \(r\)
4. 區間的總和 \(sum\)
線段樹維護 DP
對於每個樹上的節點,我們存四種資料
1. 區間中的最大連續和 \(ans\)
2. 從左開始的最大連續和 \(l\)
3.從右開始的最大連續和 \(r\)
4. 區間的總和 \(sum\)
而在節點合併時,只要做以下的算式
\(X.A = max(X_l.A, X_R.A, X_l.R+X_r.L)\)
\(X.L = max(X_l.L,X_l.sum+X_r.L)\)
\(X.R = max(X_r.R, X_l.R + X_r.sum)\)
\(X.sum = X_l.sum + X_r.sum\)
線段樹維護 DP
而在節點合併時,只要做以下的算式
\(X.A = max(X_l.A, X_R.A, X_l.R+X_r.L)\)
\(X.L = max(X_l.L,X_l.sum+X_r.L)\)
\(X.R = max(X_r.R, X_l.R + X_r.sum)\)
\(X.sum = X_l.sum + X_r.sum\)
而這樣做即可得到答案!
線段樹維護最大連續和
struct node{
ll ans, left, right, sum;
node(){}
node(ll a, ll b, ll c, ll d){
ans = a, left = b, right = c, sum = d;
}
};
node combine(node a, node b){
node c;
c.ans = max({a.ans, b.ans, a.right+b.left});
c.left = max(a.sum+b.left, a.left);
c.right = max(a.right+b.sum, b.right);
c.sum = a.sum + b.sum;
return c;
}剩下的部分皆差不多
練習題
懶惰標記
(Lazy Propagation)
我們已經知道
線段樹單點修改: \(O(\log n)\)
那如果我想要進行區間修改呢?
我們已經知道
線段樹單點修改: \(O(\log n)\)
那如果我想要進行區間修改呢?
每個點都做一次單點修改?
我們已經知道
線段樹單點修改: \(O(\log n)\)
那如果我想要進行區間修改呢?
每個點都做一次單點修改?
\(O(n \log n)\) 進行一次修改! 太慢了
讓我們看看區間詢問的作法
區間詢問
[1,1]
[2,2]
[3,3]
[4,4]
[1,2]
[3,4]
[1,4]
假設我們想要詢問 [1,3] 的最小值
修改是否也能做一樣的事呢?
區間修改?
void modify(int ml, int mr, int val, int idx, int l, int r){
if(ml <= l && r <= mr){
tr[idx] += (l-r+1) * val;
return;
}
int mid = (l+r)/2;
if(ql <= mid) modify(ml, mr, val, idx<<1, l, mid);
if(qr > mid) modify(ml, mr, val, idx<<1|1, mid+1, r);
tr[idx] = combine(tr[idx<<1],tr[idx<<1|1]);
}區間修改?
void modify(int ml, int mr, int val, int idx, int l, int r){
if(ml <= l && r <= mr){
tr[idx] += (l-r+1) * val;
return;
}
int mid = (l+r)/2;
if(ql <= mid) modify(ml, mr, val, idx<<1, l, mid);
if(qr > mid) modify(ml, mr, val, idx<<1|1, mid+1, r);
tr[idx] = combine(tr[idx<<1],tr[idx<<1|1]);
}這樣做的話,看似正確
但... 如果我們詢問這個節點以下的點呢?
區間修改?
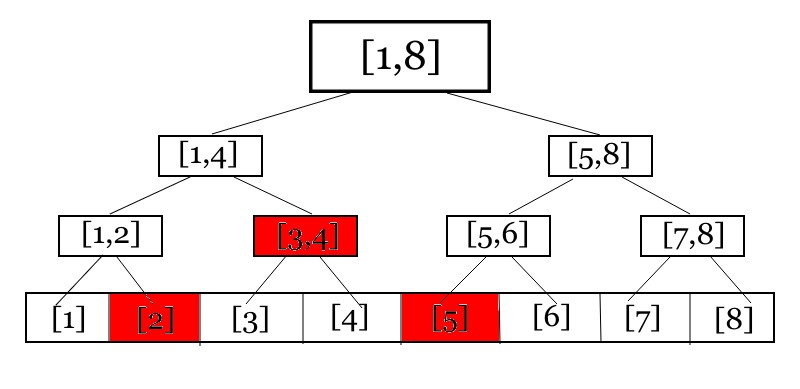
修改 [2,5] 的值
區間修改?

會發現我們修改了[2], [3,4], [5] 的位置
但要是我們詢問 [3] 的答案呢?
因此這裡我們要介紹「懶惰標記」這個東西
(很懶)
修改區間時
1. 直接去修改包含到的節點的值
2. 在節點上記錄一個標記
詢問答案時
1. 先將標記下推
2. 正常詢問答案
懶惰標記下推
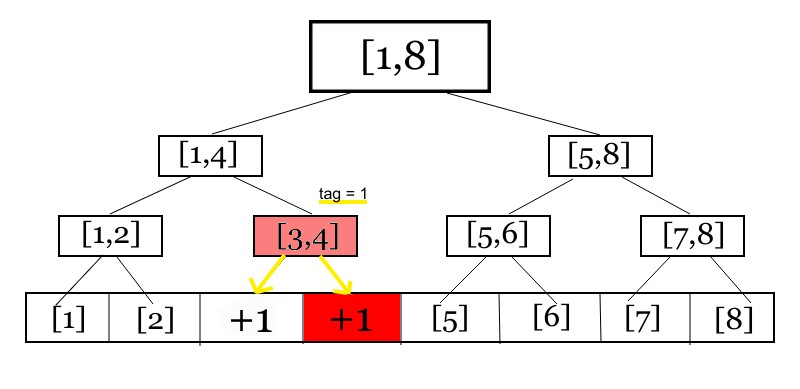
程式碼
const int MAXN = 1e5+5;
int tr[MAXN*4], arr[MAXN], tag[MAXN*4]; //線段樹的節點數量一般會開成 4n
void push(int idx){
//下推節點的標記(這裡以區間加值 區間最大值為例)
if(tag[idx]){
tr[idx<<1] += tag[idx];
tr[idx<<1|1] += tag[idx];
tag[idx<<1] += tag[idx];
tag[idx<<1|1] += tag[idx];
tag[idx] = 0;
}
}
int query(int ql, int qr, int idx, int l, int r){
if(l!=r) push(idx); //當節點並非葉節點時,下推標記
if(ql <= l && r <= qr){
return tr[idx];
}
int m = (l+r)/2;
if(ql > m){
return query(ql, qr, idx*2+1, m+1, r);
}
if(qr <= m){
return query(ql, qr, idx*2, l, m);
}
return combine(query(ql, qr, idx*2, l, m), query(ql, qr, idx*2+1, m+1, r));
}
//這裡最特別的地方,區間修改,寫法與區間詢問大致相同
void modify(int ql, int qr, int val, int idx, int l, int r){
if(l!=r) push(idx); //當節點並非葉節點時,下推標記
if(ql <= l && r <= qr){
tr[idx] += val;
return;
}
int m = (l+r)/2;
if(qr > m) modify(ql, qr, val, idx*2+1, m+1, r);
if(ql <= m) modify(ql, qr, val, idx*2, l, m);
tr[idx] = combine(tr[idx<<1],tr[idx<<1|1]);
}練習題
還有很多...
動態開點線段樹
值域太大,又無法離散化?
動態開點線段樹就派上用場了!
如果今天值域
\(a_i \le 10^9\)
但是 \(q \le 10^6\)
要怎麼辦?
會發現我們詢問次數很少
要用到的點其實最多只有 \(C \log (Q)\)
要使用到再去開點即可
常見寫法
- 指標 (空間大,不好寫)
- 偽指標 (使用陣列,非常好寫,可以預留空間)

指標型
#include <bits/stdc++.h>
#define int long long
#define fastio ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
using namespace std;
struct node{
node *lc, *rc;
int l, r, min, lz;
node(): lc(NULL), rc(NULL), l(0), r(1e9+5), min(0), lz(0){}
void ext(){
if(lc==NULL){
lc = new node();
rc = new node();
lc->l = l, lc->r = l+r>>1;
rc->l = (l+r>>1)+1, rc->r = r;
}
}
};
void range_update(node *&t, int l, int r, int val){
if(t->lz){
t->min += t->lz;
if(t->l!=t->r){
t->ext();
t->lc->lz += t->lz;
t->rc->lz += t->lz;
}
t->lz = 0;
}
if(t->l>r||t->r<l) return;
if(t->l>=l&&t->r<=r){
t->min += val;
if(t->l!=t->r){
t->ext();
t->lc->lz += val;
t->rc->lz += val;
}
return;
}
t->ext();
range_update(t->lc,l,r,val);
range_update(t->rc,l,r,val);
t->min = min(t->lc->min,t->rc->min);
}
int query(node *&t, int l, int r){
if(t->l>r||t->r<l) return 1e18;
if(t->lz){
t->min += t->lz;
if(t->l!=t->r){
t->ext();
t->lc->lz += t->lz;
t->rc->lz += t->lz;
}
t->lz = 0;
}
if(t->l>=l&&t->r<=r) return t->min;
t->ext();
return min(query(t->lc,l,r),query(t->rc,l,r));
}
signed main(){
fastio
int n,m;
cin >> n >> m;
node *t = new node();
while(m--){
int v;
cin >> v;
if(v==1){
int l,r,x;
cin >> l >> r >> x;
range_update(t,l,r-1,x);
}else{
int l,r;
cin >> l >> r;
cout << query(t,l,r-1) << "\n";
}
}
}偽指標型
#include <bits/stdc++.h>
#define int long long
#define fastio ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
using namespace std;
const int INF = 1e9+7;
struct node{
int lc, rc, l, r, mn, lz;
node(int l, int r): lc(0), rc(0), l(l), r(r), mn(INF), lz(0);
};
vector<node> nodes;
void push(int idx){
int l = nodes[idx].l, r = nodes[idx].r, m = (l+r)/2;
if(nodes[idx].lz){
if(!nodes[idx].lc) nodes[idx].lc = nodes.size(), nodes.push(node(l,m));
if(!nodes[idx].rc) nodes[idx].rc = nodes.size(), nodes.push(node(m+1,r));
nodes[nodes[idx].lc].mn += nodes[idx].lz;
nodes[nodes[idx].rc].mn += nodes[idx].lz;
nodes[idx].lz = 0;
}
}
void modify(int ml, int mr, int val, int idx){
int l = nodes[idx].l, r = nodes[idx].r;
if(l!=r) push(idx);
if(ql <= l && r <= qr){
nodes[idx].mn += val;
nodes[idx].lz += val;
}else{
int mid = (l+r)/2;
if(!nodes[idx].lc) nodes[idx].lc = nodes.size(), nodes.push(node(l,m));
if(!nodes[idx].rc) nodes[idx].rc = nodes.size(), nodes.push(node(m+1,r));
if(ql <= mid) modify(ml,mr,val,nodes[idx].lc);
if(qr > mid) modify(ml,mr,val,nodes[idx].rc);
nodes[idx].mn = min(nodes[nodes[idx].lc].mn,nodes[nodes[idx].rc].mn);
}
}
int query(int ql, int qr, int idx){
if(idx==0) return INF;
int l = nodes[idx].l, r = nodes[idx].r;
if(l!=r) push(idx);
if(ql <= l && r <= qr){
return nodes[idx].mn;
}else{
int mid = (l+r)/2;
if(qr <= mid) return query(ml,mr,val,nodes[idx].lc);
if(ql > mid) return query(ml,mr,val,nodes[idx].rc);
return min(query(ml,mr,val,nodes[idx].lc),query(ml,mr,val,nodes[idx].rc));
}
}
練習題
離線 + 區間查詢?
首先,我們來說說「在線」與「離線」
在線 (Online Algorithm)
依序將詢問輸入,並依序計算答案
離線 (Offline Algorithm)
預先將所有詢問輸入,進行 排序 等,最後再一併輸出答案
而事實上有許多離線的區間詢問算法
如:
莫隊算法
CDQ 分治
整體二分搜
(但我們這裡不講)
而我們來看看如何離線去解決一些我們不會處理的問題
給你一個陣列
每次詢問 \([l,r]\) 之間有幾個相異數字
\(1 \le n \le 10^5\)
給你一個陣列
每次詢問 \([l,r]\) 之間有幾個相異數字
\(1 \le n \le 10^5\)
要怎麼處理呢?
你可能會想到既然要相異數字
那我們就 線段樹套 set
不過這裡既然要講離線
那我們來想想要如何預先處理這些測資來讓題目變簡單
先將詢問排序?
會不會有什麼好性質呢?
想法
先將詢問排序?
會不會有什麼好性質呢?
想法
能不能將同個起點的詢問一起做
將起點固定,再一併處理詢問!
陣列
3 2 3 1 2 1 5
從左邊開始做,依序將左界往左移
\(l\)
\(r\)
陣列
3 2 3 1 2 1 5
從左邊開始做,依序將左界往左移
\(l\)
\(r\)
陣列
3 2 3 1 2 1 5
從左邊開始做,依序將左界往左移
\(l\)
\(r\)
陣列
3 2 3 1 2 1 5
從左邊開始做,依序將左界往左移
\(l\)
\(r\)
陣列
3 2 3 1 2 1 5
從左邊開始做,依序將左界往左移
\(l\)
\(r\)
陣列
3 2 3 1 2 1 5
從左邊開始做,依序將左界往左移
\(l\)
\(r\)
陣列
3 2 3 1 2 1 5
從左邊開始做,依序將左界往左移
\(l\)
\(r\)
陣列
3 2 3 1 2 1 5
從左邊開始做,依序將左界往左移
會發現每次加入一個數字,對於區間答案的影響
到數字不重複的結束點的答案都會 \(+1\)
我們來看看圖
\(l\)
\(r\)
陣列
3 2 3 1 2 1 5
\(l\)
\(r\)
紅色線為這個數字影響到的區間答案
陣列
3 2 3 1 2 1 5
\(l\)
\(r\)
紅色線為這個數字影響到的區間答案
陣列
3 2 3 1 2 1 5
\(l\)
\(r\)
紅色線為這個數字影響到的區間答案
陣列
3 2 3 1 2 1 5
\(l\)
\(r\)
紅色線為這個數字影響到的區間答案
陣列
3 2 3 1 2 1 5
\(l\)
\(r\)
紅色線為這個數字影響到的區間答案
陣列
3 2 3 1 2 1 5
\(l\)
\(r\)
紅色線為這個數字影響到的區間答案
陣列
3 2 3 1 2 1 5
\(l\)
\(r\)
紅色線為這個數字影響到的區間答案
陣列
3 2 3 1 2 1 5
\(l\)
\(r\)
紅色線為這個數字影響到的區間答案
因此,我們每次只需要進行
區間加值、單點詢問
使用 差分+BIT 或 線段樹 皆可!