最小生成樹
(Minimum Spanning Tree)
樹?
複習一下,樹是什麼?
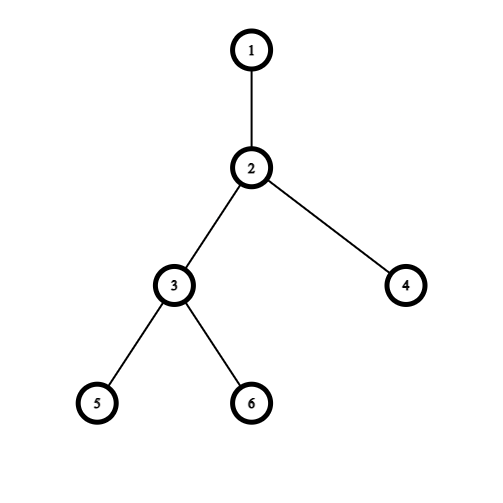
一張連通且每個點恰有一條路徑的圖
若有 \(V\) 個點,則有 \(V-1\) 條邊

樹,分為有根樹與無根樹
而這棵樹有無邊權皆可

而一棵樹的邊,不會形成環

那生成樹是什麼?
(Spanning Tree)
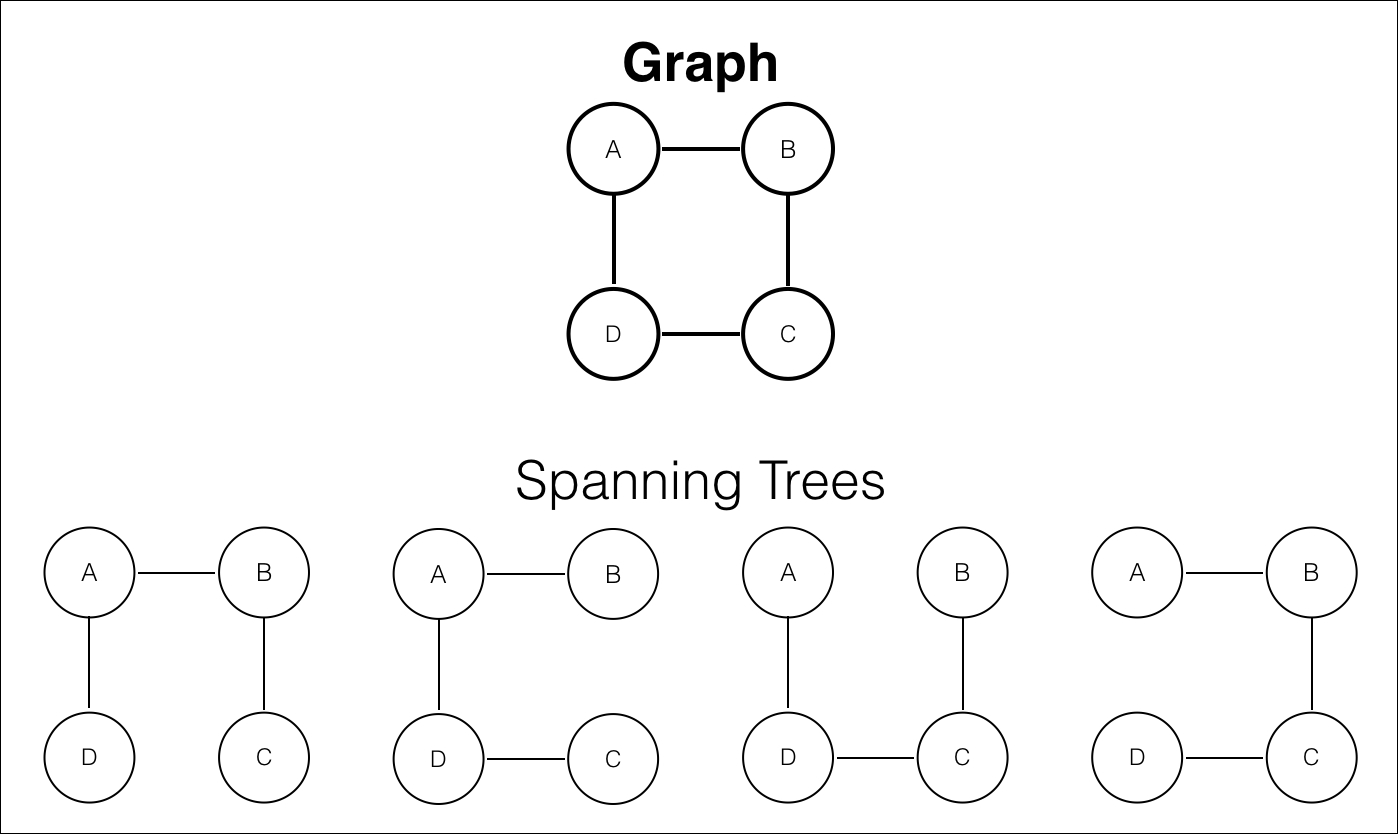
生成樹
對於一張圖 \(G=(V,E)\)
我們可以找到有 \(V\) 個點的樹 \(T=(V,E')\),且 \(E \subset E'\)
而對於一張圖,可能有多個不同的生成樹
看定義很難理解,我們來看圖
生成樹
生成樹
而生成樹根據性質有不同分類
最常見的有以下
最小生成樹 (Minimum Spanning Tree)
DFS 生成樹 (DFS Spanning Tree)
最小生成樹
DFS 生成樹
而我們今天要教的是最小生成樹
DFS 生成樹等我們講到圖的連通性時會再提
最小生成樹
最小生成樹的定義
對於一張圖的所有生成樹
樹的邊權總和最小的就被我們稱為 最小生成樹
而一張圖可能會有多個不同的 最小生成樹
我們一般簡稱 最小生成樹 為 MST
最小生成樹
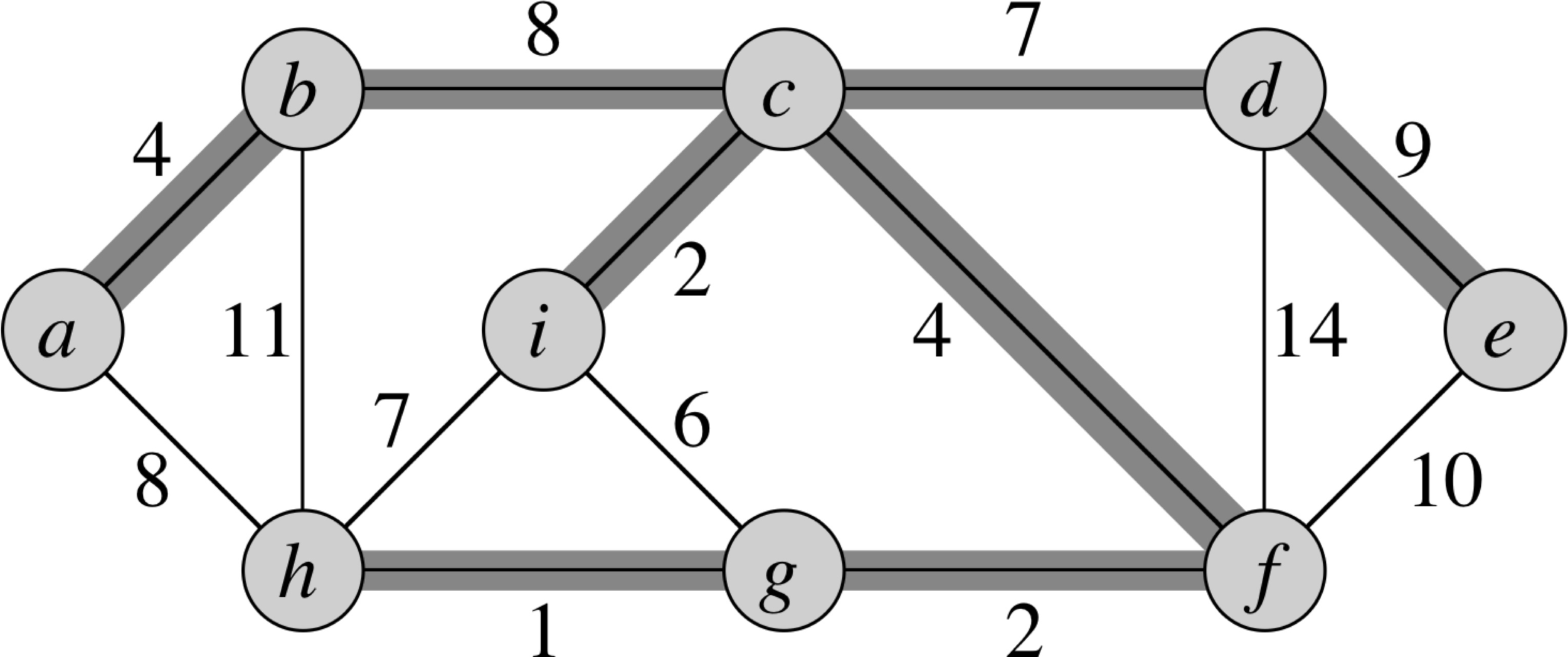
最小生成樹的兩種性質
Cycle Property
在任何一個圖 \(G\) 上的環
環上邊權最大的邊 \(e\) 一定不在 MST 上
(假設最大邊權不重複)
Cut Property
在任何一個圖 \(G\) 上的 Cut
Cut 上最小邊權的邊 \(e\) 一定在 MST 上
(假設最小邊權不重複)
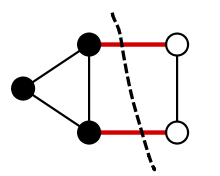
什麼時候 MST 不唯一?
Cycle Property
在任何一個圖 \(G\) 上的環
環上邊權最大的邊 \(e\) 一定不在 MST 上
(假設最大邊權不重複)

當環上有多個最大邊權的邊時
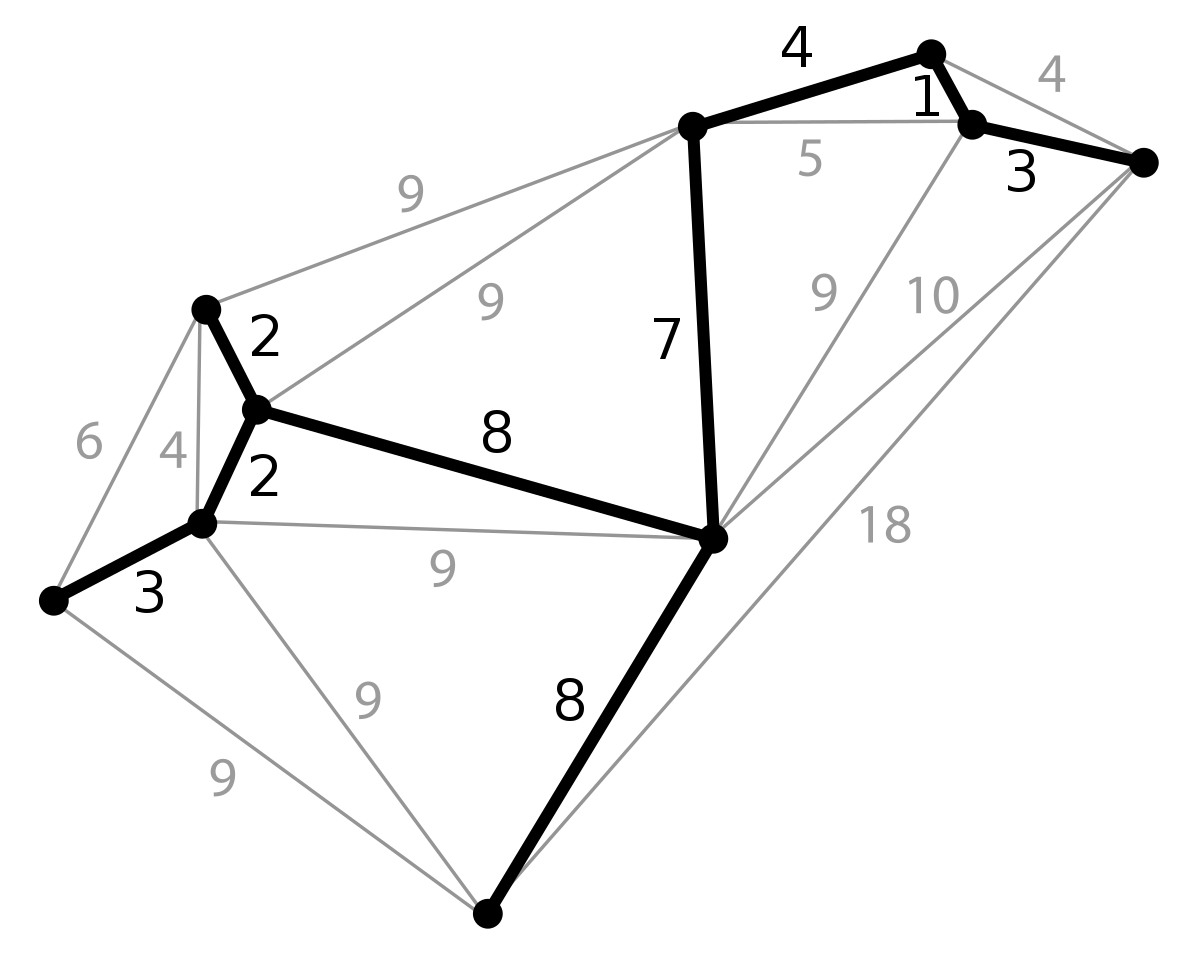
Kruskal's Algorithm
運作如下
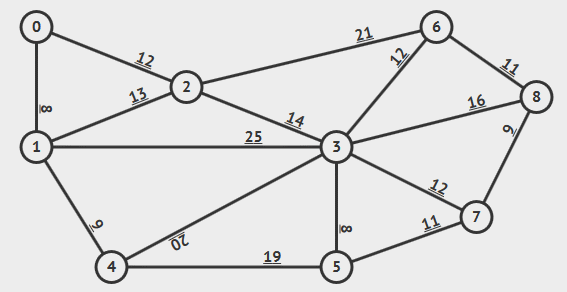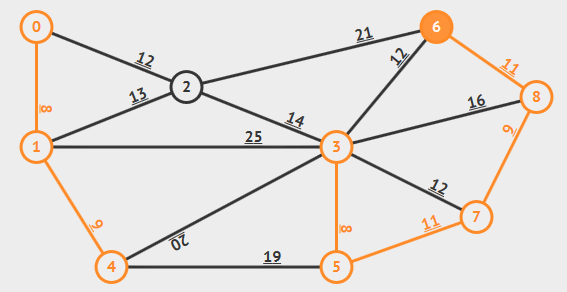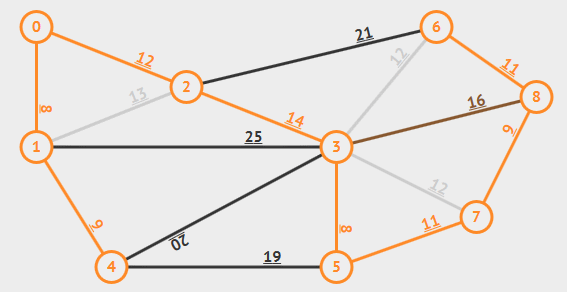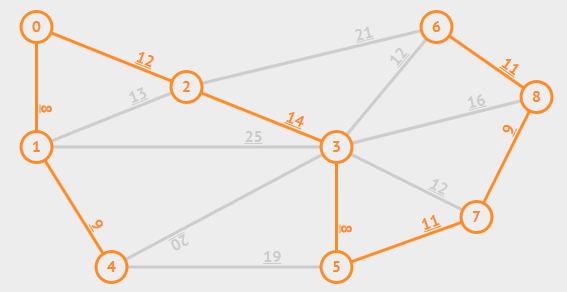
想法
既然我們想要找最小權重的一棵樹
那麼我們每次都把最小的邊加到圖上
如果這條邊加入之後,會形成環 \(\Rightarrow\) 不加
如果這條邊加入之後,不會形成環 \(\Rightarrow\) 加
最後是不是就會得到一棵最小權重和的生成樹了呢?
想法
既然我們想要找最小權重的一棵樹
那麼我們每次都把最小的邊加到圖上
如果這條邊加入之後,會形成環 \(\Rightarrow\) 不加
如果這條邊加入之後,不會形成環 \(\Rightarrow\) 加
最後是不是就會得到一棵最小權重和的生成樹了呢?
因此,這個演算法也是貪心演算法!
原理
為什麼這樣會對呢?
我們這裡就要回到剛剛所講的 Cycle Property
Cycle Property
在任何一個圖 \(G\) 上的環
環上邊權最大的邊 \(e\) 一定不在 MST 上
(假設最大邊權不重複)
原理
那麼我們只要每次都加最小的邊
若出現環就不要加
那麼我們一定不會加到環上邊權最大的邊 \(e\)
Cycle Property
在任何一個圖 \(G\) 上的環
環上邊權最大的邊 \(e\) 一定不在 MST 上
(假設最大邊權不重複)
但是這裡有個問題,我們要怎麼判斷加入這條邊之後
圖上會不會出現環呢?
但是這裡有個問題,我們要怎麼判斷加入這條邊之後
圖上會不會出現環呢?
沒錯! 只要使用 並查集 來維護即可!
實作步驟
1. 將邊根據邊權進行排序
2. 依序掃過這些邊,能加就加
3. 找到最小生成樹了!
程式碼
1. 將邊根據邊權進行排序
struct edge{
int w,u,v;
};
vector<edge> edges;
//輸入邊
sort(edges.begin(),edges.end());程式碼
1. 將邊根據邊權進行排序
struct edge{
int w,u,v;
};
vector<edge> edges;
//輸入邊
sort(edges.begin(),edges.end());
for(auto e : edges){
if(find(e.u) != find(e.v)){
//e.u, e.v 即為最小生成樹的一條邊
}
}2. 依序掃過這些邊,能加就加
程式碼
1. 將邊根據邊權進行排序
struct edge{
int w,u,v;
};
vector<edge> edges;
//輸入邊
sort(edges.begin(),edges.end());
for(auto e : edges){
if(find(e.u) != find(e.v)){
//e.u, e.v 即為最小生成樹的一條邊
}
}2. 依序掃過這些邊,能加就加
做完了!
時間複雜度?
1. 將邊根據邊權進行排序 \(\Rightarrow O(E \log E)\)
2. 依序掃過這些邊,能加就加 \(\Rightarrow O(E)\)
時間複雜度?
1. 將邊根據邊權進行排序 \(\Rightarrow O(E \log E)\)
2. 依序掃過這些邊,能加就加 \(\Rightarrow O(E)\)
總時間複雜度: \(O(E \log E)\)
或者因為 \(E \le \frac{V(V-1)}{2}\)
所以總時間複雜度也可寫成 \(O(E \log V)\)
Prim's Algorithm
運作如下
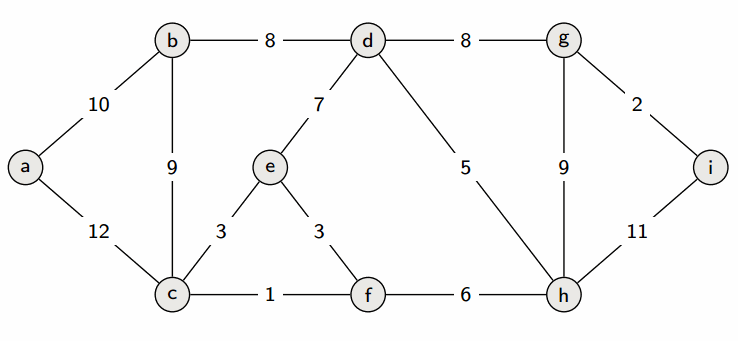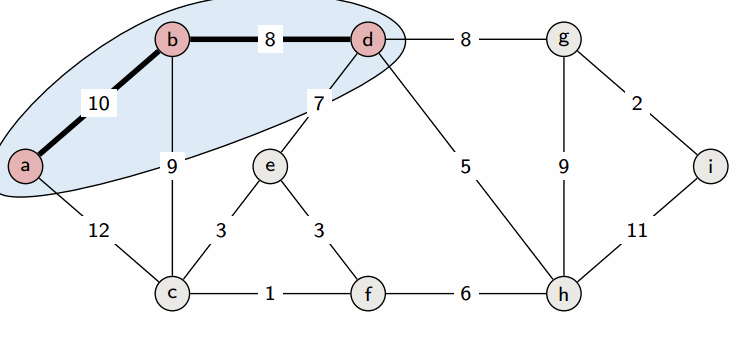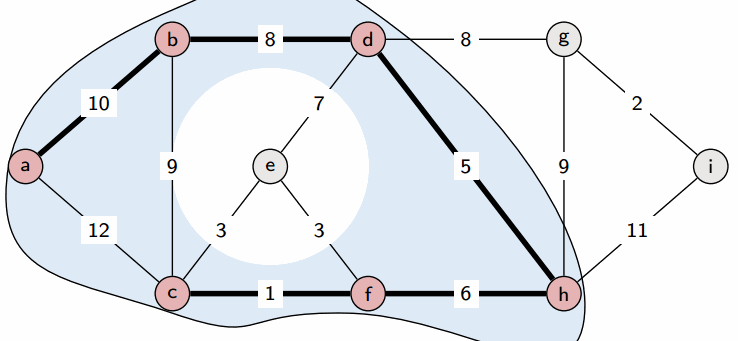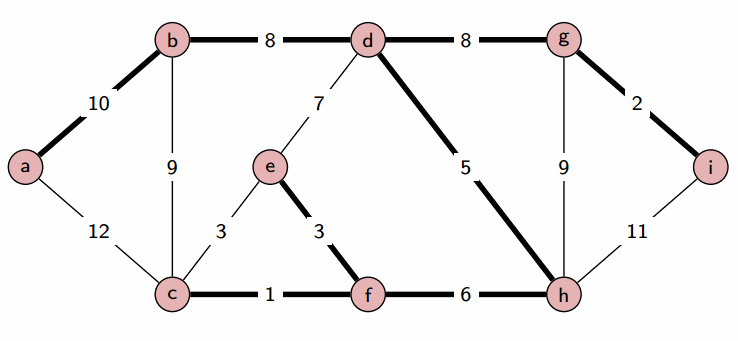
想法
既然要找 權重和最小的生成樹
那我們隨便從一個起點開始
每次都走 權重最小的邊
直到所有點都被走過
這樣是不是就會得到 最小生成樹 了呢?
想法
既然要找 權重和最小的生成樹
那我們隨便從一個起點開始
每次都走 權重最小的邊
直到所有點都被走過
這樣是不是就會得到 最小生成樹 了呢?
這也是貪心演算法!
為什麼會對?
為什麼會對?
Cut Property
在任何一個圖 \(G\) 上的 Cut
Cut 上最小邊權的邊 \(e\) 一定在 MST 上
(假設最小邊權不重複)

為什麼會對?
Cut Property
在任何一個圖 \(G\) 上的 Cut
Cut 上最小邊權的邊 \(e\) 一定在 MST 上
(假設最小邊權不重複)

因此,當我們在做 Prim's Algorithm 時
我們都會從這個連通分量走最小的邊
而這樣,我們就會符合 Cut Property
每次增加的邊皆在 MST 上
實作步驟
1. 開一個存邊的 priority_queue
2. 任選一個起點開始走
3. 當 pq 不是空的時候,看 pq 頂部的邊是否能走
4. 走到一個點時,將他相鄰的邊加進 pq
5. 走過的所有邊即形成最小生成樹
程式碼
1. 開一個存邊的 priority_queue
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<>> pq;
//邊存的是 {邊權, 走到的點}
程式碼
1. 開一個存邊的 priority_queue
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<>> pq;
//邊存的是 {邊權, 走到的點}
pq.push(1);
visited[1] = true;2. 任選一個起點開始走
程式碼
1. 開一個存邊的 priority_queue
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<>> pq;
//邊存的是 {邊權, 走到的點}
pq.push(1);
visited[1] = true;
while(!pq.empty()){
auto [w,u] = pq.top(); pq.pop();
if(visited[u]) continue;
}2. 任選一個起點開始走
3. 當 pq 不是空的時候,看 pq 頂部的邊是否能走
程式碼
1. 開一個存邊的 priority_queue
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<>> pq;
//邊存的是 {邊權, 走到的點}
pq.push(1);
visited[1] = true;
while(!pq.empty()){
auto [ww,u] = pq.top(); pq.pop();
if(visited[u]) continue;
//如果想要知道是哪個點走到 u 可以額外紀錄
//但 {from[u], u} 是最小生成樹上的一條邊
for(auto [v,w] : adj[u]){
pq.push({w,v});
}
}2. 任選一個起點開始走
3. 當 pq 不是空的時候,看 pq 頂部的邊是否能走
4. 走到一個點時,將他相鄰的邊加進 pq
時間複雜度
有一個存邊的 priority_queue
而且跑 \(E\) 次
\(O(E \log E) \Rightarrow O(E \log V)\)
如果不用 priority_queue
時間複雜度可以達到 \(O(V^2)\)
在 完全圖 時快很多
例題
有 \(n\) 個國家,而今天每個國家都有石油的需求
而今天有 \(m\) 種不同的道路可以建造,每個道路建造費用 \(w_i\)
這些國家也可以選擇自己花費 \(c_i\) 開採石油
請問讓每個國家取得石油的最少費用是多少?
這題看起來可以直接做最小生成樹
不過有 每個國家能得到石油 的限制
因此我們必須要想個方式來做到這一點
這題看起來可以直接做最小生成樹
不過有 每個國家能得到石油 的限制
因此我們必須要想個方式來做到這一點
建設虛點!
建設虛點!
將開採石油井這件事開成一個點
以 \(c_i\) 為邊權連到每個國家
跑最小生成樹演算法!
完成!
YTP 2021 決賽 p4
今天有 \(n\) 個國家,他們之間有 \(m\) 條邊
邊權為 \(w_i\),而從國家 \(u\) 派人到國家 \(v\) 的花費
為從 \(u\) 走到 \(v\) 的路徑上最大的邊
今天你想知道每個國家互相走到對方的最少花費
用 Kruskal 演算法和 並查集 維護連通塊大小
然後把答案加上 \(w_i \times cnt[find(u)] \times cnt[find(v)]\)
練習題
TIOJ 2164 - 運送蛋餅 (這題是完全圖 用Prim's)
NPSC 2018 高中組決賽 pB - 平衡的技能樹
(這題的技巧大家不會,但是可以想想看大概做法)