分治 (Divide & Conquer)
什麼是分治
什麼是分治?
分而治之
也就是將問題拆成小問題去解決!
分治的基本概念
- 將大問題想成兩個以上的小問題
- 分別解決
- 合併
主定理
Master Theorem
當你看到一個這樣的程式
int f(int l, int r){
int m = (l+r)/2;
int a = f(l,mid);
int b = f(mid+1,r);
int tmp = 0;
for(int i = l;i <= r;i++){
tmp += arr[i];
}
return a+b+tmp;
}時間複雜度如何判斷?
先將程式碼寫成數學式
int f(int l, int r){
int m = (l+r)/2;
int a = f(l,mid);
int b = f(mid+1,r);
int tmp = 0;
for(int i = l;i <= r;i++){
tmp += arr[i];
}
return a+b+tmp;
}可以使用數學歸納法找複雜度!
由於這樣的時間複雜度,與我們所知道的
Merge Sort
有幾分相似,我們知道 Merge Sort 的複雜度為 \(O(n \log n)\)
猜測這個程式的複雜度為 \(O(n \log n)\)!
因此,只要我們能證明 \(T(n) \in O(n \log n)\)
就可以證明這個程式的時間複雜度為 \(O(n \log n)\) 了!
證明方式:
- 對於 \(n=1\) 時,\(T(n) = O(n)\) 明顯成立
- 假設對於 \(n=\dfrac k 2\)時成立,意即 \(T(\dfrac n 2) = O(\dfrac{n}{2} \log \dfrac{n}{2})\),那麼 \(T(n) = 2T(\dfrac n 2) + O(n)\),得到 \(T(n) = 2O(\dfrac n 2 \log \dfrac n 2) + O(n)\),滿足 \(T(n) \in O(n \log n)\)
得證,因此這個程式的複雜度為 \(O(n \log n)\)
但每次都要猜答案並證明太麻煩了
因此,有人統整出了一種判斷方法
被稱為 主定理
主定理
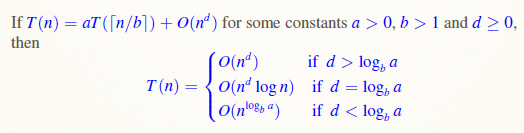
因此我們可以用這個方式去找遞迴的複雜度
Merge Sort
Merge Sort 的運行方式
一開始有一個 \(n\) 項的陣列
- 每次都拆半 \(T(\dfrac n 2)\)
- 分別去排序左右兩個陣列
- 合併 \(O(n)\)
Merge Sort 的運行方式
void merge_sort(int l, int r){
int m = (l+r)/2;
merge_sort(l,m);
merge_sort(m+1,r);
int nxt[r-l+1], p1 = l, p2 = mid+1;
for(int i = 0;i < r-l+1;i++){
if(p1==m){
nxt[i] = arr[p2++];
}else if(p2==m){
nxt[i] = arr[p1++];
}else if(arr[p1] < arr[p2]){
nxt[i] = arr[p1++];
}else{
nxt[i] = arr[p2++];
}
}
for(int i = l;i <= r;i++){
arr[i] = nxt[i-l];
}
}Merge Sort 的時間複雜度
\(T(n) = 2T(\dfrac n 2) + O(n)\)
根據主定理,得到 \(T(n) = O(n \log n)\)
逆序數對
(Inversions)
接下來,我們要定義一個東西叫做 逆序數對
對於一個陣列 \(A\), \(i \le j\) 且 \(a_i > a_j\)
的數對 \((i,j)\) 被稱作逆序數對
例如: \(A=[3,1,2]\),則 \(A\) 的逆序數對為 \((1,3),(2,3)\)
有兩個逆序數對
對於一個陣列 \(A\), \(i \le j\) 且 \(a_i > a_j\)
的數對 \((i,j)\) 被稱作逆序數對
例如: \(A=[3,1,2]\),則 \(A\) 的逆序數對為 \((1,3),(2,3)\)
有兩個逆序數對
而逆序數對的數量,等同於用氣泡排序時交換的次數
逆序數對又可以長成這樣
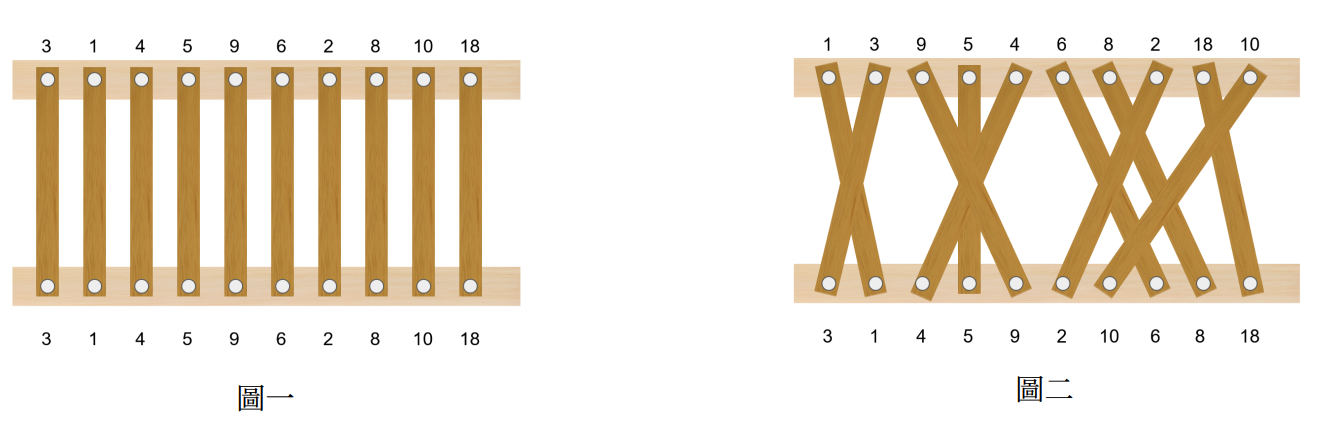
等價於木板的交點數量 (圖取自 TOI 2021 初選pC)
那要怎麼找逆序數對數量呢?
很簡單! 我們直接做一次氣泡排序不就好了嗎?
int cnt = 0;
for(int i = 1;i <= n;i++){
for(int j = 1;j <= n;j++){
if(arr[j] > arr[j+1]){
cnt++;
swap(arr[j],arr[j+1]);
}
}
}不過這樣太慢了,氣泡排序的複雜度是 \(O(n \log n)\)
因此,Merge Sort 就可以派上用場了!
void merge_sort(int l, int r){
int m = (l+r)/2;
merge_sort(l,m);
merge_sort(m+1,r);
int nxt[r-l+1], p1 = l, p2 = mid+1, cnt = 0;
for(int i = 0;i < r-l+1;i++){
if(p1==m){
cnt++;
nxt[i] = arr[p2++];
}else if(p2==m){
nxt[i] = arr[p1++];
}else if(arr[p1] < arr[p2]){
nxt[i] = arr[p1++];
}else{
cnt++;
nxt[i] = arr[p2++];
}
}
for(int i = l;i <= r;i++){
arr[i] = nxt[i-l];
}
}Merge Sort 計算逆序數對
逆序數對練習題
最近點對
(Closest Pair of Points)
請找到最近的兩個點

要在平面上找兩個最近的點
假設點的數量為 \(n\)
那最簡單的方式就是去找每兩個點,然後計算他們的距離
複雜度: \(O(n^2)\)
有沒有更好的做法?
有的! 就是分治!
做法
- 將點先依照 \(x\) 座標排序
- 將平面上的點切成 \(p_l, p_r\)
- 用 Merge Sort 排序點的 \(y\) 座標
- 分別計算 \(p_l,p_r\) 中的最短距離
- 計算跨越 \(p_l, p_r\) 的最短距離
- 注意事項: 最後會切到剩下 \(1 \times 1\) 的正方形,暴力算即可
做法
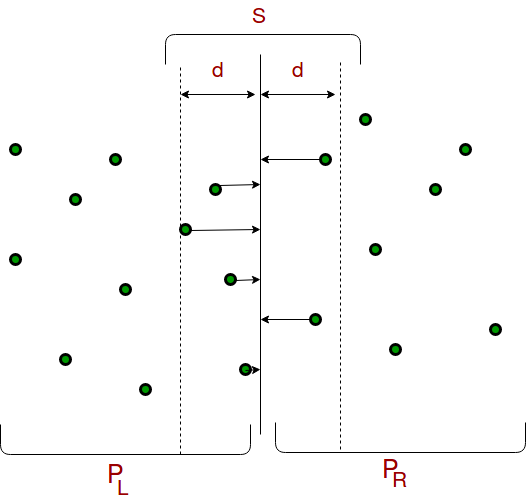
做法
vector<pt> p;
void dc(int l, int r) {
if (r - l <= 3) {
for (int i = l; i < r; ++i) {
for (int j = i + 1; j < r; ++j) {
ans = max(ans,dis(a[i], a[j]));
}
}
sort(a.begin() + l, a.begin() + r, cmp_y());
return;
}
int m = (l + r) >> 1;
int mid = a[m].x;
rec(l, m);
rec(m, r);
merge(a.begin() + l, a.begin() + m, a.begin() + m, a.begin() + r, t.begin(), cmp_y());
copy(t.begin(), t.begin() + r - l, a.begin() + l);
int now;
for (int i = l; i < r; ++i) {
if (abs(a[i].x - mid) < ans) {
for (int j = now - 1; j >= 0 && a[i].y - p[j].y < ans; --j)
ans = mid(ans,dis(a[i], p[j]));
p[now++] = a[i];
}
}
}
void init(){
sort(p.begin(),p.end(),cmp_x());
ans = 1e18;
dc(0,n);
}更多分治的應用
一些常用到的地方
- Karatsuba 演算法 (多項式乘法 \(O(n^{1.58})\))
- 快速傅立葉轉換 Fast Fourier Transform (多項式乘法 \(O(n \log n)\))
- 線段樹 (之後會講到的區間查詢資料結構)
- CDQ 分治 (使用 Merge Sort 做離線區間查詢)
- 整體二分搜 (使用分治去做多次二分搜)