最短路徑
(Shortest Path Algorithm)
找最短路徑?
假設你要從你家走到薇閣
WEGO
假設你要從你家走到薇閣
WEGO
怎麼樣走才是最快的呢?
WEGO

而這就是最短路徑演算法可以使用的地方了!
已經會的方法?
在迷宮中找最短路徑

BFS!
那一般的圖上呢?
如果邊權都是 \(1\)
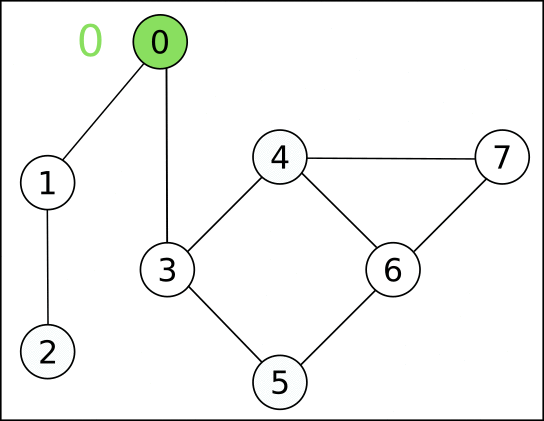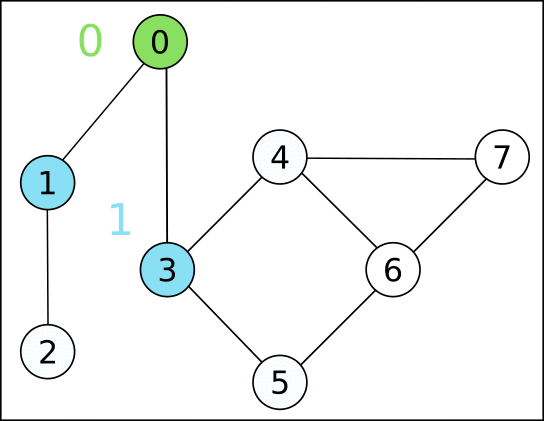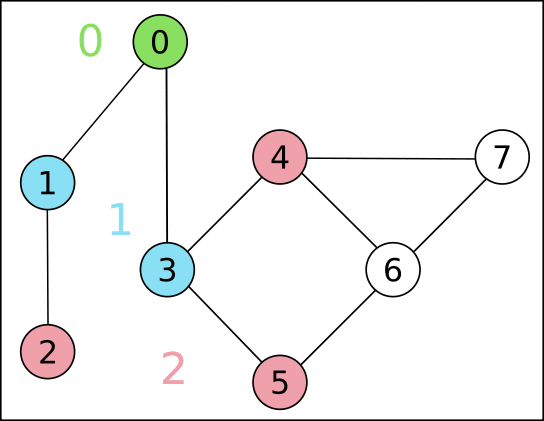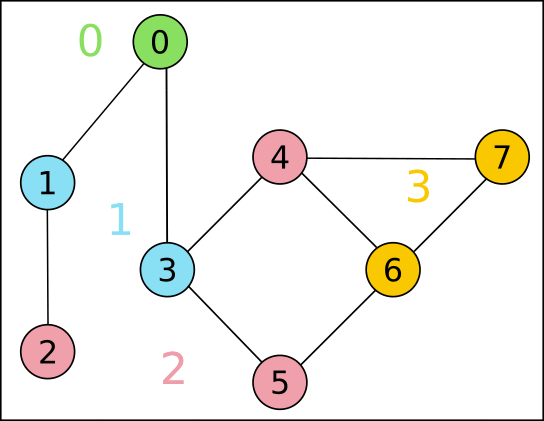
如果邊權只有 0/1 也可以 BFS
Dijkstra's Algorithm

Edsger Wybe Dijkstra
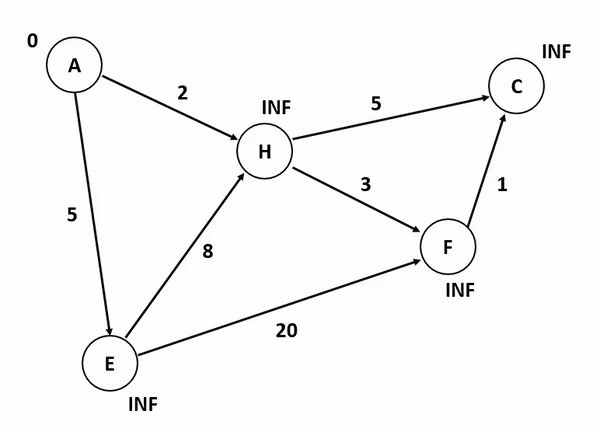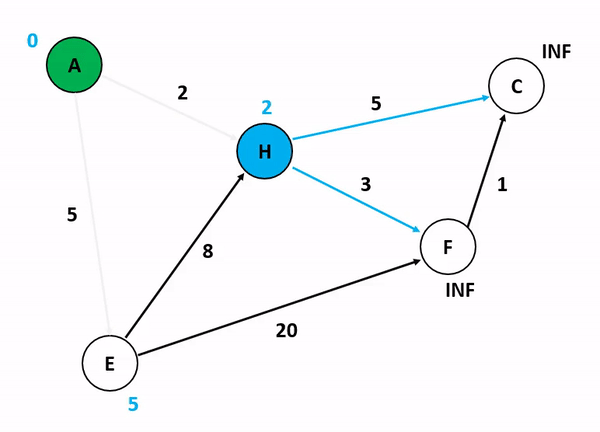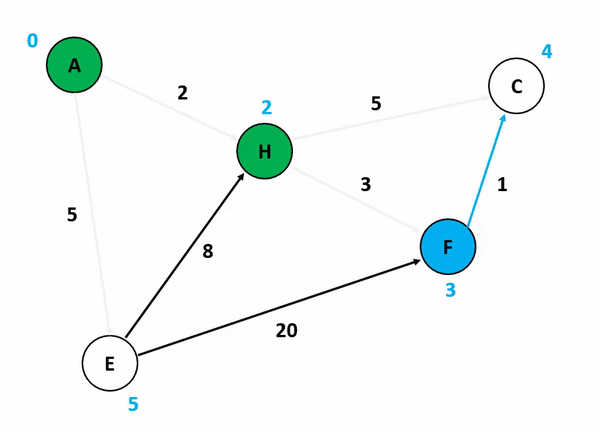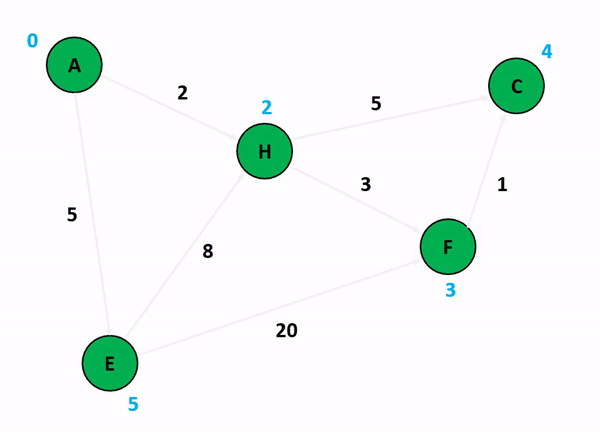
實際跑起來的樣子
那我們來談談他的想法
既然要最短路徑
- 距離如果都是 \(>0\)
- 從已經走到最近的點開始往相鄰的點走?
- 當某個點能夠由更快的方式走到,就蓋過前一個最短路?
既然要最短路徑
- 距離如果都是 \(>0\)
- 從已經走到最近的點開始往相鄰的點走?
- 當某個點能夠由更快的方式走到,就蓋過前一個最短路?
而這,其實就是一種 貪心 演算法!
所以放到程式中,做法依然相同!
Dijkstra 的實作方式
- 開一個 \(dis\) 陣列,\(dis[u]\)表示由起點 \(s\) 到 \(u\) 的最短距離
- 將 \(dis[s]\) 設為 \(0\),而當 \(u \ne s\),將 \(dis[u]\) 設為 \(\infty\)
- 開一個 Min Heap (priority_queue),依照點的距離做排序,並將 \(s\) 先放入
- 每次都拿出 Heap 中最上面的點,依序去鬆弛其他點
- 把鬆弛完的點推進 Heap
鬆弛
if(dis[v] > dis[u] + w){
dis[v] = dis[u] + w;
}
- 開一個 \(dis\) 陣列,\(dis[u]\)表示由起點 \(s\) 到 \(u\) 的最短距離
int N = 1e5+5; //圖上點的數量
int dis[N]; //起點 s 到 u 的距離Dijkstra 的實作方式
int N = 1e5+5; //圖上點的數量
int dis[N]; //起點 s 到 u 的距離
fill(dis,dis+N,INF); //INF 通常會設 10^9 或 10^18
- 開一個 \(dis\) 陣列,\(dis[u]\)表示由起點 \(s\) 到 \(u\) 的最短距離
- 將 \(dis[s]\) 設為 \(0\),而當 \(u \ne s\),將 \(dis[u]\) 設為 \(\infty\)
Dijkstra 的實作方式
int N = 1e5+5; //圖上點的數量
int dis[N]; //起點 s 到 u 的距離
fill(dis,dis+N,INF); //INF 通常會設 10^9 或 10^18
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<>> pq;
pq.push({dis[s],s});
//pair存的是 {點的距離,點}
- 開一個 \(dis\) 陣列,\(dis[u]\)表示由起點 \(s\) 到 \(u\) 的最短距離
- 將 \(dis[s]\) 設為 \(0\),而當 \(u \ne s\),將 \(dis[u]\) 設為 \(\infty\)
- 開一個 Min Heap (priority_queue),依照點的距離做排序,並將 \(s\) 先放入
Dijkstra 的實作方式
int N = 1e5+5; //圖上點的數量
int dis[N]; //起點 s 到 u 的距離
fill(dis,dis+N,INF); //INF 通常會設 10^9 或 10^18
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<>> pq;
pq.push({dis[s],s});
//pair存的是 {點的距離,點}
while(!pq.empty()){
auto [disu, u] = pq.top(); pq.pop();
if(disu > dis[u]) continue; //細節,不加會TLE
for(auto [v,w] : adj[u]){
if(dis[v] > dis[u] + w){
dis[v] = dis[u] + w;
pq.push({dis[v],v});
}
}
}
- 開一個 \(dis\) 陣列,\(dis[u]\)表示由起點 \(s\) 到 \(u\) 的最短距離
- 將 \(dis[s]\) 設為 \(0\),而當 \(u \ne s\),將 \(dis[u]\) 設為 \(\infty\)
- 開一個 Min Heap (priority_queue),依照點的距離做排序,並將 \(s\) 先放入
- 每次都拿出 Heap 中最上面的點,依序去鬆弛其他點
- 把鬆弛完的點推進 Heap
Dijkstra 的實作方式
而這樣做的時間複雜度為
Dijkstra實際上做的事
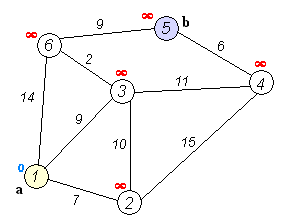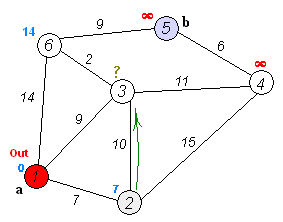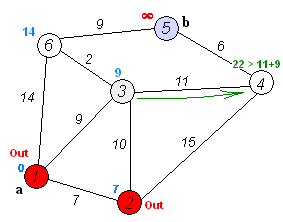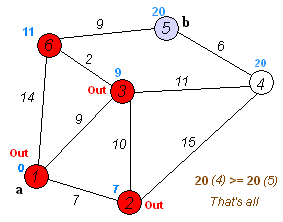
必須強調一點,Dijkstra只能用在沒有負邊的圖上,否則會得到錯誤答案
而且他是單源點的最短路
實際去寫寫看吧!
特殊的最短路
你有 \(n\) 個地區的飛機票價與航程,而你有一張折價券可以讓一次航程打五折,你要從國家 \(1\) 飛到國家 \(n\) ,請問最少要花多少錢?
這題與我們所知的最短路徑問題十分相似
不過多了一個折價券的選擇
會發現我們其實只有一張折價券
意思是到每個點的時候,只有兩種可能
已經用過折價券 或 還沒用過折價券
這裡有個特別的技巧!
建設虛點!
假設今天航班長這樣

價錢寫在圖上
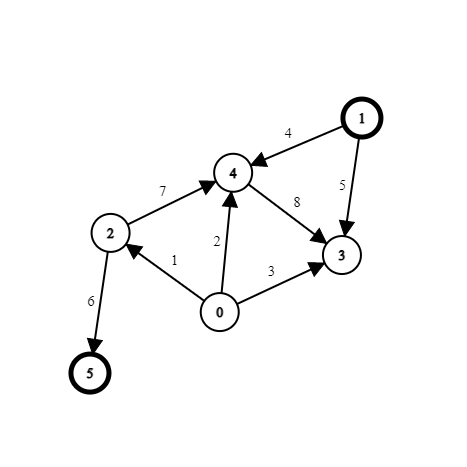
那麼,由於每個點只能有「有/無用過券」兩種可能
我們可以將原圖開兩倍的點,每個點 \(u\) 開成 \(u,u'\)
若原邊有 \(u \rightarrow v\) 則也要加入 \(u \rightarrow v'\)
以及 \(u' \rightarrow v'\)
建邊方式
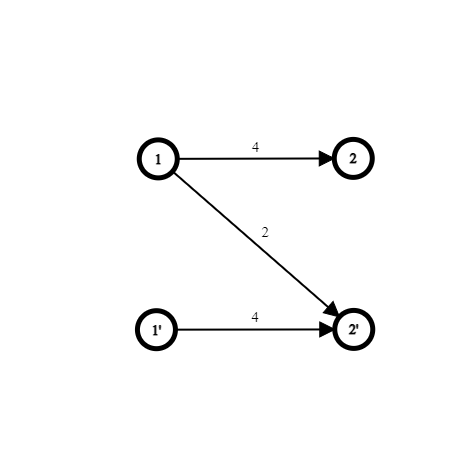
假設原本的航班在使用折價券前 \(u \rightarrow v\) 要花 \(w\) 的時間
使用折價券時,\(u \rightarrow v'\) 要花 \(\lfloor \dfrac w 2 \rfloor\) 的時間
而使用完之後,接下來的航程時間依然相同
因此,只要這樣建邊,做最短路即可
AC
其他Dijkstra練習題
Bellman-Ford
實際跑起來
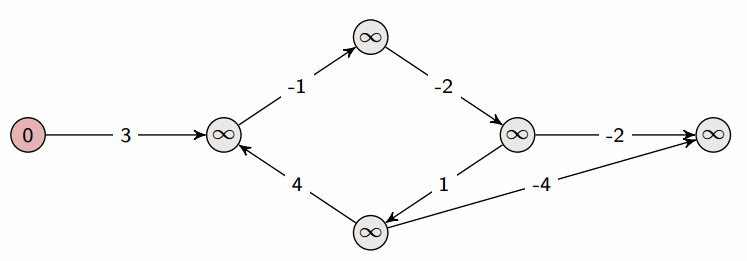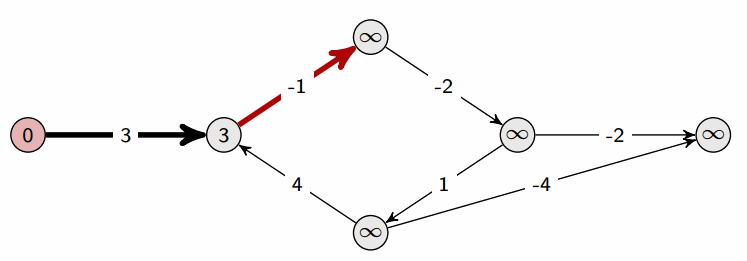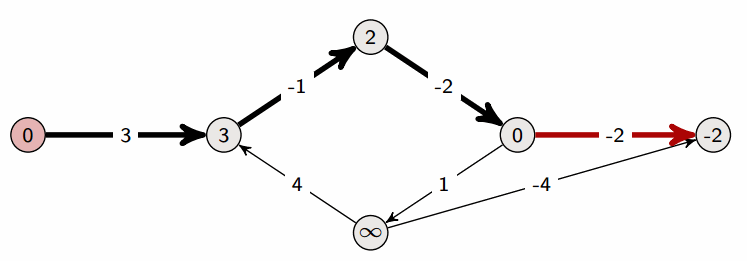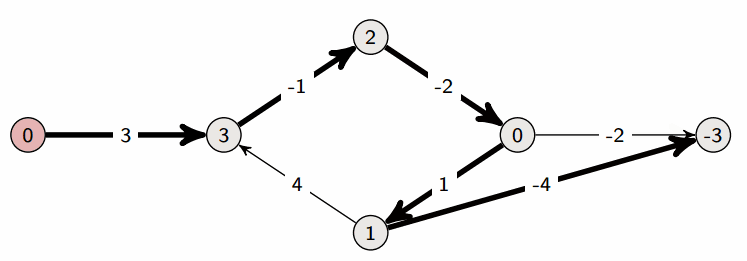
一個特別的地方是,他可以處理有負權的圖
而且可以找圖上有沒有負環
想法很簡單!
既然我們有 \(V\) 個點, \(E\) 條邊
那我們每次都去看一條邊從 \(u\) 走到 \(v\) 會不會比較快
會的話,就更新走到 \(v\) 的最短距離
不會的話,就算了
可以證明只需要做 \(n-1\) 次就可以找到最短距離了
如果還有點可以被更新,那麼圖上有負環
寫法如下
for(int i = 0;i < n-1;i++){
for(auto [u,v,w] : edges){
if(dis[v] > dis[u] + w){
dis[v] = dis[u] + w;
}
}
}
for(auto [u,v,w] : edges){
if(dis[v] > dis[u] + w){
//圖上有負環
}
}時間複雜度
\(O(VE)\)
SPFA
(Shortest Path Faster Algorithm)
他都說他 Faster 了,一定很快吧
你有沒有想過,既然BFS那麼好用
能不能拿來找最短路徑呢?
BFS?
queue<int> q;
q.push(s);
while(!q.empty()){
int u = q.front(); q.pop();
for(auto v : adj[u]){
if(dis[v] > dis[u] + w){
dis[v] = dis[u] + w;
q.push(v);
}
}
}這樣會得到TLE
queue<int> q;
q.push(s);
while(!q.empty()){
int u = q.front(); q.pop();
for(auto v : adj[u]){
if(dis[v] > dis[u] + w){
dis[v] = dis[u] + w;
q.push(v);
}
}
}但這樣呢?
int inqueue[N];
queue<int> q;
q.push(s);
inqueue[s] = true;
while(!q.empty()){
int u = q.front(); q.pop();
inqueue[u] = false;
for(auto v : adj[u]){
if(dis[v] > dis[u] + w){
dis[v] = dis[u] + w;
if(!inqueue[v]) q.push(v);
}
}
}這樣的寫法,可以被證明最差的複雜度會是
意即與 Bellman-Ford 相同
但 SPFA 在通常情況都比較快
而且甚至有可能比 Dijkstra 還快
差分約束
假設今天有四個人
他們各自有一定量的錢
而他們每個人都會跟你說他們四個人之間
所持有的錢的關係
假設今天有四個人
他們各自有一定量的錢
而他們每個人都會跟你說他們四個人之間
所持有的錢的關係
甲: 我所持有的錢比乙多 3 塊以下
乙: 我所持有的錢比丙少 4 塊以下
丙: 我所持有的錢比丁多 5 塊以下
丁: 我所持有的錢比丙少 2 塊以下
要怎麼知道他們是否說謊
假設今天有 4 個變數 \(x_1,x_2,x_3,x_4\)
他們的關係為
假設今天有 4 個變數 \(x_1,x_2,x_3,x_4\)
他們的關係為
請問是否能夠找到一組 \((x_1,x_2,x_3,x_4)\)滿足以上條件
建邊!
有負環 \(\rightarrow\) 產生矛盾
例題
全點對最短路徑
(All Pair Shortest Path)
我們前面講過的三種演算法,都是單源點
那如果今天要找兩兩點之間的距離呢?
此時,要用到全點對的最短路演算法!
最常見的兩種
- Floyd Warshall
- Johnson's Algorithm
但這裡我們只提 Floyd Warshall
Floyd-Warshall
我們講過矩陣乘法了
矩陣乘法的概念寫成數學式會長下面那樣
\(C_{ij} = \sum_{k=1}^n A_{ik} \times B_{kj}\)
想成圖論的話,會很像是去尋找 \(i\) 到 \(j\) 兩點間的路徑數量
枚舉一個中繼點 \(k\),從 \(i\) 走到 \(j\)的路徑數量
可以表達成 (\(i\) 到 \(k\) 的路徑數 \(\times\) \(k\) 到 \(j\) 的路徑數) 總和
但我們今天要找最短路徑
是否也能用類似的概念來做到呢?
是的!
最短路徑用矩陣乘法的寫法會長得像這樣
\(\displaystyle d_{ij} = \min_{k=i}^n d_{ik}+d_{kj}\)
不過是改成取最小值罷了
或者,可以用 DP 的想法
設 \(dp[i][k][j]\) 為從 \(i\) 經過 \(k\) 走到 \(j\) 的最短距離
則我們只要去枚舉 \(k\) 這個點即可!
或者,可以用 DP 的想法
設 \(dp[i][j]\) 為從 \(i\) 經過所有 \(k\) 走到 \(j\) 的最短距離
則我們只要去枚舉 \(k\) 這個點即可!
不過,順序會影響 DP 的答案!
Floyd-Warshall 寫成 Code
for(int k = 1;k <= n;k++){
for(int i = 1;i <= n;i++){
for(int j = 1;j <= n;j++){
dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
}
}
}Floyd-Warshall 寫成 Code
for(int k = 1;k <= n;k++){
for(int i = 1;i <= n;i++){
for(int j = 1;j <= n;j++){
dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
}
}
}等等,這也太短了吧
Floyd-Warshall 寫成 Code
for(int k = 1;k <= n;k++){
for(int i = 1;i <= n;i++){
for(int j = 1;j <= n;j++){
dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
}
}
}短歸短,但順序很重要,一定要記得要是 \(k, i, j\) 的迴圈順序
這樣才會得到正確答案
Floyd-Warshall 寫成 Code
for(int k = 1;k <= n;k++){
for(int i = 1;i <= n;i++){
for(int j = 1;j <= n;j++){
dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
}
}
}短歸短,但順序很重要,一定要記得要是 \(k, i, j\) 的迴圈順序
這樣才會得到正確答案
(嗎?
Floyd-Warshall 錯誤順序?
在以前一直被認為如果 Floyd-Warshall 順序錯了
會 produce 錯誤的答案
不過,在一篇 2019 年的論文當中
有人發現就算順序錯了,也只要多跑幾次即可!
Floyd-Warshall 錯誤順序?
如果迴圈順序是 IJK,那只要跑三次就正確了!
如果迴圈順序是 IKJ,那只要跑兩次就正確了!
很神奇吧! 連順序都不影響正確答案!
時間複雜度: \(O(V^3)\)
跑一次 Floyd-Warshall
會跑三個做 \(V\) 次的迴圈
因此時間複雜度很明顯了!
如果有負環呢?
跑完之後,如果有任何一個點使得 \(d_{ii} < 0\)
則表示有負環
例題
最小環
(Minimum Cycle)
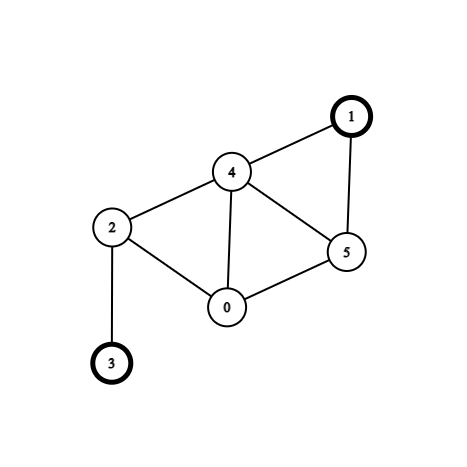
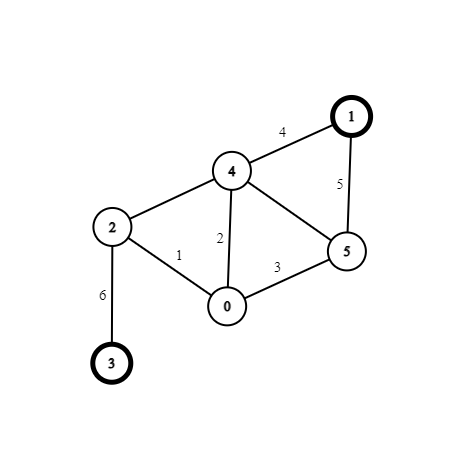
給你一張圖,問最小的環的長度為何?
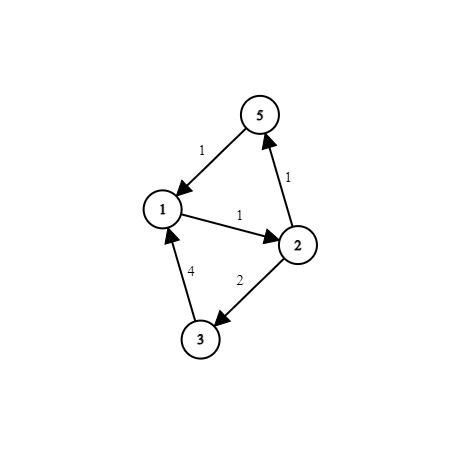
給你一張圖,問最小的環的長度為何?

這裡的最小環為 \(1,2,5\),長度為 \(3\)
這裡有個想法
把每條邊先刪掉之後,以 \(u\) 當起點跑最短路,看 \(d_{uv}\) 是多少,答案會是 \(\min (d_{uv}+w)\)
應該滿合理的對吧
這裡有個想法
把每條邊先刪掉之後,以 \(u\) 當起點跑最短路,看 \(d_{uv}\) 是多少,答案會是 \(\min (d_{uv}+w)\)
應該滿合理的對吧
時間複雜度: \(O(m(n+m)\log(n))\)
把每條邊先刪掉之後,以 \(u\) 當起點跑最短路,看 \(d_{uv}\) 是多少,答案會是 \(\min (d_{uv}+w)\)
時間複雜度: \(O(E(V+E)\log(V))\)
不過,當這張圖是完全圖呢?
\(E\) 最多有可能會是 \(\dfrac{V(V-1)}{2}\)
複雜度會變成 \(O(V^4 \log V)\)
就算使用在完全圖上的 Dijkstra
複雜度也會是 \(O(V^4)\)
因此換個想法,如果我們邊找最短路邊做呢?
因此換個想法,如果我們邊找最短路邊做呢?
也就是當我們在使用 Floyd-Warshall 時,順便去更新最小環
因此換個想法,如果我們邊找最短路邊做呢?
也就是當我們在使用 Floyd-Warshall 時,順便去更新最小環
for(int k = 1;k <= n;k++){
for(int i = 1;i <= n;i++){
for(int j = 1;j <= n;j++){
ans = min(ans,dis[i][j]+e[i][k]+e[k][j]); //e 是 i,j 之間的邊權
}
}
for(int i = 1;i <= n;i++){
for(int j = 1;j <= n;j++){
dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
}
}
}