DP 優化
目錄
矩陣快速冪
單調隊列優化
斜率優化
四邊形優化
分治優化
Aliens 優化
矩陣快速冪優化
(Matrix Exponentiation Optimization)
經典例題
有一個 \(n\) 階的階梯,你每次可以走 \(1\) 或 \(2\) 階
問總共有幾種走法?
\(dp[i] = dp[i-1]+dp[i-2]\)
費氏數列! 我們可以在 \(O(n)\) 的時間解決
然後你仔細看題目:
\(n \le 10^{18}\)
使用矩陣乘法來優化轉移過程!
矩陣 (Matrix)
\(\begin{bmatrix}a_{11} & \cdots & a_{1n} \\ \vdots & \ddots & \vdots \\ a_{m1} & \cdots & a_{mn}\end{bmatrix}\)
兩個矩陣 \(A,B\) 相乘得到的 \(C\)
\(c_{ij}=a_{ik} \times b_{kj}\)
兩個矩陣 \(A,B\) 相乘得到的 \(C\)
\(c_{ij}=a_{ik} \times b_{kj}\)
舉例:
\(\begin{bmatrix}1 & 2 \\ 3 & 4\end{bmatrix} \begin{bmatrix}1 & 3 \\ 2 & 4 \end{bmatrix} \)
\(\begin{bmatrix}1 \times 1 + 2 \times 2 & 1 \times 3 + 2 \times 4 \\ 3 \times 1 + 4 \times 2 & 3 \times 3 + 4 \times 4\end{bmatrix}\)
\(dp[i] = dp[i-1]+dp[i-2]\)
回到原本的轉移式
而我們知道 \(dp[1] = 1, dp[0] = 1\)
會發現其實可以將其寫為
\(\begin{bmatrix} dp[i] \\ dp[i-1] \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} dp[i-1] \\ dp[i-2] \end{bmatrix}\)
因此,我們會得到以下的結論
\(\begin{bmatrix} dp[n] \\ dp[n-1] \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}^{n-1} \begin{bmatrix} dp[1] \\ dp[0] \end{bmatrix}\)
使用快速冪,即可在 \(O(2^3 \log n)\) 做完
而這樣的優化方式可以被使用在任何形如
\(dp[i] = a_1 dp[i-1] + a_2 dp[i-2] + \ldots\)
的轉移式
這種轉移式,被稱為「線性遞迴」
另一種常見的矩陣快速冪應用
給你一個有向圖,問從 \(u\) 開始走了 \(k\) 步
有幾種到達 \(v\) 的路徑?
另一種常見的矩陣快速冪應用
給你一個有向圖,問從 \(u\) 開始走了 \(k\) 步
有幾種到達 \(v\) 的路徑?
我們可以設 DP 狀態為
\(dp[u][v][k]\) 表示從 \(u\) 到 \(v\) 走了 \(k\) 步的路徑數
另一種常見的矩陣快速冪應用
給你一個有向圖,問從 \(u\) 開始走了 \(k\) 步
有幾種到達 \(v\) 的路徑?
發現到在鄰接矩陣中
\(A_{ij}\) 代表的意義與 \(i\) 走 \(1\) 步到 \(j\) 到路徑數概念是一樣的
我們直接將其變成 \(A^k\),那麼 \((A^k)_{uv}\) 即為答案
練習題
單調隊列優化
(Monotonic Queue Optimization)
回想一下,在基礎資結的時候
我們曾經介紹過一種方式可以計算以下的題目
Sliding Minimum
給你一個 \(n\) 項的陣列
請依序輸出長度為 \(k\) 的子陣列中區間的最小值
Sliding Minimum
給你一個 \(n\) 項的陣列
請依序輸出長度為 \(k\) 的子陣列中區間的最小值
作法
1. 依序從左到右開始做
2. 維護一個 deque,最前面存的是 sliding window 的最小值
Sliding Minimum
| 5 | 3 | 2 | 4 | 1 |
|---|
\(k = 4\)
Deque
Sliding Minimum
| 5 | 3 | 2 | 4 | 1 |
|---|
\(k = 4\)
Deque
| 5 |
|---|
Sliding Minimum
| 5 | 3 | 2 | 4 | 1 |
|---|
\(k = 4\)
Deque
| 3 |
|---|
Sliding Minimum
| 5 | 3 | 2 | 4 | 1 |
|---|
\(k = 4\)
Deque
| 2 |
|---|
Sliding Minimum
| 5 | 3 | 2 | 4 | 1 |
|---|
\(k = 4\)
Deque
| 2 | 4 |
|---|
輸出 2
Sliding Minimum
| 5 | 3 | 2 | 4 | 1 |
|---|
\(k = 4\)
Deque
| 1 |
|---|
輸出 1
那我們要如何將這個概念放到 DP 轉移上呢?
同樣來看一個經典例題
走階梯
今天有一個 \(n\) 階的階梯
每一階上面有一個權值 \(v_i\)
你每次可以走 \(1 \sim k\) 階
問最小可以拿到的權值為何
測資範圍:
\(1 \le k \le n \le 10^6\)
\(|v_i| \le 10^9\)
走階梯
觀察到,我們可以很輕易的將原本的轉移式寫成
\(dp[i] = \max\limits_{j=i-k}^{i-1}(dp[j]) + v_i\)
發現到 \(k\) 是固定的,因此可以用單調隊列
在 \(O(n)\) 的時間完成轉移
單調隊列優化的題目
有時候使用 pq 等資結進行優化 照樣能夠通過
複雜度較差,但題目通常不會故意卡 (?
練習題
斜率優化
(Convex Hull Trick)
「凸包優化」、「CHT」都是同個東西
斜率優化
通常 DP 的轉移式會長的像這樣
\(dp[i] = c_i + \max\{a_j x_i + b_j\}\)
也就是直線的形式
斜率優化
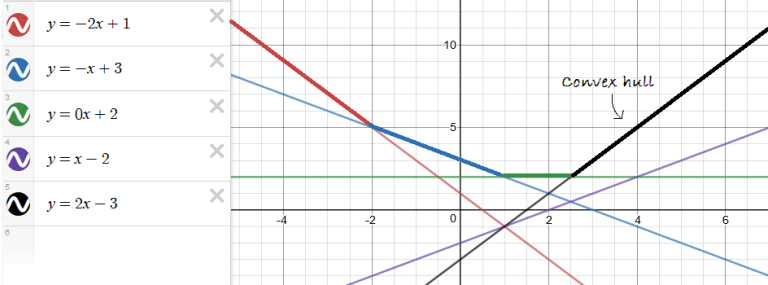
(圖取自 CF)
會發現很多個直線在某個 \(x\) 時的最大值
他們會形成一個下凸包
斜率優化
而斜率優化主要分成幾種
1. 斜率單調、轉移點單調
2. 斜率不單調、轉移點單調
3. 斜率不單調、轉移點不單調
斜率單調、轉移點單調
有 \(n\) 個關卡,你有一個技能值 \(x\)
在某個關卡,打敗該關卡怪物的時間為 \(s_i x\)
而你的技能值會變為 \(f_i\)
在途中,你可以選擇逃跑或打怪物
不過最後一關的怪物一定要打
問最少要花多少時間,才能通過這個遊戲
\(n \le 2 \times 10^5\)
\(x > f_1 > f_2 > \ldots > f_n\)
\(s_1 < s_2 < \ldots < s_n\)
我們可以設 dp 狀態為
也就是很多個斜率是 \(f_j\),截距是 \(dp[j]\) 的直線
由於斜率都是單調的
我們可以觀察到,我們可以用單調隊列維護
而當詢問也是單調時,有什麼特別的性質呢?
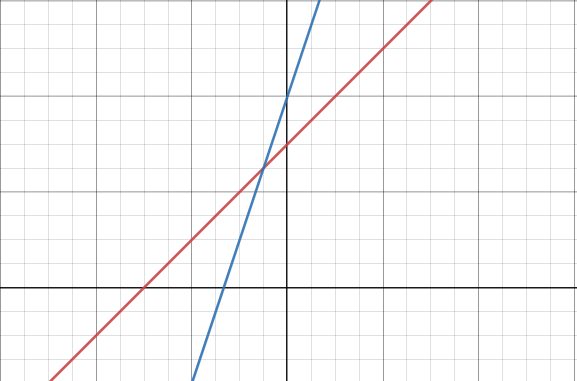

發現到,斜率比較大的直線(藍)
會在某一個時間點 \(x\) 時,超越斜率小的

如果在當前的詢問
在要加入的直線大於 deque 最後方的直線
就將 deque pop back!
這題就可以使用單調隊列在 \(O(n)\) 完成了!
參考程式碼
這題就可以使用單調隊列在 \(O(n)\) 完成了!
不過,斜率或轉移點不單調怎麼辦?
想想看,在尋找某個區間的最大值時
我們會使用什麼樣的資結來達到這一點呢?
線段樹!
如果有個方便的資料結構
可以讓我們隨時增加新的直線
並詢問在 \(x\) 時的答案
我們是不是就能很輕易的做完斜率優化了呢?
李超線段樹
(Li Chao Segment Tree)
李超線段樹是一種很方便的資結
他可以支援以下兩種操作
1. 插入一個直線 \(ax+b\)
2. 詢問在某個位置 \(x\) 時,已插入的直線在該位置的最大值
實際上的寫法也與正常的線段樹非常相似
讓我們來看看要怎麼寫李超線段樹
李超線段樹
李超線段樹,實際上就是一棵存直線的線段樹
因此,我們會先寫出
struct line{
int m, b;
bool operator () (int x){
return m*x+b;
}
};
line tr[N<<2];李超線段樹
在插入直線時,寫法與單點修改線段樹很像
我們依序從中間開始切開某個區間
然後去比較兩條直線
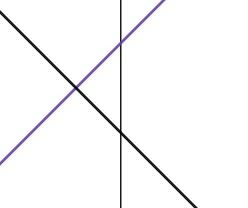
(紫色的線是我們要加入的,黑色是已經在裡面的)
李超線段樹

發現紫色的線在 mid 的值 > 黑色
就把區間的直線替換成紫線
然後我們將黑線往左邊的區間丟包
李超線段樹
其他的 Case 也很類似
寫成 code 會變成底下這樣
void insert(Line seg, int idx = 1, int l = 0, int r = N){
if(l==r){
if(seg(l) > tr[idx](l)) tr[idx] = seg;
return;
}
int mid = l+r>>1;
if(tr[idx].m > seg.m) swap(tr[idx],seg);
if(tr[idx](mid) < seg(mid)){
swap(tr[idx],seg);
insert(seg, idx<<1, l,mid);
}else{
insert(seg, idx<<1|1, mid+1,r);
}
}李超線段樹
詢問的話,與單點修改的線段樹非常像
int query(int x, int idx = 1, int l = 0, int r = N-1){
if(l==r) return tr[idx](x);
int mid = l+r>>1;
if(x <= mid) return max(tr[idx](x), query(x, idx<<1, l, mid));
else return max(tr[idx](x),query(x,idx<<1|1,mid+1,r));
}李超線段樹
而整棵樹就會長的像這樣
const int N = 5e5+5, INF = 1e18;
struct Line{
int m,b;
int operator()(int x) {
return m*x+b;
}
};
Line tr[N<<2];
void insert(Line seg, int idx = 1, int l = 0, int r = N-1){
if(l==r){
if(seg(l) > tr[idx](l)){
tr[idx] = seg;
}
return;
}
int mid = l+r>>1;
if(tr[idx].m > seg.m) swap(tr[idx],seg);
if(tr[idx](mid) < seg(mid)){
swap(tr[idx],seg);
insert(seg,idx<<1,l,mid);
}else insert(seg,idx<<1|1,mid+1,r);
}
int query(int x, int idx = 1, int l = 0, int r = N-1){
if(l==r) return tr[idx](x);
int mid = l+r>>1;
if(x <= mid) return max(tr[idx](x), query(x, idx<<1, l, mid));
else return max(tr[idx](x),query(x,idx<<1|1,mid+1,r));
}