Basic Graph Theory

UMD CP Club Summer CP Week 6

What is a Graph?

Graph Terminology

A graph \(G = (V,E)\) is a structure consisting of a vertex set \(V\) and edge set \(E\)

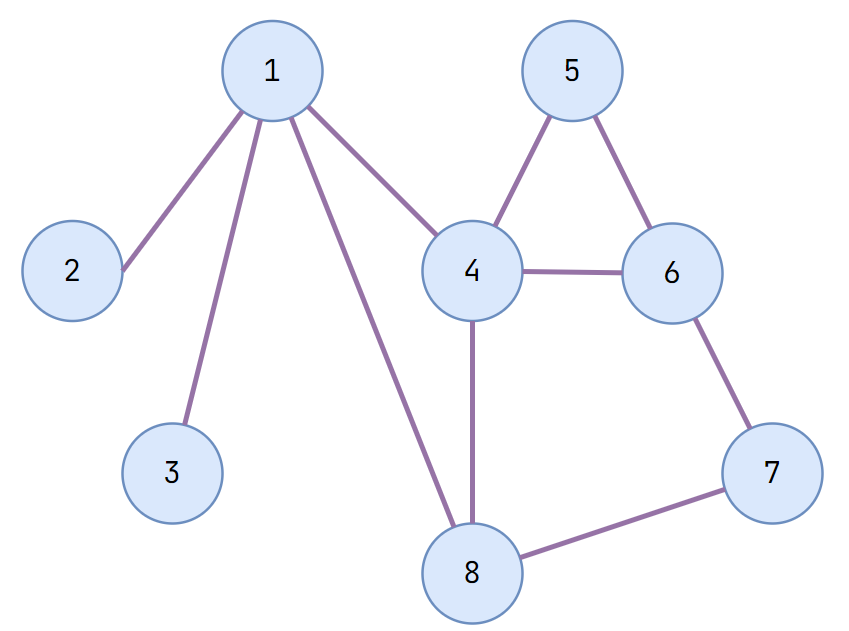
Graph Terminology

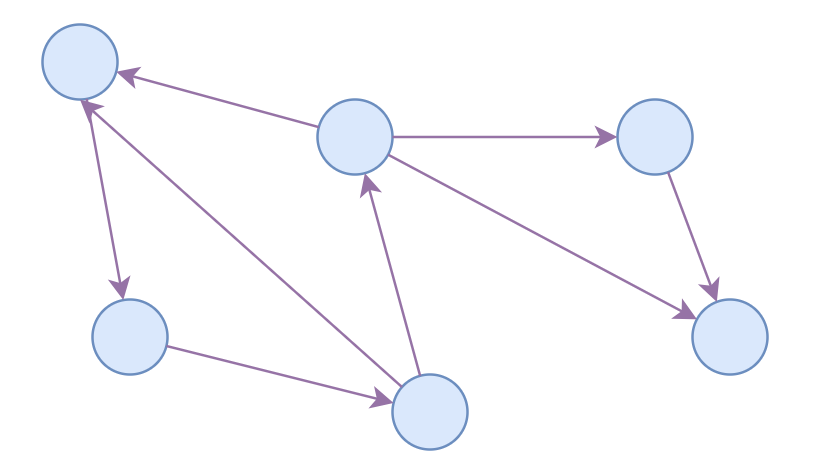
Directed Graph

Undirected Graph

Graph Terminology

There can be weight on edges, and we call the graph weighted

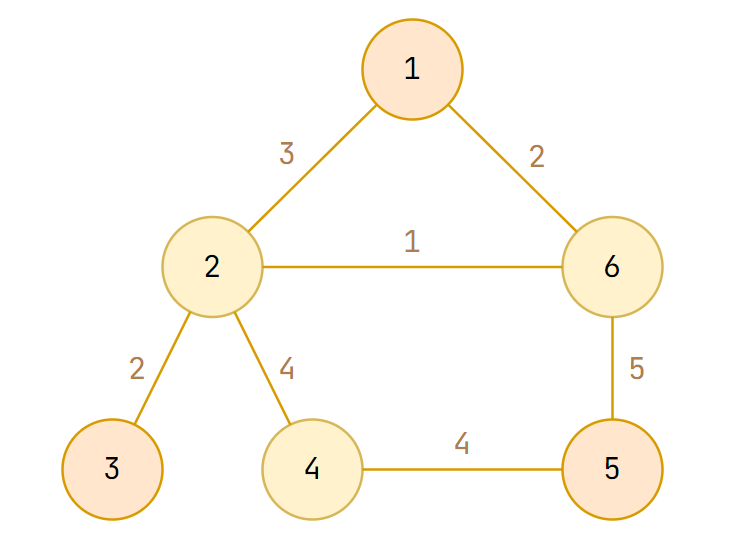
Graph Terminology

An outdegree of a vertex \(u\) is the number of edge in a form of \((u,v)\)

An indegree of a vertex \(u\) is the number of edge in a form of \((v,u)\)

An degree of a vertex \(u\) is the number of edges incident to \(u\)

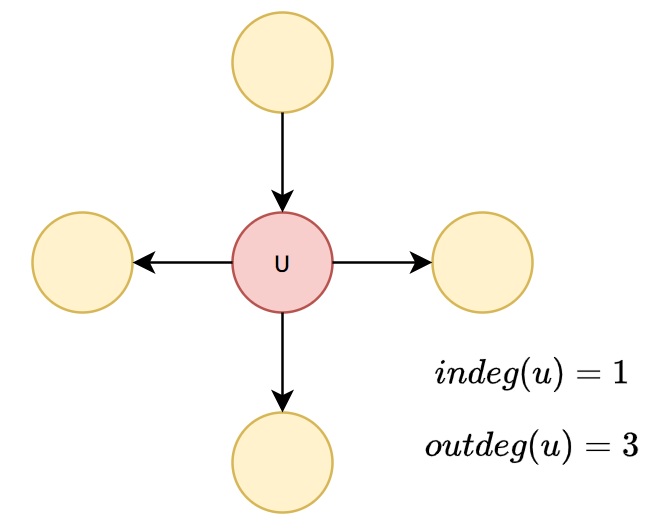
Graph Terminology

  • A path is a sequence of vertices \(v_1, v_2, \cdots, v_n\)
  • A simple path does not include repeating vertices
  • A cycle is a path that starts and ends with same vertex
  • A circuit is a cycle that goes through all vertices 

Graph Terminology

Two vertices \(u,v\) are connected if you can reach \(v\) from \(u\) and \(u\) from \(v\)

The connected components are the set of vertices that are connected 

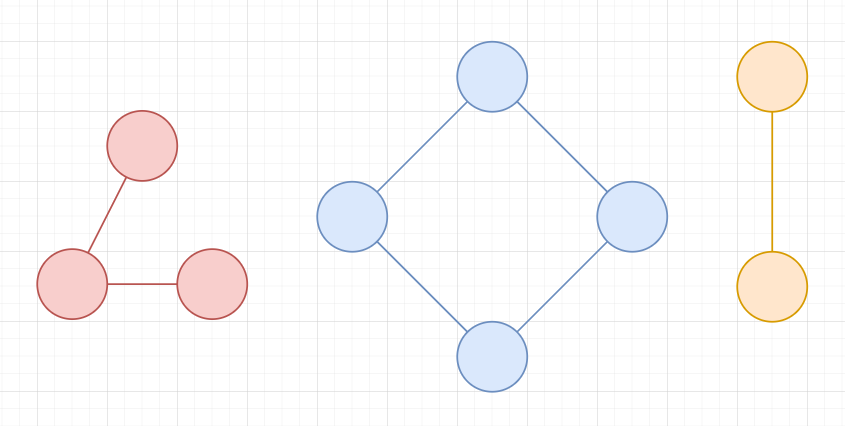
Graph Terminology

Two vertices \(u,v\) are connected if you can reach \(v\) from \(u\) and \(u\) from \(v\)

The connected components are the set of vertices that are connected 

Graph Terminology

A tree is a connected graph without cycles, it can be rooted or not

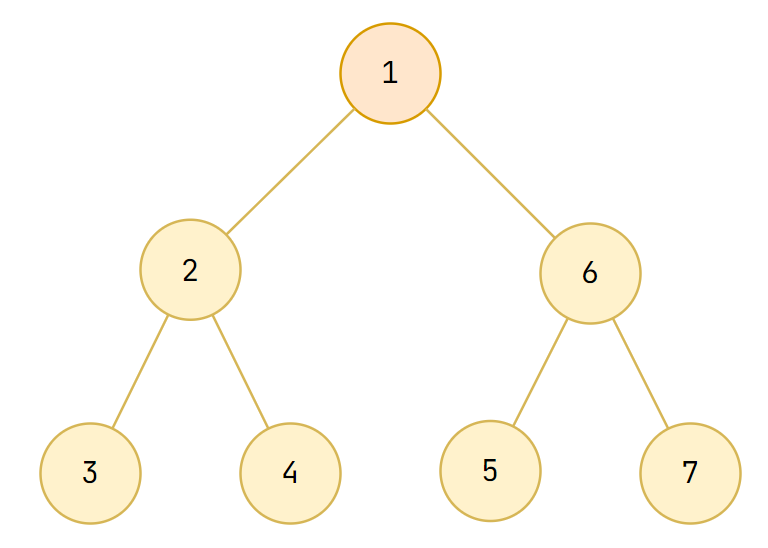
Graph Terminology

A directed acyclic graph (DAG) is a directed graph without cycles

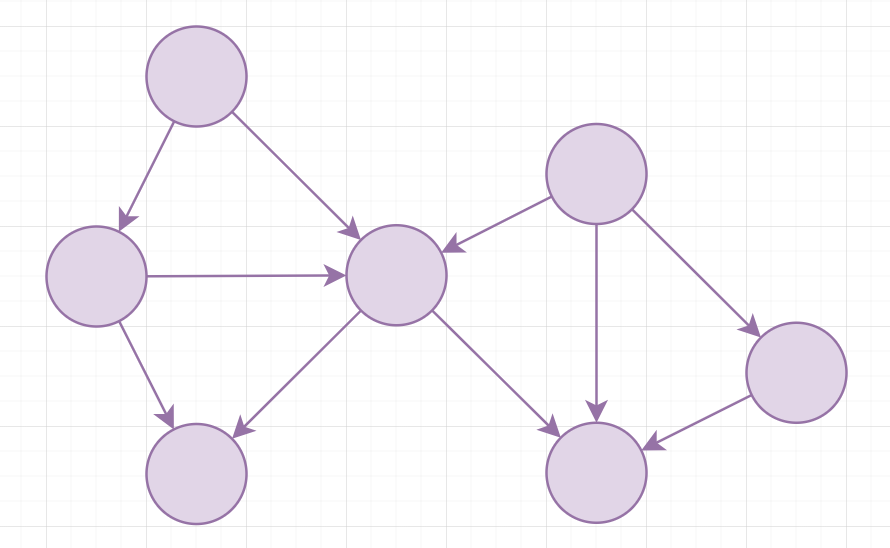
It is possible to find a topological order

Graph Terminology

A functional graph is a directed graph where all vertices has outdegree exactly 1

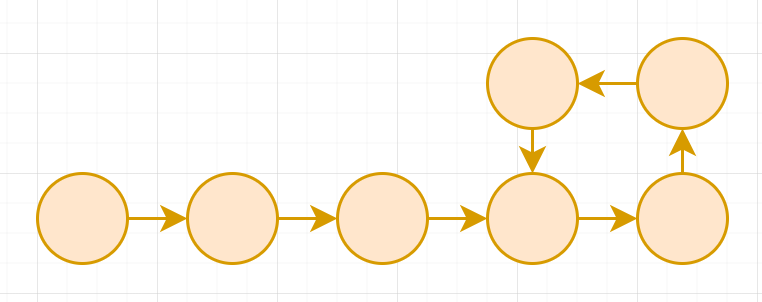
A permutation can be drawn into a functional graph

Graph Terminology

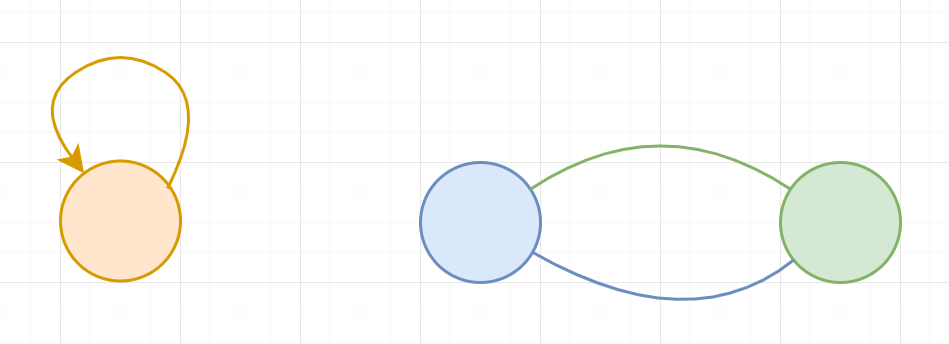
A simple graph is a graph that does not contain self loops or multi-edge

How to store Graphs

What do we want?

Suppose you are given a graph, and you want to know whether two vertices are adjacent, how will you do it?

A Simple Solution

Let's start an 2D Array \(A\), and we call it the adjacency matrix

A[u][v] = \begin{cases} 1 &, \text{ if } u,v \text{ are connected} \\ 0 &, \text{ otherwise} \end{cases}

A Simple Solution

Let's start an 2D Array \(A\), and we call it the adjacency matrix

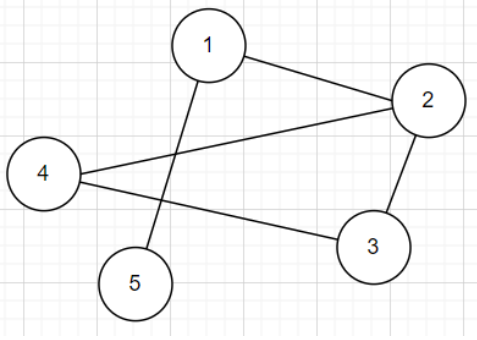
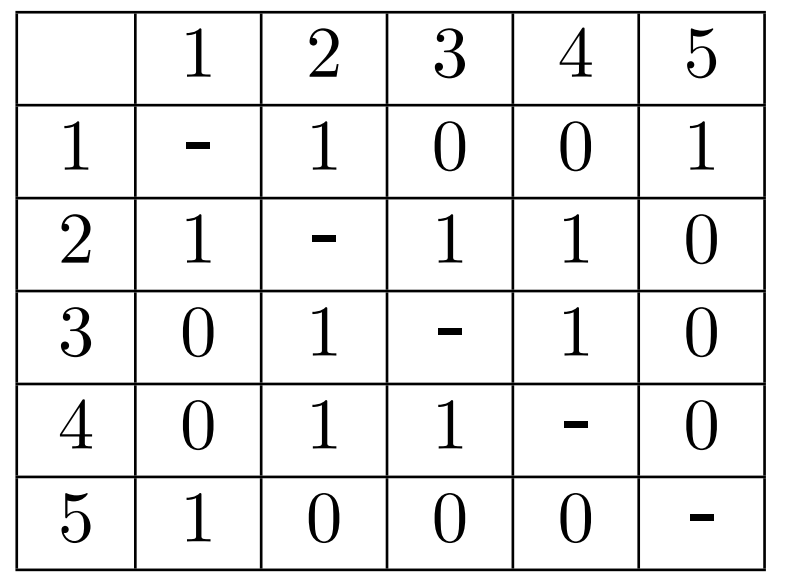
A Simple Solution

This enables us to know whether \(u,v\) are adjacent in \(O(1)\), but it requires \(O(|V|^2)\) space

An Arising Problem

While the previous way makes it easy to know whether two vertices are adjacent

It is actually not too useful for us later on

An Arising Problem

Is there a way to reduce memory usage?

Adjacency List

Consider storing an array of lists \(A\), and \(A[u]\) stores all \(v\) connected to \(u\)

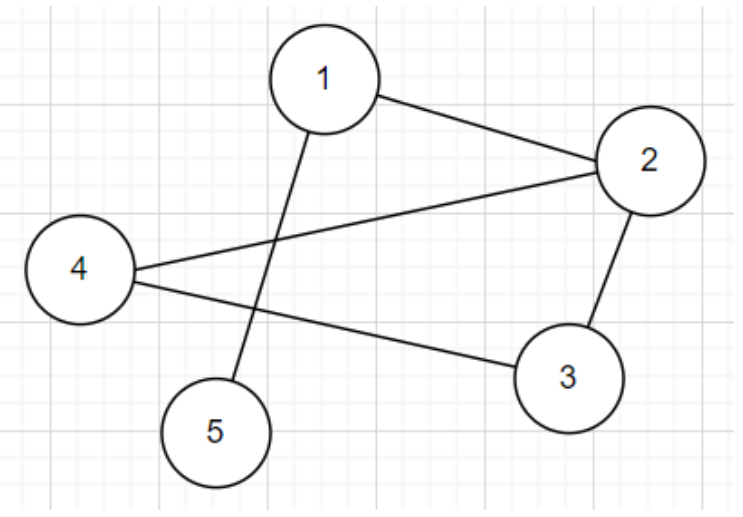
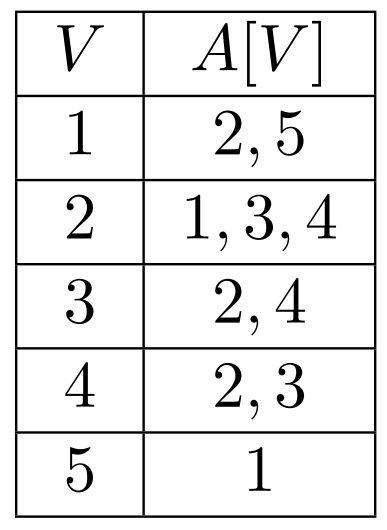
Adjacency List

This makes finding whether \(u, v\) are connected into \(O(|V|)\)

But it will make traversing the graph easier

Code

const int N = 5005;
int adj[N][N];

int main(){
    int n,m;
    cin >> n >> m;
    for(int i = 0; i < m; i++){
        int u,v;
        cin >> u >> v;
        adj[u][v] = 1;
        adj[v][u] = 1; //if undirected
    }
}

Adjacency Matrix

const int N = 1e6+5;
vector<int> adj[N];

int main(){
    int n,m;
    cin >> n >> m;
    for(int i = 0; i < m; i++){
        int u,v;
        cin >> u >> v;
        adj[u].push_back(v);
        adj[v].push_back(u); //if undirected
    }
}

Adjacency List

Graph Traversal

Graph Traversal

There are two ways of doing graph traversal

 

DFS (Depth First Search)

 

BFS (Breath First Search)

Depth First Search

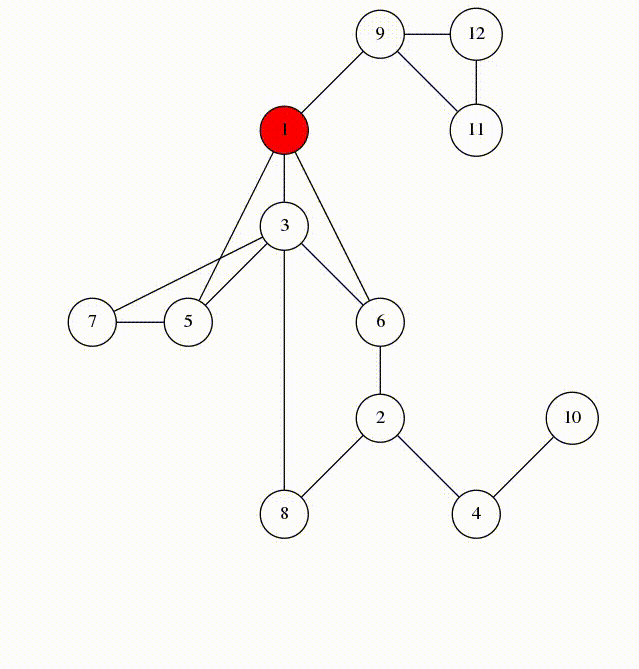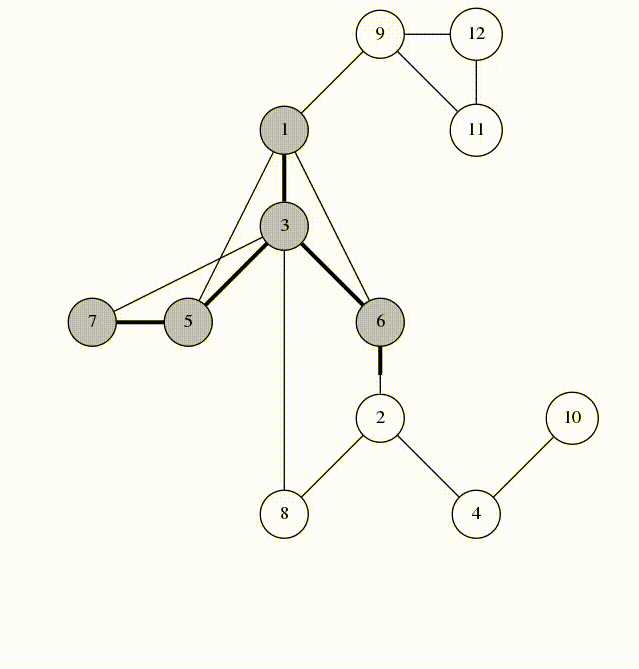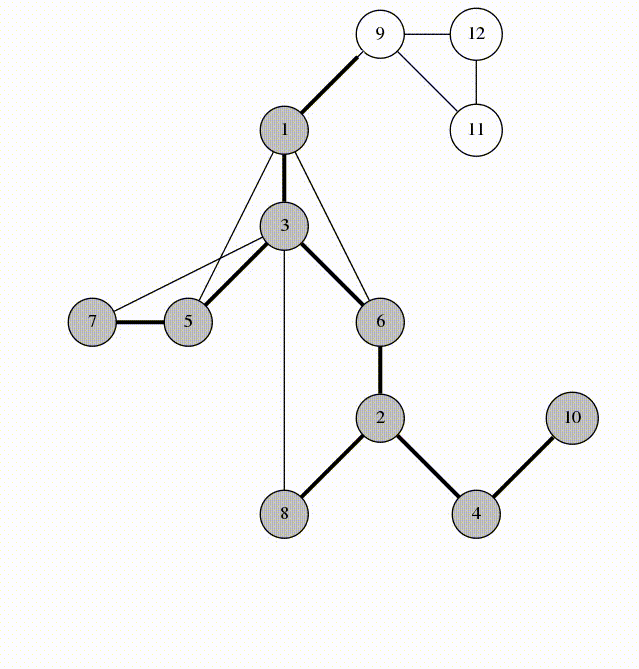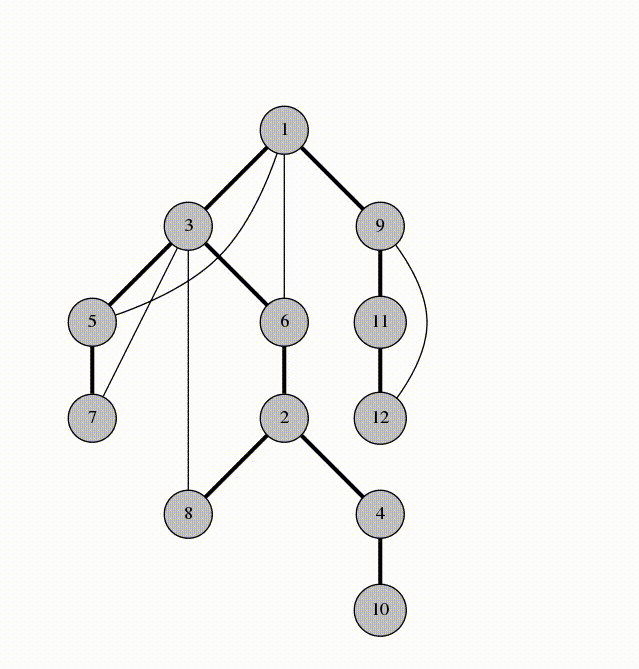
We will visit by depth, the idea is similar to using a stack

animation from codeforces

Depth First Search

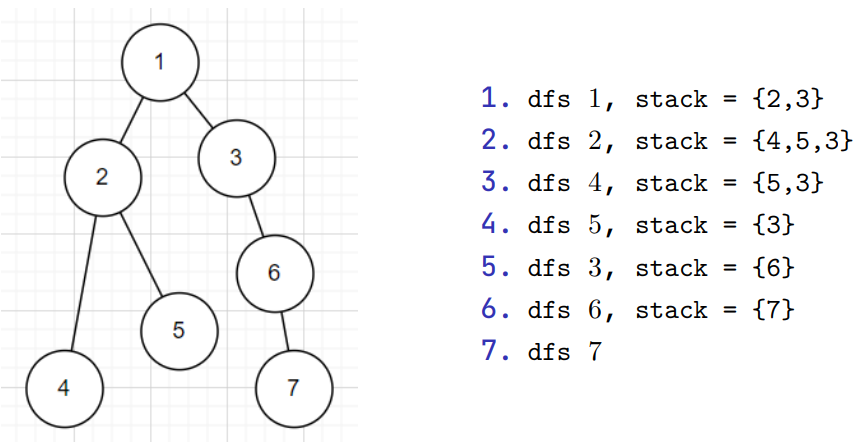
Depth First Search

void dfs(int u){
    visited[u] = true;
    for (int v = 1; v <= n; v++){
        if (!adj[u][v] || visited[v]) continue;
        dfs(v, u);
    }
}

DFS using an adjacency matrix

Time Complexity: \(O(|V|^2)\)

Depth First Search

void dfs(int u){
    visited[u] = true;
    for (int v : adj[u]){
        if (visited[v]) continue;
        dfs(v, u);
    }
}

DFS using an adjacency list

Time Complexity: \(O(|V| + |E|)\)

Breath First Search

For breath first search, we search the vertices closest to the starting vertex

We usually use a queue to do this

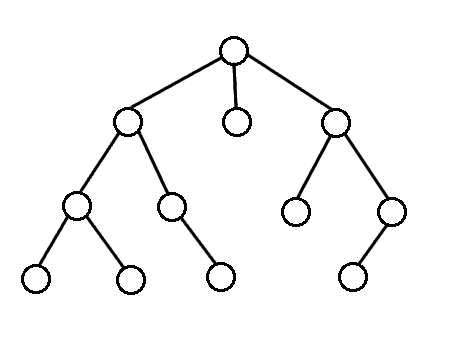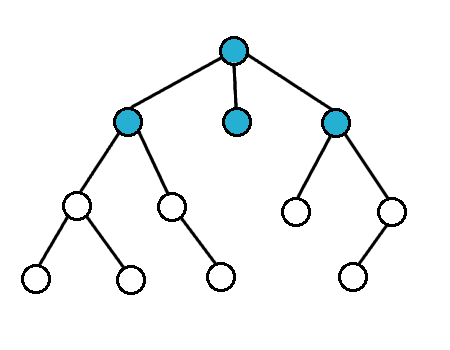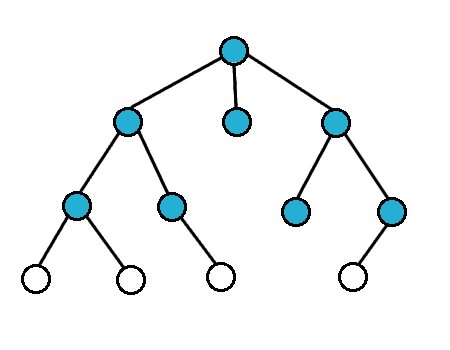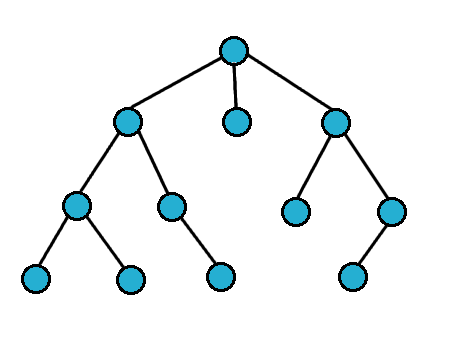
Breath First Search

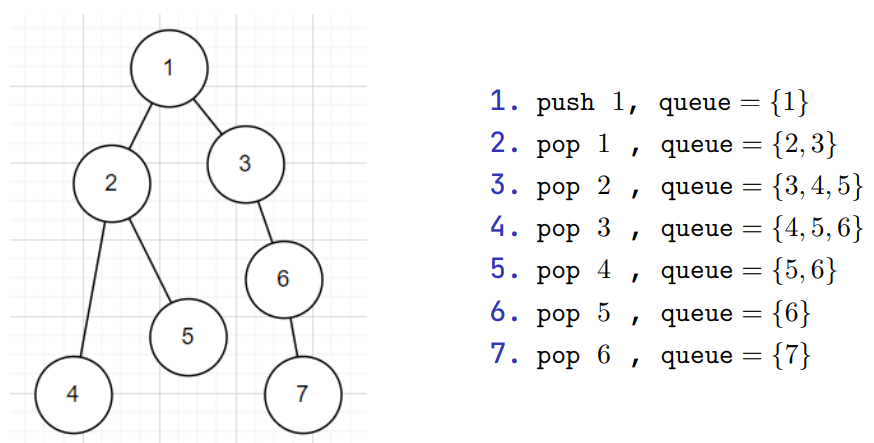
Breath First Search

queue<int> q;
q.push(1);
while(!q.empty()){
    int u = q.front(); q.pop();
    for(int v = 1; v <= n; v++){
        if(!adj[u][v] || visited[v]) continue;
        q.push(v);
    }
}

BFS with adjacency matrix

Time Complexity: \(O(|V|^2)\)

Breath First Search

queue<int> q;
q.push(1);
while(!q.empty()){
    int u = q.front(); q.pop();
    for(int v : adj[u]){
        if(visited[v]) continue;
        q.push(v);
    }
}

BFS with adjacency list

Time Complexity: \(O(|V| + |E|)\)

Some Practice Problems

Bipartite Coloring

A bipartite graph is a graph where you can color the vertices into two colors where no adjacent vertices has same color

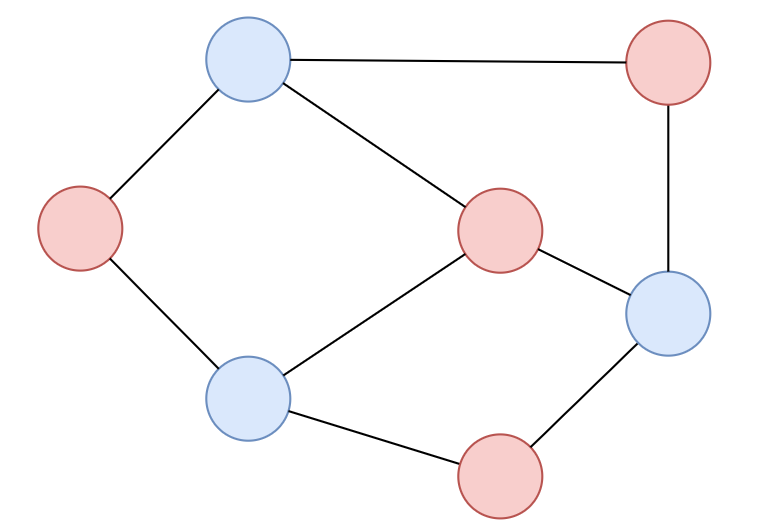
Bipartite Coloring

Fix a vertex, and try coloring the vertices

If there exists some conflicts, then the graph is not bipartite 

Eulerian & Hamiltonian Circuit

Eulerian Graph

Can you draw a graph in one pen stroke without going through same edges

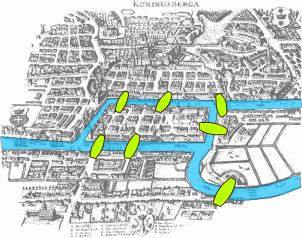
Eulerian Graph

  • Eulerian Path: A path that visits all edge but does no have repeating edges
  • Eulerian Circuit: Eulerian Path but starts and ends at same vertex
  • Chinese Postman Problem: Find the shortest eulerian path (weighted graph)

Eulerian Graph

You can prove a conclusion

  • If a connected graph has exactly \(0\) odd degree vertices \(\implies\) Has Eulerian Circuit
  • If a connected graph has exactly \(2\) odd degree vertices \(\implies\) Has Eulerian Path
  • If a connected graph has \(> 2\) odd degree vertices \(\implies\) not Eulerian

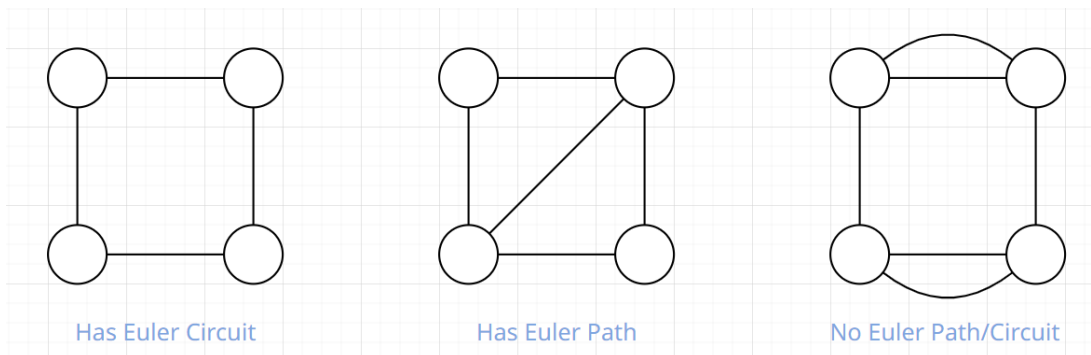
How to Find Eulerian Path?

  • If there are exactly \(0\) odd degree vertices \(\implies\) start from any vertex, you will always find an Eulerian circuit
  • If there are exactly \(2\) odd degree vertices \(\implies\) start from any odd degree vertex, you will always find an Eulerian path

Hamiltonian Graph

  • Hamiltonian Path: A path that visits all vertices but does no have repeating vertex
  • Hamiltonian Circuit: Hamiltonian Path but starts and ends at same vertex
  • Travelling Saleman Problem: Find the shortest Hamiltonian Path (weighted graph)

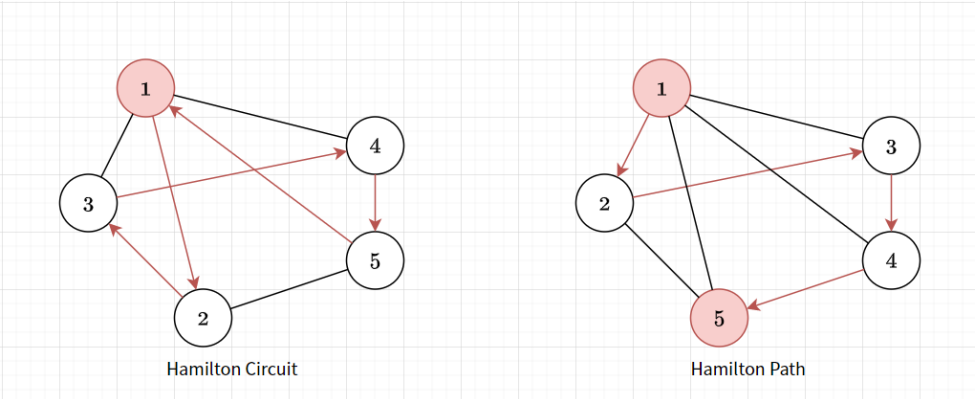
Hamiltonian Graph

There is no easy way to find Hamiltonian Path/Circuit

Usually we will have to use Bitmask DP to solve problems related to this

DAG & Topological Sort

Topological Order of DAG

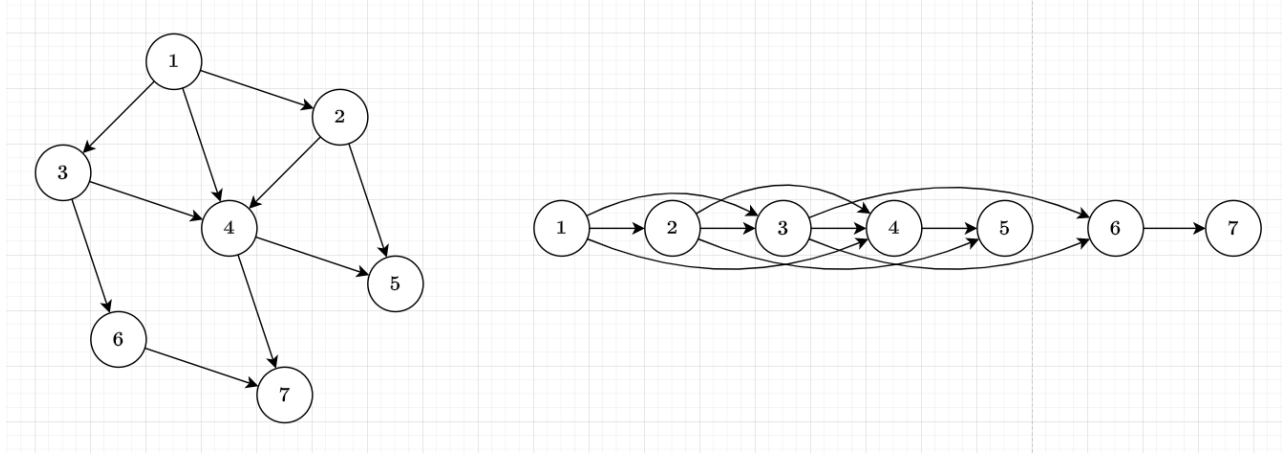
Topological Order of DAG

Think about taking courses in university

Some classes have prerequisites, then we can draw it into a graph

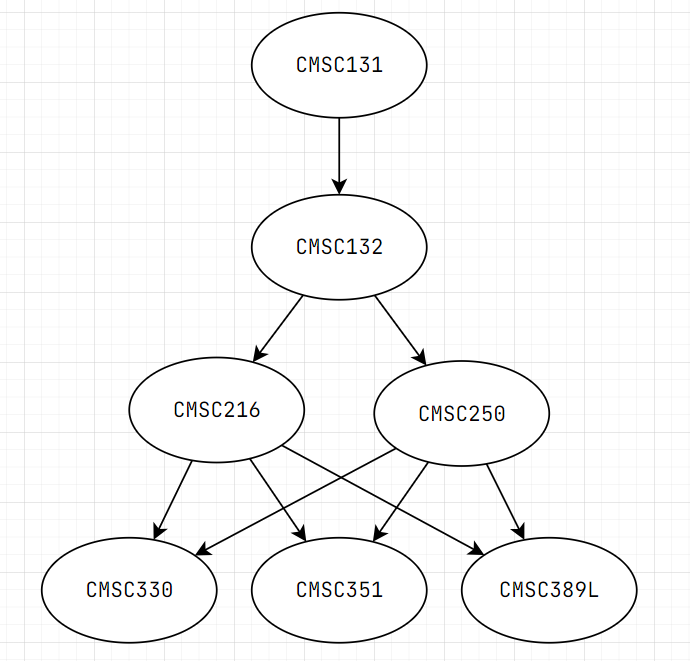
Topological Order of DAG

Therefore, we have the idea of sorting the vertices by their order

The edges will only go from the vertices in front of the order to back

Topological Order of DAG

The algorithm

  1. Start from the vertices with indeg[u] = 0
  2. We will do BFS, push all the vertices with indeg 0 into the queue
  3. Remove the vertex, and decrement the indeg[v]
  4. If the indegree of \(v\) becomes \(0\), then push it into a queue

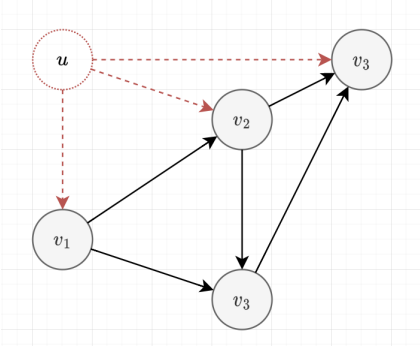
Topological Order of DAG

queue<int> q;
vector<int> topo;
for(int i = 1; i <= n; i++){
    if(deg[i] == 0)
        q.push(i);
}

while(!q.empty()){
    int u = q.front(); q.pop();
    topo.push_back(u);
    for(int v : adj[u]){
        deg[v]--;
        if(deg[v] == 0)
            q.push(v);
    }
}
//if topo.size() == n, then the graph is a DAG

Codeforces 510C - Fox and Names

DP On DAGs

CSES - Longest Flight Route

CSES - Game Route

Disjoint Set Union

We want a data structure that can

  1. Connect two vertices \(u, v\)
  2. Answer if \(u,v\) are connected with each other

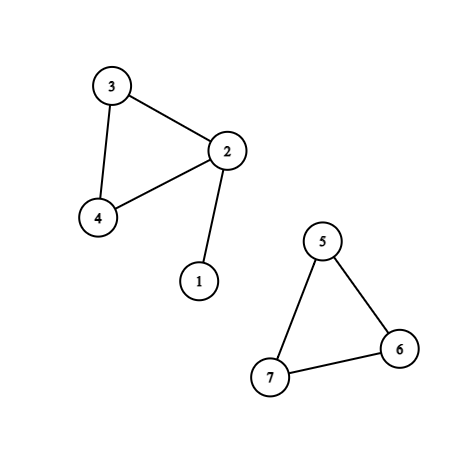
Disjoint Set Union

We introduce the data structure Disjoint Set Union (DSU)

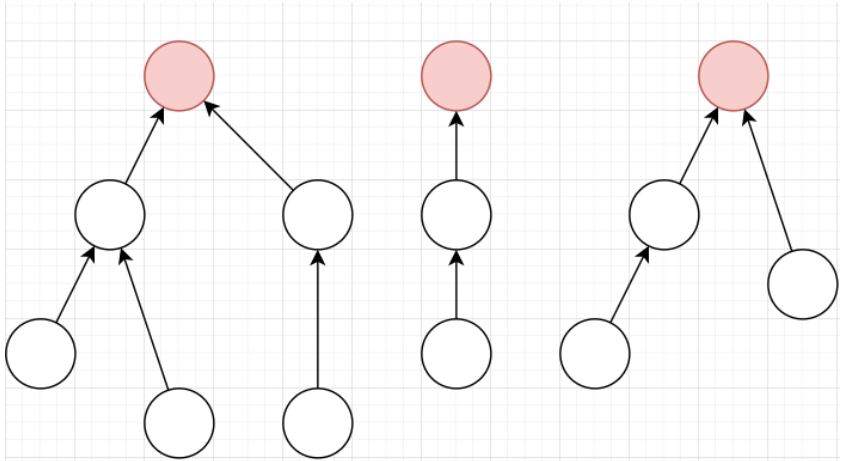
Disjoint Set Union

For an undirected graph, we connect each vertices in the same connected components with a directed arrow

Disjoint Set Union

When we want to know whether two vertices are connected

We check if their roots are the same

u
v

Disjoint Set Union

When we want to know whether two vertices are connected

We check if their roots are the same

u
v

Disjoint Set Union

We will declare an array dsu, where dsu[u]is the vertex \(u\) points to

1
2
dsu[1] = 2

Disjoint Set Union

Initialize the data structure

for(int i = 1; i <= n; i++)
    dsu[i] = i;

//or you can do
iota(dsu, dsu+MAXN, 0);

Time Complexity: \(O(|V|)\)

Disjoint Set Union

To find the root of each vertex

void find(int u) {
    if(dsu[u] == u) return u;
    return find(dsu[u]);
}

Time Complexity: \(O(|V|)\)

Disjoint Set Union

To connect two vertices, we connect the roots of both vertex

void unite(int u, int v){
    u = find(v), v = find(v);
    if(dsu[u] == dsu[v]) continue;
    dsu[u] = v;
}

Time Complexity: \(O(1)\)

Disjoint Set Union

However, notice that finding whether \(u,v\) are connected is same as just doing DFS/BFS from one vertex

How can we speed this up?

Disjoint Set Union

The problem for finding is that, every time we will have to go through all vertices on the chain

What if we shorten the chain?

Path Compression

Each time we query a vertex, we connect all the vertices on the path to the root

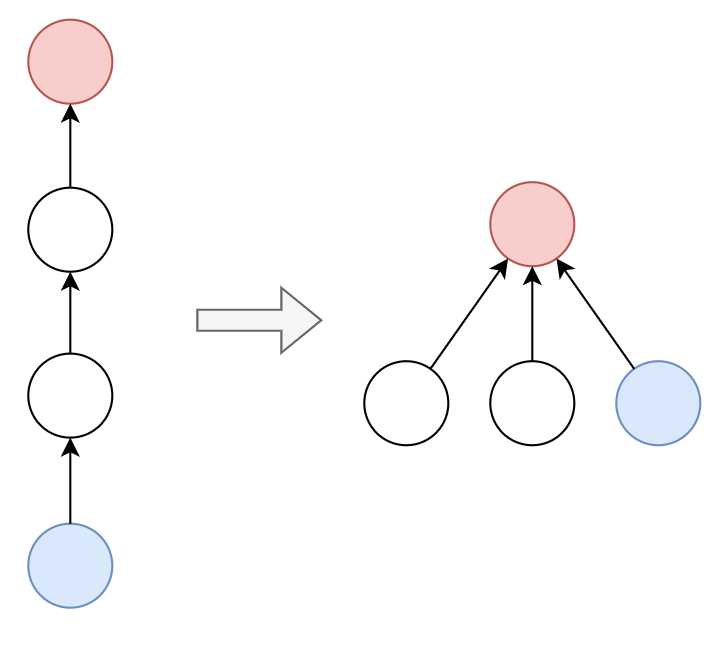
Path Compression

void find(int u) {
    if(dsu[u] == u) return u;
    return dsu[u] = find(dsu[u]);
}

Time Complexity: \(O(\log n)\) amortized

Union By Size

There is another way to speed up DSU operations

We maintain the size of each component in sz[rt]

Union By Size

There is another way to speed up DSU operations

We maintain the size of each component in sz[rt]

void unite(int u, int v){
    u = find(u), v = find(v);
    if(u == v) return;
    dsu[u] = v;
    sz[v] += sz[u];
}

Union By Size

We connect the smaller to the larger one

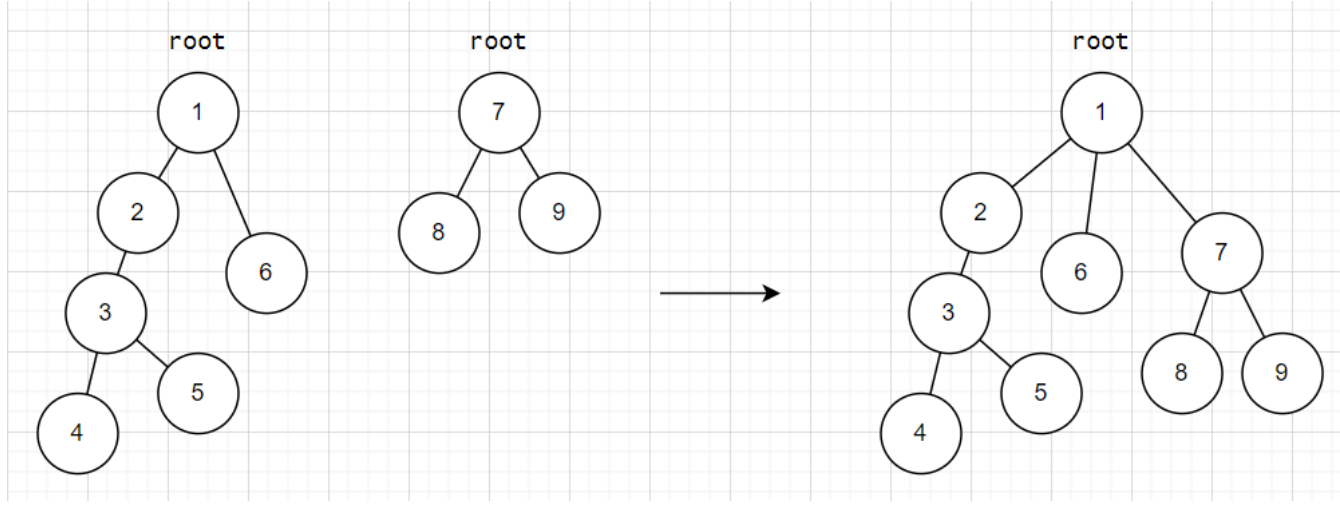
Union By Size

Doing this technique, you can prove the complexity will become \(O(\log n)\) amortized

Union By Size

void unite(int u, int v){
    u = find(u), v = find(v);
    if(u == v) return;
    if(sz[u] > sz[v]) swap(u, v);
    dsu[u] = v;
    sz[v] += sz[u];
}

Time Complexity: \(O(\log n)\) amortized

Using Both Optimizations

Both optimizations can be used independently

If you use both optimizations, the time complexity of each operations becomes 

\(O(\alpha(n))\) amoritzed

The \(\alpha\) here is the inverse Ackermann function

You can consider it almost as a constant

Problems

Codeforces EDU - Experience

Codeforces EDU - Cutting a Graph

Codeforces EDU - Monkeys

Bipartite Checking

Codeforces EDU - Bipartite Graph

Made with Slides.com