Dynamic Programming
UMD CP Club Summer CP Week 4


Consider this problem

Consider this problem
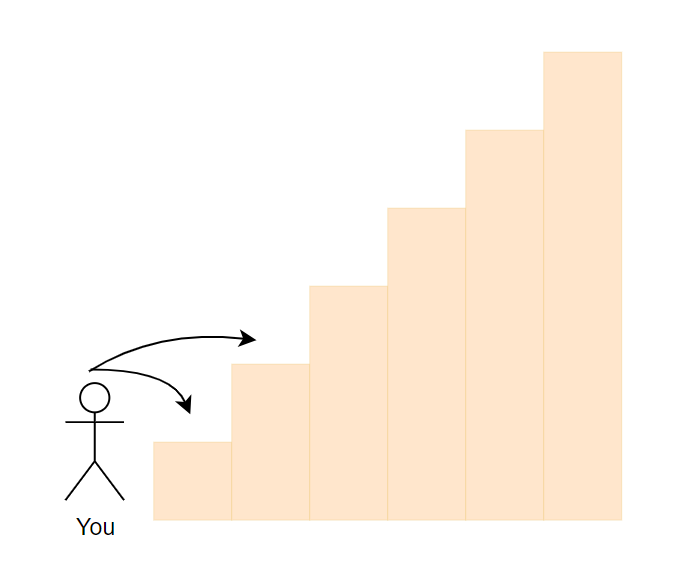

Consider this problem
There is a stairs with \(n\) levels, you can walk \(1\) or \(2\) steps each time. What is the number of possible paths you can go?

Let's search for the answer

Let's search for the answer
int cnt(int n) {
if (n == 0) return 1;
else if(n == 1) return 1;
else return cnt(n-1) + cnt(n-2);
}What is the time complexity?

Let's search for the answer
int cnt(int n) {
if (n == 0) return 1;
else if(n == 1) return 1;
else return cnt(n-1) + cnt(n-2);
}What is the time complexity?

Why is this so slow?

Why is this so slow?
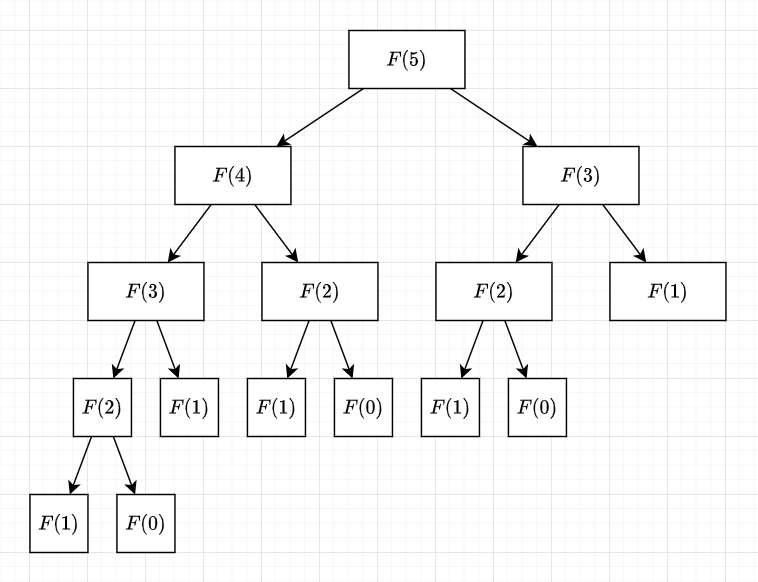
We recomputed same state multiple times!

Why is this so slow?
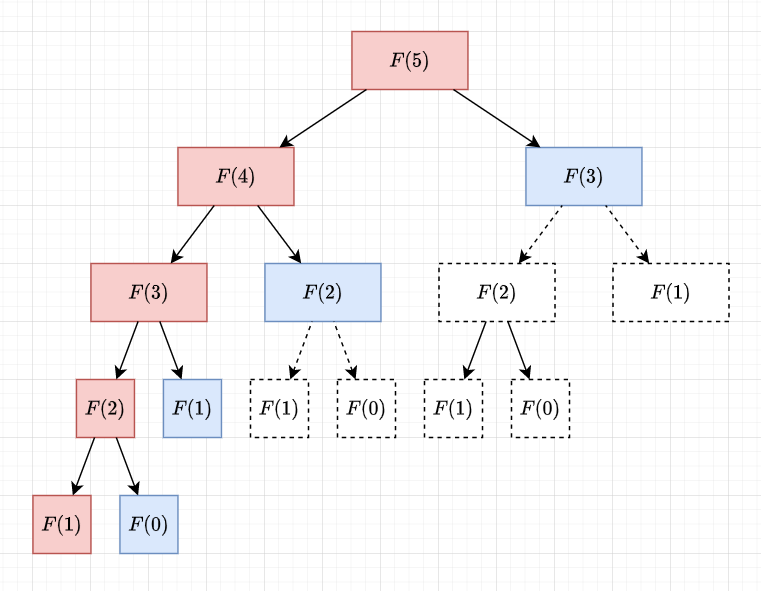
We actually only need \(O(n)\) states!

int arr[MAXN];
int cnt(int n) {
if (arr[n]) return arr[n];
if (n == 0) return arr[n] = 1;
else if(n == 1) return arr[n] = 1;
else return arr[n] = cnt(n-1) + cnt(n-2);
}We change the code into
This becomes \(O(n)\)

What we just did is called Memoization
and this is the basic idea of Dynamic Programming!

What is Dynamic Programming?

What is Dynamic Programming?
It is usually abbreviated with DP
Instead of an algorithm, it is more like an idea or a trick
It can also be the name of array

What is Dynamic Programming?
Two main types of problems that it can solve
1. Overlapping Subproblems
2. Optimal Substructures

What is Dynamic Programming?
1. Overlapping Subproblems
.Same type of problems might be recalculated
.Can be sped up with memoization to prevent recalculations
2. Optimal Substructures
.An optimal solution can be calculated from the subproblems

What is Dynamic Programming?
There is a stairs with \(n\) levels, there are \(a_i\) coins on each level, you can walk \(1\) or \(2\) steps each time. What is the maximum coins you can get?
2. Optimal Substructures
.An optimal solution can be calculated from the subproblems
Let \(f(n)\) be the maximum coins you get when you get to \(n\)

What is Dynamic Programming?
There are three steps for approaching a DP problem

What is Dynamic Programming?
There are three steps for approaching a DP problem
Define the States
Let \(f(n)\) be the maximum coins you get when you get to \(n\)

What is Dynamic Programming?
There are three steps for approaching a DP problem
Define the States \(\implies\) Find Transition
Let \(f(n)\) be the maximum coins you get when you get to \(n\)

What is Dynamic Programming?
There are three steps for approaching a DP problem
Define the States \(\implies\) Find Transition \(\implies\) Base Cases
Let \(f(n)\) be the maximum coins you get when you get to \(n\)
We know \(f(0) = 0\)

What is Dynamic Programming?
There are also two different ways of solving a DP Problem

What is Dynamic Programming?
There are also two different ways of solving a DP Problem
int f(int n) {
if (dp[n]) return dp[n];
if (n <= 1) return dp[n] = 1;
else return dp[n] = f(n-1) + f(n-2);
}This is called Top-Down approach

What is Dynamic Programming?
int dp[n+1] = {};
dp[0] = dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = dp[i-1] + dp[i-2]
}There are also two different ways of solving a DP Problem
This is called Bottom-Up approach

What is Dynamic Programming?
Both ways are good, and it depends on which you like more
However, I personally like bottom-up more then top-down
So later, all of my code will be bottom-up

Classic DP Problems



To approach a DP Problem, we need to define our states

Let's define the state!
Then the answer will be \(dp[n]\)

Let's find the transition!
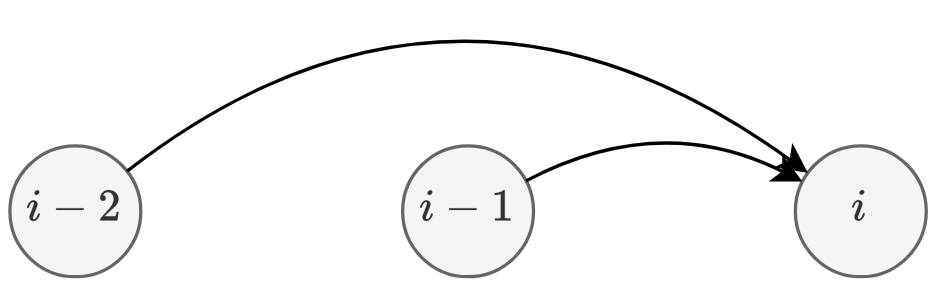

What is the base case?
That's it!

Let's write this into code!

Let's write this into code!
int dp[n+1];
//Let dp[i] be the minimum cost for the frog to jump to stone i
dp[0] = 0; //Base Case
for (int i = 1; i <= n; i++) {
for (int j = i-1; j >= max(0, i-k); j++) {
//Transition
dp[i] = max(dp[j] + abs(h[i] - h[j]));
}
}
cout << dp[n] << "\n"; //Answer
Let's write this into code!
int dp[n+1];
//Let dp[i] be the minimum cost for the frog to jump to stone i
dp[0] = 0; //Base Case
for (int i = 1; i <= n; i++) {
for (int j = i-1; j >= max(0, i-k); j++) {
//Transition
dp[i] = max(dp[j] + abs(h[i] - h[j]));
}
}
cout << dp[n] << "\n"; //Answer
There are \(n\) houses, and you are a robber. You want to steal valuable items from the houses. However, you cannot steal adjacent houses.
For the \(i\)th house, the items has a value of \(a_i\). Find the maximum total value you can get from the \(n\) houses

Define the States
Then the answer will be \(\max(dp[1], dp[2], \cdots, dp[n])\)

Find the Transition

Base Cases
We have \(n\) states and the transition is \(O(1)\)
we can do this in \(O(n)\)

You are on a vacation for \(n\) days, each day, you can do three activities
- Swim in the sea, and get \(a_i\) happiness
- Catch bugs, and get \(b_i\) happiness
- Do homework, and get \(c_i\) happiness
However, you cannot do same activities on consecutive days
What is the maximum happiness you can have?

Define the state!
But what would happen when you want to find the transition?

Define the state!
Answer would be \(\max(dp[n][0], dp[n][1], dp[n][2])\)

Find the transition!

Define the base cases!
We have \(O(n)\) states, and each transition is \(O(1)\)
We can do this in \(O(n)\)

int dp[n+1][3]; //The state we define
dp[0][0] = dp[0][1] = dp[0][2] = 0; //Base Cases
for (int i = 1; i <= n; i++) {
//Transition
dp[i][0] = max(dp[i-1][1],dp[i-1][2]) + a[i];
dp[i][1] = max(dp[i-1][0],dp[i-1][2]) + b[i];
dp[i][2] = max(dp[i-1][0],dp[i-1][1]) + c[i];
}
cout<< max({dp[n][0],dp[n][1],dp[n][2]}) <<'\n';
Can you use similar idea on House Robber?

Define the States
Answer would be \(\max(dp[n][0], dp[n][1])\)

Find the transition!

Base Cases
This is an idea that would simplify our thoughts a lot

You are given two strings \(s,t\)
You want to find their Longest Common Subsequence (LCS)

You are given two strings \(s,t\)
You want to find their Longest Common Subsequence (LCS)
If s = \(\texttt{abcdgh}\), t = \(\texttt{aedfhr}\), then their LCS is a,d,h

Define the states
\(i,j\) can be seen as string lengths

Find The Transition

Base Cases
There are \(|s||t|\) states, and transition is \(O(1)\)
Therefore, we can do this in \(O(|s||t|)\)

How do we actually find the subsequence?

Let \(from[i][j]\) be \(\{x,y\}\) where the value of \(dp[i][j]\) is from
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (s[i-1] == s[j-1]) {
dp[i][j] = dp[i-1][j-1] + 1;
from[i][j] = {i-1, j-1};
}
if (dp[i-1][j] > dp[i][j]) {
dp[i][j] = dp[i-1][j];
from[i][j] = {i-1, j};
}
if (dp[i][j-1] > dp[i][j]) {
dp[i][j] = dp[i][j-1];
from[i][j] = {i, j-1};
}
}
}


Similar to LCS, let's define the states as

Similar to LCS, let's define the states as
Define the states
\(i,j\) can be seen as string lengths

Find the transition

Base Cases
There are \(|s||t|\) states, and transition is \(O(1)\)
Therefore, we can do this in \(O(|s||t|)\)



Define the States
The answer would be \(dp[n][n]\)

Find the transitions!

Base Cases
The state is \(O(n^2)\) and the transition is \(O(1)\)
Therefore we can do this in \(O(n^2)\)


Knapsack Problem

You have a knapsack with weight capacity \(W\)
There are \(n\) items, each with \(w_i\) weight and value \(v_i\)
What is the maximum sum of values you can bring?
- \(1 \le n \le 100\)
- \(1 \le w_i \le 10^5\)
- \(1 \le v_i \le 10^9\)

We talked about how to solve this problem by searching through all subsets

We talked about how to solve this problem by searching through all subsets
int ans = 0;
for (int mask = 0; mask < (1 << n); i++) {
int sum = 0, cap = 0;
for (int i = 0; i < n; i++) {
if (mask & (1 << i)) {
sum += v[i];
cap += w[i];
}
if(cap <= W) ans = max(ans, sum);
}
}
But now, the number of item is much more
and the maximum weight is lower!

Define the States
The answer would be \(dp[n][W]\)

Find the Transition!

Find the Transition!
Not Take
Take

Base Cases
\(dp[0][i] = dp[j][0] = 0 \text{ for all } i,j\)
We have \(O(nW)\) states and transition is \(O(1)\)
Therefore, the time is \(O(nW)\)

int dp[n+1][W+1] = {}; //The state we define and base case
for(int i = 1;i < n;i++){
for(int j = 1;j <= W;j++){
//Transition
dp[i][j] = dp[i-1][j];
if(j >= w[i]) dp[i][j] = max(dp[i][j],dp[i-1][j-w[i]] + v[i]);
}
}
cout << dp[n][W] << "\n"; //Answer
Do we really need the first dimension for dp?
NO!

for(int i = 1; i <= n; i++){
for(int j = W; j >= 0; j--){
if(j >= w[i])
dp[j] = max(dp[j], dp[j-w[i]] + v[i]);
}
}This way, we did it in 1D DP
and now, the state is

This is the original transition
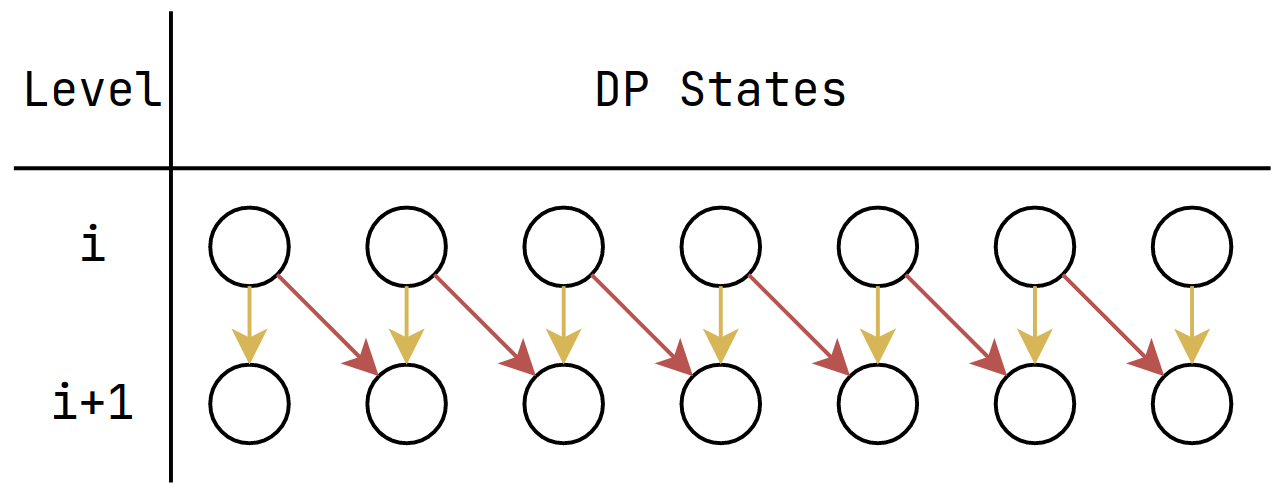

This is the original transition


Compressed DP State should be like this
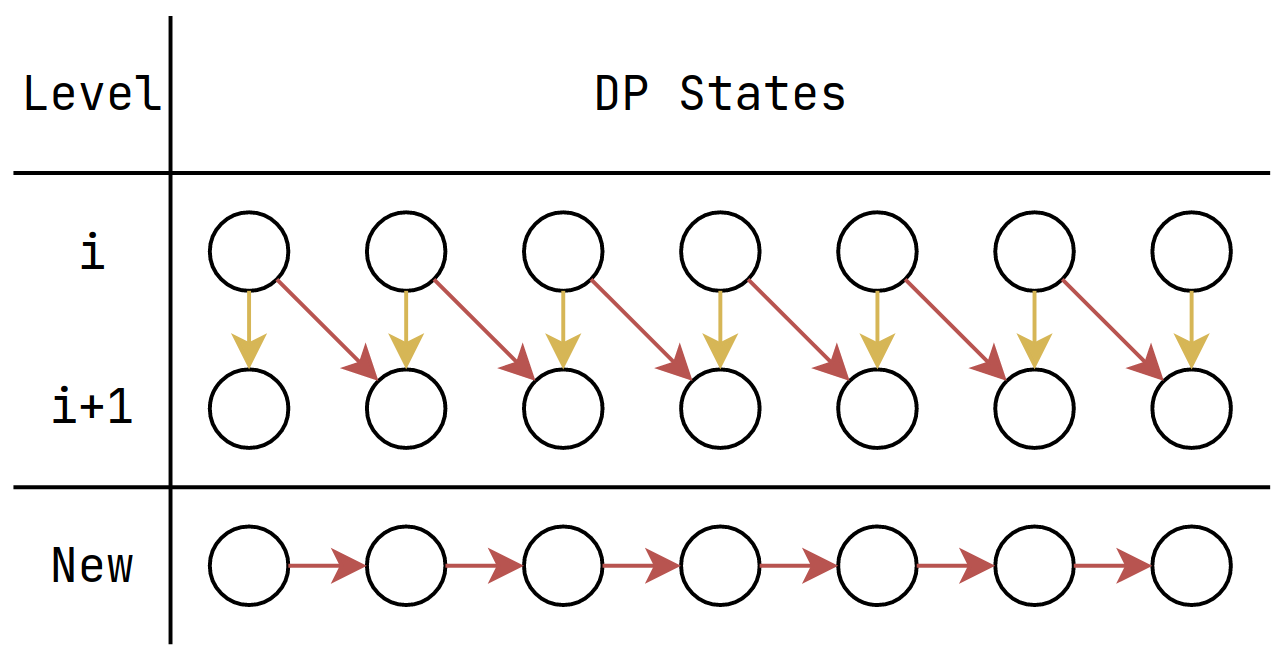

Infinite Knapsack Problem / Coin Change
What if now, you can take a single item multiple times

Infinite Knapsack Problem / Coin Change
The idea is basically the same, we can define everything the same, but for transition

Infinite Knapsack Problem / Coin Change
The idea is basically the same, we can define everything the same, but for transition
for(int i = 1; i <= n; i++){
for(int j = 0; j <= W; j++){
if(j >= w[i])
dp[j] = max(dp[j], dp[j-w[i]] + v[i]);
}
}
Infinite Knapsack Problem / Coin Change


Other Problems


