Deep Learning HMC

Building Topological Samplers for Lattice QCD

Sam Foreman

May, 2021

saforem2/l2hmc-qcd
arXiv:2105.03418

Text

MCMC in Lattice QCD

  • Generating independent gauge configurations is a MAJOR bottleneck for LatticeQCD.
  • As the lattice spacing, \(a \rightarrow 0\), the MCMC updates tend to get stuck in sectors of fixed gauge topology.
    • This causes the number of steps needed to adequately sample different topological sectors to increase exponentially.

Critical slowing down!

Markov Chain Monte Carlo (MCMC)

  • Goal: Draw independent samples from a target distribution, \(p(x)\)
x^{\prime} = x_{0} + \delta,\quad \delta\sim\mathcal{N}(0, \mathbb{1})
  • Starting from some initial state \(x_{0}\sim \mathcal{N}(0, \mathbb{1})\) , we generate proposal configurations \(x^{\prime}\)
  • Use Metropolis-Hastings acceptance criteria
x_{i+1} = \begin{cases} x^{\prime},\quad\text{with probability } A(x^{\prime}|x)\\ x,\quad\text{with probability } 1 - A(x^{\prime}|x) \end{cases}
A(x^{\prime}|x) = \min\left\{1, \frac{p(x^{\prime})}{p(x)}\left|\frac{\partial x^{\prime}}{\partial x^{T}}\right|\right\}

\(\big\{ x_{0},  x_{1},  x_{2},  \ldots,   x_{m-1},  x_{m},  x_{m+1},   \ldots,   x_{n-2},  x_{n-1},  x_{n} \big\}\)

 1. Construct chain:

\(\big\{ x_{0},  x_{1},  x_{2},  \ldots,   x_{m-1},  x_{m},  x_{m+1},   \ldots,   x_{n-2},  x_{n-1},  x_{n} \big\}\)

 2. Thermalize ("burn-in"):

\(\big\{ x_{0},  x_{1},  x_{2},  \ldots,   x_{m-1},  x_{m},  x_{m+1},   \ldots,   x_{n-2},  x_{n-1},  x_{n} \big\}\)

 3. Drop correlated samples ("thinning"):

dropped configurations

Inefficient!

Issues with MCMC

  • Generate proposal \(x^{\prime}\):

\(x^{\prime} = x  + \delta\), where \(\delta \sim \mathcal{N}(0, \mathbb{1})\)

random walk

Hamiltonian Monte Carlo (HMC)

  • Introduce fictitious momentum:

\(v\sim\mathcal{N}(0, 1)\)

  • Target distribution:

\(p(x)\propto e^{-S(x)}\)

  • Joint target distribution:

p(x, v) = p(x)\cdot p(v) = e^{-S(x)}\cdot e^{-\frac{1}{2}v^{T}v} = e^{-\mathcal{H(x,v)}}

  • The joint \((x, v)\) system obeys Hamilton's Equations:

\dot{x} = \frac{\partial\mathcal{H}}{\partial v},
\dot{v} = -\frac{\partial\mathcal{H}}{\partial x}
p(x, v) = p(x|v)p(v)

lift to phase space

v\sim \mathcal{N}(0, \mathbb{1})
\mathcal{H}=\mathrm{const}

HMC: Leapfrog Integrator

(trajectory)

  • Hamilton's Eqs:

\dot{x}=\frac{\partial\mathcal{H}}{\partial v}, \dot{v}=-\frac{\partial{\mathcal{H}}}{\partial x}
\mathcal{H}(x, v) = S(x) + \frac{1}{2}v^{T}v

  • Hamiltonian:

(x_{0}, v_{0})\rightarrow \cdots \rightarrow(x_{N_{\mathrm{LF}}}, v_{N_{\mathrm{LF}}})

  • \(N_{\mathrm{LF}}\) leapfrog steps:

\Longrightarrow

Leapfrog Integrator

x^{\prime} = x + \varepsilon v^{1/2}
v^{\prime} = v^{1/2} - \frac{\varepsilon}{2}\partial_{x}S(x^{\prime})
v^{1/2} = v - \frac{\varepsilon}{2}\partial_{x}S(x)

2. Full-step \(x\)-update:

3. Half-step \(v\)-update:

1. Half-step \(v\)-update:

HMC: Issues

  • Cannot easily traverse low-density zones.
  • What do we want in a good sampler?
  • Fast mixing
  • Fast burn-in
  • Mix across energy levels
  • Mix between modes
  • Energy levels selected randomly \(\longrightarrow\) slow mixing!

Stuck!

Leapfrog Layer

  • Introduce a persistent direction \(d \sim \mathcal{U}(+,-)\)  (forward/backward)
  • Introduce a discrete index \(k \in \{1, 2, \ldots, N_{\mathrm{LF}}\}\) to denote the current leapfrog step
  • Let \(\xi = (x, v, \pm)\) denote a complete state, then the target distribution is given by
p(\xi) = p(x)\cdot p(v)\cdot p(d)
  • Each leapfrog step transforms \(\xi_{k} = (x_{k}, v_{k}, \pm) \rightarrow (x''_{k}, v''_{k} \pm) = \xi''_{k}\) by passing it through the \(k^{\mathrm{th}}\) leapfrog layer

Leapfrog Layer

where \((s_{v}^{k}, q^{k}_{v}, t^{k}_{v})\), and \((s_{x}^{k}, q^{k}_{x}, t^{k}_{x})\), are parameterized by neural networks

  • \(x\)-update \((d = +)\):
x^{\prime}_{k} = \Lambda^{+}_{k}(x_{k};\zeta_{x_{k}})
\zeta_{x_{k}}\equiv \big(\quad\odot x_{k}, \partial_{x}S(x_{k})\big)
\bar{m}_{t}

(\(m_{t}\)\(\odot  x\)) -independent

\,\quad= x_{k}\odot\exp\left(\varepsilon^{k}_{x}s^{k}_{x}(\zeta_{x_{k}})\right) + \varepsilon^{k}_{x}\left[v^{\prime}_{k}\odot\exp\left(\varepsilon^{k}_{x}q^{k}_{x}(\zeta_{x_{k}})\right)+t^{k}_{x}(\zeta_{x_{k}})\right]

masks:

m_{t}
\bar{m}_{t}
= \mathbb{1}
+

Momentum (\(v_{k}\)) scaling

Gradient \(\partial_{x}S(x_{k})\) scaling

Translation

\,\quad\equiv\, v_{k}\odot \exp\left(\frac{\varepsilon^{k}_{v}}{2}s^{k}_{v}(\zeta_{v_{k}})\right) - \frac{\varepsilon^{k}_{v}}{2}\left[\partial_{x}S(x_{k})\odot\exp\left(\varepsilon^{k}_{v}q^{k}_{v}(\zeta_{v_{k}})\right) \,+\,t^{k}_{v}(\zeta_{v_{k}})\right]
\zeta_{v_{k}}\equiv \big(x_{k}, \partial_{x}S(x_{k})\big)
  • \(v\)-update \((d = +)\):
v^{\prime}_{k} = \Gamma^{+}_{k}(v_{k};\zeta_{v_{k}} )
\overbrace{\hspace{80px}}
\overbrace{\hspace{100px}}
\overbrace{\hspace{30px}}

(\(v\)-independent)

  • Each leapfrog step transforms 
\xi_{k} = (x_{k}, v_{k}, \pm)\longrightarrow (x''_{k}, v''_{k}, \pm)=\xi''_{k}

by passing it through the \(k^{\mathrm{th}}\) leapfrog layer.

L2HMC: Generalized Leapfrog

  • Complete (generalized) update:
    1. Half-step \(v\) update:
    2. Full-step \(\frac{1}{2} x\) update:
    3. Full-step \(\frac{1}{2} x\) update:
    4. Half-step \(v\) update:
v^{\prime}_{k} = \Gamma^{\pm}(v_{k};\zeta_{v_{k}})
x^{\prime}_{k} = \hspace{14px}\odot x_{k} + \hspace{14px}\odot \Lambda^{\pm}(x_{k};\zeta_{x_{k}})
\bar{m}^{t}
m^{t}
x^{\prime\prime}_{k} = \hspace{14px}\odot \Lambda^{\pm}_{k}(x^{\prime}_{k};\zeta_{x^{\prime}_{k}}) + \hspace{14px}\odot x^{\prime}_{k}
\bar{m}^{t}
m^{t}
v^{\prime\prime}_{k} = \Gamma^{\pm}(v^{\prime}_{k};\zeta_{v^{\prime}_{k}})

Leapfrog Layer

masks:

Stack of fully-connected layers

Example: GMM \(\in\mathbb{R}^{2}\)

\(A(\xi',\xi)\) = acceptance probability

\(A(\xi'|\xi)\cdot\delta(\xi',\xi)\) = avg. distance

Note:

\(\xi'\) = proposed state

\(\xi\) = initial state

  • Maximize expected squared jump distance:
\mathcal{L}_{\theta}\left(\theta\right) \equiv \mathbb{E}_{p(\xi)}\left[A(\xi'|\xi)\cdot \delta(\xi',\xi)\right]
  • Define the squared jump distance:
\delta(\xi^{\prime}, \xi) = \|x^{\prime} - x\|^{2}_{2}

HMC

L2HMC

Training Algorithm

     construct
trajectory
Compute loss
  + backprop
 Metropolis-Hastings 
       accept/reject

     re-sample    
      momentum
   + direction

Annealing Schedule

\left\{\gamma_{t}\right\}_{t=0}^{N} = \left\{\gamma_{0}, \gamma_{1}, \ldots, \gamma_{N-1}, \gamma_{N}\right\},
\gamma_{0} < \gamma_{1} < \ldots < \gamma_{N} \equiv 1
\gamma_{t+1} - \gamma_{t} \ll 1
  • Introduce an annealing schedule during the training phase:

(varied slowly)

 e.g. \( \{0.1, 0.2, \ldots, 0.9, 1.0\}\)

(increasing)

p_{t}(x)\propto e^{-\gamma_{t}S(x)},\quad\text{for}\quad t=0, 1,\ldots, N
  • Target distribution becomes:
  • For \(\|\gamma_{t}\| < 1\), this helps to rescale (shrink) the energy barriers between isolated modes
    • Allows our sampler to explore previously inaccessible regions of the target distribution
  • Wilson action:
S_{\beta}(x)=\beta \sum_{P}1-\cos x_{P}
x_{P} = x_{\mu}(n) + x_{\nu}(n+\hat{\mu}) - x_{\mu}(n+\hat{\nu}) - x_{\nu}(n)
  • Topological charge:

continuous, differentiable

discrete, hard to work with

\left\lfloor x_{P}\right\rfloor = x_{P} - 2\pi\left\lfloor\frac{x_{P}+\pi}{2\pi}\right\rfloor
\mathcal{Q}_{\mathbb{Z}} = \frac{1}{2\pi}\sum_{P}\left\lfloor x_{P}\right\rfloor\hspace{6pt} \in\mathbb{Z}
\mathcal{Q}_{\mathbb{R}} = \frac{1}{2\pi}\sum_{P}\sin x_{P}\in\mathbb{R}
  • Link variables:
U_{\mu}(x) = e^{i x_{\mu}(n)} \in U(1)
x_{\mu}(n) \in [-\pi,\pi]

Lattice Gauge Theory

  • We maximize the expected squared charge difference:

Loss function: \(\mathcal{L}(\theta)\)

\delta \mathcal{Q}_{\mathbb{R}}^{2}(\xi',\xi) \equiv \left(\mathcal{Q}_{\mathbb{R}}(x') - \mathcal{Q}_{\mathbb{R}}(x)\right)^{2}
\mathcal{L}(\theta) = \mathbb{E}_{p(\xi)}\left[-\delta\mathcal{Q}^{2}_{\mathbb{R}}(\xi',\xi)\cdot A(\xi'|\xi)\right]
A(\xi'|\xi) = \min\left\{1, \frac{p(\xi')}{p(\xi)} \left|\frac{\partial\xi'}{\partial\xi^{T}}\right|\right\}

Results

  • We maximize the expected squared charge difference:
\delta \mathcal{Q}_{\mathbb{R}}^{2}(\xi',\xi) \equiv \left(\mathcal{Q}_{\mathbb{R}}(x') - \mathcal{Q}_{\mathbb{R}}(x)\right)^{2}
\mathcal{L}(\theta) = \mathbb{E}_{p(\xi)}\left[-\delta\mathcal{Q}^{2}_{\mathbb{R}}(\xi',\xi)\cdot A(\xi'|\xi)\right]
A(\xi'|\xi) = \min\left\{1, \frac{p(\xi')}{p(\xi)} \left|\frac{\partial\xi'}{\partial\xi^{T}}\right|\right\}

Interpretation

  • Look at how different quantities evolve over a single trajectory
    • See that the sampler artificially increases the energy during the first half of the trajectory (before returning to original value)

Leapfrog step

variation in the avg plaquette

continuous topological charge

shifted energy

Text

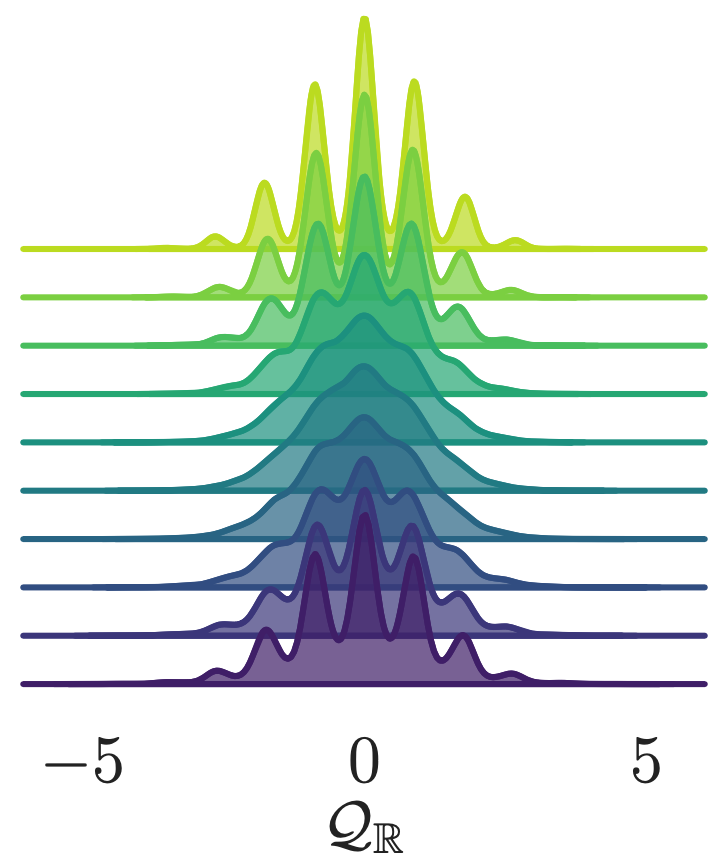
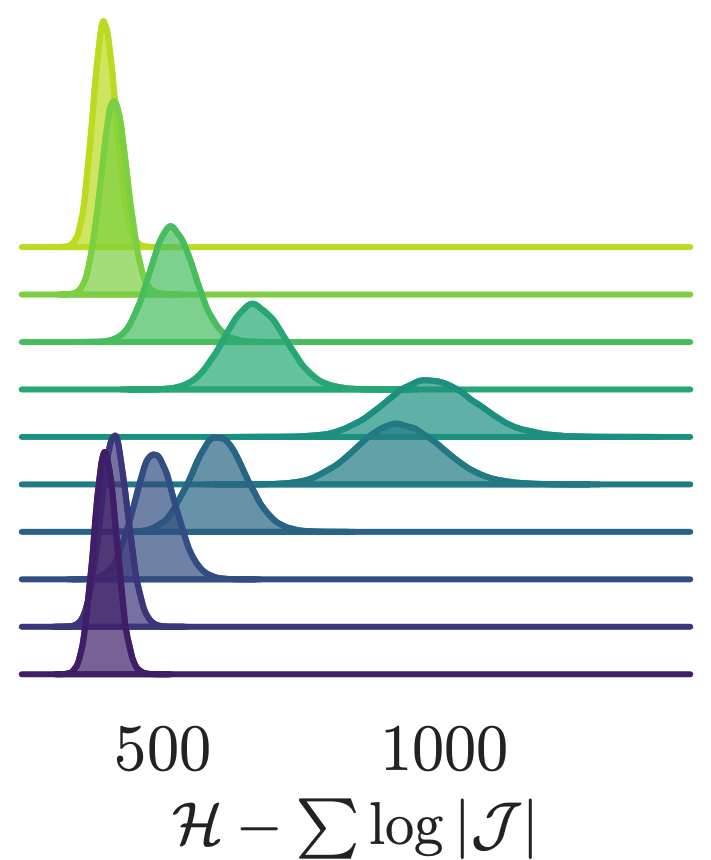
Leapfrog step

variation in the avg plaquette

continuous topological charge

shifted energy

\langle x_{P}-x^{*}_{p}\rangle
\text{leapfrog step}

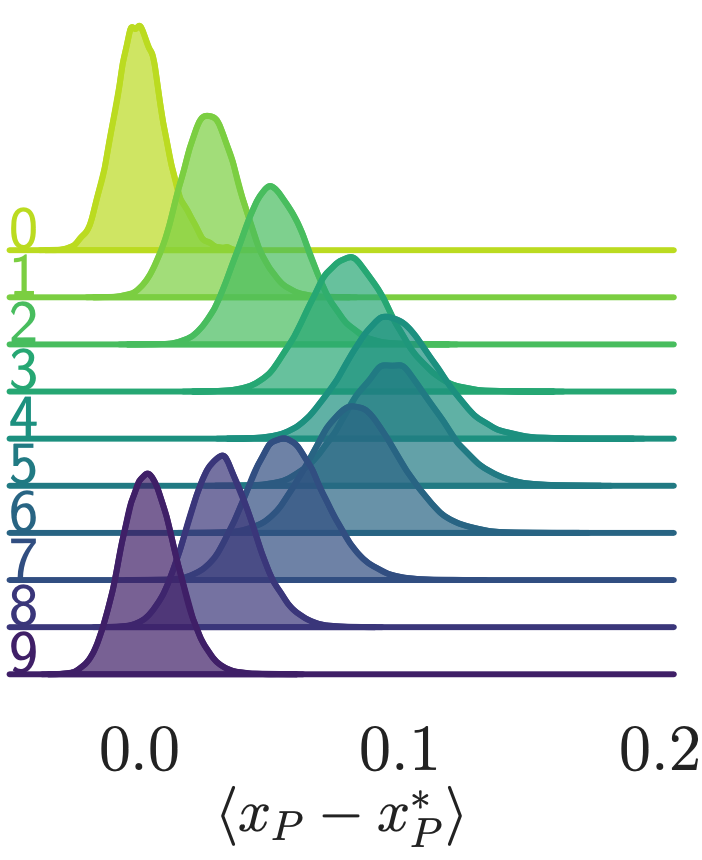
Interpretation

  • Look at how the variation in \(\langle\delta x_{P}\rangle\) varies for different values of \(\beta\)

 \(\beta = 7\) 

\(\simeq \beta = 3\)

\(\beta = 5\)

\(\beta = 6\)

\(\beta = 7\)

Integrated Autocorrelation Time

  • Want to calculate: \(\langle \mathcal{O}\rangle\propto \int \left[\mathcal{D} x\right] \mathcal{O}(x)e^{-S[x]}\)
  • Instead, we account for the autocorrelation, so the variance becomes: \(\sigma^{2} = \frac{\tau^{\mathcal{O}}_{int}}{N}\mathrm{Var}\left[\mathcal{O}(x)\right]\)
  • If we had independent configurations, we could approximate by \(\langle\mathcal{O}\rangle \simeq \frac{1}{N}\sum_{n=1}^{N} \mathcal{O}(x_{n})\longrightarrow \sigma^{2}=\frac{1}{N}\mathrm{Var}\left[\mathcal{O}(x)\right]\propto\frac{1}{N}\)

Thanks for listening!

Interested?

 

arXiv:2105.03418
saforem2/l2hmc-qcd

4096

8192

1024

2048

512

Scaling test: Training

\(4096 \sim 1.73\times\)

\(8192 \sim 2.19\times\)

\(1024 \sim 1.04\times\)

\(2048 \sim 1.29\times\)

\(512\sim 1\times\)

Scaling test: Training

Scaling test: Training

\(8192\sim \times\)

4096

1024

2048

512

Scaling test: Inference

Made with Slides.com