Towards a robust exploration of the Dark Sector with Euclid and Stage-IV surveys within the next decade

Santiago Casas

Postdoctoral Researcher

TTK, RWTH Aachen University

@santiagocasas @sant87casas

Towards a robust exploration of the Dark Sector with Euclid and Stage-IV surveys within the next decade

Santiago Casas

Postdoctoral Researcher

TTK, RWTH Aachen University

@santiagocasas @sant87casas

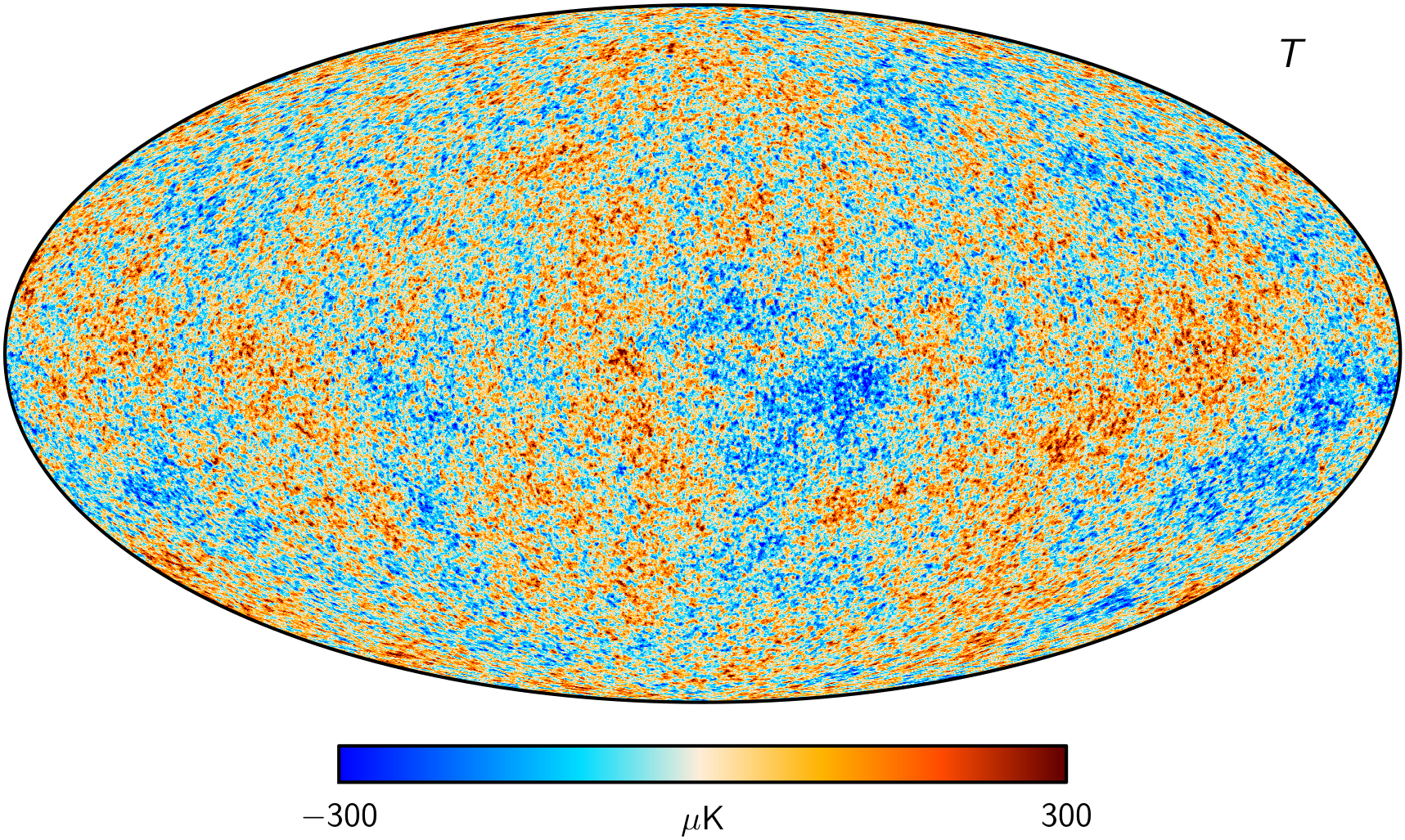
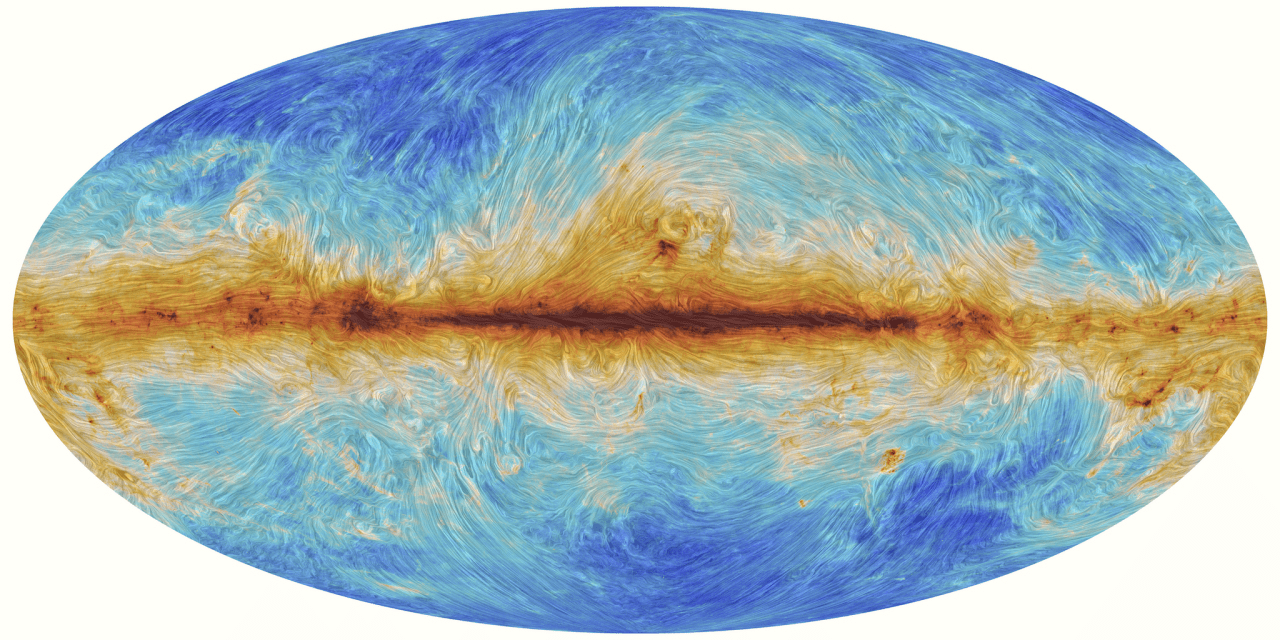
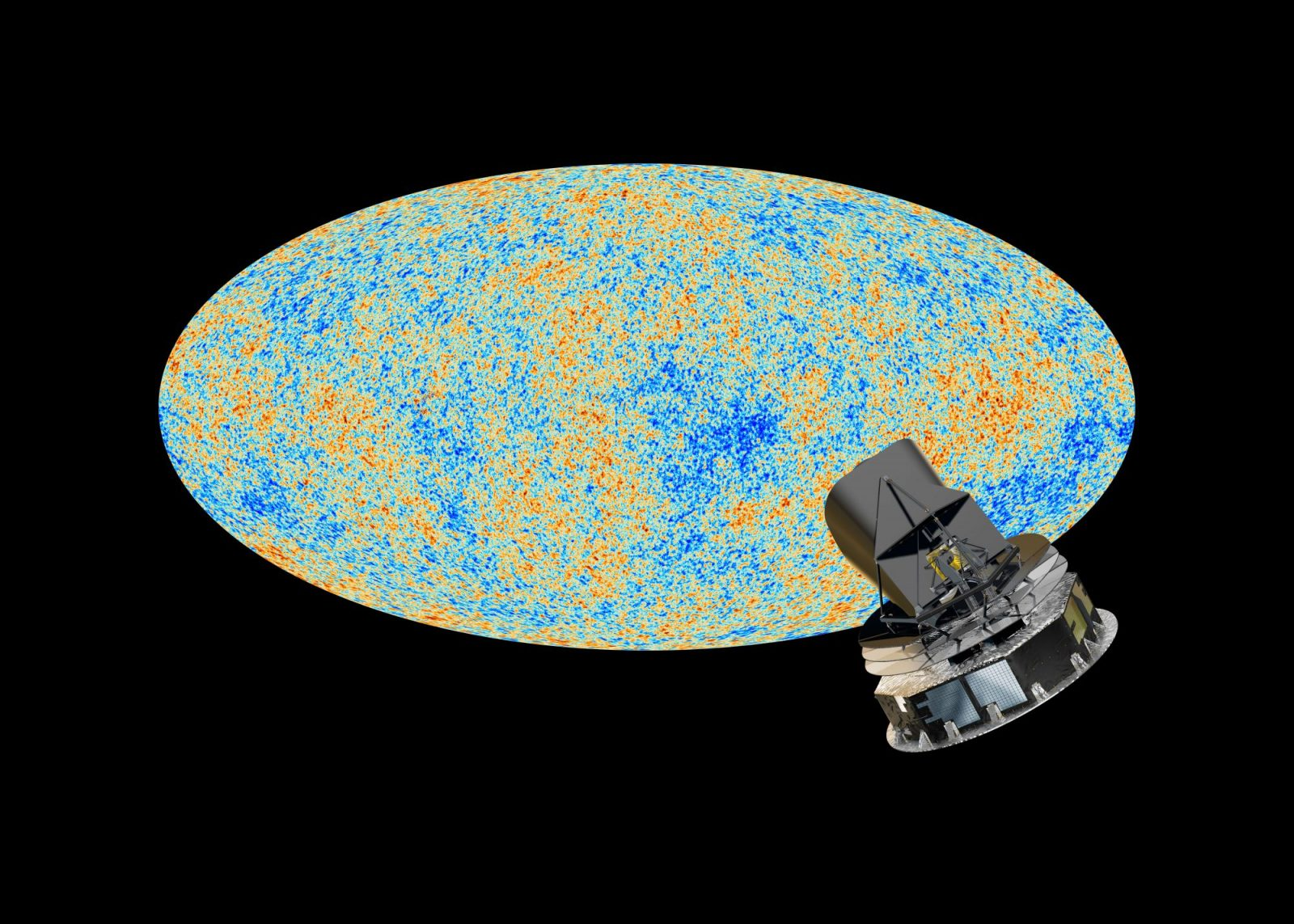
Planck 2018 CMB Temperature map (Commander) . wiki.cosmos.esa.int/planck-legacy-archive/index.php/CMB_maps

Cosmic microwave background

Planck 2018 Cosmological Results (1807.06209)

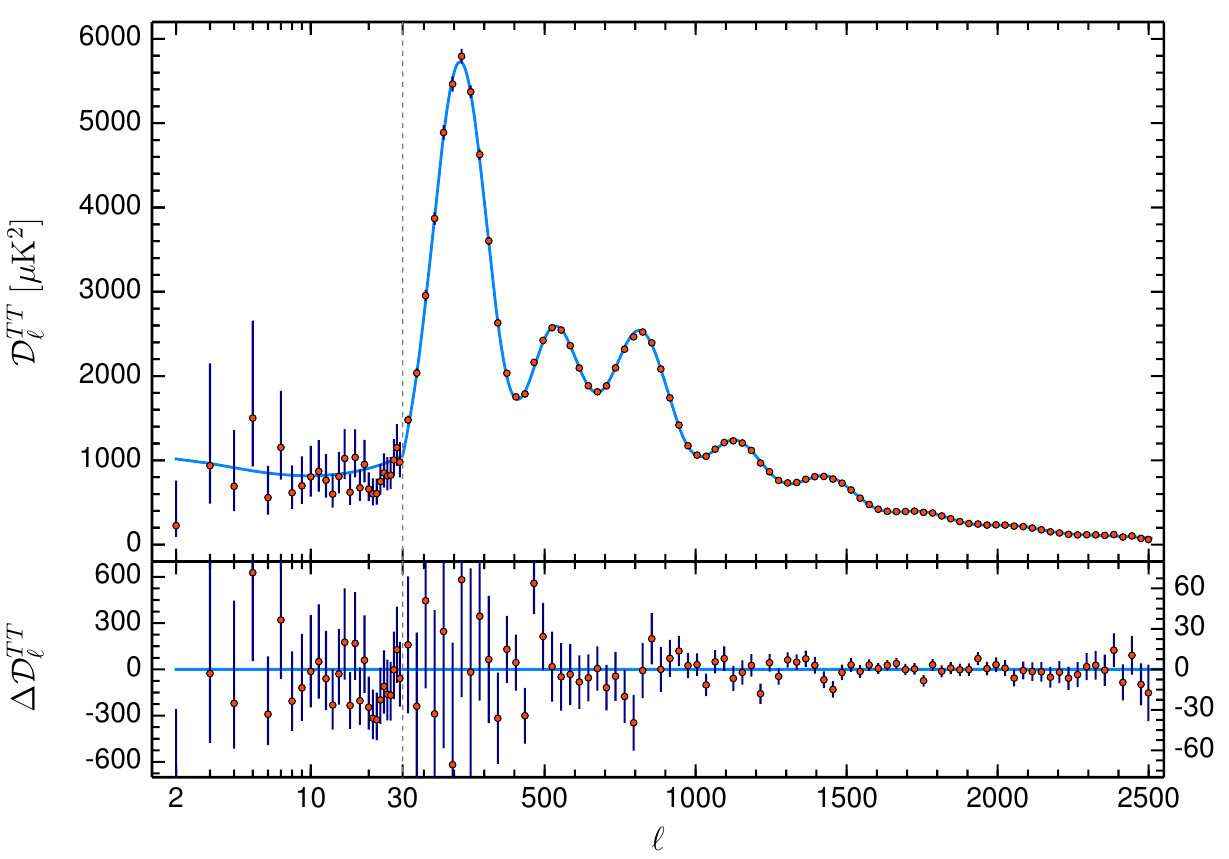
Planck 2018 measurements

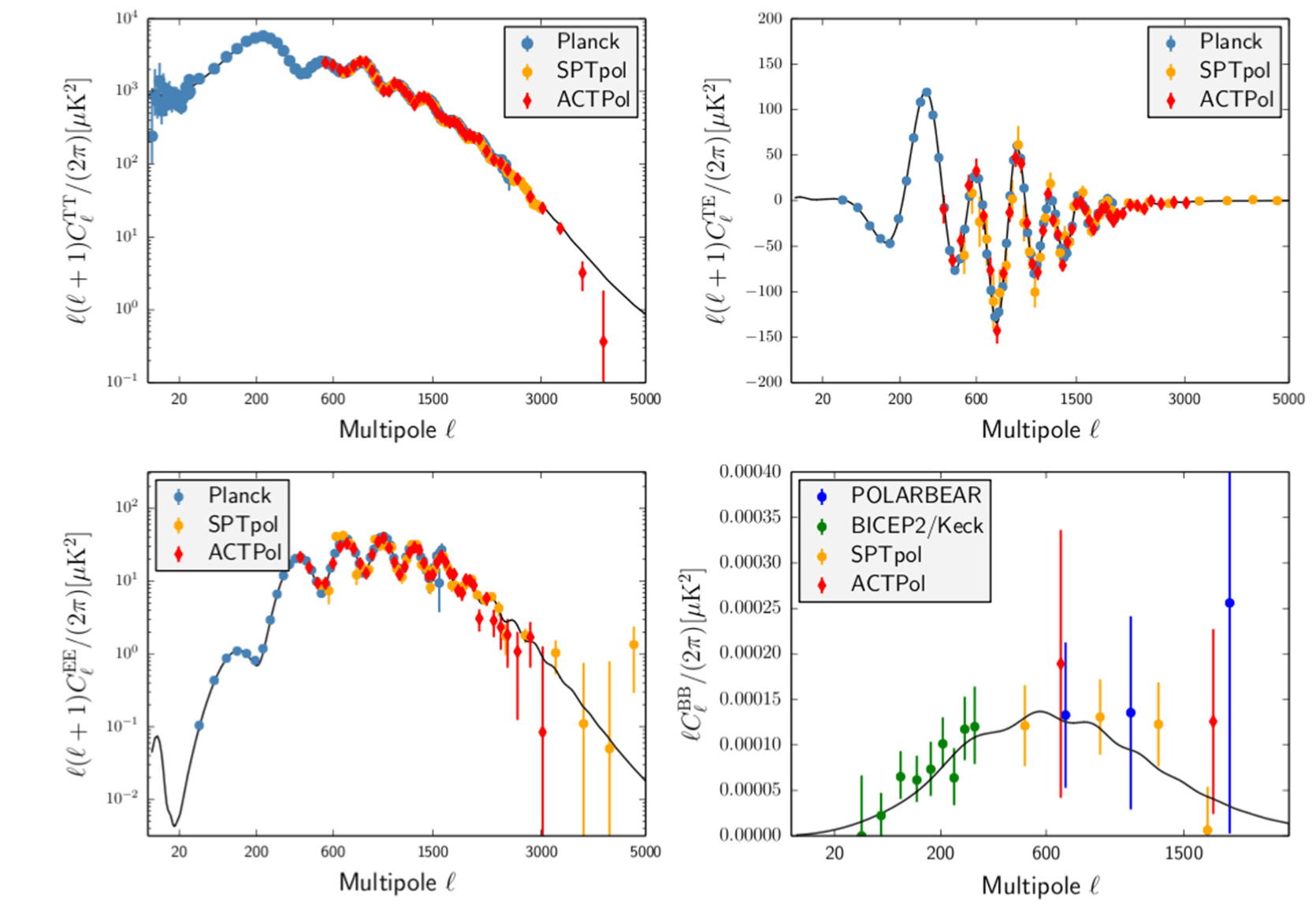
SPT and ACT review: Staggs, Dunkley, Page (2018)

Data in Temperature and Polarization agree well with a $\Lambda$CDM model
Some 1$\sigma$ anomalies have been reported, but they tend to go away, after accounting for i.e. look-elsewhere-effects

CMB: A (Gaussian) Success story

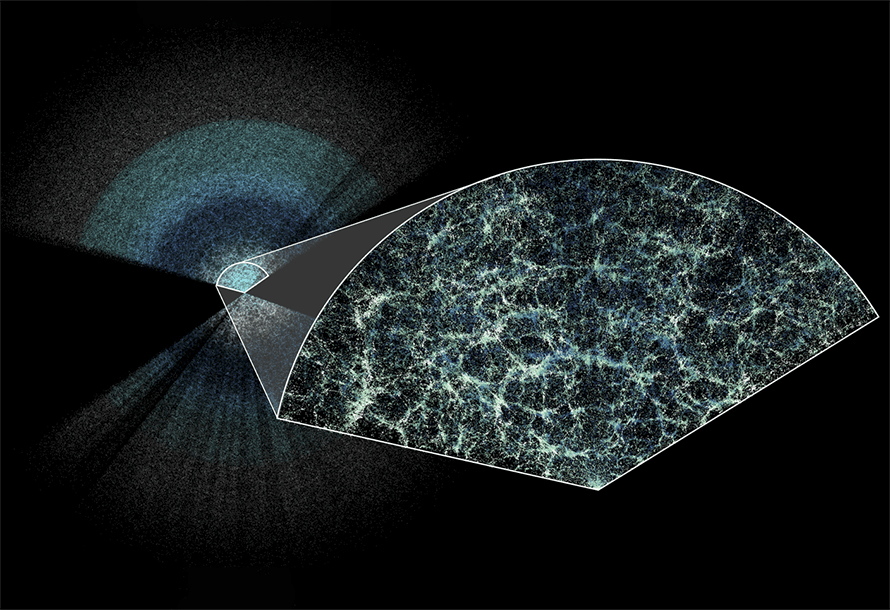
Large Scale StructureS

Illustris Simulation: www.nature.com/articles/nature13316

However, the Universe is not as nice and simple. It is a non-linear mess:

Dark Matter

Baryons

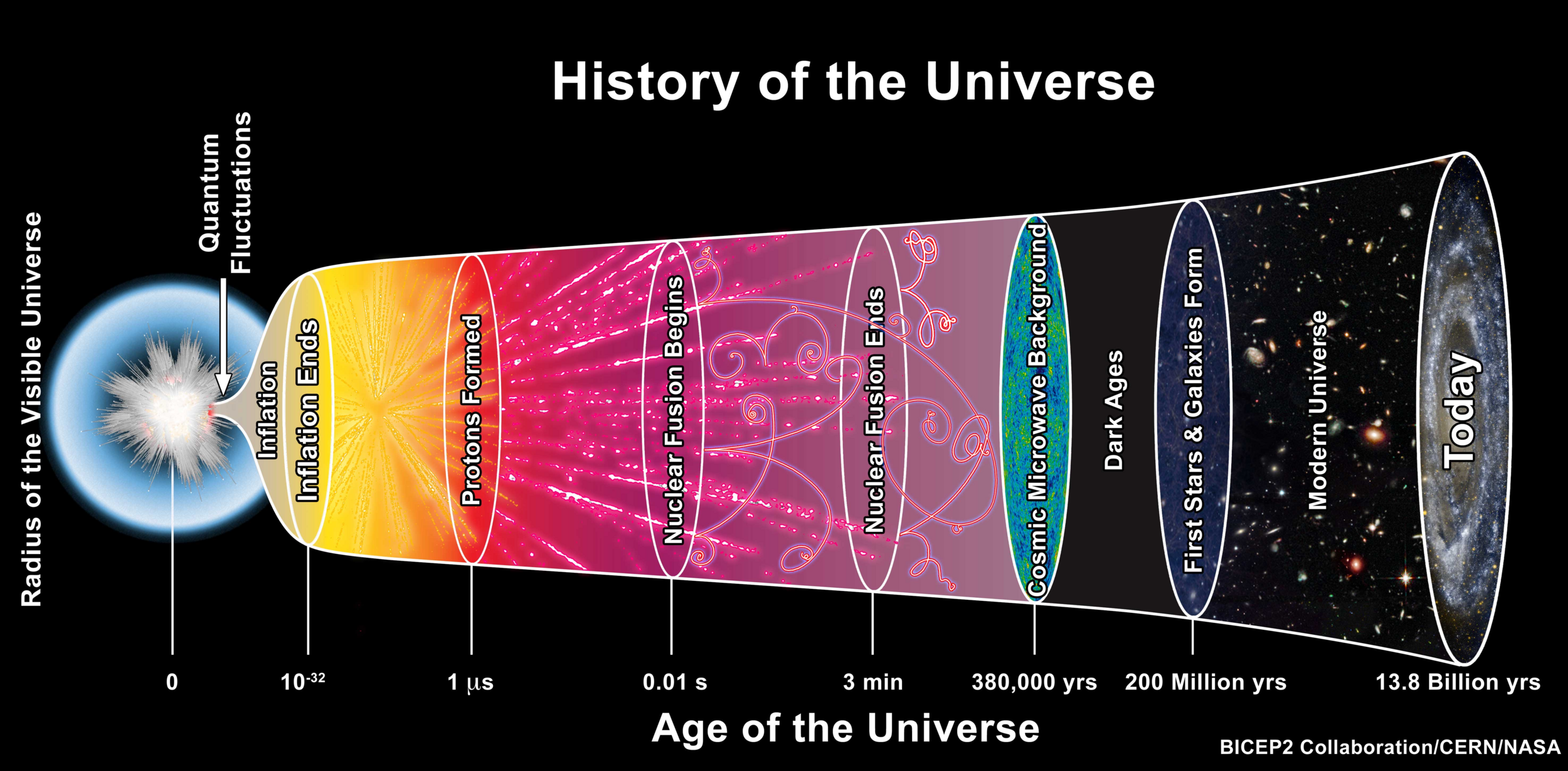
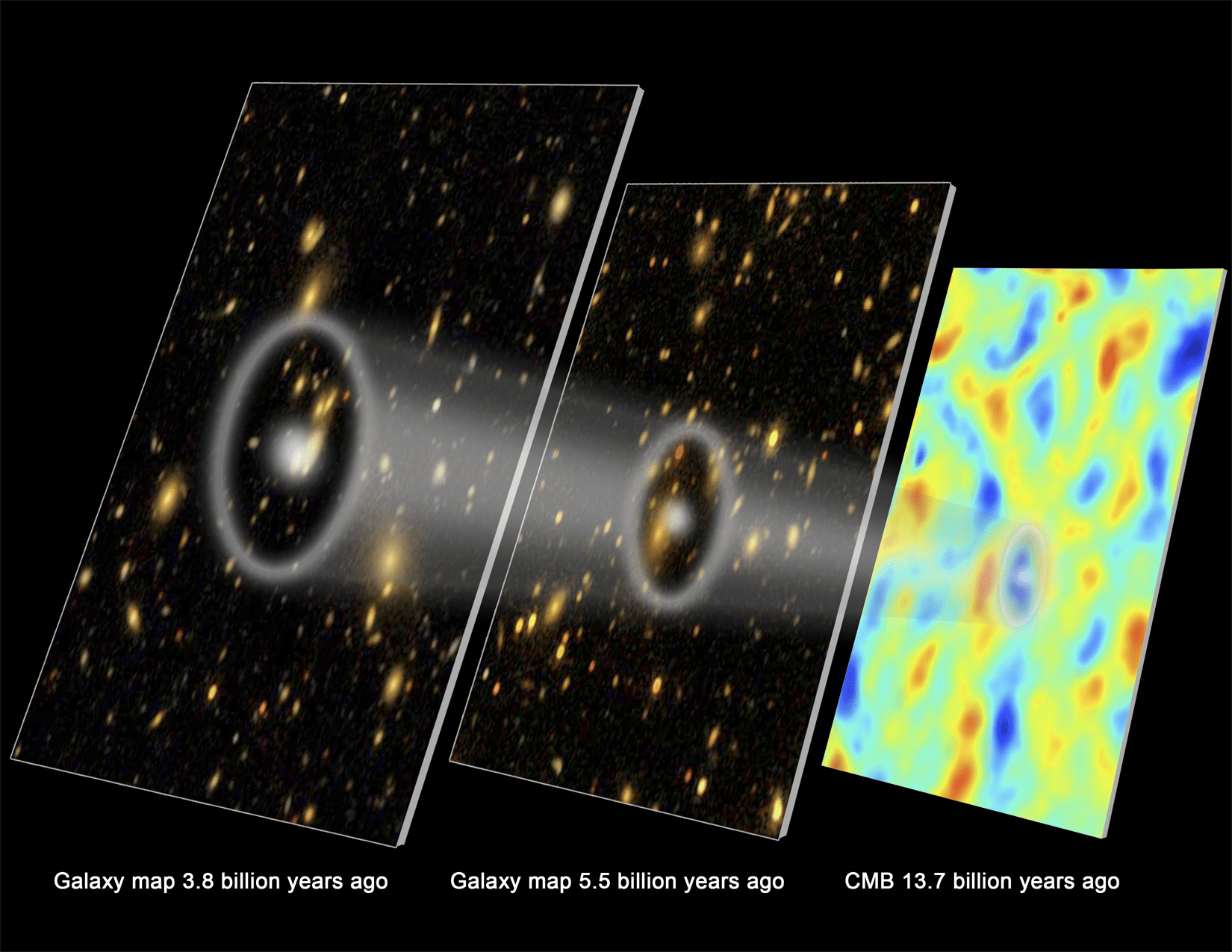
What happened between z=1000 and z=0?

Cosmologists looked up:

What happened between z=1000 and z=0?

(Image credit: DESI Collaboration/KPNO/NOIRLab/NSF/AURA/P. Horálek/R. Proctor)

we Basically KNOW how to measure:

Positions of galaxies in the sky (angles)
Redshifts of galaxies (photo or Spectro)
Shapes (ellipticities of galaxies)

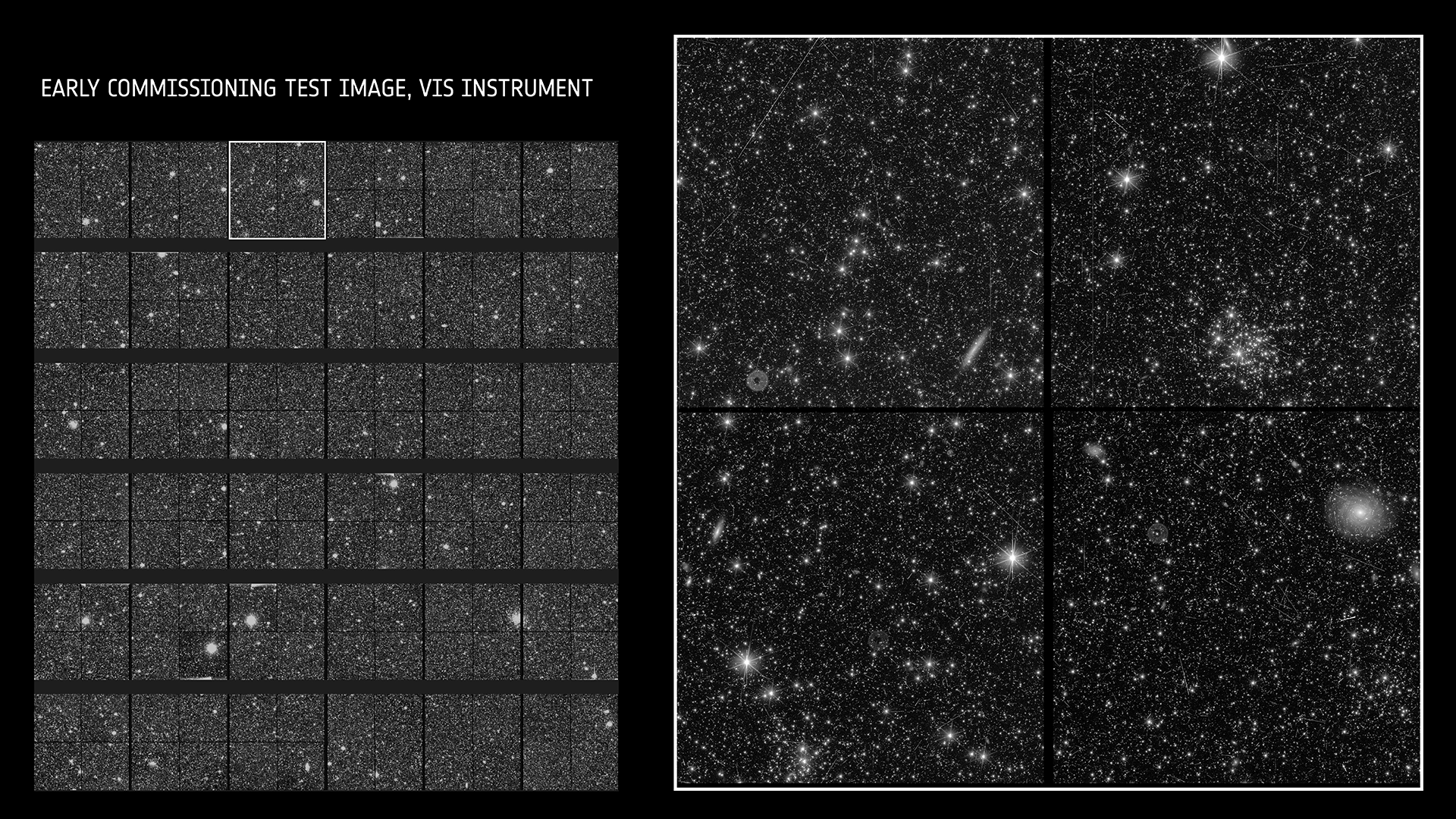
https://www.esa.int/Science_Exploration/Space_Science/Euclid/Euclid_test_images_tease_of_riches_to_come

Do galaxies just randomly spread out across the sky?

https://www.esa.int/Science_Exploration/Space_Science/Euclid/Euclid_test_images_tease_of_riches_to_come

No they do not, there is actually a 2-point correlation (and higher orders) among them

Expresses the excess probabilty of finding another galaxy as a function of scale

Strong hint that some physical mechanism is at play!!

https://www.esa.int/Science_Exploration/Space_Science/Euclid/Euclid_test_images_tease_of_riches_to_come

Shape and orientation of galaxies is also correlated -- due to Weak Gravitational Lensing -- and this tells us about the content of (dark) mass-energy in the Universe

Some successful (STAGE-III) missions exploring these two aspects so far:

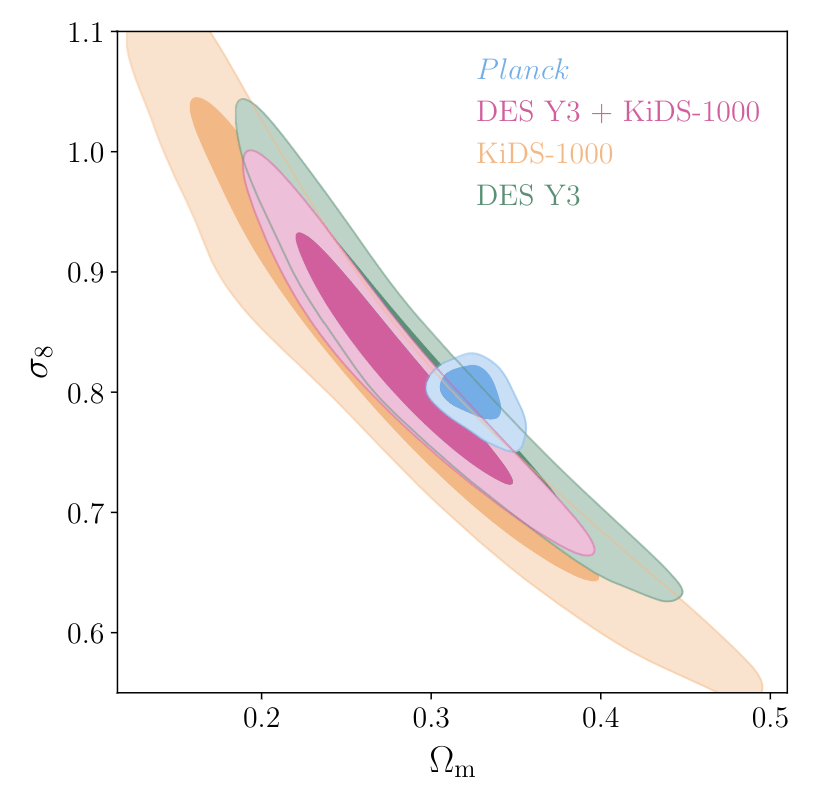
DES (Dark Energy Survey) and KiDS (Kilo-degree survey): photometric WL and Galaxy Clustering (angular)

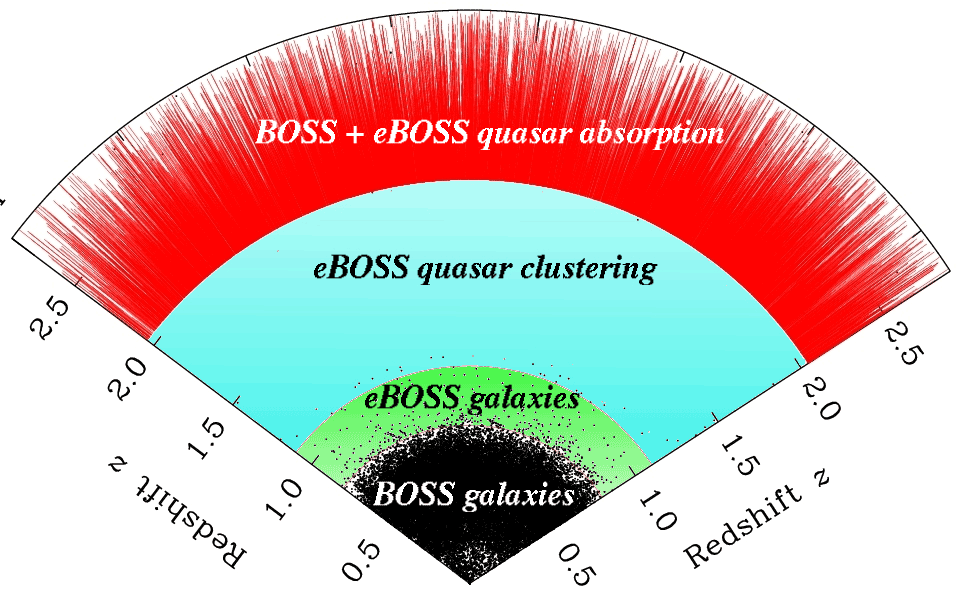
SDSS, BOSS, eBOSS:

spectroscopic galaxy clustering

DES Y3 + KIDS-1000: CONSISTENT COSMOLOGY COMBINING COSMIC SHEAR SURVEYS (2305.17173v2)

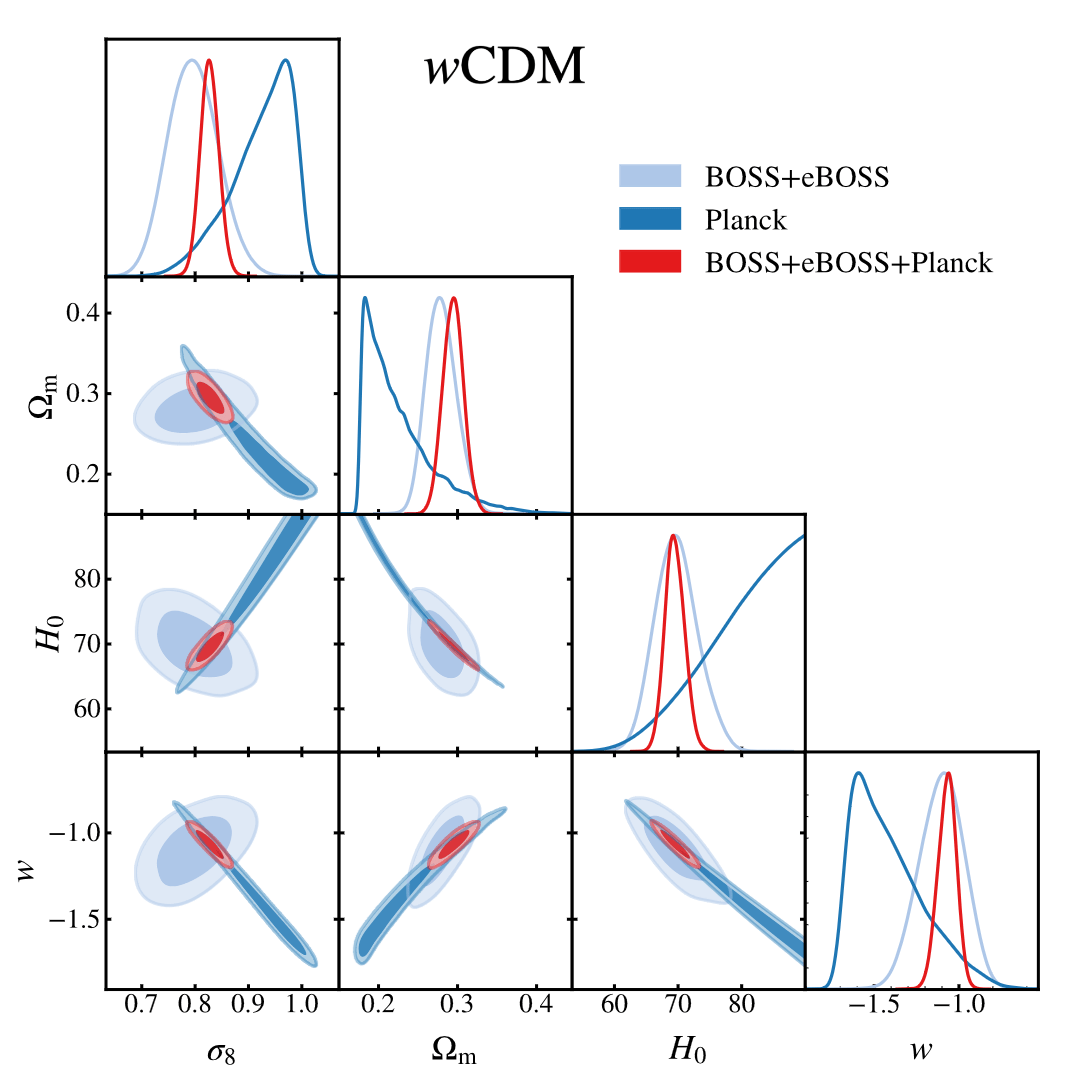
Beyond - ΛCDM constraints from the full shape clustering measurements
from BOSS and eBOSS (2210.07304)

Everything roughly so far so good....

The Standard $\Lambda$CDM model

G_{\mu \nu} + \Lambda g_{\mu \nu} = 8\pi G T_{\mu \nu}

$\Lambda$CDM is still best fit to observations.
Some questions remain:
$\Lambda$ and CDM.
CDM hasn't been found directly
Cosmological Constant Problem:

Quantum Gravity?

O(100) orders of magnitude wrong
(Zeldovich 1967, Weinberg 1989, Martin 2012).
Composed of fine-tuning, hierarchy and coincidence
sub-problems, among others.

String Theory Landscape?

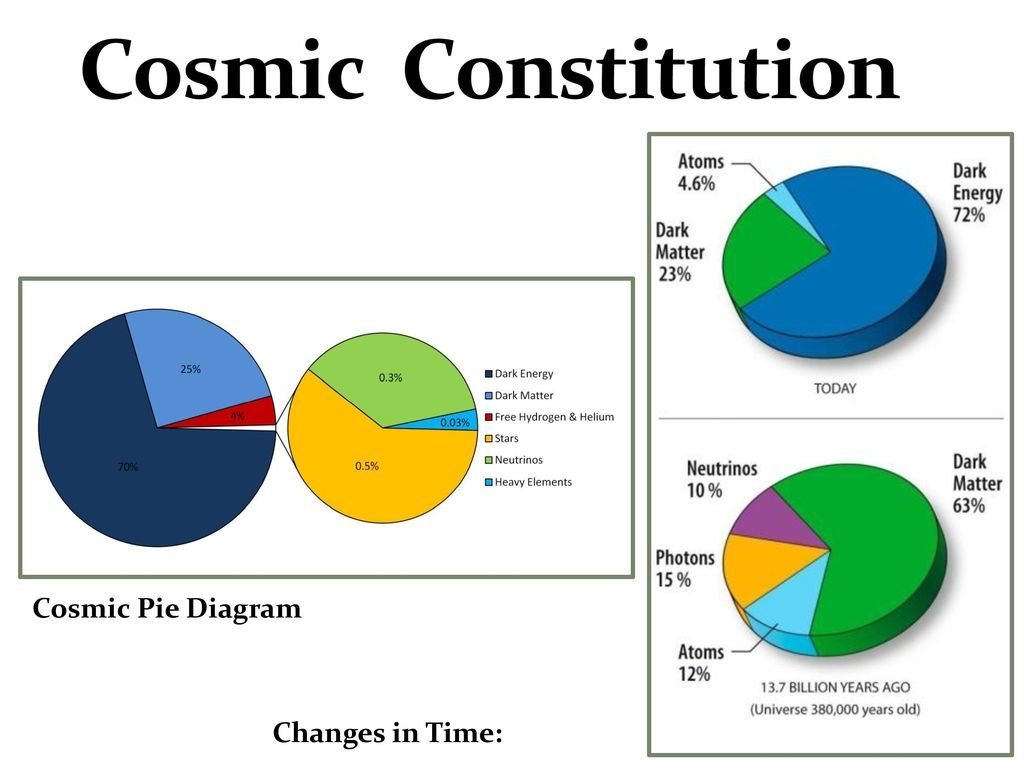
68% Dark Energy

5% Baryons

27% Dark Matter

The expansion History

$\phi$ ?

baryogenesis? $_3^7\textrm{Li}$?

H0 tension?

z_reio?

$\Lambda$ ?

DM? PBH ?

Tensions IN $\Lambda$CDM

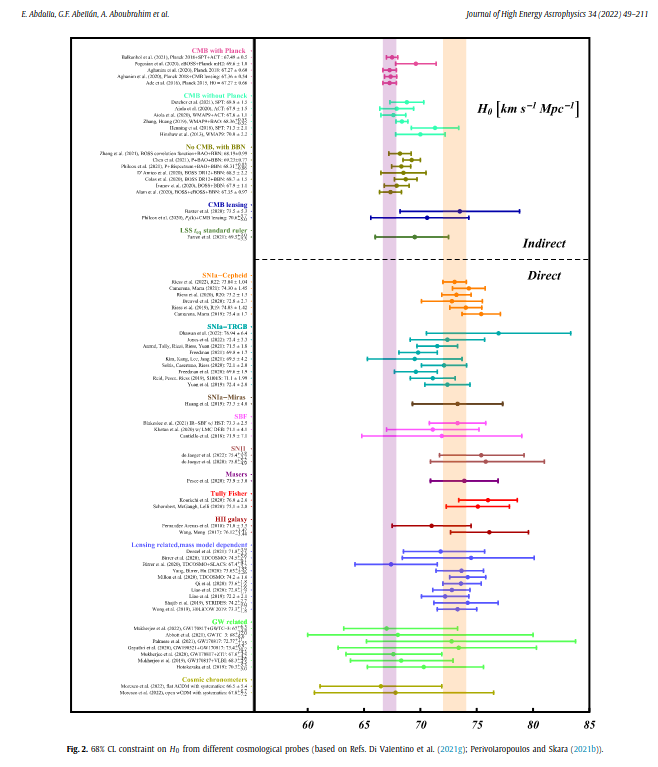
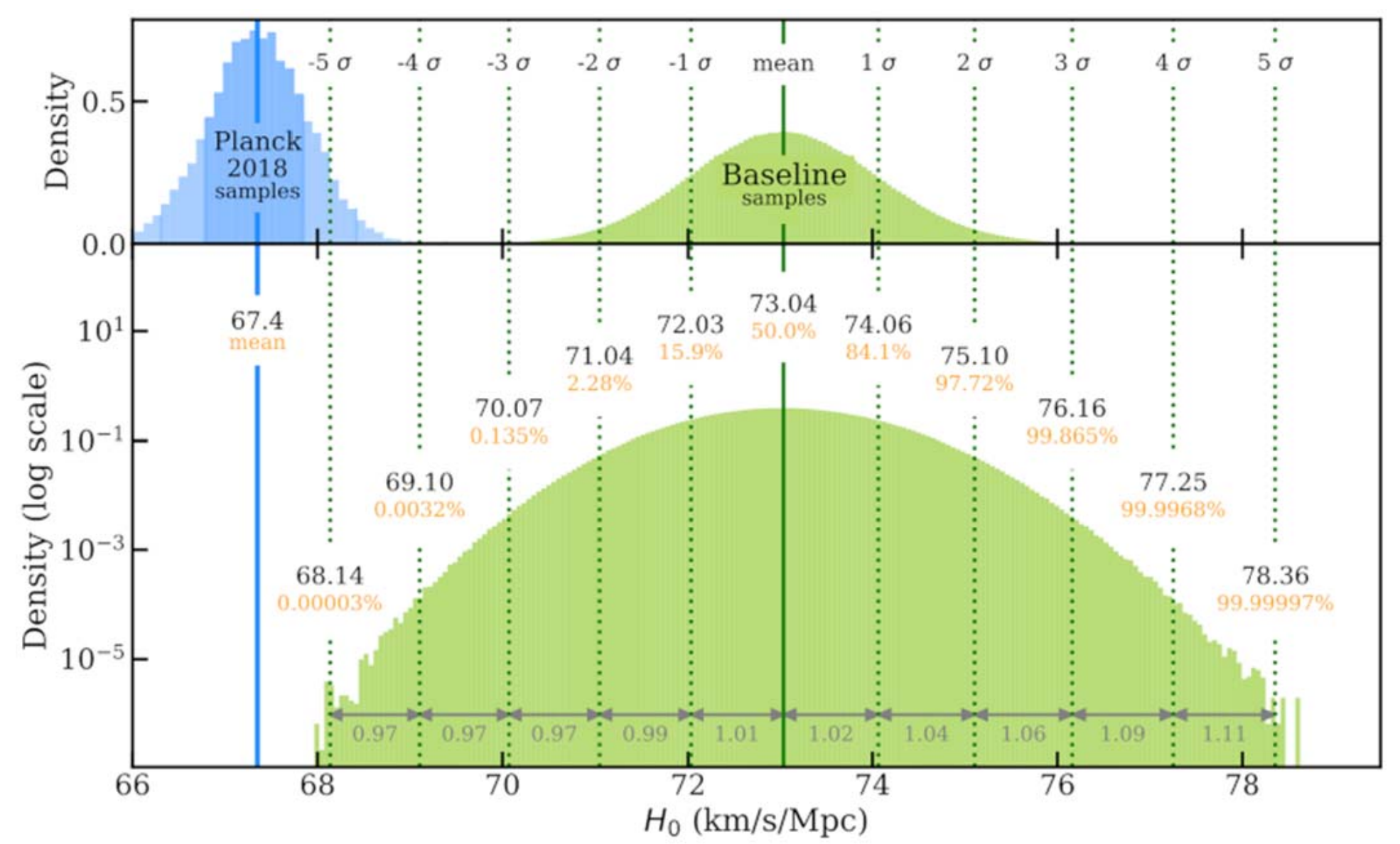
$H_0$ tension at 5$\sigma$

Tensions between local and sound-horizon-based measurements

Freedman et al

SH0ES, Riess et al

Planck 2018, VI

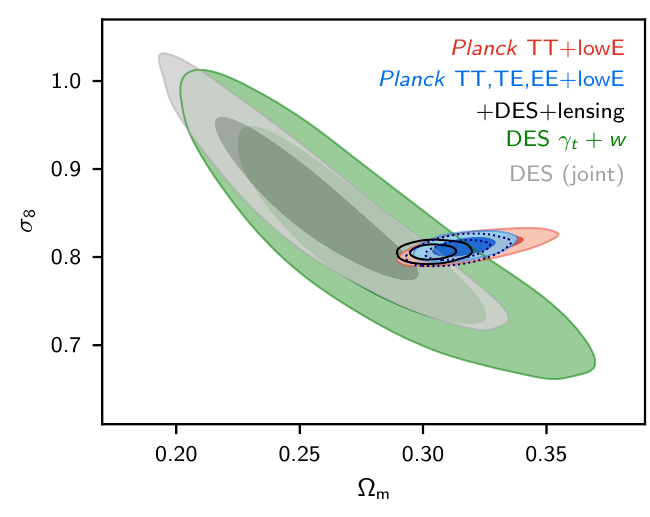
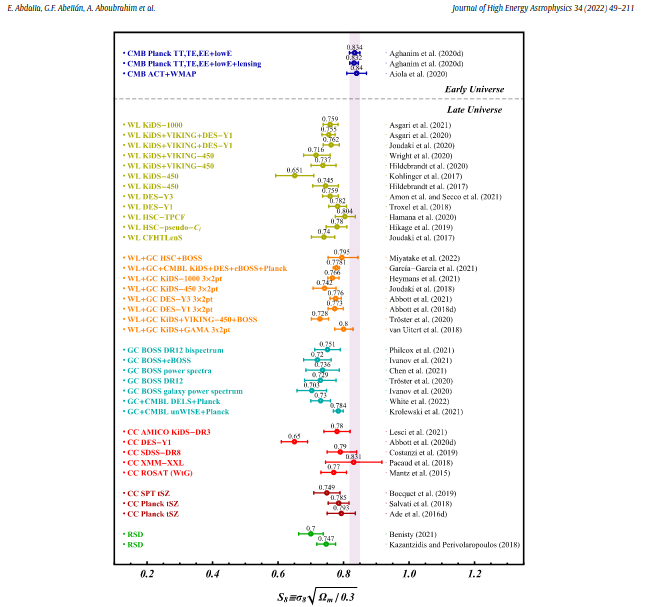
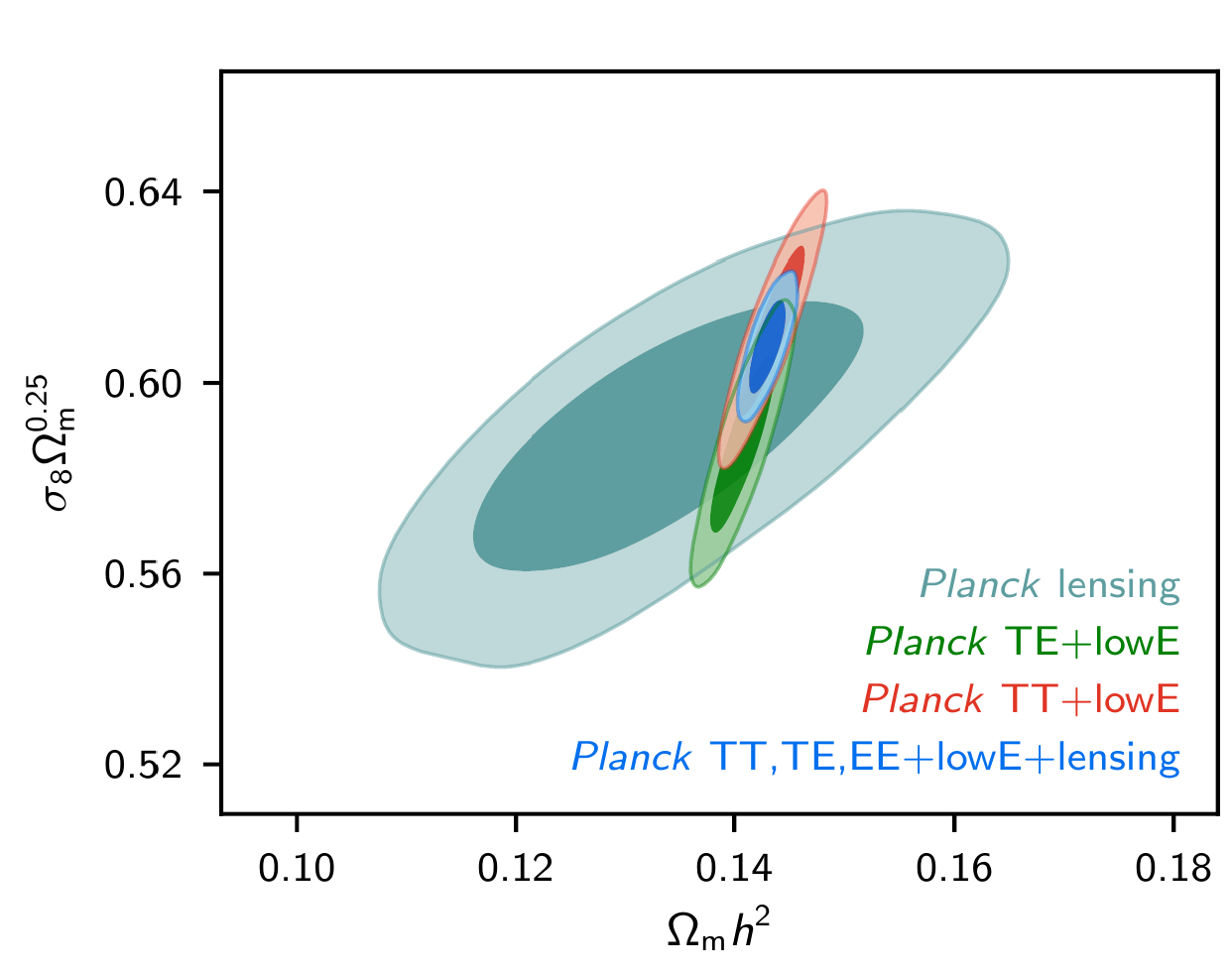
Tension with Planck in the
$\sigma8$ - $\Omega_m$ plane

Lange et al. arXiv: 2301.08692

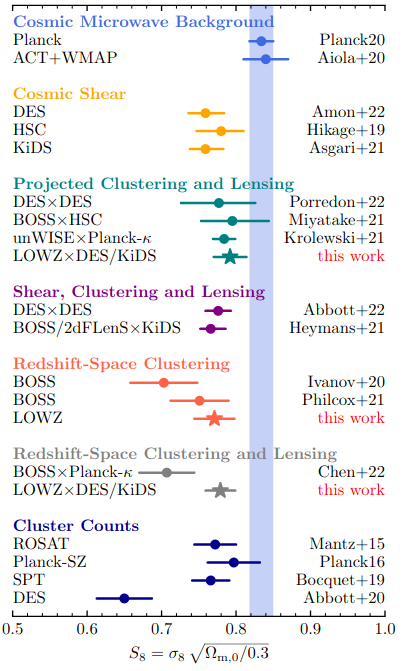
$ S_8 = \sigma_8 \sqrt{\Omega_{m,0}/0.3} $
So called "lensing is low" problem or S8 problem.
At the moment just a discrepancy (no tension) at 2-3 $\sigma$
Blind comparisons among surveys can rule out usual systematics below z<0.54 (A. Leauthaud et al.)
Beyond $\Lambda$CDM modelling does not help with current nonlinear analysis

Planck 2018, VI

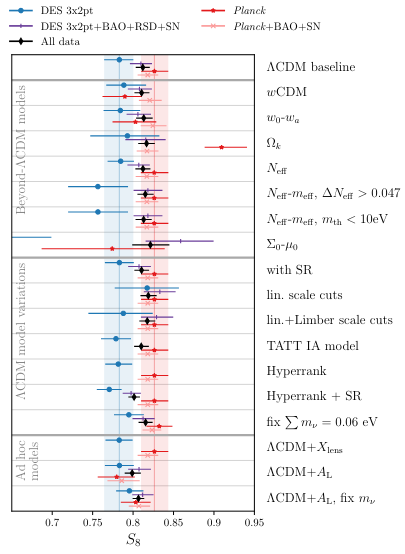
DES DRY3 arxiv:2207.05766

Tensions IN $\Lambda$CDM

Stage-IV surveys to the rescue?

https://www.esa.int/Science_Exploration/Space_Science/Euclid/Euclid_test_images_tease_of_riches_to_come

With Stage-IV surveys we will have $\approx 10^9$ galaxy shapes with photometric (approximate) and $\approx 10^6$ (precise) redshifts and positions

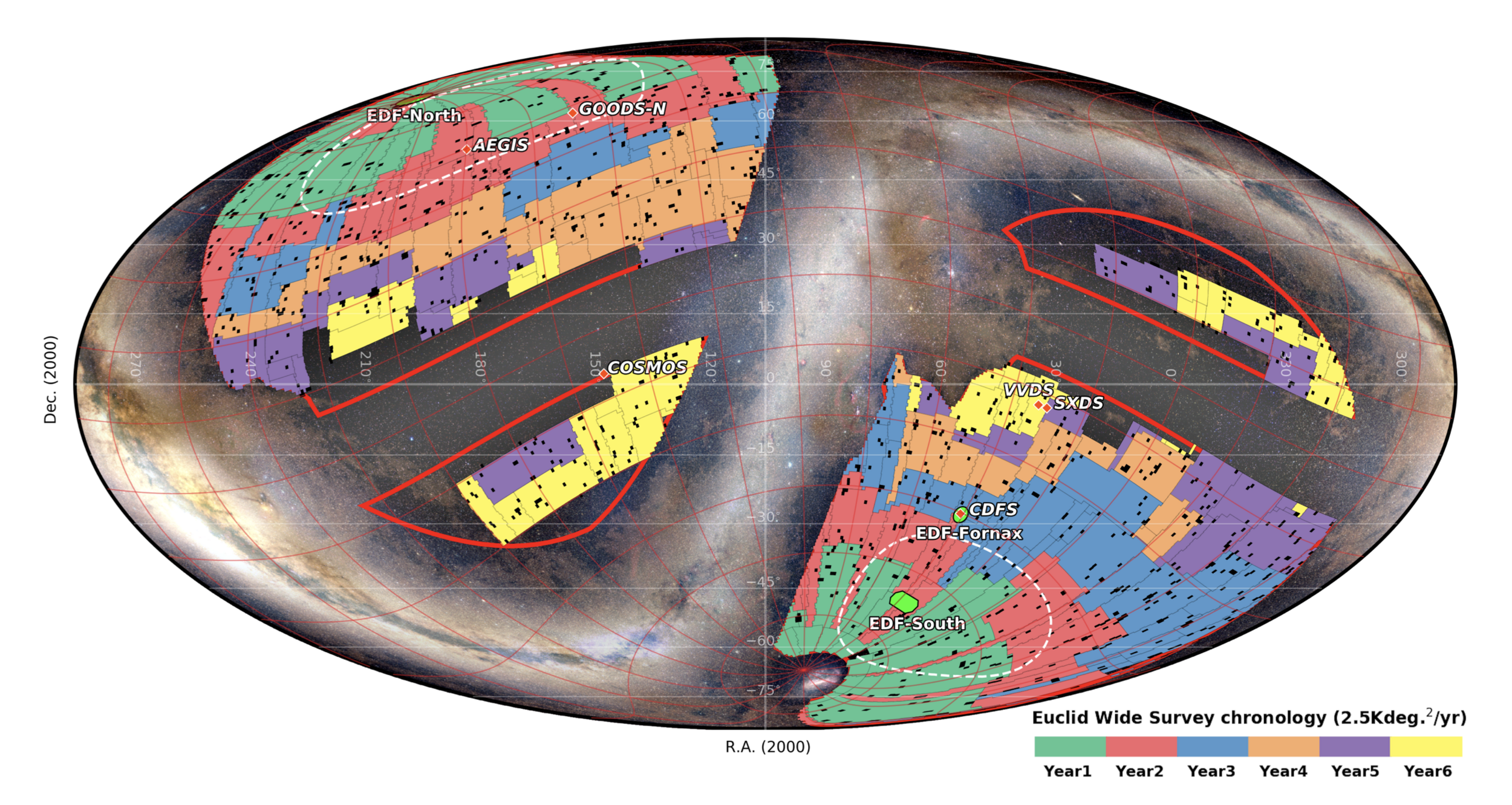
Only 1/64th of the complete Euclid field of view is represented here, which in turn is equivalent to a mere quarter of the apparent size of the Moon. Consider the vast expanse of 15,000 square degrees, encompassing one-third of the entire sky!

Euclid Space Satellite

ESA class M2 space mission, Launched 1st July 2023 with a SpaceX Falcon9 rocket

Credits: www.esa.int/Science_Exploration/Space_Science/Euclid, www.euclid-ec.org, ESA/NASA/SpaceX, Euclid Consortium

Sun-Earth Lagrange point 2, 1.5 million km from Earth

Euclid consortium scientist visits Cannes. Credits: ThalesAlenia Space

The Euclid Consortium fingertip galaxy, thanks to the contribution of many scientists within the EC, courtesy of Lisa Pettibone, Tom Kitching and ESA

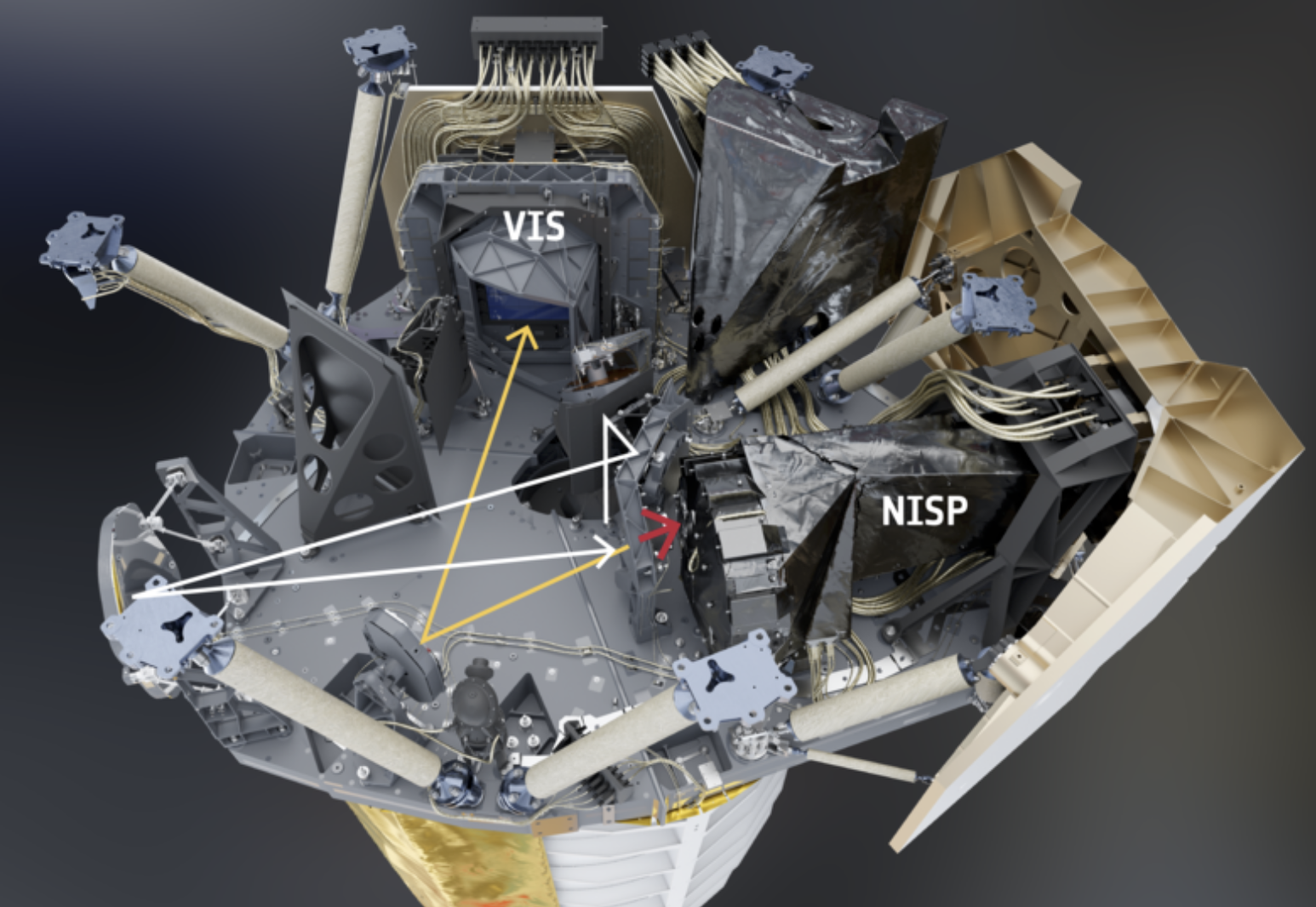
Euclid Space Satellite

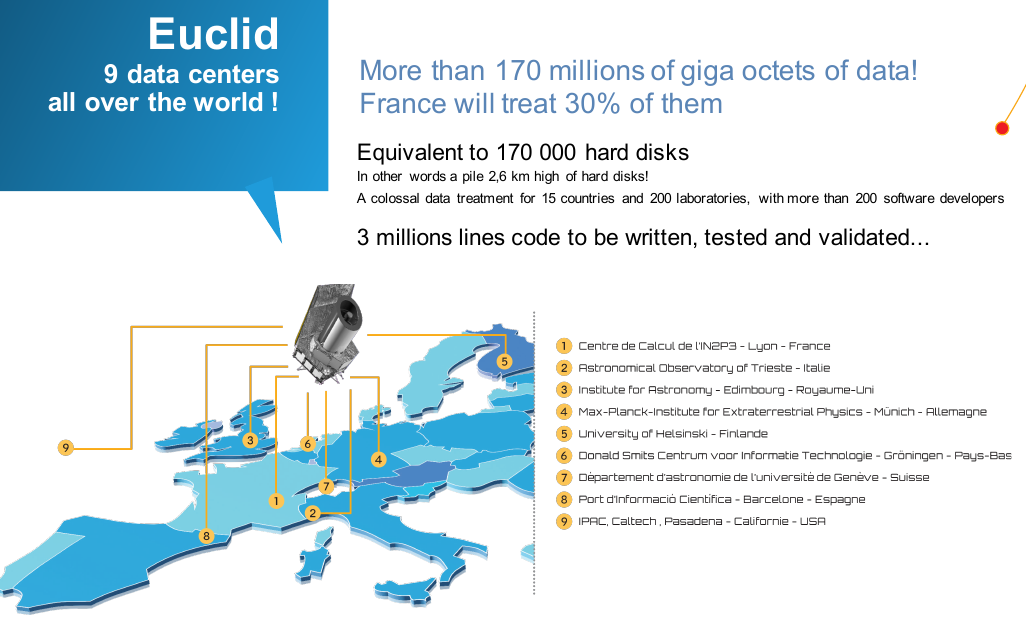
Two instruments:
VIS (visible photometer): shape and orientation of ~1 billion galaxies!
NISP (near infrared spectrograph): ~20 million galaxy spectra !
6 years nominal mission

15 000 square degrees in the sky
16 countries, ~1500 members
~170 Petabyte of data!

VIS cosmic shear map

https://www.euclid-ec.org/blog/

Euclid preparation: I. The Euclid Wide Survey of ESA, R. Scaramella et al.

VIS cosmic shear map

Vera Rubin LSST

Located in Chile, 8.4m telescope
3.2 Gigapixel camera!
20 billion galaxies
Redshifts: 0 < z ~< 3 (photometric)
18,000 square degrees
11 years of observation
3x2pt, clusters, SNIa and more!

By LSST Project Office - http://www.lsst.org/gallery/telescope-rendering-2013, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=42054166

Vera Rubin LSST

DESI telescope

14 000 square degrees in the sky
20-40 million accurate spectra
Redshifts: 0 < z < 2 (spectroscopic)
Quasars up to z~3.5
5 years of observation
Starting 2021
Power spectra, Bispectra, Corr. Func.

DESI Data Release 1

5000 robotically controlled optical fibers

Tucson, Arizona, in the Schuk Toak District on the Tohono O’odham Nation

Credits: https://www.desi.lbl.gov

Vera Rubin LSST

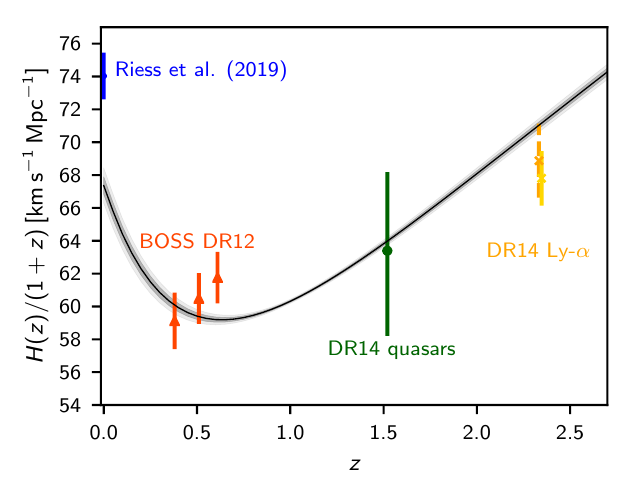
DESI Baryon Acoustic Oscillations

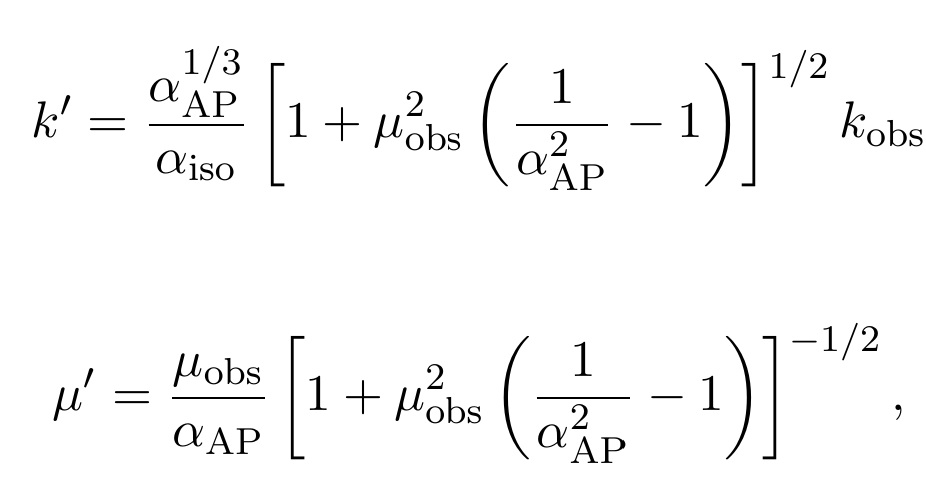
In a nutshell: Measure a geometric scale that was imprinted on LSS at recombination

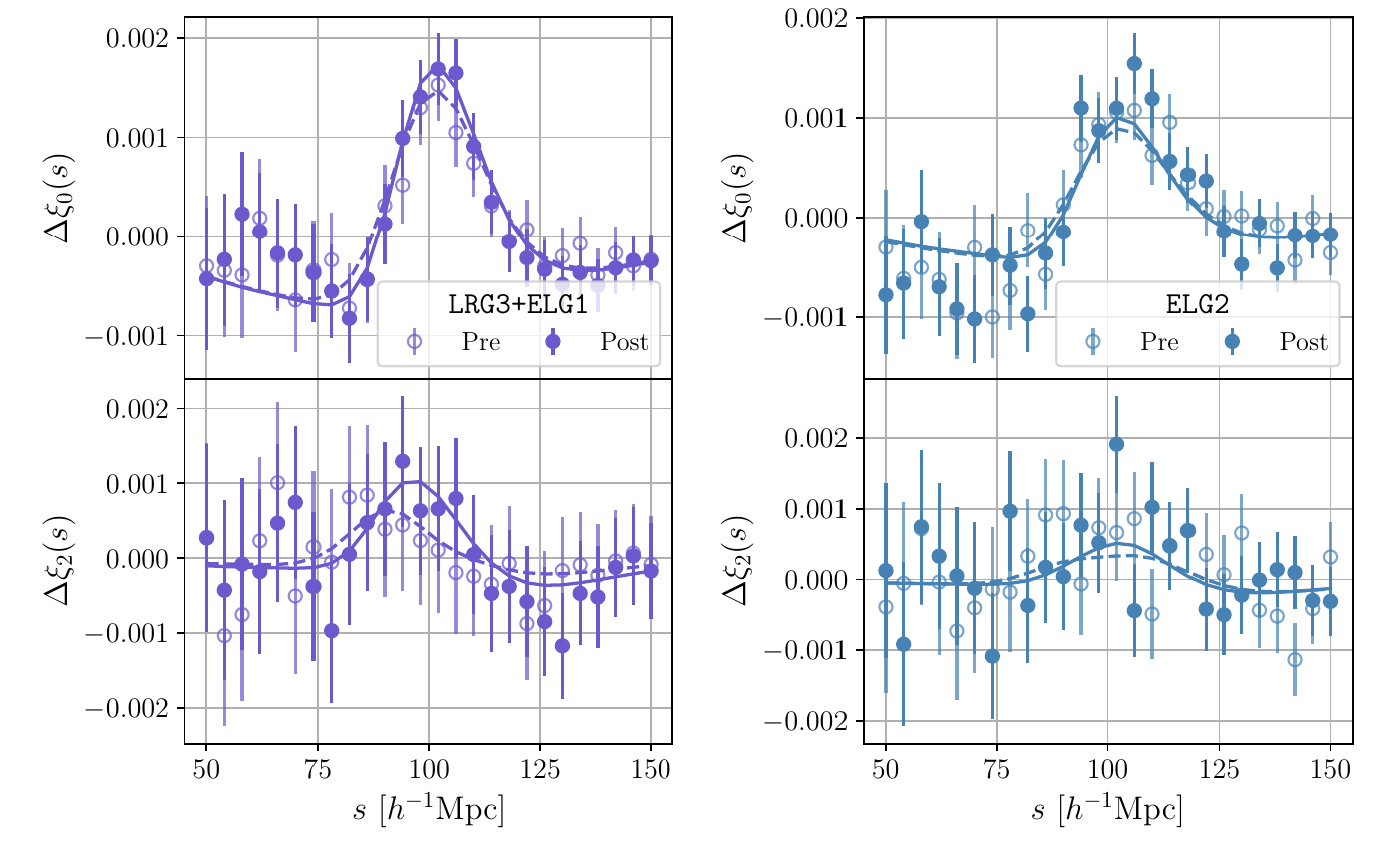
https://data.desi.lbl.gov/doc/papers/

Another tension we need to explain?

Vera Rubin LSST

Square kilometer array (SKAO)

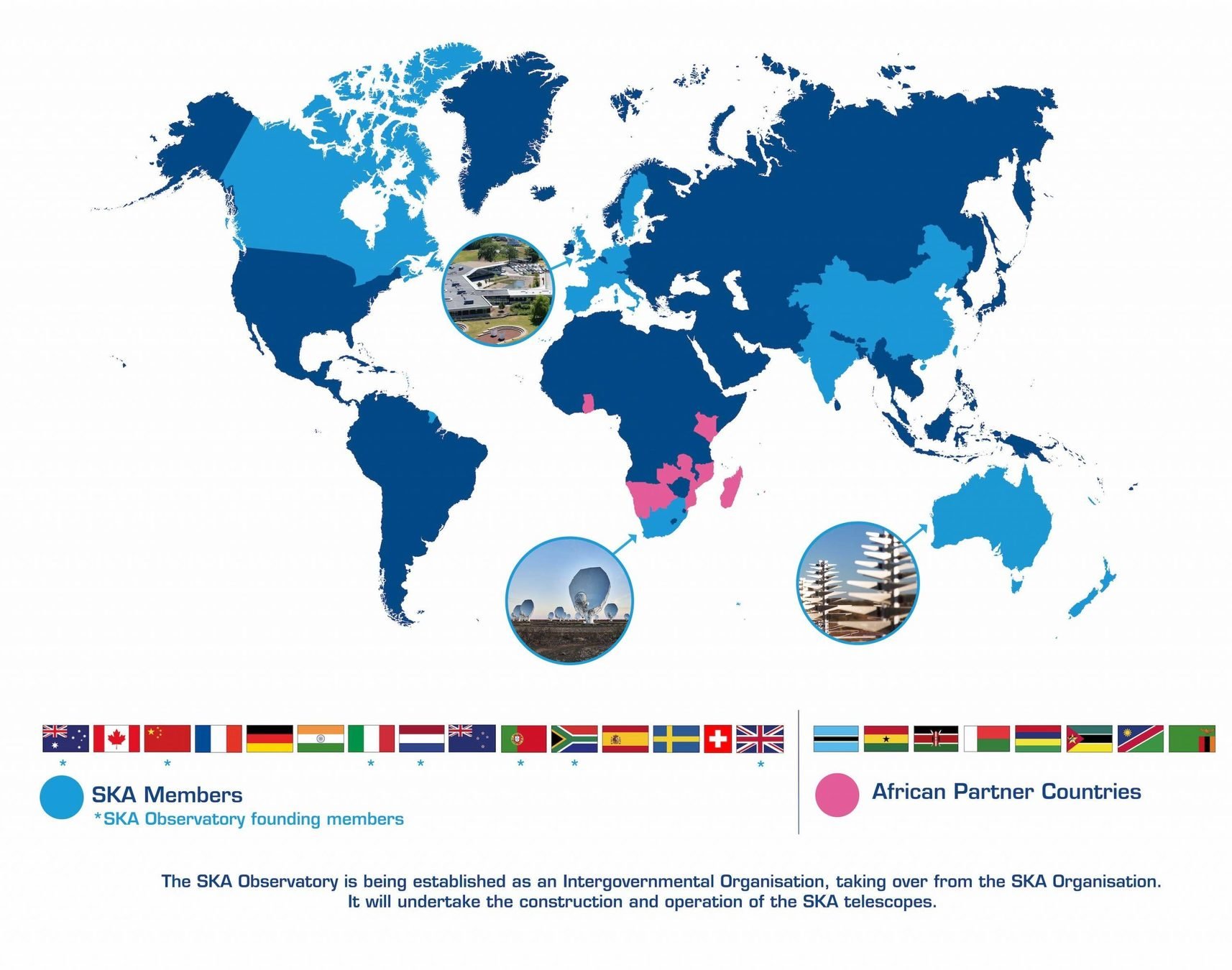
SKA Phase 1: SKA1-Low and SKA1-Mid
SKA1-Low: 130,000 dipole antennas, 65km max. baseline (Australia)
SKA1-Mid: ~200 dishes of ~15m diameter, max. baseline 150km (South Africa)
Precursors: ASKAP, MEERKAT, HERA...
€1.3 Billion, 16 countries, 710 Petabytes, 8 years construction

Google maps

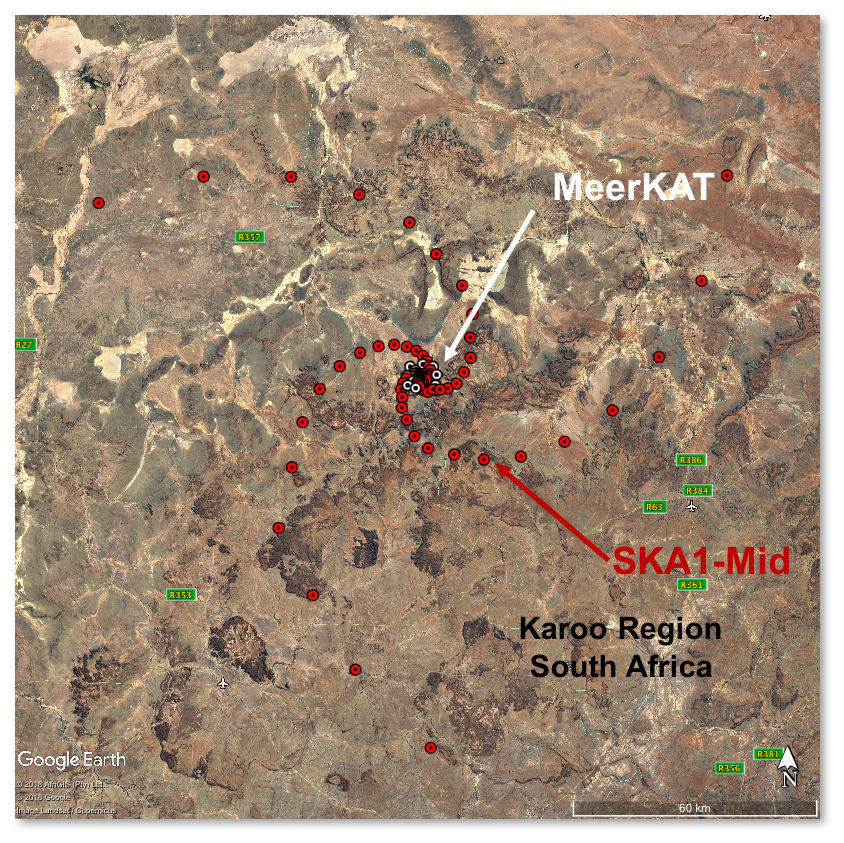
https://www.skao.int/

Other Large Scale Structure Probes I WOn't MENTION IN THIS TALK:

CMB LEnSING and ITS Cross-Correlation with LSS
Cosmic VOIDS
NON-Gaussian and HIGHER ORDER STatistics
CLUSTERS of GALAXIES
....

We have many problems/Mysteries in cosmology

BUT let's focus on a classical one

why is the universe accelerating?

(assuming we don't like $\Lambda$)

First Step: Modify Gravity

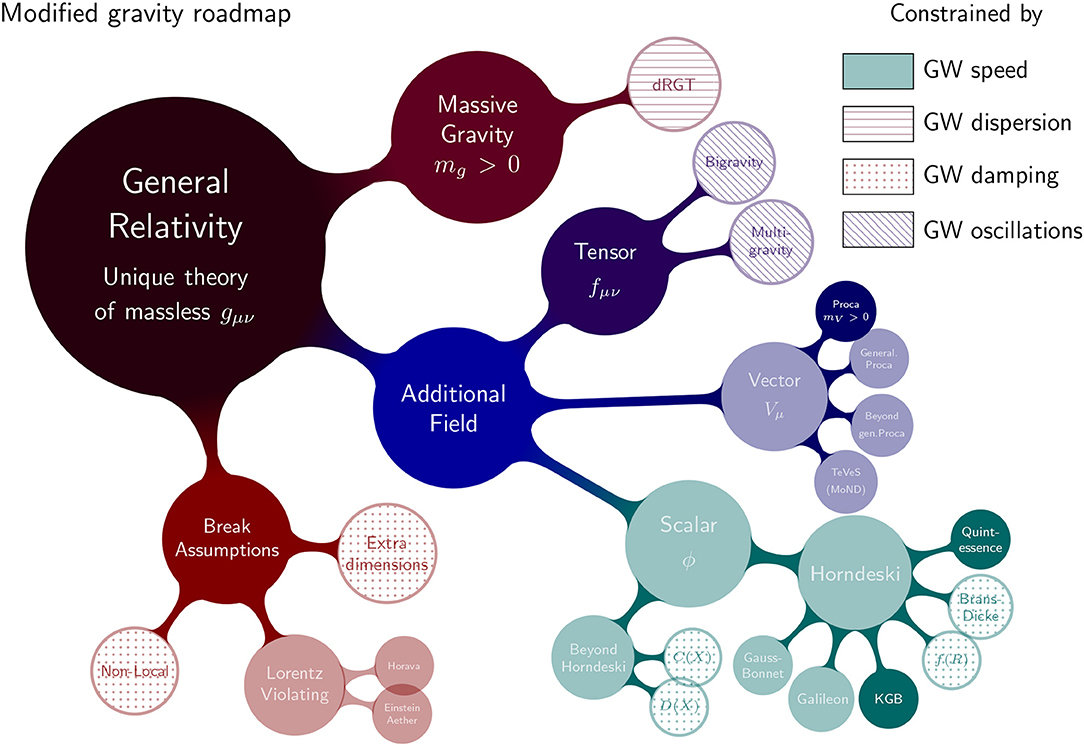
Ezquiaga, Zumalacárregui, Front. Astron. Space Sci., 2018

Dynamical Dark Energy

Dark Energy: Any dynamical cause for the accelerated expansion.

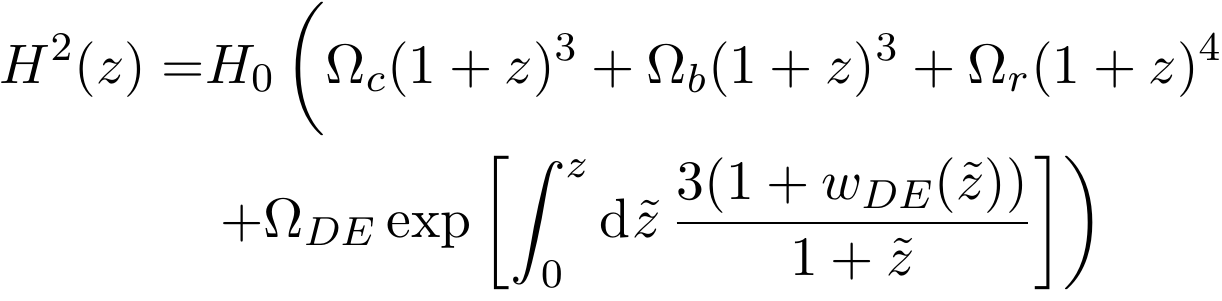
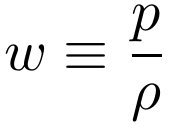
Euclid was commissioned to test with observations the most common parametrization (CPL):

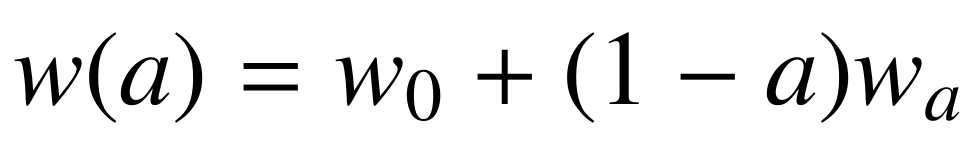
And possible deviations of the growth of structures

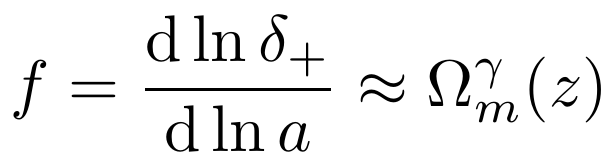
M. Chevallier and D. Polarski (2001), and E. Linder (2003),
Cosmology and Fundamental Physics with the Euclid Satellite (Amendola et al , Living Reviews in Relativity, 2018)

Dynamical Dark Energy

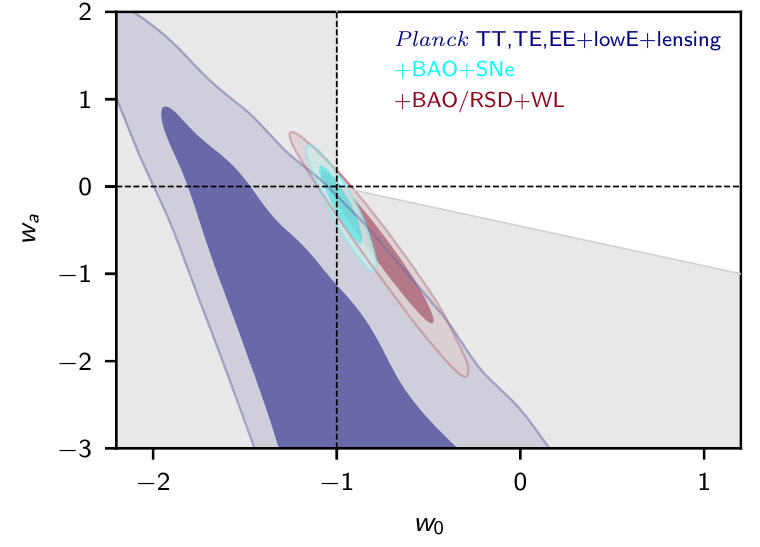
Current bounds from CMB and LSS alone
$\mathcal{O}(1)$ for $w_0$ combining Planck+GC+WL+SNIa
$\mathcal{O}(0.01)$ with Euclid

Here: Flat $w_0 w_a\mathrm{CDM}$
GCsp+WL+GCph+XC
Figure of Merit (~inverse area of ellipse):
1257 (flat)
Non-flat FoM:
500
Optimistic flat:
$\sigma_{w_0}=0.025$
$\sigma_{w_a}=0.092$

Euclid preparation: VII. Forecast validation for Euclid cosmological probes, Blanchard et al. arXiv:1910.09273

Awardees of the Euclid STAR Prize Team 2019

Dynamical Dark Energy

Current bounds from CMB and LSS alone
$\mathcal{O}(1)$ for $w_0$ combining Planck+GC+WL+SNIa
$\mathcal{O}(0.01)$ with Euclid

Here: Flat $w_0 w_a\mathrm{CDM}$
GCsp+WL+GCph+XC
Figure of Merit (~inverse area of ellipse):
1257 (flat)
Non-flat FoM:
500
Optimistic flat:
$\sigma_{w_0}=0.025$
$\sigma_{w_a}=0.092$

Awardees of the Euclid STAR Prize Team 2019

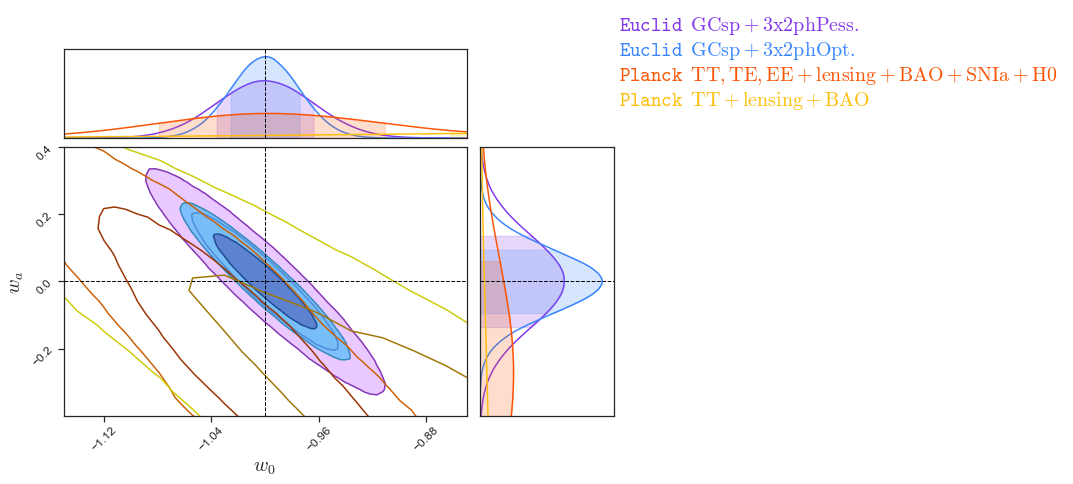
Euclid preparation: VII. Forecast validation for Euclid cosmological probes, Blanchard et al. arXiv:1910.09273

Dynamical Dark Energy

Wolf, Ferreira 2310.07482

Problems with Dynamical DE CPL parametrization:

It is just a first order Taylor expansion around $a=1$
It is underdetermined, prior- and data-dependent
parts of $ w_0 - w_a $ space do not match any meaningful model
Many physical Quintessence models can recover same parameters even if we find $ w_0 \neq -1 , w_a \neq 0 $

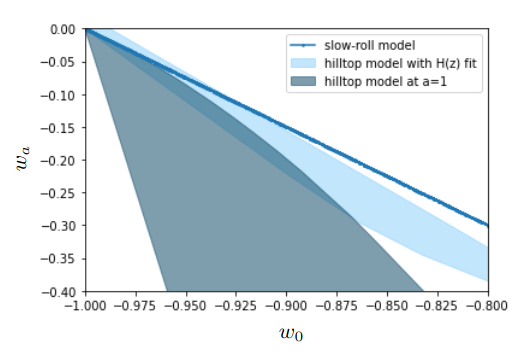
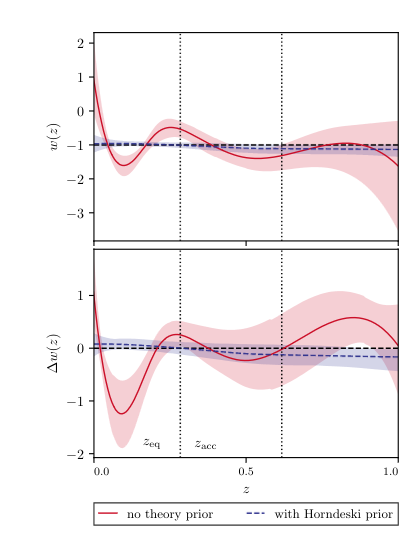
Raveri et al, 2107.12990

how do we do these forecasts again?

spectroscopic probe

BAO / AP-effect

Clustering

RSD

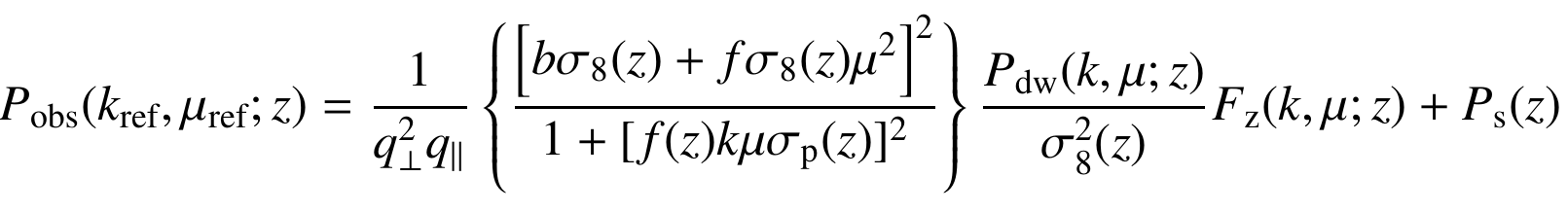
Spec-z

Euclid will also measure the 2pt corr-func of spectroscopic galaxies in redshift space

Euclid preparation: VII. Forecast validation for Euclid cosmological probes, Blanchard et al. arXiv:1910.09273

FoG

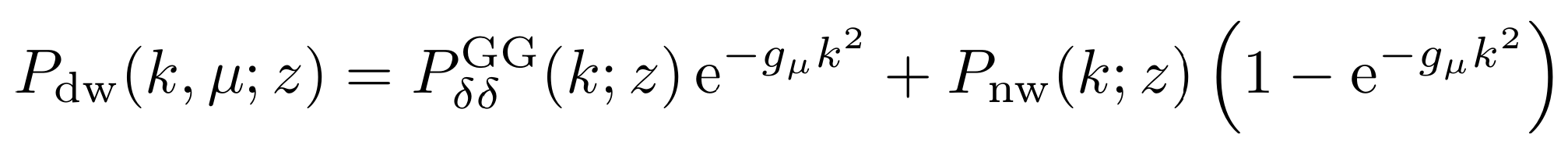
BAO-damping / IR-resummation

photometric primary probe

Euclid preparation: VII. Forecast validation for Euclid cosmological probes, Blanchard et al. arXiv:1910.09273

photometric primary probe

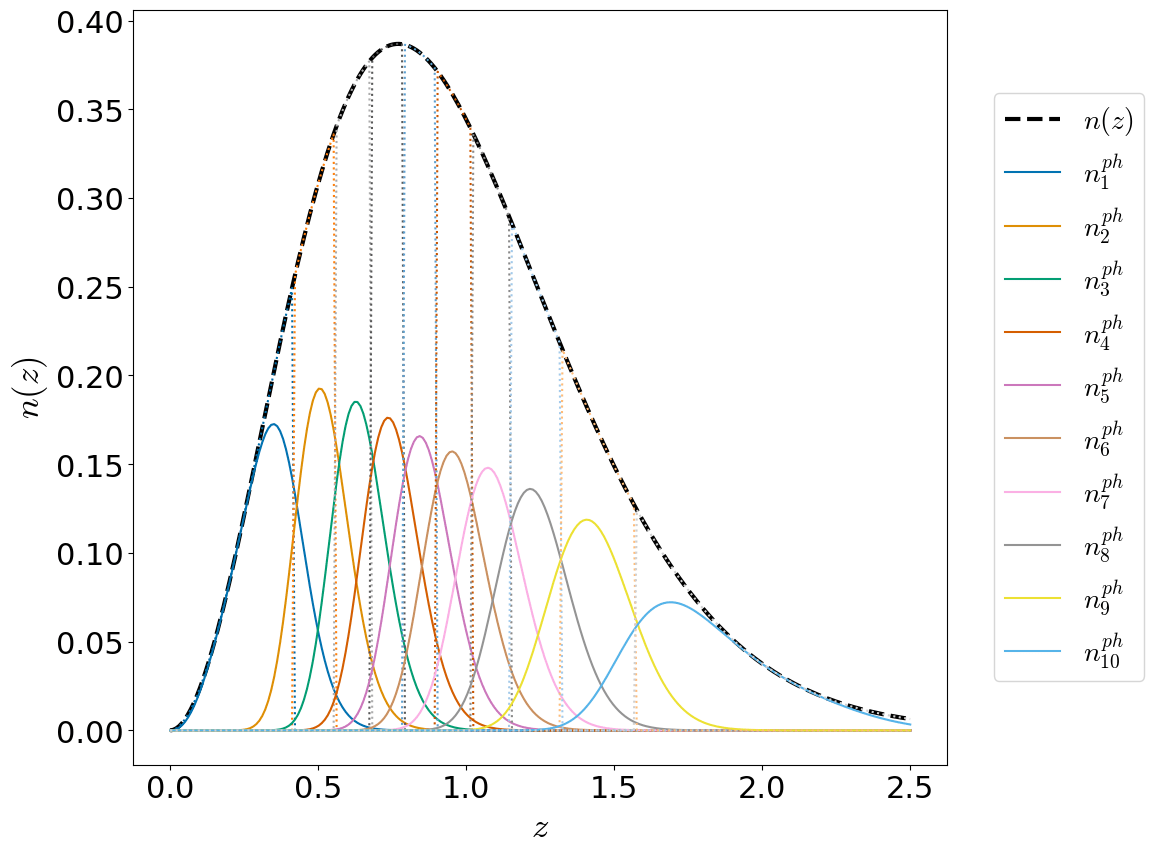
Photometric galaxy density distribution.
Bins convolved with photometric redshift PDF
10-15 bins in future Stage-IV surveys

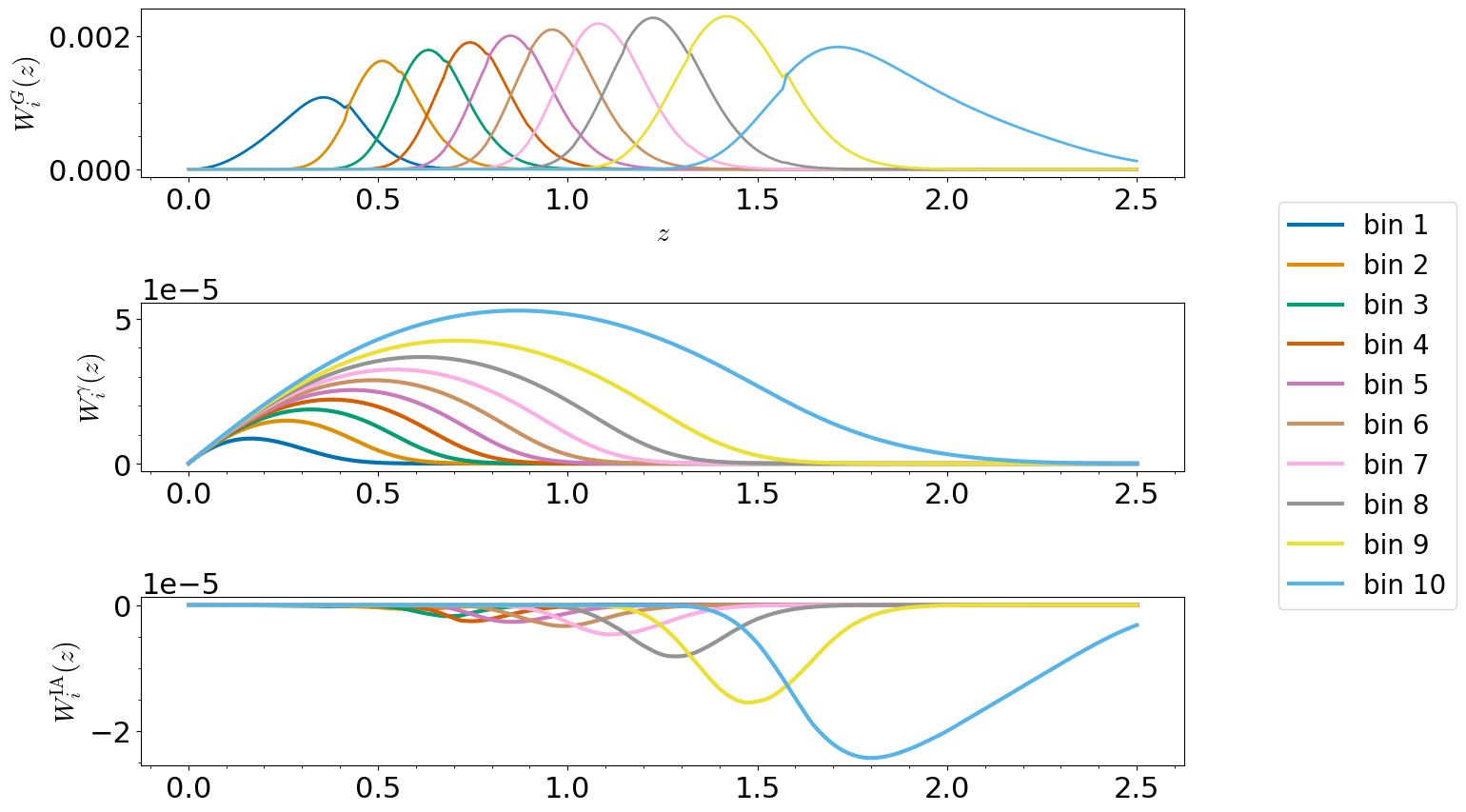
Window functions (Kernels projecting correlations into angular space) -> Limber
Cosmic Shear Kernels are "delocalized" in z -> k
Localization techniques such as BNT to allow for clear cuts

Euclid: Forecasts for $k$ -cut $3 \times 2$ Point Statistics, P. Taylor, V. Cardone, ..., SC, et al. 2012.04672

Fisher Matrix Forecasts

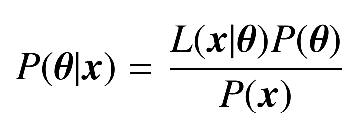
Bayes Theorem:

Probability of the model parameters given the data

Fisher Information Matrix:

Curvature (Hessian) of the Likelihood

Gaussian Likelihood in data space:

-2\ln {L}({\bm x}|{\bm\theta})=\left({\bm x}-{\bm \mu}({\bm\theta})\right)^t{ C}^{-1}\left({\bm x}-{\bm \mu}({\bm\theta})\right)

How do we actually perform those forecasts?

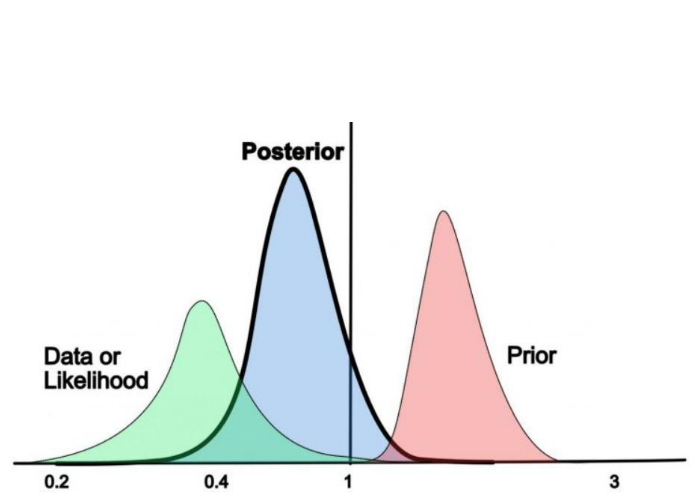
J. Schaffmeister

Euclid preparation: VII. Forecast validation for Euclid cosmological probes, Blanchard et al. arXiv:1910.09273

Fisher Matrix Forecasts

Fisher Matrix for a Gaussian likelihood of angular power spectra:

Parameter covariance:

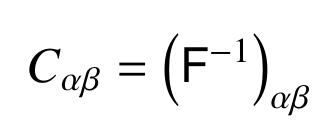
Defines an ellipse:

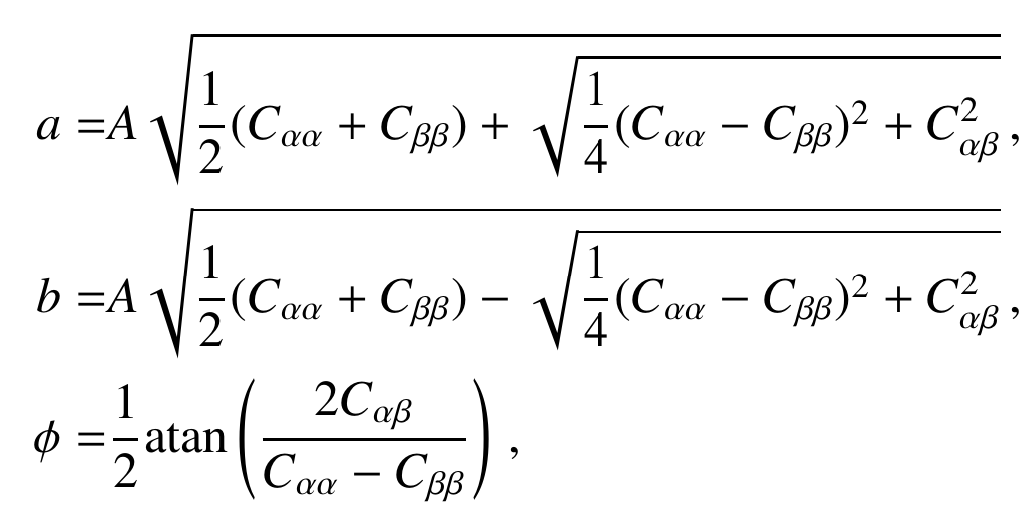
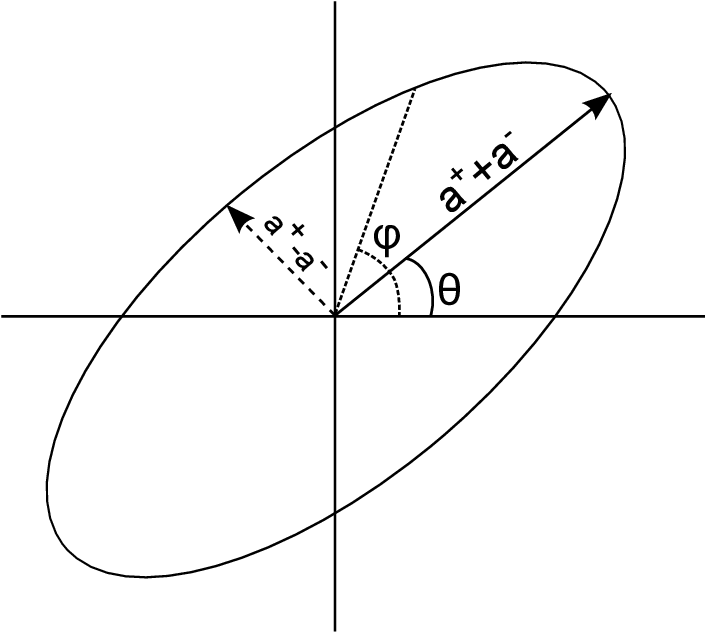
Euclid preparation: VII. Forecast validation for Euclid cosmological probes, Blanchard et al. arXiv:1910.09273

Fisher Matrix Forecasts

Euclid preparation: VII. Forecast validation for Euclid cosmological probes, Blanchard et al. arXiv:1910.09273

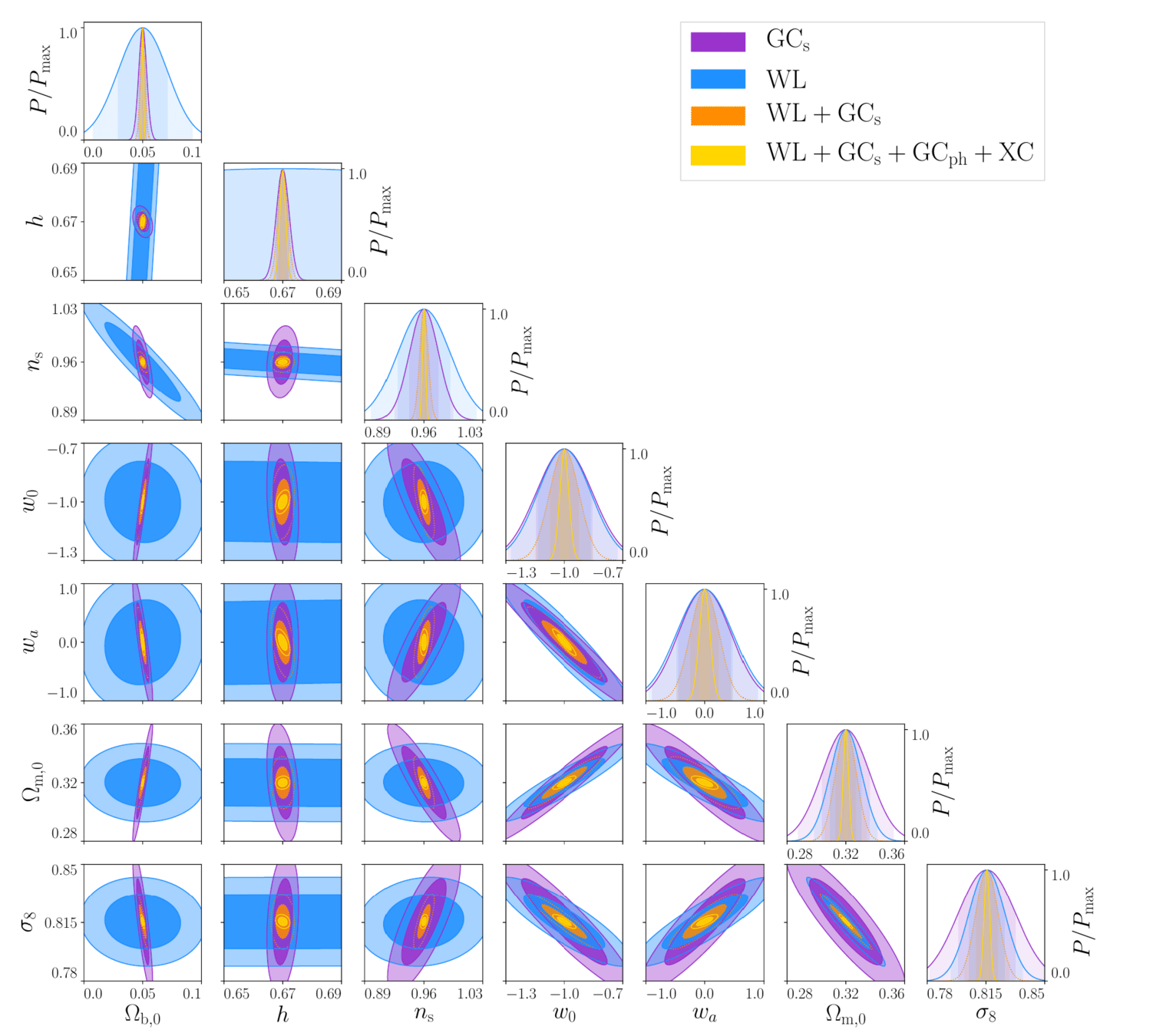
Here: Flat $w_0 w_a\mathrm{CDM}$
GCsp+WL+GCph+XC
Figure of Merit (~inverse area of ellipse):
1257 (flat)
Non-flat FoM:
500
Optimistic flat:
$\sigma_{w_0}=0.025$
$\sigma_{w_a}=0.092$

Can we trust Fisher constraints?

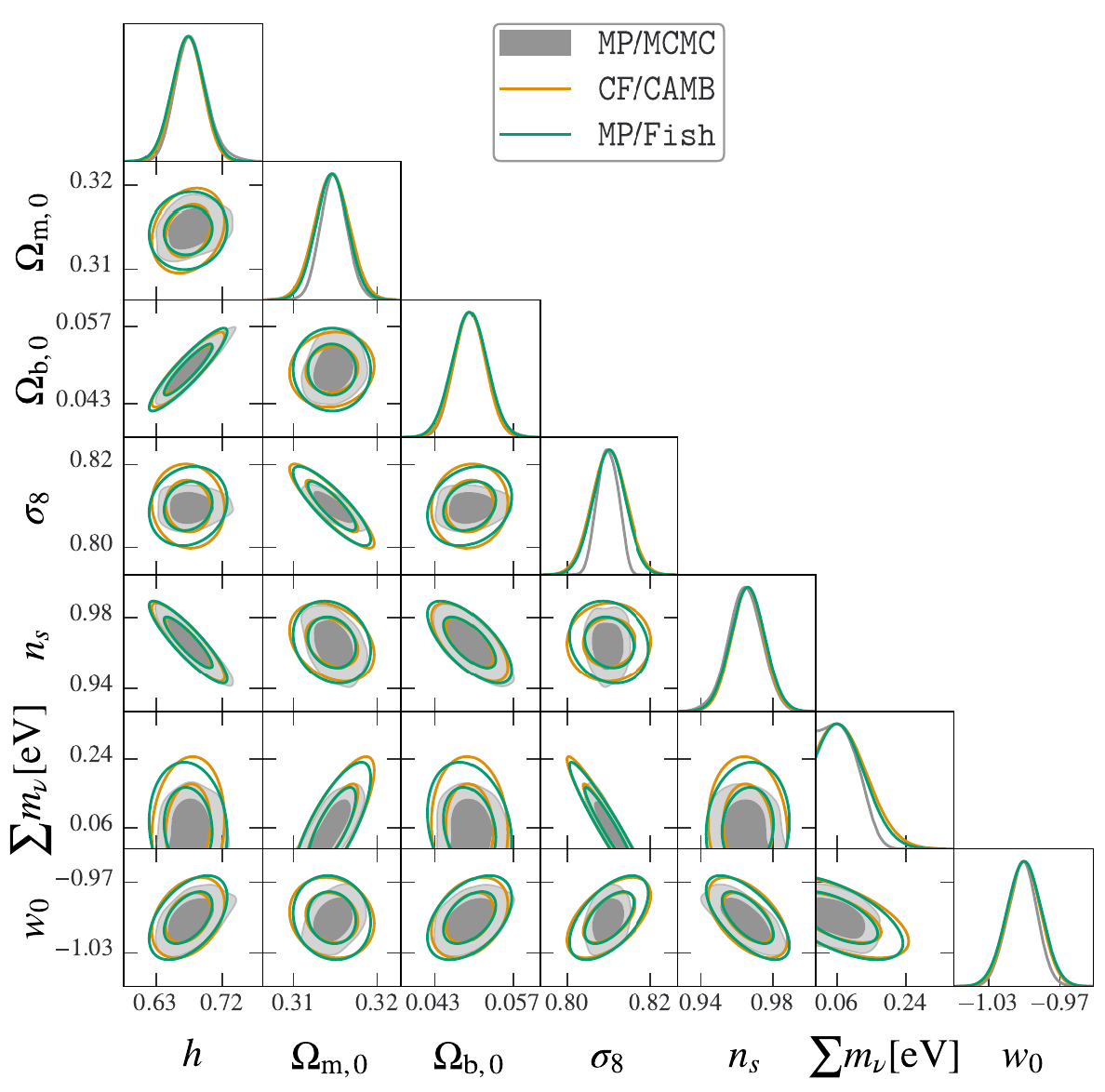
Euclid: Validation of the MontePython forecasting tools, 2303.09451 , SC, Lesgourgues, Schöneberg, et al.

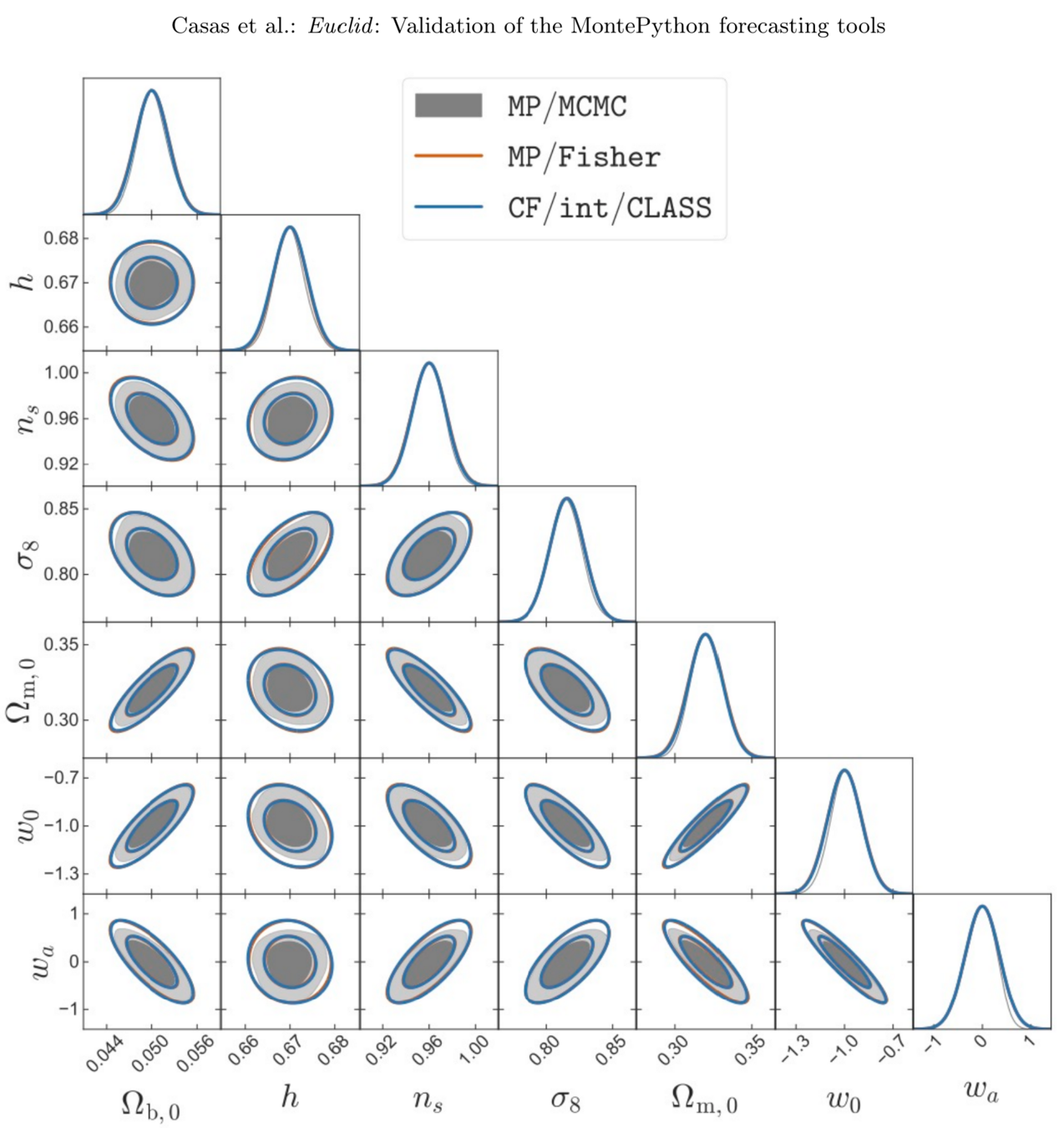
Validated IST:F Fisher forecasts against MCMCs with MontePython -> Gaussian posteriors for $w_0, w_a$
It turns out Fisher approx. is good for a full 6yr data release of Euclid-like specs (optimistic and pessimistic).
We also validated CAMB and CLASS to each other, the main Einstein-Boltzmann-Solvers on the market.
We tested precise numerical accuracy of non-linear methods (Halofit and HMCode) and found differences in CAMB vs. CLASS.

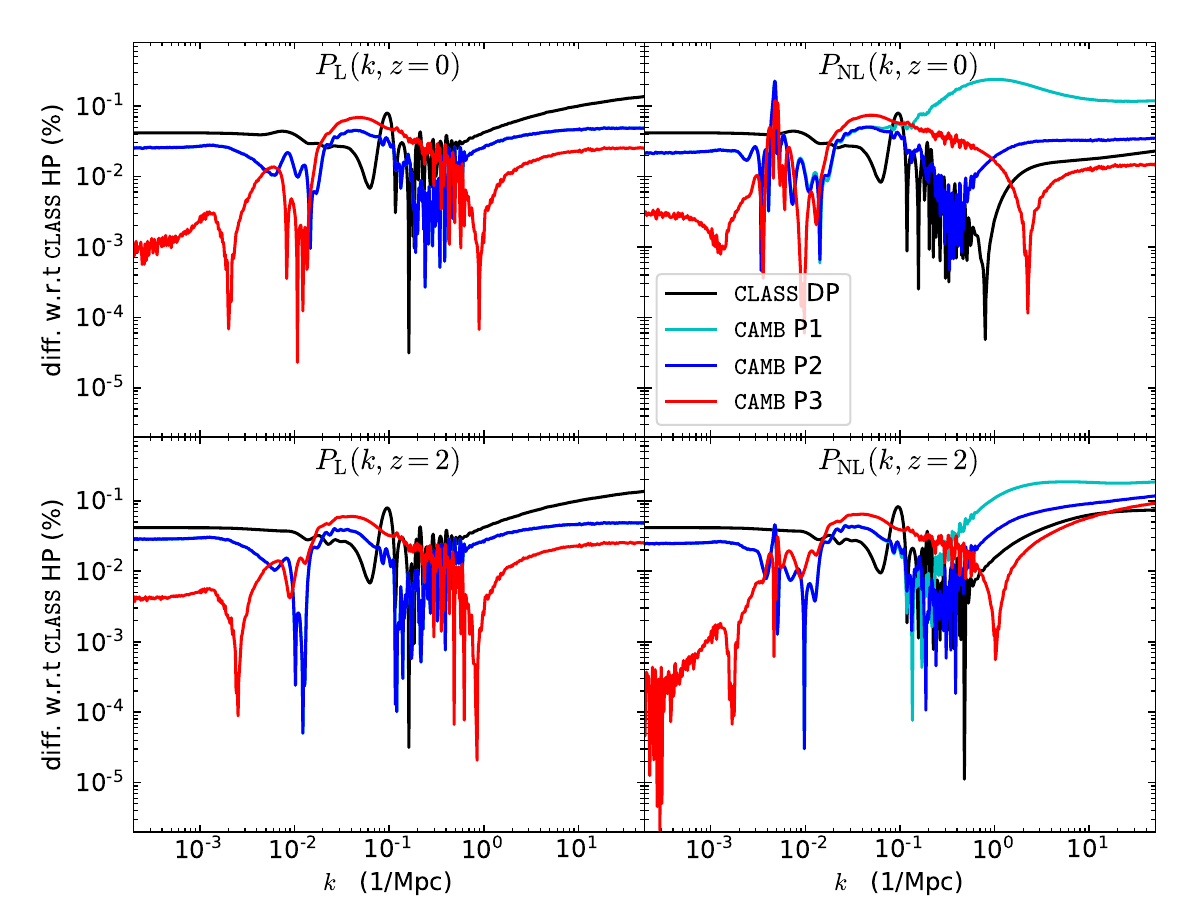
The effect of Neutrinos

Simulations and images by my bachelor student: Yun Ling (RWTH), using CoNCEPT, developed by J. Dakin (Aarhus, U. Zürich)

Can we trust Fisher constraints also in this case?

The effect of Neutrinos

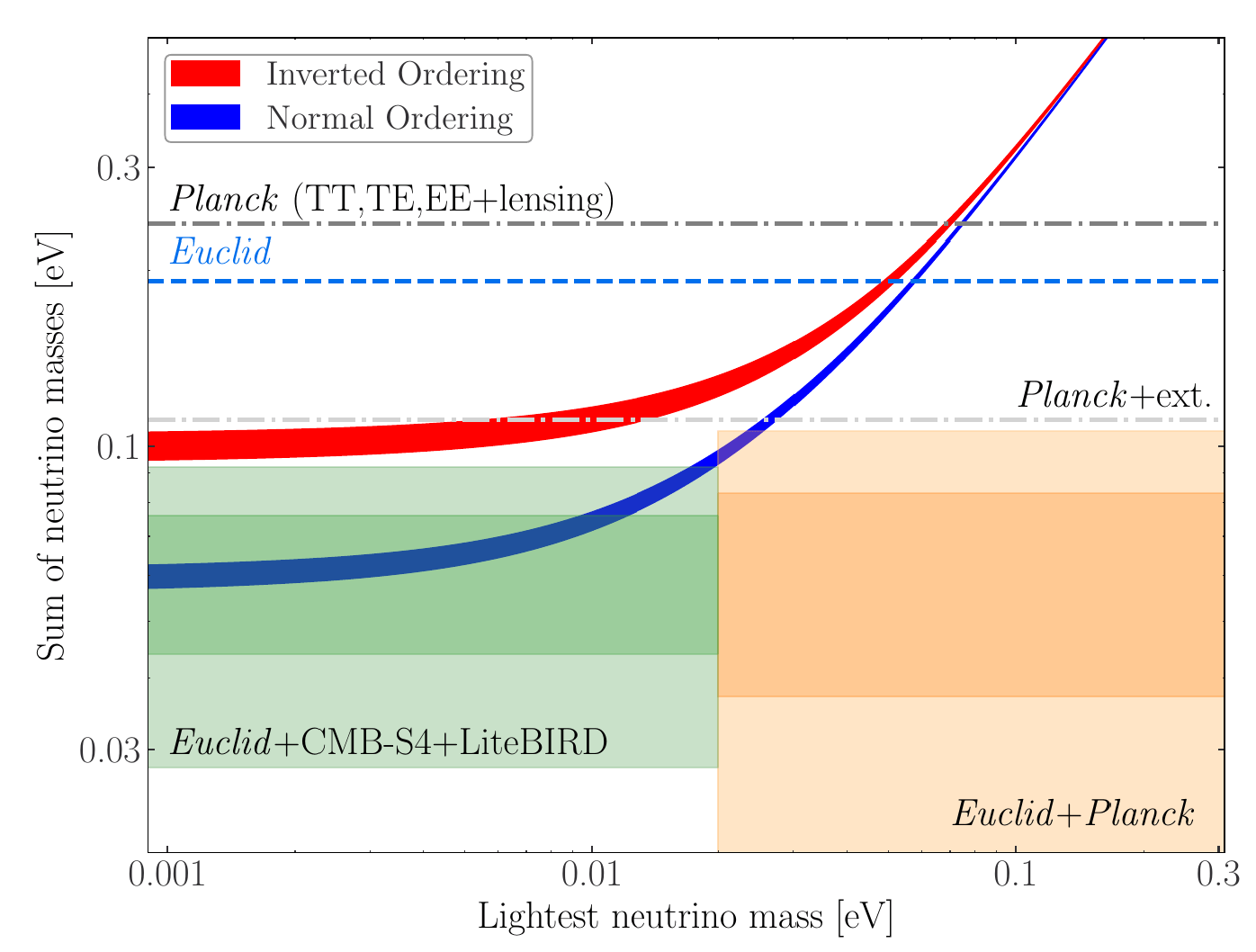
Euclid Preparation: Sensitivity to Neutrino parameters. (Under internal review). Archidiacono, Lesgourgues, SC, Pamuk, et al.

EUCLID PRELIMINARY

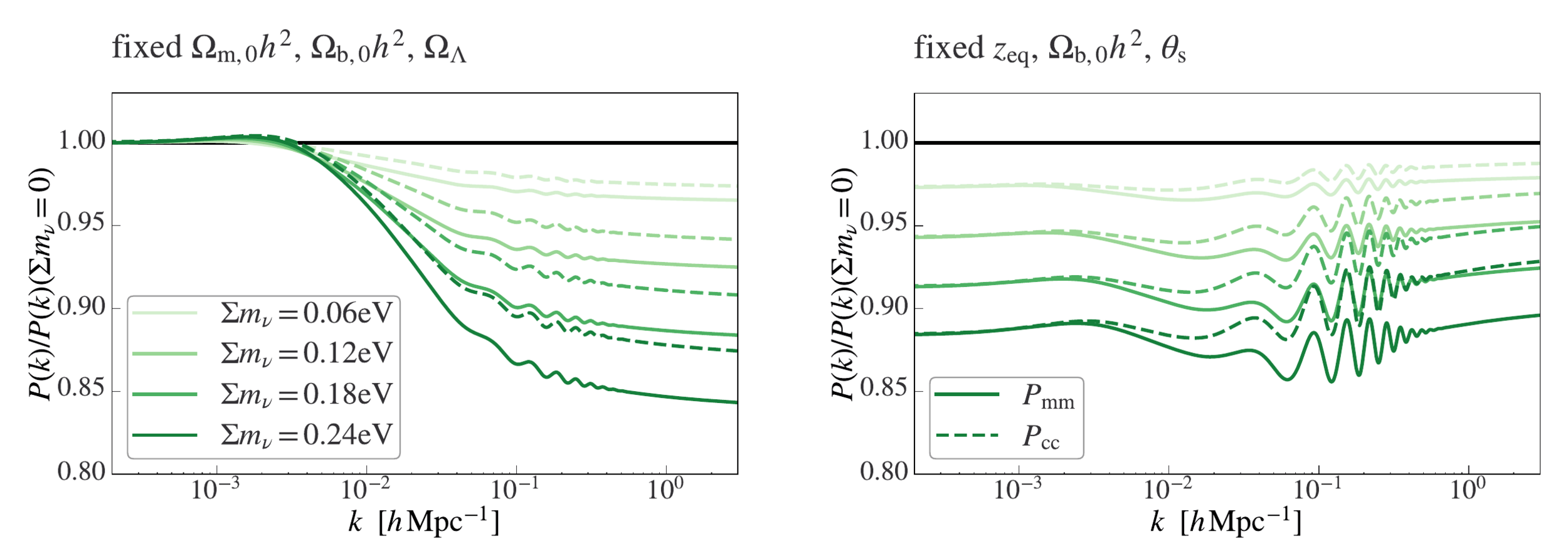
Neutrinos free stream below a scale of $k_{FS}$.
They do not cluster below that scale.
Suppression of the power spectrum.
The non-relativistic transition imposes a minimum in $k_{FS}$

Dynamical Dark Energy + Neutrinos

Euclid Preparation: Sensitivity to Neutrino parameters. (Under internal review). Archidiacono, Lesgourgues, SC, Pamuk, et al.

EUCLID PRELIMINARY

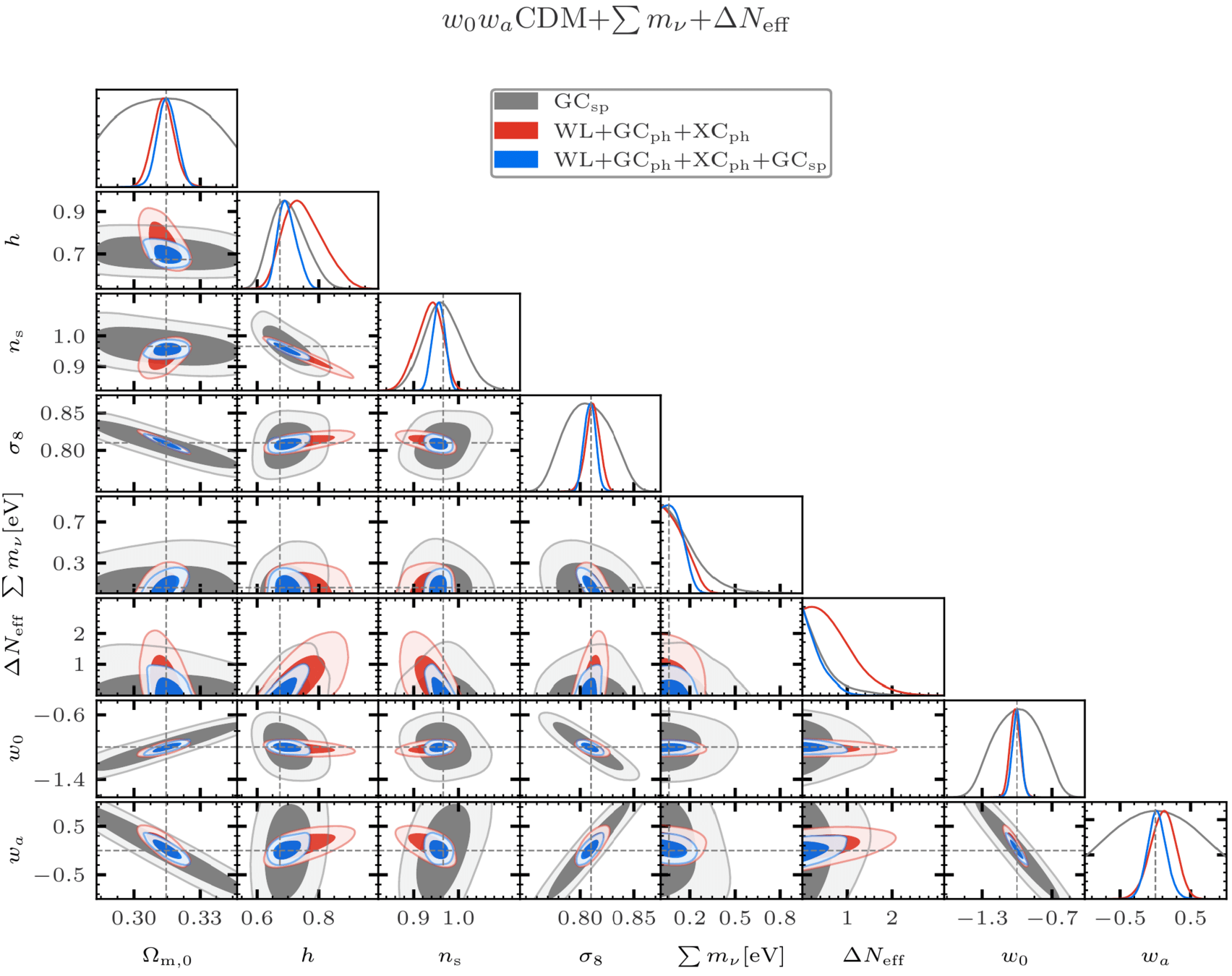
Use more "realistic" settings (HMcode, P_cb, no-fluid approx....) :
$\sigma_{w_0} \approx 0.04$
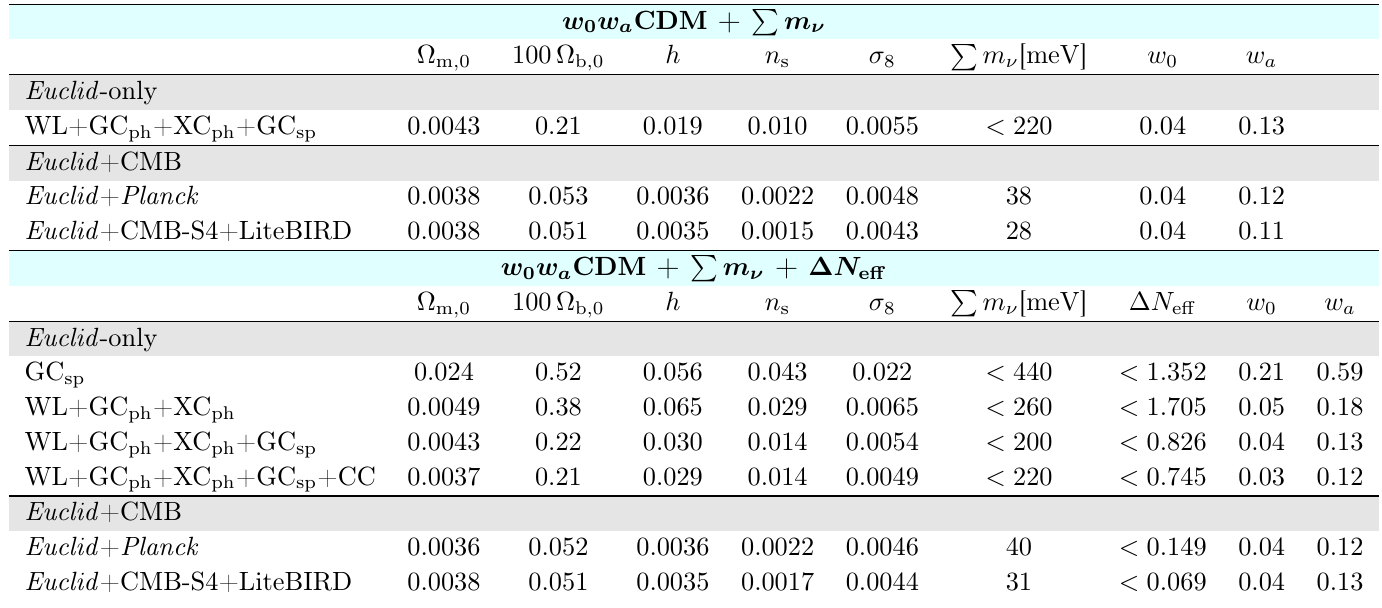
$\sigma_{w_a} \approx 0.13$
$ m_{\nu} \lt 200 \rm{ meV}$
Euclid + Planck
$\sigma_{w_0} \approx 0.04$
$\sigma_{w_a} \approx 0.12$,
$ m_{\nu} \approx 60 \pm 40 \, \rm{ meV}$

Fisher is not so reliable anymore, with 7, 8 or 9 free cosmological parameters!!

Dynamical Dark Energy + Neutrinos

Euclid Preparation: Sensitivity to Neutrino parameters. (Under internal review). Archidiacono, Lesgourgues, SC, Pamuk, et al.

EUCLID PRELIMINARY

Let's go to even more realistic settings

Euclid: Likelihood and Nonlinear Challenges

GCspectro: EFT 1-loop RSD in multipoles
3x2pt photo:
- Covariance, nonlinear Super-Sample
- Bias expansion
- Emulators for nonlinear, HMCode, Halofit, Bacco, EuclidEmu
- Baryonic Feedback

Different emulators with systematic offsets
Euclid error bars can distinguish among them
Biases in parameter estimation to be resolved

EUCLID PRELIMINARY

Credit: P. Carrilho

Credit: SC, for IST:NL

Cosmological Likelihood for Observables in Euclid

Euclid: Likelihood and Nonlinear Challenges

EUCLID PRELIMINARY

Credit: SC, for IST:L

Cosmological Likelihood for Observables in Euclid

Weak Lensing

(Cosmic Shear)

+ Baryonic feedback

+ Intrinsic alignment

+ multiplicative bias

+ dnz uncertainties

= 34 parameters

for LCDM flat

6x8 cores x 6 days

spectroscopic probe: Full Shape

Linde, Moradinezhad, Rademacher, SC, Lesgourgues (2402.09778)

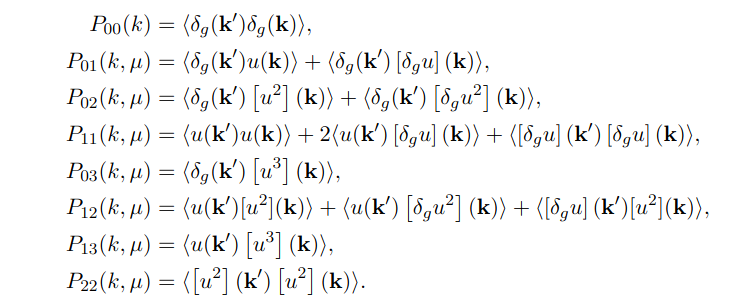
The more-realistic GCspectro model, based on Senatore, Ivanov, Simonovic, Vlah, et al

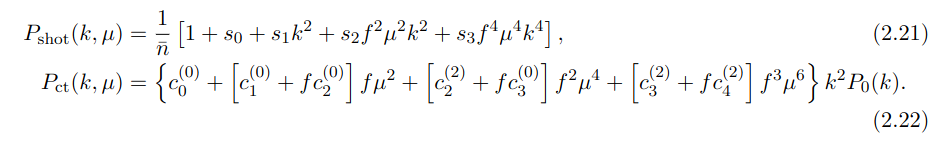
CLASS 1-loop Code in development in Aachen, RWTH

Validated against CLASS-PT, Velocileptors

1-loop PT of density and velocity in redshift space

4 counterterms, 4 shot-noise, 4 higher-order biases

Trade-off: larger error bars, more accuracy, less biasing
Compared against IST:F model at different scales
Many free parameters, good fit to ABACUS simulations

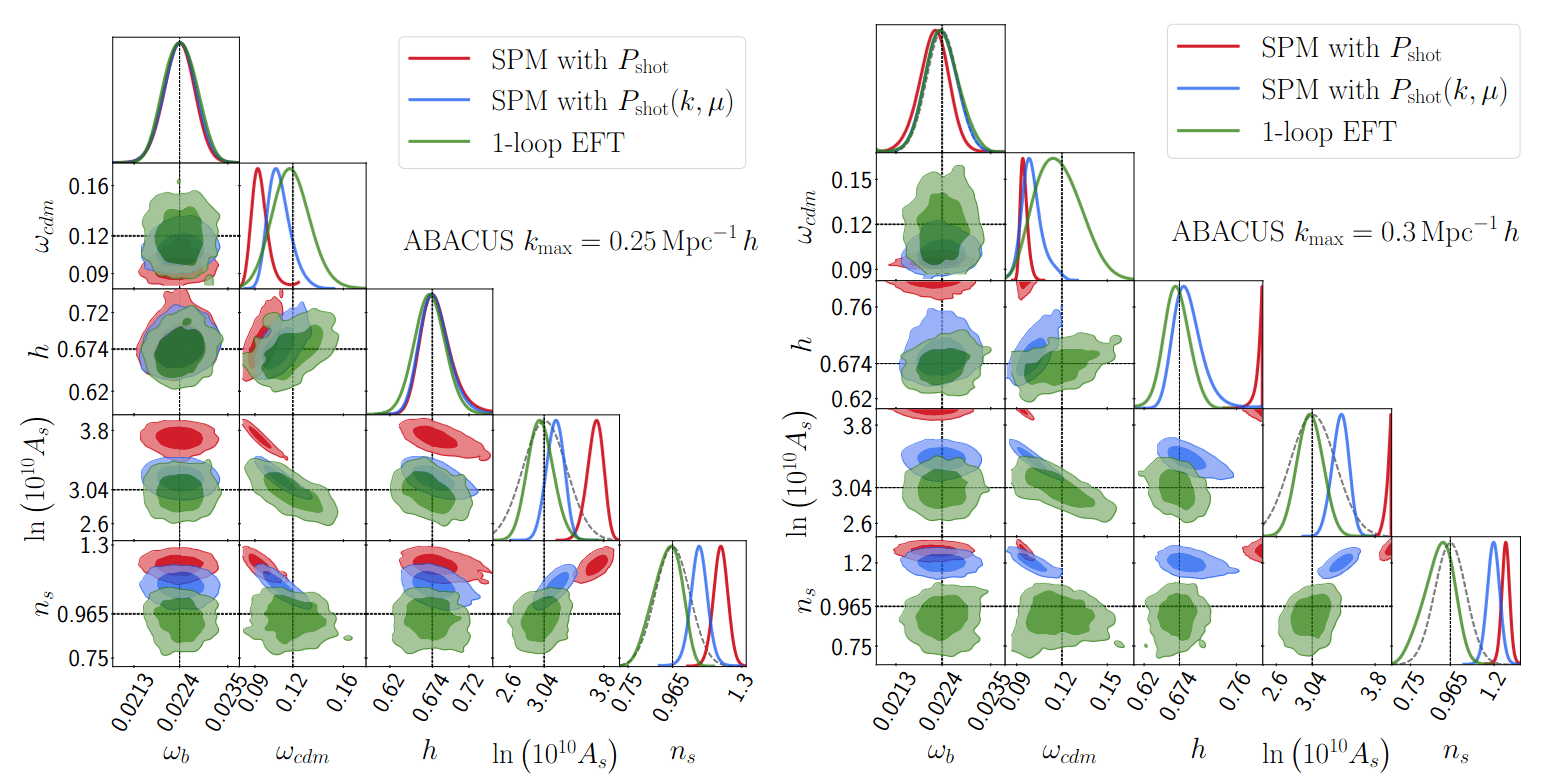
spectroscopic probe: Full Shape

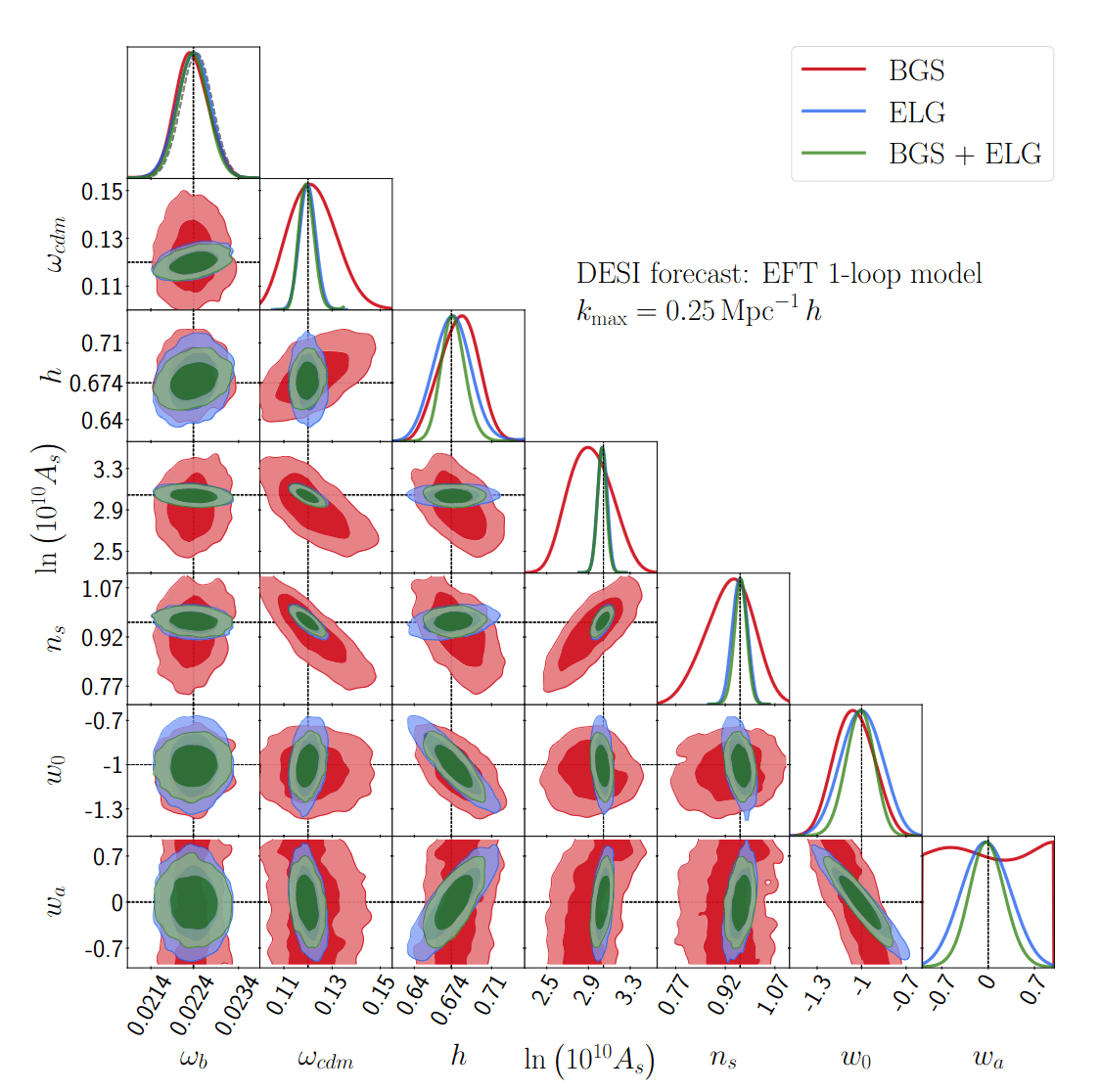
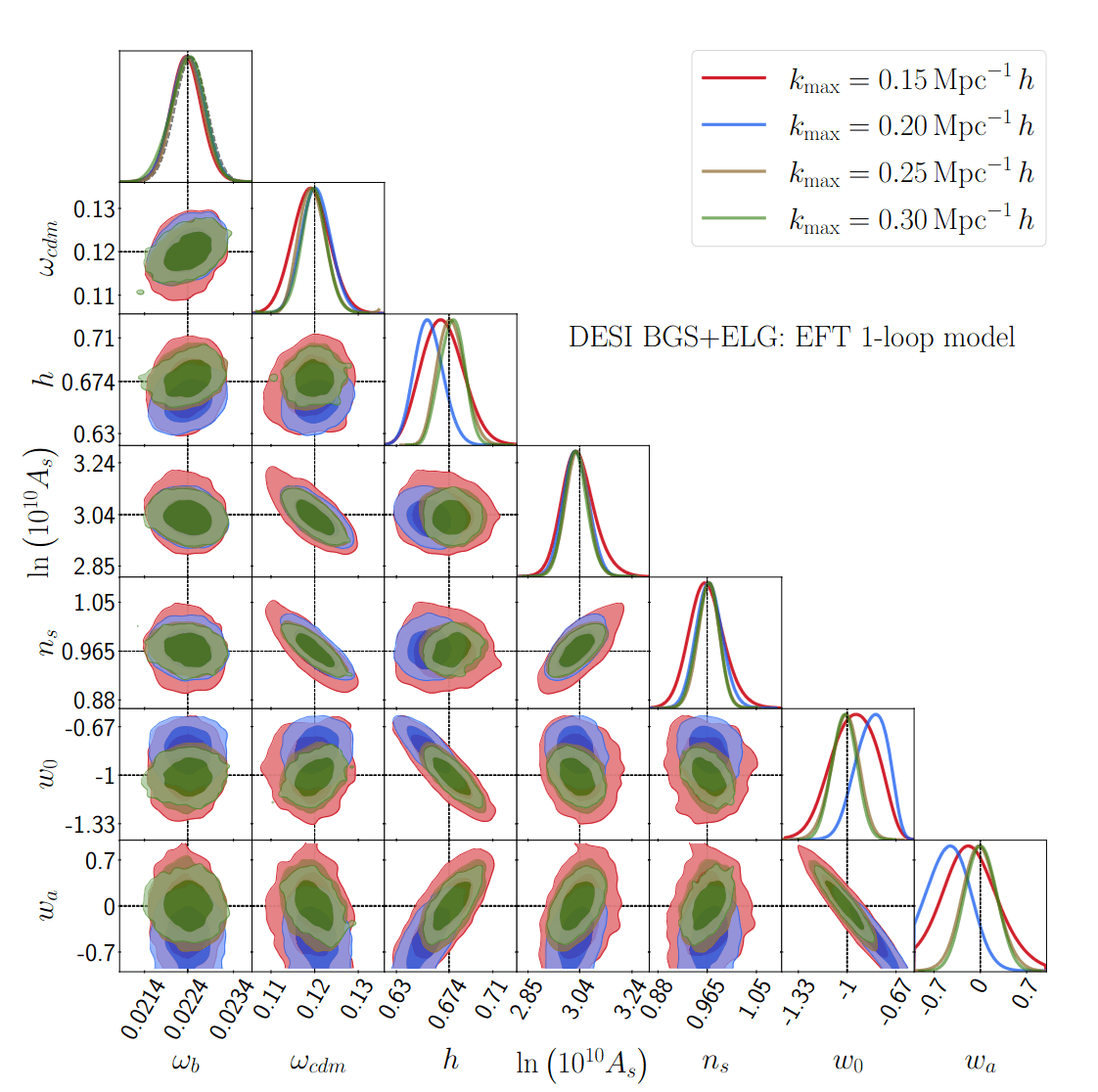
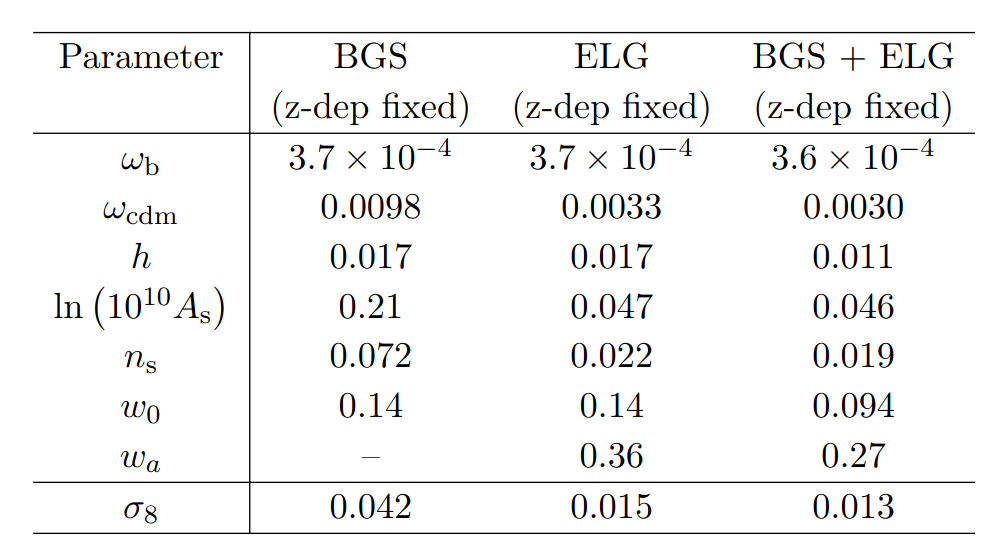
DESI full shape forecasts for w0, wa
BGS and ELG
As a function of k_max

Let's go Back to modified gravity

Modified Gravity and Dark Energy

Add a scalar degree of freedom to the Einstein-Hilbert action
(Non-)Minimal coupling, Kinetic terms

a SCALAR-tensor theory

Gregory Horndeski
https://www.horndeskicontemporary.com/works

And in the Lorentz Institute seminar room!

Costa Rica - Arenal Volcano

Horndeski theory: most general theory for an extra scalar degree of freedom, with second order equations of motion in 4D and no ghosts
4 Lagrangian terms, which have been largely ruled out by:
- Late-ISW
- GW170817
- No self-acceleration -> uninteresting?

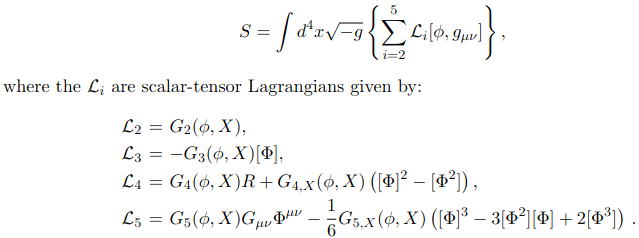
Gregory Horndeski
https://www.horndeskicontemporary.com/works

Parametrized modified gravity

\rm{d}s^2 = -(1+2\Psi) \rm{d}t^2 + a^2(1-2\Phi) \rm{d}x^2

Beyond $\Lambda$CDM the two linear gravitational potentials $\Psi$ and $\Phi$ are not equal to each other

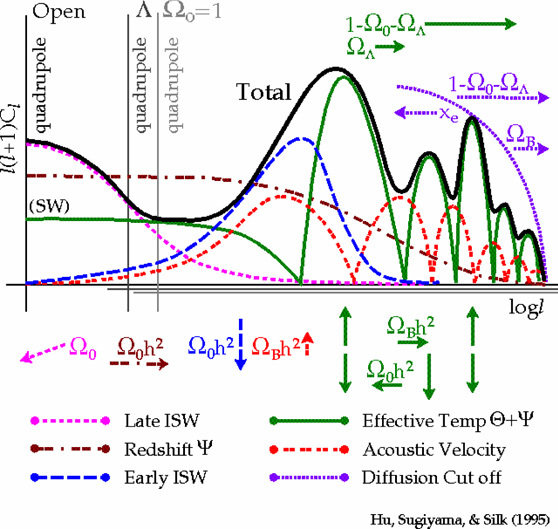
We can describe general modifications of gravity (of the metric) at the linear perturbation level with 2 functions of scale ($k$) and time ($a$)

\Sigma(a,k) = \frac{1}{2}\mu(a,k)(1+\eta(a,k))

Only two independent functions!

Parametrized approach for perturbations:

Parametrized modified gravity

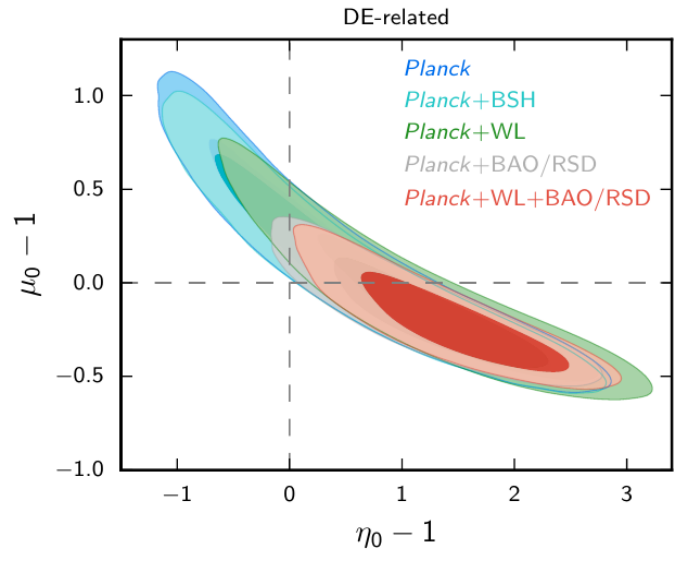
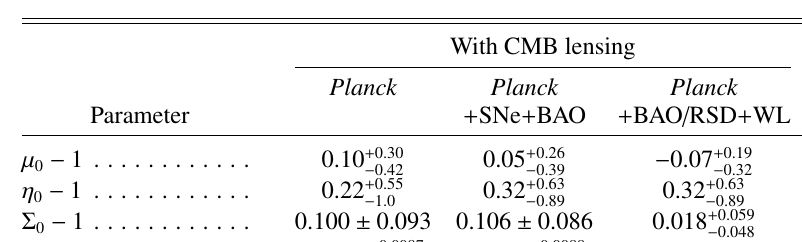
Using Planck satellite data in 2015 and 2018, constraints were obtained on these two functions $\mu$ and $\eta$.
Late-time parametrization: dependent on Dark Energy fraction

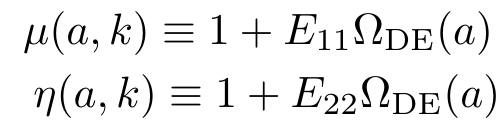
Planck 2018 results VI, arXiv:1807.06209

Planck 2015 results XIV, arXiv:1502.01590

Planck alone relatively unconstrained: 100-500% errors

Parametrized modified gravity

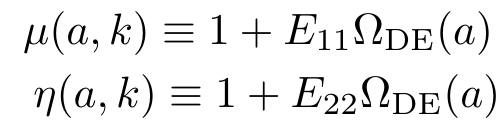
Forecasts for Stage-IV : Euclid, DESI, SKA1, SKA2, only GC and WL

SC, Kunz, Martinelli, Pettorino, Phys.Dark Univ. 18 1703.01271

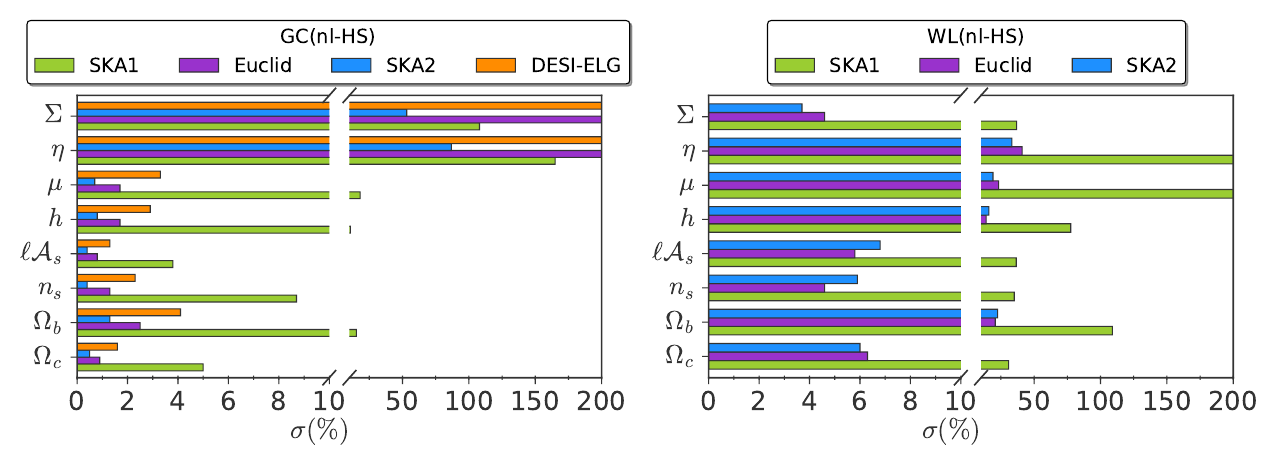
Study more general case of free $\mu$, $\eta$ functions at each bin
Non-linearities crucial for constraints
Z-PCA decorrelation
Constraints on $\mu$, $\eta$ of O(10%)

For late-time and early-time scenario:
Constraints on $\mu$, $\eta$ of O(3%)
When combining GC+WL+Planck priors

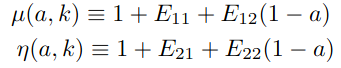
Vera Rubin LSST

Square kilometer array (SKAO)

Modelling is very analogous to GCsp, with brightness temperature on top and different biases
GCsp-IM Cross-correlation in overlapping bins
DESI : Two galaxy samples
SKAO: HI Galaxies and 21cm-IM

$P^{\rm IM}(z,k) = \bar{T}_{IM}(z)^2 \rm{AP}(z) K_{\rm rsd}^2(z, \mu; b_{\rm HI}) $
$FoG(z,k,\mu_\theta) \\ \times P_{\delta\delta,dw}(z,k) $

$ K_{\rm rsd}(z, \mu; b_{\rm HI}) = [b_{\rm HI}(z)^2+f(z)\mu^2] $

$ b_{\rm HI}(z) = 0.3(1+z) + 0.6 $

$ \bar{T}_{\mathrm{IM}}(z)= 189h \frac{(1+z)^2 H_0}{H(z)}\Omega_{HI}(z) \,\,{\rm mK} $

$\Omega_{HI} = 4(1+z)^{0.6} \times 10^{-4} $

Carucci et al (2020) 2006.05996

Jolicoeur et al (2020) 2009.06197

$P^{{\rm IM} \times \rm{g}}(z,k) = \bar{T}_{\rm IM}(z) {\rm AP} (z) r_{\rm IM,opt} K_{\rm rsd}(z, \mu; b_{\rm HI}) $
$ \times K_{\rm rsd}(z, \mu; b_{\rm g}) FoG(z,k,\mu_\theta) P_{\delta\delta,dw}(z,k) $

$ \times \exp[-\frac{1}{2} k^2 \mu^2 (\sigma_{\rm IM}(z)^2+\sigma_{\rm sp}(z)^2)] $

SC, Carucci, Pettorino et al (2022) 2210.05705

Brightness temperature of 21cm emission line

Fraction of neutral hydrogen in the Universe

Vera Rubin LSST

Radio x Optical Cosmology

SC, Carucci, Pettorino et al (2022) 2210.05705

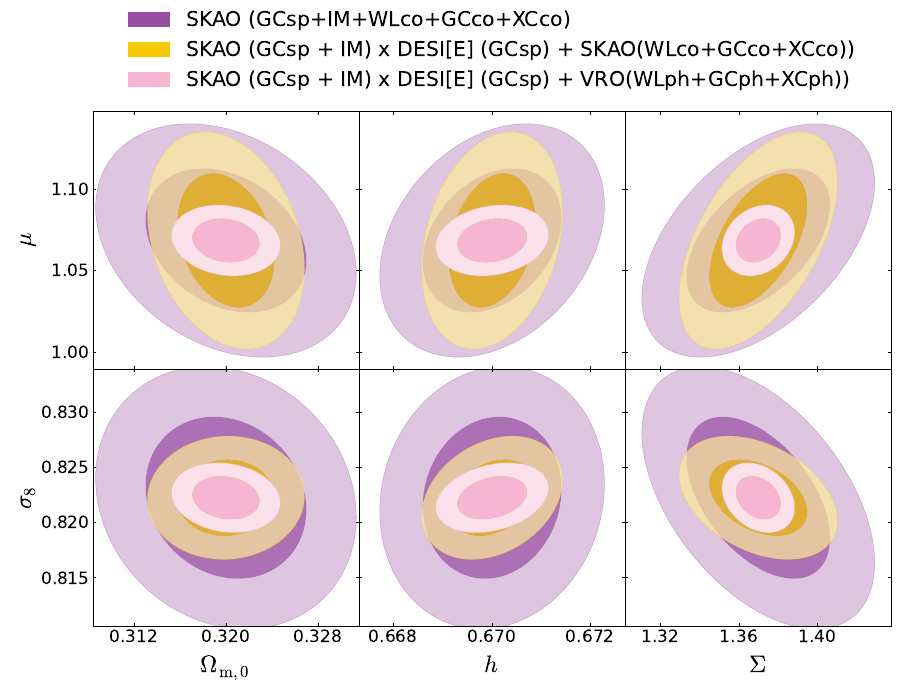
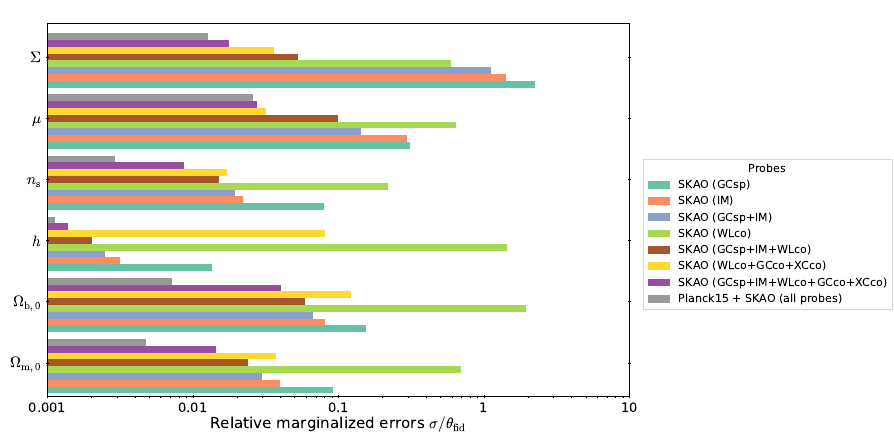
WL is better at measuring $\Sigma$ (40% relative error)
GC is better at measuring $\mu$ (20% relative error)
SKAO-all-probes constrains at 3-5% relative error
At Planck best fits

DESI(GCsp)xSKAO(IM) helps in $h, \sigma_8$ but not in MG parameters
Combination of SKAO + one Stage-IV probe is as good as two Stage-IV
Different noise and systematics -> break degeneracies

Classifying by screening

Modified Gravity theories should recover GR at small scales, especially in dense regions, screening needed!

Brax, SC, Desmond, Elder 2201.10817, Universe 8 (2021), Review: Testing Screened Modified Gravity

G_{\rm eff}=\left(1+ \frac{2\beta^2(\phi_0)}{Z(\phi_0)}e^{-m(\phi_0)r}\right) G_N

Perturbations of $\phi$ and matter coupled in Jordan frame -> Yukawa-like fifth forces:

Different types of screening:

Chameleon: The mass $m(\phi_0)$ increases sharply inside matter
Damour-Polyakov: The coupling $\beta(\phi_0)$ vanishes inside matter
K-mouflage and Vainshtein: $Z(\phi_0) \gg 1$

Classifying by screening

Screening mechanisms can be characterized by the inequality:

\nabla^k \Phi_N \gtrsim C

Chameleon: $k=0$ (surface N. potential is large)
K-mouflage: $k=1$ (N. acceleration is large)
Vainshtein: $k=2$ (curvature is large)

$ f(R) $ Hu-Sawicki (see later)
$k$-essence + univ. coupling
nDGP (3+1)d brane embedded in 5d

For DE applications and under some assumptions:

Chameleon screens everything above a certain potential threshold
K-mouflage does not screen galaxy clusters
Vainshtein screens all structures that turn non-linear

Brax, SC, Desmond, Elder 2201.10817, Universe 8 (2021), Review: Testing Screened Modified Gravity

Text

SC et al, Euclid: Constraints on f(R) cosmologies from the spectroscopic and photometric primary probes, 2306.11053

f(R) Hu-Sawicki model

\newcommand{\sg}{\ensuremath{\sigma_{8}}} \newcommand{\de}{\mathrm{d}} S = \frac{c^4}{16\pi G} \int{\de^4 x \sqrt{-g} \left[R+f(R)\right]}

-k^2\Psi =\frac{4\pi\,G}{c^4} \,a^2\mu\bar\rho\Delta\,

Modification of the Einstein-Hilbert action

-k^2\left(\Phi+\Psi\right) = \frac{8\pi\,G}{c^4}\,a^2 \Sigma \bar\rho\Delta

Induces changes in the gravitational potentials *

\mu(a,k) = \frac{1}{1+f_R(a)}\frac {1+4k^2a^{-2}m_{f_R}^{-2}(a) }{1+3k^2a^{-2}m_{f_R}^{-2}(a)}

Scale-dependent growth of matter perturbations

Small changes in lensing potential

\Sigma(a)=\frac{1}{1+f_{R}(a)}\,

*for negligible matter anisotropic stress

Free parameter: $f_{R0}$

f(R) = - 6 \Omega_{\rm DE} H_0^2 + |f_{R0}| \frac{\bar R_0^2}{R}\,

$\lambda_C =32 \rm{Mpc}\sqrt{|f_{R0}|/10^{-4}}$

"Fifth-force" scale for cosmological densities

Hu, Sawicki (2007)

Text

f(R) Hu-Sawicki model

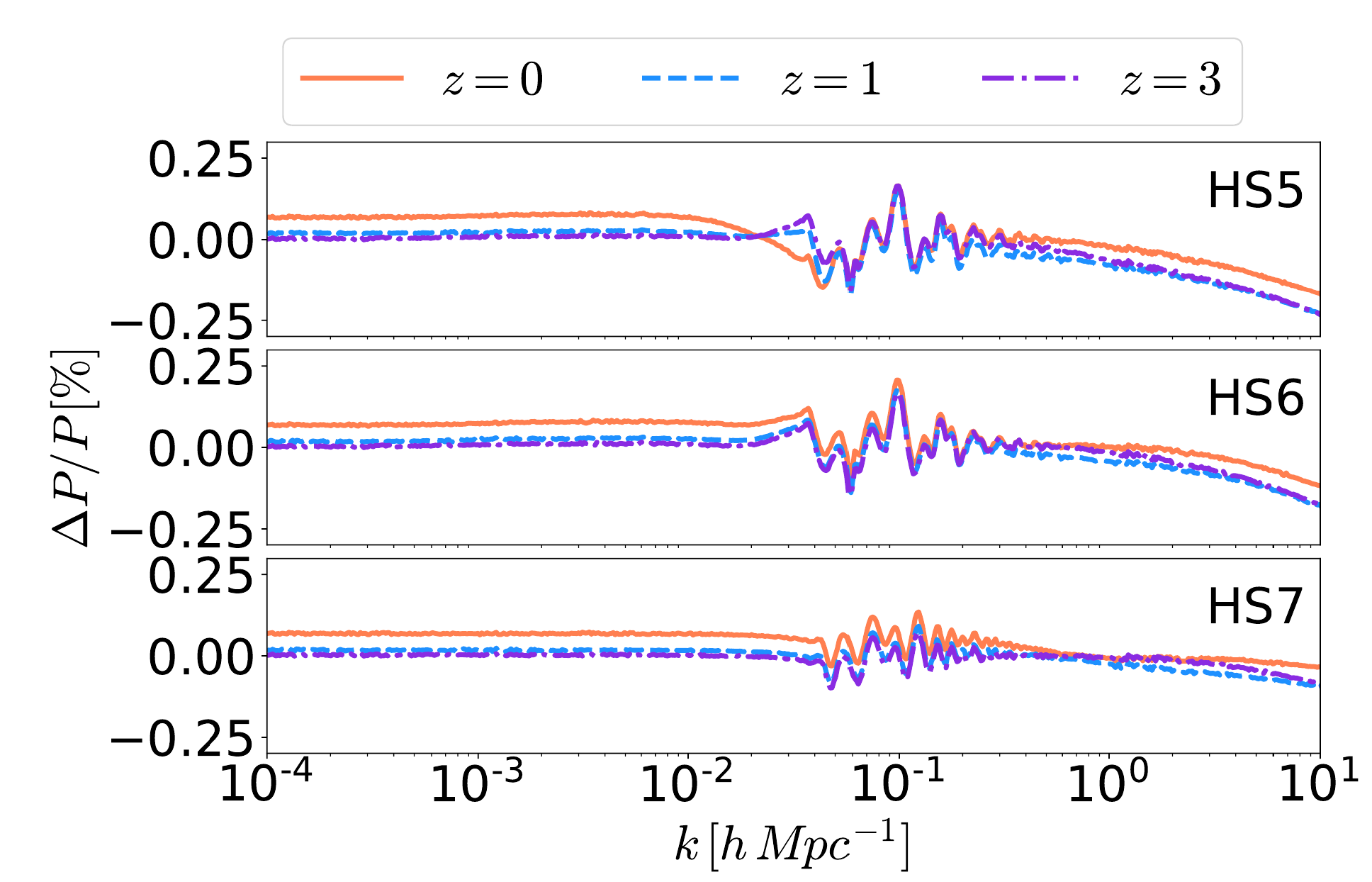
Codes used: for background and scale-dependent linear perturbations: MGCAMB and EFTCAMB

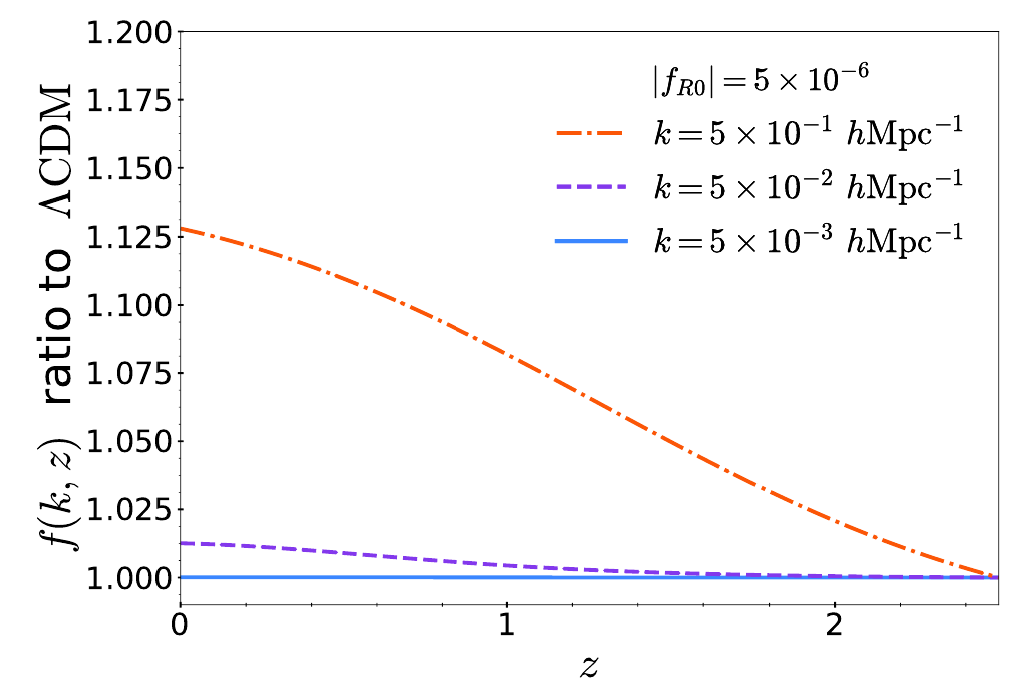
Non-linear matter power spectrum:

Winther et al (2019) fitting formula

Scale-dependent growth, change in forecasting pipeline

Current Euclid KP-JC6-SP paper in preparation (ledy by Kazuya), investigating biasing by Emulators/ReACT compared to simulations

SC et al, Euclid: Constraints on f(R) cosmologies from the spectroscopic and photometric primary probes, 2306.11053

Text

f(R) Hu-Sawicki model

$\sigma_{\log f_{R0}}=0.05$ (1%)

Current cosmological limits ~approx:

$ |f_{R0}|<10^{-6}$

Full probe combination, optimistic Euclid constraints:

$f_{R0}=(5.0^{+ 0.58}_{-0.52} \times 10^{-6})$

Paper also contains impact of:

Non-linear scales
Cross-correlations
Pessimistic settings
LCDM-limit (numerical)

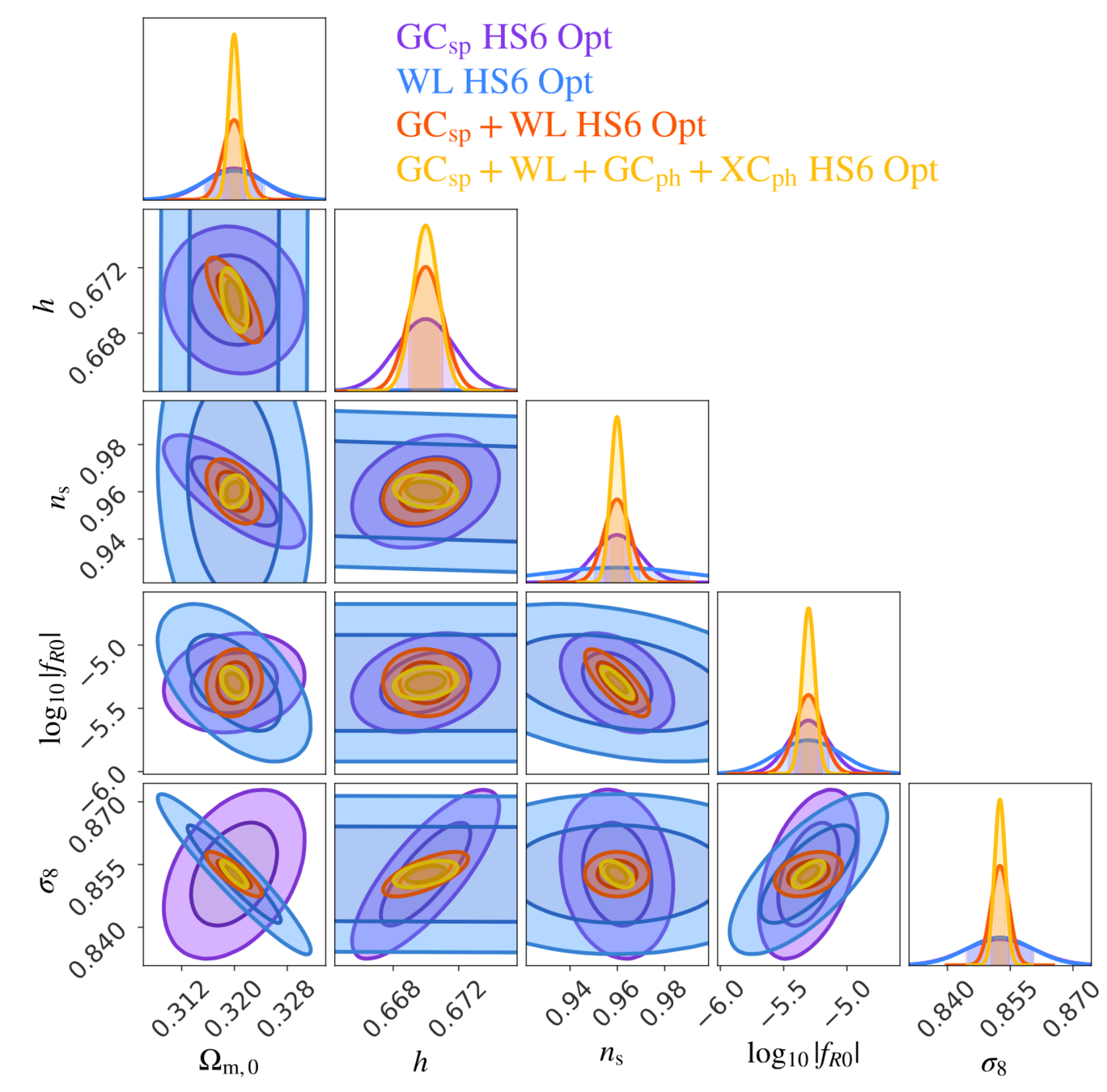
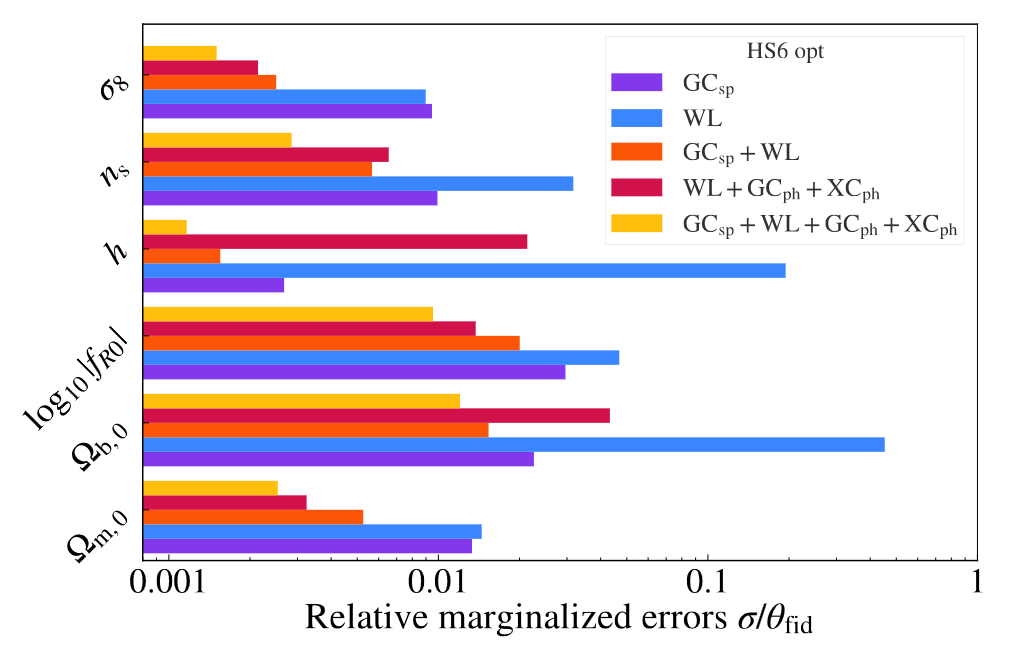
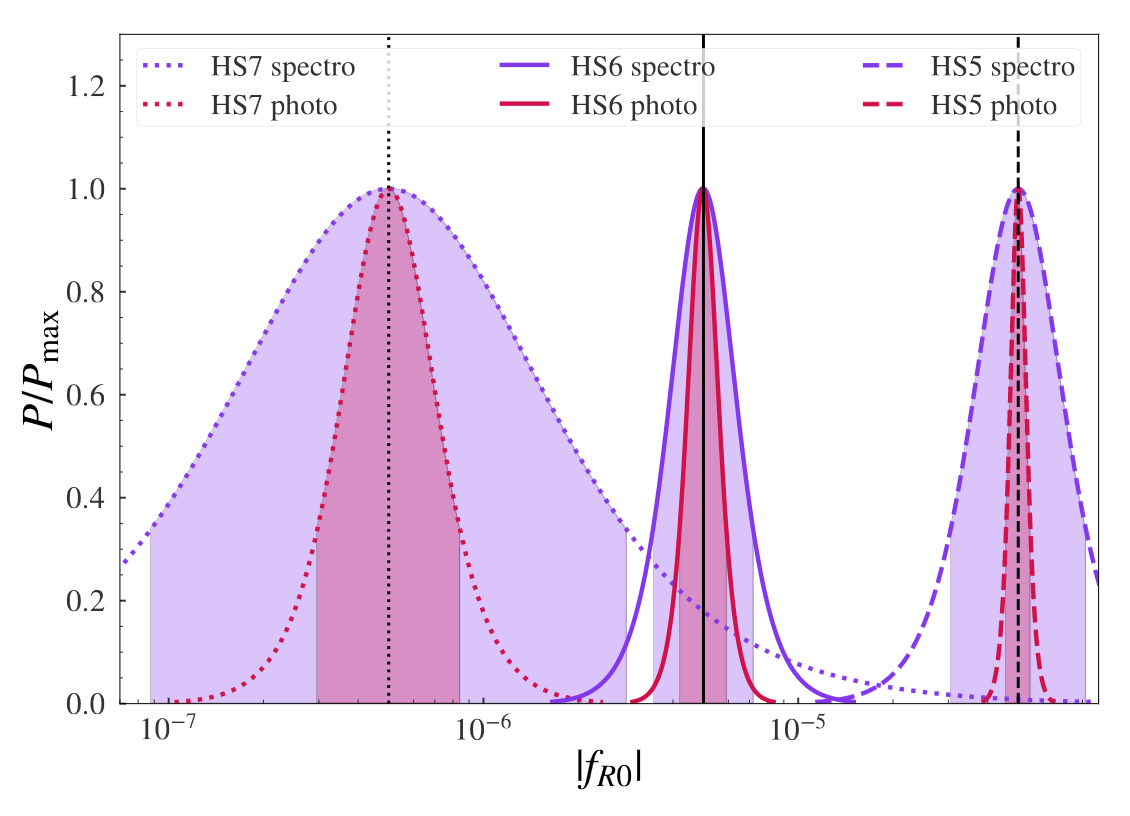
SC et al, Euclid: Constraints on f(R) cosmologies from the spectroscopic and photometric primary probes, 2306.11053

Text

f(R) Hu-Sawicki model

Euclid preparation: Simulations and nonlinearities beyond ΛCDM
Constraints on f (R) models from the photometric primary probes, Kazuya, SC, Pamuk, Bose, et al, (in prep.)

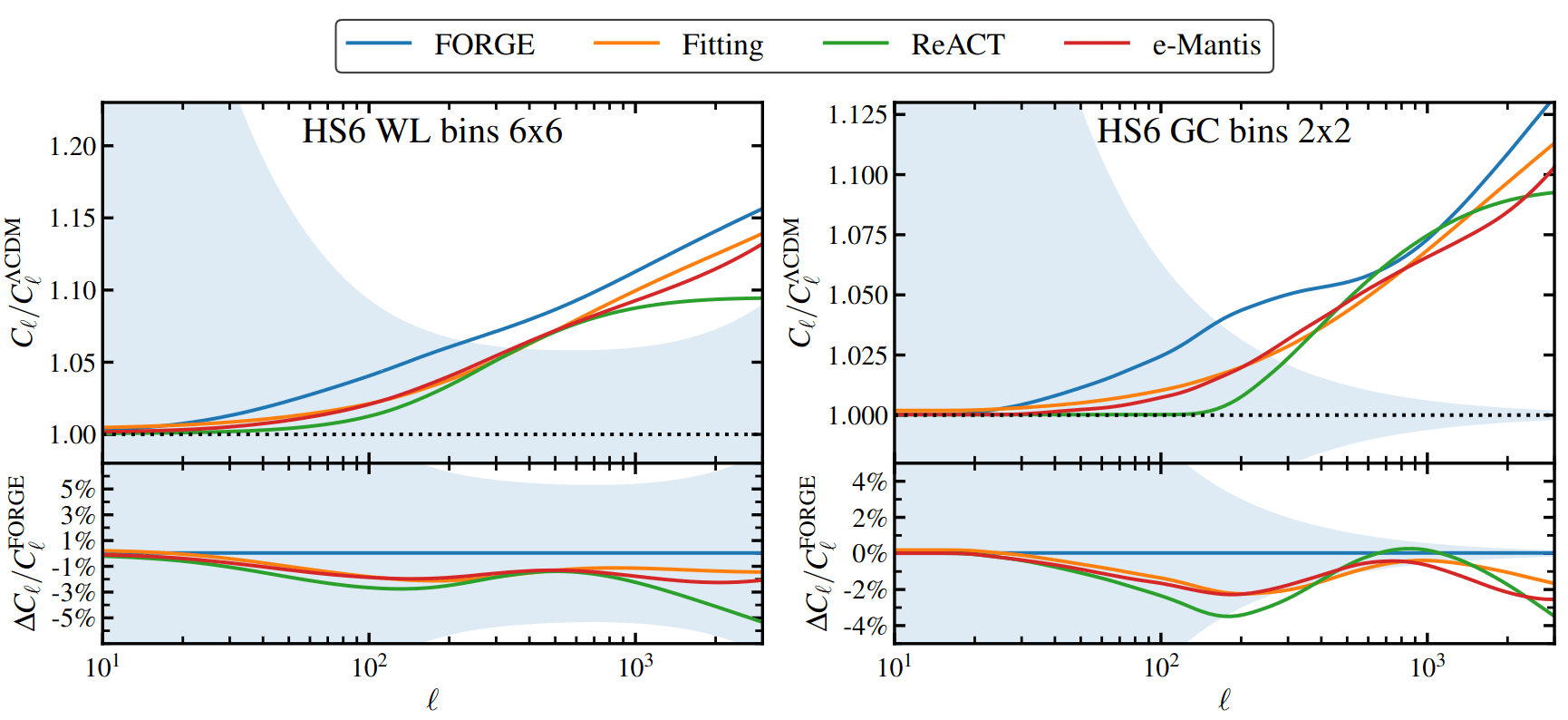
What happens if we go to MCMC, can we trust our modelling?
Not only fitting formulae, but many emulators available in the community
Disagreements above the predicted Euclid error bars
Baryonic modelling still unsufficient (and too degenerate) for full-analysis

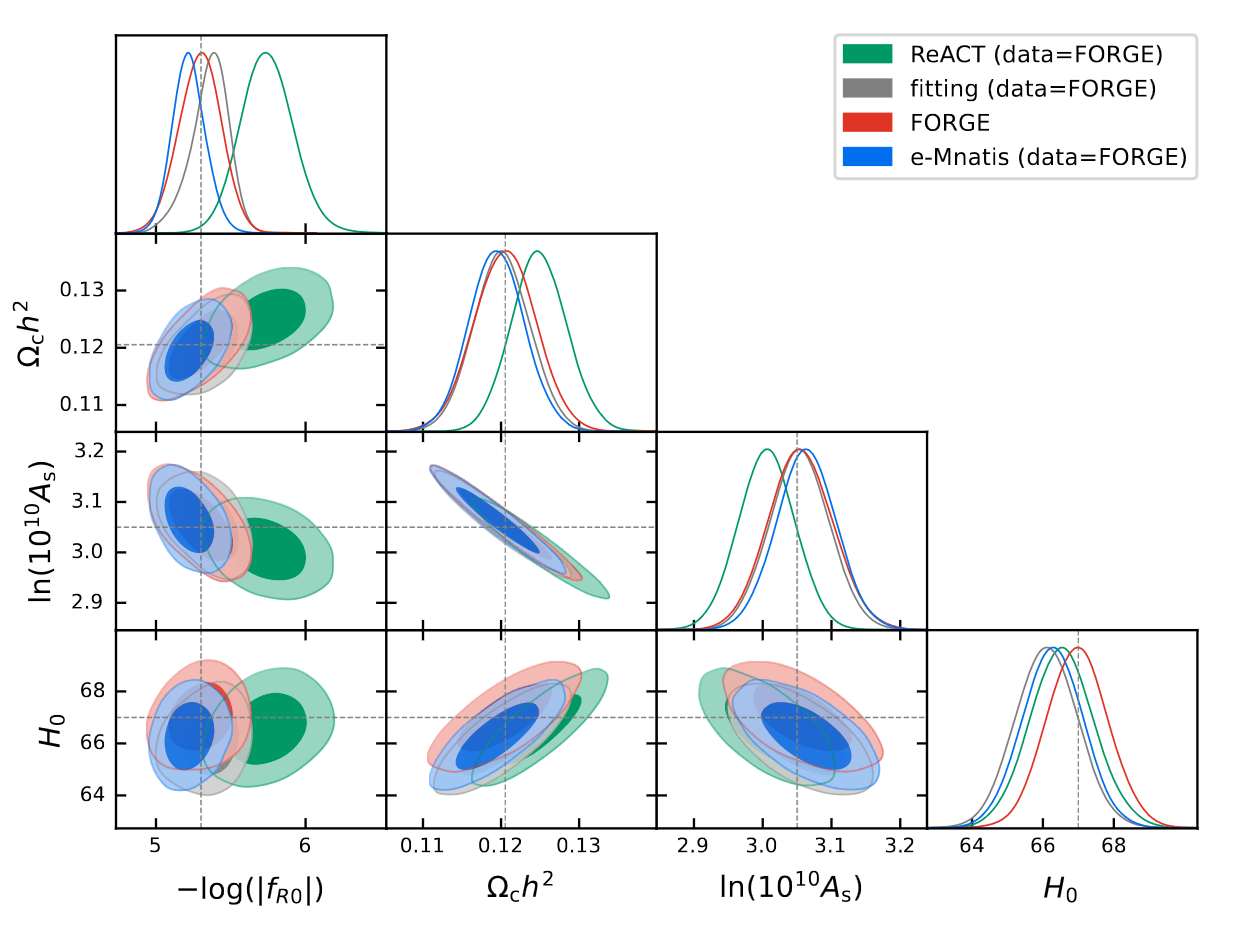
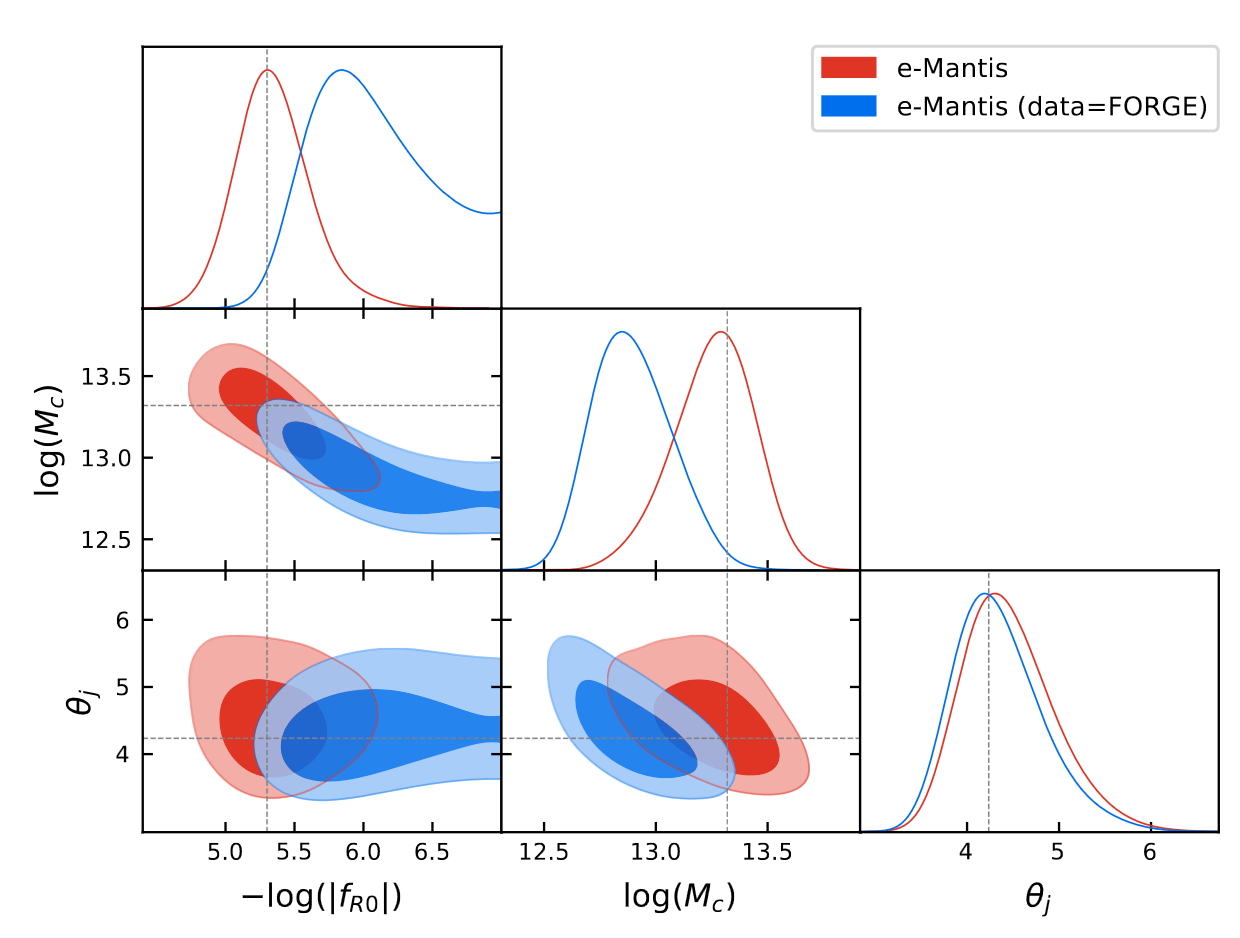
EUCLID PRELIMINARY

Text

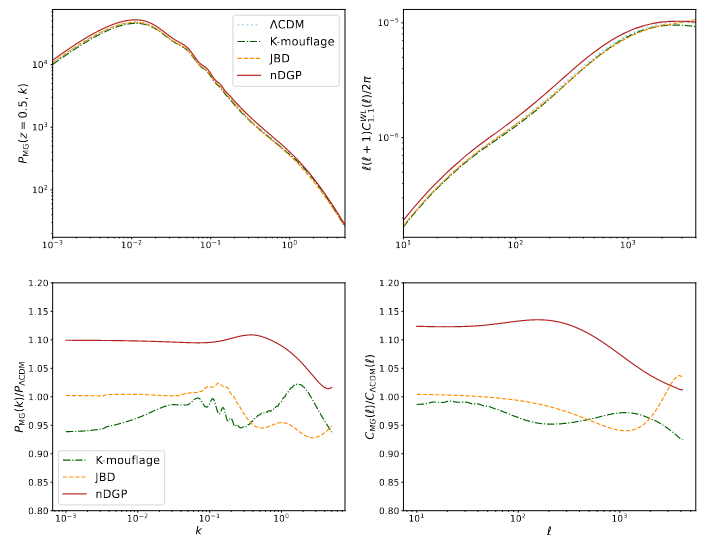
Scale-independent Modifications of GR

Forecasts for:

Jordan-Brans-Dicke (no-screening)
nDGP (5D brane model)
k-Mouflage
We work mostly in QSA MGCAMB or hiclass and non-linear modelling: Halo model or fits to simulations

Fruciante, Pace, Cardone, SC et al, Euclid: Constraining linearly scale-independent modifications of
gravity with the spectroscopic and photometric primary probes, 2306.12368

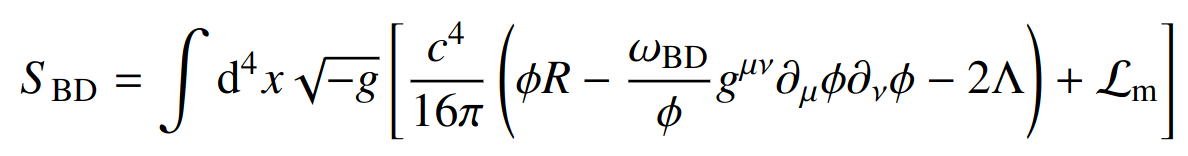
Current cosmo bounds $\omega_{BD} \gtrapprox 1000 $, GR: $\omega_{BD} \rightarrow \infty $

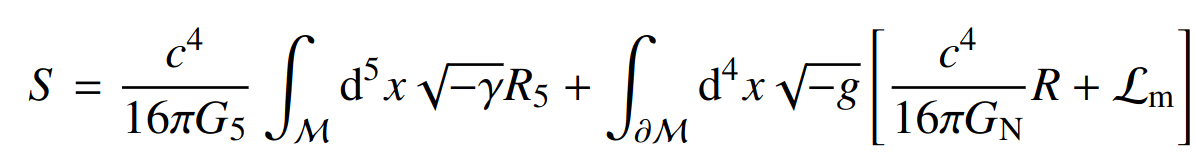
$r_c = G_5 / 2G_N \, , \Omega_{rc} \equiv c^2 / (4 r_c^2 H_0^2 ) $

Current cosmo bounds $\Omega_{rc} \lessapprox 0.27 $, GR: $r_{c} \rightarrow \infty $

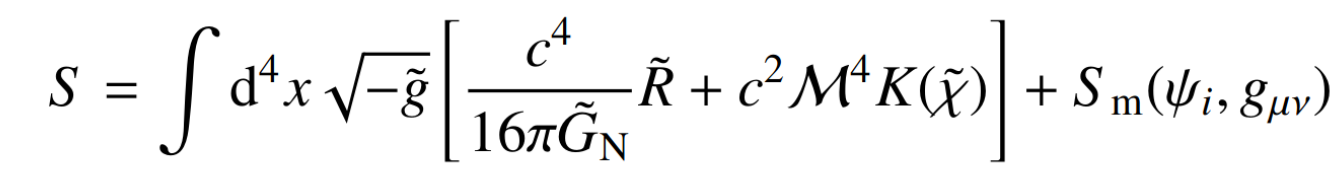
Vary just $\epsilon_{2,0}$ which in the limit $\epsilon_{2,0} \rightarrow 0 $ turns the Kinetic term into a cosmological constant

Current cosmo bounds $ −0.04 \lessapprox \epsilon_{2,0} \lessapprox 0$

Perform forecasts for limits close-to and far-from LCDM

Text

Scale-independent Modifications of GR

Example of result for JBD $\sigma(\log \omega_{BD}) $:

(other results see paper)

Fruciante, Pace, Cardone, SC et al, Euclid: Constraining linearly scale-independent modifications of
gravity with the spectroscopic and photometric primary probes, 2306.12368

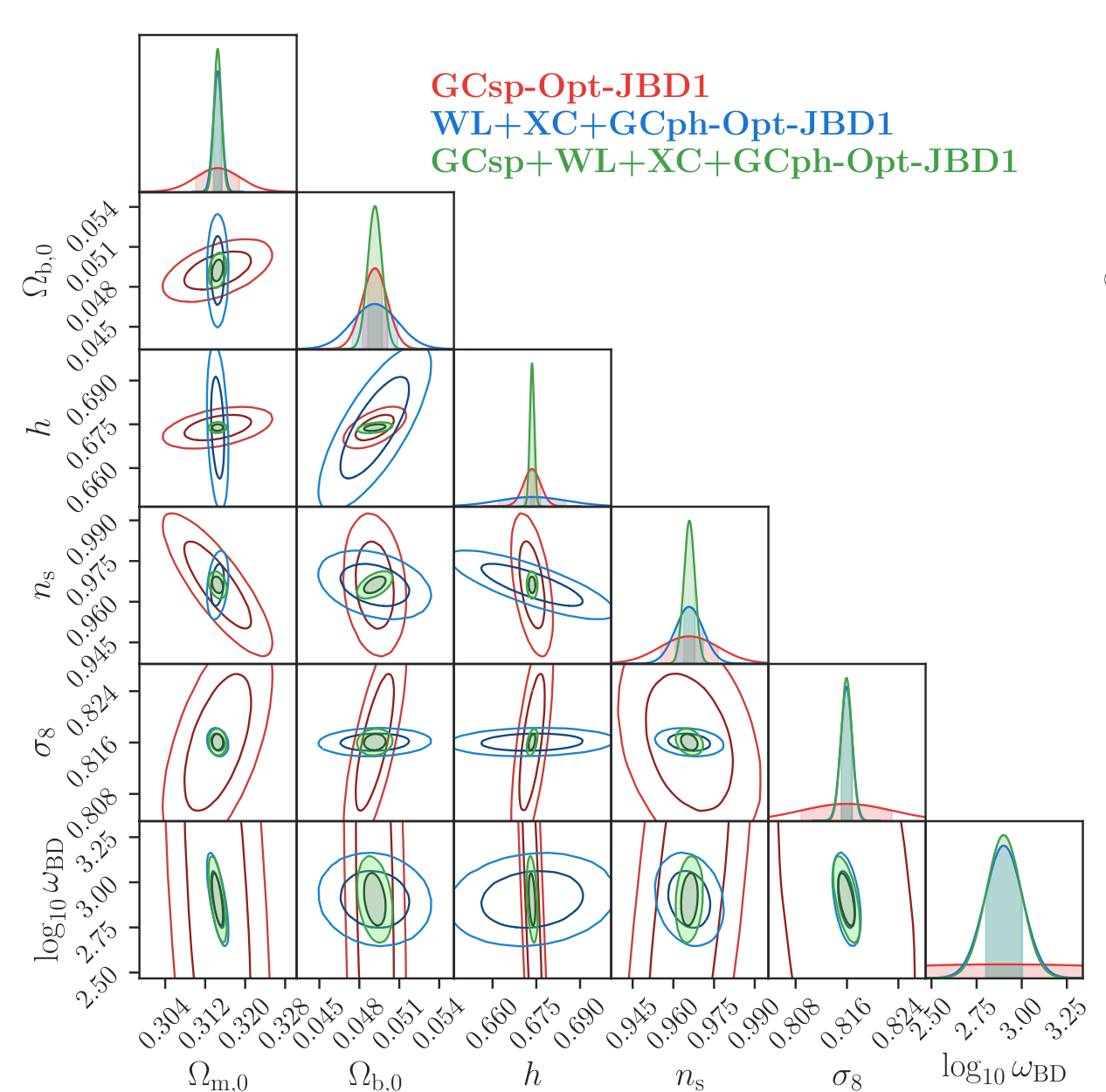
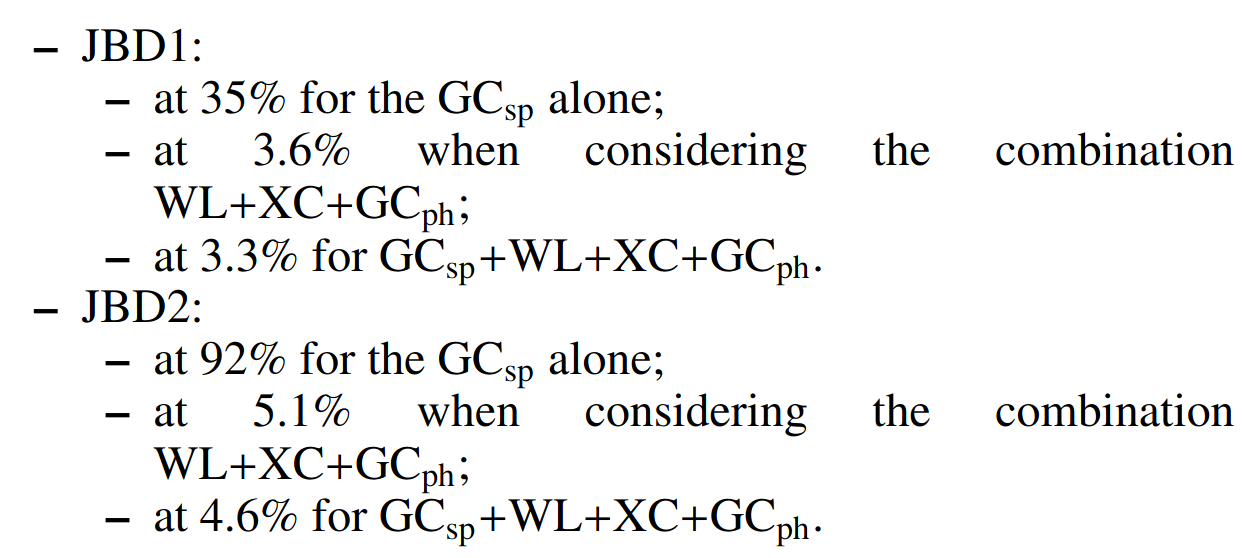
Full Euclid:

JBD1: $\omega_{BD} = 800 ^{+200}_{-160}$
JBD1: $\omega_{BD} = 2500 ^{+1070}_{-750}$

other models (To Be tested) with STAGE-IV

SC, Rubio, Pauly et al (2017) 1712.04956

Higgs-Dilaton inflation: early-late Universe connection

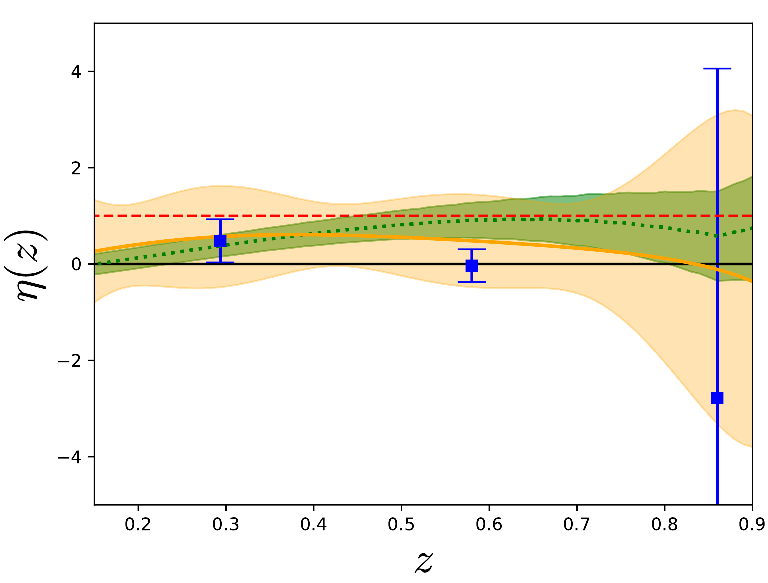
Model-independent anisotropic-stress $\eta$

Amendola, Pinho, SC 1805.00027

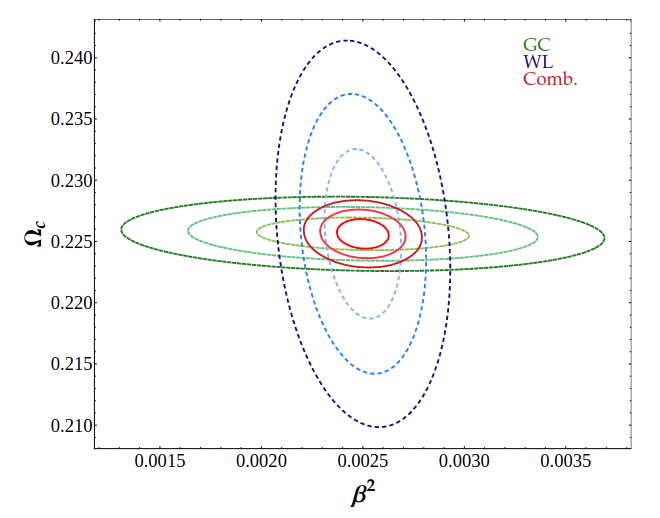
SC, Amendola, Baldi, Pettorino et al 1508.07208

Coupled Quintessence: DM-DE

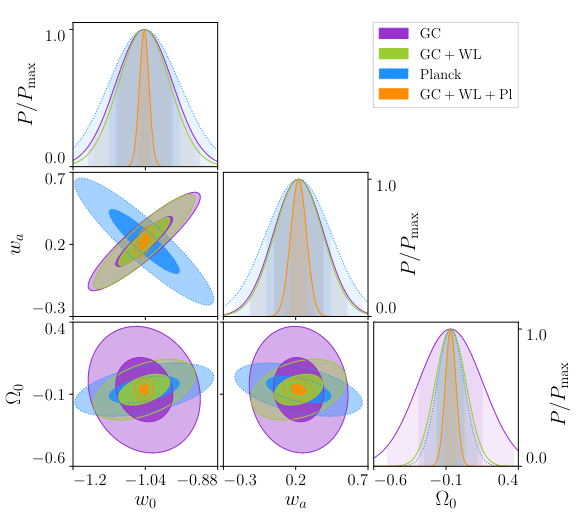
Surviving Horndeski EFT

Frusciante, Peirone, SC, Lima, 1810.10521, Phys.Rev.D 99

Text

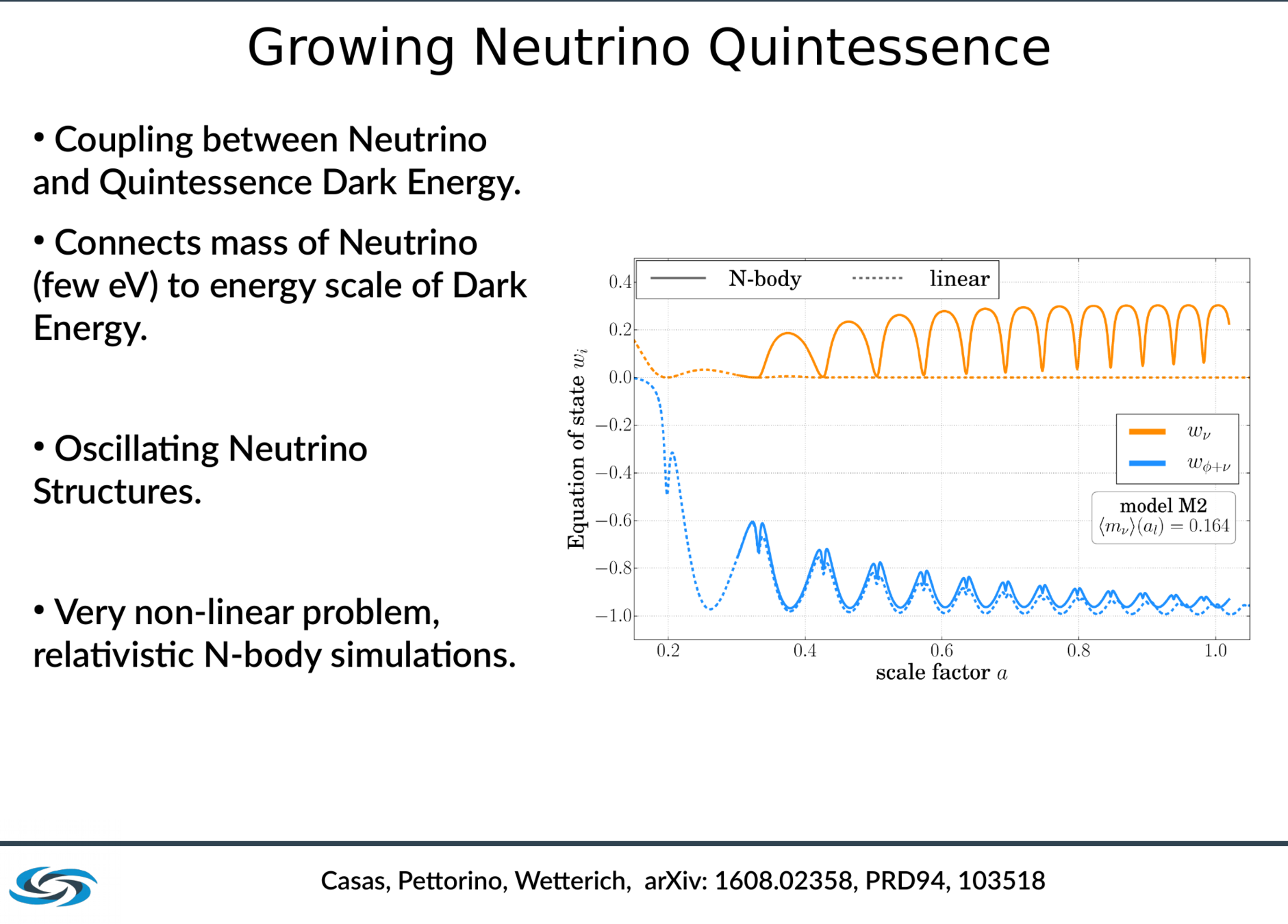
Growing Neutrino Quintessence

SC, Pettorino, Wetterich 1608.02358

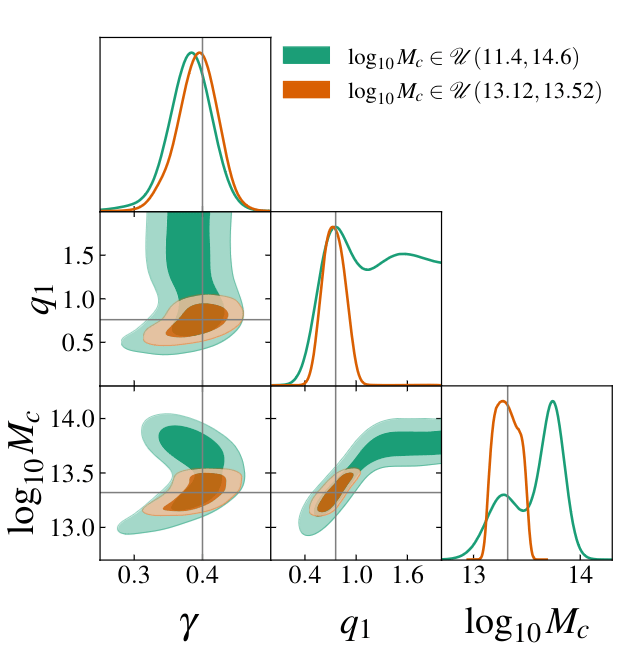
Linder-Gamma and nDGP with baryons and WL

Tsedrik, Bose, Carrilho, Pourtsidou,S.
Pamuk, Casas, Lesgourgues, 2404.11508

CosmicFish Code

Code: CosmicFish

S.Casas, M.Martinelli and M.Raveri

Soon to be released: New full pythonic version

https://github.com/santiagocasas/cosmicfishpie

Fisher Information Matrix:

Curvature (Hessian) of the Likelihood

Example: Fisher Matrix for a Gaussian likelihood of angular power spectra:

machine Learning and variational methods

In era of Big Data (billions of raw data points) and hundreds of possible models and simulations:
- Important to be as computationally efficient as possible
Likelihood codes for Euclid 2-3s per evaluation, Einstein-Boltzmann codes 1-100 seconds (depending on model -> too slow!!
Automatic-Differentiable (AD) codes: Leverage variational methods, such as Hamilton MC, AD-Variational Inference, Exact Fisher and beyond

In collaboration with Johanna Schaffmeister and Sven Günther

jaxcosmo library https://github.com/DifferentiableUniverseInitiative

Campagne, Lanusse, Zuntz, SC, et al, 2302.05163

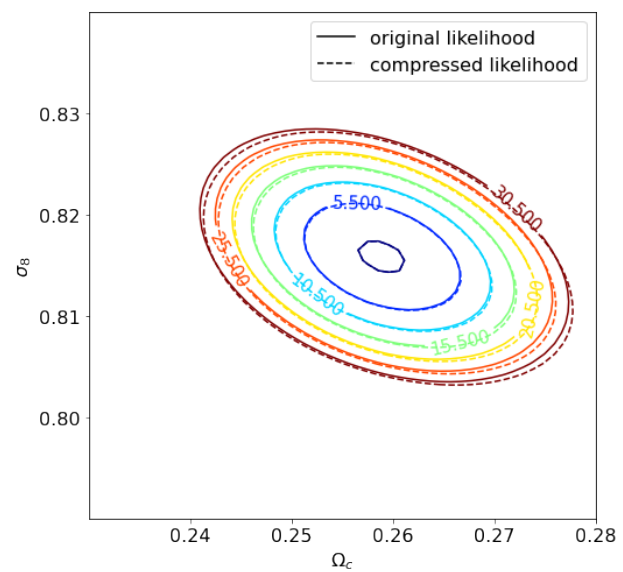
Text

Conclusions

$\Lambda$CDM paradigm still best fit to observations, but tensions, unknowns and discrepancies start to show cracks in the model.
Several avenues of research important: Modified Gravity, cosmological Neutrinos, Early-Late time interaction.
Stage-IV surveys, infrarred, optical and radio will improve error bars by one order of magnitude.
Theoretical modelling (especially at non-linear scales) has to keep up with accuracy.
Big Data challenge to be resolved with ML and AI
Unknown unknowns awaiting for us in the data !

Merci!!

BACKUP

Cosmic Microwave Background

Planck 2018 CMB Temperature map (Commander) . wiki.cosmos.esa.int/planck-legacy-archive/index.php/CMB_maps

What happened in between, if in its infancy it was a fairly Gaussian, linearly perturbed, homogenous and isotropic Universe?

the road ahead of horndeski

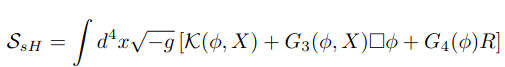
The "surviving Horndeski" Lagrangian:

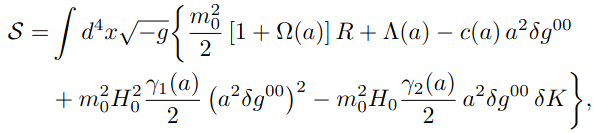
In the EFT formalism, FLRW, linear and
(unitary gauge time $\rightarrow \phi$ ) :

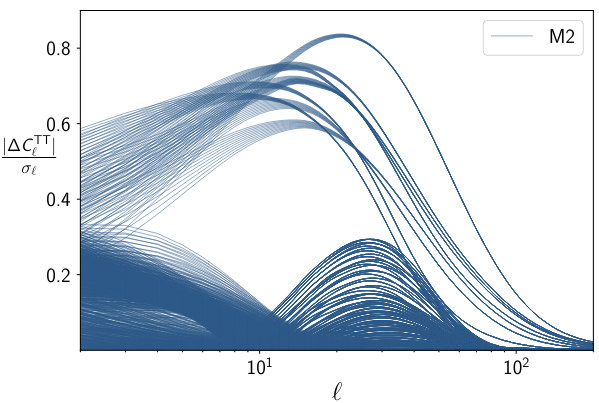
Parametrize free functions and check for stability in solutions

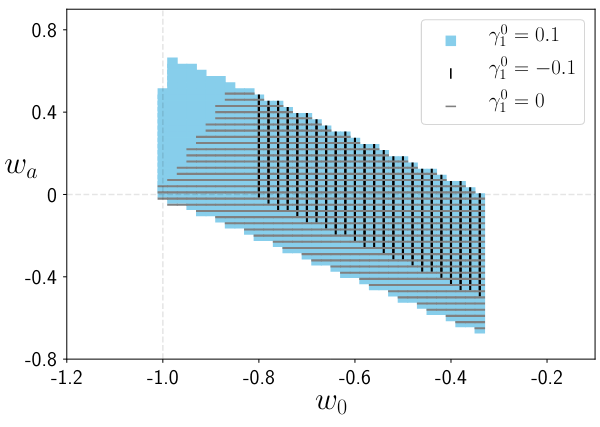
We have shown that certain classes of models will not be distinguishable from LCDM, even with future surveys, at 1$\sigma$, while others will be measured with 10%-60% precision in their parameters

Frusciante, Peirone, SC, Lima, 1810.10521, Phys.Rev.D 99

photometric primary probe

Directly constrains MG function $\Sigma$ through Weyl potential

-k^2(\Phi(a,k)+\Psi(a,k)) \equiv 8\pi G a^2 \Sigma(a,k)\rho(a)\delta(a,k)

P_{\delta \delta} \rightarrow \Sigma^2 P_{m}

http://caastro.org/research-highlights/science-animations/

In this 2-point correlation function we can see geometric features that are directly related to the expansion history of the Universe

Credits: Tobias Liaudat, CosmoStat

Euclid Shape Pipeline

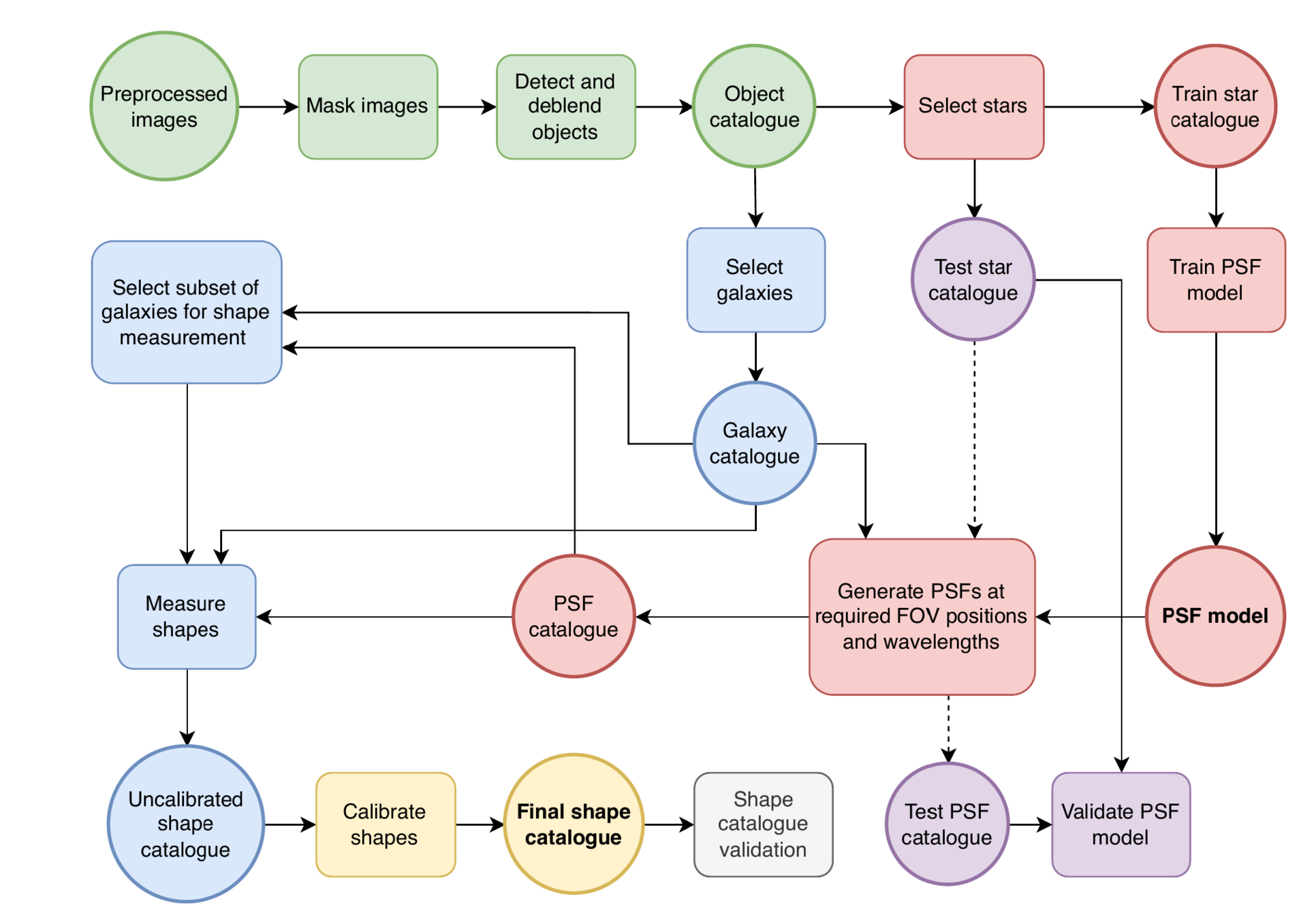
Credits: Rodlophe Cledassou, CNES

Euclid

Big bang nucleosynthesis

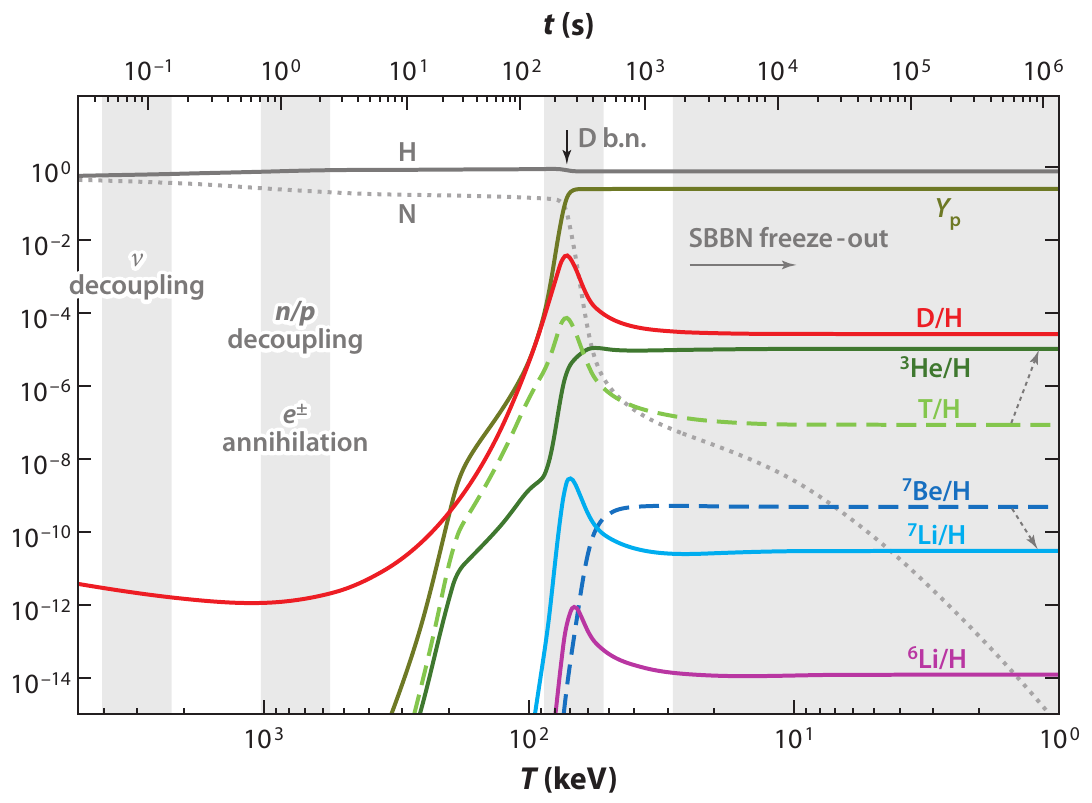
doi: 10.1146/annurev.nucl.012809.104521

Age of the Universe

Temperature of the Universe

Cosmic microwave background

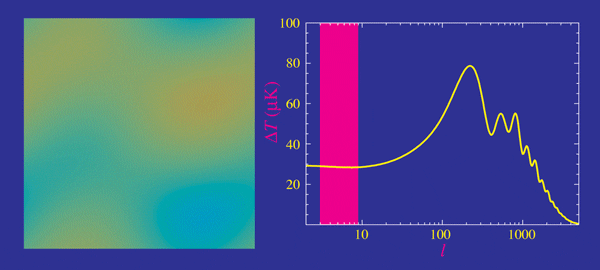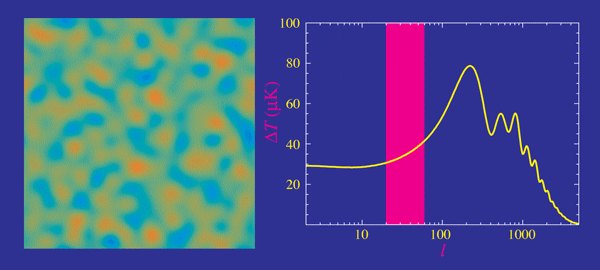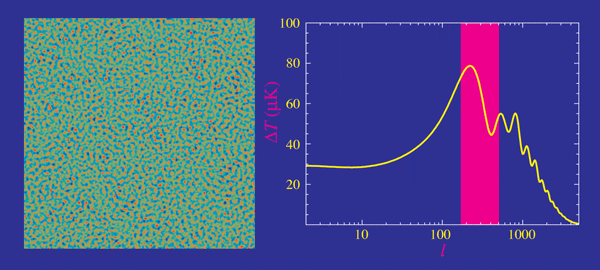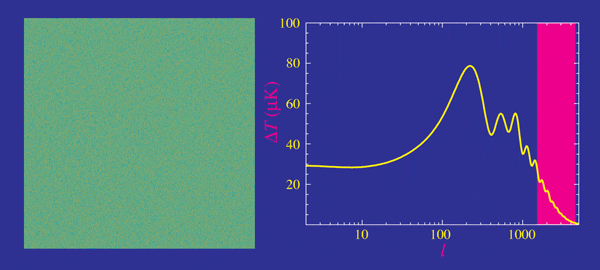
Planck measurements, essentially cosmic-variance limited in TT
Percent precision in cosmological parameters
Degeneracies in $\Omega_k$, $\Omega_m$ and $H_0$ broken with BAO and lensing
$H_0 = 67.37 \pm 0.54 \, \textrm{km/s/Mpc}$

Planck 2018 results. VI. Cosmological parameters https://arxiv.org/abs/1807.06209

https://www.cosmos.esa.int/web/planck

Possible solutions and new directions

$\Lambda$ ?
Inflation ?
$m_{\nu}$ ?
LSS ?
Big data?

Outline of working fields

Coupled Quintessence
Higgs-Dilaton
Modified Gravity
Horndeski/EFToDE
EFToLSS
Emulators
Machine Learning
Variational inference
Stage-IV surveys
Radio and Optical

Galaxy Clustering and Cosmic Shear

Weak gravitational lensing

Galaxy Clustering

Orientation and ellipticities

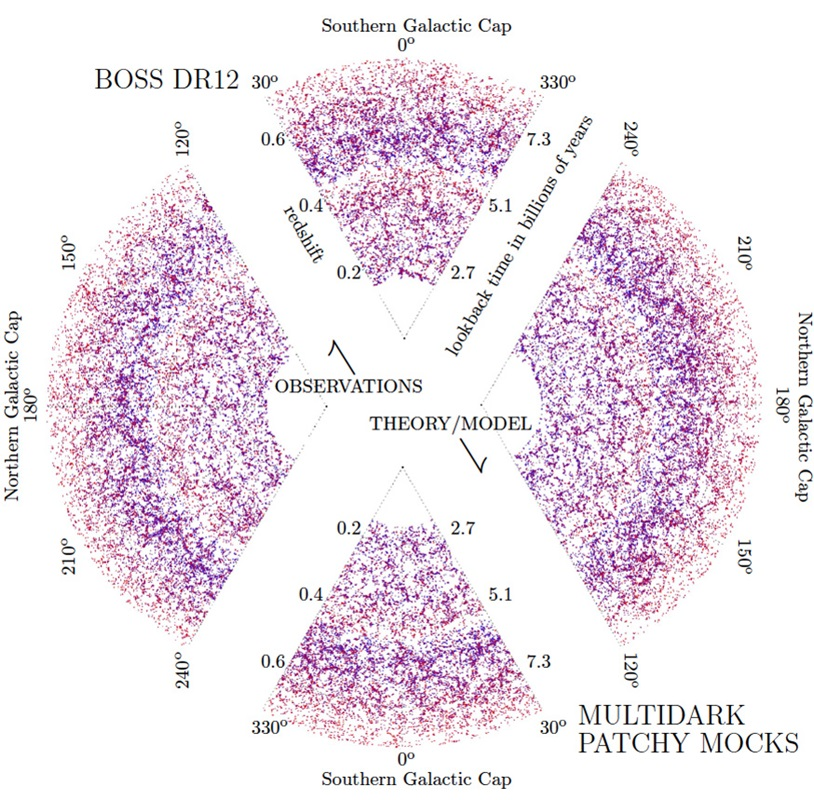
Angles and redshifts

Supernovae Type Ia and Local H0

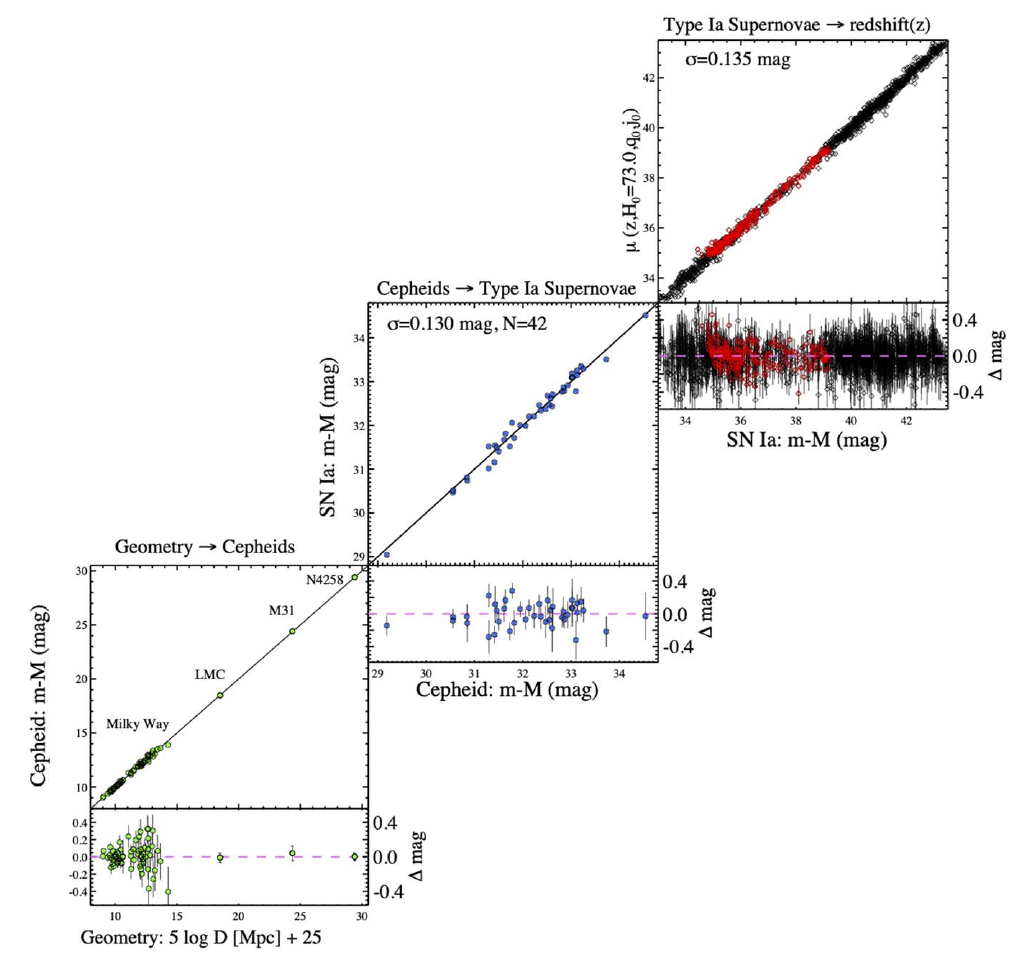
In general: confidence on the distance ladder
Concerns on calibration, anchors dust or
metallicity, have basically
faded out
Riess et al 2022*:
$H_0 = 73.30 \pm 1.04 \, \textrm{km/s/Mpc}$

using Cepheids and
high-z SNIa

* The Astrophysical Journal Letters, 934:L7 (52pp), 2022 July 20

Neutrinos Masivos en Cosmologia

Neutrinos masivos: Free streaming

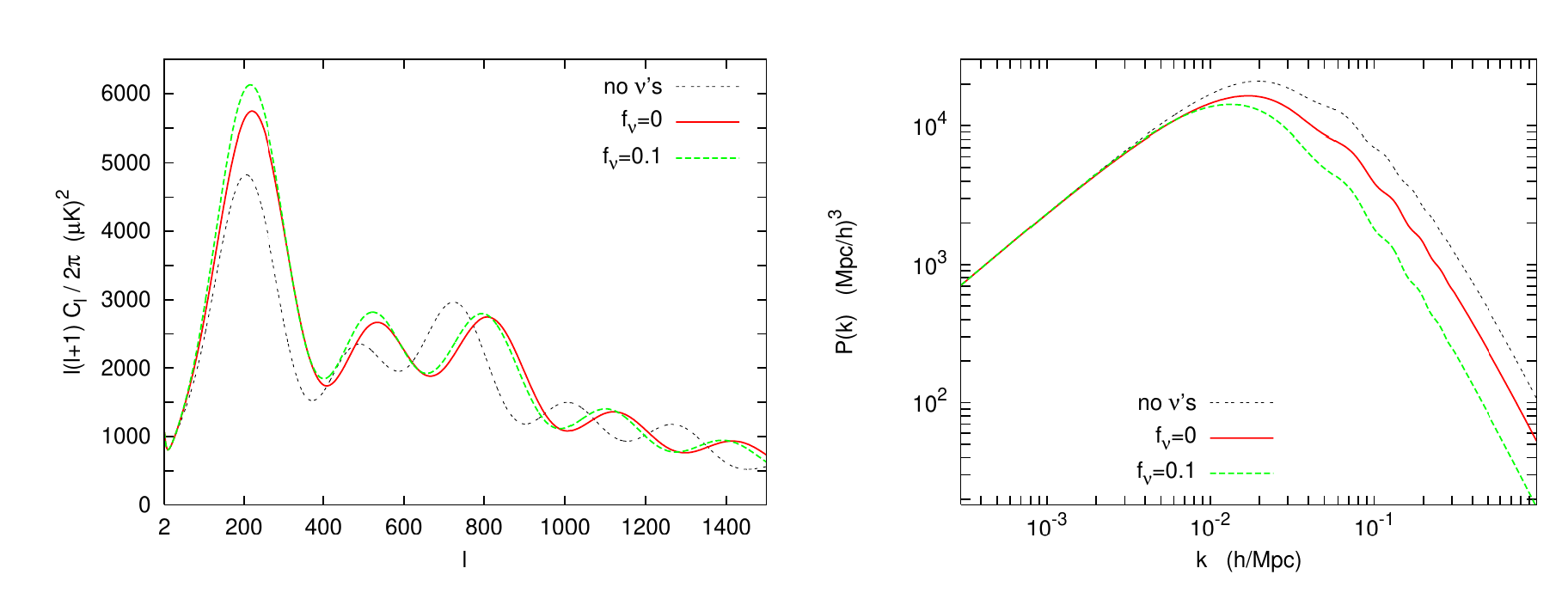
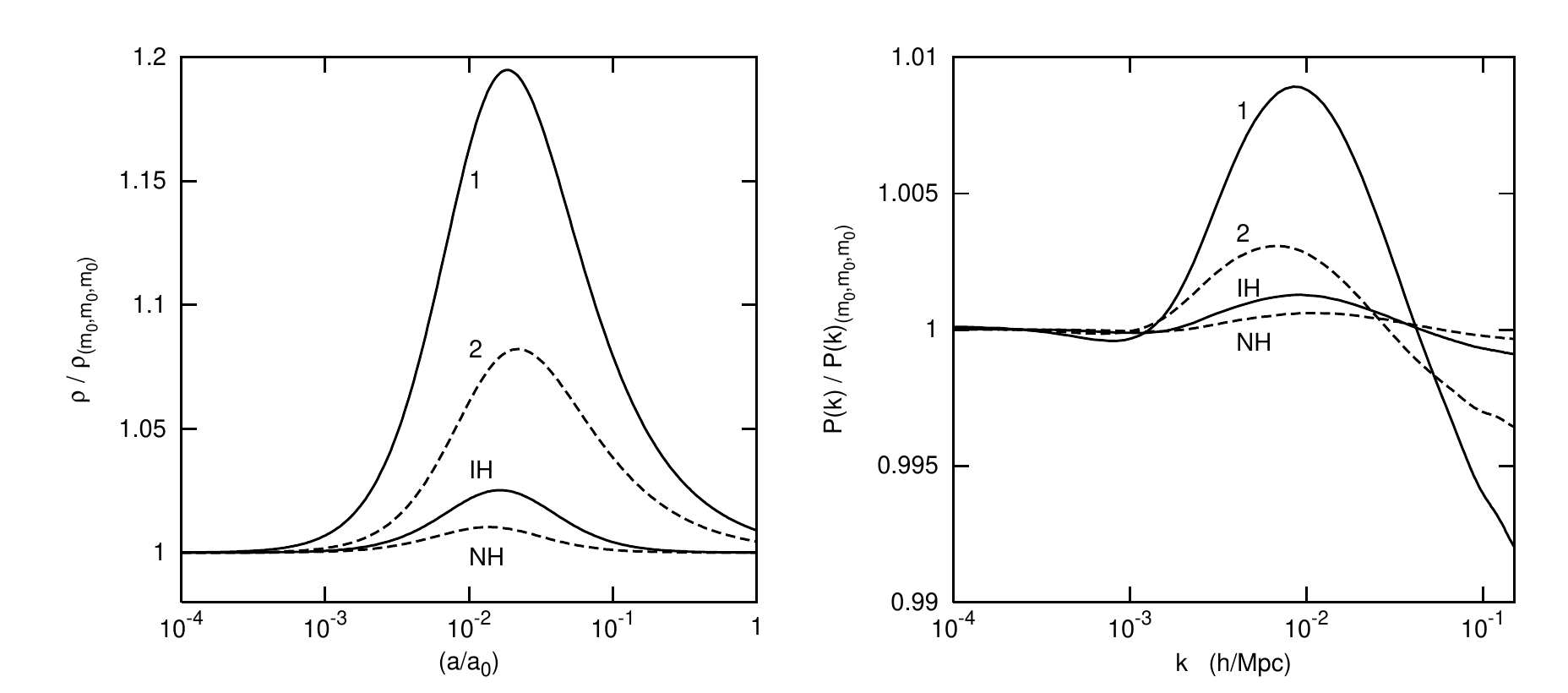
CMB angular spectrum and matter power spectrum are both dependent on neutrino mass, N_eff and ordering

Linear Perturbations

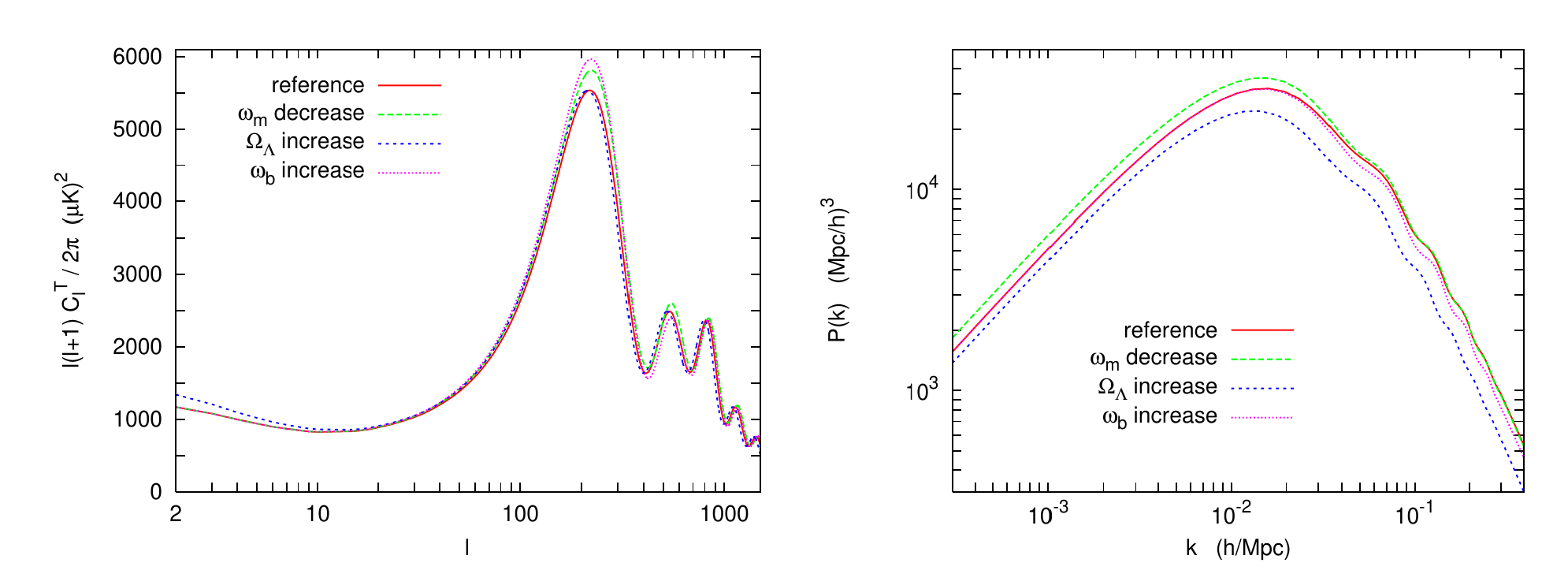
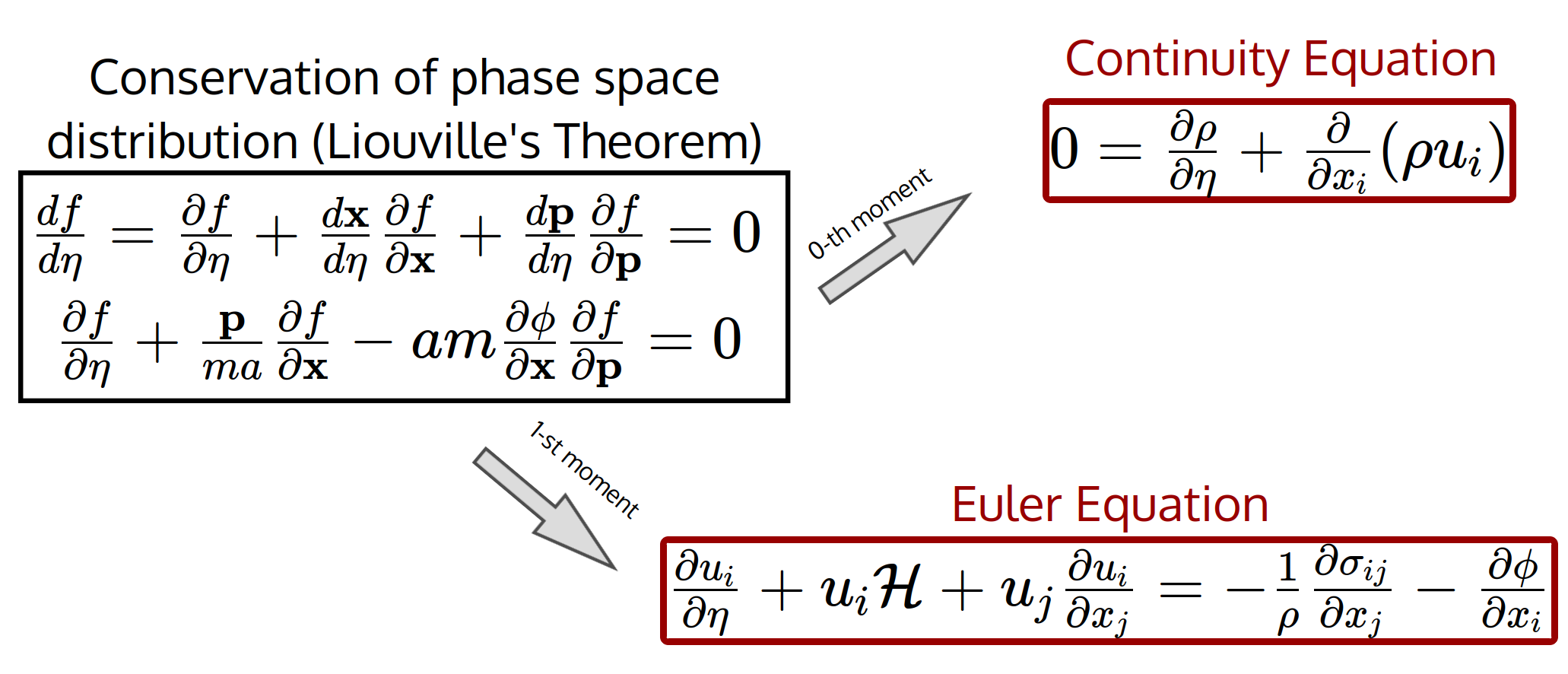
Vlasov-Poisson system is a set of diff.eqn. in which all matter-radiation species are coupled

Slides by: Dennis Linde

https://www.pablocarlosbudassi.com/2021/02/the-infographic-and-artistic-work-named.html

f(R) Hu-Sawicki model

Text

Modification of the Einstein-Hilbert action

\newcommand{\sg}{\ensuremath{\sigma_{8}}} \newcommand{\de}{\mathrm{d}} S = \frac{c^4}{16\pi G} \int{\de^4 x \sqrt{-g} \left[R+f(R)\right]}

Induces changes in the gravitational potentials *

*for negligible matter anisotropic stress

-k^2\Psi =\frac{4\pi\,G}{c^4} \,a^2\mu\bar\rho\Delta\,

-k^2\left(\Phi+\Psi\right) = \frac{8\pi\,G}{c^4}\,a^2 \Sigma \bar\rho\Delta

Scale-dependent growth of matter perturbations

Small changes in lensing potential

\mu(a,k) = \frac{1}{1+f_R(a)}\frac {1+4k^2a^{-2}m_{f_R}^{-2}(a) }{1+3k^2a^{-2}m_{f_R}^{-2}(a)}

\Sigma(a)=\frac{1}{1+f_{R}(a)}\,

Free parameter: $f_{R0}$

f(R) = - 6 \Omega_{\rm DE} H_0^2 + |f_{R0}| \frac{\bar R_0^2}{R}\,

Hu, Sawicki (2007)

"Fifth-force" scale for cosmological densities

$\lambda_C =32 \rm{Mpc}\sqrt{|f_{R0}|/10^{-4}}$

Euclid: Casas et al (2022) in preparation

f(R) Hu-Sawicki model

Text

Euclid: Casas et al (2022) in preparation

Codes used: for background and scale-dependent linear perturbations: MGCAMB and EFTCAMB

For non-linear power spectrum:

Winther et al (2019) fitting formula

Towards a robust exploration of the Dark Sector with Euclid and Stage-IV surveys within the next decade

@santiagocasas @sant87casas

Towards a robust exploration of the Dark Sector with Euclid and Stage-IV surveys within the next decade

@santiagocasas @sant87casas

Cosmic microwave background

CMB: A (Gaussian) Success story

Large Scale StructureS

However, the Universe is not as nice and simple. It is a non-linear mess:

What happened between z=1000 and z=0?

Cosmologists looked up:

What happened between z=1000 and z=0?

we Basically KNOW how to measure:

Positions of galaxies in the sky (angles)

Redshifts of galaxies (photo or Spectro)

Shapes (ellipticities of galaxies)

Some successful (STAGE-III) missions exploring these two aspects so far:

The Standard \(\Lambda\)CDM model

The expansion History

The expansion History

Tensions IN \(\Lambda\)CDM

Tensions IN \(\Lambda\)CDM

Stage-IV surveys to the rescue?

Euclid Space Satellite

Euclid Space Satellite

Vera Rubin LSST

Vera Rubin LSST

DESI telescope

Vera Rubin LSST

DESI Baryon Acoustic Oscillations

Vera Rubin LSST

Square kilometer array (SKAO)

Other Large Scale Structure Probes I WOn't MENTION IN THIS TALK:

CMB LEnSING and ITS Cross-Correlation with LSS

Cosmic VOIDS

NON-Gaussian and HIGHER ORDER STatistics

CLUSTERS of GALAXIES

We have many problems/Mysteries in cosmology

BUT let's focus on a classical one

why is the universe accelerating?

(assuming we don't like \(\Lambda\))

First Step: Modify Gravity

Dynamical Dark Energy

Dynamical Dark Energy

Dynamical Dark Energy

Dynamical Dark Energy

Problems with Dynamical DE CPL parametrization:

how do we do these forecasts again?

spectroscopic probe

photometric primary probe

photometric primary probe

Fisher Matrix Forecasts

Fisher Matrix Forecasts

Fisher Matrix Forecasts

Can we trust Fisher constraints?

The effect of Neutrinos

Can we trust Fisher constraints also in this case?

The effect of Neutrinos

Dynamical Dark Energy + Neutrinos

Dynamical Dark Energy + Neutrinos

Let's go to even more realistic settings

Euclid: Likelihood and Nonlinear Challenges

Euclid: Likelihood and Nonlinear Challenges

spectroscopic probe: Full Shape

spectroscopic probe: Full Shape

Let's go Back to modified gravity

Modified Gravity and Dark Energy

a SCALAR-tensor theory

Parametrized modified gravity

Parametrized modified gravity

Parametrized modified gravity

Vera Rubin LSST

Square kilometer array (SKAO)

Vera Rubin LSST

Radio x Optical Cosmology

Classifying by screening

Classifying by screening

f(R) Hu-Sawicki model

f(R) Hu-Sawicki model

f(R) Hu-Sawicki model

f(R) Hu-Sawicki model