An exploration of physics beyond the standard model with next generation cosmological observations
Santiago Casas
Postdoctoral Researcher
TTK, RWTH Aachen University





@santiagocasas @sant87casas


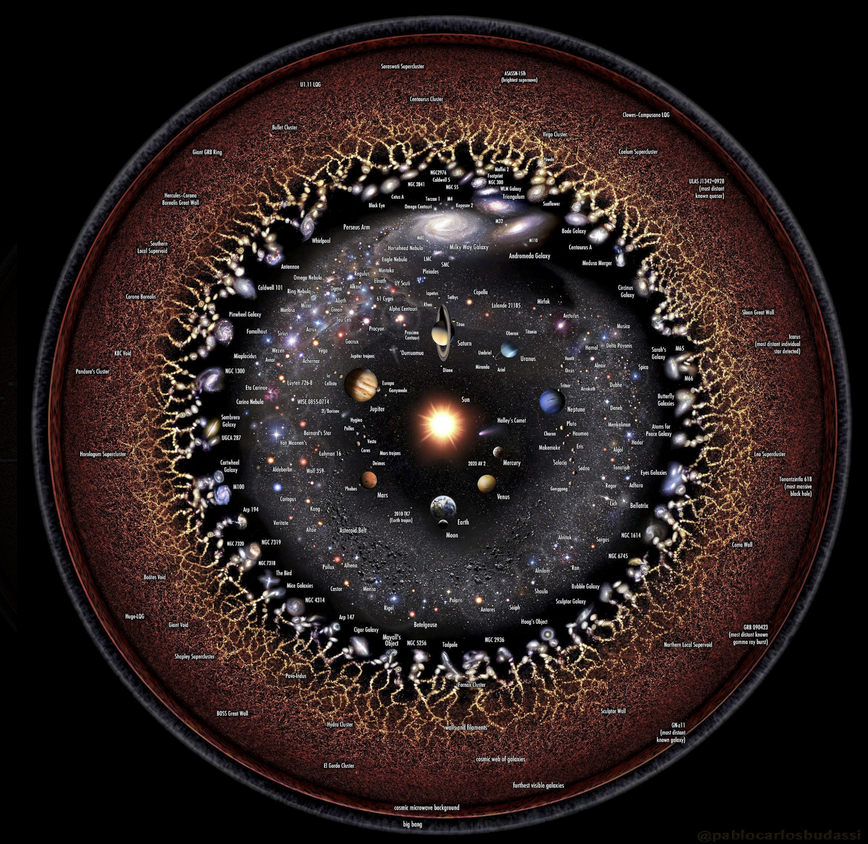
https://www.pablocarlosbudassi.com/2021/02/the-infographic-and-artistic-work-named.html
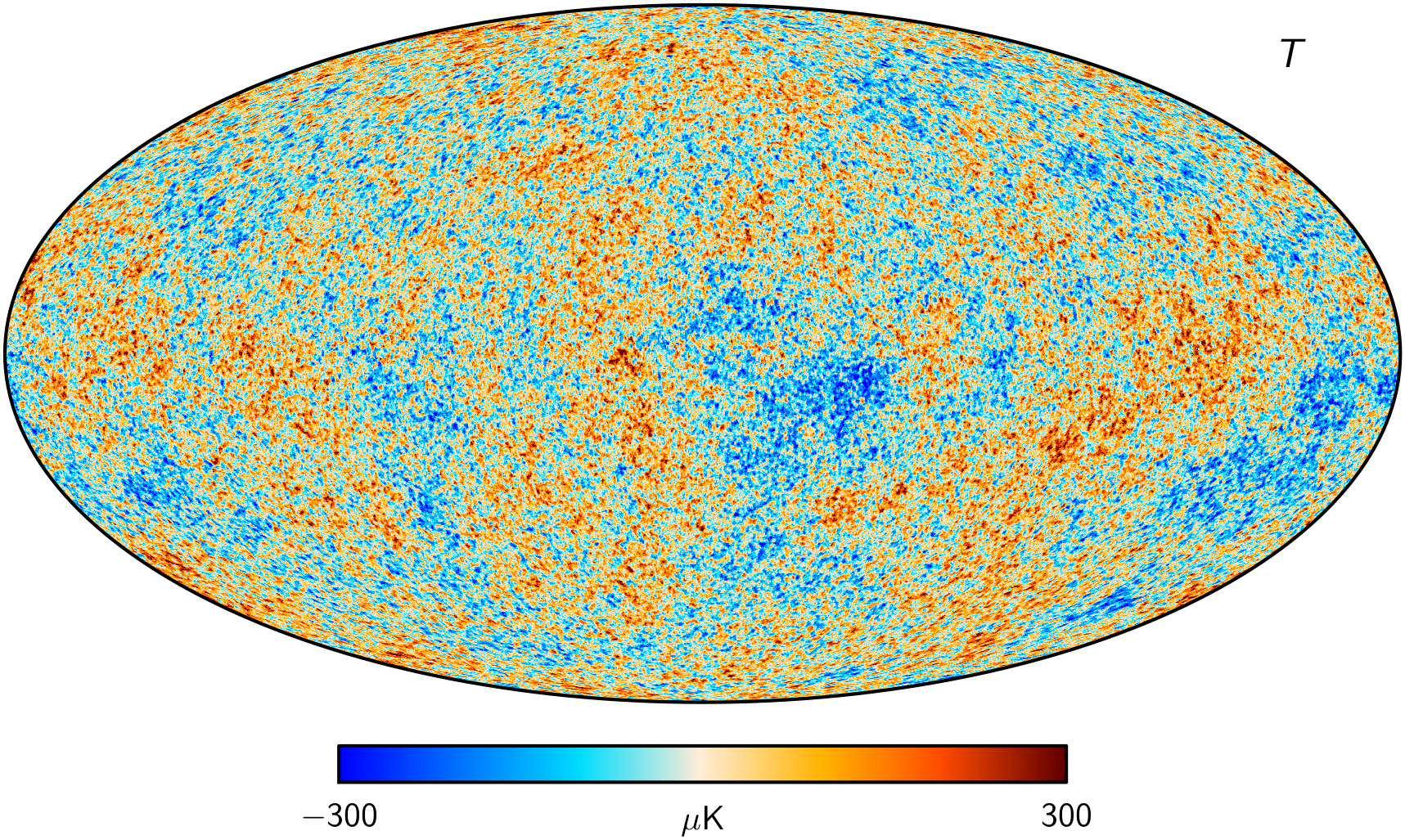
Cosmic Microwave Background
Planck 2018 CMB Temperature map (Commander) . wiki.cosmos.esa.int/planck-legacy-archive/index.php/CMB_maps

Large Scale Structure
Illustris Simulation: www.nature.com/articles/nature13316
The Standard \(\Lambda\)CDM model
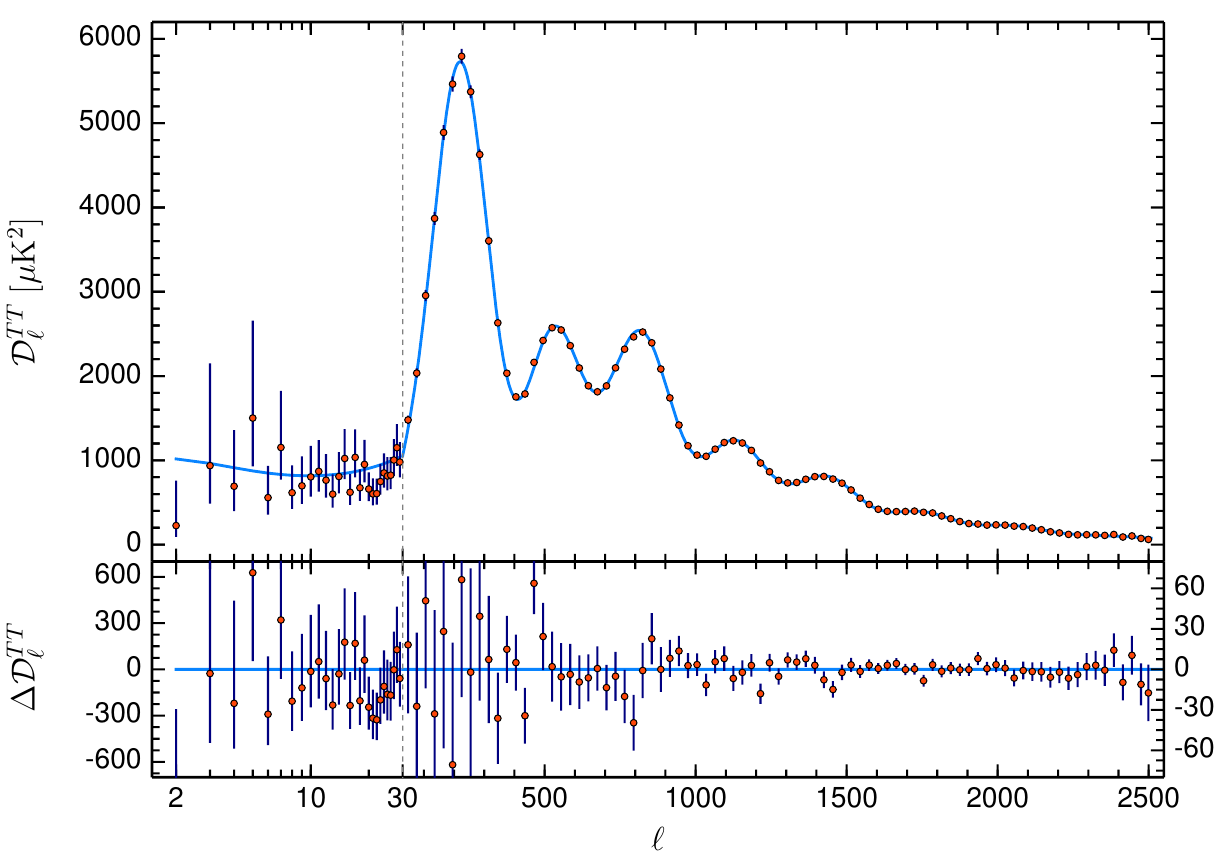
- \(\Lambda\)CDM is best fit to observations.
- Predictive model with few free parameters.
Concordance Cosmology:
- Lensing
- CMB
- Clustering
- Supernovae
- Clusters
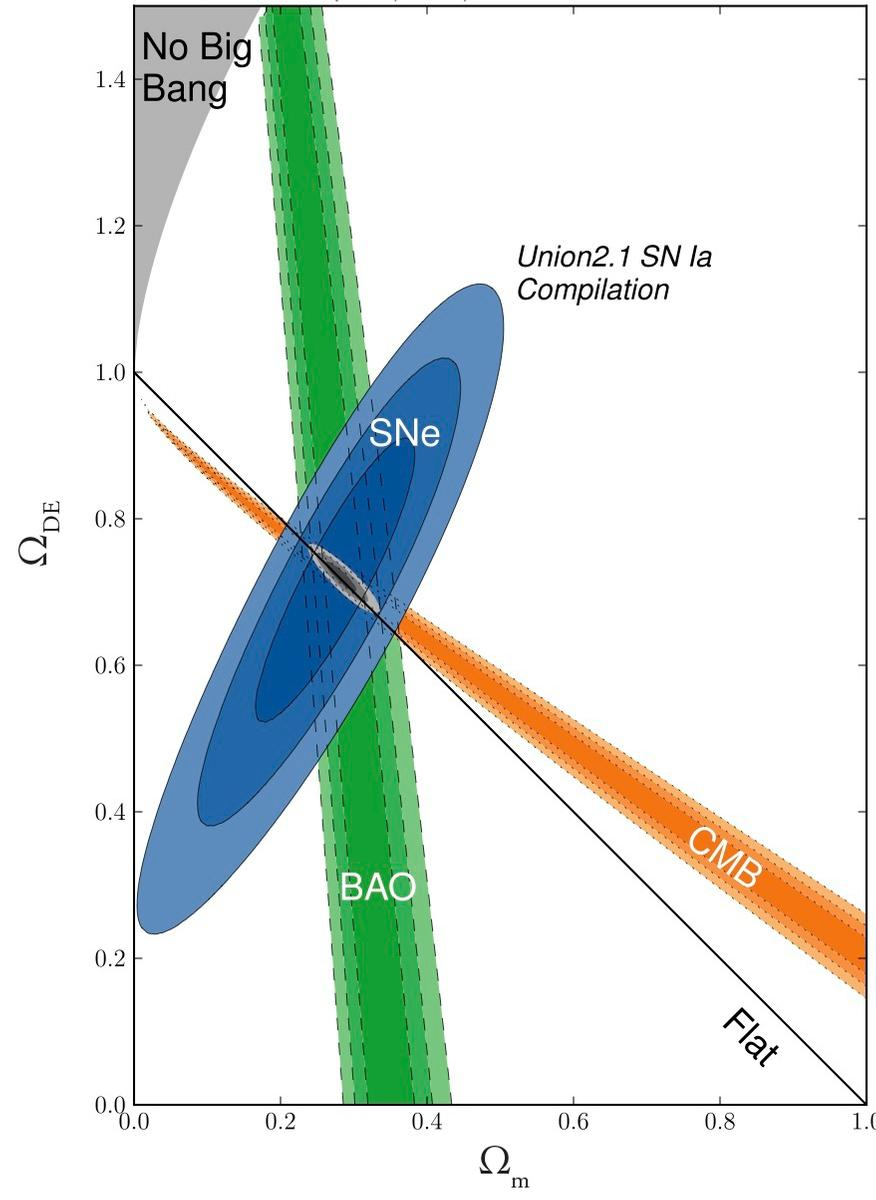
https://www.cosmos.esa.int/web/planck/publications
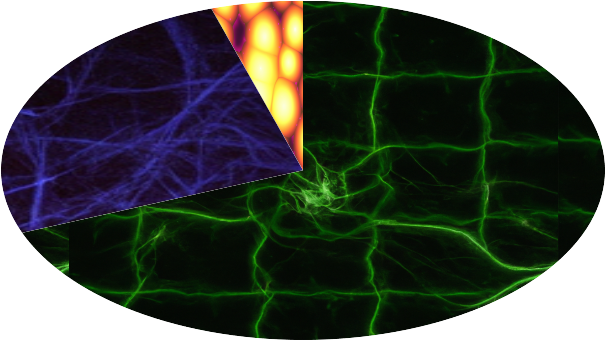
68% Dark Energy
5% Baryons
27% Dark Matter
Textures created with DALL-E
The Standard \(\Lambda\)CDM model
- \(\Lambda\)CDM is still best fit to observations.
- Some questions remain:
- \(\Lambda\) and CDM.
- CDM hasn't been found
- Cosmological Constant Problem:

Quantum Gravity?
O(100) orders of magnitude wrong
(Zeldovich 1967, Weinberg 1989, Martin 2012).
Composed of fine-tuning, hierarchy and coincidence
sub-problems, among others.
String Theory Landscape?
The expansion History
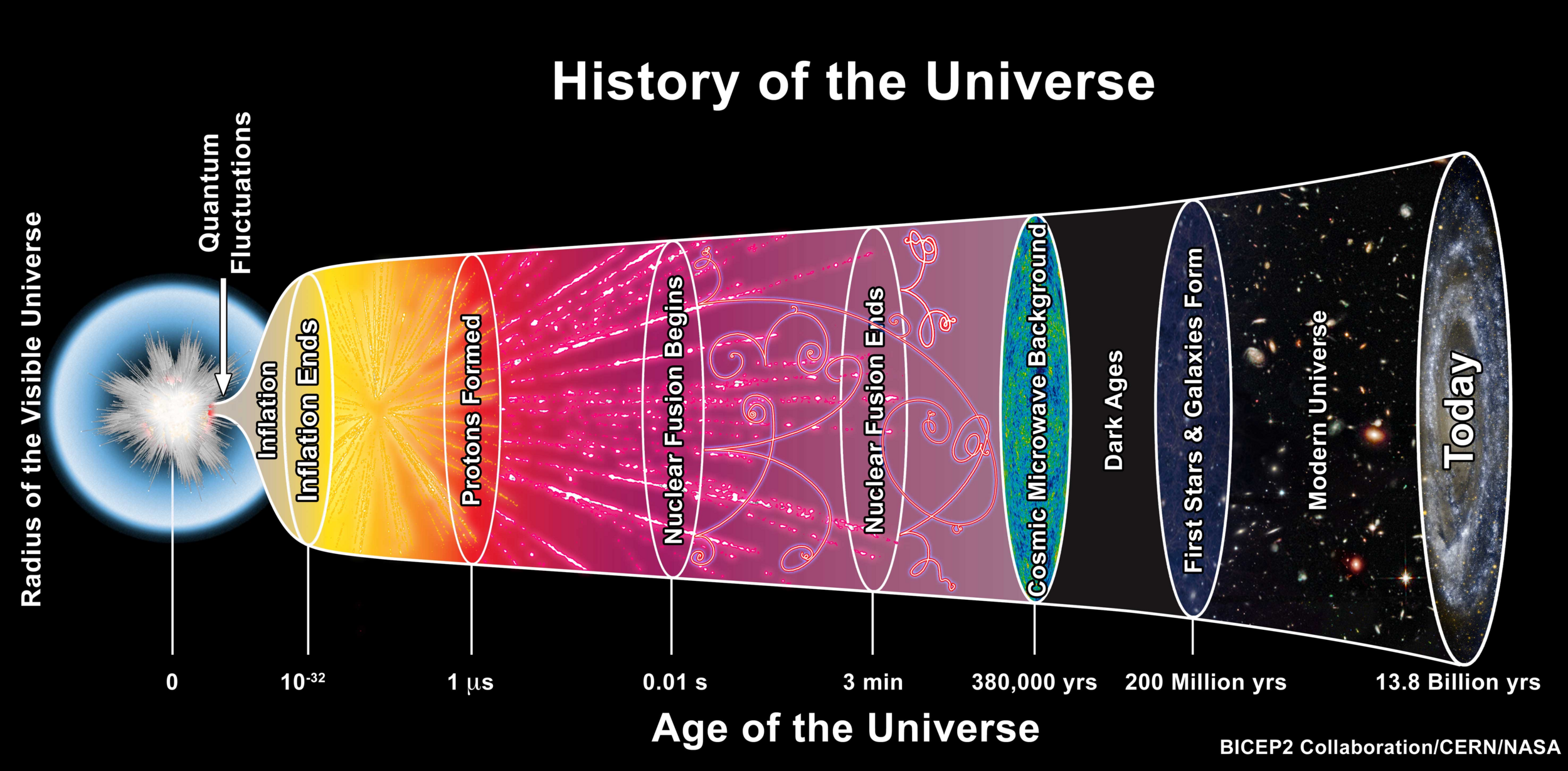
The expansion History

\(\phi\) ?
baryogenesis? \(_3^7\textrm{Li}\)?
H0 tension?
z_reio?
\(\Lambda\) ?
DM? PBH ?
-
Things We Think we knoW
-
THINGS WE kNOW WE DON'T understand
-
UNKNOWN UNKNOWNS
HOW to classify our ignorance?
What do we think we know?
Big bang nucleosynthesis
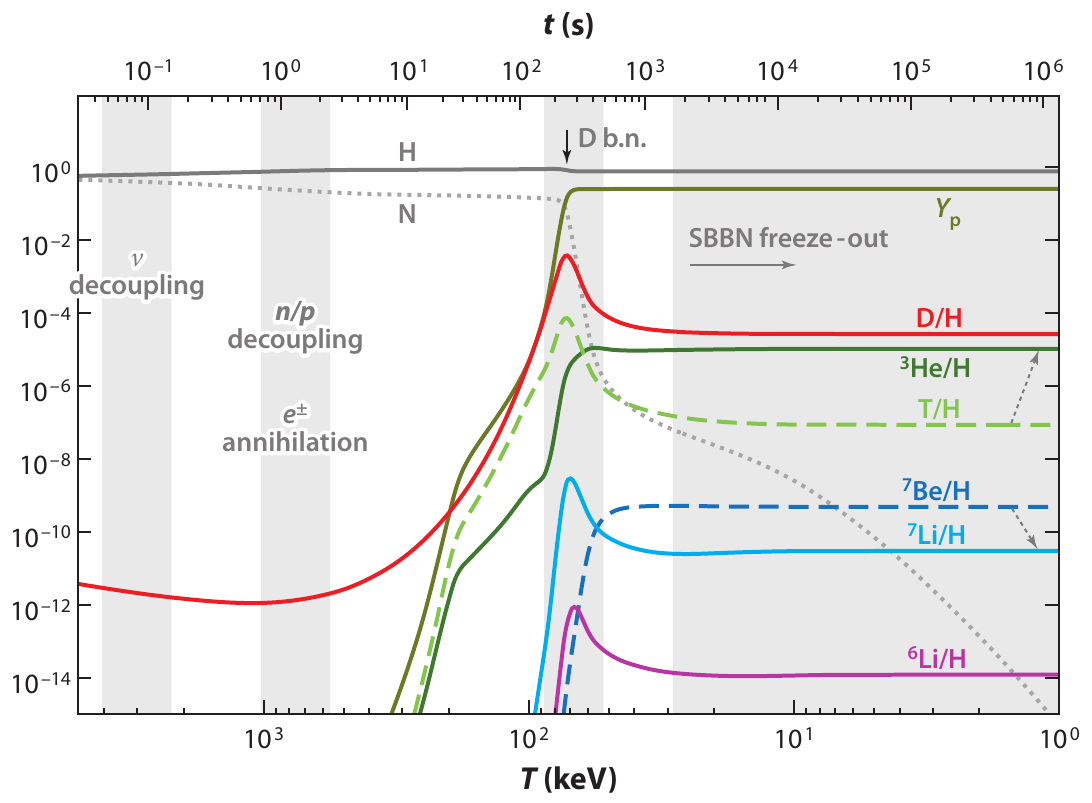
doi: 10.1146/annurev.nucl.012809.104521
Age of the Universe
Temperature of the Universe
Cosmic microwave background
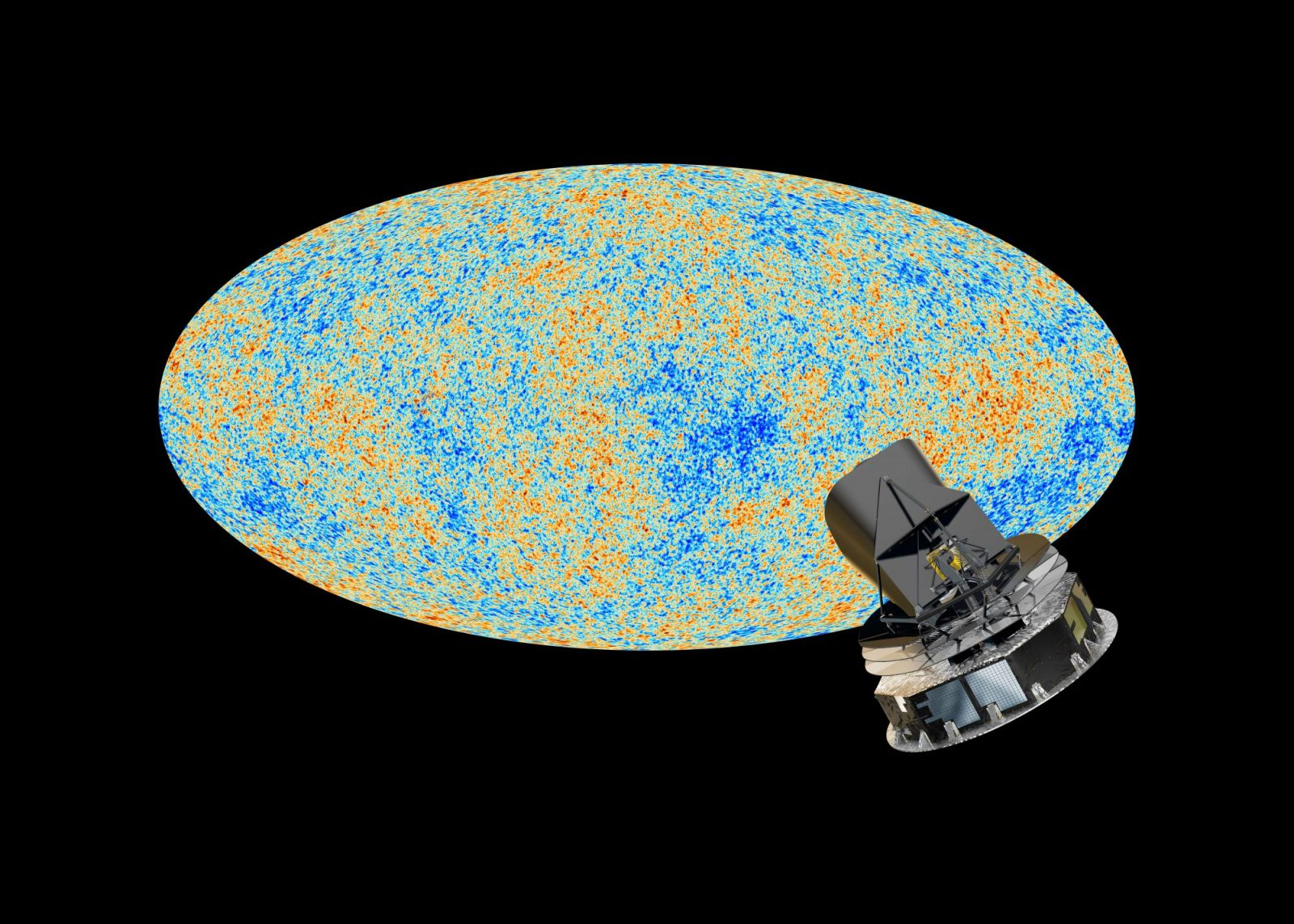
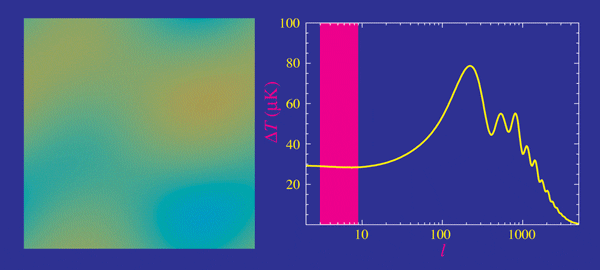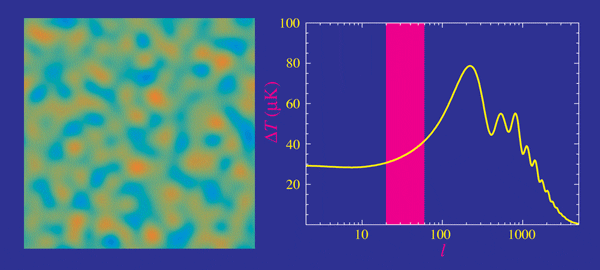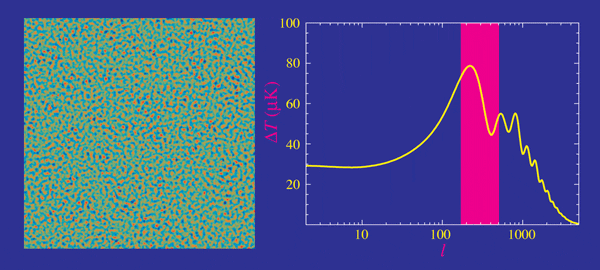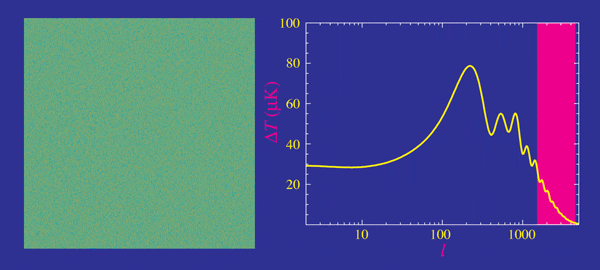
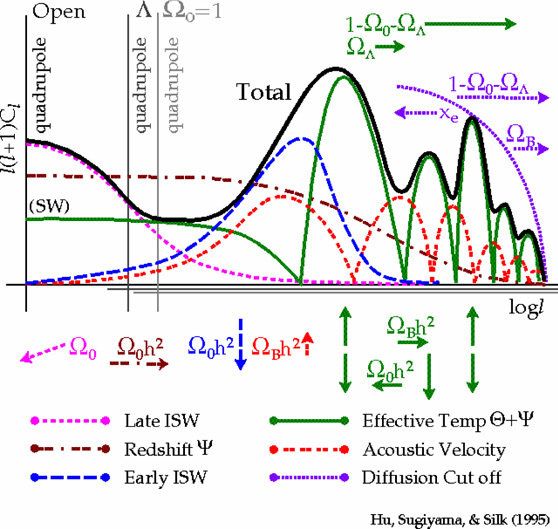

- Planck measurements, essentially cosmic-variance limited in TT
- Percent precision in cosmological parameters
- Degeneracies in \(\Omega_k\), \(\Omega_m\) and \(H_0\) broken with BAO and lensing
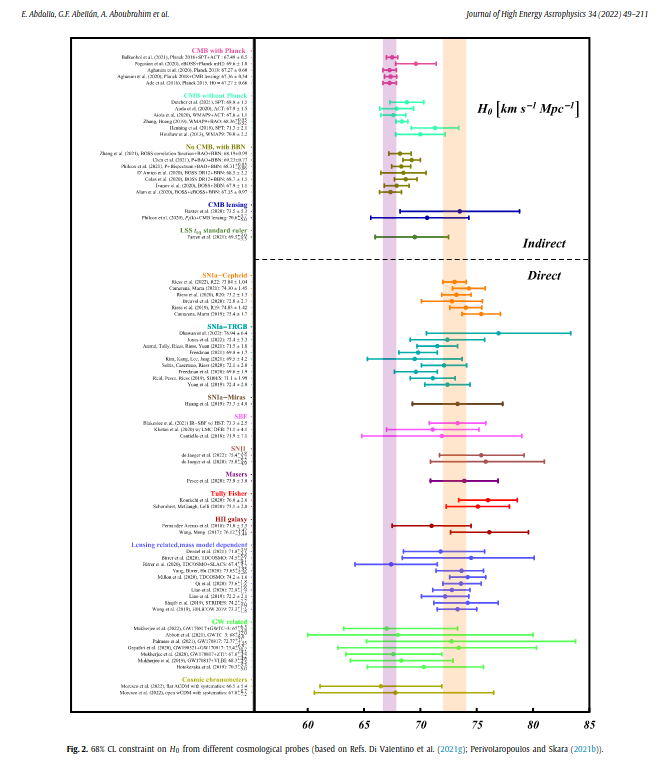
- \(H_0 = 67.37 \pm 0.54 \, \textrm{km/s/Mpc}\)
Planck 2018 results. VI. Cosmological parameters https://arxiv.org/abs/1807.06209
https://www.cosmos.esa.int/web/planck
Supernovae Type Ia and Local H0
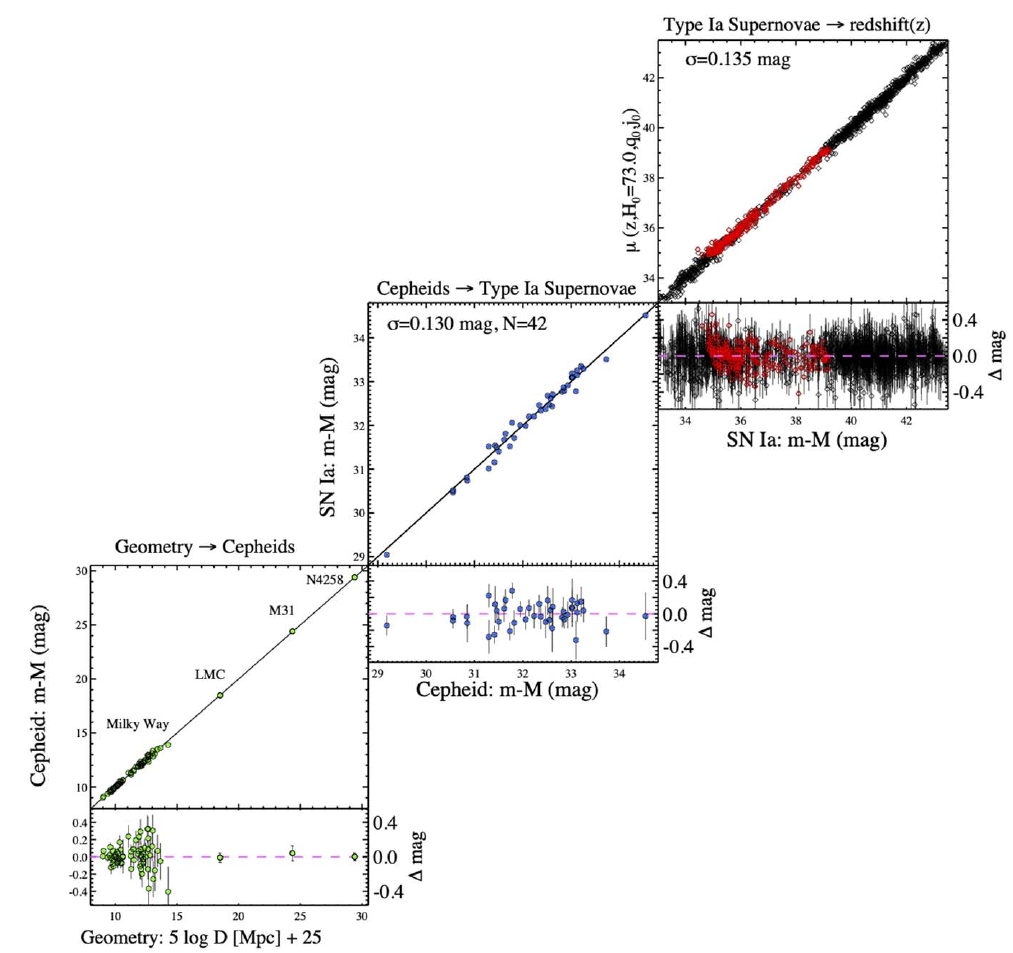
- In general: confidence on the distance ladder
- Concerns on calibration, anchors dust or
metallicity, have basically
faded out - Riess et al 2022*:
\(H_0 = 73.30 \pm 1.04 \, \textrm{km/s/Mpc}\)
using Cepheids and
high-z SNIa
* The Astrophysical Journal Letters, 934:L7 (52pp), 2022 July 20
Tensions IN \(\Lambda\)CDM

\(H_0\) tension at 5\(\sigma\)
- Tensions between local and recombination-based measurements
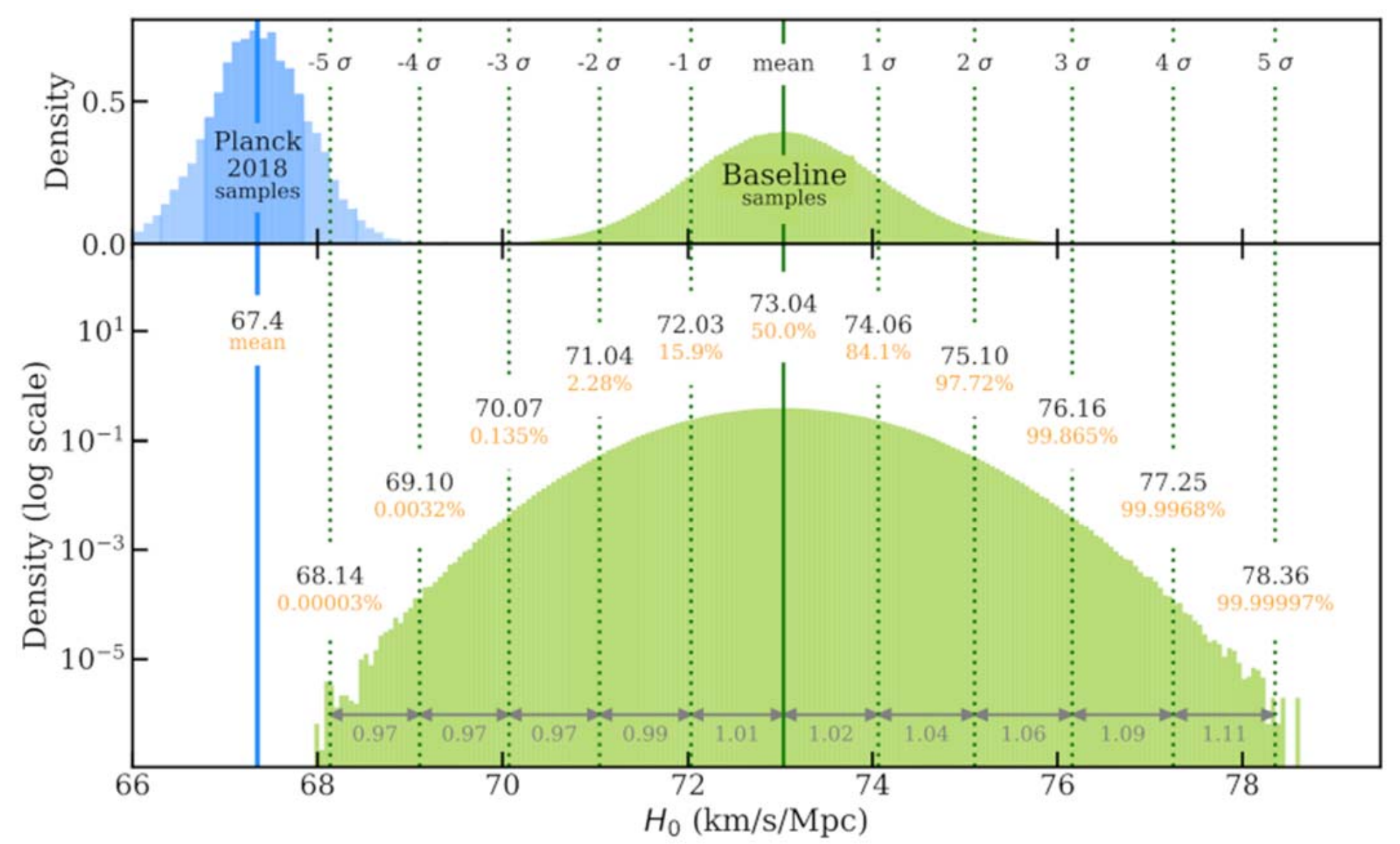
Freedman et al
SH0ES, Riess et al
Planck 2018, VI
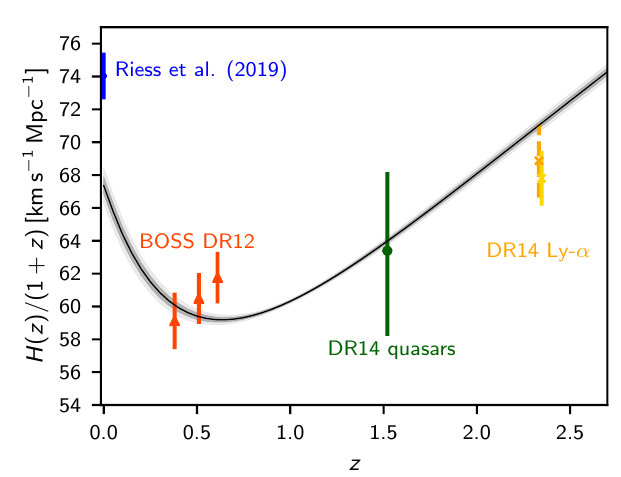
What else do we think we know?
How to measure:
-
Positions of galaxies in the sky (angles)
-
Redshifts of galaxies (photo or Spectro)
-
Shapes (ellipticities of galaxies)
Galaxy Clustering and Cosmic Shear
Weak gravitational lensing
Galaxy Clustering
Orientation and ellipticities

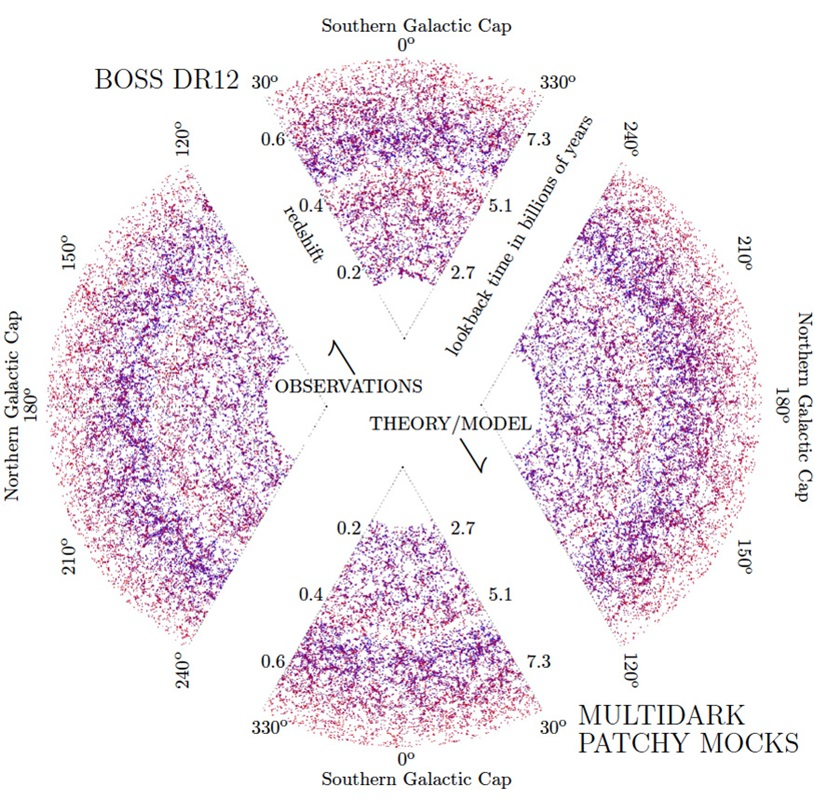
Angles and redshifts
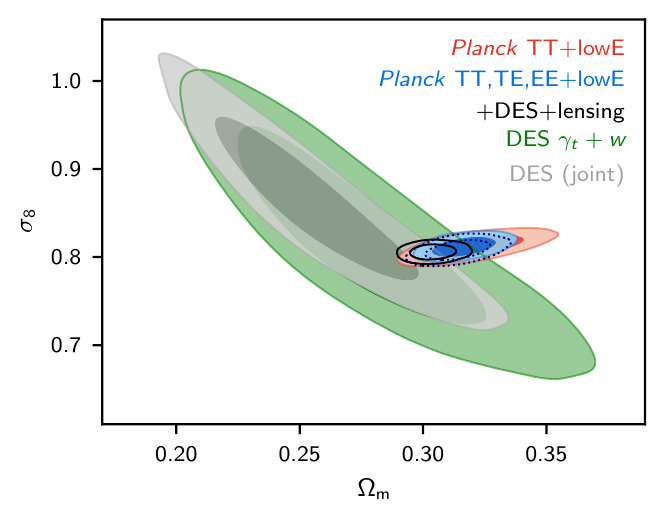
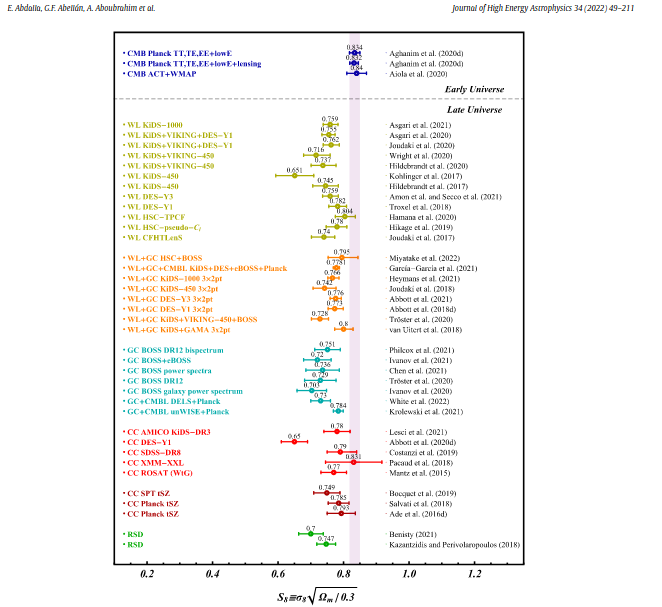
Tension with Planck in the
\(\sigma8\) - \(\Omega_m\) plane
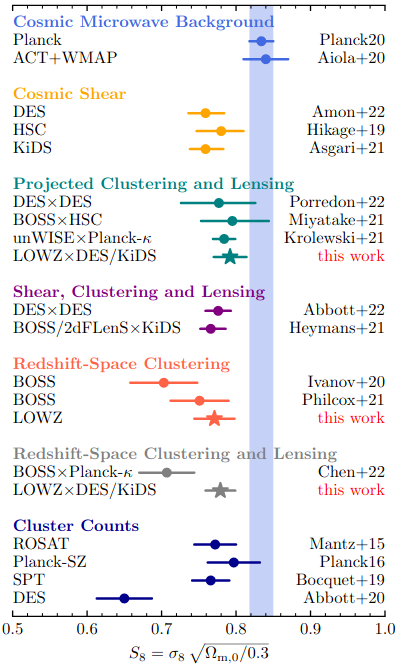
Lange et al. arXiv: 2301.08692
- So called "lensing is low" problem.
- At the moment just a discrepancy (no tension) at 2-3 \(\sigma\)
- Blind comparisons among surveys can rule out usual systematics below z<0.54 (A. Leauthaud et al.)
- Beyond \(\Lambda\)CDM modelling does not help with current nonlinear analysis
Planck 2018, VI
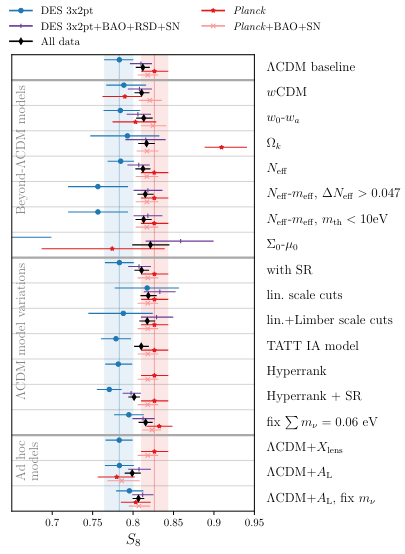
DES DRY3 arxiv:2207.05766
Tensions IN \(\Lambda\)CDM

Tension with Planck in the
\(\sigma8\) - \(\Omega_m\) plane

Lange et al. arXiv: 2301.08692
- So called "lensing is low" problem.
- At the moment just a discrepancy (no tension) at 2-3 \(\sigma\)
- Blind comparisons among surveys can rule out usual systematics below z<0.54 (A. Leauthaud et al.)
- Beyond \(\Lambda\)CDM modelling does not help with current nonlinear analysis
Planck 2018, VI

Tensions IN \(\Lambda\)CDM
Possible solutions and new directions
- \(\Lambda\) ?
- Inflation ?
- \(m_{\nu}\) ?
- LSS ?
- Big data?
Outline of working fields
- Coupled Quintessence
- Higgs-Dilaton
- Modified Gravity
- Horndeski/EFToDE
- EFToLSS
- Emulators
- Machine Learning
- Variational inference
- Stage-IV surveys
Radio and Optical

First Step: Modify Gravity
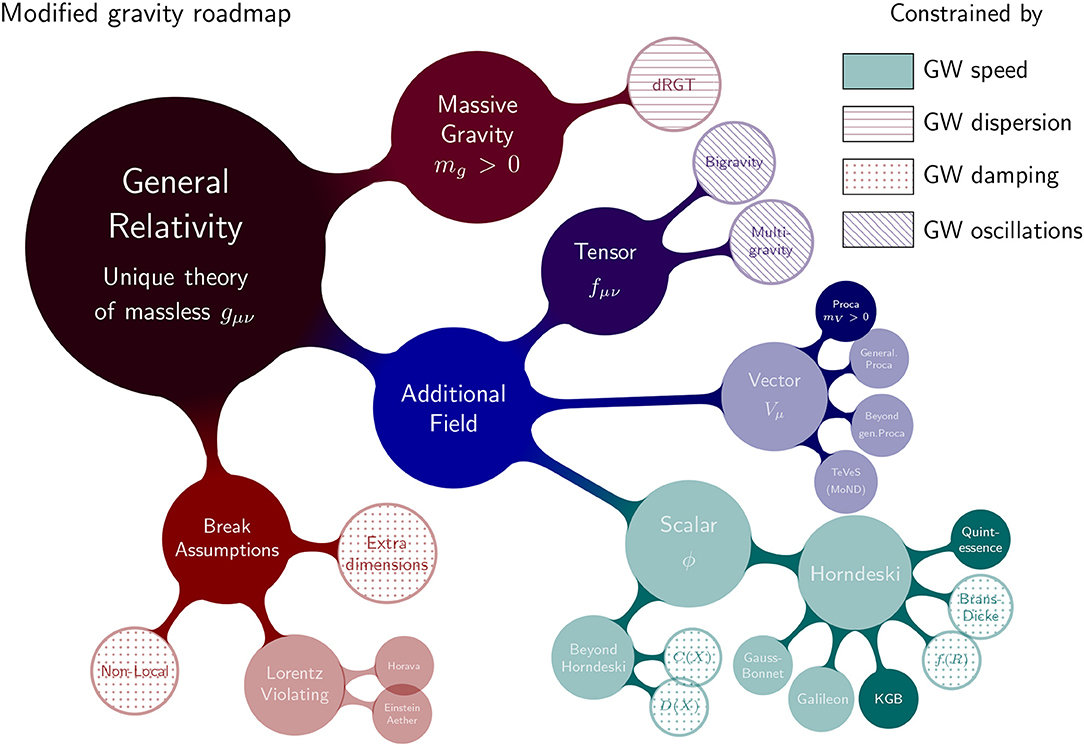
Ezquiaga, Zumalacárregui, Front. Astron. Space Sci., 2018
Modified Gravity and Dark Energy

- Add a scalar degree of freedom to the Einstein-Hilbert action
- (Non-)Minimal coupling, Kinetic terms
a SCALAR-tensor theory



Gregory Horndeski
https://www.horndeskicontemporary.com/works
Costa Rica - Arenal Volcano
- Horndeski theory: most general theory for an extra scalar degree of freedom, with second order equations of motion in 4D and no ghosts
- 5 Lagrangian terms, which have been largely ruled out by:
- Late-ISW
- GW170817
- No self-acceleration -> uninteresting
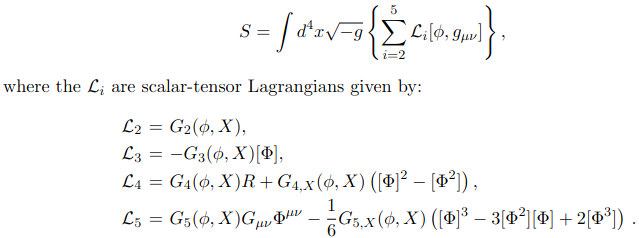
the road ahead of horndeski
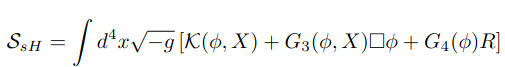
The "surviving Horndeski" Lagrangian:
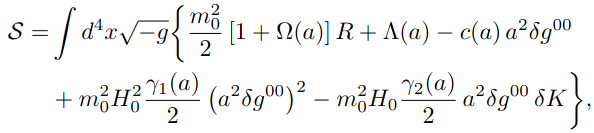
In the EFT formalism, FLRW, linear and
(unitary gauge time \(\rightarrow \phi\) ) :
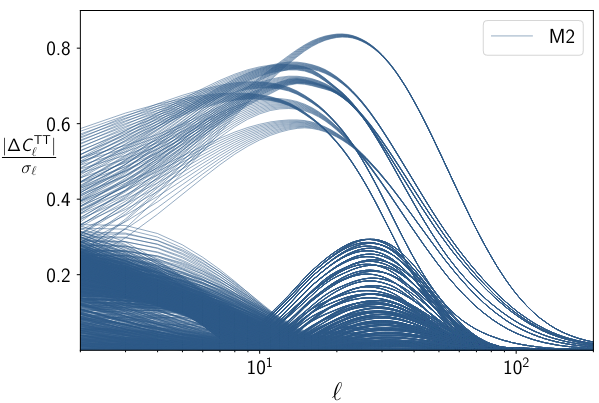
Parametrize free functions and check for stability in solutions
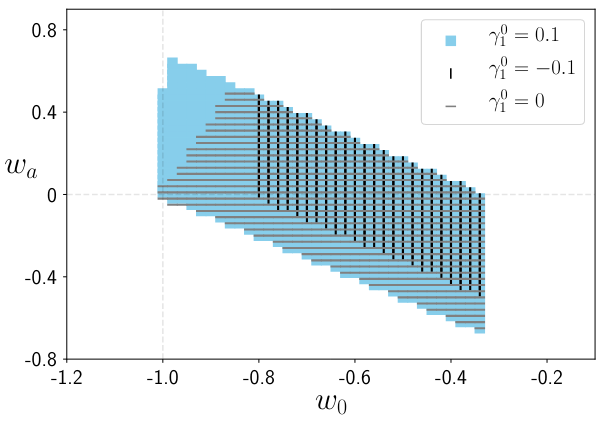
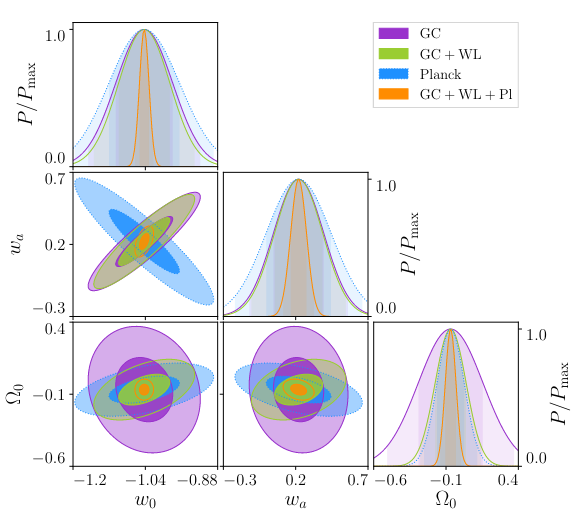
We have shown that certain classes of models will not be distinguishable from LCDM, even with future surveys, at 1\(\sigma\), while others will be measured with 10%-60% precision in their parameters
Frusciante, Peirone, SC, Lima, 1810.10521, Phys.Rev.D 99
Classifying by screening
- Modified Gravity theories should recover GR at small scales, especially in dense regions, screening needed!
Brax, SC, Desmond, Elder 2201.10817 Universe 8
- Perturbations of \(\phi\) and matter coupled in Jordan frame -> Yukawa-like fifth forces:
Different types of screening:
- Chameleon: The mass \(m(\phi_0)\) increases sharply inside matter
- Damour-Polyakov: The coupling \(\beta(\phi_0)\) vanishes inside matter
- K-mouflage and Vainshtein: \(Z(\phi_0) \gg 1\)
Classifying by screening
Brax, SC, Desmond, Elder 2201.10817 Universe 8
Screening mechanisms can be characterized by the inequality:
- Chameleon: \(k=0\) (surface N. potential is large)
- K-mouflage: \(k=1\) (N. acceleration is large)
- Vainshtein: \(k=2\) (curvature is large)
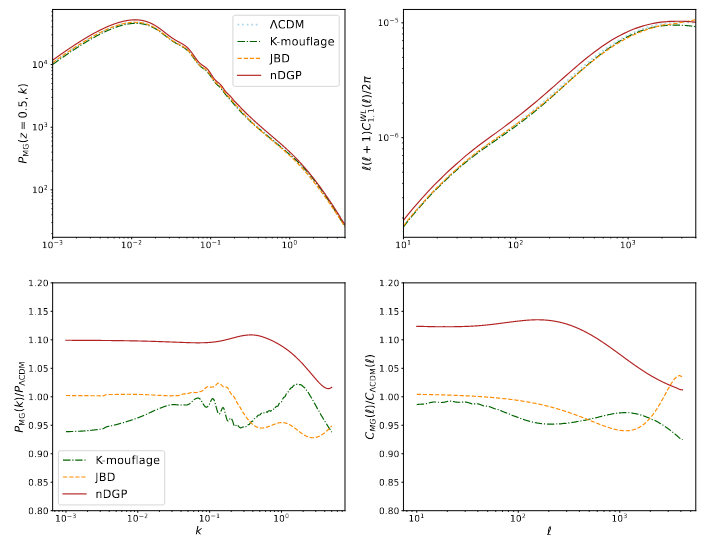
- \( f(R) \) Hu-Sawicki (see later)
- \(k\)-essence + univ. coupling
- nDGP (3+1)d brane embedded in 5d
For DE applications and under some assumptions:
- Chameleon screens everything above a certain potential threshold
- K-mouflage does not screen galaxy clusters
- Vainshtein screens all structures that turn non-linear
Parametrized modified gravity

Beyond \(\Lambda\)CDM the two linear gravitational potentials \(\Psi\) and \(\Phi\) are not equal to each other
We can describe general modifications of gravity (of the metric) at the linear perturbation level with 2 functions of scale (\(k\)) and time (\(a\))
Only two independent functions!
Another approach:
Parametrized modified gravity
- Using Planck satellite data in 2015 and 2018, constraints were obtained on these two functions \(\mu\) and \(\eta\).
- Late-time parametrization: dependent on Dark Energy fraction
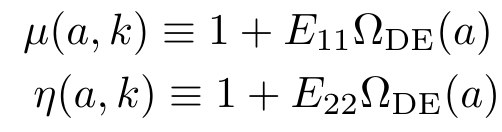
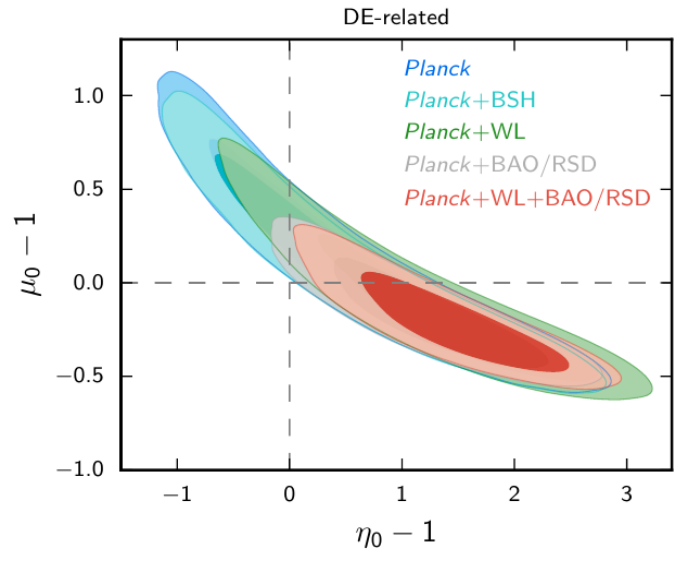
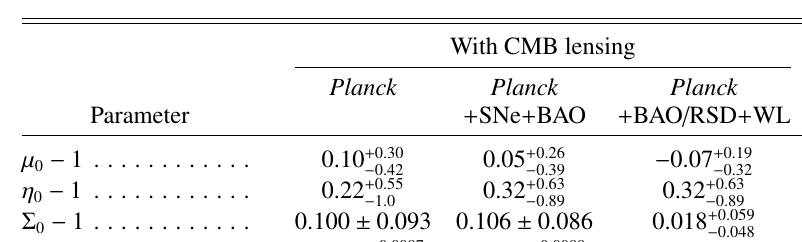
Planck 2018 results VI, arXiv:1807.06209
Planck 2015 results XIV, arXiv:1502.01590
Planck alone relatively unconstrained: 100-500% errors
Parametrized modified gravity
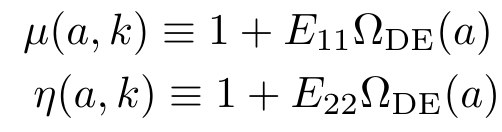
Forecasts for Stage-IV : Euclid, DESI, SKA1, SKA2, only GC and WL
SC, Kunz, Martinelli, Pettorino, Phys.Dark Univ. 18 1703.01271

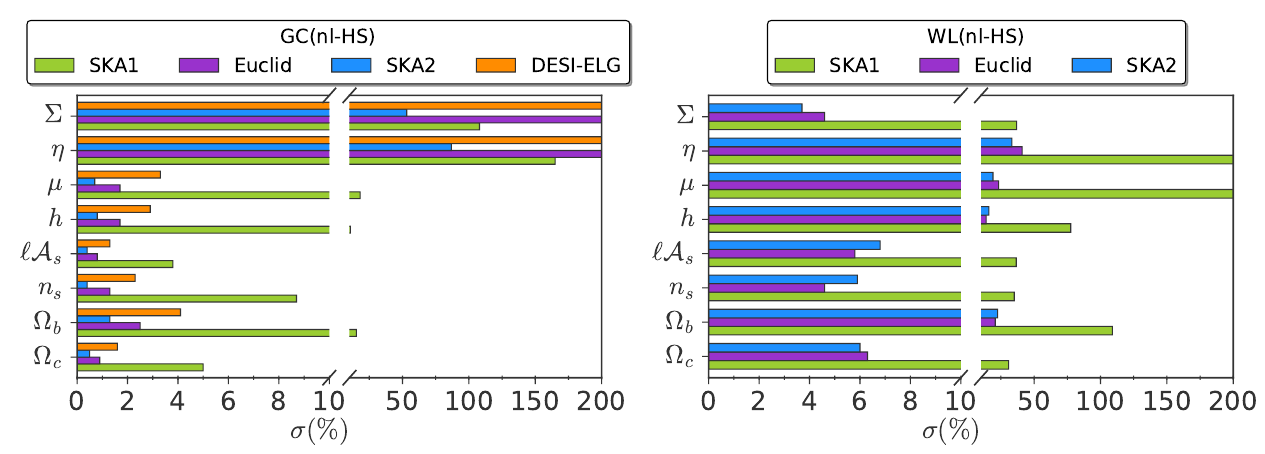
- Study more general case of free \(\mu\), \(\eta\) functions at each bin
- Non-linearities crucial for constraints
- Z-PCA decorrelation
- Constraints on \(\mu\), \(\eta\) of O(10%)
- For late-time and early-time scenario:
Constraints on \(\mu\), \(\eta\) of O(3%) - When combining GC+WL+Planck priors
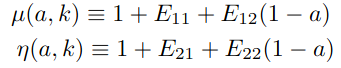
Stage IV Surveys
- Stage IV surveys get their name from the fourth generation of cosmological surveys
- Provide constraints on cosmological parameters, at least one order of magnitude better than current data
- Euclid, LSST (Vera Rubin Obs), WFIRST (Nancy Roman Telescope), SKAO, CMB S-IV, DESI
Euclid Space Satellite

ESA class M2 space mission
Currently in Cannes, waiting to be shipped to Cape Canaveral
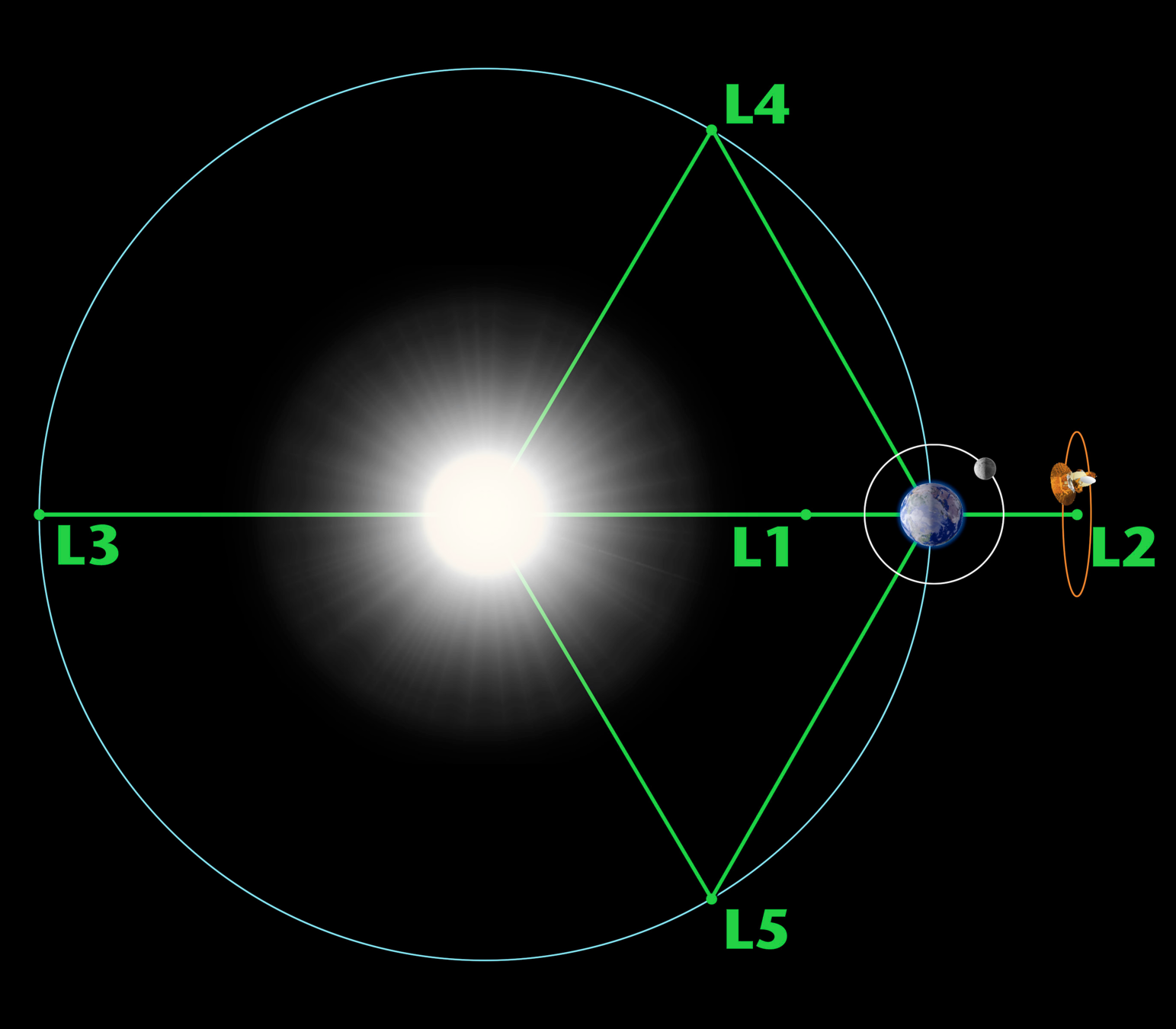
https://www.esa.int/Science_Exploration/Space_Science/Euclid
Sun-Earth Lagrange point 2, 1.5 million km from Earth
Launch vehicle: SpaceX Falcon 9

Euclid Space Satellite
- Two instruments:
- VIS (visible photometer): shape and orientation of ~1.5 billion galaxies!
- NISP (near infrared spectrograph): ~30 million galaxy spectra !
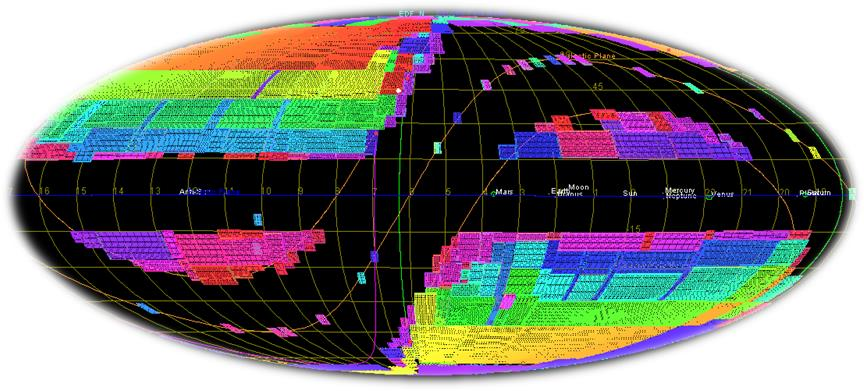


- 15 000 square degrees in the sky
- 16 countries, ~1500 members
- ~170 Petabyte of data!
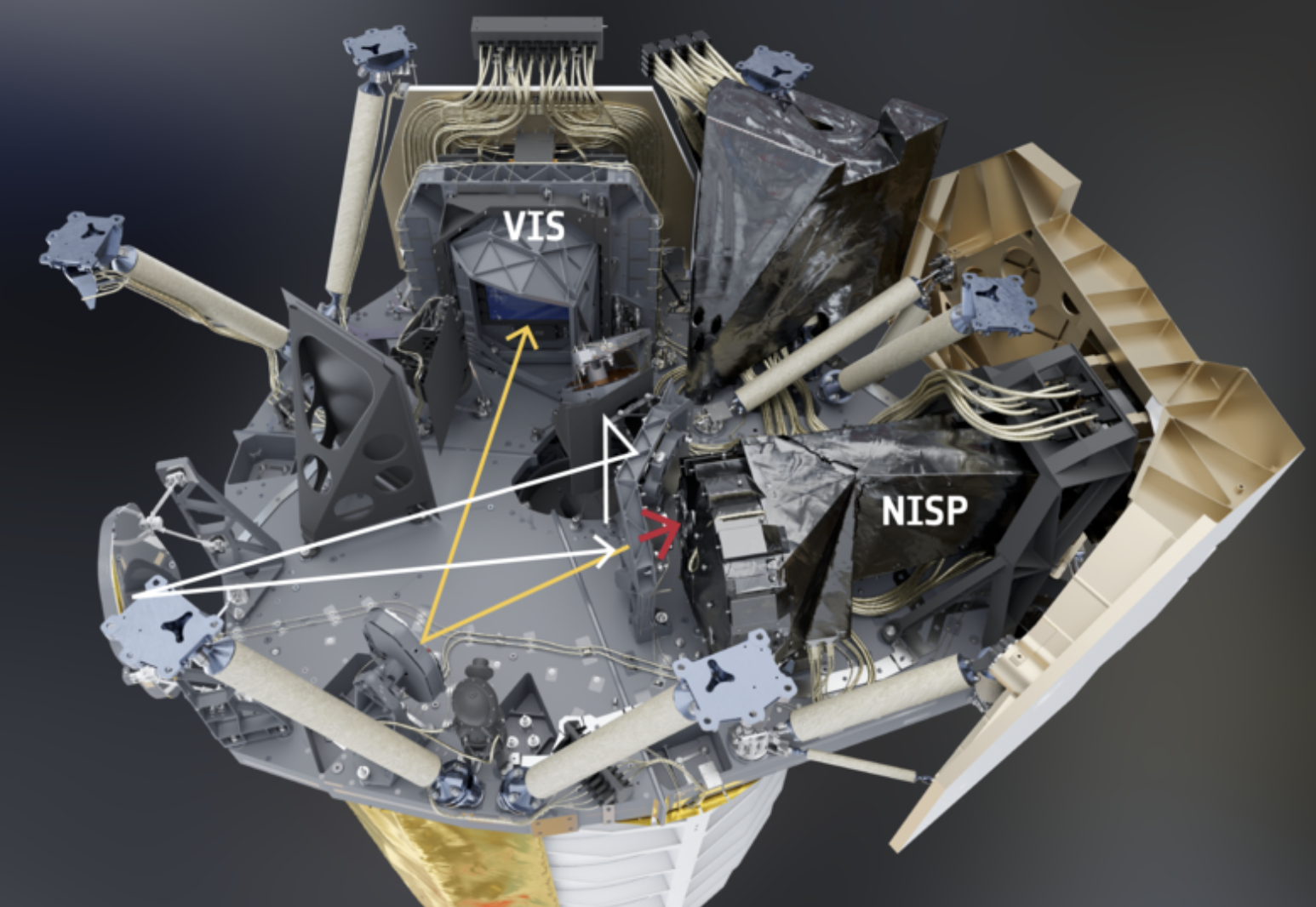

photometric primary probe

Euclid will measure the photometric 3x2pt function
Directly constrains MG function \(\Sigma\) through Weyl potential
spectroscopic probe
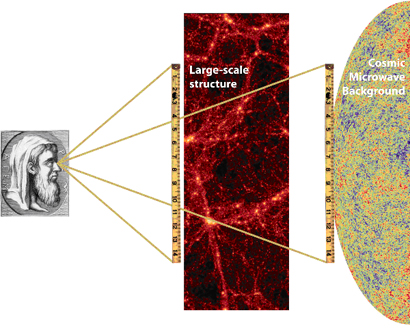

BAO
Clustering
RSD
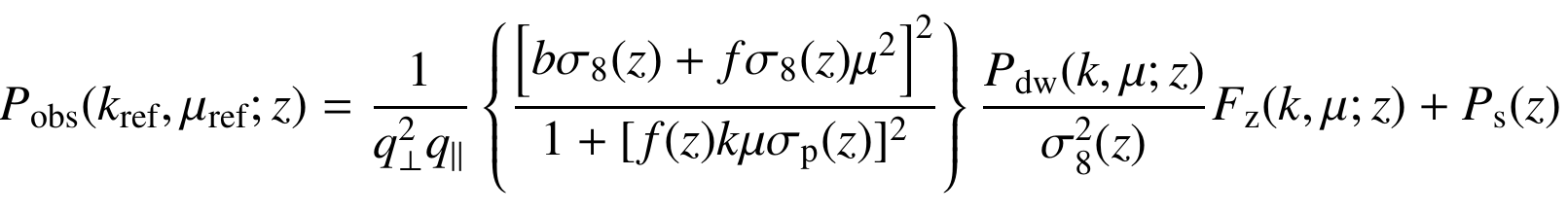
Spec-z
Euclid Collaboration, IST:Forecasts, arXiv: 1910.09273
Euclid will also measure the 2pt corr-func of spectroscopic galaxies in redshift space
The Matter Power Spectrum
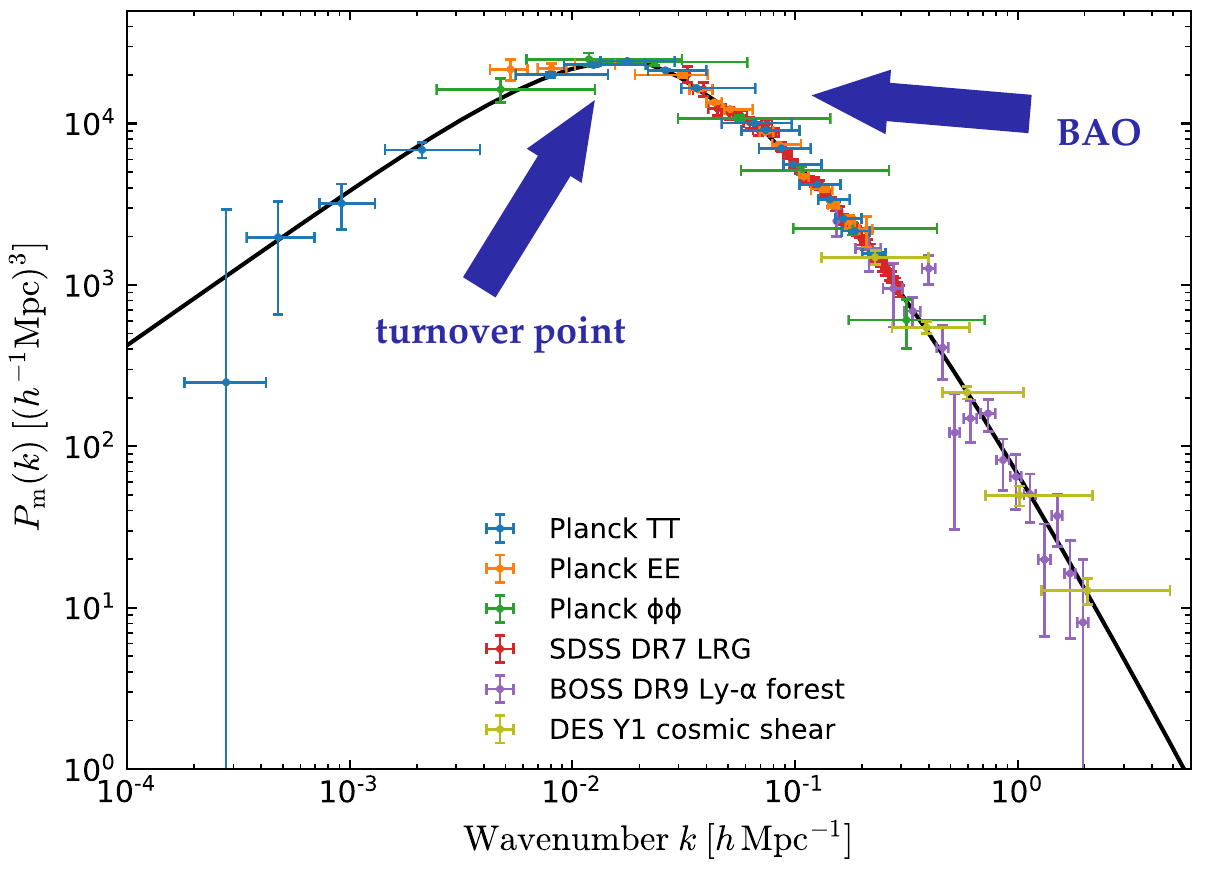
Current data:
Image: https://www.cosmos.esa.int/web/planck/picture-gallery
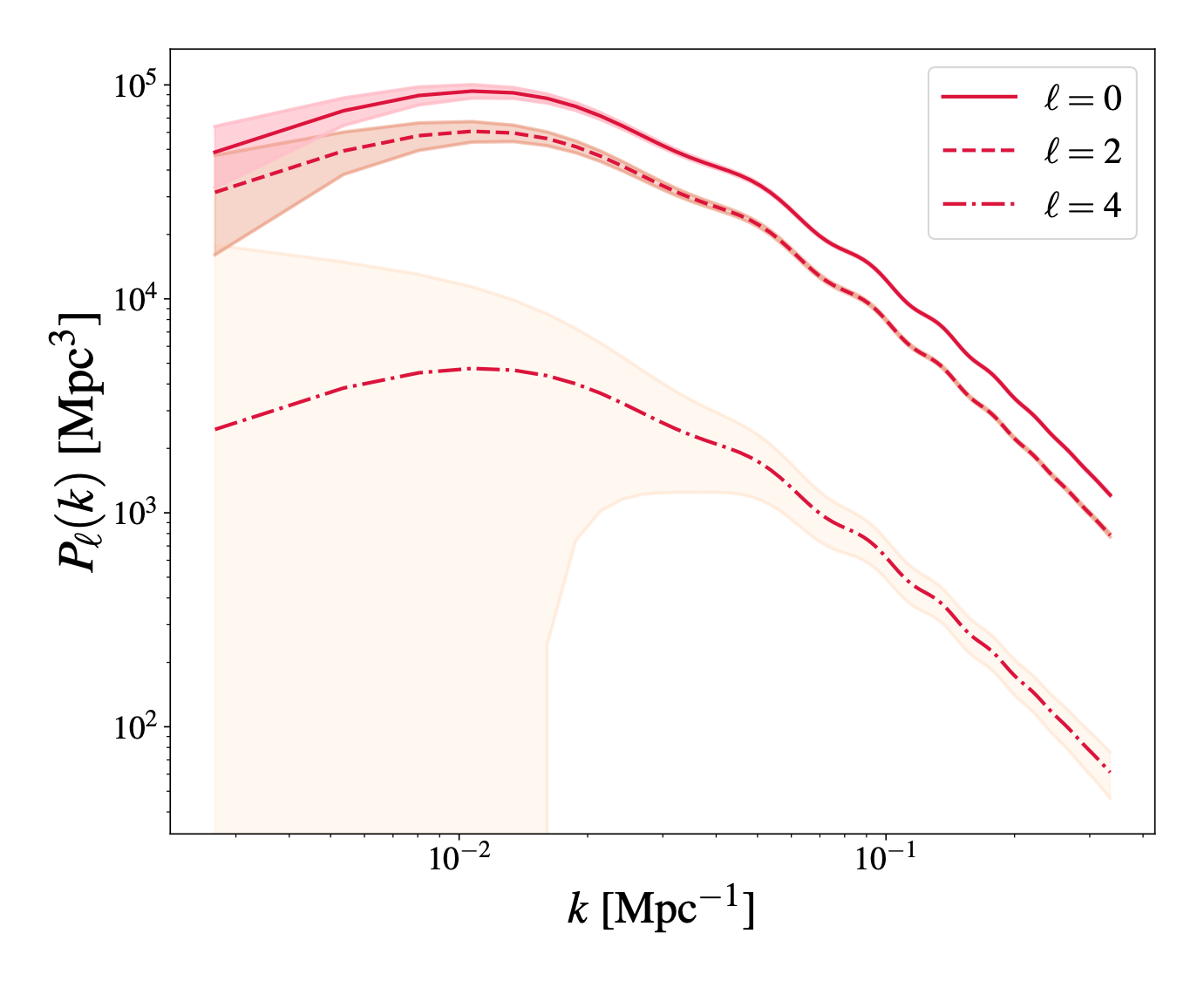
The Matter Power Spectrum
Slides provided by: Guadalupe Cañas-Herrera

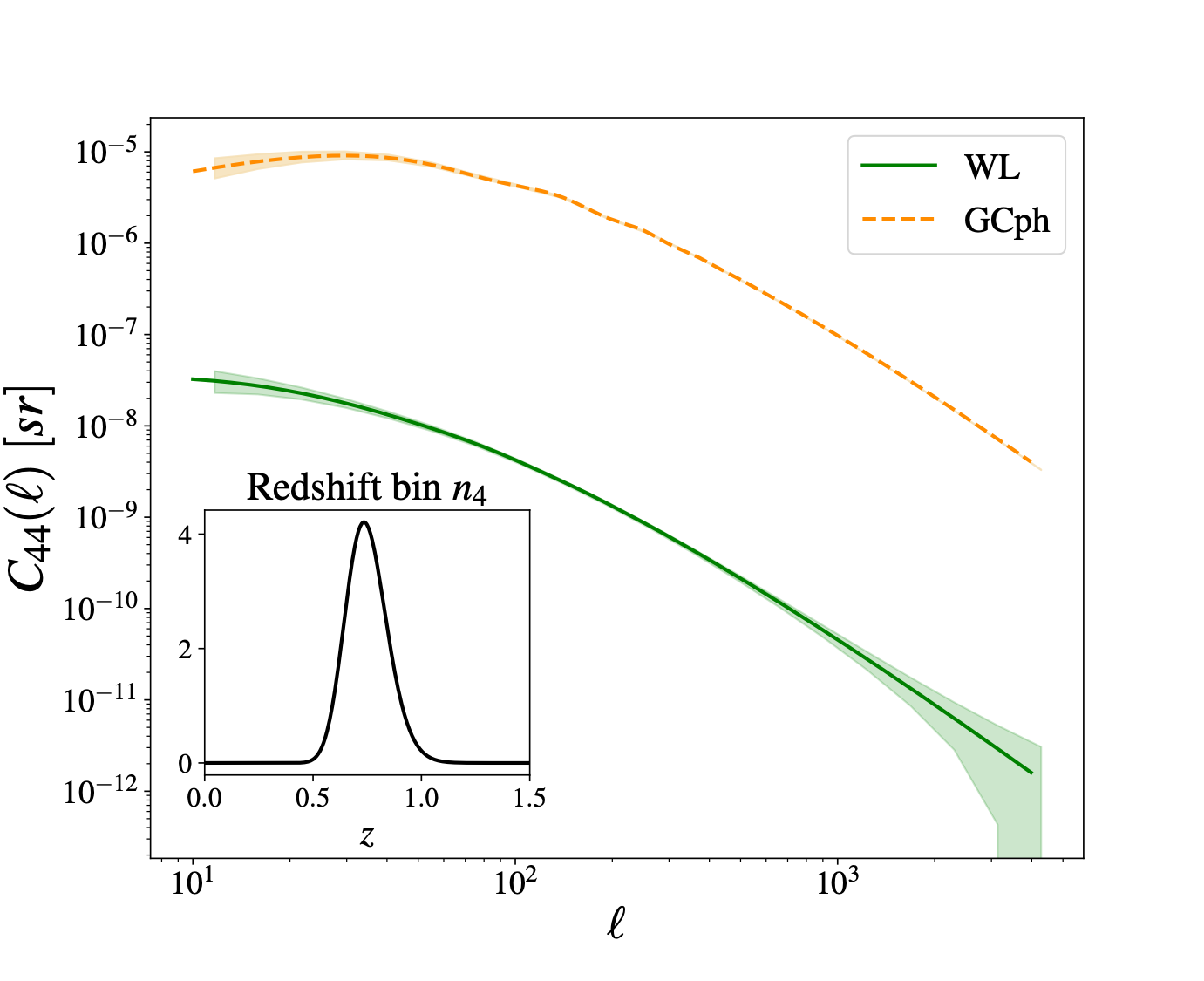
EUCLID PRELIMINARY
spectroscopic GC
photometric WL and GC
Euclid: IST:Forecasts

Awardees of the Euclid STAR Prize Team 2019
Euclid preparation: VII. Forecast validation for Euclid cosmological probes. arXiv:1910.09273


IST:F (forecasting taskforce), spent a few years refining, validating and comparing recipes, codes and forecasts
Euclid was commissioned to measure \(w_0, w_a , \gamma\)
Vera Rubin LSST
- Located in Chile, 8.4m telescope
- 20 billion galaxies
- Redshifts: 0 < z ~< 3 (photometric)
- 18,000 square degrees
- 11 years of observation
- 3x2pt, clusters, SNIa

Vera Rubin LSST
DESI telescope
- 14 000 square degrees in the sky
- 30 million accurate galaxy spectra
- Redshifts: 0 < z < 2 (spectroscopic)
- Quasars up to z~3.5
- 5 years of observation
- Starting 2021
- Power spectra, Bispectra, Corr. Func.

Vera Rubin LSST
Euclid vs. DESI+Rubin
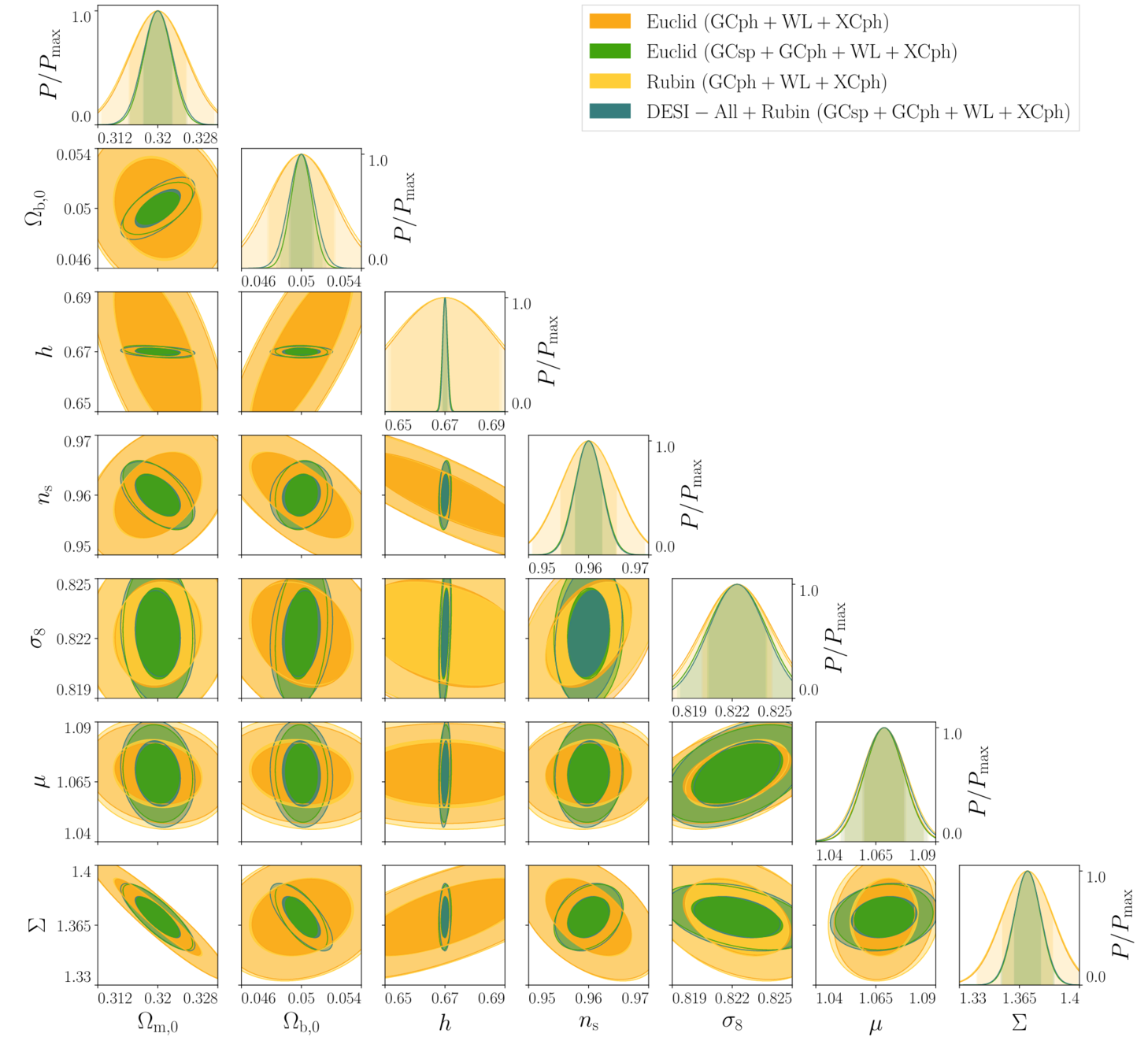
- Forecasts for Modfied Gravity parametrizations
- Euclid using spectroscopic and photometric probes, is roughly as powerful as Rubin+DESI
EUCLID PRELIMINARY
Vera Rubin LSST
21cm Intensity mapping
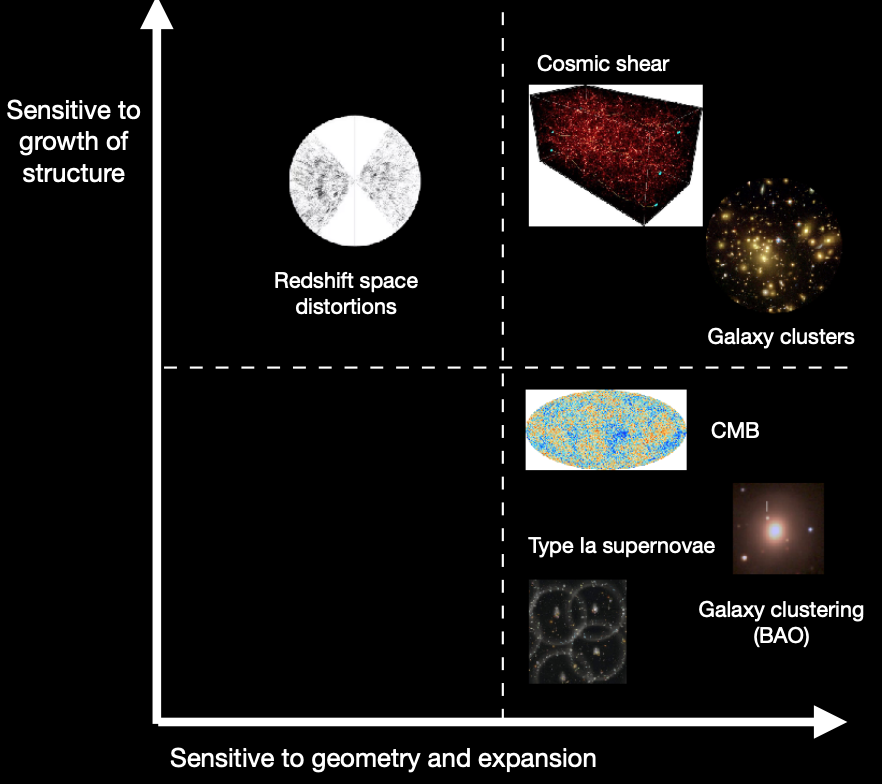
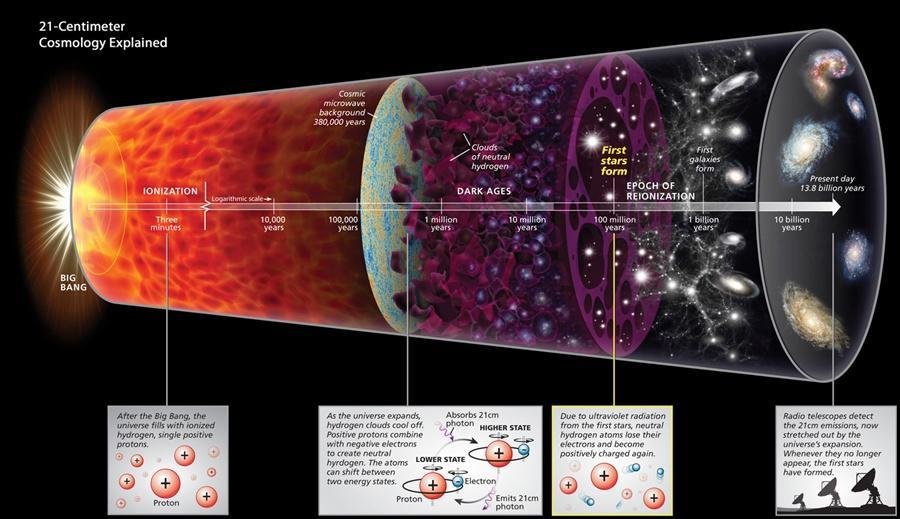
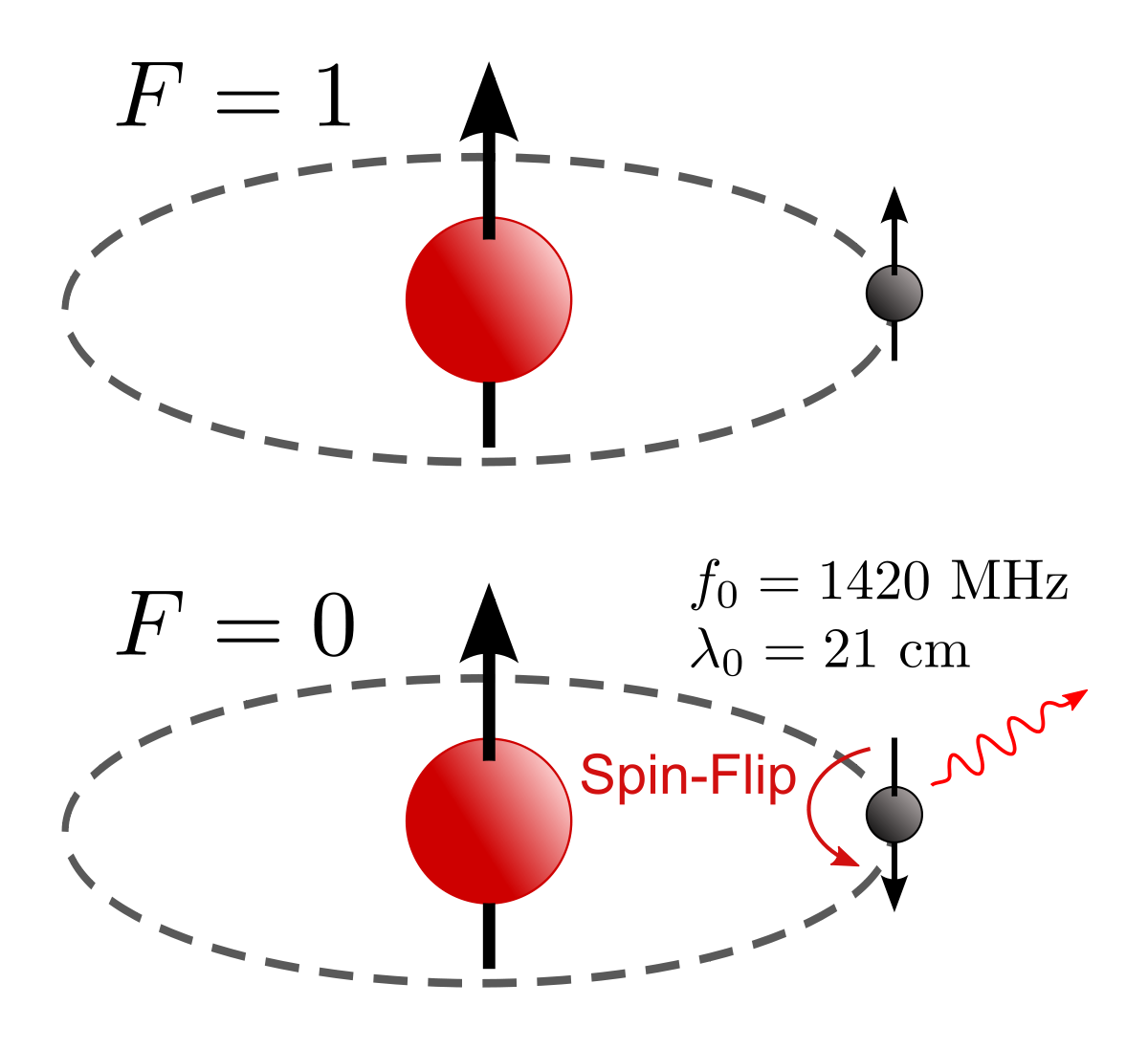

21cm Intensity mapping
Image credit: Sunayana Bhargava
- Novel probe for cosmology in the 21st century
- Access to yet unexplored redshifts
- Very different systematics, hybrid of techniques between CMB and GCsp
- Tracer of DM-Halos where neutral H resides
- Information about dark ages
- Very good redshift resolution, bad angular resolution
Vera Rubin LSST
Square kilometer array (SKAO)

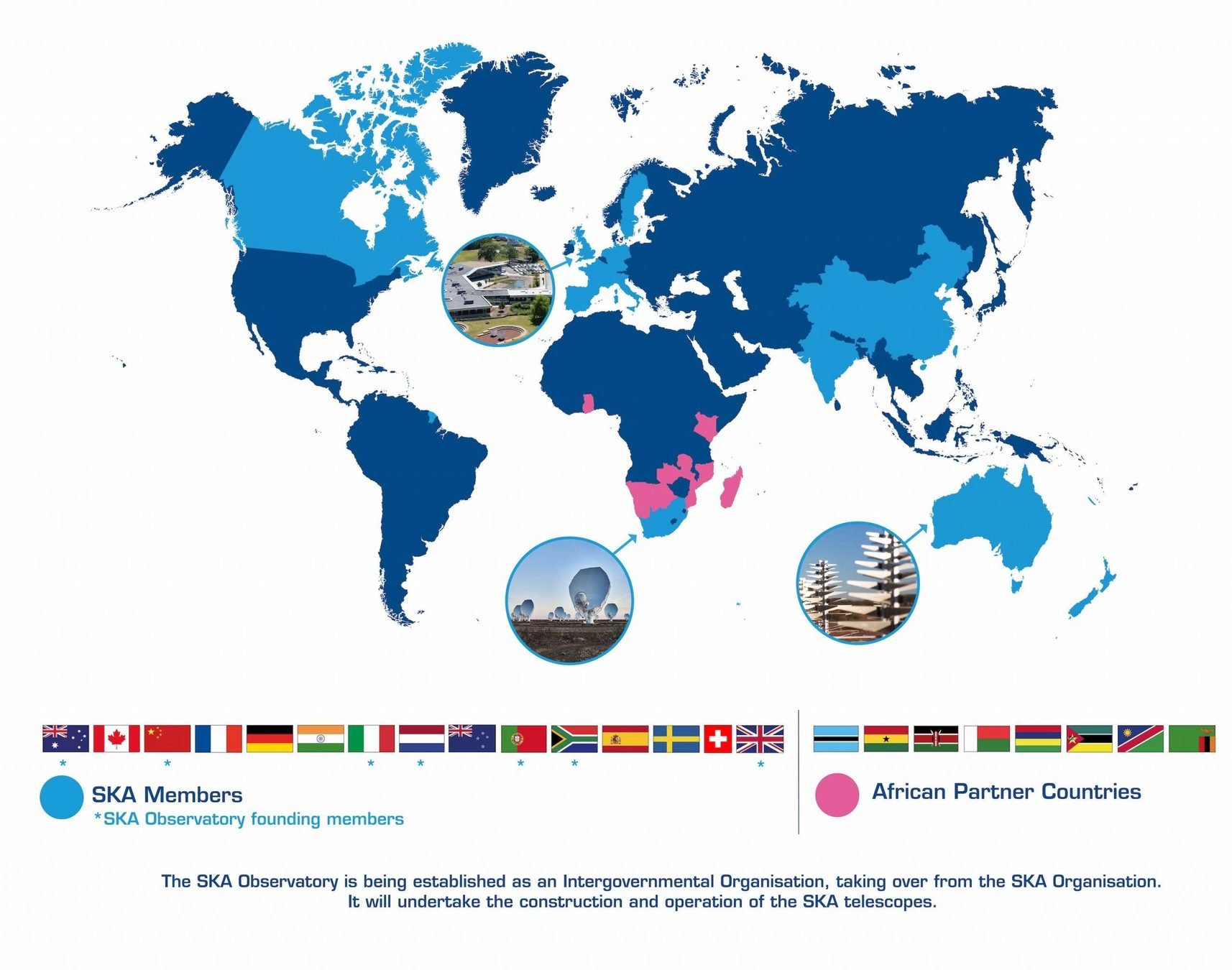
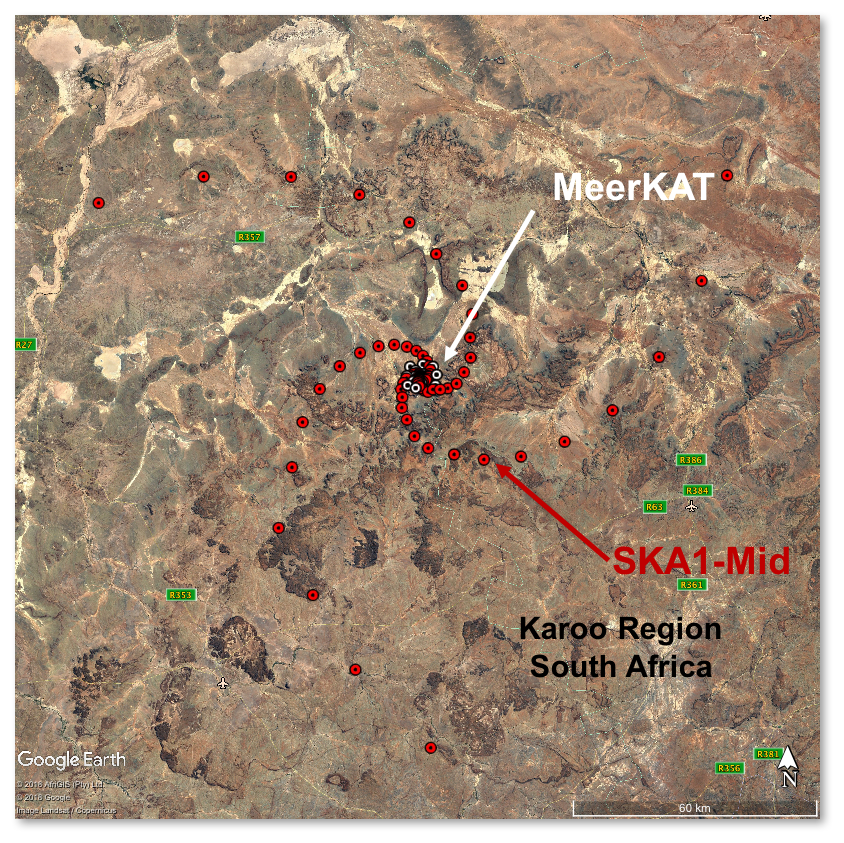
- SKA Phase 1: SKA1-Low and SKA1-Mid
- SKA1-Low: 130,000 dipole antennas, 65km max. baseline (Australia)
- SKA1-Mid: ~200 dishes of ~15m diameter, max. baseline 150km (South Africa)
- Precursors: ASKAP, MEERKAT, HERA...
- €1.3 Billion, 16 countries, 710 Petabytes, 8 years construction



https://www.skao.int/
Vera Rubin LSST
Square kilometer array (SKAO)


- Modelling is very analogous to GCsp, with brightness temperature on top and different biases
- GCsp-IM Cross-correlation in overlapping bins
- DESI : Two galaxy samples
- SKAO: HI Galaxies and 21cm-IM
\(P^{\rm IM}(z,k) = \bar{T}_{IM}(z)^2 \rm{AP}(z) K_{\rm rsd}^2(z, \mu; b_{\rm HI}) \)
\(FoG(z,k,\mu_\theta) \\ \times P_{\delta\delta,dw}(z,k) \)
\( K_{\rm rsd}(z, \mu; b_{\rm HI}) = [b_{\rm HI}(z)^2+f(z)\mu^2] \)
\( b_{\rm HI}(z) = 0.3(1+z) + 0.6 \)
\( \bar{T}_{\mathrm{IM}}(z)= 189h \frac{(1+z)^2 H_0}{H(z)}\Omega_{HI}(z) \,\,{\rm mK} \)
\(\Omega_{HI} = 4(1+z)^{0.6} \times 10^{-4} \)
Carucci et al (2020) 2006.05996
Jolicoeur et al (2020) 2009.06197
\(P^{{\rm IM} \times \rm{g}}(z,k) = \bar{T}_{\rm IM}(z) {\rm AP} (z) r_{\rm IM,opt} K_{\rm rsd}(z, \mu; b_{\rm HI}) \)
\( \times K_{\rm rsd}(z, \mu; b_{\rm g}) FoG(z,k,\mu_\theta) P_{\delta\delta,dw}(z,k) \)
\( \times \exp[-\frac{1}{2} k^2 \mu^2 (\sigma_{\rm IM}(z)^2+\sigma_{\rm sp}(z)^2)] \)
SC, Carucci, Pettorino et al (2022) 2210.05705
Brightness temperature of 21cm emission line
Fraction of neutral hydrogen in the Universe
Vera Rubin LSST
Square kilometer array (SKAO)

SC, Carucci, Pettorino et al (2022) 2210.05705
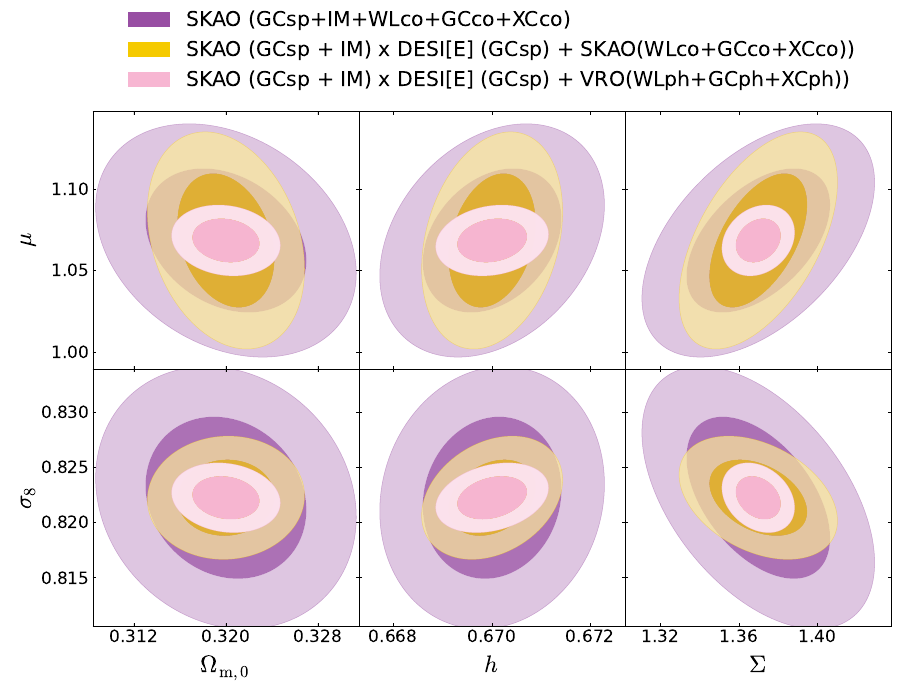

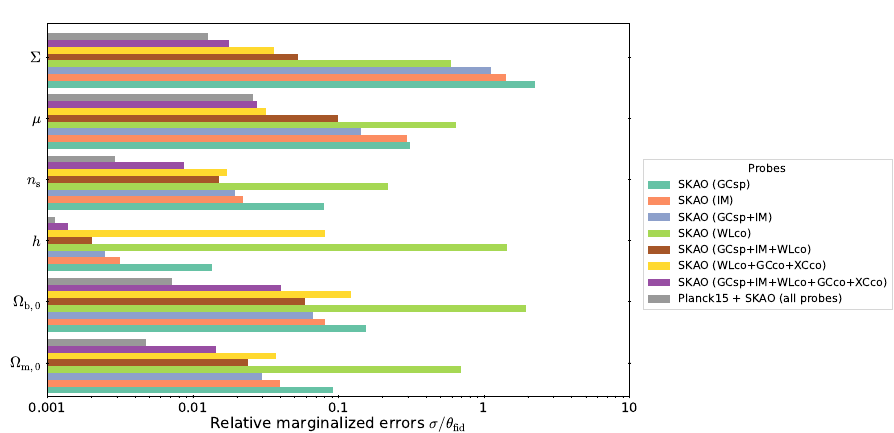
- WL is better at measuring \(\Sigma\)
- GC is better at measuring \(\mu\)
- SKAO-all-probes constrains at 3% already
- DESI(GCsp)xSKAO(IM) helps in \(h, \sigma_8\) but not in MG parameters
- Combination of SKAO + one Stage-IV probe is as good as two Stage-IV
- Different noise and systematics -> break degeneracies
Fisher Matrix Forecasts
Euclid preparation: VII. Forecast validation for Euclid cosmological probes. arXiv:1910.09273
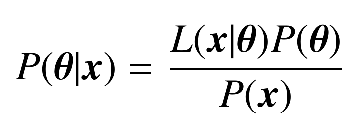
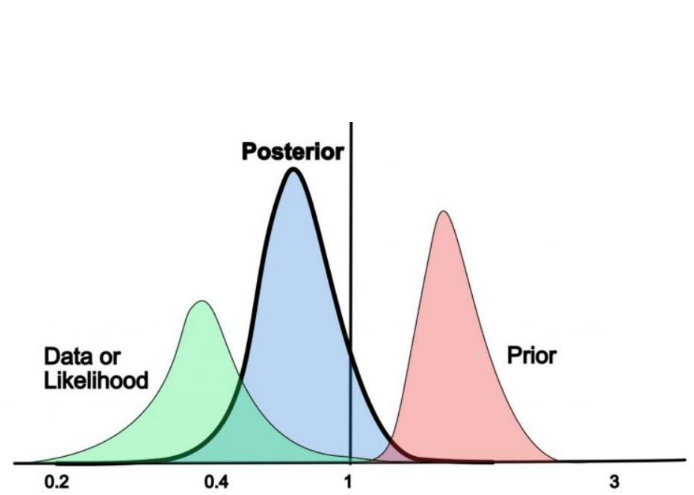
Bayes Theorem:
Probability of the model parameters given the data

Fisher Information Matrix:
Curvature (Hessian) of the Likelihood
Gaussian Likelihood in data space:
How do we actually perform those forecasts?
J. Schaffmeister
Fisher Matrix Forecasts
Euclid preparation: VII. Forecast validation for Euclid cosmological probes. arXiv:1910.09273
Fisher Matrix for a Gaussian likelihood of angular power spectra:
Parameter covariance:
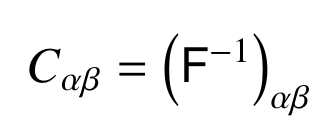
Defines an ellipse:
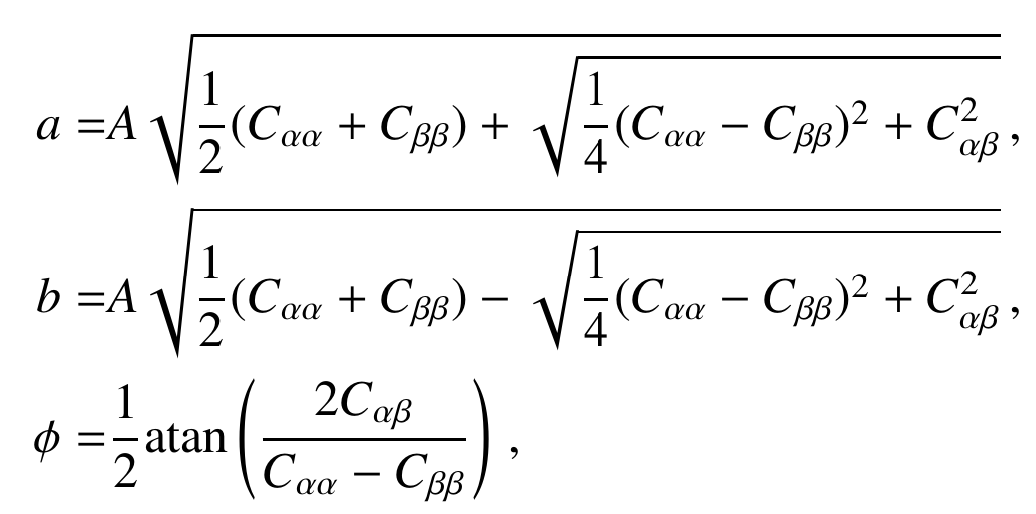
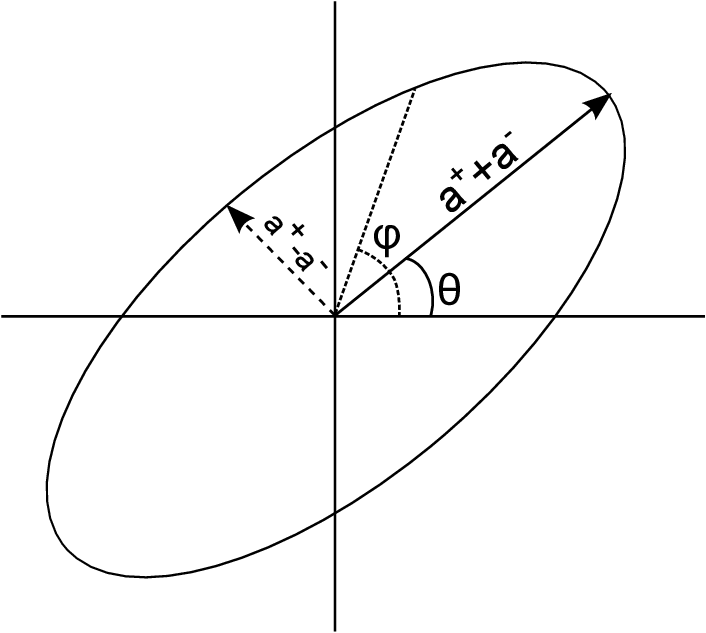

CosmicFish Code

Code: CosmicFish
S.Casas, M.Martinelli and M.Raveri
Soon to be released: New full pythonic version
https://github.com/CosmicFish/CosmicFish
Neutrino forecasts for Euclid
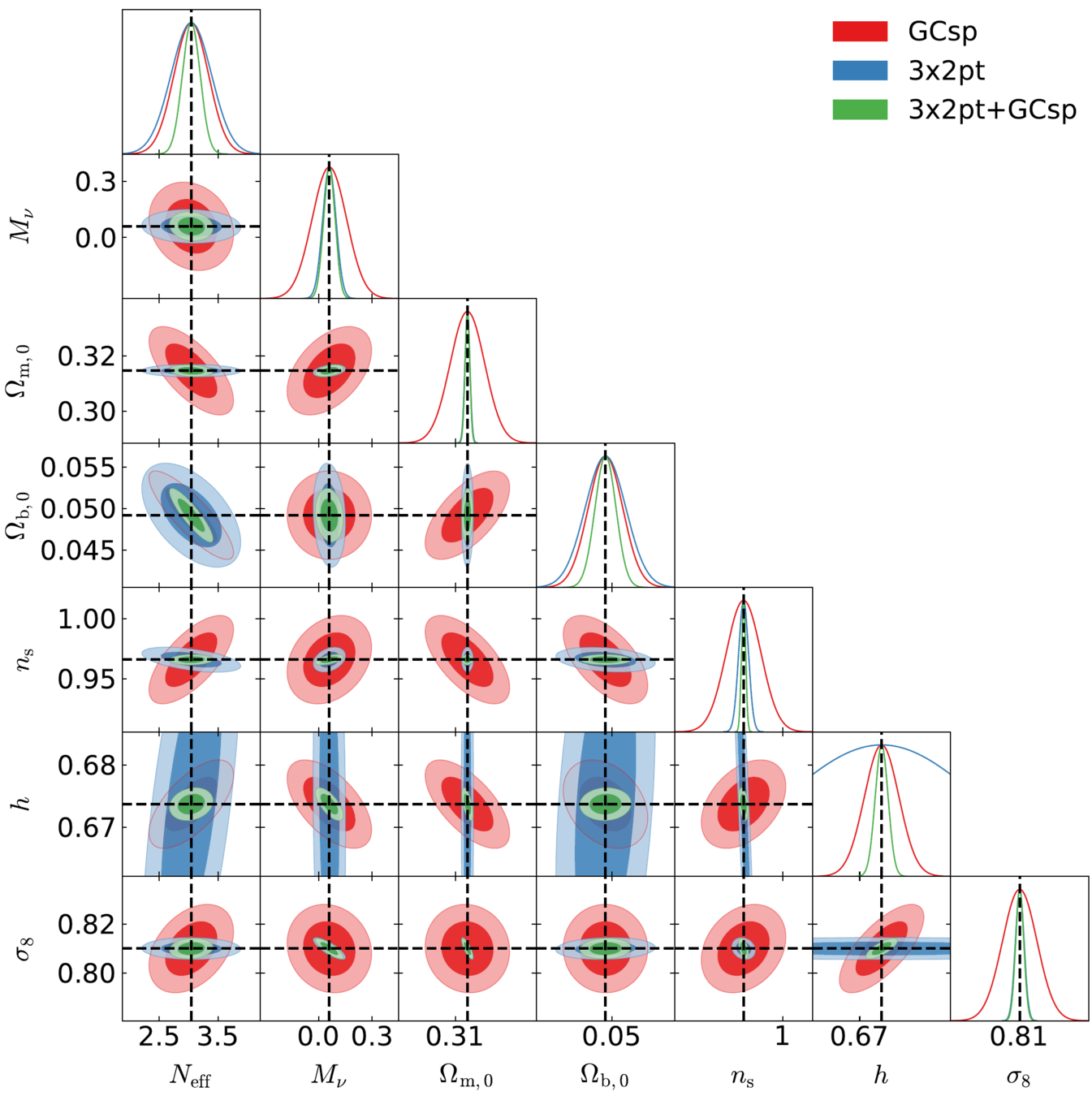
Plots by: Sabarish Sabarish Venkataramani
Euclid Full:
GC spectro + 3x2pt photo
Code: CosmicFish
S.Casas and M.Martinelli
Neutrino constraints from Planck
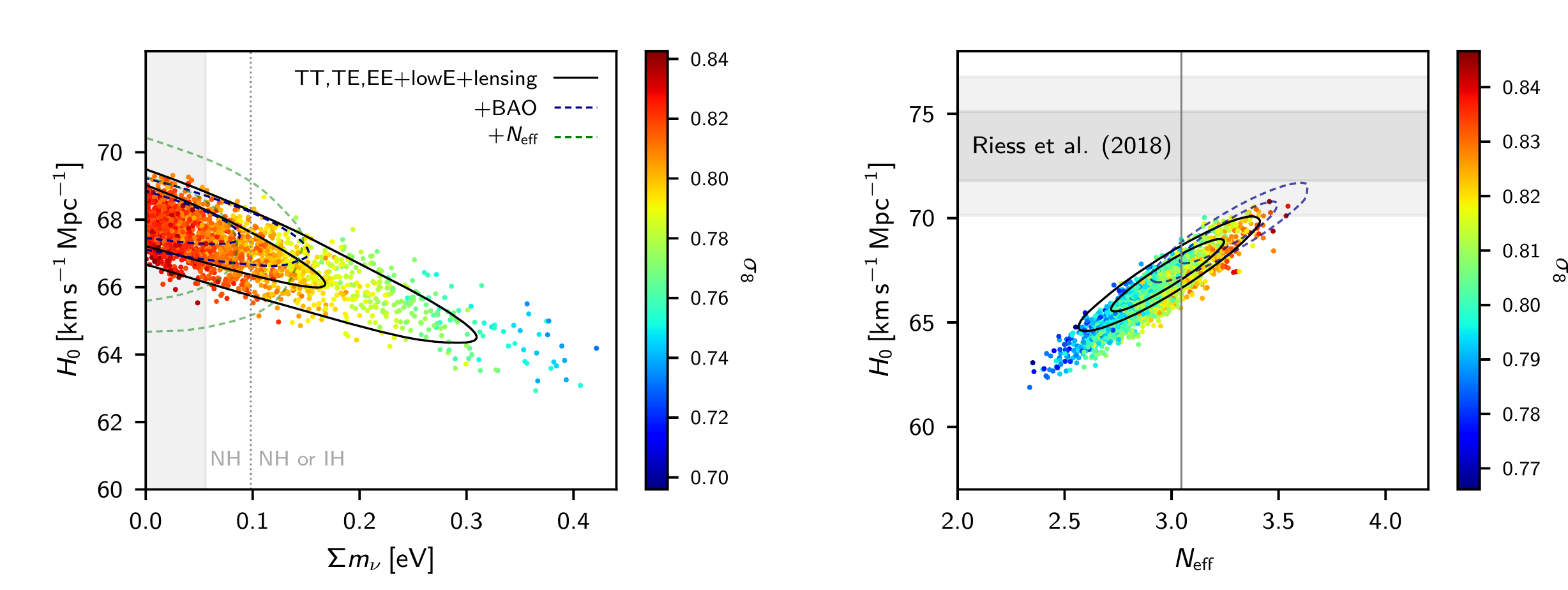
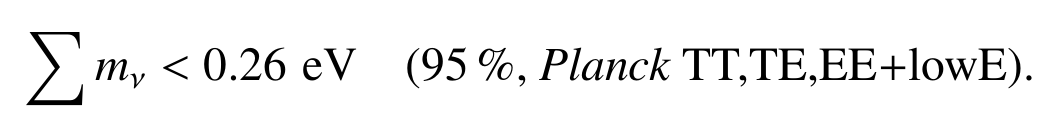

Planck 2018 results VI, arXiv:1807.06209
MASSIVE Neutrinos in Cosmology
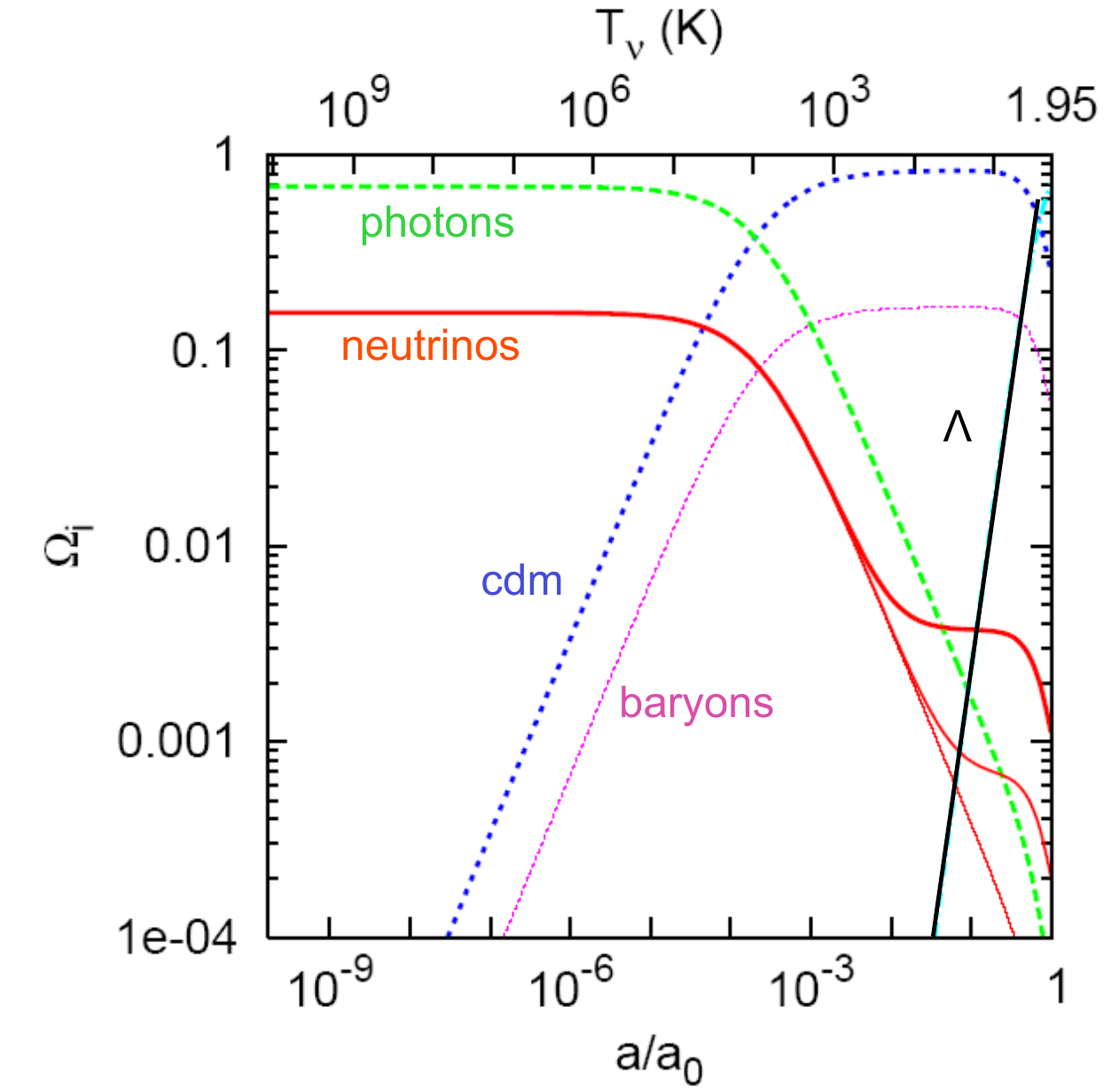
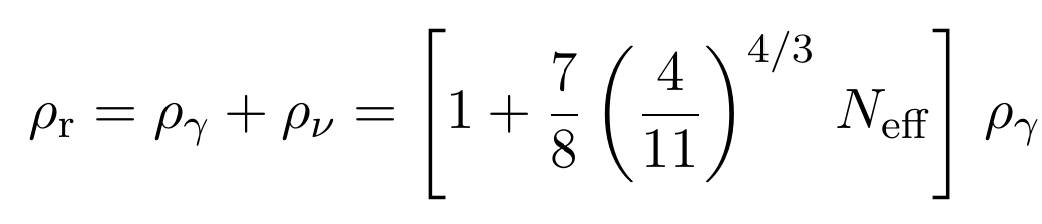
Froustey et al, arXiv:2008.01074, arXiv: 2110.11296
- If neutrinos are massless: relativistic, dilute as \(a^{-4}\)
- If massive: non-relativistic, one has to follow the Friedmann function evolution
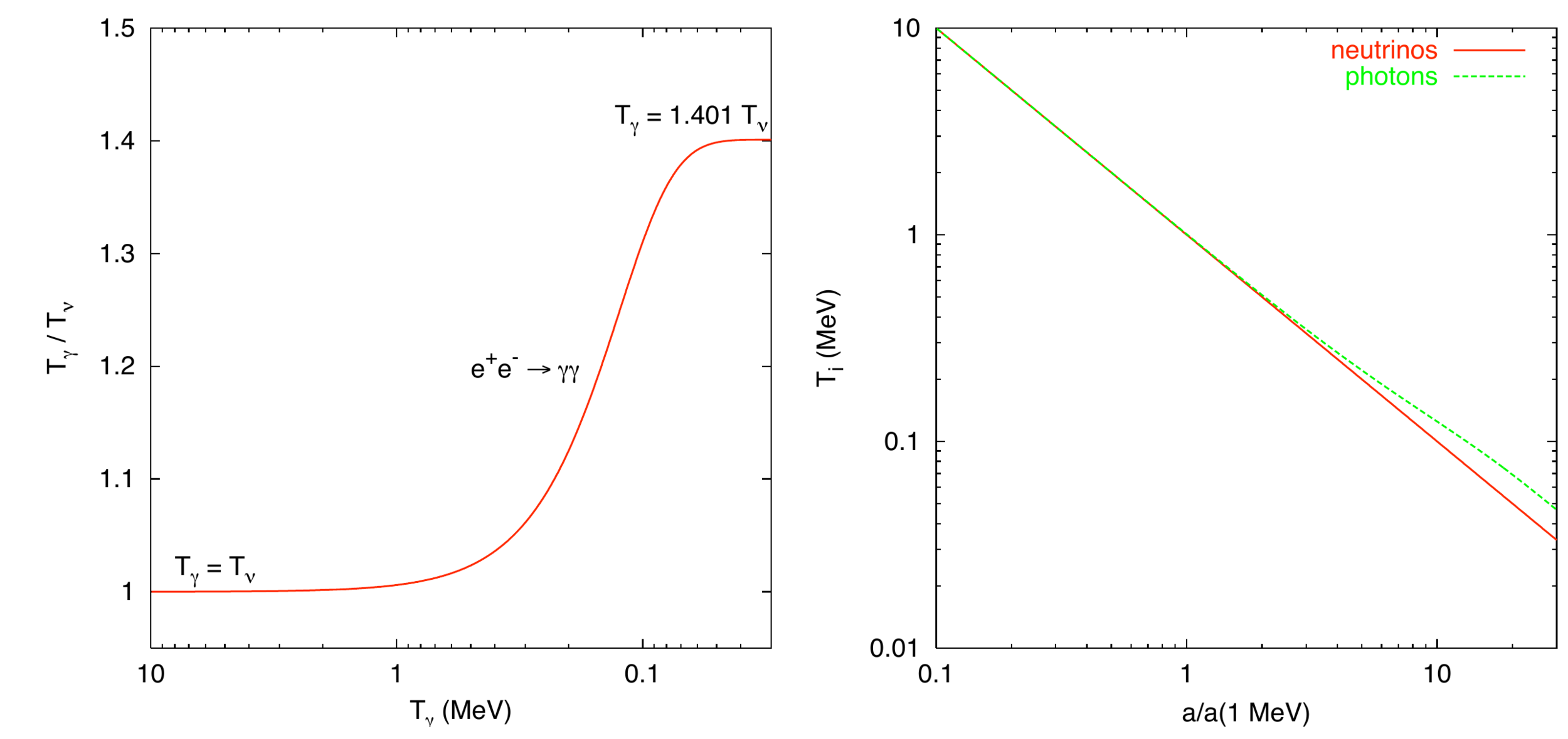
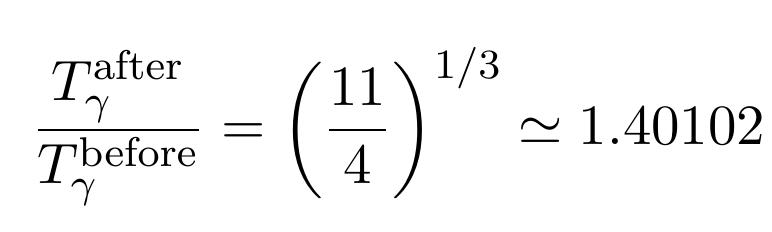
- Neutrinos and Photons initially at thermal equilibrium
- Neutrinos decouple at \(\approx\) 1MeV
- Energy injection into photons from \(e^+ e^- \) annihilation
massive Neutrinos: Free streaming


- Neutrinos free stream below a scale of \(k_{FS}\)
- They do not cluster below that scale
- Suppression of the total power spectrum
- The non-relativistic transition imposes a minimum in \(k_{FS}\)
- Cosmology-dependent
Suppression of the power spectrum, at first order depends on energy density ratios
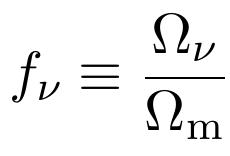
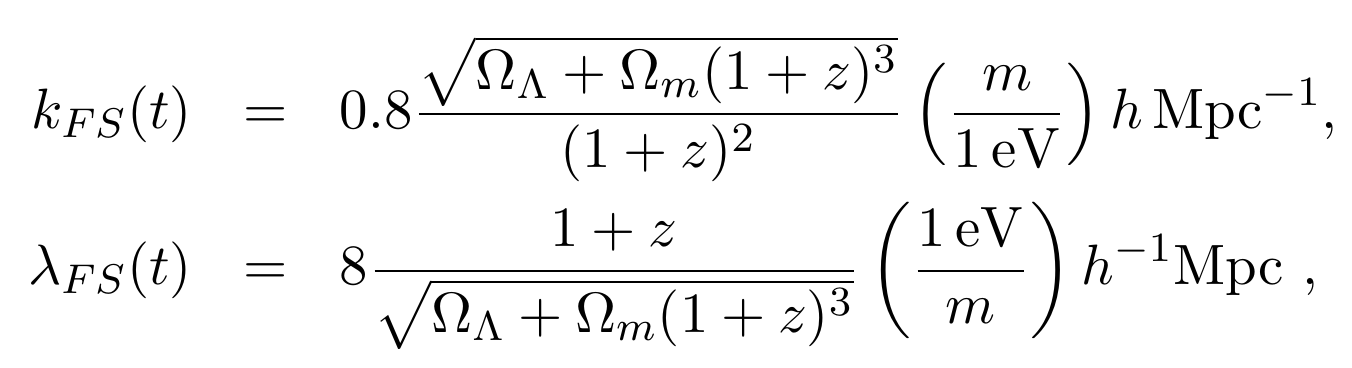
Likelihood Sampling
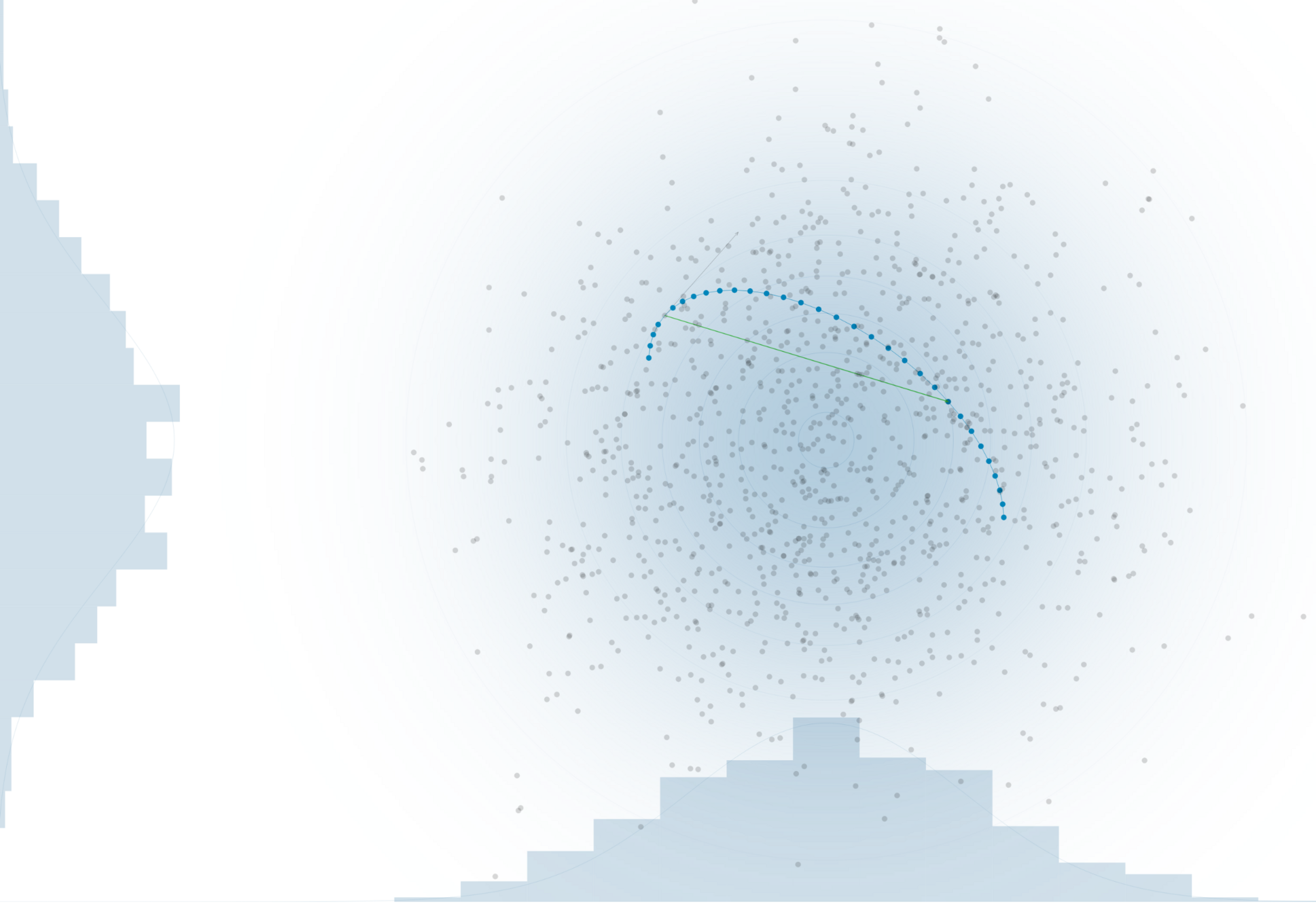
Markov Chain Monte Carlo explorations -> inefficient, but standard way of exploring complicated likelihoods with non-Gaussian posteriors
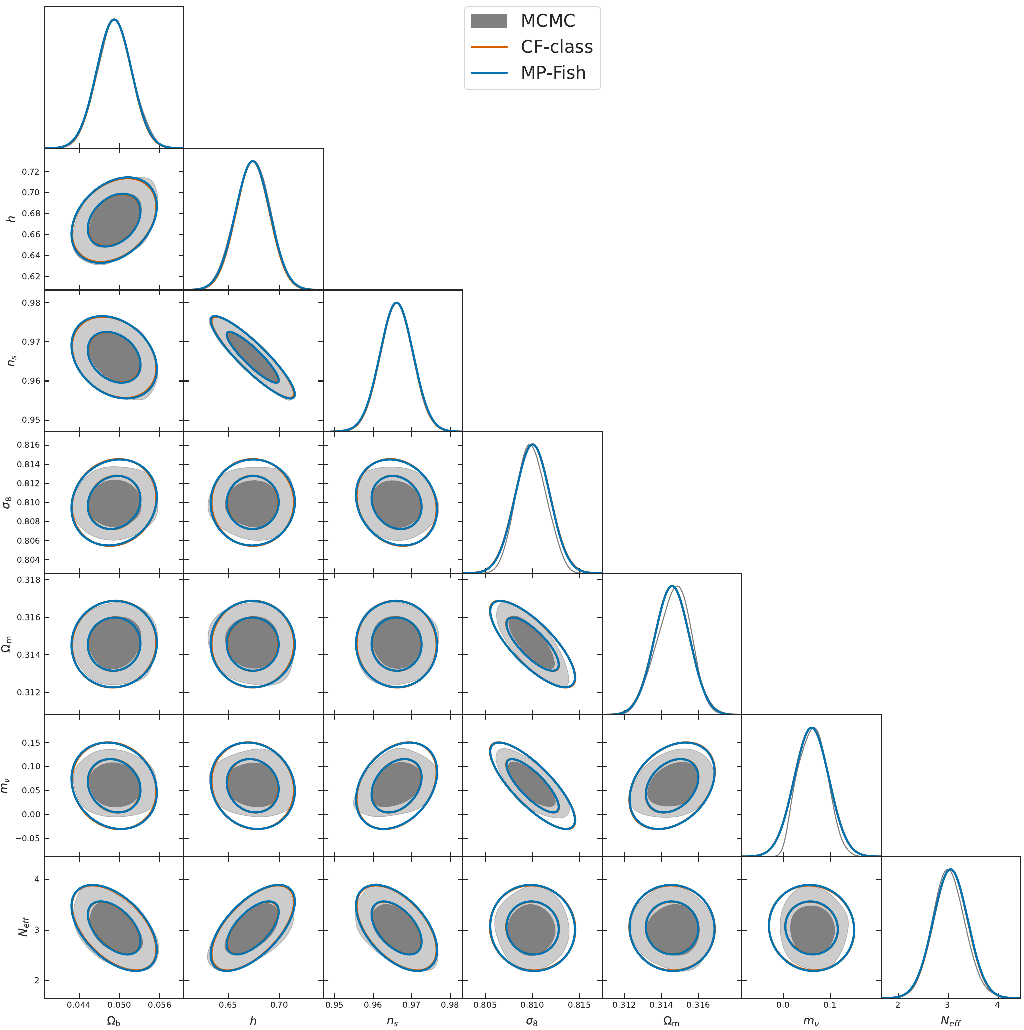
MontePython MCMC vs. CosmicFish, for the 3x2pt photo probe of Euclid with neutrino mass and N_eff. Plot by: Sefa Pamuk
- Recent Euclid SP paper (SC, Lesgourgues, Schöneberg, et al) validating MontePython Fishers against IST:F results (in internal review)
- Validation of Einstein-Boltzmann codes CLASS and CAMB using CosmicFish
- Good agreement between Fisher matrices and MCMC contours for Euclid specs.
- Tools used now in several Euclid KP and SP papers.
Galaxy Clustering beyond Linear

Slide by: Dennis Linde
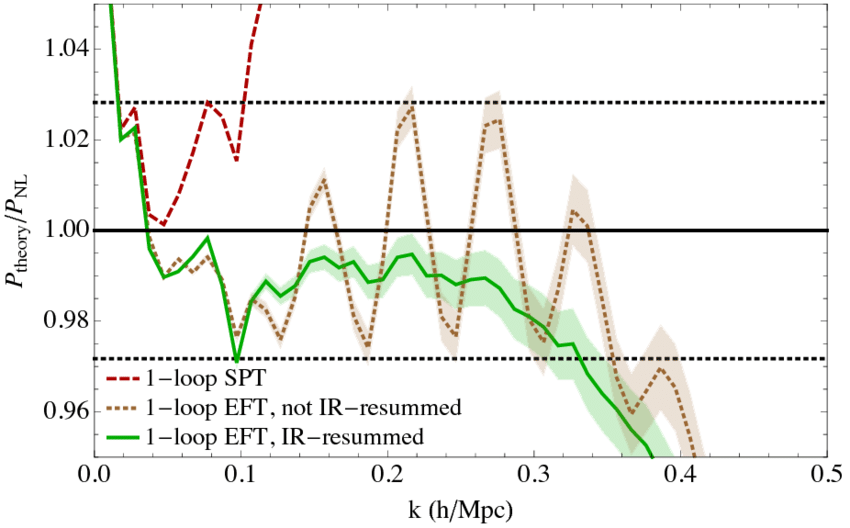
- Start from Vlasov-Poisson system
- Take non-linear terms into Fourier space
- Compute mode-coupling kernels
- Integrate out small scale physics
Text
- Pros: More accuracy, BAO damping, correct bias and RSD expansion
- Cons: Many more free parameters
- Implementing currently into CLASS à la FFTLog (Simonovic et al, arxiv:1708.08130)
Angulo et al, 1406.4143
Euclid likelihood development IST:L

CLOE team, Oslo 2022

Cosmological Likelihood for Observables in Euclid
- In charge of implementing the likelihood for spectroscopic and photometric observables
- Samplers, emulators, Boltzmann codes
- Theory prediction code
- Data, covariance reader and handler
- Group of ~15 people
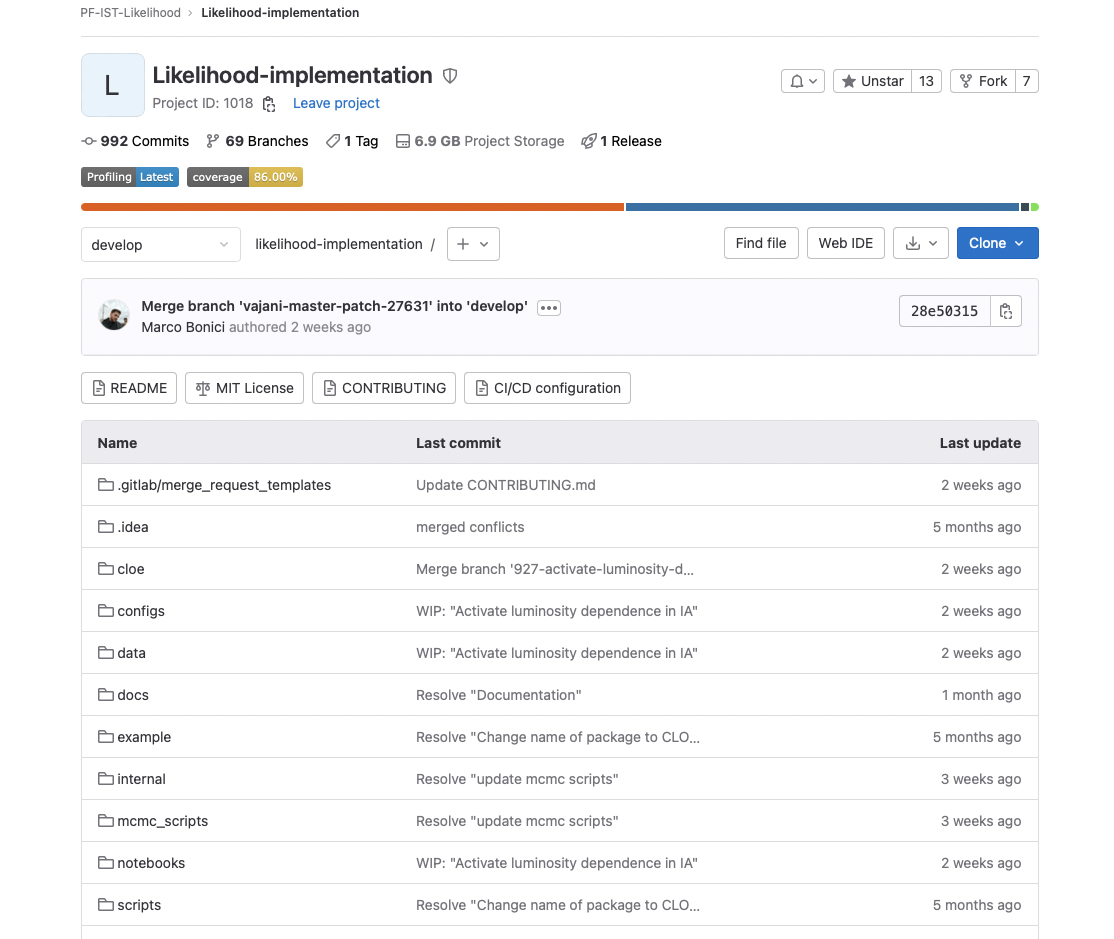
Agile: Recently -> 1000 tasks!
Euclid likelihood NONLINEAR IST:NL
- Group of ~10 people
In charge of implementing the non-linear prescriptions for IST:Likelihood - GCspectro: EFT 1-loop RSD in multipoles
- 3x2pt photo:
- Covariance, nonlinear Super-Sample
- Bias expansion
- Emulators for nonlinear, HMCode, Halofit, Bacco, EuclidEmu
- Baryonic Feedback
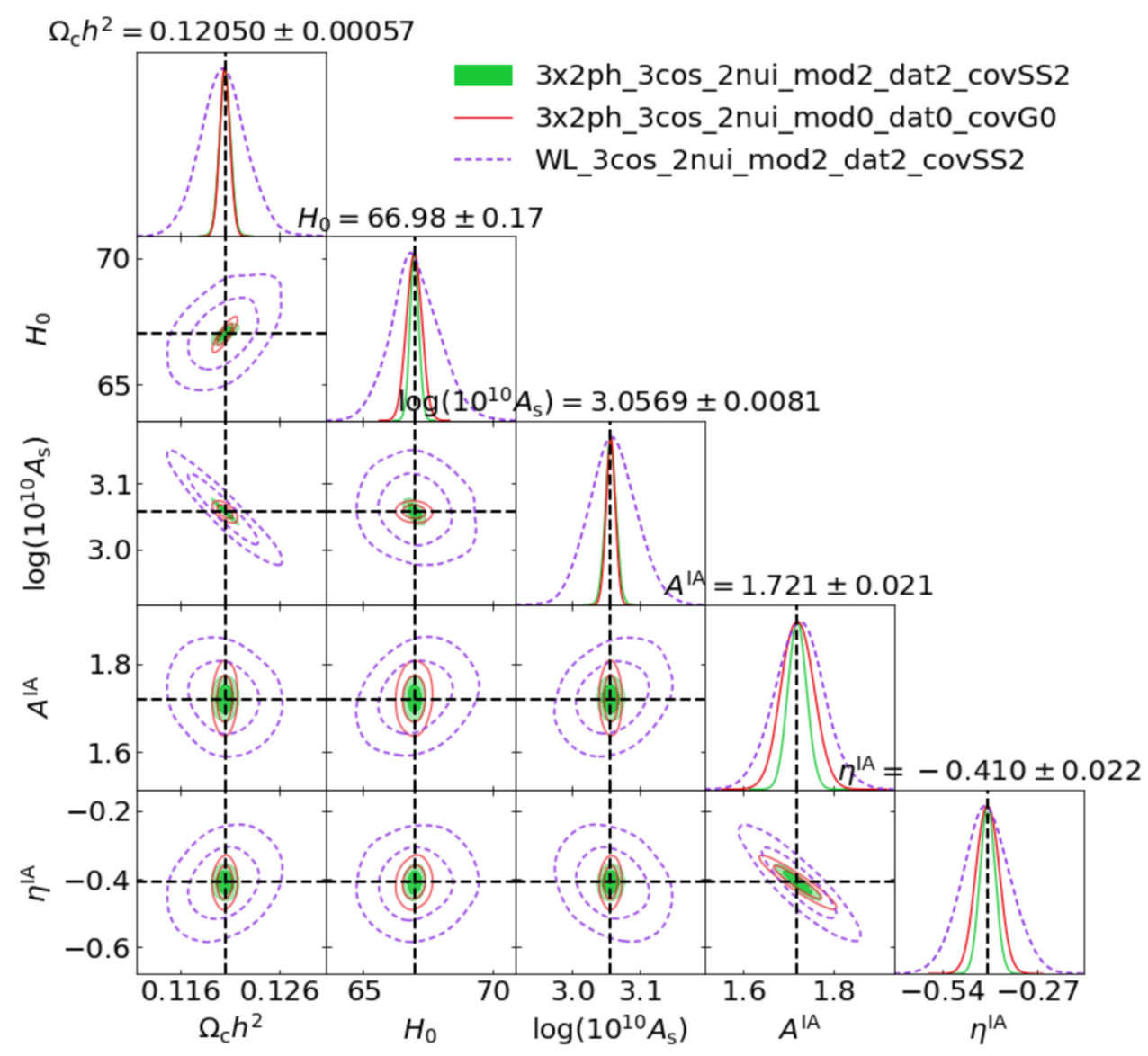
WL NonLin, 3x2pt Lin, 3x2pt NonLin
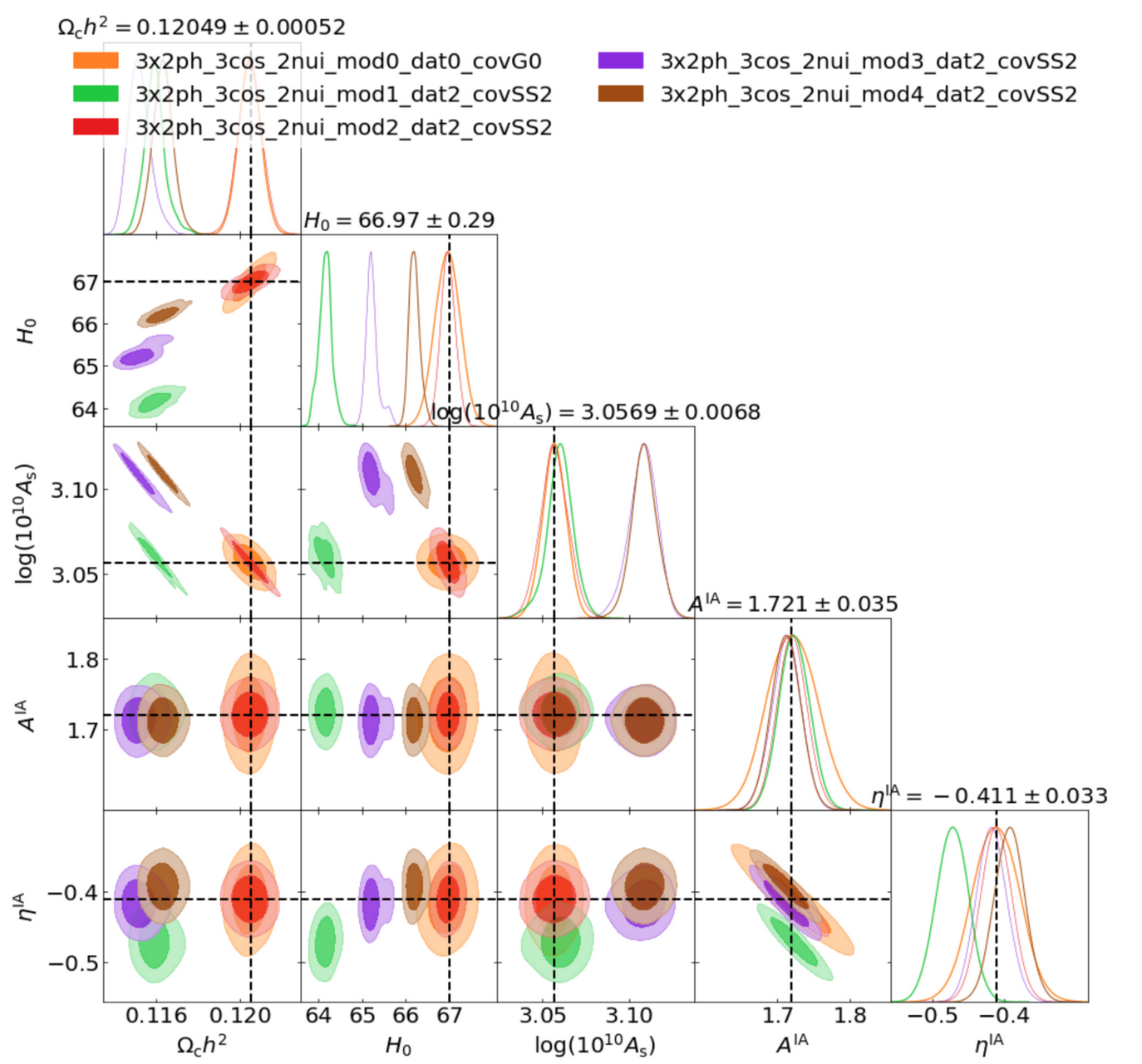
- Different emulators with systematic offsets
- Euclid optimistic error bars can distinguish them
- Biases in parameter estimation to be resolved
- S.Casas, P. Carrilho, C. Moretti to lead KP papers
EUCLID PRELIMINARY
other models tested with STAGE-IV
Euclid: SC et al (2022) in review
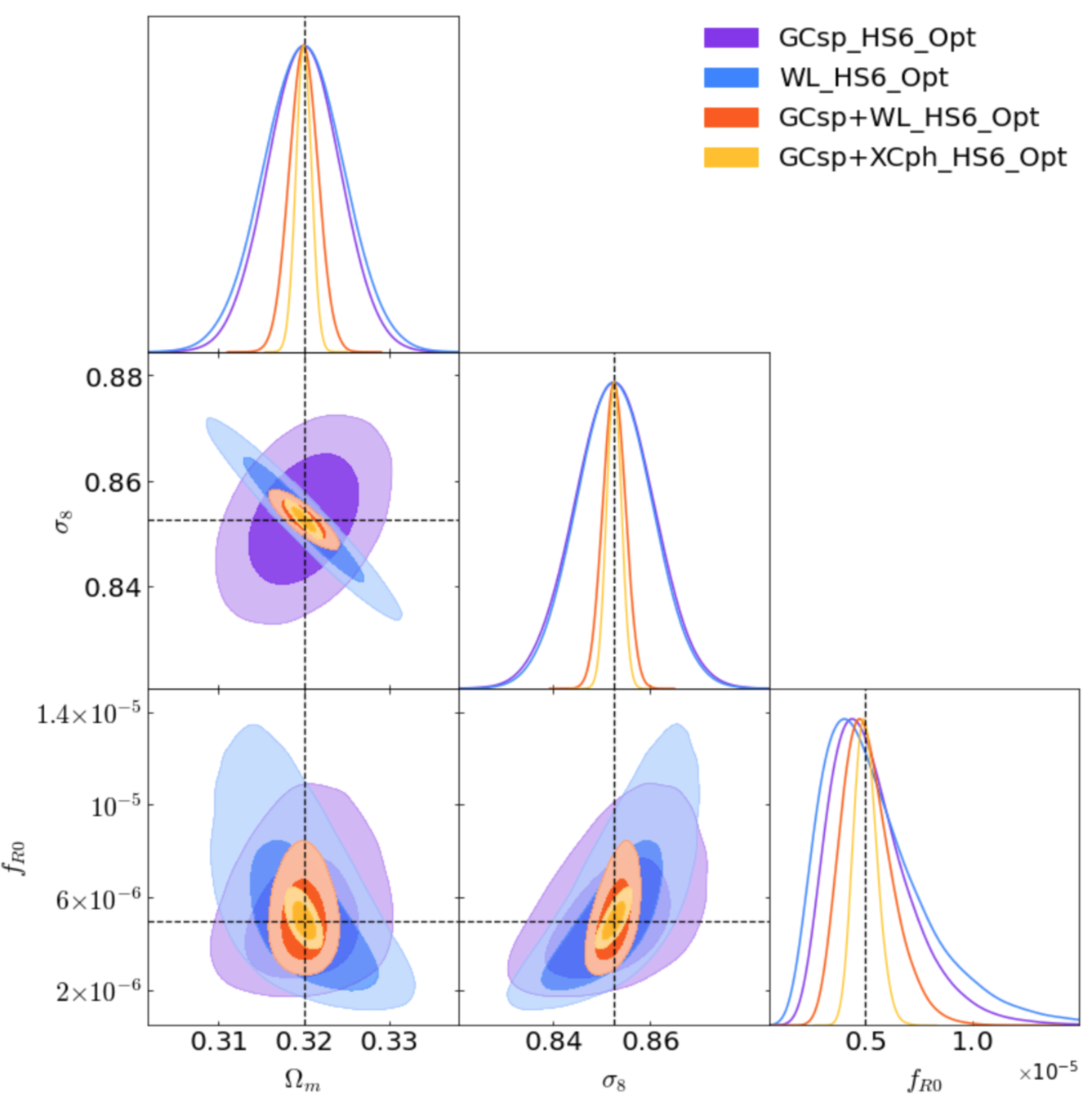
\(f_{R0}=(5.0^{+ 0.58}_{-0.52} \times 10^{-6})\)
f(R) Hu-Sawicki
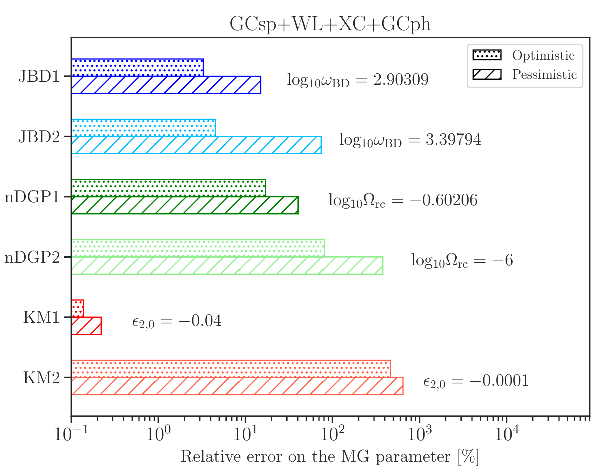
scale-independent scalar-tensor theories
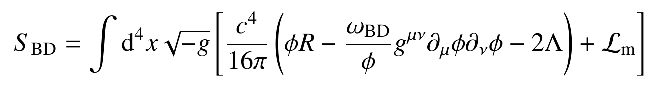
Euclid: Frusciante, Pace, Cardone, SC et al (2022) in review
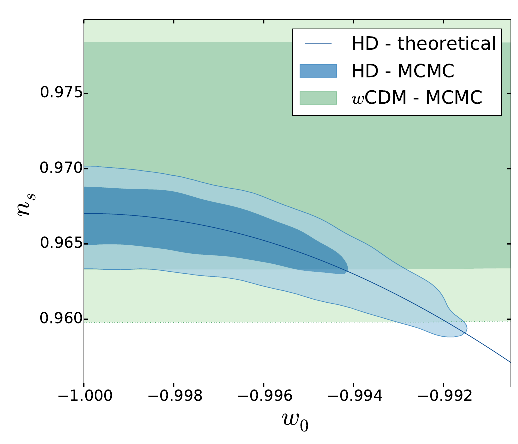
SC, Rubio, Pauly et al (2017) 1712.04956
Higgs-Dilaton inflation: early-late Universe connection
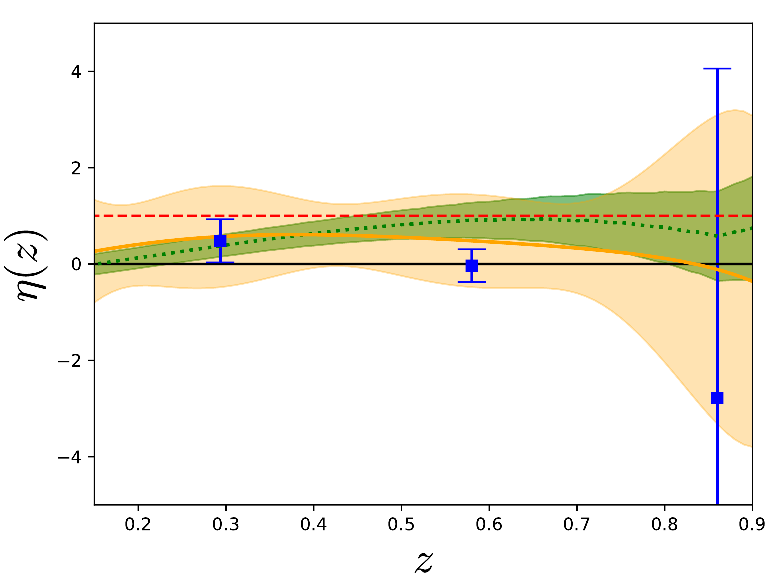
Model-independent anisotropic-stress \(\eta\)
Amendola, Pinho, SC 1805.00027
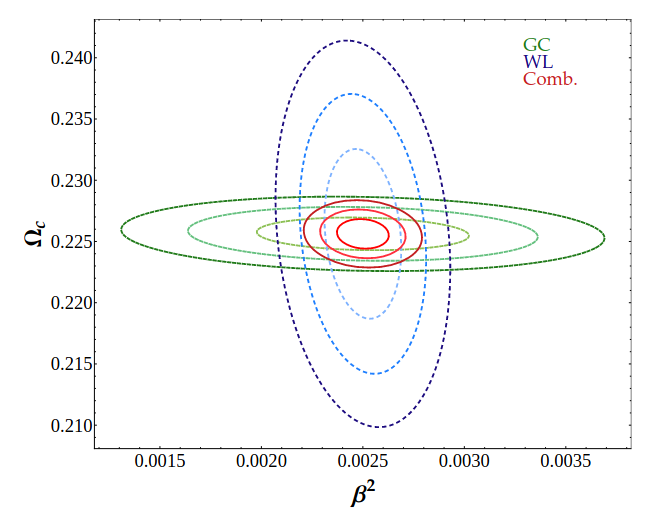
SC, Amendola, Baldi, Pettorino et al 1508.07208
Coupled Quintessence: DM-DE
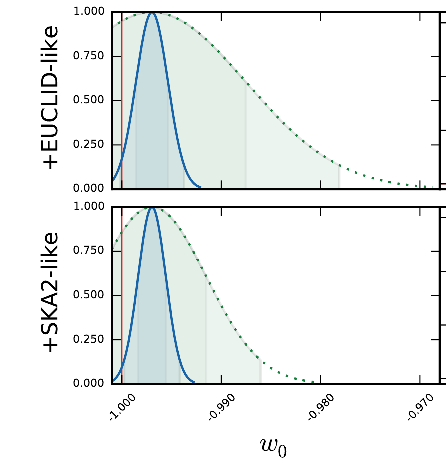
More exotic models
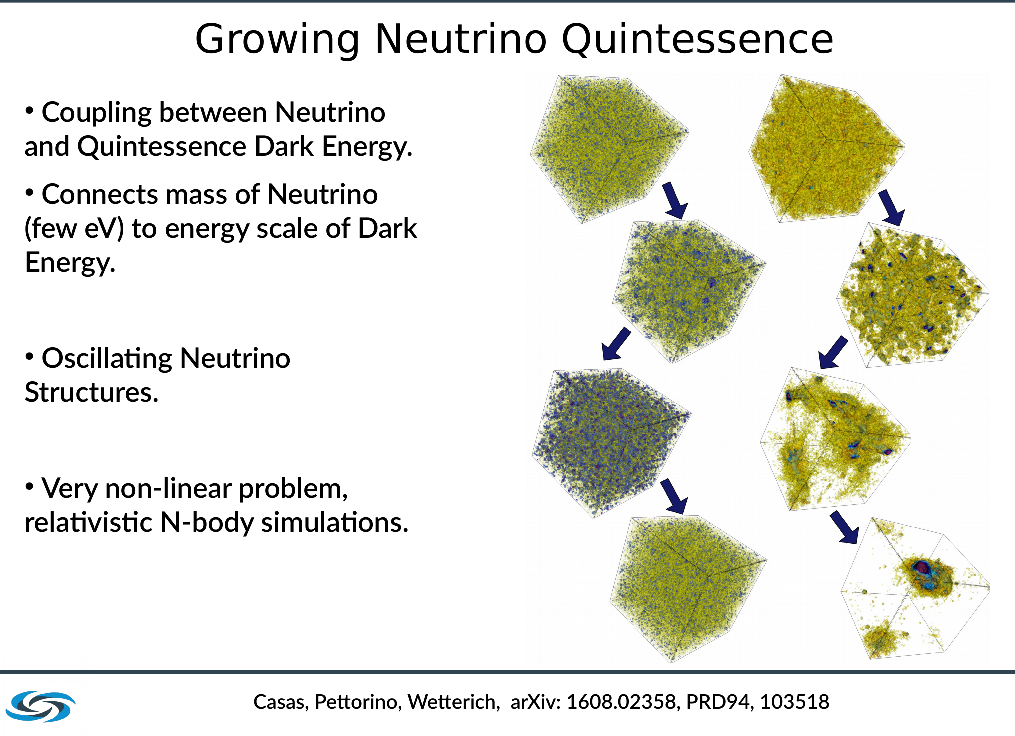
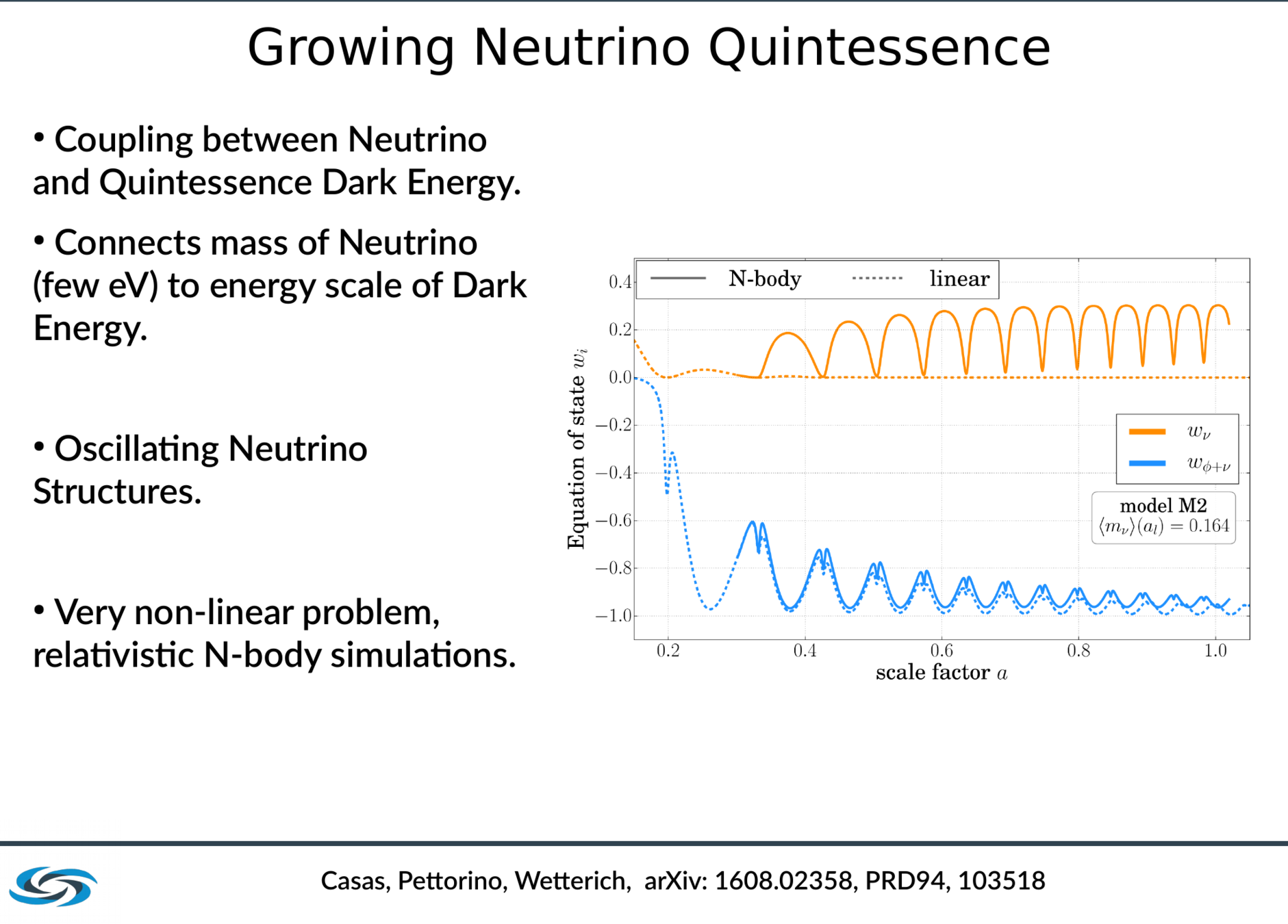
More exotic models
machine Learning and variational methods
- In era of Big Data (billions of raw data points) and hundreds of possible models and simulations:
- Important to be as computationally efficient as possible
- Important to be as computationally efficient as possible
- Likelihood codes for Euclid 2-3s per evaluation, Einstein-Boltzmann codes 1-10 seconds (depending on model)
- Emulators for linear and nonlinear codes (CLASS, N-body, Lensing)
- Bayesian Neural Networks give also uncertainty estimations
- Bayesian Neural Networks give also uncertainty estimations
- Automatic-Differentiable (AD) codes: Leverage variational methods, such as Hamilton MC, AD-Variational Inference, Exact Fisher and beyond

In collaboration with Johanna Schaffmeister and Sven Günther
jaxcosmo library https://github.com/DifferentiableUniverseInitiative
Campagne, Lanusse, Zuntz, SC
to appear in the arXiv in the next few days
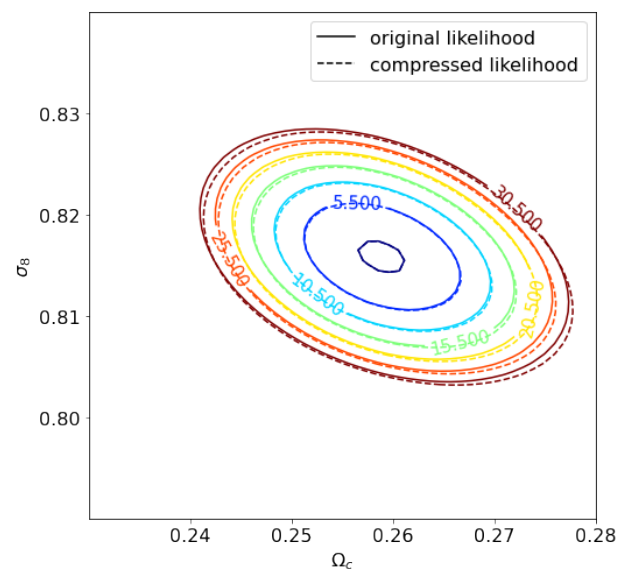
Text
Conclusions
- \(\Lambda\)CDM paradigm still best fit to observations, but tensions, unknowns and discrepancies start to crack the model.
- Several avenues of research important: Modified Gravity, cosmological Neutrinos, Early-Late time interaction.
- Stage-IV surveys, infrarred, optical and radio will improve error bars by one order of magnitude.
- Theoretical modelling (especially at non-linear scales) has to keep up with accuracy.
- Combination and synergies of surveys will break degeneracies.
- Big Data challenge needs to be resolved with ML and AI
- Unexpected unknowns awaiting for us in the data this decade!
Merci!!
BACKUP
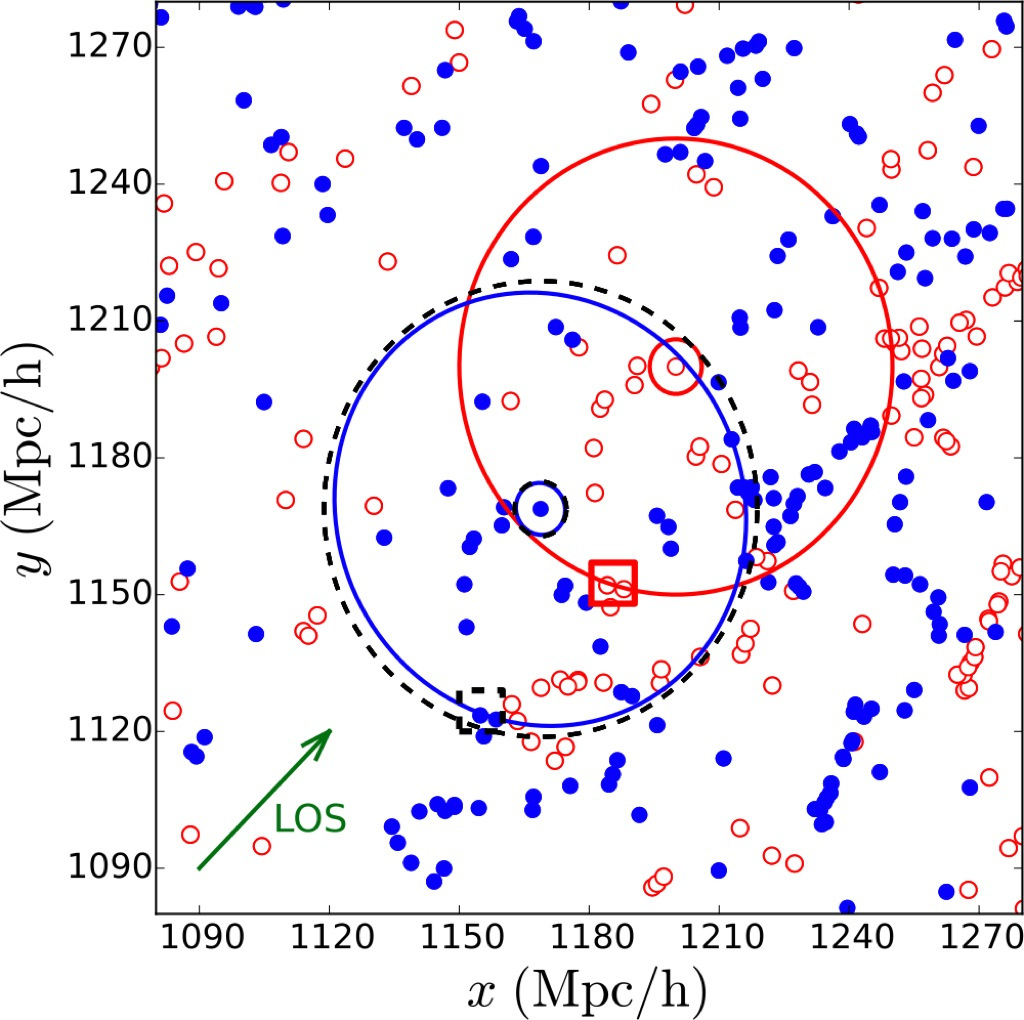
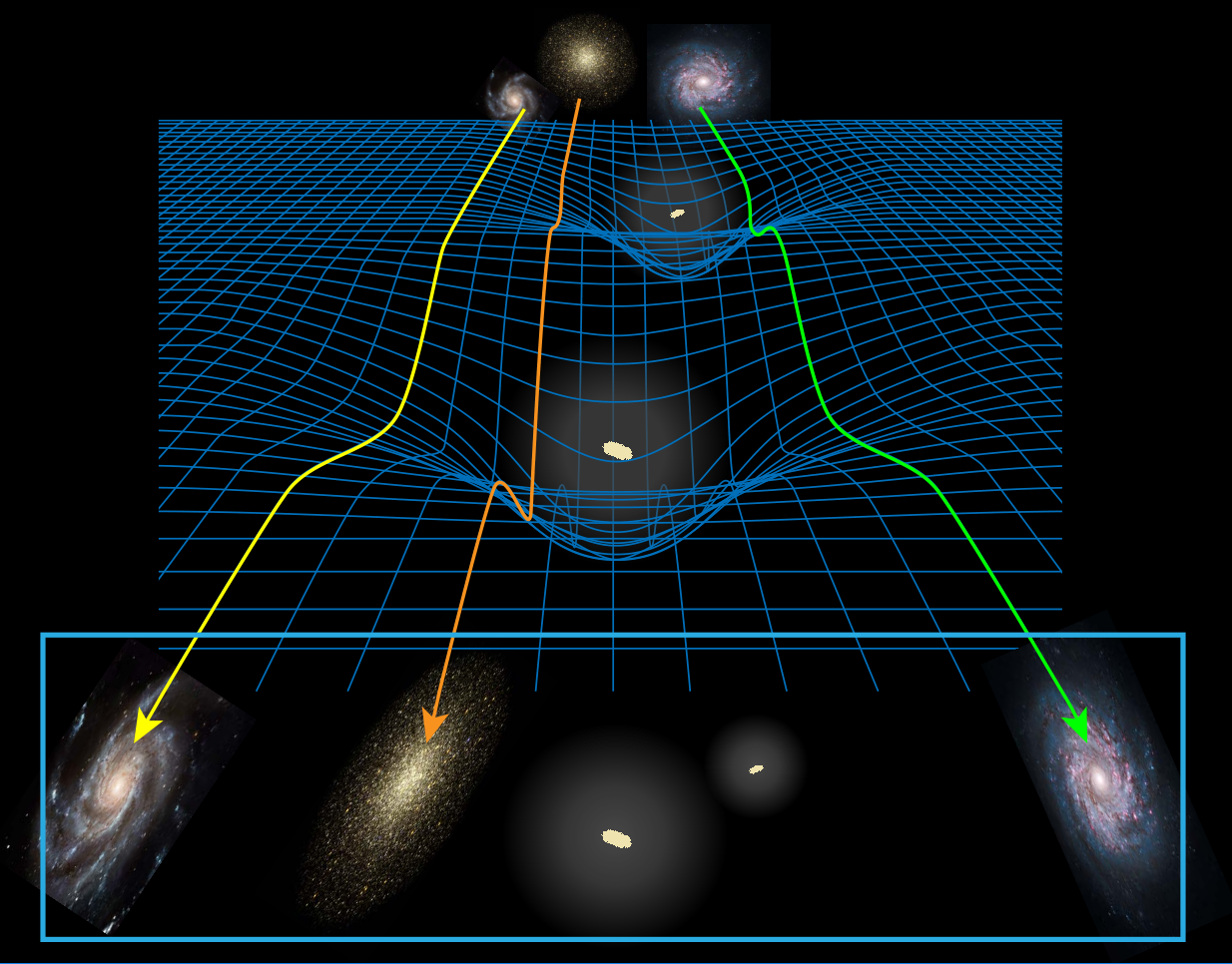
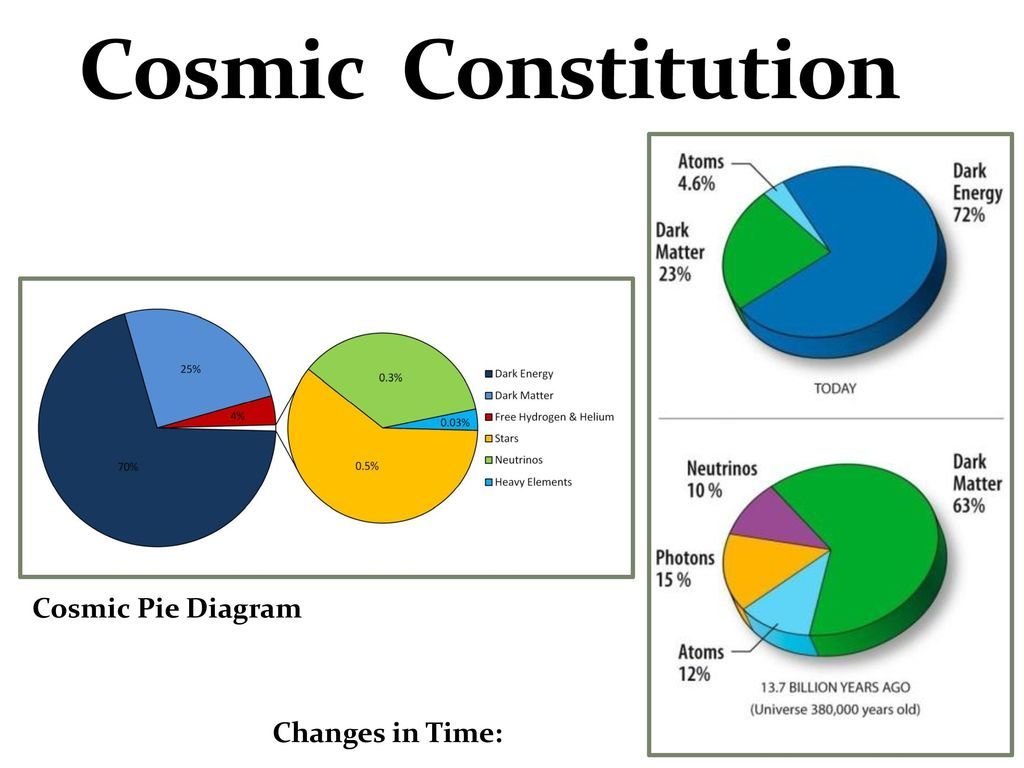
Credits: Tobias Liaudat, CosmoStat
Euclid Shape Pipeline
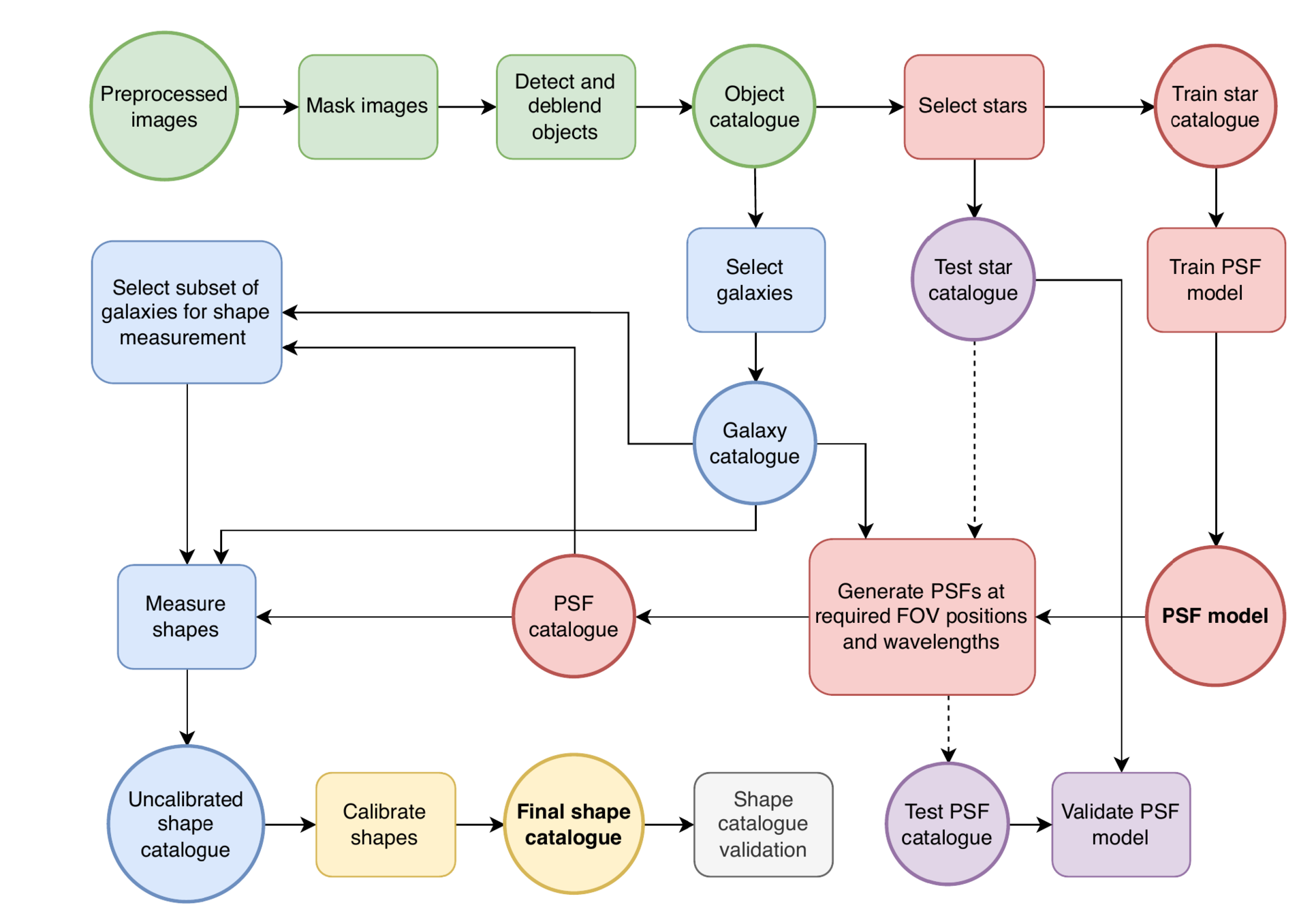
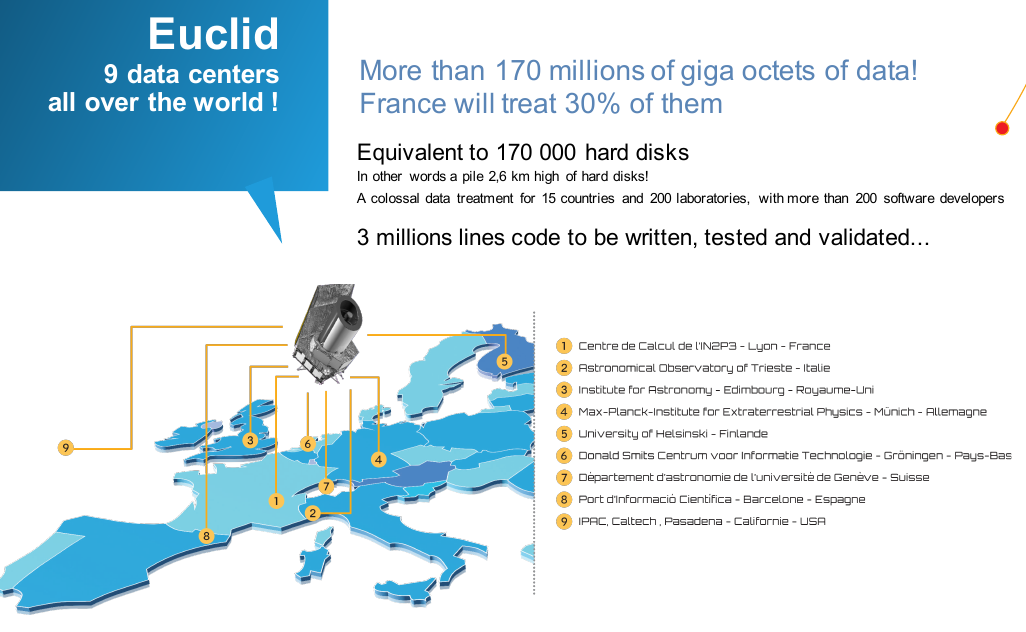
Credits: Rodlophe Cledassou, CNES
Euclid
Neutrinos Masivos en Cosmologia

Neutrinos masivos: Free streaming
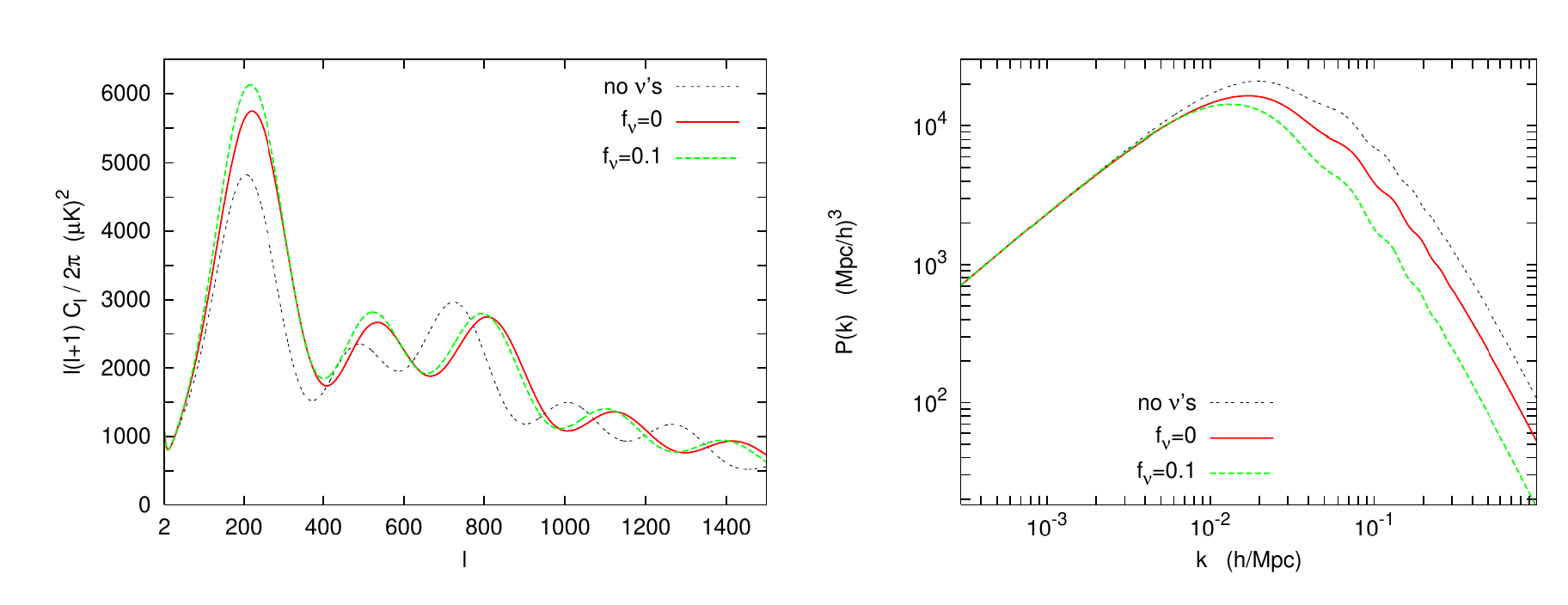
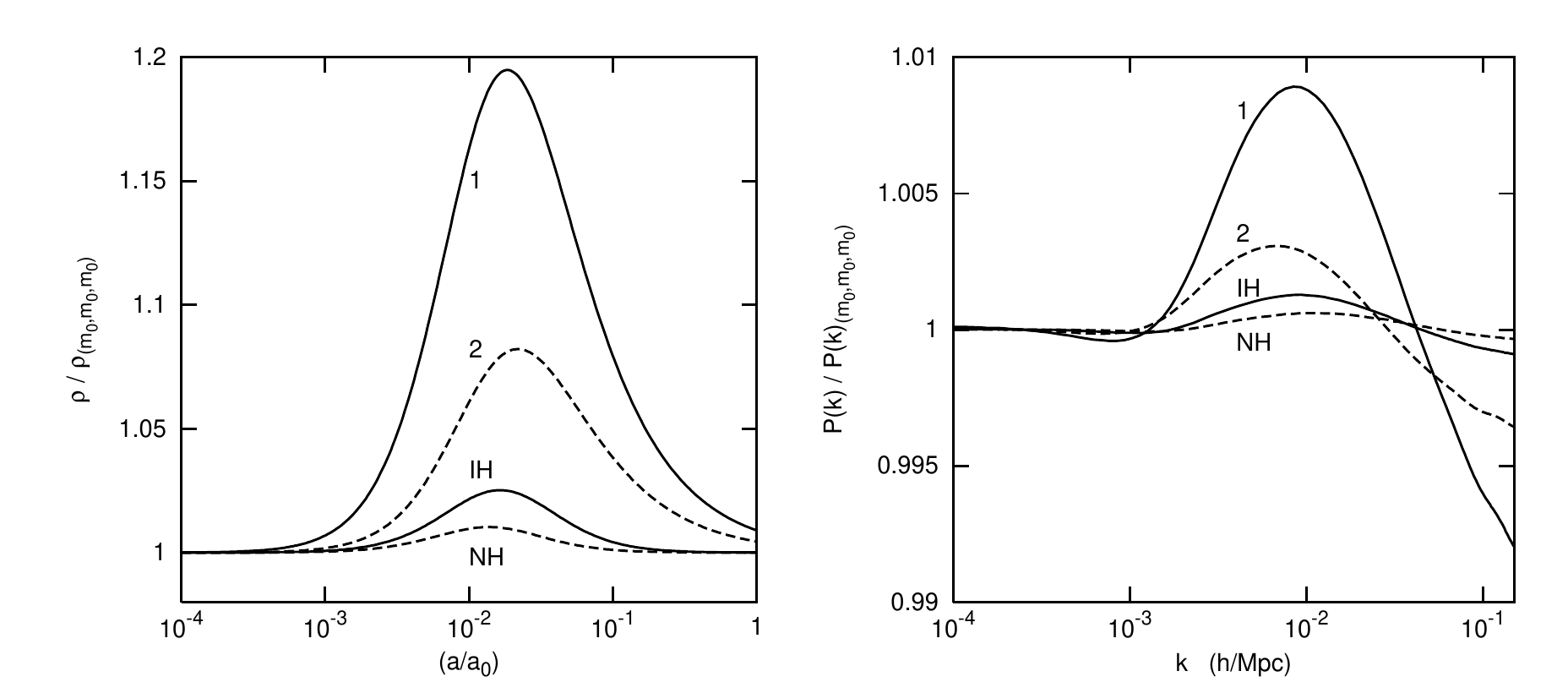
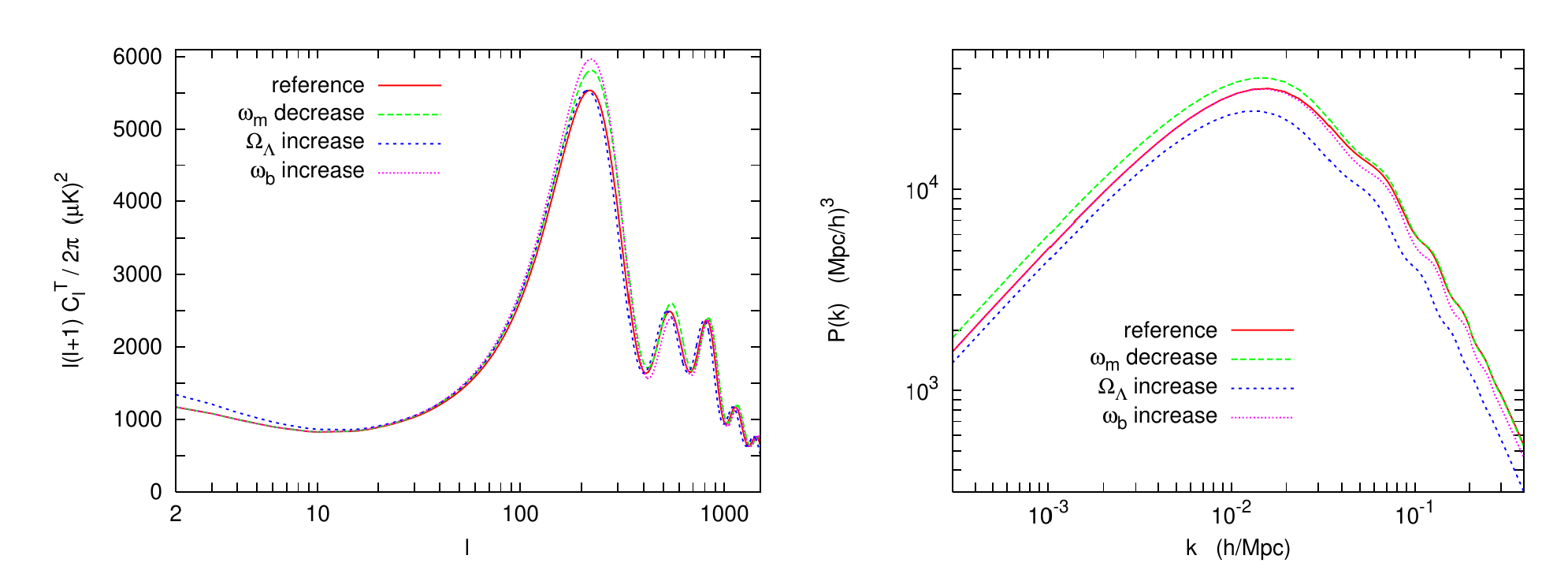
CMB angular spectrum and matter power spectrum are both dependent on neutrino mass, N_eff and ordering
Linear Perturbations
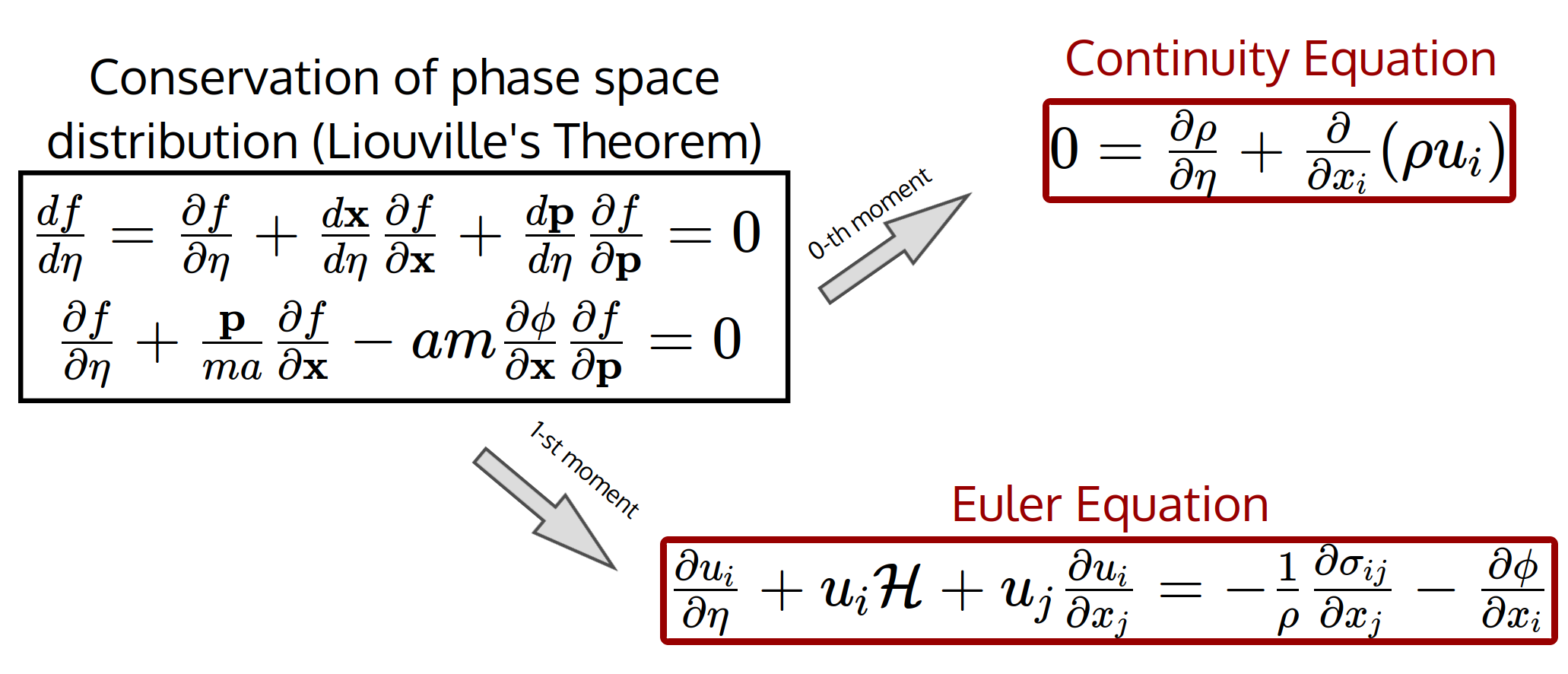
Vlasov-Poisson system is a set of diff.eqn. in which all matter-radiation species are coupled
Slides by: Dennis Linde
f(R) Hu-Sawicki model
Text
Modification of the Einstein-Hilbert action
Induces changes in the gravitational potentials *
*for negligible matter anisotropic stress
Scale-dependent growth of matter perturbations
Small changes in lensing potential
Free parameter: \(f_{R0}\)
Hu, Sawicki (2007)
"Fifth-force" scale for cosmological densities
\(\lambda_C =32 \rm{Mpc}\sqrt{|f_{R0}|/10^{-4}}\)
Euclid: Casas et al (2022) in preparation
f(R) Hu-Sawicki model
Text
Euclid: Casas et al (2022) in preparation
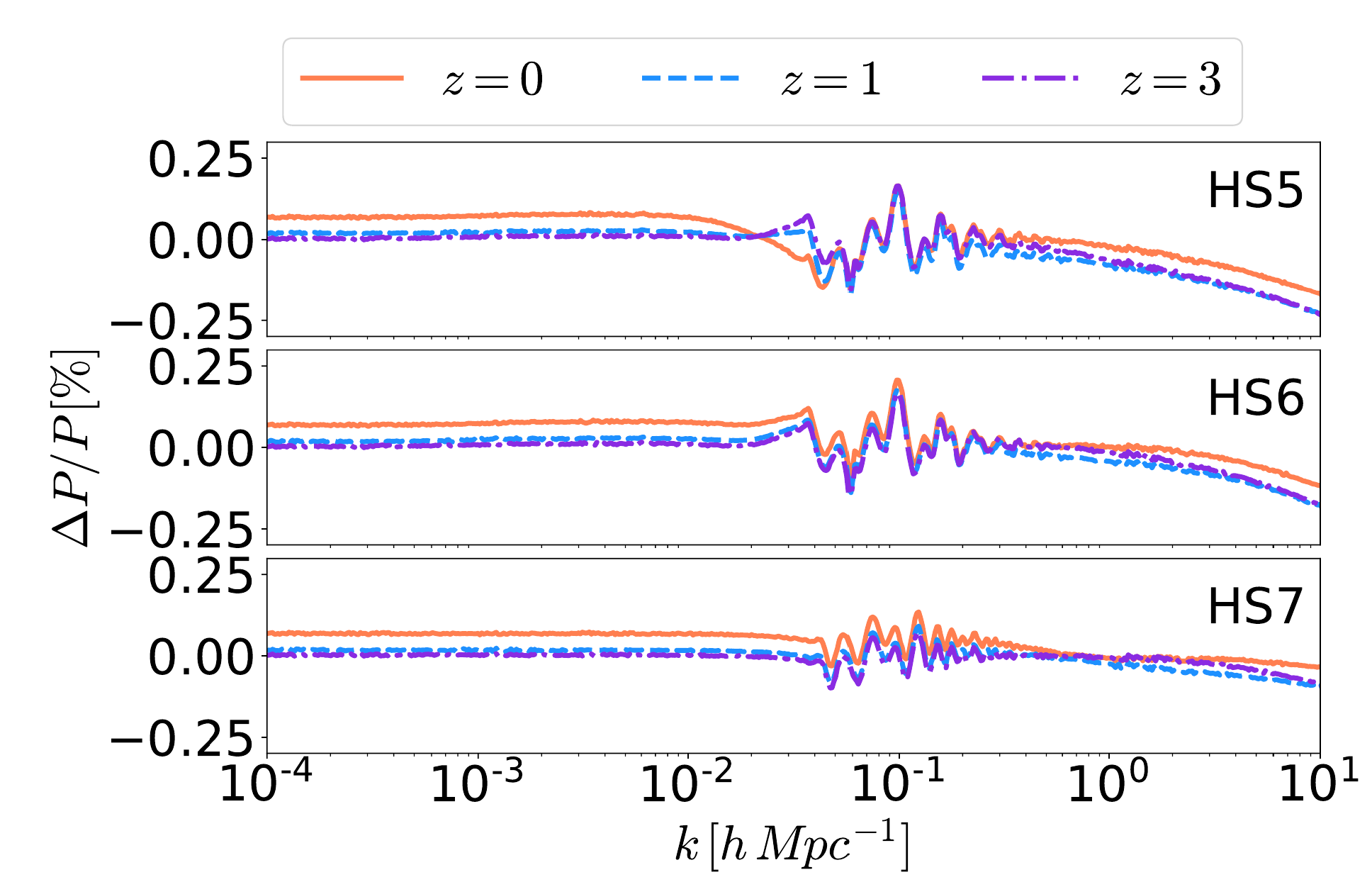
Codes used: for background and scale-dependent linear perturbations: MGCAMB and EFTCAMB
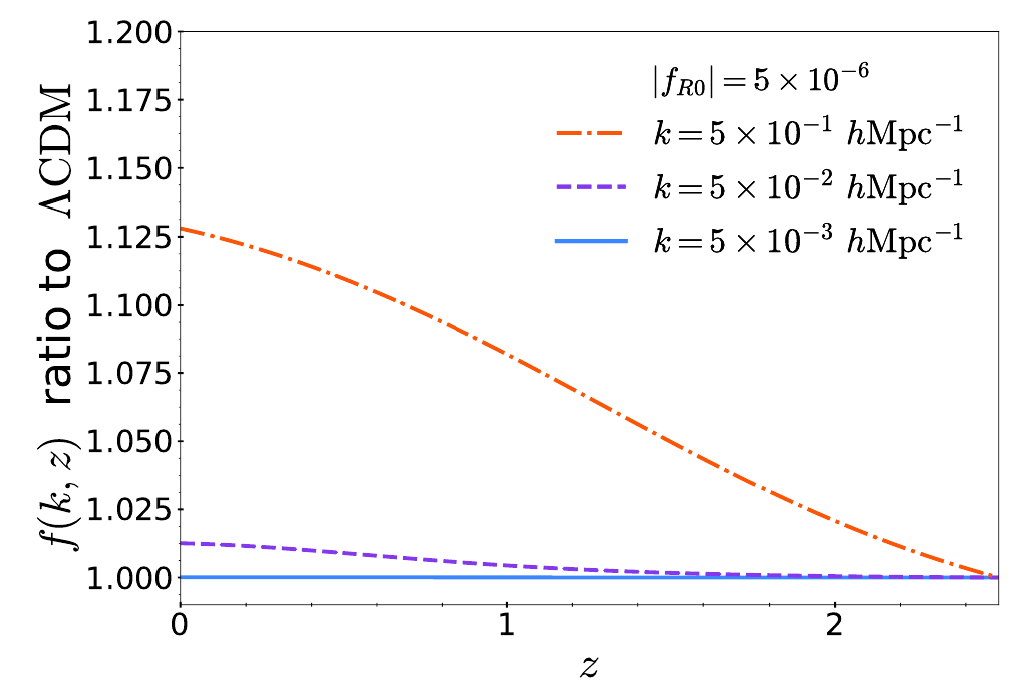
For non-linear power spectrum:
Winther et al (2019) fitting formula