Constraining modifications of gravity using Galaxy Clustering, Weak Lensing and Intensity Mapping with SKA-1
Santiago Casas,
Isabella Carucci, Valeria Pettorino,
Stefano Camera, Matteo Martinelli

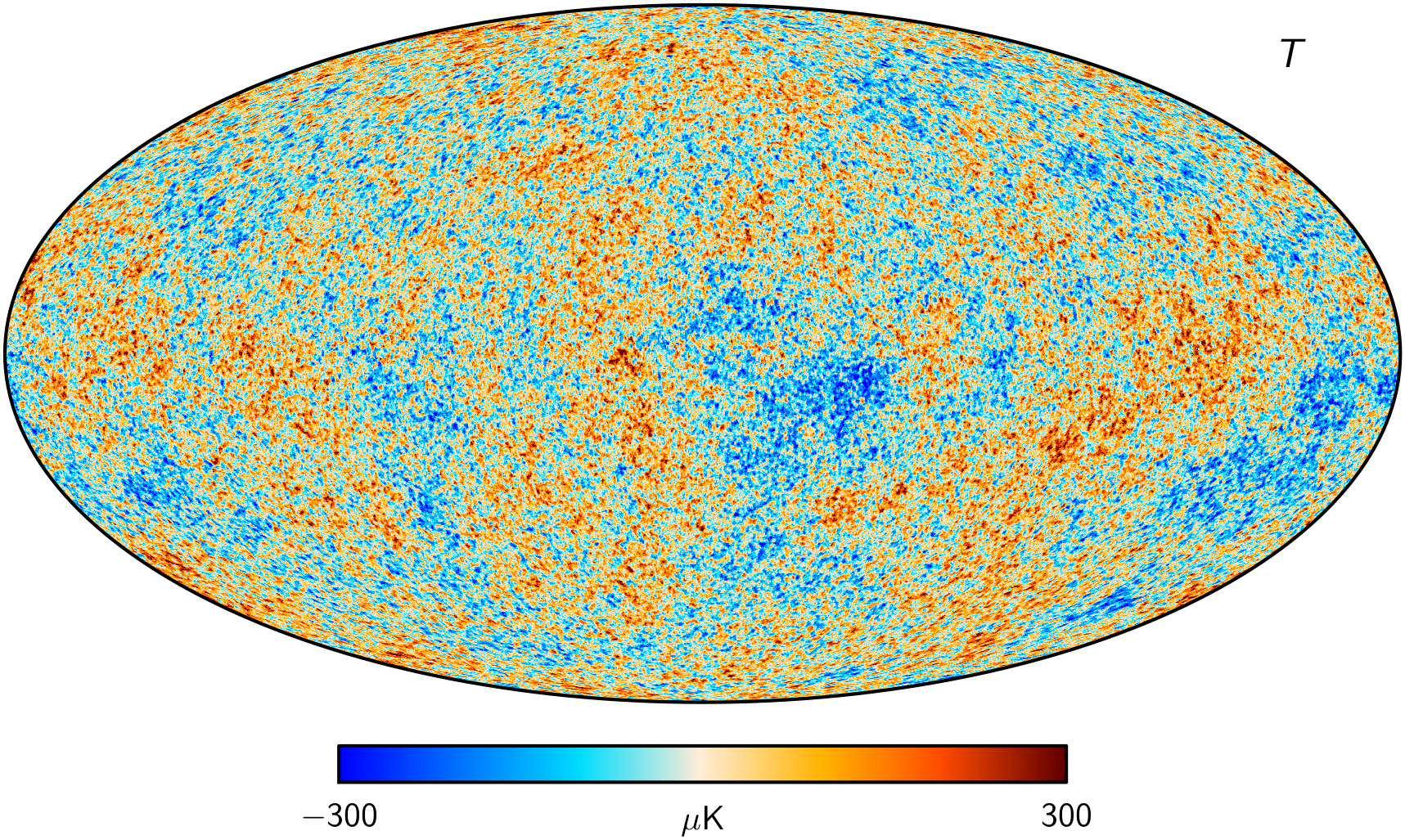
Cosmic Microwave Background
Planck 2018 CMB Temperature map (Commander) . wiki.cosmos.esa.int/planck-legacy-archive/index.php/CMB_maps

Large Scale Structure
Illustris Simulation: www.nature.com/articles/nature13316
Santiago Casas, 15.04.21
The Standard \(\Lambda\)CDM model
- \(\Lambda\)CDM is still best fit to observations.
- Predictive model with few free parameters.
- Lensing
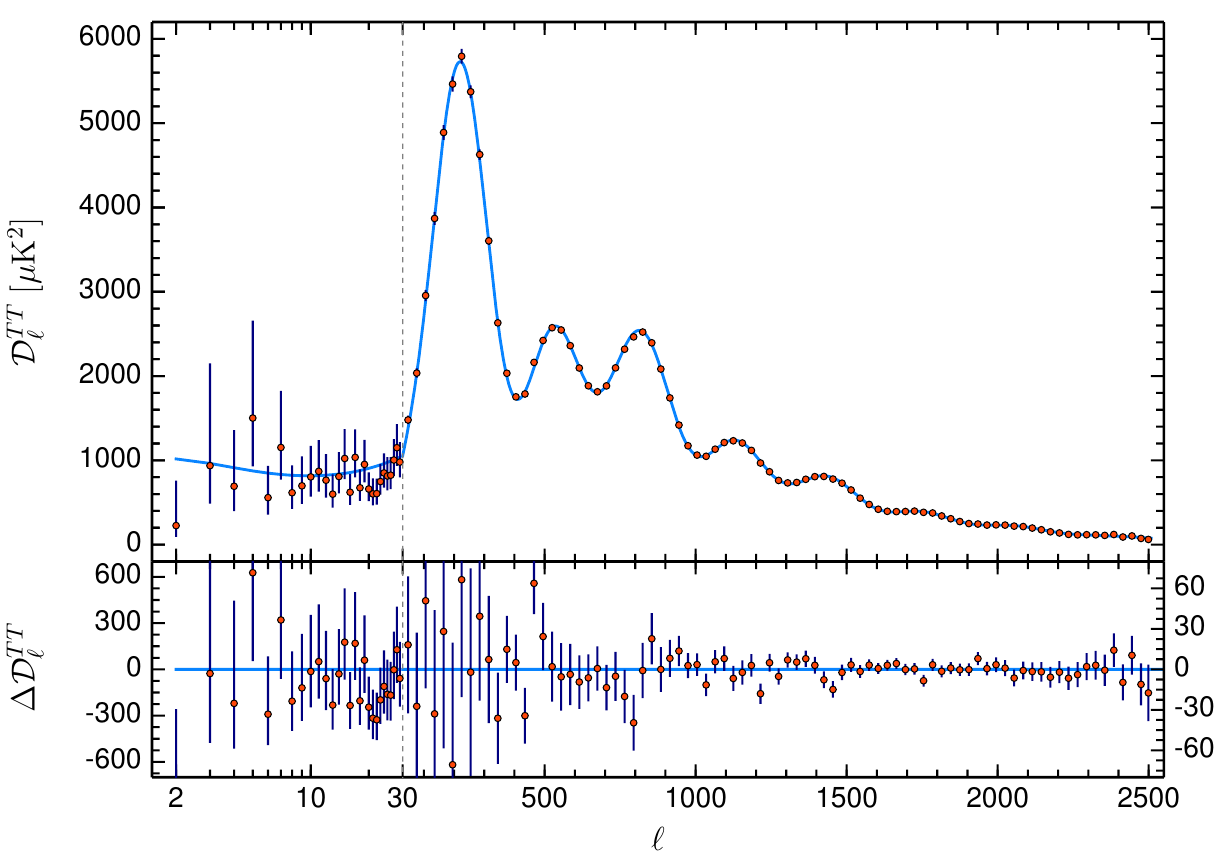
- CMB
- Clustering
- Supernovae
- Clusters
Concordance Cosmology:
Santiago Casas, 15.04.21
The Standard \(\Lambda\)CDM model
- \(\Lambda\)CDM is still best fit to observations.
- Some questions remain:
- \(\Lambda\) and CDM.
- Cosmological Constant Problem:

O(100) orders of magnitude wrong
(Zeldovich 1967, Weinberg 1989, Martin 2012).
Composed of naturalness and coincidence
sub-problems, among others.
Quantum Gravity?
Santiago Casas, 15.04.21
Tensions in the \(\Lambda\)CDM model
- \(\Lambda\)CDM is still best fit to observations.
- Some questions remain:
- H0 tension, now ~5\(\sigma\)

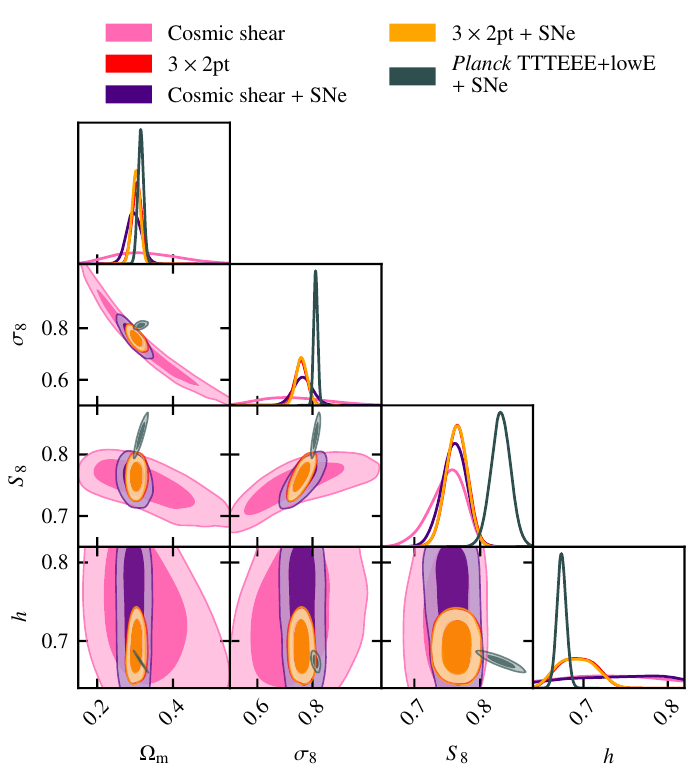
Planck, Clusters and Lensing tension on clustering amplitude \(\sigma_8\)
KiDS 1000 Cosmology, arXiv:2010:16416
L.Verde, et al 2019. arXiv:1907.10625
Santiago Casas, 15.04.21
Alternatives to \(\Lambda\)CDM
Ezquiaga, Zumalacárregui, Front. Astron. Space Sci., 2018
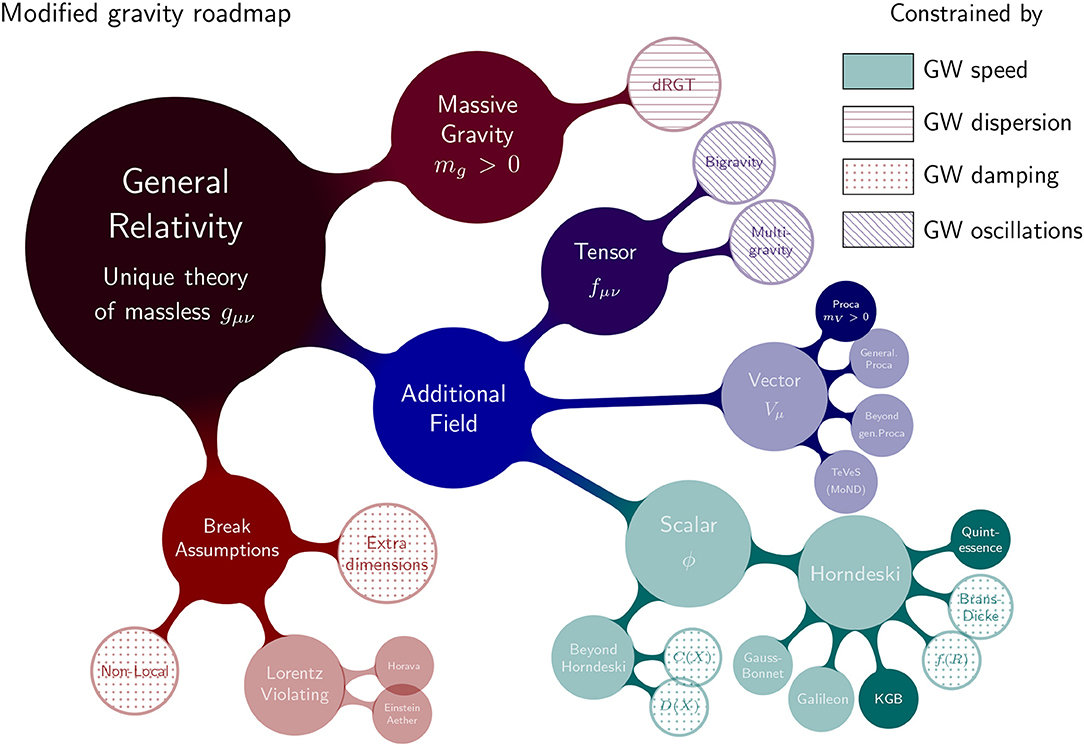
Santiago Casas, 15.04.21
Parametrized modified gravity

In \(\Lambda\)CDM the two linear gravitational potentials \(\Psi\) and \(\Phi\) are equal to each other
We can describe general modifications of gravity (of the metric) at the linear level with 2 functions of scale (\(k\)) and time (\(a\))
Only two independent functions
Santiago Casas, 15.04.21
Late-time parametrization: Planck constraints
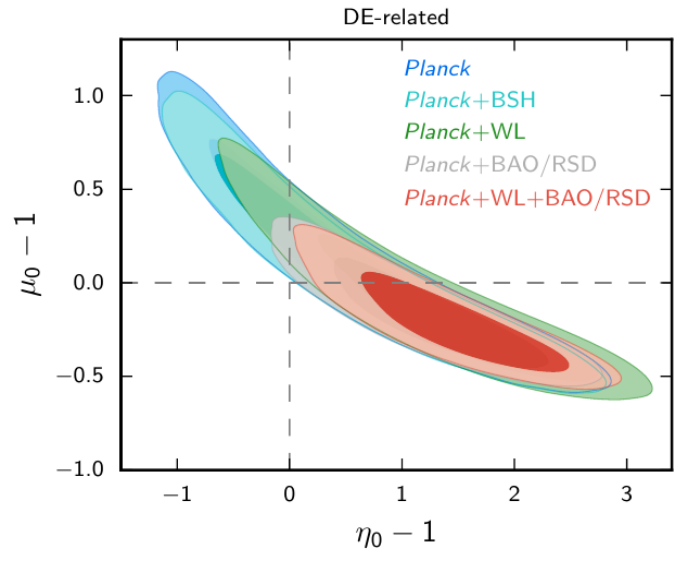
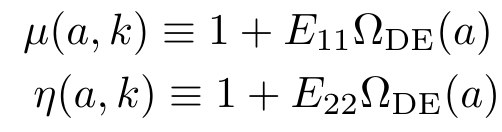
- Using Planck satellite data in 2015 and 2018, constraints were obtained on these two functions \(\mu\) and \(\eta\).
- Late-time parametrization: dependent on Dark Energy fraction
Planck 2015 results XIV, arXiv:1502.01590
Planck 2018 results VI, arXiv:1807.06209
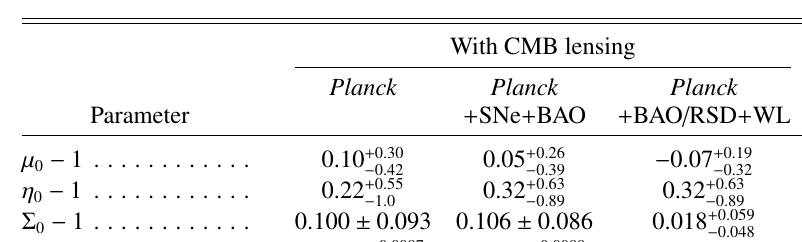
Casas et al (2017), arXiv:1703.01271
Forecasts for Stage-IV surveys in:
Santiago Casas, 15.04.21
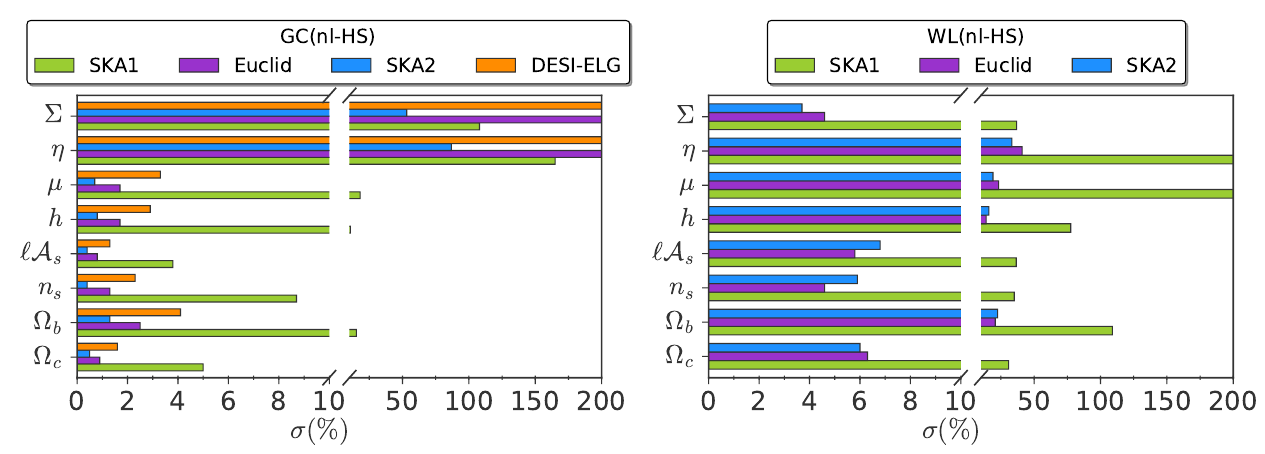
Late-time: Old SKA1, Euclid forecasts
Casas et al (2017), arXiv:1703.01271
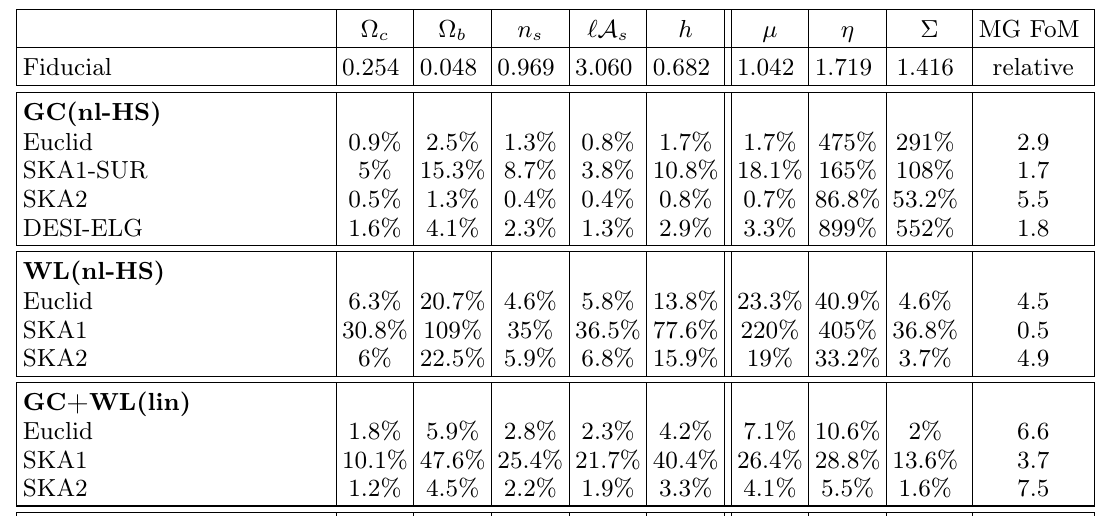
- Old SKA1 forecasts contain only WL continuum and GCsp from HI galaxies
- Linear GCsp formalism and no IA params in WL
Santiago Casas, 15.04.21
Late-time: Old SKA1, Euclid forecasts
Casas et al (2017), arXiv:1703.01271
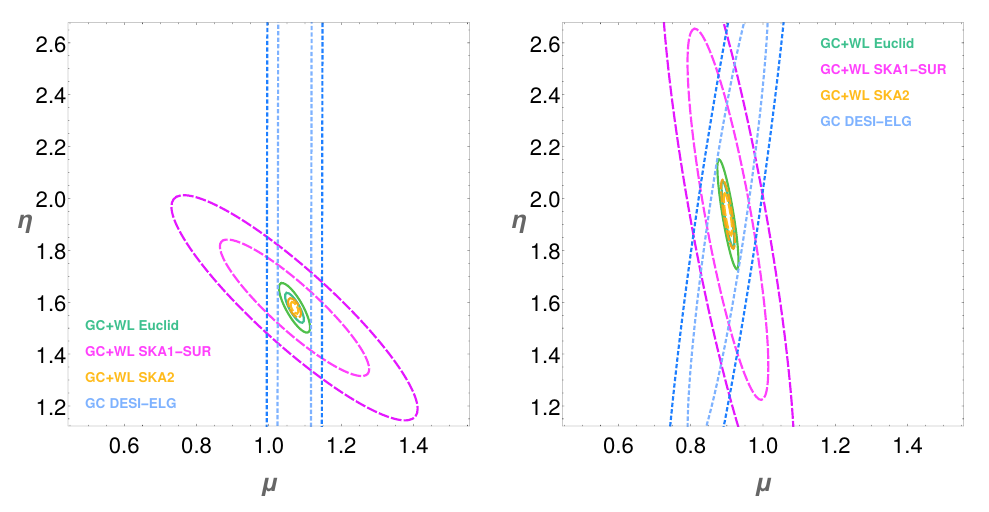
- However, we do roughly recover the same contour orientations and constraints with the new WL SKA1 forecasts.
- Deeply non-linear Pk recipe is the same, using an interpolation to recover GR at small scales.

Santiago Casas, 15.04.21
SKA Probes
Image credit: Isabella Carucci
-
Continuum emission: Allows detection of position and shapes of galaxies.
-
Line emission of neutral Hydrogen (HI, 21cm):
-
Using redshifted HI line -> spectroscopic galaxy survey
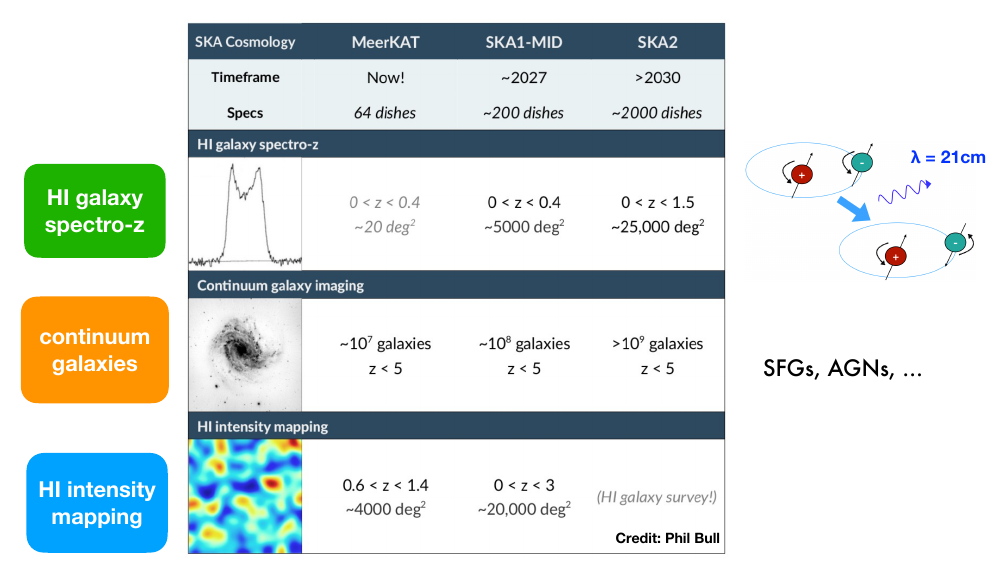
2. Intensity Mapping: Large scale correlations in HI brightness temperature -> very good redshift resolution,
good probe of structres

Santiago Casas, 15.04.21

SKA Probes
Image credit: Isabella Carucci
-
Continuum emission: Allows detection of position and shapes of galaxies.
-
Line emission of neutral Hydrogen (HI, 21cm):
-
Using redshifted HI line -> spectroscopic galaxy survey
2. Intensity Mapping: Large scale correlations in HI brightness temperature -> very good redshift resolution,
good probe of structres
Santiago Casas, 15.04.21
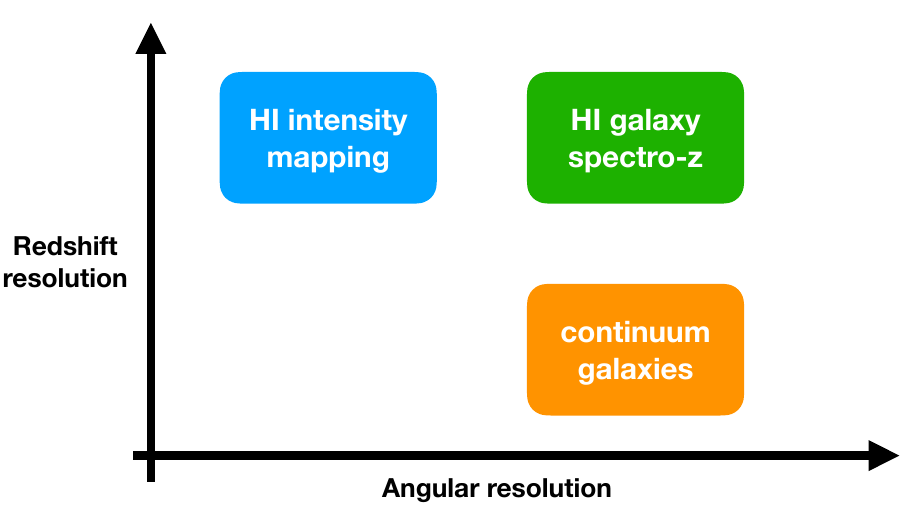
SKA1 Surveys
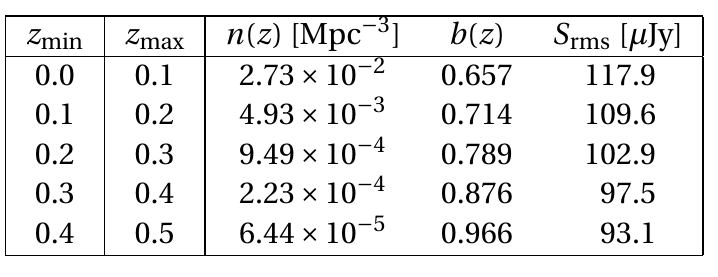
HI galaxies spectroscopic survey
- GCsp: HI galaxy spec. redshift survey: \(0.0 < z < 0.5\)
probes 3D matter power spectrum in Fourier space.
SKA1 Redbook 2018, arXiv:1811.02743
SKA1 Medium Deep Band 2: \(5000 \, \rm{deg}^2\)
Santiago Casas, 15.04.21
Galaxy Clustering Recipe

BAO
Clustering
RSD
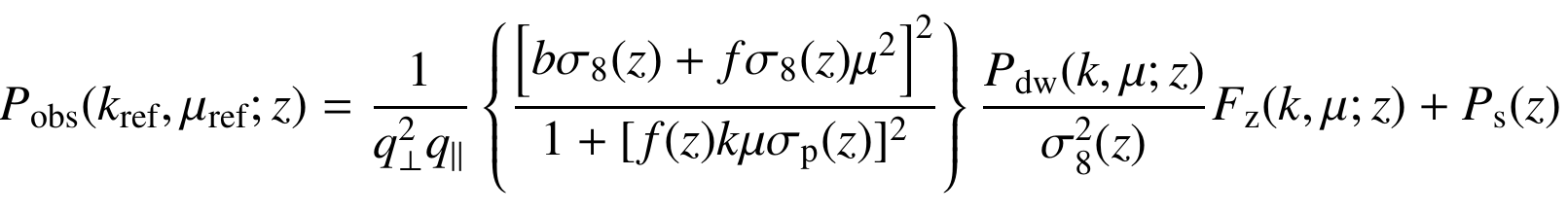
Spec-z
Euclid Collaboration, IST:Forecasts, arXiv: 1910.09273
Santiago Casas, 15.04.21
SKA1 Surveys
- GCsp: HI galaxy spec. redshift survey: \(0.0 < z < 0.5\)
probes 3D matter power spectrum in Fourier space -
GCco + WL + XCco (Continuum): \(0.0 < z < 3.0 \)
probes angular clustering of galaxies, Weak Lensing (Weyl potential) and galaxy-galaxy-lensing.
Angular number density:
\( n \approx 3.2 \rm{arcmin}^{-2}\)
SKA1 Redbook 2018, arXiv:1811.02743
SKA1 Medium Deep Band 2: \(5000 \, \rm{deg}^2\)
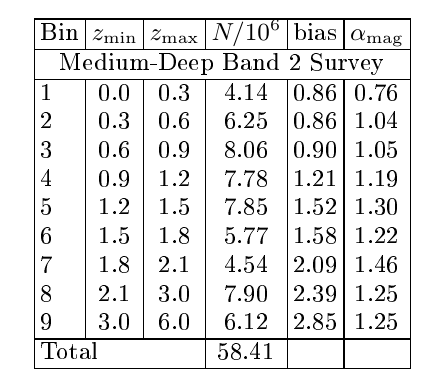
Continuum galaxy survey
Santiago Casas, 15.04.21
SKA1 Surveys
- GCsp: HI galaxy spec. redshift survey: \(0.0 < z < 0.5\)
probes 3D matter power spectrum in Fourier space -
GCco + WL + XCco (Continuum): \(0.0 < z < 3.0 \)
probes angular clustering of galaxies, Weak Lensing (Weyl potential) and galaxy-galaxy-lensing.
Angular number density:
\( n \approx 3.2 \rm{arcmin}^{-2}\)
*kindly provided by Stefano Camera
SKA1 Medium Deep Band 2: \(5000 \, \rm{deg}^2\)
Continuum galaxy survey
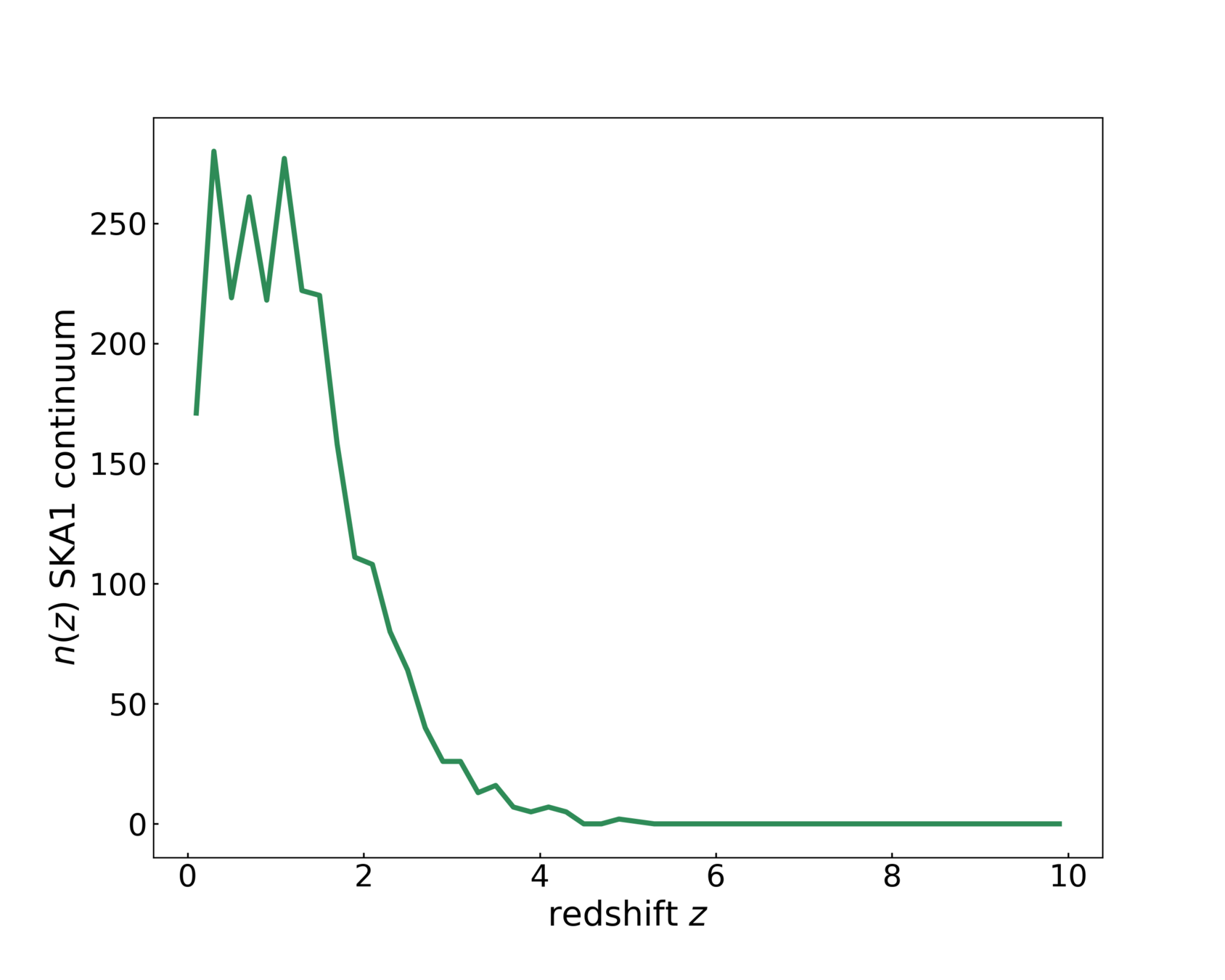
Santiago Casas, 15.04.21
Weak Lensing
- Influence of matter-energy: galaxies align and get distorted
- Correlation function
of cosmic shear: information about matter content
and expansion.
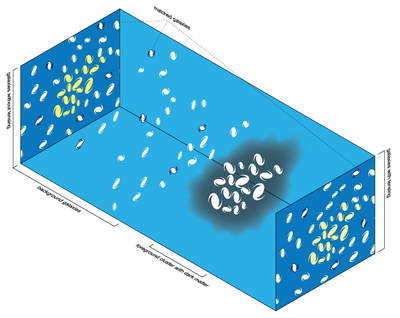
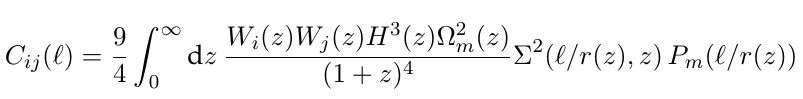
Directly constrains MG function \(\Sigma\) through Weyl potential

Santiago Casas, 15.04.21

SKA Surveys
- IM: Intensity mapping survey
\(0.4 < z < 2.5\) - Very good redshift resolution: \(\Delta z \approx \mathcal{O}(10^{-3}) \)
- We use: 11 redshift bins
-
Single dish mode:
\(N_d = 197\)
\(t_{obs} = 10000 \, \rm{hr} \)
We limit to the scales
\(0.001 < k < 0.25 \, [h/\rm{Mpc}] \)
SKA1 Medium Deep Band 1: \(20000 \,\rm{deg}^2\)

Santiago Casas, 15.04.21

Intensity Mapping
- IM probes the underlying matter power spectrum.
- There is a density bias given by the HI mass contained in dark matter halos.
- 21cm brightness temperature depends on cosmological background evolution and the energy fraction of neutral Hydrogen in the Universe \(\Omega_{HI}\).
- \(P_{\delta\delta,zs}(z,k) \) is the redshift space matter power spectrum
\(P^{\rm IM}(z,k) = \bar{T}_{IM}(z)^2[b_{\rm IM}(z)^2+f(z)\mu^2]^2P_{\delta\delta,zs}(z,k) \)
\( b_{IM}(z) = 0.3(1+z) + 0.6 \)
\(\Omega_{HI} = 4(1+z)^{0.6} \times 10^{-4} \)
\( \bar{T}_{\mathrm{IM}}(z)= 189h \frac{(1+z)^2 H_0}{H(z)}\Omega_{HI}(z) \,\,{\rm mK} \)
Jolicoeur et al (2020) arXiv:2009.06197
Carucci et al (2020) arXiv:2006.05996
Santiago Casas, 15.04.21
Intensity Mapping x GCsp
- The cross correlation combines one term of brightness temperature with one Kaiser term for each "redshift sample".
- Same underlying matter power spectrum for both probes.
- A combined redshift error (damping along the line of sight), where "sp" dominates, since the IM resolution is 1-2 orders of magnitude better.
\( b_{\rm g}(z) = \) fit to simulations for given galaxy sample
Jolicoeur et al (2020) arXiv:2009.06197
Wolz et al (2021) arXiv:2102.04946
\(\sigma_i(z) = \frac{c}{H(z)}(1+z) \delta_z\)
\(P^{{\rm IM} \times \rm{GC}}(z,k) = \bar{T}_{\rm IM}(z) [b_{\rm IM}(z)^2+f(z)\mu^2] \times [b_{\rm g}(z)^2+f(z)\mu^2] P_{\delta\delta,zs}(z,k) \times \exp[-\frac{1}{2} k^2 \mu^2 (\sigma_{\rm IM}(z)^2+\sigma_{\rm sp}(z)^2)] r_{\rm IM,opt} \)
Santiago Casas, 15.04.21
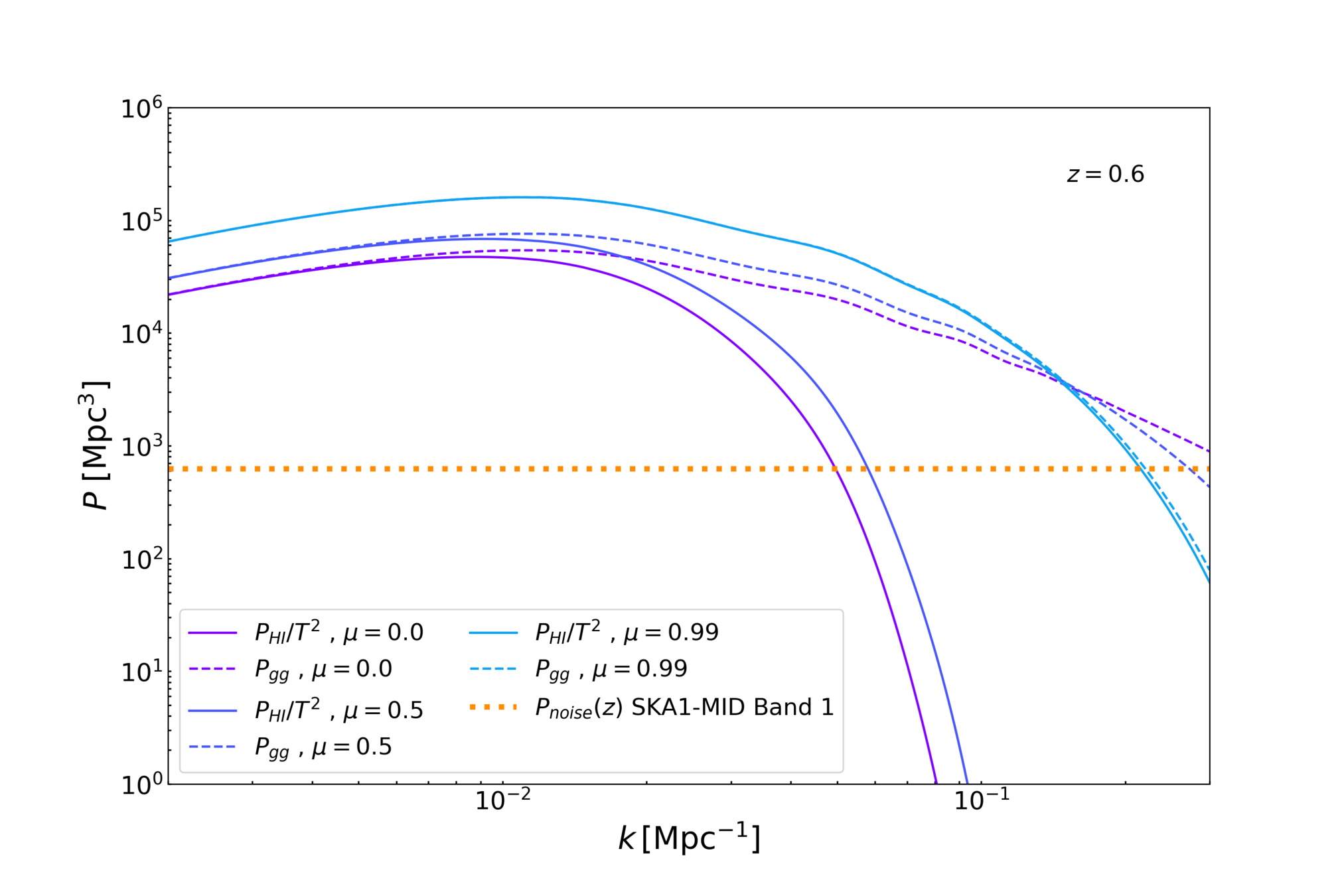
Intensity Mapping
- \(P_{gg}\) underlying galaxy power spectrum.
- \(P_{HI}/T_{HI}^2\) IM power spectrum.
- \(P_{noise} \) for single dish mode in SKA1-MID Band 1 survey.
- Angle-dependent beam effect is in the signal.
Santiago Casas, 15.04.21
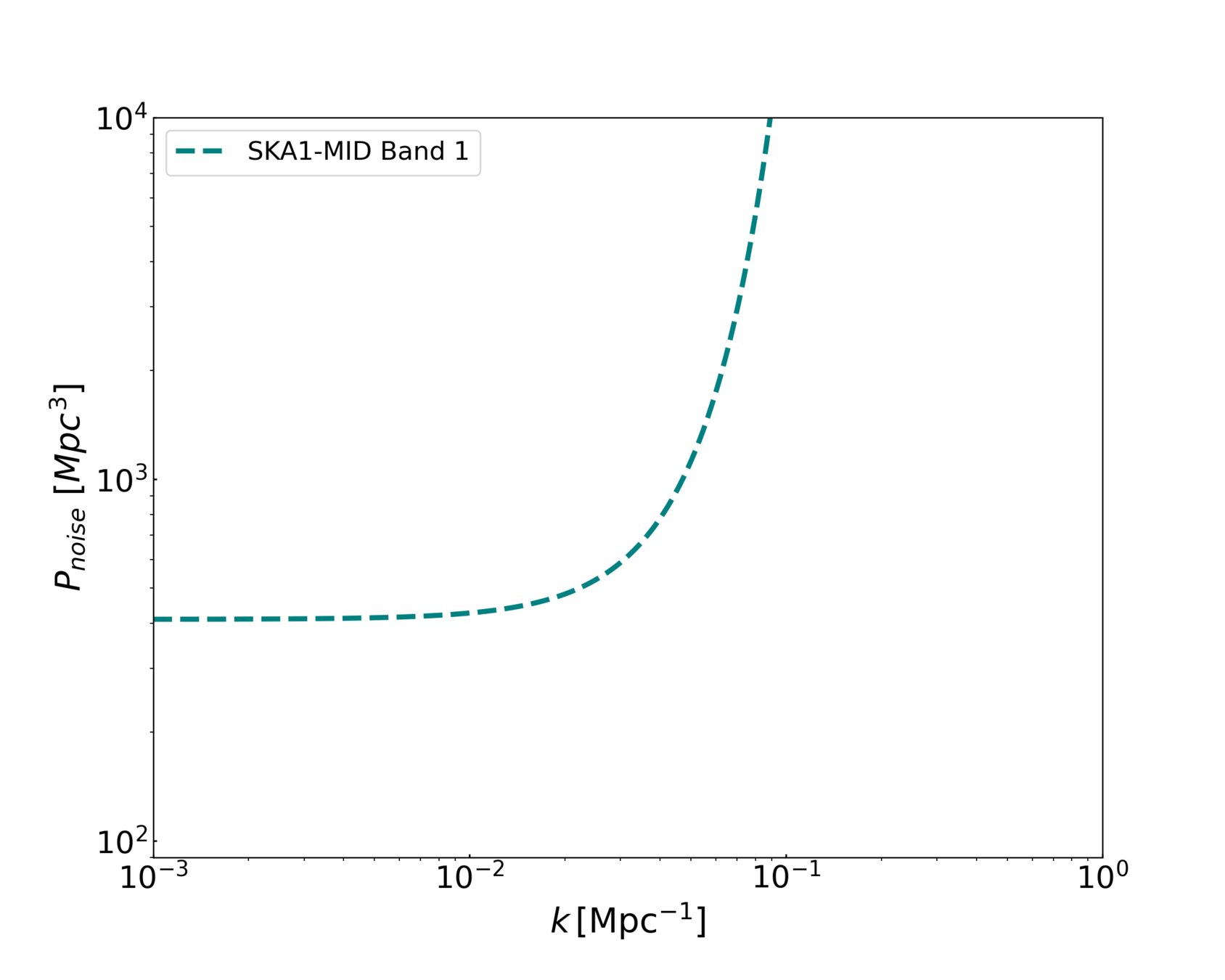
Intensity Mapping Noise Terms
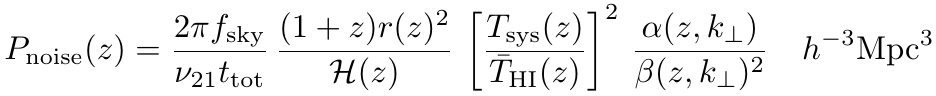
Number of dishes
Effective beam
\(\beta_{SD} = \exp[-\frac{k_\perp r(z)^2 \theta_b (z)^2}{8 \ln 2}] \)
\( \alpha_{SD} = \frac{1}{N_d} \)
Jolicoeur et al (2020) arXiv:2009.06197

Santiago Casas, 15.04.21

Euclid space satellite


Santiago Casas, 15.04.21

Euclid space satellite
- Two instruments:
- VIS (visible photometer): shape and orientation of 1.5 billion galaxies!
- NISP (near infrared spectrograph): 30 million galaxy spectra!




Santiago Casas, 15.04.21

Galaxy Clustering - IM Synergies
- SKA1 and Euclid probe complementary redshifts in spectroscopic GC.
- IM and GC cross-correlation offers gain in information and reduction of systematics

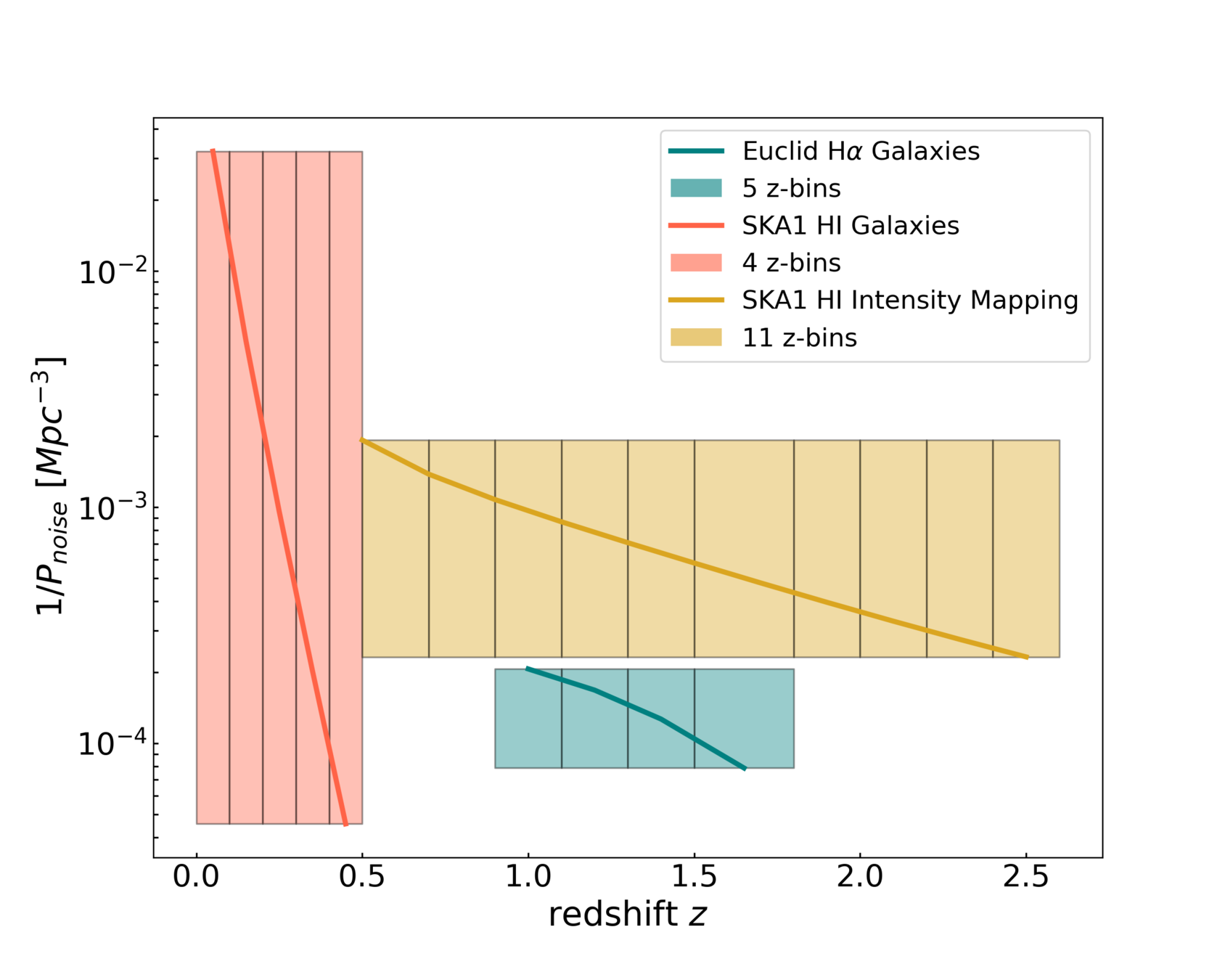

Santiago Casas, 15.04.21

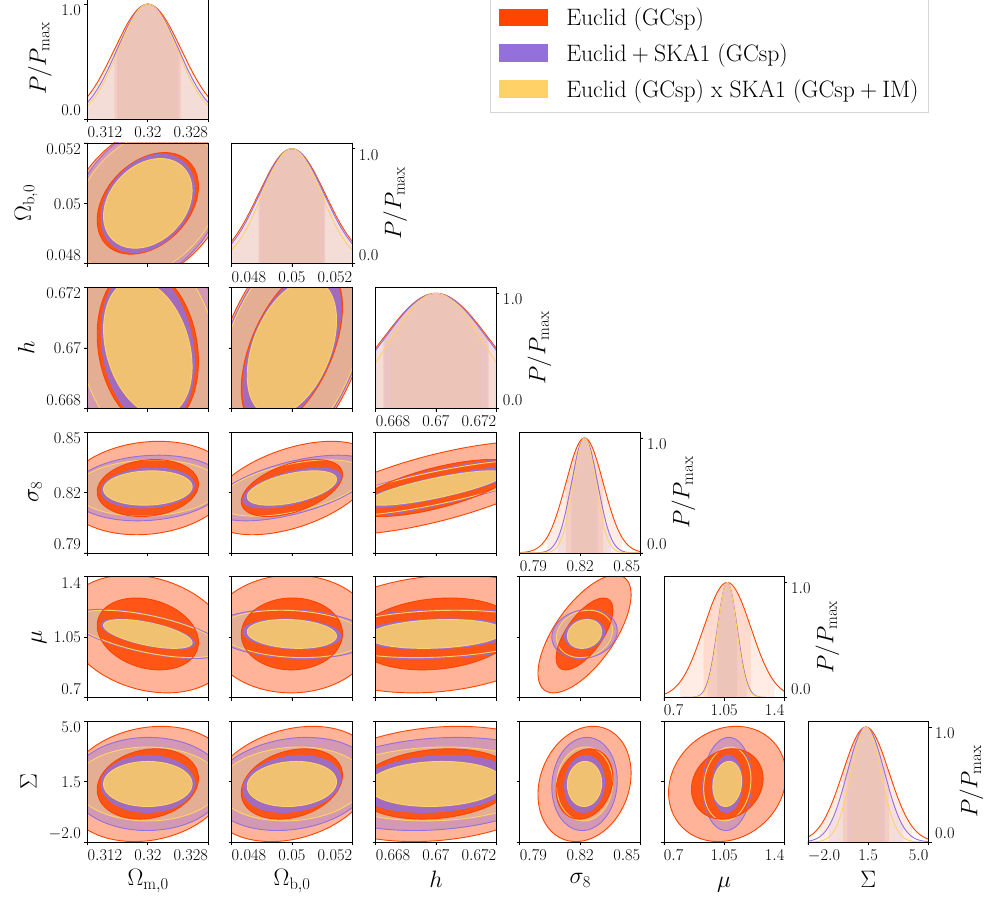
SKA1 Results
Euclid GCsp
+
SKA1 GCsp (HI galaxies)
- Improved constraints on \(\mu\) since it covers a larger redshift range at small \(z\) where \(\mu\) becomes important.
PRELIMINARY

Santiago Casas, 15.04.21

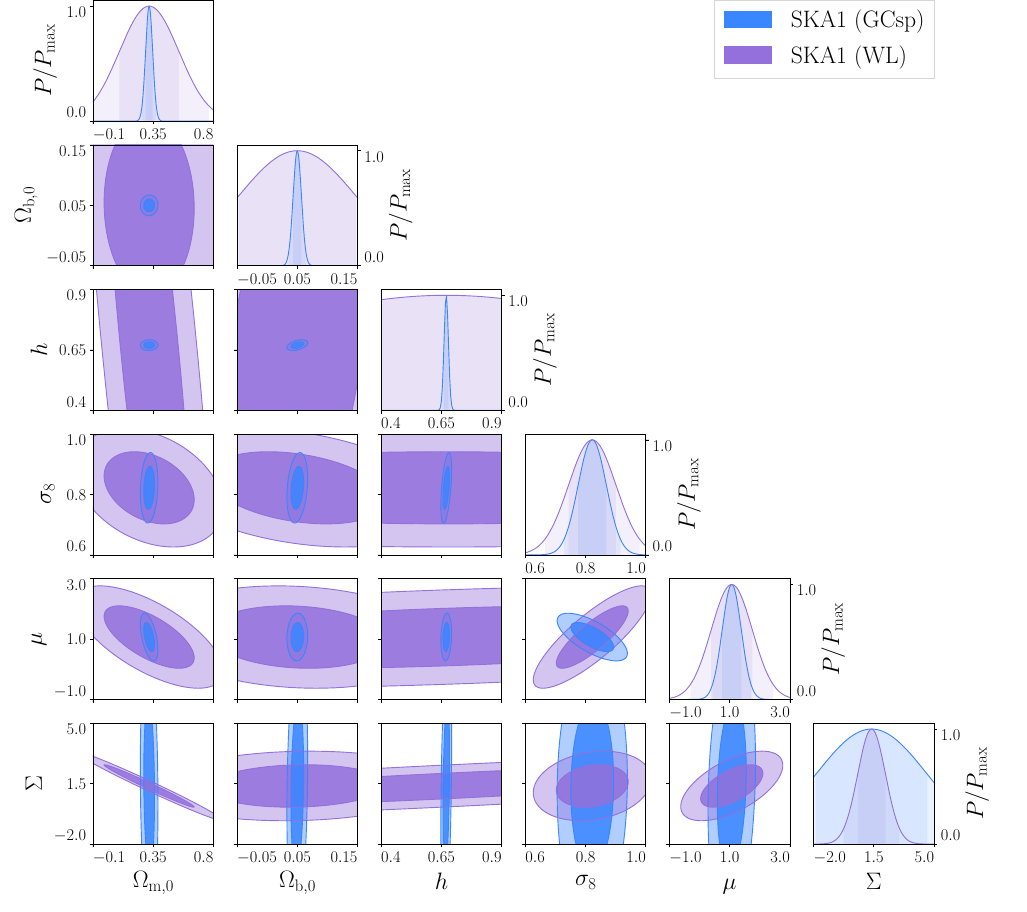
SKA1 Results
SKA1:
GCsp (HI galaxies)
WL (Continuum)
- WL is more constraining on \(\Sigma\) as expected.
PRELIMINARY

Santiago Casas, 15.04.21

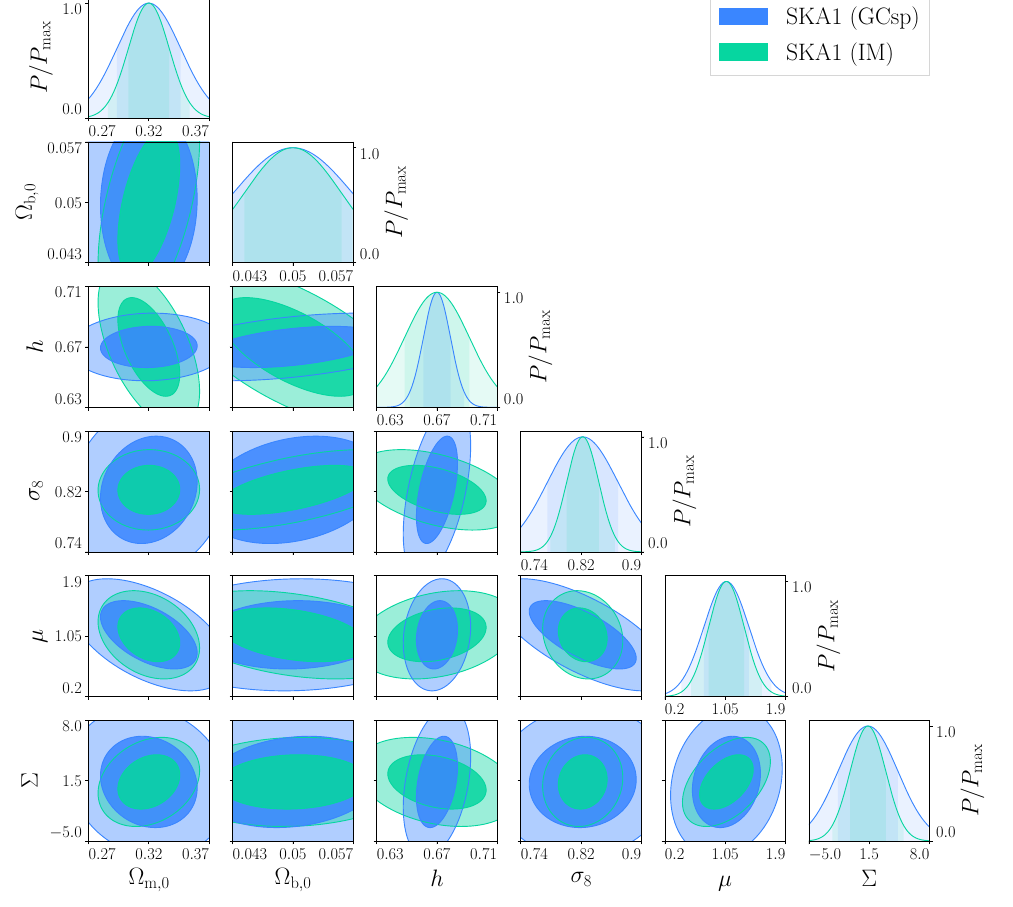
SKA1 Results
SKA1:
GCsp (HI galaxies)
IM
(21cm HI)
- IM is more constraining in almost all parameters. Except \(h\), where GCsp is better.
PRELIMINARY

Santiago Casas, 15.04.21

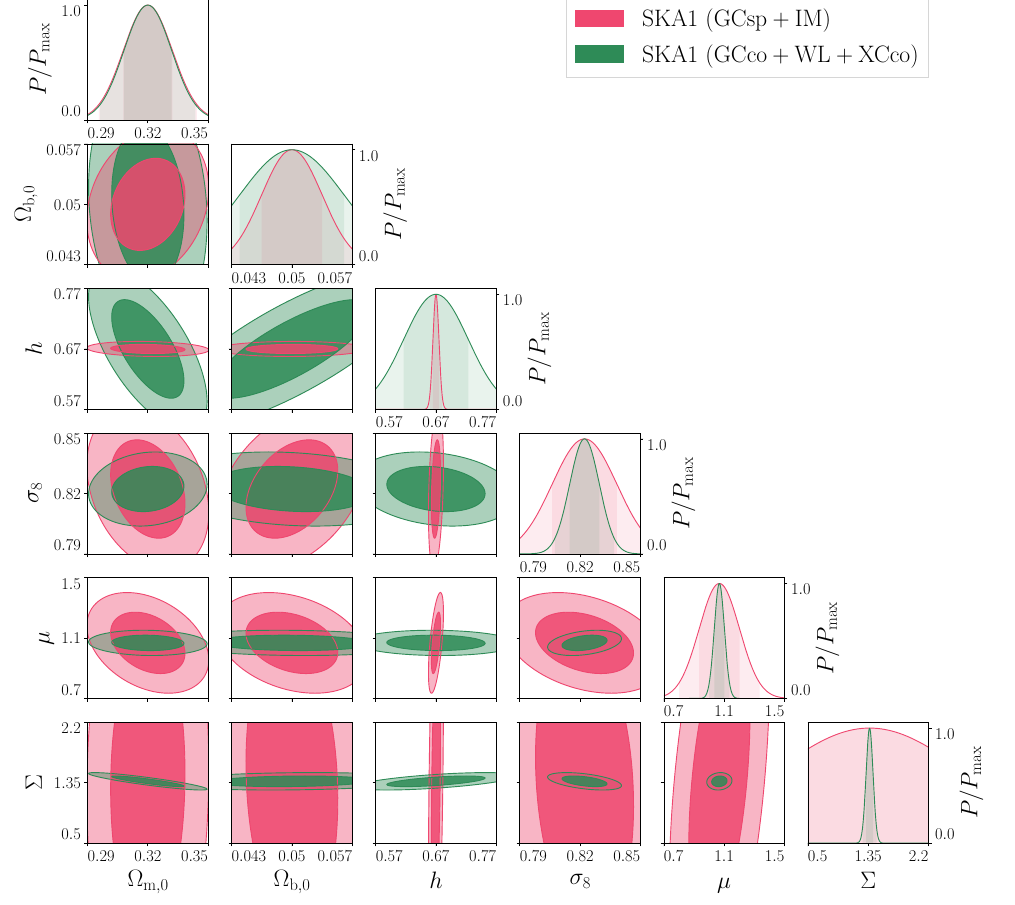
SKA1 Results
SKA1:
GCsp (HI galaxies)+IM (HI 21cm)
vs.
GC+WL+XC (Continuum)
- The combination of WL and angular galaxy correlations, (3x2pt) is very good at constraining \(\Sigma\) as expected, but not so good in \(h\), which is constrained by the Pk probes.
PRELIMINARY

Santiago Casas, 15.04.21

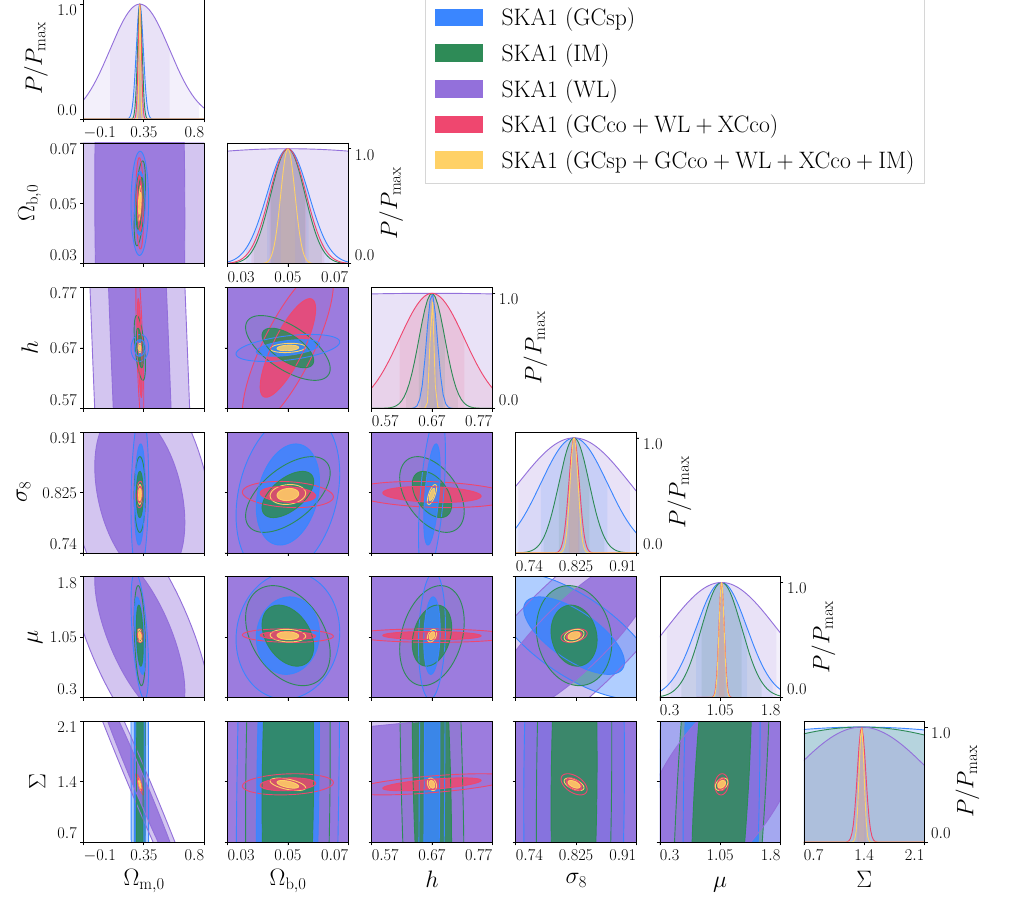
SKA1 Results
SKA1:
GCsp (HI galaxies) +
GC+WL+XC (Continuum)
+ IM (HI 21cm)
-
HI galaxies at small z, IM at higher z and angular resolution of continuum galaxies provide good complementary constraints.
PRELIMINARY

Santiago Casas, 15.04.21

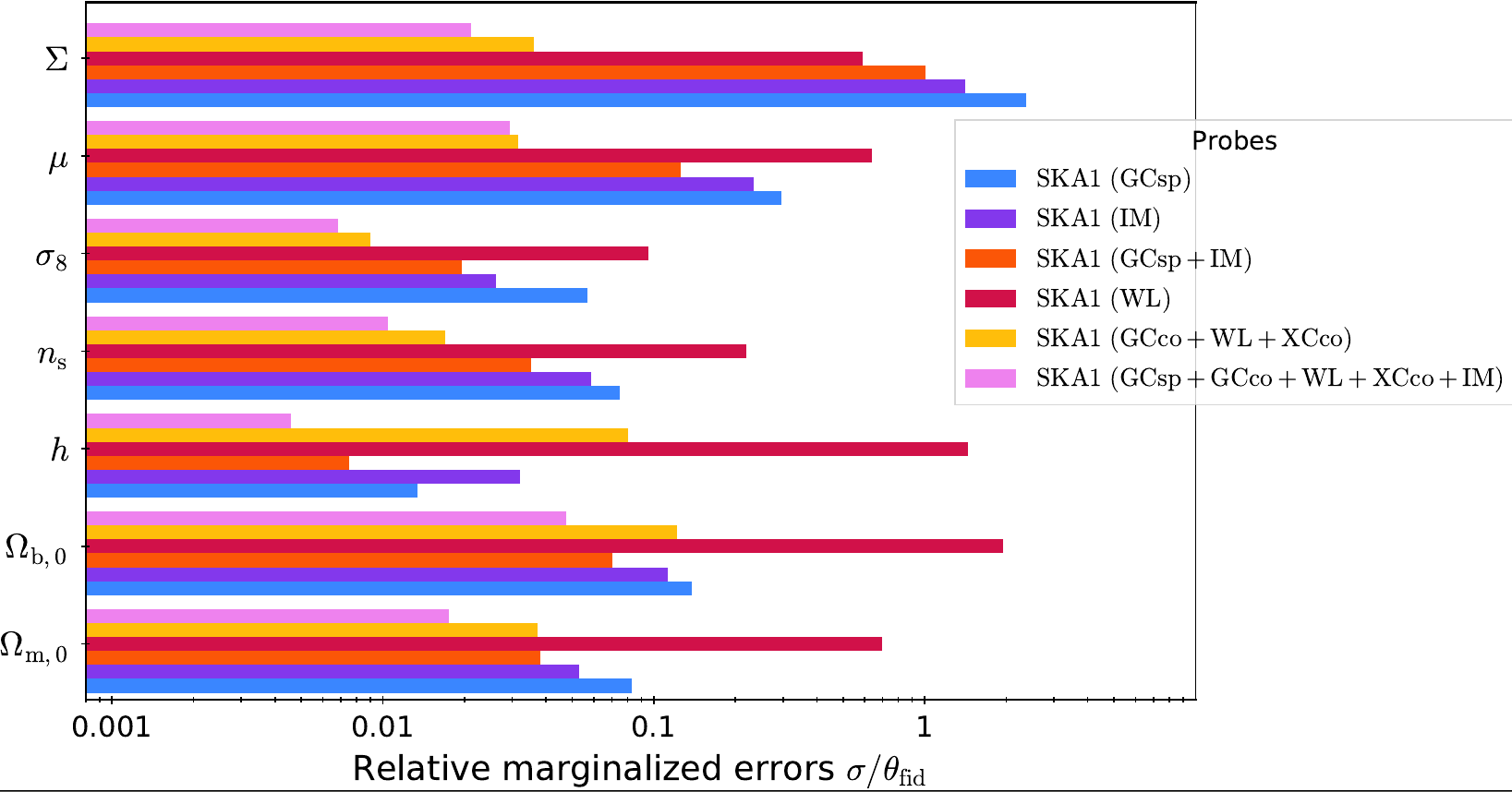
SKA1 Results
SKA1:
GCsp (HI galaxies) , GC+WL+XC (Continuum), + IM (HI 21cm)
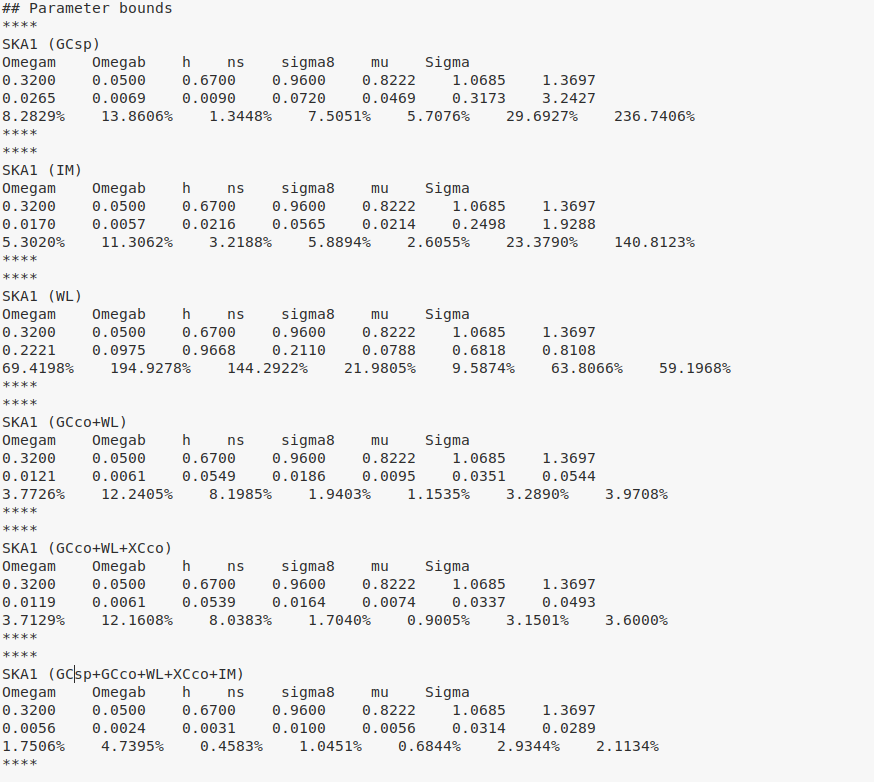
Combined constraints on \(\mu\)-\(\Sigma\) ~ 3%
PRELIMINARY

Santiago Casas, 15.04.21

SKA1 Results
SKA1:
GC+WL+XC (Continuum) +
IM (HI 21cm) + GCsp(HI)
and Planck'15
- Planck provides information on \(\Omega_{b}, \, \Omega_{m}\) but also on the MG parameter \(\Sigma\).
- In the \(\mu\)-\(\Sigma\) plane it complements very well with the IM constraints
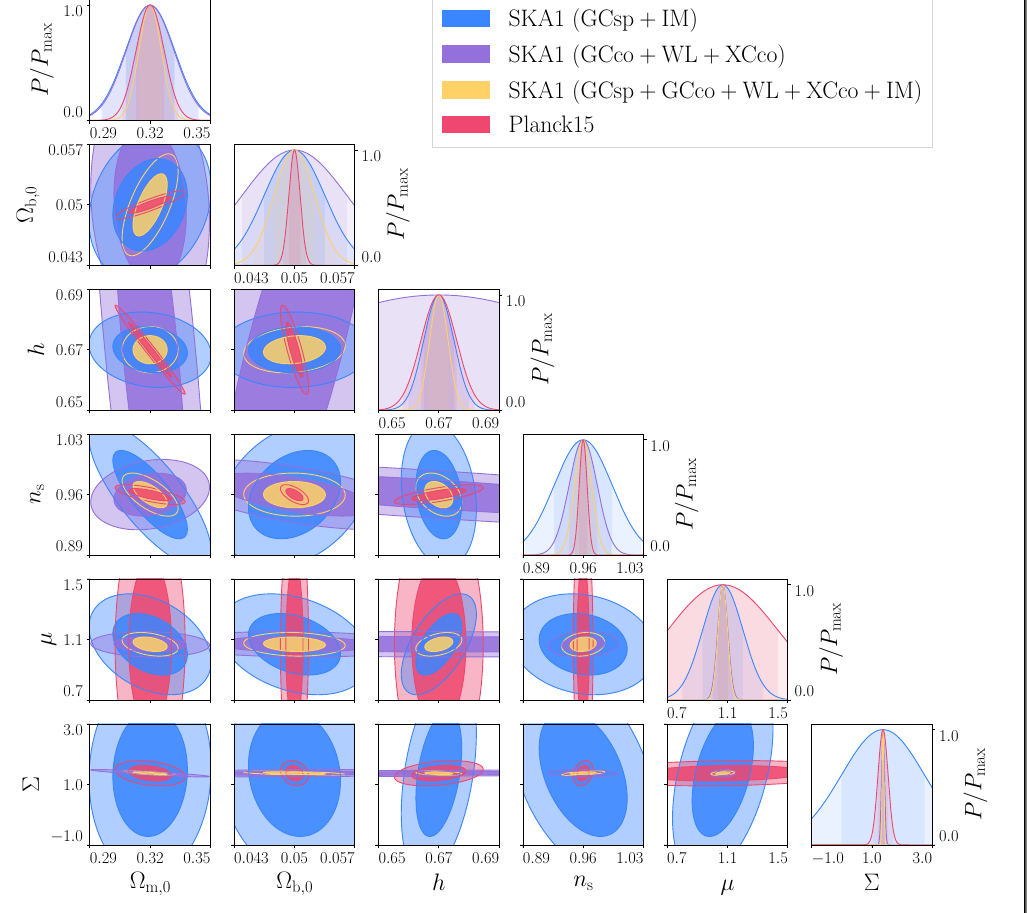
PRELIMINARY

Santiago Casas, 15.04.21

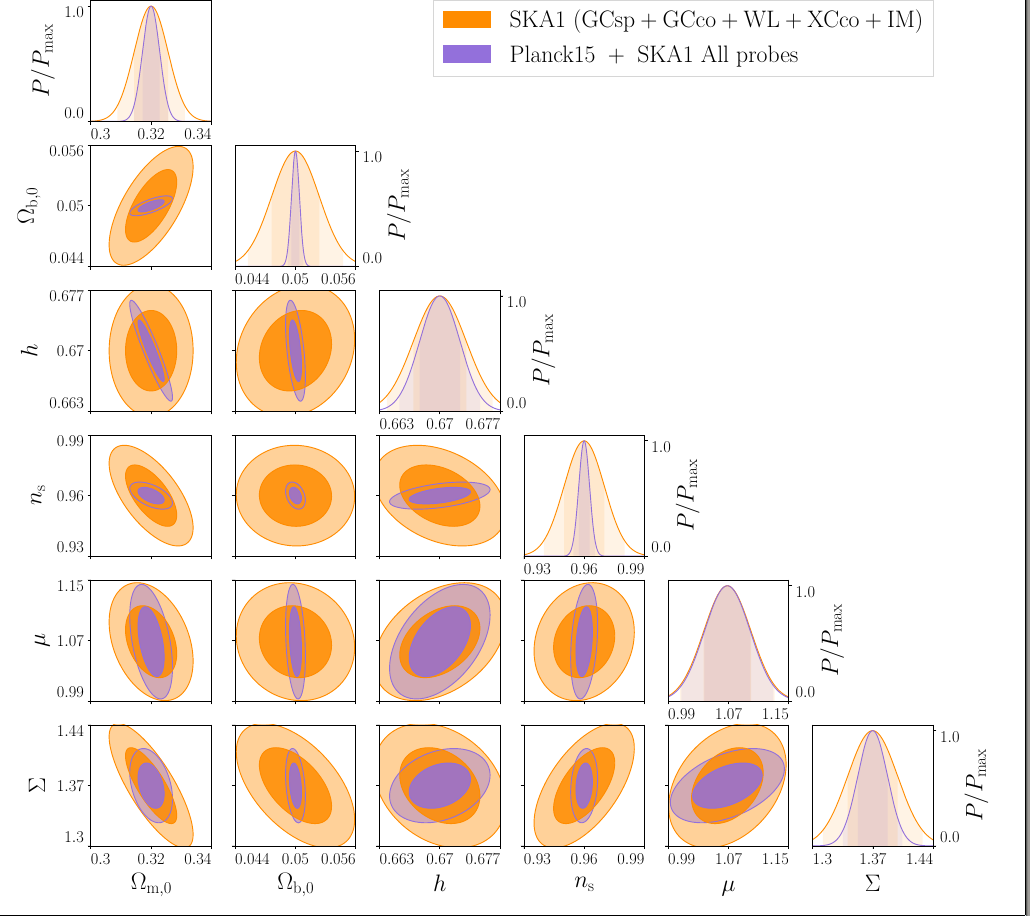
SKA1 Results
SKA1:
GC+WL+XC (Continuum) +
IM (HI 21cm) + GCsp(HI)
+ Planck'15
- Planck provides information on \(\Omega_{b}, \, \Omega_{m}\) but also on the MG parameter \(\Sigma\).
- In the \(\mu\)-\(\Sigma\) plane it complements very well with the IM constraints.
- Combined constraints on \(\Sigma\) ~ 1.5%
PRELIMINARY

Santiago Casas, 15.04.21

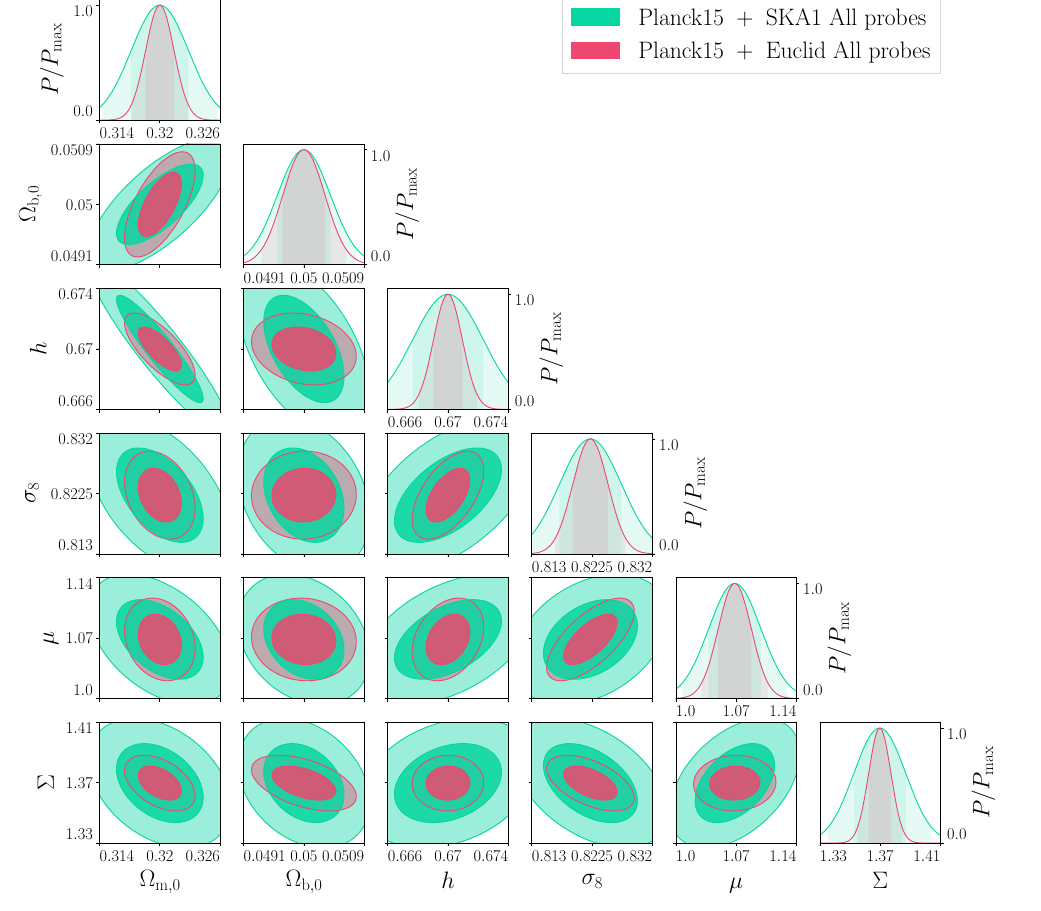
SKA1 vs Euclid and Planck
SKA1-All+Planck:
\(\sigma\)[\(\mu\)-\(\Sigma\)] ~ [3, 1.5]%
Euclid-All+Planck:
\(\sigma\)[\(\mu\)-\(\Sigma\)] ~ [1.8, 0.5]%
*Optimistic scenario
PRELIMINARY

Santiago Casas, 15.04.21

Bonus: w0waCDM
PRELIMINARY
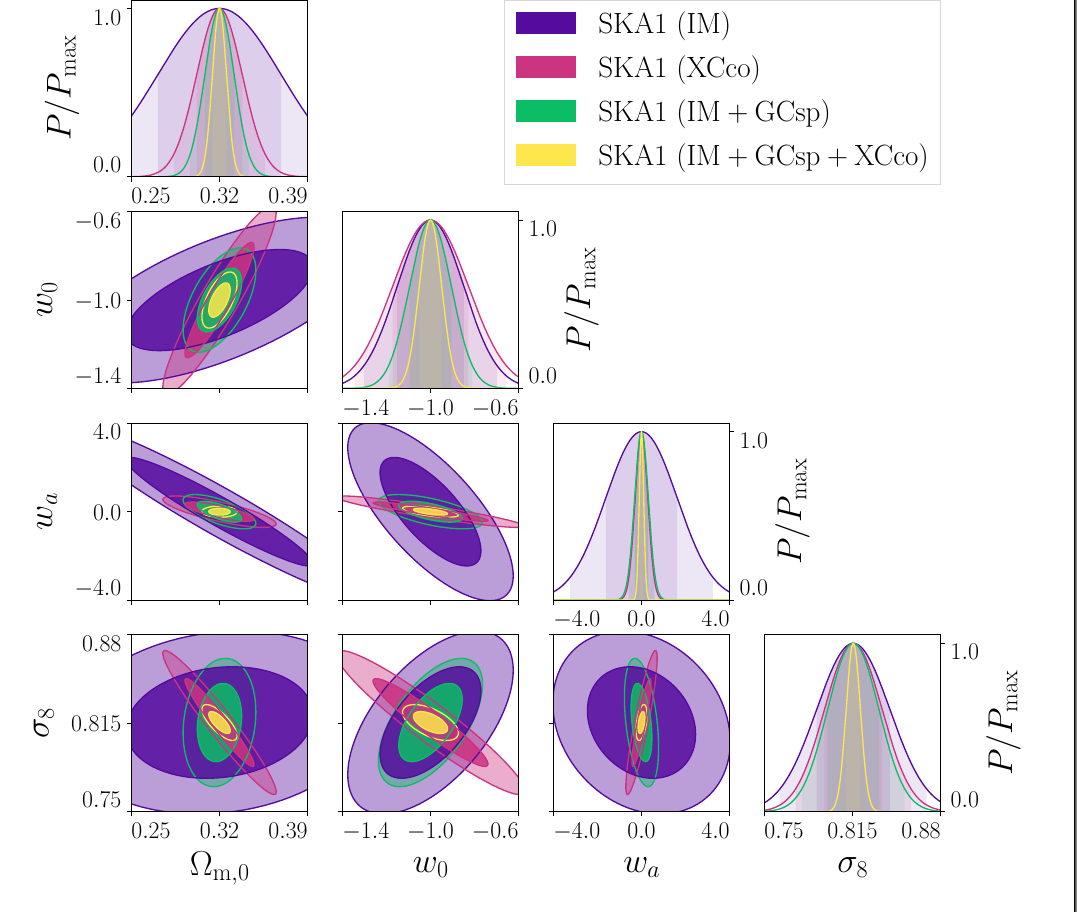
SKA1:
GC+WL+XC (Continuum) +
IM (HI 21cm) + GCsp(HI)
- Some updated constraints on LCDM and w0waCDM, since all combinations cannot be found on the redbook.
- Preliminary numbers:
- \(\sigma(w_0)\approx 0.05,\sigma(w_a) \approx 0.1 \)

Santiago Casas, 15.04.21

Text
Conclusions
- \(\Lambda\)CDM is still the best fit to observations, however certain theoretical uncertainties and tensions in data are still of concern.
- Constraining modifications of gravity at the level of perturbations -> hints for alternative models.
- SKA1 will be able to probe weak lensing and matter density perturbations in novel and independent ways compared to optical surveys.
- This will place constraints on deviations of standard gravity at yet unexplored redshifts.
- Synergies with optical surveys, like Euclid, including cross-correlations are promising (work in progress).
- Using the good z-resolution of SKA1 HI could place tight constraints on redshift-binned parametrizations.

Santiago Casas, 15.04.21

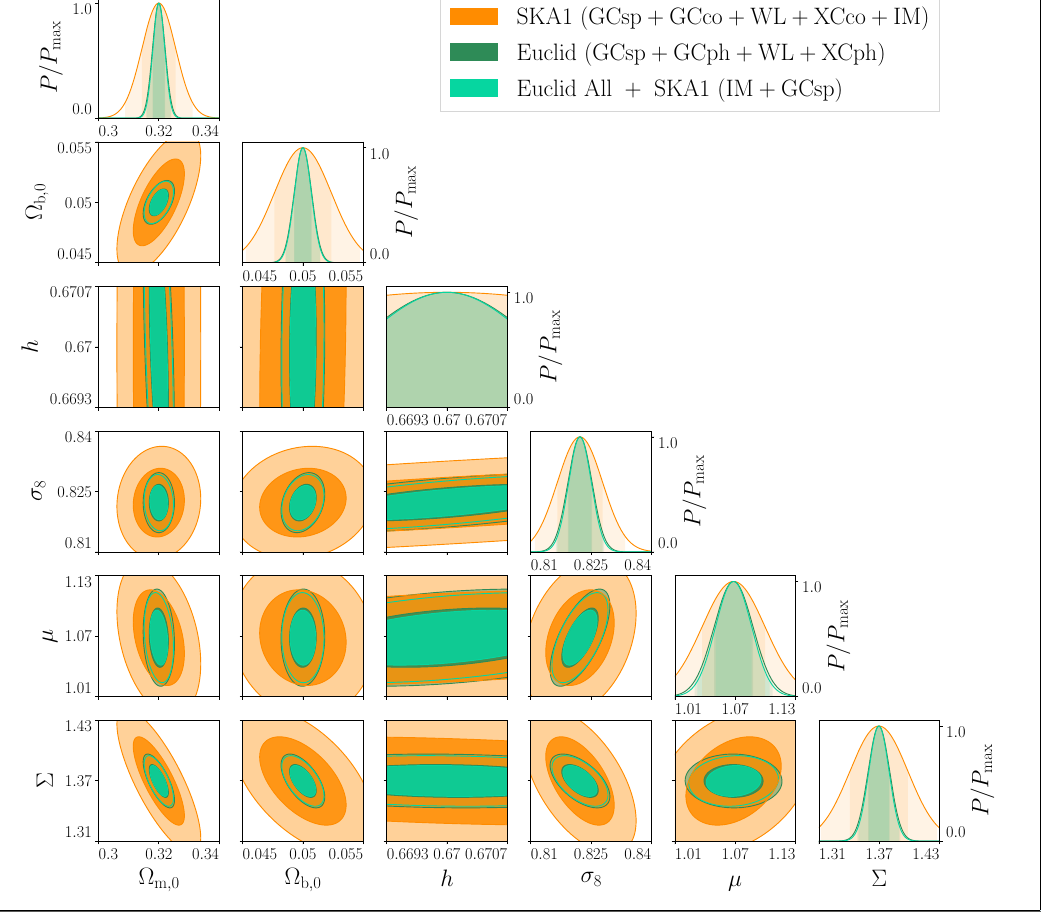
SKA1 vs Euclid
SKA1:
GC+WL+XC (Continuum) +
IM (HI 21cm) + GCsp(HI)
vs
Euclid
(Gcsp+GCph+WL+XCph)
vs
Euclid
(Gcsp+GCph+WL+XCph)+SKA1 Pk-probes.
Unfortunately, the \(\mu\) constraints from Euclid alone dominate over the improvement that SKA1 "Pk-probes" add
PRELIMINARY
Backup slide
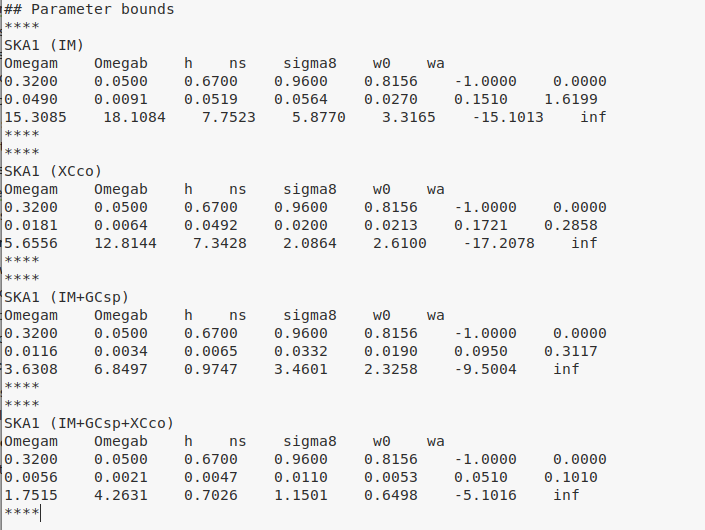
Backup slide

Backup slide

Backup slide

Backup slide

Backup slide