Relevancy of
Functional programming

paradigms in Real World

Sathish Kumar

Flipkart Ads Team

Outline

  • Imperative vs Functional programming (FP)
  • Functional programming (FP) in Software Industry
  • Functional programming (FP) in Flipkart Ads systems
  • Ads Problem statements
    • Functional solutions
    • Java 8 vs Haskell
    • Abstractions - Lambdas, Functors, Monads

Imperative/OO programming

Double calculateTotalCashback(Order order){
    Double totalCashback = 0.0;
    for (OrderItem orderItem : order.getOrderItems()) {
        if(orderItem.hasOffer() && 
            orderItem.getOffer().getCashback() > 0.0) {
                totalCashback += orderItem.getOffer().getCashback();
        }
    }
    return totalCashback;
}

Mutable State

Reasoning about code - How vs What

Lock based concurrency

Functional programming

Quick Sort in Haskell

qsort [] = []
qsort (x:xs) = qsort small ++ [x] ++ qsort large
  where small = [y | y <- xs, y <= x]
        large = [y | y <- xs, y > x]

No side effects (or) state changes

Type safety and Type inference

Immutable data - Multicore concurrency

Pivot

Larger than Pivot

Smaller than Pivot

Functional programming

Infinite Fibonacci in Lisp

Lazy evaluation

Functions are composable

(define (fib a b)
  (cons-stream a (fib b (+ a b))))

(take 10 (filter isEven fib))

Infinite recursion

Higher order functions

FP in Academia - 1990

Why functional programming matters - John Hughes

http://www.cse.chalmers.se/~rjmh/Papers/whyfp.pdf

FP in Industry

2010

2011

Twitter uses Scala for backend services

https://blog.twitter.com/2011/finagle-a-protocol-agnostic-rpc-system

FP in Industry

2012

Haskell at Standard Chartered

http://code.haskell.org/~dons/talks/padl-keynote-2012-01-24.pdf

2014

Ocaml at Jane Street

https://www.infoq.com/presentations/jane-street-caml-ocaml     

Wall street's secret sauce

FP in Industry

2014

WhatsApp: Scaling to Billions of messages in Erlang

https://www.infoq.com/presentations/whatsapp-scalability

FP in Industry

2015

Facebook: Fighting Spam with Haskell

https://code.facebook.com/posts/745068642270222/fighting-spam-with-haskell/

FP in Industry

  • Lambdas
  • First class functions
  • Higher order functions
  • Streams
  • Optional
  • Function composition

2014

Java 8: Functional features

FP in Industry

Functional style

No matter what language you work in, programming in a functional style provides benefits. You should do it whenever it is convenient, and you should think hard about the decision when it isn't convenient"

- John Carmack (Creator of Quake, Doom, Wolf)

https://youtu.be/1PhArSujR_A

Flow of ideas

Imperative / OOP

Functional 

Math

Java

Python/Ruby

Javascript

Scala

Lisp

Haskell

Lambda Calculus

Category Theory

A language that doesn't affect the way you think about programming, is not worth knowing."

- Alan J. Perlis

Ads Serving

App

Desktop

Exchange

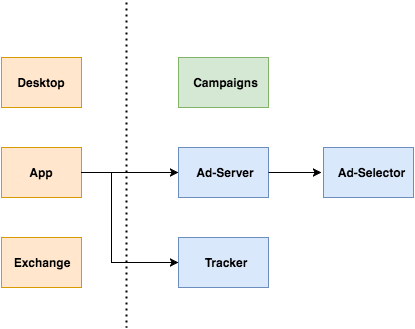
Ads Serving Stack

Campaign Impressions Clicks
101 100,000 1000
102 200,000 2000

Ad Selection flow

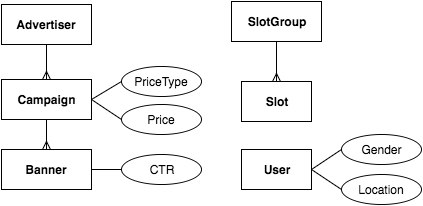
Data Model

Conventions

Functional concept

# foo

foo :: String -> String
foo x = "Hello " ++ x
public String foo(String name){
    return "Hello " + name;
}

Haskell code example

Java code example

Data Model

# Type

# Type alias

type Price = Double
type CTR = Double
data PriceType = CPM | CPV | CPC

type Id = Int
type Score = Double

data Advertiser = Advertiser Id
data Campaign = Campaign Id Advertiser PriceType Price
data Banner = Banner Id Campaign
data Slot = Slot Id
data User = UnknownUser | User Id 


data SlotGroup = SlotGroup Id [Slot]

Campaign, Banner attrs

Advertiser, Campaign, Banner

Slot, User

   constructors

Relevance - Campaigns

1. Active

2. Gender targeting

Relevance - Campaigns

relevantCampaigns :: Context -> Map[Slot, [Campaign]]

1. Active

2. Gender targeting

isActive = \campaign -> isActive campaign
isGenderTargeted = \campaign, context ->
  case (getGender campaign) of
    Nothing -> True
    Just (gender) -> gender == getGender (getUser context)

# Type signature

# Lambdas

Predicate<Campaign> isActive = campaign -> campaign.isActive();

Predicate<Campaign> isGenderTargeted(Context context) {
    return campaign -> context.getUser()
            .map(gender -> gender.equals(campaign.getGender()))
            .orElse(true);
}

# Predicate

Relevance - Campaigns

List<Campaign> getRelevantCampaigns(Context context){
    return campaignStore.getAll().stream()
        .filter(isActive())
        .filter(isGenderTargeted(context))
        .collect(toList());
}

Combining predicates - AND

# Streams

# Filter

Relevance - Campaigns

Combining predicates - AND

# Function

Predicate<Campaign> getRelevanceFilters(Context context){
    return isActive()
            .and(isGenderTargeted(context))
            .and(isFrequencyCapped(context));
}

Adding a new relevance rule is

as simple as adding a predicate

  composition

Relevance - Banners

1. Matches template

2. Matches width and height

Relevance - Banners

relevantBanners :: Map[Slot, [Campaign]] -> Map[Slot, [Banner]]

1. Matches template

Predicate<Banner> forTemplate(Context context){
    return banner -> banner.getTemplate().equals(context.getTemplate());
}

2. Matches width and height

Predicate<Banner> forDimension(Context context){
    return banner -> banner.getWidth().equals(context.getWidth()) &&
                        banner.getHeight().equals(context.getHeight());
}
Predicate<Banner> getFilters(Context context){
    return forTemplate(context)
            .or(forDimension(context));
}

List<Banner> getRelevantBanners(Context context, List<Campaign> campaigns){
    return bannerStore.getAll(campaigns).stream()
        .filter(getFilters(context))
        .collect(toList());
}

Relevance - Banners

Combining predicates - OR

[1,2,3] ++ [] == [1,2,3]
[1,2] ++ ([3,4] ++ [5,6]) == ([1,2] ++ [3,4]) ++ [5,6]

[] ++ [1,2,3] == [1,2,3]

List

Sum

5 + 0 == 5
(1 + 2) + 3 == 1 + (2 + 3)

0 + 5 == 5

Product

5 * 1 == 5
(1 * 2) * 3 == 1 * (2 * 3)

1 * 5 == 5

False && True == False
(True && True) && False == True && (True && False)

True && False == False

Boolean AND

True || False == True
(True || True) || False == True || (True || False)

False || True == True

Boolean OR

All of these are binary operations with Identity and Associativity

Monoid is an abstraction of this common pattern

Detour: Monoid

# Monoid

Detour: Monoid

Any

mconcat [Any False, Any False] == Any False
mconcat [Any False, Any True] == Any True

All

mconcat [All True, All False] == All False
mconcat [All True, All True] == All True

Monoid: if you define identity and append, you get concat for free

isRelevant campaign = mconcat (map (\f -> f campaign) filters)
isRelevant banner = mconcat (map (\f -> f banner) filters)

With these abstractions, Relevance simplifies to:

Ranking

1. Score banners by criteria

2. Sort banners by score

1. Samsung (score: 0.85)

2. Sony (score: 0.75)

3. BPL (score: 0.65)

Ranking

rankBanners :: Map[Slot, [Banner]] -> Map[Slot, [BannerScore]]

1. Score banners by criteria

2. Sort banners by score

What is the common pattern here?

relevantBanners :: Map[Slot, [Campaign]] -> Map[Slot, [Banner]]

rankBanners :: Map[Slot, [Banner]] -> Map[Slot, [BannerScore]] 

Map<K, B> mapValues(Map<K, A> input, Function<A, B> transformer) {
    return input.keySet().stream()
            .collect(toMap(Function.identity(), transformer));
}

# Higher order

Ranking

functions

Ranking

mapValues(relevantBanners, bannerScorer())


public Map<Slot, List<BannerScore>> rankBanners(Map[Slot, List[Banner]] relevantBanners){
  return mapValues(relevantBanners, scorer());
}

Function<Slot, List<BannerScore>> bannerScorer(){
    return slot -> {
        List<Price> prices = getPrices(banners);
        List<CTR> ctrs = getCTRs(banners);
        return StreamUtils.zip(
                    prices.stream(),
                    ctrs.stream(),
                    (price, ctr) -> calculate(price, ctr))
                .collect(toList());
    }
}

mapValues takes function as argument

bannerScorer returns function as output

# First class

   functions

# zip

CTR Prediction Model

1. CTR: Click Through Rate

2. Logistic Regression Model

3. Input: Supply, Demand, User features

4. Output: Predicted CTR

z=\theta_{0} + \theta_{1} * x_{1} + \theta_{2} * x_{2} ... + \theta_{n} * x_{n}
z=θ0+θ1∗x1+θ2∗x2...+θn∗xnz=\theta_{0} + \theta_{1} * x_{1} + \theta_{2} * x_{2} ... + \theta_{n} * x_{n}
pCTR = \frac{1}{1+e^{-z}}
pCTR=11+e−zpCTR = \frac{1}{1+e^{-z}}

n features

θi - Model coefficients

Xi - Boolean value of features 

CTR Prediction Model

Features

1. Slot : slot:123 (0.001) or slot:default (-0.005)

2. Campaign : campaign:123 (0.002) or campaign:default (-0.005)

3. Gender : gender:male (0.003) or gender:female (0.003) or gender:default (-0.005)

4. Stores : store:books (0.004), store:mobiles (0.005), store:default (-0.005)

z = - 5.0 + 0.001 + 0.002 + 0.003 - 0.005

pCTR = 0.7%

CTR Prediction Model

# Optional

# Null safety

Feature genderFeature = context.getUser().getGender()
    .map(value -> new Feature("gender:" + value))
    .orElse(new Feature("gender:default"))

Single valued features

Optional [Gender]

1. user.gender is present - Just [Gender] - map

 

 

2. user.gender is null - Nothing - orElse

 

 

Detour: Functors

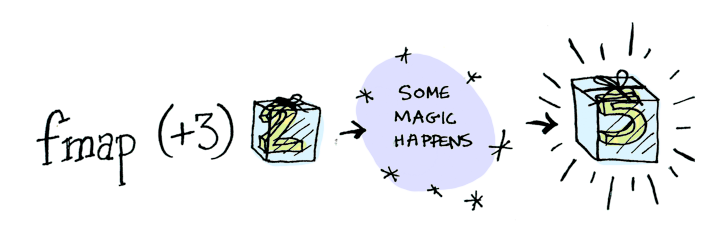
* http://adit.io/posts/2013-04-17-functors,_applicatives,_and_monads_in_pictures.html

Functors apply a function to a value in a box

*

# Functors

value -> new Feature("gender:" + value)

Gender

Feature

getGender() :: Maybe[Gender]

Optional[Gender]

"gender:female"

Feature

map

Java 8 Optional is a functor

Feature genderFeature = context.getUser()
    .flatMap(user -> user.getGender())
    .map(value -> new Feature("gender:" + value))
    .orElse(new Feature("gender:default"))

1. Optional [User]

user is present: flatMap

user is null: orElse

 

2. Optional [Gender]

user.gender is present: map

user.gender is null: orElse

 

 

# flatMap

CTR Prediction Model

# Monads

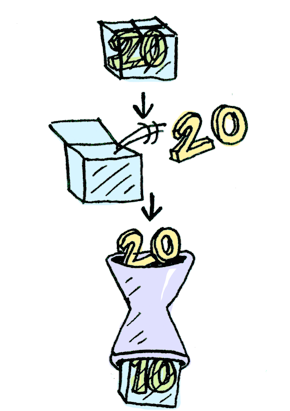
* http://adit.io/posts/2013-04-17-functors,_applicatives,_and_monads_in_pictures.html

*

Monads apply a value in a box to a function that returns a value in a box

Detour : Maybe Monad

half()

map on Optional

flatMap on Optional

value -> new Feature("gender:" + value)

Gender

Feature

getGender() :: Maybe[Gender]

Optional[Gender]

"gender:female"

Feature

map

user -> user.getGender()

User

Optional[Gender]

getUser() :: Maybe[User]

Optional[User]

Optional[Gender]

flatMap

Java 8 Optional is a monad

Deduplication

1. Serve unique ads across multiple slots

2. Uniqueness can be by advertiser or campaign or banner

 

Dedup options:

1. None 2. By Advertiser 3. By Campaign 4. By Banner

dedupCriteria = Nothing
dedupCriteria = Just (\banner -> (advertiser (campaign banner)))
dedupCriteria = Just (\banner -> (campaign banner))
dedupCriteria = Just (\banner -> banner)
dedupBanners :: Map[Slot, [BannerScore]] -> Map[Slot, Maybe[Banner]]

Deduplication

Workflow

# Function composition

Workflow is just function composition

compose :: (b -> c) -> (a -> b) -> a -> c
relevantCampaigns :: Context -> [Campaign]
relevantBanners :: [Campaign] -> [Banner]
rankBanners :: [Banner] -> [BannerScore]
dedupBanners :: [BannerScore] -> Maybe[Banner]
selectAds :: Context -> Maybe[Banner]
selectAds = dedupBanners . rankBanners . relevantBanners . relevantCampaigns

Summary

  • Immutability
  • Elegant and Expressive
  • Reusability - Lambdas, Higher order functions
  • Null safe code using Optional
  • Functors, Monads - Function application patterns
  • Functional languages change the way you think about programming

Questions?

Made with Slides.com