Understanding Python's DataStructure: Dictionary
Sayan Chowdhury
@chowdhury_sayan
The Dictionary
>>> d = {
... 'Fedora': 21,
... 3.1415: 'pi',
... 9 : 'Planets',
... (1, 4, 17): 'Django version',
...}
keys can be anything.
A dictionary is really a list
>>> # An empty dictionary is an 8-element list!
>>> d = {}
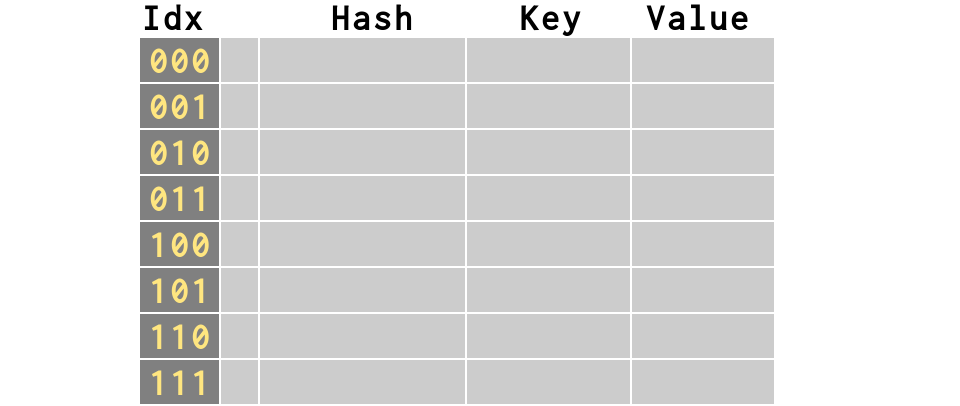
>>> # This actually creates a `hash table`
>>> # containing `slots`

Keys are hashed to produce indexes
How the hashing is done?
Python uses the built-in hash() function.
Let's hash some keys now!
>>> def bits(n):
... n += 2**32
... return bin(n)[-32:] # remove '0b'
...
>>> print bits(1)
00000000000000000000000000000001
>>> print bits(-1)
11111111111111111111111111111111
>>> for key in 'Monty', 3.1415, (1, 4, 17): ... print bits(hash(key)), key 10011000011001101001001100000010 Monty 01101010101011010000100100000010 3.1415 11000111101010001110010110011011 (1, 4, 17)
>>> k1 = bits(hash('Monty')) >>> k2 = bits(hash('Money')) >>> diff = ('^ '[a==b] for a,b in zip(k1, k2)) >>> print k1; print k2; print ''.join(diff) 10011000011001101001001100000010 10011001010010110111010100010111 ^ ^ ^^ ^^^^ ^^ ^ ^ ^
Even minor change in value can lead to drastic change in hashed value
Same value returns the same hash
for key in 3.1415, 3.1415, 3.1415:
... print bits(hash(key)), key
01101010101011010000100100000010 3.1415
01101010101011010000100100000010 3.1415
01101010101011010000100100000010 3.1415
Now, let me show something interesting!
>>> for key in 9, 9.0, complex(9):
... print bits(hash(key)), key
00000000000000000000000000001001 9
00000000000000000000000000001001 9.0
00000000000000000000000000001001 (9+0j)
Keys <===> Indexes
#1. Keys are hashed.
#2. To build an index, Python uses the bottom
n bits of the hash
>>> d['ftp'] = 21
>>> b = bits(hash('ftp'))
>>> print b
11010010011111111001001010100001
>>> print b[-3:] # last 3 bits = 8 combinations
001

>>> d['ssh'] = 22
>>> print bits(hash('ssh'))[-3:]
101

>>> d['ssh'] = 22
>>> print bits(hash('ssh'))[-3:]
101
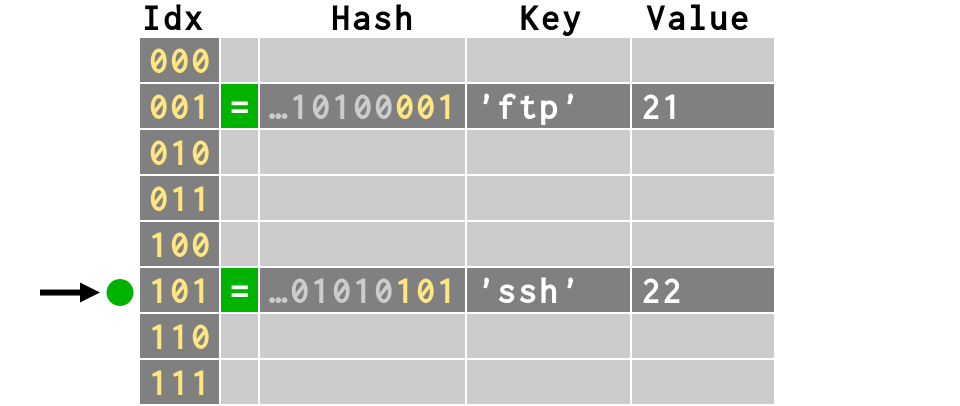
>>> d['smtp'] = 25
>>> print bits(hash('smtp'))[-3:]
100
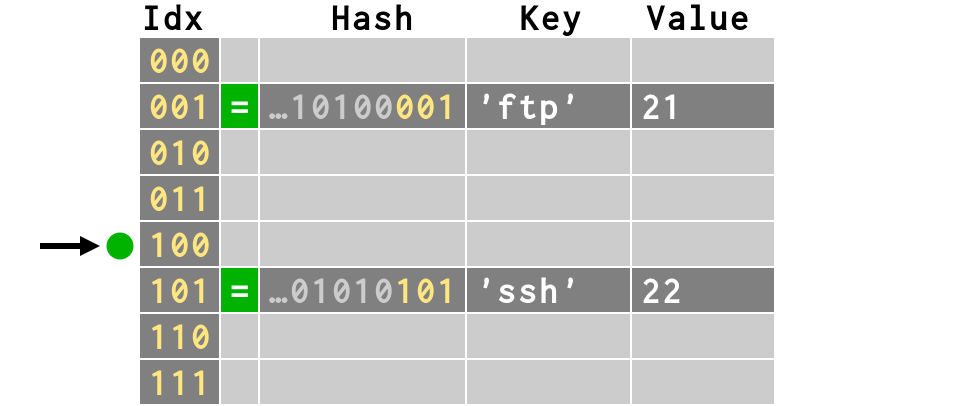
>>> d['smtp'] = 25
>>> print bits(hash('smtp'))[-3:]
100

>>> d['time'] = 37
>>> print bits(hash('time'))[-3:]
111

>>> d['time'] = 37
>>> print bits(hash('time'))[-3:]
111

>>> d['www'] = 80
>>> print bits(hash('www'))[-3:]
010

>>> d['www'] = 80
>>> print bits(hash('www'))[-3:]
010

d = {'ftp': 21, 'ssh': 22,
'smtp': 25, 'time': 37,
'www': 80}

Lookup?
-
compute hash
-
get the index using `i` bits
-
search in the hash table
>>> print d['smtp'] 25 >>> print bits(hash('smtp'))[-3:] 100
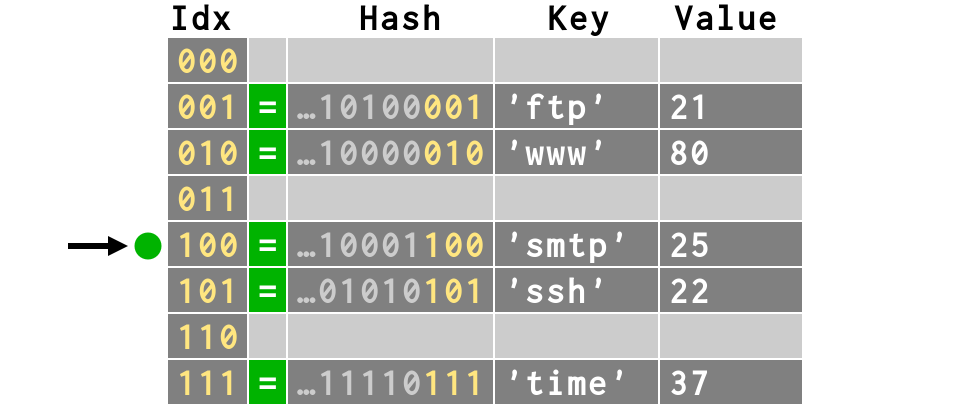
Ever noticed the crazy order of a dictionary ?
>>> # Different than our insertion order:
>>> print d
{'ftp': 21, 'www': 80, 'smtp': 25, 'ssh': 22,
'time': 37}
>>> # But same order as in the hash table!

>>> # keys and values also in table order
>>> d.keys()
['ftp', 'www', 'smtp', 'ssh', 'time']
>>> d.values()
[21, 80, 25, 22, 37]

Collision
What happens when two keys need the same slot?
>>> # start over with a new dictionary
>>> d = {}
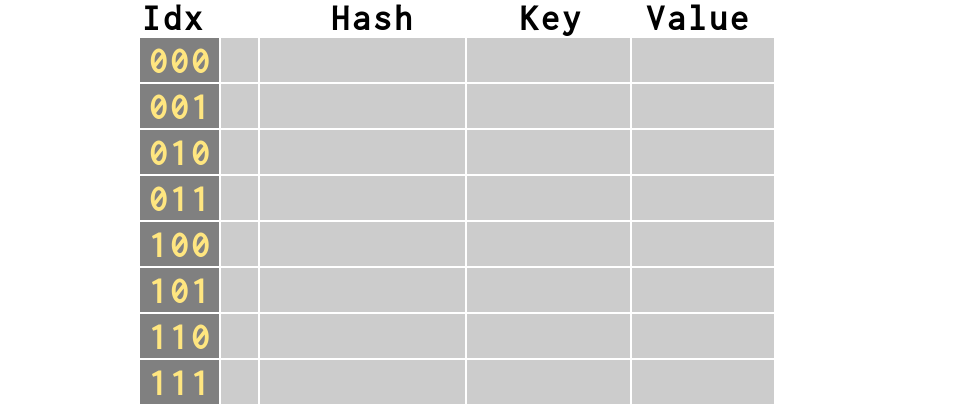
>>> # first item inserts fine
>>> d['smtp'] = 21
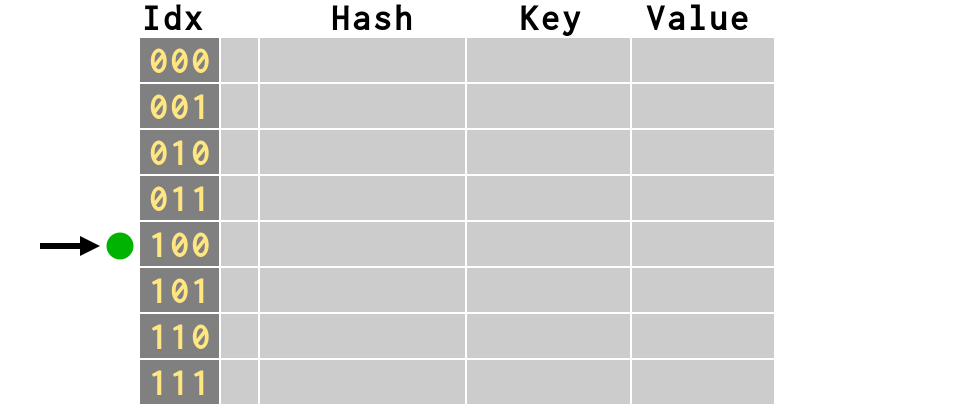
>>> # first item inserts fine
>>> d['smtp'] = 21
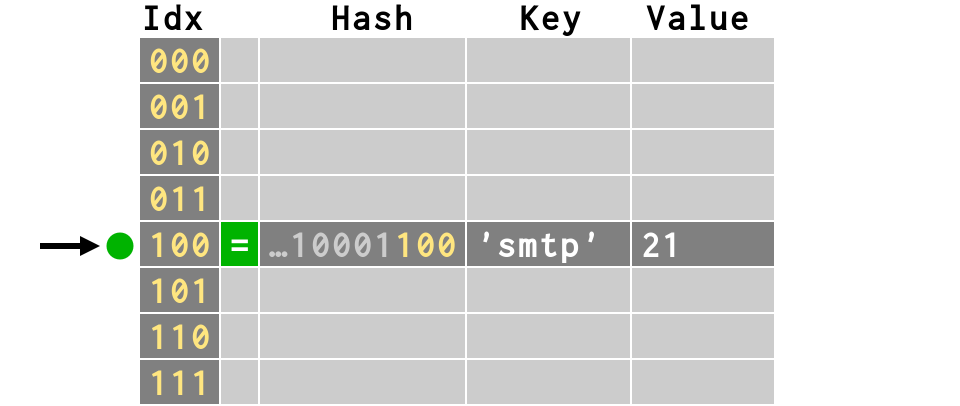
>>> # second item collides! >>> d['dict'] = 2628
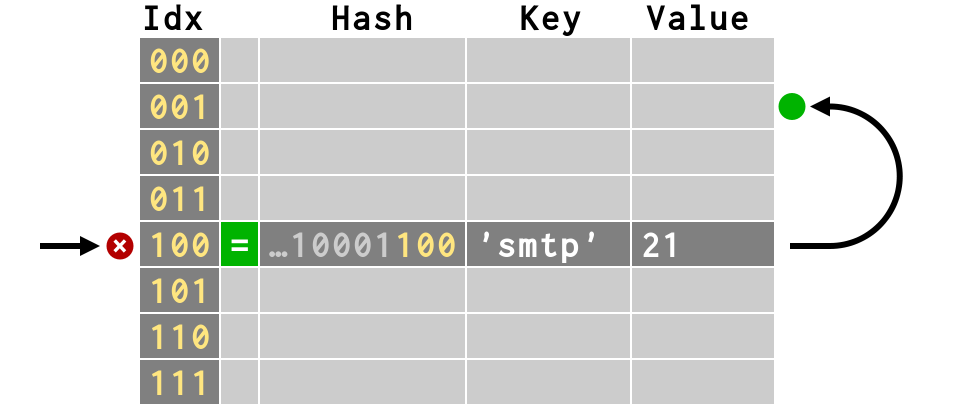
>>> # second item collides!
>>> d['dict'] = 2628
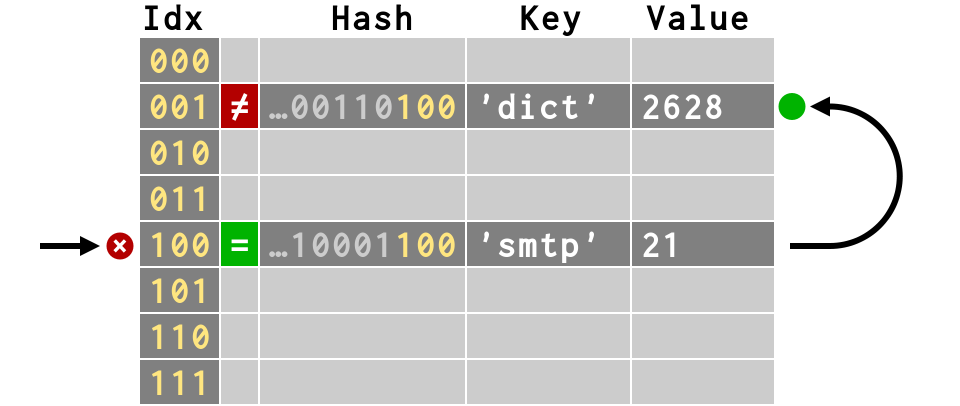
>>> # third item also finds empty slot
>>> d['svn'] = 3690
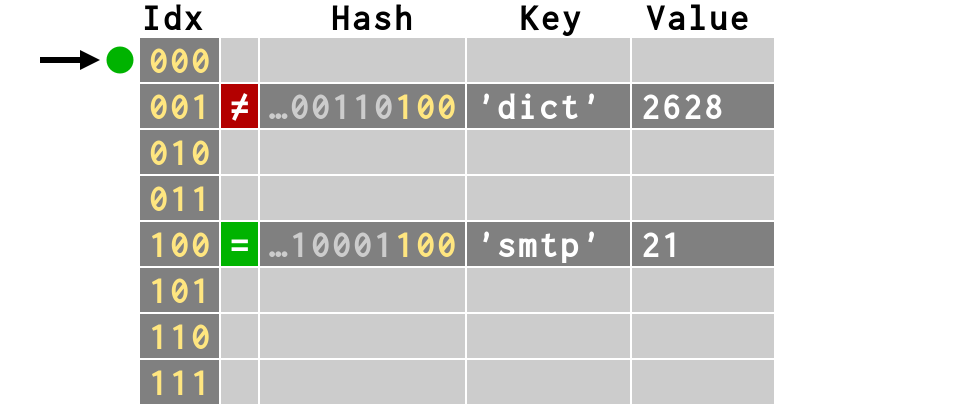
>>> # third item also finds empty slot
>>> d['svn'] = 3690
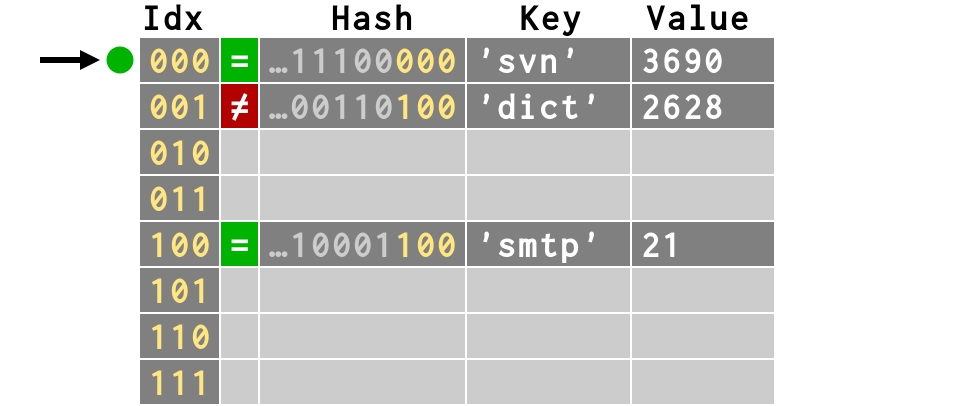
>>> # fourth item has multiple collisions
>>> d['ircd'] = 6667

>>> # fifth item collides, but less deeply
>>> d['zope'] = 9673

>>> # fifth item collides, but less deeply
>>> d['zope'] = 9673

>>> # fifth item collides, but less deeply
>>> d['zope'] = 9673

Because collisions move keys
away from their natural hash values,
key order is quite sensitive
to dictionary history
>>> d = {'smtp': 21, 'dict': 2628,
... 'svn': 3690, 'ircd': 6667, 'zope': 9673}
>>> d.keys()
['svn', 'dict', 'zope', 'smtp', 'ircd']

>>> e = {'ircd': 6667, 'zope': 9673,
... 'smtp': 21, 'dict': 2628, 'svn': 3690}
>>> e.keys()
['ircd', 'zope', 'smtp', 'svn', 'dict']

We are same yet so different!
>>> d == e
True
>>> d.keys()
['svn', 'dict', 'zope', 'smtp', 'ircd']
>>> e.keys()
['ircd', 'zope', 'smtp', 'svn', 'dict']
These dictionaries are same,
yet different by the order of keys in hash table.
>>> # Successful lookup, length 1
>>> # Compares HASHES then compares VALUES
>>> d['svn']
3690

>>> # Successful lookup, length 1
>>> # Compares HASHES then compares VALUES
>>> d['svn']
3690

>>> # Successful lookup, length 4
>>> d['ircd']
6667

>>> # Unsuccessful lookup, length 1
>>> d['nsca']
Traceback (most recent call last):
...
KeyError: 'nsca'

>>> # Unsuccessful lookup, length 4
>>> d['netstat']
Traceback (most recent call last):
...
KeyError: 'netstat'

Remember, lookups are costly !
Not all lookups are created equal.
Some finish at their first slot
Some loop over several slots
threes = {
3: 1, 3+8: 2, 3+16: 3,
3+24: 4, 3+32: 5
}

# Thanks to piling collisions atop each
# other, we can make lookup more expensive
timeit('d[3]', 'd=%r' % threes) # -> 0.078
timeit('d[3+32]', 'd=%r' % threes) # -> 0.082


An interesting consequence!
what happens to lookups when we delete keys?
del d['smtp']
# Can we simply make its slot empty?

del d['smtp']
# But what would happen to d['ircd']?

When a key is deleted, its slot cannot simply
be marked as empty
Otherwise, lookups for any keys that collided would be now be impossible to find!
So we create a <dummy> key instead
>>> # Creates a <dummy> slot that
>>> # can be re-used as storage
>>> del d['smtp']

>>> # That way, we can still find d['ircd']
>>> d['ircd']
6667

>>> del d['svn'], d['dict'], d['zope']
>>> d['ircd']
6667
>>> # Still requires 4 steps!
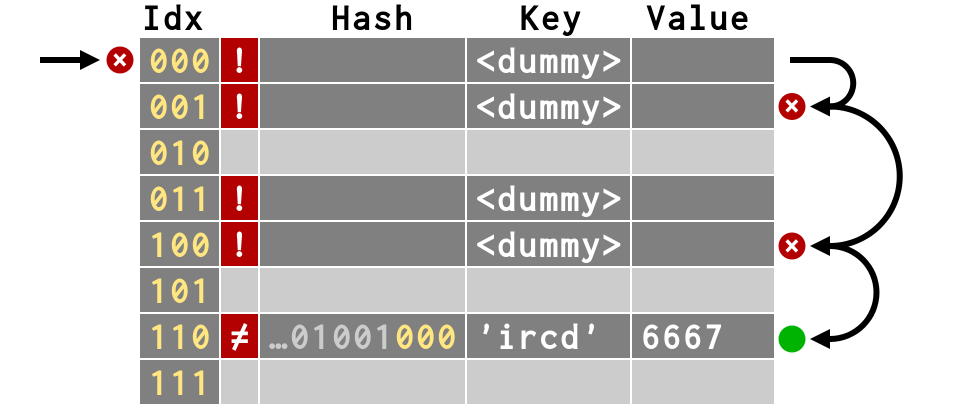
Dictionary resize when they get full
To keep collisions rare, dicts resize when only ⅔ full
>>> wordfile = open('/home/sayan/words')
>>> text = wordfile.read().decode('utf-8')
>>> words = [ w for w in text.split()
... if w == w.lower() and len(w) < 6 ]
>>> words
[u'a', u'abaci', u'aback', u'abaft', u'abase',
..., u'zoom', u'zooms', u'zoos', ...]
d = {}
# Again, an empty dict has 8 slots
# Let's start filling it with keys
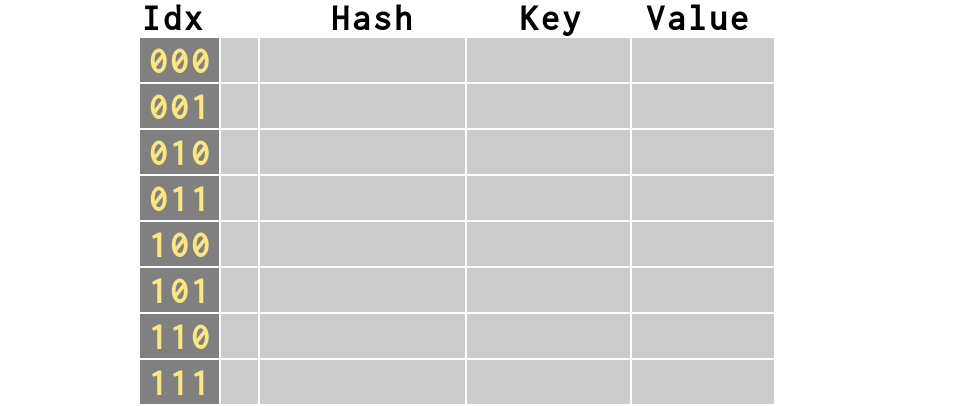
d = dict.fromkeys(words[:5])
# collision rate 40%
# but now ⅔ full — on verge of resizing!

d['abash'] = None
# Resizes ×4 to 32, collision rate drops to 0%
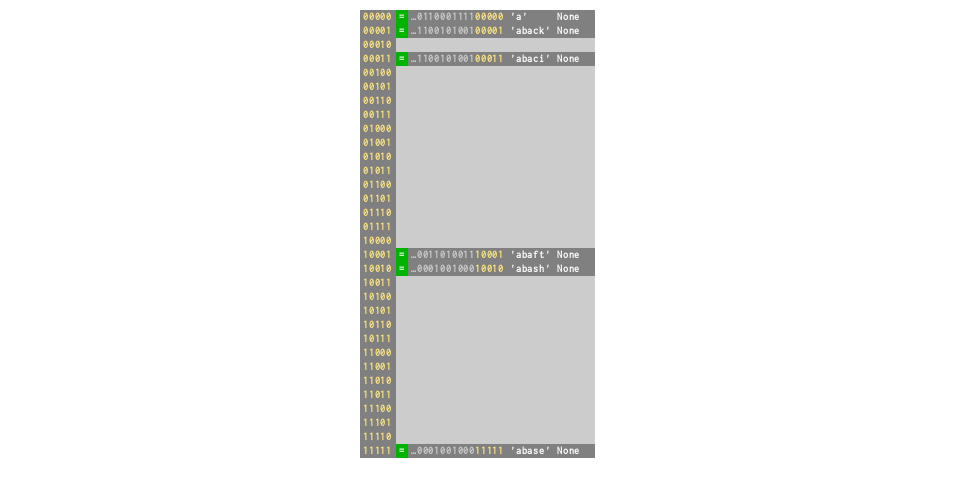
d = dict.fromkeys(words[:21])
# ⅔ full again — collision rate 29%
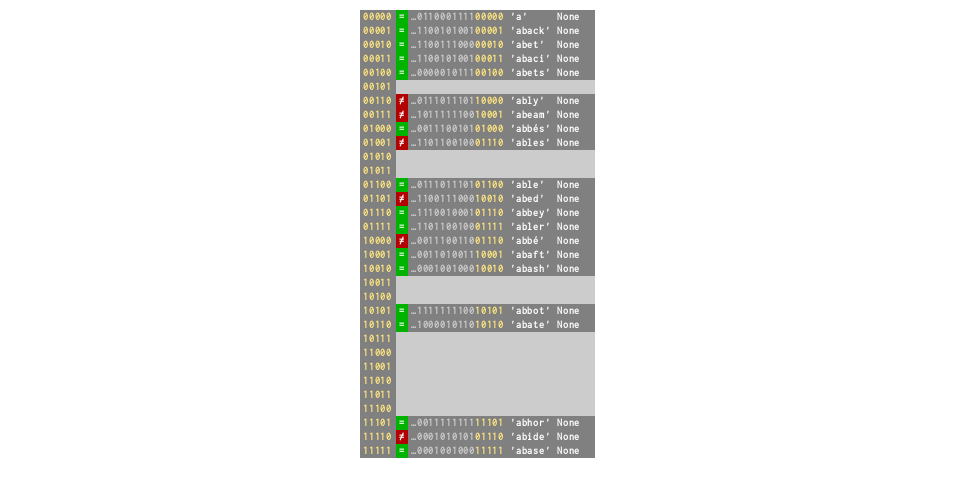
d['abode'] = None
# Resizes ×4 to 128, collision rate drops to 9%
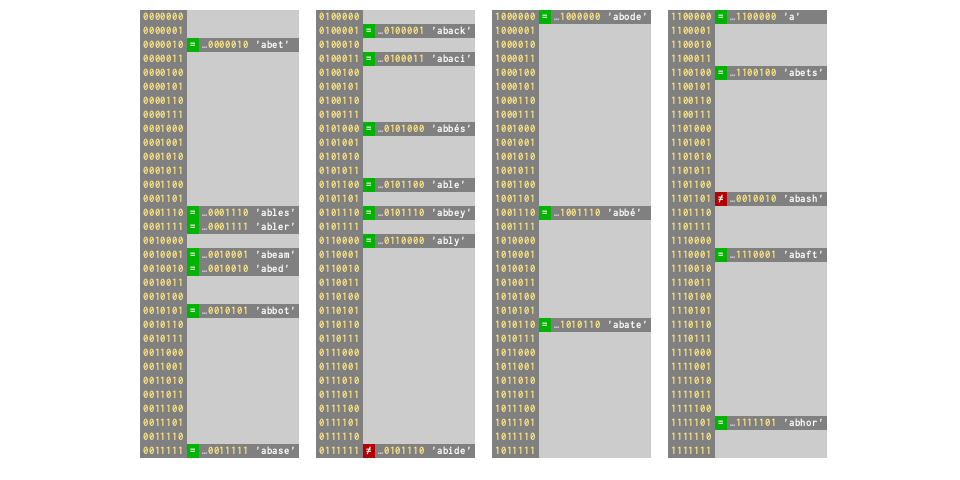
d = dict.fromkeys(words[:85])
# ⅔ full again — collision rate 33%
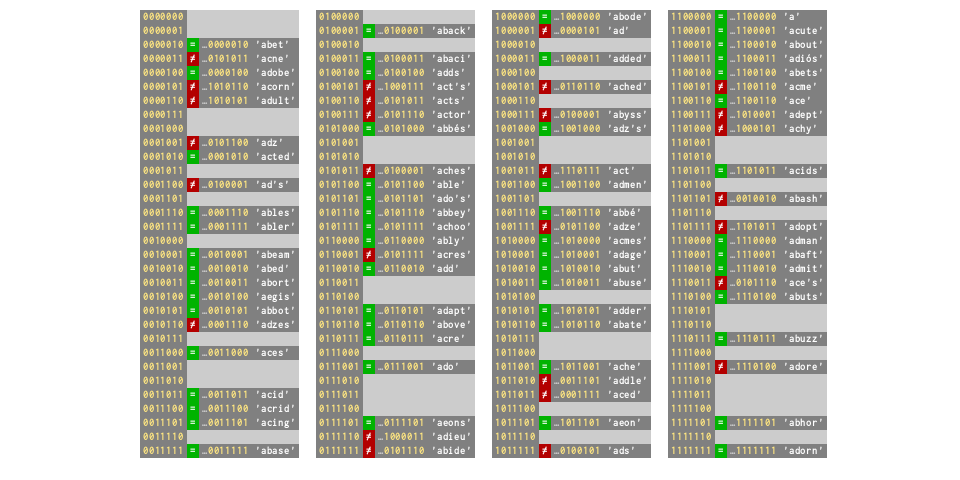
So, dictionary size increase as the keys become crowded
Average dictionary
performance is excellent
A dictionary of common words:
>>> wfile = open('/usr/sayan/words')
>>> words = wfile.read().split()[:1365]
>>> print words
['A', "A's", ..., "Backus's", 'Bacon', "Bacon's"]
>>> pmap = _dictinfo.probe_all_steps(words)
Some are lucky enough to hit in first try
>>> pmap['Ajax']
[1330]
>>> pmap['Agamemnon']
[2020]
While some of them where not that lucky enough!
>>> pmap['Aristarchus'] # requires 5 probes
[864, 1089, 801, 1108, 74]
>>> pmap['Baal'] # requires 16 probes!
[916, 1401, 250, 1359, 399, 1156, 1722, 420, 53,
266, 1331, 512, 513, 518, 543, 668]
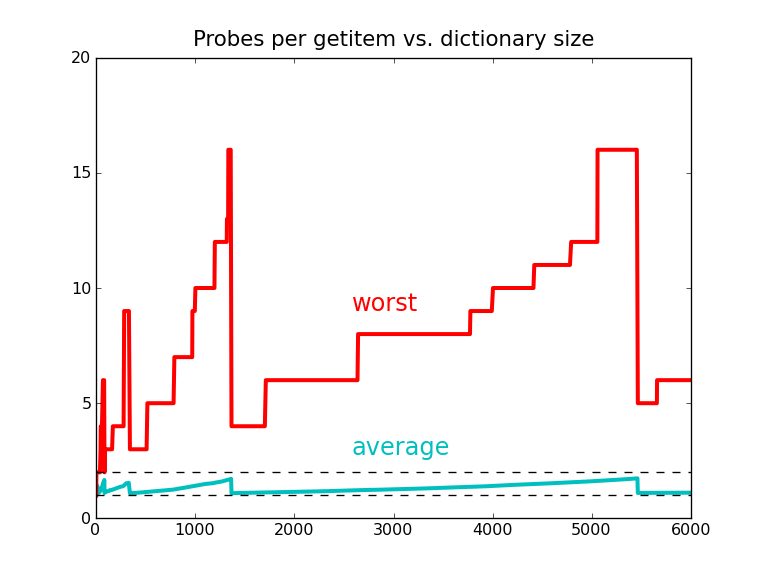
Probes sound to be slow ? right?
But they aren't !
>>> setup = "d=dict.fromkeys(%r)" % words
>>> fast = timeit("d['Ajax']", setup)
>>> slow = timeit("d['Baal']", setup)
>>> '%.1f' % (slow/fast)
'1.7'
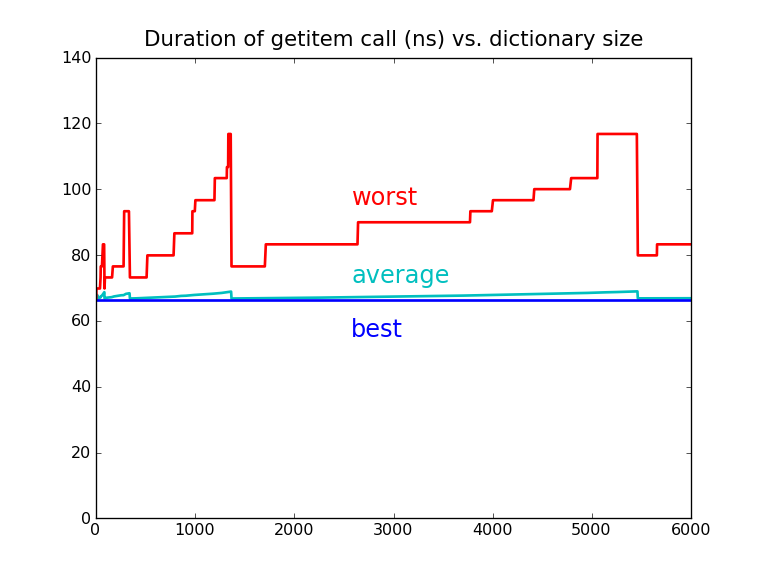
An insert can completely reorder a dictionary during resizing!
>>> d = {'Double': 1, 'double': 2, 'toil': 3,
... 'and': 4, 'trouble': 5}
>>> d.keys()
['toil', 'Double', 'and', 'trouble', 'double']
>>> d['fire'] = 6
>>> d.keys()
['and', 'fire', 'Double', 'double', 'toil',
'trouble']
Because an insert can radically reorder a dictionary, key insertion
is prohibited during iteration
>>> d = {'Double': 1, 'double': 2, 'toil': 3,
... 'and': 4, 'trouble': 5}
>>> for key in d:
... d['fire'] = 6
Traceback (most recent call last):
...
RuntimeError: dictionary changed size during
iteration
Rules to follow!
- Don't rely on the order
- Don't insert while iterating
- Mutable keys not allowed
- Dictionaries trade space for time
Equal values should have equal hashes
regardless of their type!
>>> hash(9)
9
>>> hash(9.0)
9
>>> hash(complex(9, 0))
9
>>> dict = { 9: 'nine' }
9
>>> dict[9]
'nine'
>>> dict[9.0]
'nine'
>>> dict[complex(9)]
'nine'
References
- The Mighty Dictionary by Brandon Rhodes - https://www.youtube.com/watch?v=C4Kc8xzcA68
- http://svn.python.org/projects/python/trunk/Objects/dictnotes.txt
- http://svn.python.org/projects/python/trunk/Objects/dictobject.c
- https://gist.github.com/avances123/9497630