Intro To
By Casey Allred
@sbditto85

Who am I?
- PHP Developer
- Haskell Hobbyist/Developer
- Father of two beautiful girls
Outline
- Compare to typical OOP language 'X'
- Functions!
- Types and Type Classes
- Lists
- Functor, Applicative, and Monads
- Monad Transformers
- Tools
Side note
How many of us know everything about electricity?
How many of us can flip a switch to turn on the lights?
Why Haskell?
- Good practices for any language/paradigm
- Enjoy the science of computing
- Expand your comfort zone
- Mature language that is ever evolving
- It's FUN!
https://xkcd.com/1312/

Haskell vs OOP

What's the same?
- Turing Complete
What's Different
- Everything Else
- Lazy
- Strongly and Statically typed
- Pure
- Functional
Why do I care about differences?
- Because you have to approach problems differently
- Need to forget typical OOP approaches
- Need to forget OOP jargon and learn FP jargon
- You will struggle
Functions!
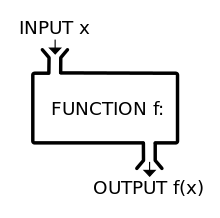
Functions
- "Bread and butter" of Haskell
- Behave like math function f(x) = x + 2 (stateless)
- Parameters separated by spaces
- Curried by default
- Can take or return other functions
- No Objects, so Data and Functions are separate
- Operators (+, -, ==, <$>) are functions too!
Hello World
module Main where
main :: IO ()
main = putStrLn "Hello World"Hello World (Compared)
module Main where
main :: IO ()
main = putStrLn "Hello World"//CPP from https://en.wikibooks.org/wiki/C%2B%2B_Programming/Examples/Hello_world
#include <iostream>
int main()
{
std::cout
<< "Hello World!"
<< std::endl;
return 0;
}Addition
module Main where
main :: IO ()
main = print (addInt 3 4)
addInt :: Int -> Int -> Int
addInt x y = x + y
addThree :: Int -> Int
addThree = addInt 3Addition
module Main where
main :: IO ()
main = print (addInt 3 4)
addInt :: Int -> Int -> Int
addInt x y = x + y
--To call a function
x `addInt` y -- is infix
addInt x y -- is prefix
x + y -- is infix
(+) x y -- is prefixAddition (Compared)
addInt :: Int -> Int -> Int
addInt x y = x + yint addInt(int x, int y) {
return x + y;
}Fibonacci
The formula for the Fibonacci sequence is:
Fn = F(n-1) + F(n-2)
with F(0) = 0 and F(1) = 1
Fibonacci
module Main where
main :: IO ()
main = print (fibN 10)
fibN 0 = 0
fibN 1 = 1
fibN n = fibN (n-1) + fibN (n-2)
-- Output: 55Fibonacci
module Main where
main :: IO ()
main = print (fibN 10)
fibN :: (Eq a, Num a) => a -> a
fibN 0 = 0
fibN 1 = 1
fibN n = fibN (n-1) + fibN (n-2)Fibonacci
module Main where
main :: IO ()
main = print (fibN 10)
fibN i =
(head . drop i) fibs
fibs =
0 : 1 : zipWith (+) fibs (tail fibs)Function Composition
- In math you would do:
- executes right to left
- types must line up
funOne :: Int -> String
funTwo :: String -> Bool
combined :: Int -> Bool
combined x = (funTwo . funOne) xFactorial
module Main where
main :: IO ()
main = print (factorial 5)
factorial 1 = 1
factorial n = n * factorial (n - 1)
{-
OUTPUT: 120
-}factorial 1 = 1
factorial n = n * factorial (n-1)
Factorial
module Main where
main :: IO ()
main = print (factorial 5)
factorial n = product [1..n]
{-
OUTPUT: 120
-}Factorial
module Main where
main :: IO ()
main = print (factorial 5)
factorial :: (Enum a, Num a) => a -> a
factorial n = product [1..n]
{-
OUTPUT: 120
-}FizzBuzz
module Main where
import Control.Monad
import Lib
main :: IO ()
main = forM_ fizzBuzz putStrLn
module Lib
( fizzBuzz
) where
fizzBuzz :: [ String ]
fizzBuzz =
map fizzInt [1..100]
where
fizzInt :: Int -> String
fizzInt i =
case (i `mod` 3 == 0, i `mod` 5 == 0) of
(True, True) -> "FizzBuzz"
(True, False) -> "Fizz"
(False, True) -> "Buzz"
(False, False) -> show i
Divisible by 3 put "Fizz"
Divisible by 5 put "Buzz"
Otherwise put the number
FizzBuzz
module Main where
import Control.Monad
import Lib
main :: IO ()
main = forM_ fizzBuzz putStrLn
module Lib
( fizzBuzz
, fizzInt
) where
fizzBuzz :: [ String ]
fizzBuzz =
map fizzInt [1..100]
where
fizzInt :: Int -> String
fizzInt i
| i `mod` 3 == 0 && i `mod` 5 == 0 = "fizzbuzz"
| i `mod` 5 == 0 = "buzz"
| i `mod` 3 == 0 = "fizz"
| otherwise = show i
FizzBuzz
module Main where
import Control.Monad
import Lib
main :: IO ()
main = forM_ fizzBuzz putStrLn
module Lib
( fizzBuzz
, fizzInt
) where
fizzBuzz :: [ String ]
fizzBuzz =
map fizzInt [1..100]
fizzInt :: Int -> String
fizzInt i
| isMod3 && isMod5 = "fizzbuzz"
| isMod5 = "buzz"
| isMod3 = "fizz"
| otherwise = show i
where
isMod3 :: Bool
isMod3 = i `mod` 3 == 0
isMod5 :: Bool
isMod5 = i `mod` 5 == 0Lambda Functions
- Anonymous functions
- Can be written inline
- Like other functions can be assigned to a name
addInt :: Int -> Int -> Int
addInt x y = x + y -- addInt 1 2 == 3
lambdaAdd :: Int -> Int -> Int
lambdaAdd = \x y -> x + y -- lambdaAdd 1 2 == 3
map (\i -> i + 1) [1..4] -- [2, 3, 4, 5]
map (+1) [1..4] -- [2, 3, 4, 5]Types and Type Classes

Built in Types
- Int, Integer
- Float, Double
- Char
- Bool
- String == [Char]
Creating Your Own Types
- type - for creating an alias
- data - for creating a new type
type (alias)
type String = [ Char ]
type PeoplesNames = [ String ]
type Person = ( String, String, Int )data
data Bool = True | False
data WeekDays = Monday | Tuesday | Wednesday | Thursday | Friday
data Person = Person String String Int
data Worker = Employee String String Int | Manager String String Int
getFirstName (Employee firstName _ _) = firstName
data Employee = Employee { getFirstName :: String
, getLastName :: String
, getAge :: Int
}
emp = Employee "Jonny" "Jon" 40
getFirstName emp -- "Jonny"Type Parameters
data Maybe a = Just a | Nothing
data [a] = a : [a] | []
data List a = Cons a (List a) | EmptyType Parameters
data Maybe a = Just a | Nothing
a = Just "hello" -- Maybe String
b = Just 5 -- Maybe Int
c = Nothing -- Maybe aType Classes
- Like interfaces
- Allow us to keep functionality and data separate
- Useful for polymorphism
myFunc :: (Num a) => a -> a -> a
myFunc x y = x + yCommon Type Classes
- Eq = can they be compared equal
- Ord = can they be compared > or < etc
- Show = can it be turned into a String
- Read = can it be converted from a String
- Enum = can it be enumerated
- Bounded = does it have a min and max
- Num = is it a number
- Intergral = is it a whole number
- Floating = is it a real number
The Num Type Class
class Num a where
(+) :: a -> a -> a
(-) :: a -> a -> a
(*) :: a -> a -> a
negate :: a -> a
abs :: a -> a
{-*SNIP*-}The Eq Type Class
class Eq a where
(==) :: a -> a -> Bool
(/=) :: a -> a -> Bool
x == y = not (x /= y)
x /= y = not (x == y)
data TrafficLight = Red | Yellow | Green
instance Eq TrafficLight where
Red == Red = True
Green == Green = True
Yellow == Yellow = True
_ == _ = False The Eq Type Class
areEq :: (Eq a) => a -> a-> Bool
areEq first second = first == secondDeriving Type Classes
When creating a type, if its composed of types that already implement a Type Class, you can then just derive that Type Class for your new type.
data Employee = Employee { getFirstName :: String
, getLastName :: String
, getAge :: Int
} deriving ( Show, Eq )Lists
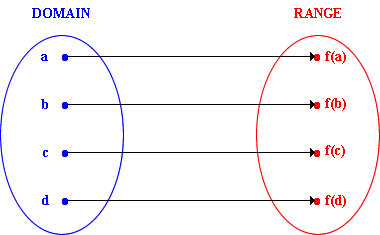
Lists
- Singly linked list
- Can be infinite
- Can be used like an array but be careful
data List a = a : [a] | []
data List a = Cons a (List a) | EmptyList
[1, 2, 3, 4, 5]
1 : 2 : 3 : 4 : 5 : []
Cons 1 (Cons 2 (Cons 3 ( Cons 4 (Cons 5 EmtpyList))))Infinite Lists
- Possible due to Haskell being lazy
- Only computed up to what is used
- Can get stuck in an 'infinite loop'
infinteList = [1..]
oddInfiniteList = [1,3..]
finiteList = take 10 infiniteList
otherFiniteList = (take 10) . (drop 5) oddInfiniteListMap
- Like a foreach that applies a function to each value
- Don't care how it works, just do it
list = [1, 2, 3, 4]
newList = map (+1) listint arr[] = {1, 2, 3, 4};
int newArr[] = {0, 0, 0, 0};
int size = 4;
for(int i = 0; i < size; i++) {
newArr[i] = arr[i] + 1;
}Filter
- Like a foreach that only adds a value if a condition is true
- Don't care how it works, just do it
list = [1, 2, 3, 4]
newList = filter (<3) listvector<int> arr = {1, 2, 3, 4};
vector<int> newArr;
for(int i = 0; i < arr.size; i++) {
if(arr[i] < 3) {
newArr.push(arr[i]);
}
}List Comprehension
myList = [x | x <- [1..10] ] --[1,2,3,4,5,6,7,8,9,10]
myList = [x + 1 | x <- [1..10] ] --[2,3,4,5,6,7,8,9,10,11]
myList = [x | x <- [1..10], x < 3] --[1,2]
myList = [x + 1 | x <- [1..10], x < 3] --[2,3]Functor, Applicative, and Monads
Functor
class Functor f where
fmap :: (a -> b) -> f a -> f bApply a function to a computational context
Common Functors
- Maybe
- []
- IO
Functor
myFunc :: Int -> Bool
mayExistInt :: Maybe Int
-- How do I use myFunc with mayExistInt?
result = fmap myFunc mayExistInt
result = myFunc <$> mayExistInt
-- which will result in
result :: Maybe BoolWhy do we care?
Ok, what about multiple params?
Applicative
class Functor f => Applicative f where
pure :: a -> f a
(<*>) :: f (a -> b) -> f a -> f bApply a function in a context to a context
Common Applicatives
- Maybe
- []
- IO
Applicative
myFunc :: Int -> String -> Bool
mayExistInt :: Maybe Int
mayExistString :: Maybe String
-- How do I use myFunc with mayExistInt and mayExistString?
result = fmap myFunc mayExistInt <*> mayExistString
result = myFunc <$> mayExistInt <*> mayExistString
-- which will result in
result :: Maybe BoolWhy do we care?
Monads
What if I have a value in a context but the function takes a normal value and return a value in a context?
class Applicative m => Monad m where
(>>=) :: m a -> (a -> m b) -> m b
return :: a -> m a
-- Applicative
pure :: a -> m aMonads
What do you think the following program does?
module Main where
main :: IO ()
main = do
hello <- return "hello"
world <- return "world"
print (hello ++ world)Common Monads
- Maybe
- []
- IO
Monads
myFunc :: Int -> Maybe Bool
mayExistInt :: Maybe Int
-- How do I use myFunc with mayExistInt?
result = mayExistInt >>= myFunc
result = do
i <- mayExistInt
myFunc i
-- which will result in
result :: Maybe BoolWhy do we care?
Monads
instance Monad Maybe where
(>>=) :: Maybe a -> (a -> Maybe b) -> Maybe b
(>>=) (Just a) f = f a
(>>=) Nothing _ = Nothing
mayExistInt >>= myFunc
-- if mayExistInt == Nothing :
Nothing
-- if mayExistInt == Just x then f == myFunc and a == x :
myFunc x :: Maybe BoolWhats happening behind the Maybe >>= curtain?
Monads
getLine :: IO String -- from the prelude
myFunc :: String -> IO Bool
myFunc2 :: Bool -> IO String
putStrLn :: String -> IO () -- from the prelude
result = do inputString <- getLine
myBool <- myFunc inputString
computeString <- myFunc2 myBool
putStrLn computeString
-- which will result in
result :: IO () --and the appropriate IO actionsWhy do we care?
Monad Transformers

Monad Transformers
- This is one way we get "real" programs
- Instead of nesting we stack them like legos
- Then we just require something has the ability to do a context not the context itself
- i.e. requiring MonadIO instead of IO


Tools

GHC/GHCI
- Compiler (GHC)
- REPL (GHCI)
- Read
- Eval
- Loop
stack
- www.haskellstack.org
- build tool
- package manager
- project manager
- Setup a new project
- stack new my-project
- cd my-project
- stack setup
- stack build
- stack exec my-project-exe
Searching for libs/functions
- https://www.haskell.org/hoogle/
- Generic search
- Can search by function parameters
- https://www.stackage.org/snapshots
- Pick a stack snapshot
- Search just like you would for Hoogle
Links
- http://learnyouahaskell.com/chapters
- http://haskellbook.com/
- http://adit.io/posts/2013-04-17-functors,_applicatives,_and_monads_in_pictures.html
- https://github.com/sbditto85/intro-to-haskell-code
- http://lorepub.com/post/2016-12-17-Haskell-Pitfalls