基礎圖論
圖
就是一些點和一些邊
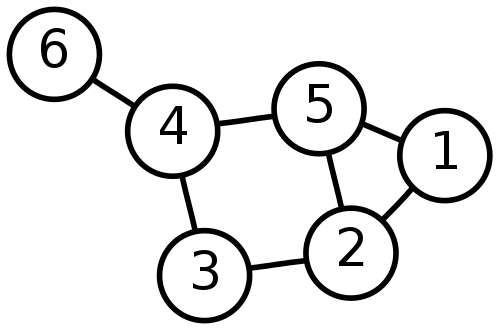
名詞介紹
-
點:就是點
-
邊:連接兩個點
-
無向邊:沒有方向性的邊
-
有向邊:有方向性的邊
-
權重:給邊或點加上一個數值,例如距離
路徑
從一個點\(v_0\)經過一些邊\((v_0, v_1), (v_1, v_2) ... (v_{k - 1}, v_k)\)到達另一個點\(v_k\)
的序列稱為路徑
可表示成經過的點的序列\((v_0, v_1, ... v_k)\)
簡單路徑
路徑上沒有經過重複的點
最短路徑
就最短,可以是路徑上的邊權總和
環
一條路徑的起點和終點相同稱為環
就是可以走一圈回到原點
無向圖
無向邊組成的圖
連通圖
連通塊
任意兩點之間都有路徑存在
就是可以從任意點走到其他所有點
圖中一些點,互相都有路徑存在,且不能被包含在其他連通塊內
就是其他的點都跟這些點不連通
有向圖
有向邊組成的圖
有向無環圖(DAG)
沒有環的有向圖
儲存方式
鄰接矩陣
點的數量是\(n\),編號為\(0\)~\(n-1\)
開一個\(n\times n\)的二維陣列A
如果A[i][j]=1,代表有一條邊從點i連接到點j
鄰接串列
當邊的數量很少時,鄰接矩陣很多空間會浪費掉
鄰接串列只儲存有邊的資料
可用vector實作
圖的遍歷
遍歷
走過所有的點
DFS
深度優先搜尋
像人走路一樣
,選一條路一直走,走到不能再走之後退回來繼續找路
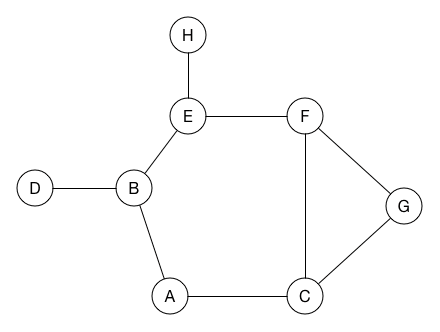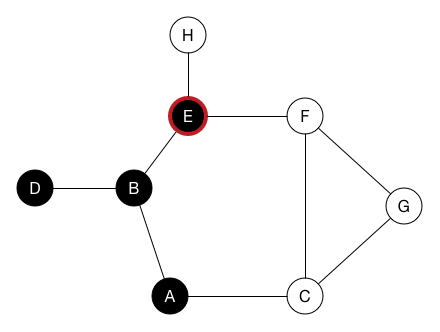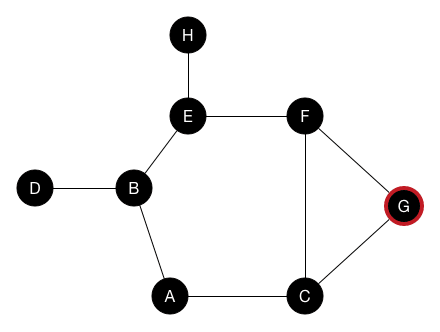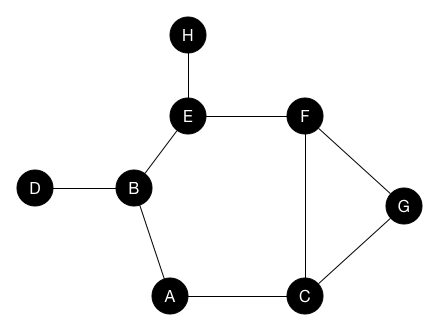
實作方式
遞迴
vector<int> edge[100005];
bool visit[100005];
void dfs(int x) {
visit[x] = 1;
for (int i = 0; i < edge[x].size(); i++) {
if (!visit[edge[x][i]]) {
dfs(edge[x][i]);
}
}
}C++11小技巧
for(auto i:edge[x]){
if(visit[i]){
dfs(i);
}
}BFS
廣度優先搜尋
像是倒水
每次會先遍歷完所有經過一條邊可以到的點,接這遍歷兩條邊,以此類推
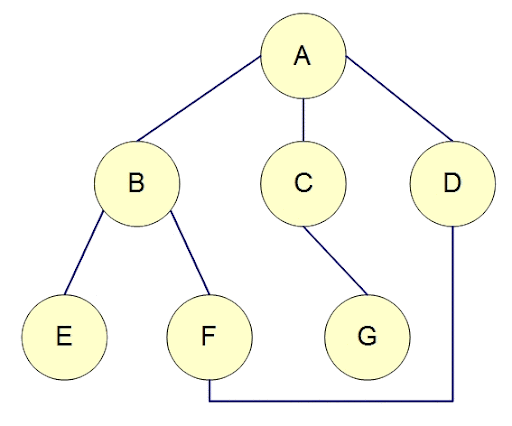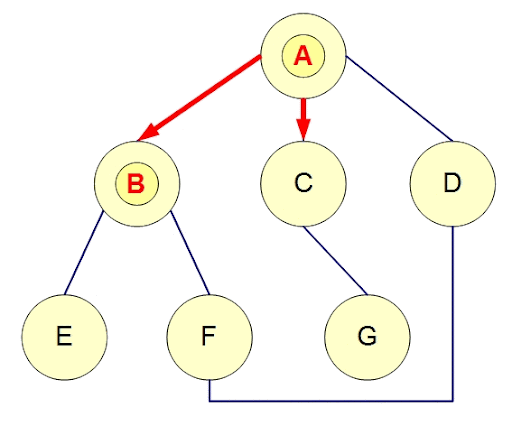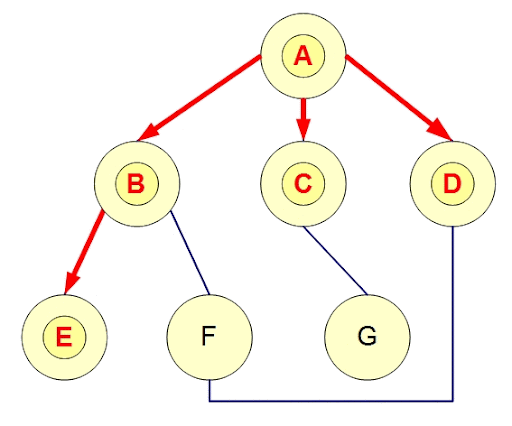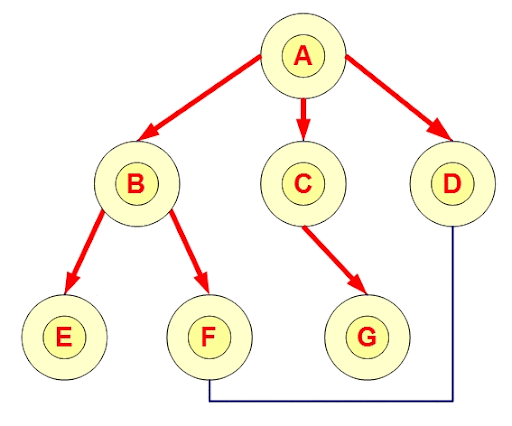
實作方式
queue
把第一個拿出來,看有哪些點跟他連接且還沒被看過,把他們丟到queue後面
vector<int> edge[100005];
bool visit[100005];
void bfs(int x) {
queue<int> q;
q.push(x);
visit[x] = 1;
while (!q.empty()) {
int now = q.front();
q.pop();
for (auto i : edge[x]) {
if (!visit[i]) {
q.push(i);
visit[i] = 1;
}
}
}
}練習題
試著用dfs和bfs寫寫看
樹
圖的範圍太廣
太複雜
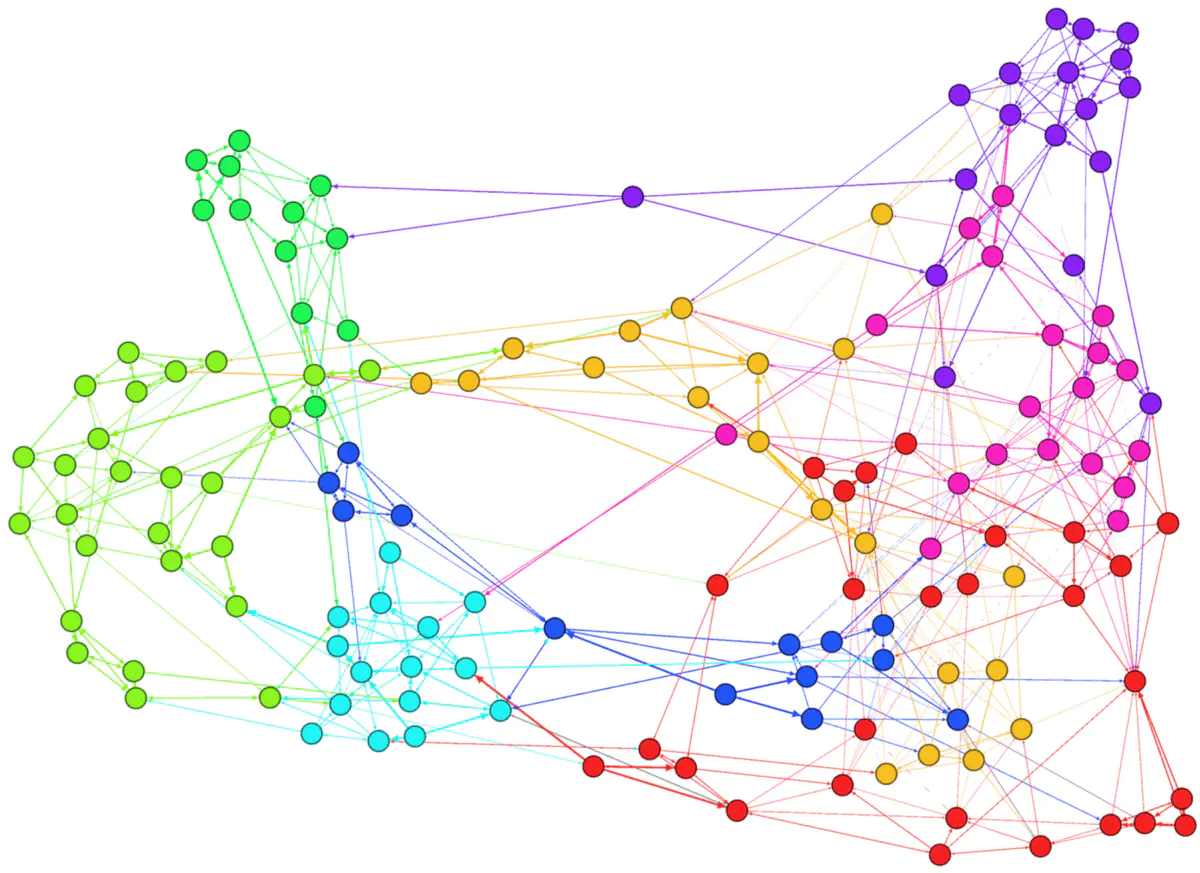
樹
- 一種圖
- 就像樹枝一樣
- 沒有環
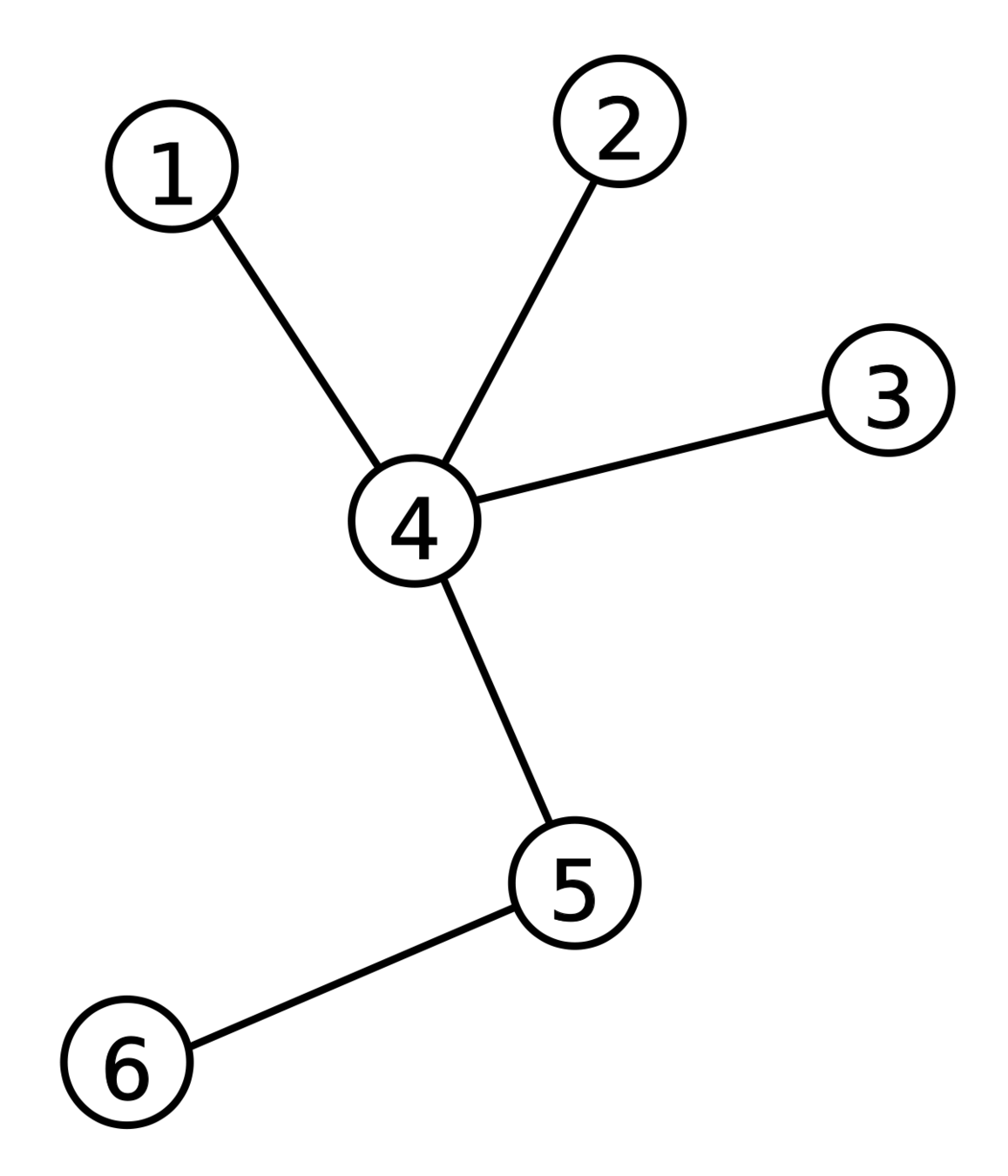
這樣就會出現一些很好的性質
- 樹上任兩點間只有一條簡單路徑
- 對於一棵樹,邊的數量是點數-1
練習題:
zerojudge b517
有根樹和無根樹
有根樹有一個最頂端的根
有根樹上的問題比無根樹上簡單很多
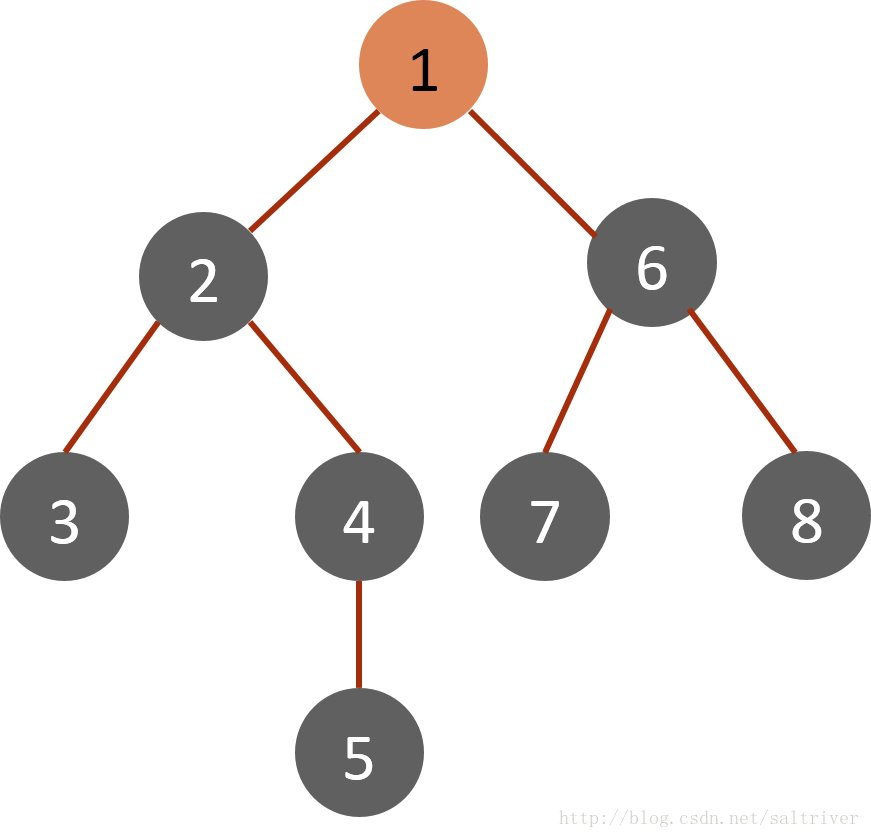
有根樹
根節點
最上面的點
有根樹
根節點
最上面的點
父節點
一個點上面那一層的點,除了根節點外的點都只有一個父節點
有根樹
根節點
最上面的點
父節點
一個點上面那一層的點,除了根節點外的點都只有一個父節點
子節點
一個點下面一層的點,可以有多個
有根樹
根節點
最上面的點
父節點
一個點上面那一層的點,除了根節點外的點都只有一個父節點
子節點
一個點下面一層的點,可以有多個
葉節點
沒有子節點的點
有根樹
祖先
一個點的父節點和父節點的父節點....
也可以說是一個點到根節點路徑上的所有點
練習題:
tcirc judge d102
DAG
directed acyclic graph
DAG
有向無環圖
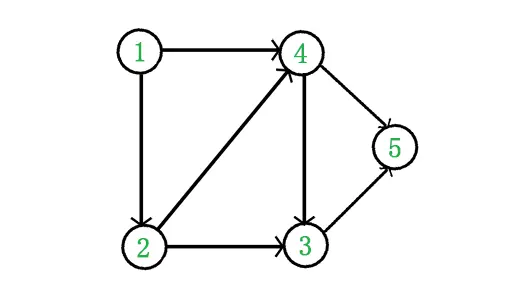
可以幹嘛?
工作排程問題
有n個工作,每個工作可能有一個或多個前置工作,問是否可以完成所有工作?
對於a工作,如果前置工作有b,
就連一條邊從b指向a
必須是DAG才有解
怎麼輸出解?
拓撲排序
每次把沒有被指向的點拔掉
拔到沒有點為止
拔掉的順序就是一種答案
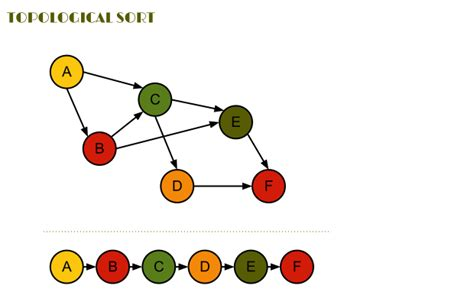
如果每個工作有完成所需時間
同時可以進行多個工作
求做完所有工作的最短時間
tcirc d099