Copy of Chalmers_symplectic_space

Underline = Cmd+u

More symplectic structures

on the space of space curves

(and the space of wave functions)

April 2025 @ Chalmers University of Technology (online)

Sadashige Ishida (ISTA)

Purpose of this talk

To discuss a collaborative project

To introduce myself and some taste of my work

Introduction to myself

Sadashige, a PhD student @ ISTA (near Vienna)

Introduction to myself

Geometry & Dynamics in Math

Sadashige, a PhD student @ ISTA (near Vienna)

Introduction to myself

Geometry & Dynamics in Math, Physics, CS

Sadashige, a PhD student @ ISTA (near Vienna)

Dynamics as $\infty$-dim geometry

e.g. fluids, optimal transport, shapes

Introduction to myself

Geometry & Dynamics in Math, Physics, CS

Sadashige, a PhD student @ ISTA (near Vienna)

Dynamics as $\infty$-dim geometry

e.g. fluids, optimal transport, shapes

+ their finite-dim approximations

a.k.a. discretization

Introduction to myself

Dynamics as $\infty$-dim geometry

e.g. fluids, optimal transport, shapes

Geometry & Dynamics in Math, Physics, CS

+ their finite-dim approximations

a.k.a. discretization

Sadashige, a PhD student @ ISTA (near Vienna)

Introduction to myself

Geometry & Dynamics in Math, Physics, CS

Sadashige, a final year PhD student @ ISTA (near Vienna)

Introduction to myself

Dynamics as $\infty$-dim geometry

e.g. fluids, optimal transport, shapes

Geometry & Dynamics in Math, Physics, CS

+ their finite-dim approximations

a.k.a. discretization

Sadashige, a final year PhD student @ ISTA (near Vienna)

Introduction to myself

Dynamics as $\infty$-dim geometry

e.g. fluids, optimal transport, shapes

Geometry & Dynamics in Math, Physics, CS

+ their finite-dim approximations

a.k.a. discretization

Sadashige, a final year PhD student @ ISTA (near Vienna)

Overview

On the shape space of space curves,

only one symplectic structure was known.

We found more.

Joint with

Martin Bauer Peter Michor

Overview

This is an experimental study.

One can define different dynamics by inputting different Hamiltonians.

But what if we use different symplectic structures to invoke different dynamics?

We tried it for space curves

Symplectic structure is a sandbox

for Hamiltonian dynamics

Space with

a symplectic structure $\Omega$

A function $H$

Dynamics $V_H$

Symplectic structure is a sandbox

for Hamiltonian dynamics

A symplectic structure $\Omega$

A function $H$

Dynamics

Symplectic structure is a sandbox

for Hamiltonian dynamics

A symplectic structure $\Omega$

A function $H$

Dynamics

i.e. 2-form

closed $d\Omega=0$
non-degenerate $\operatorname{ker}\Omega = 0$

$$ dH = \Omega(V_H, \cdot)$$

$$ \dot x =V_H$$

Symplectic structure is a sandbox

for Hamiltonian dynamics

A symplectic structure $\Omega$ is a 2-form on a manifold $X$ s.t.

Symplectic structure is a sandbox

for Hamiltonian dynamics

A symplectic structure $\Omega$ is a 2-form on a manifold $X$ s.t.

closed i.e. $d\Omega=0$

Symplectic structure is a sandbox

for Hamiltonian dynamics

A symplectic structure $\Omega$ is a 2-form on a manifold $X$ s.t.

non-degenerate i.e. the map $$\flat: TX\to T^*X$$ $$ \qquad v\to \Omega(v, \cdot )$$ is injective

closed i.e. $d\Omega=0$

Symplectic structure is a sandbox

for Hamiltonian dynamics

Symplectic structure is a sandbox

for Hamiltonian dynamics

For $H \colon X\to \mathbb{R}$,

Hamiltonian vector field $V_H\in \Gamma(TX)$ is the one

$$ dH = \Omega(V_H, \cdot). $$

Symplectic structure is a sandbox

for Hamiltonian dynamics

For $H \colon X\to \mathbb{R}$,

Hamiltonian vector field $V_H\in \Gamma(TX)$ is the one

$$ dH = \Omega(V_H, \cdot). $$

The Hamiltonian dynamics

$$\dot x=V_H(x).$$

Why Hamiltonian dynamics?

Has nice properties.

E.g.

$H$ is preserved in dynamics.
If $H$ is invariant under some group action, there is a conserved quantity.

Spaces with symplectic structures

and Hamiltonian dynamics

$T^*M^n$

$T^*\operatorname{SDiff}(M)$

Celestial mechanics

$C^\infty(M,\mathbb{C})$

Schrödinger equation

Incompressible fluids

Spaces with symplectic structures

and Hamiltonian dynamics

$T^*M^n$

$T^*\operatorname{SDiff}(M)$

Celestial mechanics

$C^\infty(M,\mathbb{C})$

Schrödinger equation

Incompressible fluids

We consider the space of space curves

Spaces with symplectic structures

and Hamiltonian dynamics

$T^*M^n$

$T^*\operatorname{SDiff}(M)$

Celestial mechanics

$C^\infty(M,\mathbb{C})$

Schrödinger equation

Incompressible fluids

We consider the space of space curves

(and the space of wave functions).

We consider the space of space curves

Spaces with symplectic structures

and Hamiltonian dynamics

The space of space curves

$$\operatorname{Imm}(\mathbb{S}^1,\mathbb{R}^3)=\{ c\colon \mathbb{S}^1\to\mathbb{R}^3, \partial_\theta c\neq 0 \ \forall \theta\in\mathbb{S}^1 \}$$

Parametrized curves

The space of space curves

$$\operatorname{Imm}(\mathbb{S}^1,\mathbb{R}^3)=\{ c\colon \mathbb{S}^1\to\mathbb{R}^3, \partial_\theta c\neq 0 \ \forall \theta\in\mathbb{S}^1 \}$$

Parametrized curves

$$T_c\operatorname{Imm}(\mathbb{S}^1,\mathbb{R}^3)=C^\infty(\mathbb{S}^1,\mathbb{R}^3)$$

Tangent space

The space of space curves

$$\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)=\operatorname{Imm}(\mathbb{S}^1,\mathbb{R}^3)/\operatorname{Diff}^+(\mathbb{S}^1)$$

Unparametrized curves a.k.a. shape space

The space of space curves

$$\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)=\operatorname{Imm}(\mathbb{S}^1,\mathbb{R}^3)/\operatorname{Diff}^+(\mathbb{S}^1)$$

Unparametrized curves a.k.a. shape space

$$\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)$$

$$\operatorname{Imm}(\mathbb{S}^1,\mathbb{R}^3)$$

\[\Bigg\downarrow \pi\]

\[\curvearrowright\]

$$\operatorname{Diff}^+(\mathbb{S}^1)$$

The space of space curves

$$\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)=\operatorname{Imm}(\mathbb{S}^1,\mathbb{R}^3)/\operatorname{Diff}^+(\mathbb{S}^1)$$

Unparametrized curves a.k.a. shape space

Tangent space

$$T_{[c]}\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)=T_c\operatorname{Imm}(\mathbb{S}^1,\mathbb{R}^3)/\ker d\pi_c$$

$$\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)$$

$$\operatorname{Imm}(\mathbb{S}^1,\mathbb{R}^3)$$

\[\Bigg\downarrow \pi\]

\[\curvearrowright\]

$$\operatorname{Diff}^+(\mathbb{S}^1)$$

The space of space curves

$$\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)=\operatorname{Imm}(\mathbb{S}^1,\mathbb{R}^3)/\operatorname{Diff}^+(\mathbb{S}^1)$$

Unparametrized curves a.k.a. shape space

Tangent space

$$T_{[c]}\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)=T_c\operatorname{Imm}(\mathbb{S}^1,\mathbb{R}^3)/\ker d\pi_c$$

$$\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)$$

$$\operatorname{Imm}(\mathbb{S}^1,\mathbb{R}^3)$$

\[\Bigg\downarrow \pi\]

\[\curvearrowright\]

$$\operatorname{Diff}^+(\mathbb{S}^1)$$

$\{a.\partial_\theta c \mid a\in C^\infty(\mathbb{S}^1)\}$

curve tangent

The space of space curves

$$\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)=\operatorname{Imm}(\mathbb{S}^1,\mathbb{R}^3)/\operatorname{Diff}^+(\mathbb{S}^1)$$

Unparametrized curves a.k.a. shape space

Tangent space

$$T_{[c]}\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)=T_c\operatorname{Imm}(\mathbb{S}^1,\mathbb{R}^3)/\ker d\pi_c$$

$$\eqsim\{h \in T_c \operatorname{Imm}(\mathbb{S}^1,\mathbb{R}^3)\mid h\perp \partial_\theta c \}$$

$$\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)$$

$$\operatorname{Imm}(\mathbb{S}^1,\mathbb{R}^3)$$

\[\Bigg\downarrow \pi\]

\[\curvearrowright\]

$$\operatorname{Diff}^+(\mathbb{S}^1)$$

$\{a.\partial_\theta c \mid a\in C^\infty(\mathbb{S}^1)\}$

curve tangent

Canonical symplectic structure on $\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)$

The Marsden-Weinstein structure

\[\Omega_{[c]}\colon T_{[ c]}\operatorname{UImm}\times T_{[ c]}\operatorname{UImm}\to \mathbb{R},\]

Canonical symplectic structure on $\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)$

\[\Omega_{[c]}\colon T_{[ c]}\operatorname{UImm}\times T_{[ c]}\operatorname{UImm}\to \mathbb{R},\]

The Marsden-Weinstein structure

\[\Omega_{[c]}([h],[k])=\int_{\mathbb{S}^1}\langle D_s c\times h, k\rangle ds\]

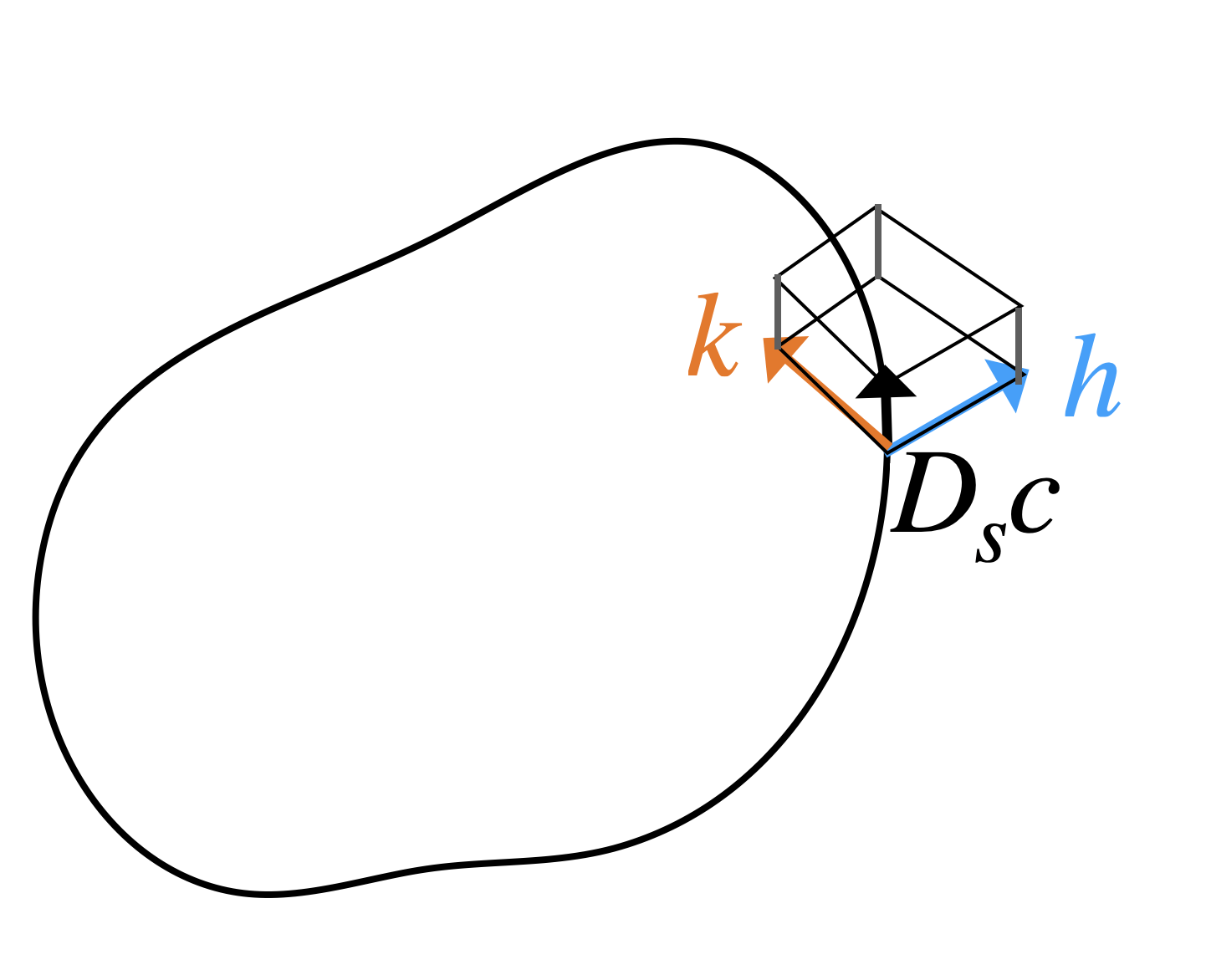
where

\[D_s = \frac{\partial_\theta }{|\partial_\theta c|}, \quad ds = |\partial_\theta c| d\theta \]

unit tangent

Canonical symplectic structure on $\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)$

\[\Omega_{[c]}\colon T_{[ c]}\operatorname{UImm}\times T_{[ c]}\operatorname{UImm}\to \mathbb{R},\]

Symplectic!

The Marsden-Weinstein structure

\[\Omega_{[c]}([h],[k])=\int_{\mathbb{S}^1}\langle D_s c\times h, k\rangle ds\]

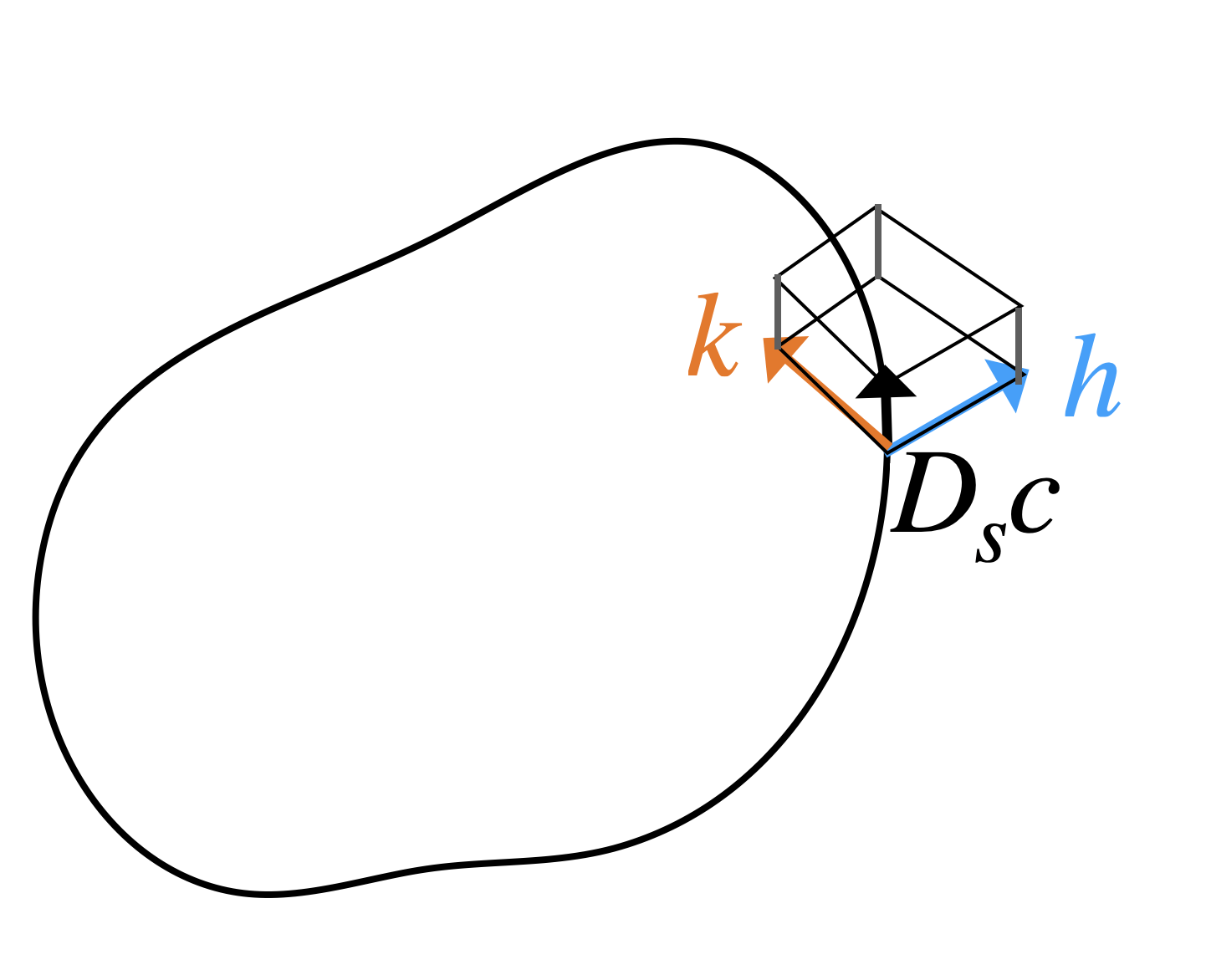
where

\[D_s = \frac{\partial_\theta }{|\partial_\theta c|}, \quad ds = |\partial_\theta c| d\theta \]

unit tangent

Canonical symplectic structure on $\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)$

\[\Omega_{[c]}\colon T_{[ c]}\operatorname{UImm}\times T_{[ c]}\operatorname{UImm}\to \mathbb{R},\]

Closed $d\Omega=0$,

Symplectic!

The Marsden-Weinstein structure

\[\Omega_{[c]}([h],[k])=\int_{\mathbb{S}^1}\langle D_s c\times h, k\rangle ds\]

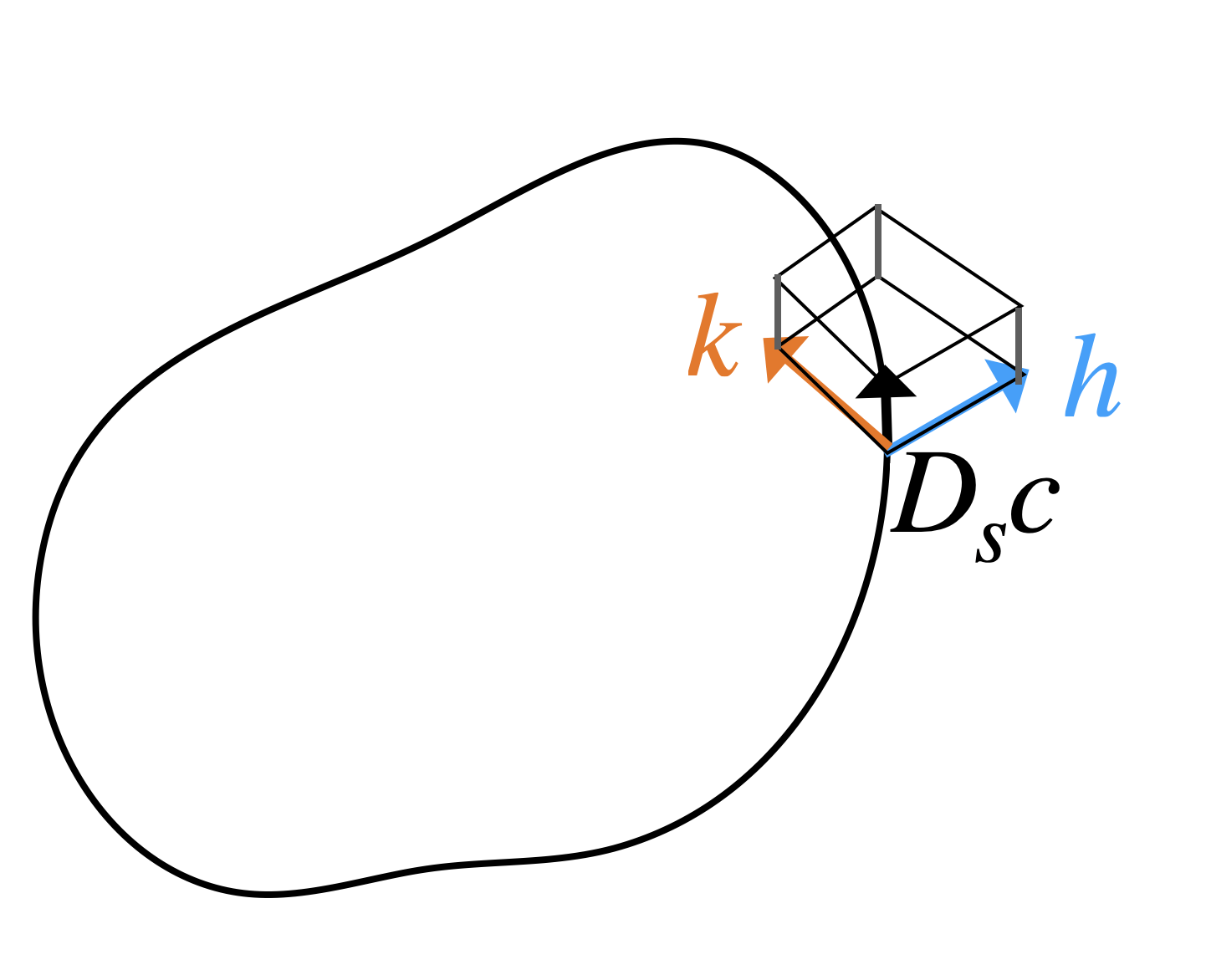
where

\[D_s = \frac{\partial_\theta }{|\partial_\theta c|}, \quad ds = |\partial_\theta c| d\theta \]

unit tangent

Canonical symplectic structure on $\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)$

\[\Omega_{[c]}\colon T_{[ c]}\operatorname{UImm}\times T_{[ c]}\operatorname{UImm}\to \mathbb{R},\]

Closed $d\Omega=0$,

Symplectic!

The Marsden-Weinstein structure

\[\Omega_{[c]}([h],[k])=\int_{\mathbb{S}^1}\langle D_s c\times h, k\rangle ds\]

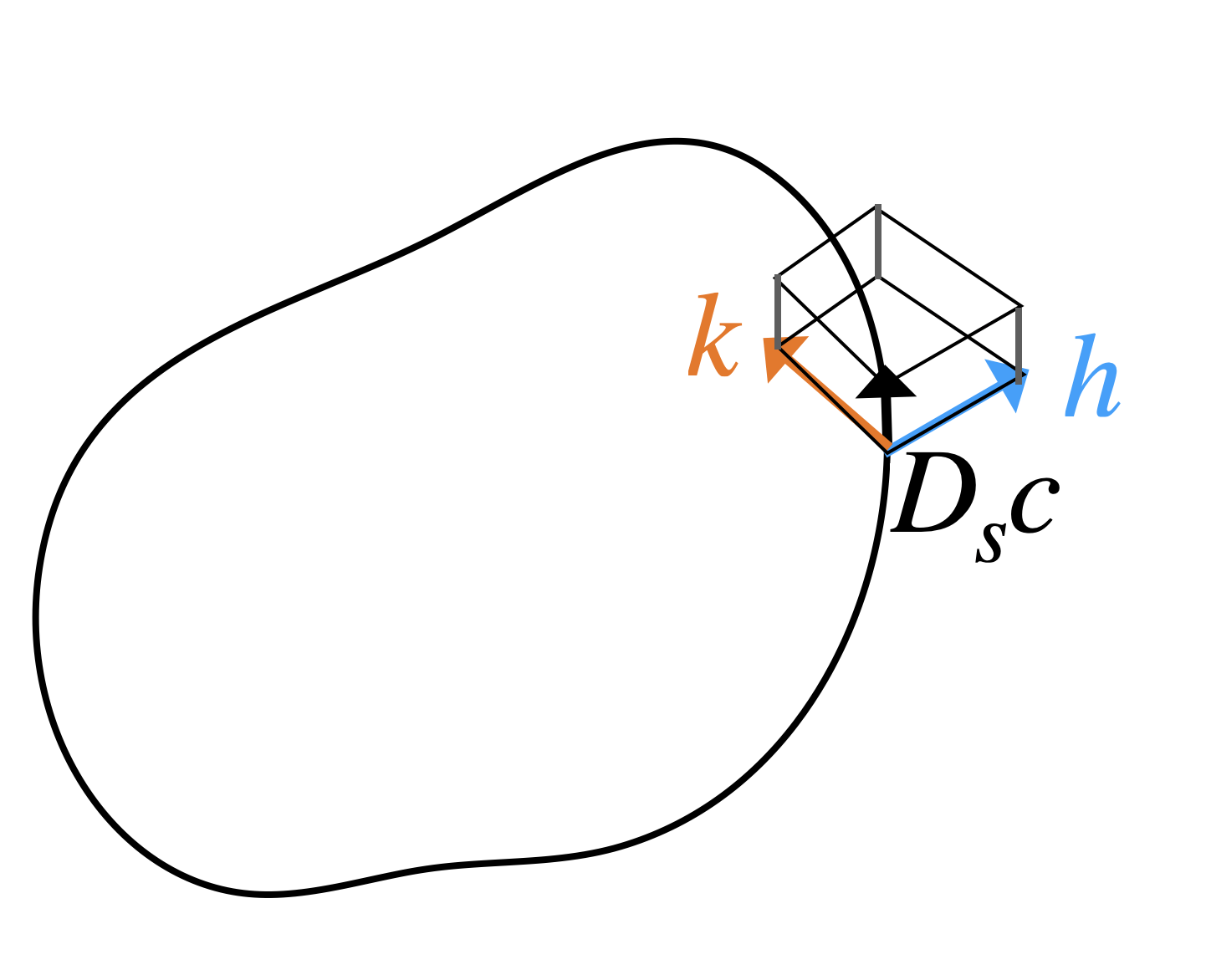
where

\[D_s = \frac{\partial_\theta }{|\partial_\theta c|}, \quad ds = |\partial_\theta c| d\theta \]

Non-degenerate $\ker \Omega_{[c]}=[0]=\{a.D_s c \mid a \in C^\infty(\mathbb{S}^1)\}$

unit tangent

Hamiltonian flow

E.g.

Hamiltonian $H = \operatorname{Length}([c])$

Binormal flow

Dynamics $V_H=[D_s c \times D_s^2 c]$

Hamiltonian flow

E.g.

Hamiltonian $H = \operatorname{Length}([c])$

Binormal flow

Dynamics $V_H=[D_s c \times D_s^2 c]$

A completely integrable system

More symplectic structures?

Remember

A symplectic structure $\Omega$ defines a Hamiltonian dynamics $V_H$ via $$dH=\Omega(V_H,\cdot).$$

More symplectic structures?

A different $\Omega$ defines different $V_H$.

Remember

A symplectic structure $\Omega$ defines a Hamiltonian dynamics $V_H$ via $$dH=\Omega(V_H,\cdot).$$

More symplectic structures?

A different $\Omega$ defines different $V_H$.

But only one $\Omega$ is known on $\operatorname{UImm}$.

Remember

A symplectic structure $\Omega$ defines a Hamiltonian dynamics $V_H$ via $$dH=\Omega(V_H,\cdot).$$

More symplectic structures?

A different $\Omega$ defines different $V_H$.

We found more

But only one $\Omega$ is known on $\operatorname{UImm}$.

Remember

A symplectic structure $\Omega$ defines a Hamiltonian dynamics $V_H$ via $$dH=\Omega(V_H,\cdot).$$

More symplectic structures?

A different $\Omega$ defines different $V_H$.

We found more

But only one $\Omega$ is known on $\operatorname{UImm}$.

Remember

A symplectic structure $\Omega$ defines a Hamiltonian dynamics $V_H$ via $$dH=\Omega(V_H,\cdot).$$

by combining 2 hints.

Hint 1. Trend in shape analysis

a Riemannian metric on $\operatorname{Imm}$

$$ g(h,k)=\int_{\mathbb{S}^1} \langle h,k\rangle ds$$

Hint 1. Trend in shape analysis

a Riemannian metric on $\operatorname{Imm}$

$$ g(h,k)=\int_{\mathbb{S}^1} \langle h,k\rangle ds$$

a suitable operator

$$L\colon T\operatorname{Imm}\to T\operatorname{Imm}. $$

Hint 1. Trend in shape analysis

a Riemannian metric on $\operatorname{Imm}$

$$ g(h,k)=\int_{\mathbb{S}^1} \langle h,k\rangle ds$$

New metric $$g^L(h,k)\coloneqq g(h,Lk) $$

a suitable operator

$$L\colon T\operatorname{Imm}\to T\operatorname{Imm}. $$

e.g. $L_c=\operatorname{id}_c$,

$$g^{\operatorname{id}}_c(h,k)=\int_{\mathbb{S}^1} \langle h,k\rangle ds$$

Hint 1. Trend in shape analysis

e.g. $L_c=\operatorname{id}_c$,

$$g^{\operatorname{id}}_c(h,k)=\int_{\mathbb{S}^1} \langle h,k\rangle ds$$

e.g. $L_c=\lambda(c)$ with a conformal factor $\lambda\colon \operatorname{Imm}\to \mathbb{R}_{>0}$

$$g^{\lambda}_c(h,k)=\lambda(c)\int_{\mathbb{S}^1} \langle h,k\rangle ds$$

Hint 1. Trend in shape analysis

e.g. $L_c=\operatorname{id}_c$,

$$g^{\operatorname{id}}_c(h,k)=\int_{\mathbb{S}^1} \langle h,k\rangle ds$$

e.g. Sobolev-type differential operator $L_c=\operatorname{id}-D_s^2$

$$g^{\operatorname{id}-D_s^2}_c(h,k)=\int_{\mathbb{S}^1} \langle h,k\rangle -\langle h, D_s^2 k \rangle ds = \int_{\mathbb{S}^1} \langle h,k\rangle + \langle D_s h, D_s k \rangle ds $$

Hint 1. Trend in shape analysis

e.g. $L_c=\lambda(c)$ with a conformal factor $\lambda\colon \operatorname{Imm}\to \mathbb{R}_{>0}$

$$g^{\lambda}_c(h,k)=\lambda(c)\int_{\mathbb{S}^1} \langle h,k\rangle ds$$

Hint 2. Liouville form

i.e. there is a 1-form $\Theta$ s.t. $\Omega=d\Theta$.

Marsden-Weinstein form $\Omega$ is exact

Hint 2. Liouville form

Marsden-Weinstein form $\Omega$ is exact

$\Theta$ is given by

$$\Theta_{[c]}([h])=\frac{1}{3}\int_{\mathbb{S}^1}\langle D_s c\times c, h\rangle ds=g^{\operatorname{id}}\left(\frac{1}{3}D_s c\times c, h\right).$$

i.e. there is a 1-form $\Theta$ s.t. $\Omega=d\Theta$.

Hint 1 + Hint 2

Let's define a 1-form

$$\Theta_{[c]}^{\color{blue}L}([h])\coloneqq g^{\color{blue}L}\left(\frac{1}{3}D_s c\times c, h\right)= \frac{1}{3} \int_{\mathbb{S}^1} \langle D_s c \times c, {\color{blue}L} h\rangle ds $$

Hint 1 + Hint 2

and a 2-form $$\Omega^L\coloneqq d\Theta^L$$

Let's define a 1-form

$$\Theta_{[c]}^{\color{blue}L}([h])\coloneqq g^{\color{blue}L}\left(\frac{1}{3}D_s c\times c, h\right)= \frac{1}{3} \int_{\mathbb{S}^1} \langle D_s c \times c, {\color{blue}L} h\rangle ds $$

$$\Omega^L\coloneqq d\Theta^L$$

Does $\Omega^L$ define a symplectic structure on $\operatorname{UImm}$?

Hint 1 + Hint 2

with $\Theta_{[c]}^L([h])\coloneqq \frac{1}{3} \int_{\mathbb{S}^1} \langle D_s c \times c, L h\rangle ds $

Closeness. OK because it is exact $d\Omega^L=dd\Theta^L=0$

$$\Omega^L\coloneqq d\Theta^L$$

Does $\Omega^L$ define a symplectic structure on $\operatorname{UImm}$?

Hint 1 + Hint 2

with $\Theta_{[c]}^L([h])\coloneqq \frac{1}{3} \int_{\mathbb{S}^1} \langle D_s c \times c, L h\rangle ds $

Closeness. OK because it is exact $d\Omega^L=dd\Theta^L=0$

$$\Omega^L\coloneqq d\Theta^L$$

Does $\Omega^L$ define a symplectic structure on $\operatorname{UImm}$?

Hint 1 + Hint 2

with $\Theta_{[c]}^L([h])\coloneqq \frac{1}{3} \int_{\mathbb{S}^1} \langle D_s c \times c, L h\rangle ds $

Non-degeneracy on $\operatorname{UImm}$ ?

i.e. $\ker \Omega_c^L = [0] = \{a. D_s c \mid a \in C^\infty(\mathbb{S}^1)\}$

Closeness. OK because it is exact $d\Omega^L=dd\Theta^L=0$

$$\Omega^L\coloneqq d\Theta^L$$

Does $\Omega^L$ define a symplectic structure on $\operatorname{UImm}$?

Non-degeneracy on $\operatorname{UImm}$ ?

i.e. $\ker \Omega_c^L = [0] = \{a. D_s c \mid a \in C^\infty(\mathbb{S}^1)\}$

Need to check case by case.

Hint 1 + Hint 2

with $\Theta_{[c]}^L([h])\coloneqq \frac{1}{3} \int_{\mathbb{S}^1} \langle D_s c \times c, L h\rangle ds $

Symplectic structure

induced by a conformal factor

$$\Omega^\lambda\coloneqq d\Theta^\lambda$$

Theorem

With a conformal factor $\lambda\colon \operatorname{UImm}\to \mathbb{R}_{>0} $,

is a symplectic structure on $\operatorname{UImm}$

Symplectic structure

induced by a conformal factor

$$\Omega^\lambda\coloneqq d\Theta^\lambda$$

Theorem

With a conformal factor $\lambda\colon \operatorname{UImm}\to \mathbb{R}_{>0} $,

is a symplectic structure on $\operatorname{UImm}$

if $\Theta^\lambda$ is NOT invariant under scaling ($c\to c+t c$ with $t >0$).

Symplectic structure

induced by a conformal factor

$$\Omega^\lambda\coloneqq d\Theta^\lambda$$

Theorem

With a conformal factor $\lambda\colon \operatorname{UImm}\to \mathbb{R}_{>0} $,

is a symplectic structure on $\operatorname{UImm}$

If $\Theta^\lambda$ is invariant under scaling, $\Omega^\lambda$ is NOT symplectic on $\operatorname{UImm}$,

but becomes symplectic in another space! (Check out our paper)

if $\Theta^\lambda$ is NOT invariant under scaling ($c\to c+t c$ with $t >0$).

Open problem

Is there a non-conformal $L$ making $\Omega^L\coloneqq d\Theta^L$ symplectic?

Open problem

Is there a non-conformal $L$ making $\Omega^L\coloneqq d\Theta^L$ symplectic?

Conjecture

Squared curvature $L|_\theta=1+\kappa^2_c(\theta)$ defines a symplectic structure.

Open problem

Is there a non-conformal $L$ making $\Omega^L\coloneqq d\Theta^L$ symplectic?

Conjecture

Squared curvature $L|_\theta=1+\kappa^2_c(\theta)$ defines a symplectic structure.

Result in preparation

Squared scale $L|_\theta=|c(\theta)|^2$ defines a symplectic structure.

Remember, different symplectic structures induce different dynamics $V_H$ from the same Hamiltonian $H$.

Hamiltonian dynamics from $\Omega^\lambda$

Remember, different symplectic structures induce different dynamics $V_H$ from the same Hamiltonian $H$.

Hamiltonian dynamics from $\Omega^\lambda$

From $\Omega^\lambda$ with a conformal factor $\lambda\colon \operatorname{UImm}\to \mathbb{R}_{>0}$, we get

$V_H$

(Marsden-Weinstein)

$\Omega^{\operatorname{id}}$

$\Omega^{\operatorname{Length}([c])^{-1/10}}$

$\Omega^{\operatorname{Length}([c])^{2}}$

Simulation of Hamiltonian dynamics

Hamiltonian dynamics $V_H$ of total squared-scale $$H([c])=\int_{\mathbb{S}^1}|c|^2 ds$$

$H$ is preserved in all of them.

Our paper has a disclaimer

We do not guarantee any correctness of (even short-time behavior) dynamics in our simulation

Simulation of Hamiltonian dynamics

Future work

Symplectic structure on the space of discrete space curves?

Toward a symplectic integrator for space curves.

Our paper has a disclaimer

We do not guarantee any correctness of (even short-time behavior) dynamics in our simulation

Simulation of Hamiltonian dynamics

Other spaces?

The linear Schrödinger equation

$$i\partial_t \psi + \Delta \psi =0$$

Other spaces?

The linear Schrödinger equation

$$i\partial_t \psi + \Delta \psi =0$$
is the Hamiltonian flow for $$H(\psi)=\int\frac{1}{2} |\nabla\psi|^2 dx $$

Other spaces?

The linear Schrödinger equation

$$i\partial_t \psi + \Delta \psi =0$$
is the Hamiltonian flow for $$H(\psi)=\int\frac{1}{2} |\nabla\psi|^2 dx $$

on the space of wave functions $X=C^\infty(\mathbb{T}^d,\mathbb{C})$

Other spaces?

$$\Omega_\psi(h,k)=\int \operatorname{Im} h\bar k \ dx\quad \quad h,k \in T_\psi X=C^\infty(\mathbb{T}^d,\mathbb{C}) $$

with a symplectic structure $\Omega$

More symplectic structures?

This symplectic structure $\Omega$ has a Liouville form $\Theta$

i.e. $\Omega=d\Theta$.

More symplectic structures?

This symplectic structure $\Omega$ has a Liouville form $\Theta$

i.e. $\Omega=d\Theta$.

Can get more symplectic structures by

$$\Omega^L=d\Theta^L$$

with different operators $L\colon TC^\infty(\mathbb{T}^d,\mathbb{C})\to T C^\infty(\mathbb{T}^d,\mathbb{C})$ ?

More symplectic structures?

This symplectic structure $\Omega$ has a Liouville form $\Theta$

i.e. $\Omega=d\Theta$.

Can get more symplectic structures by

$$\Omega^L=d\Theta^L$$

with different operators $L\colon TC^\infty(\mathbb{T}^d,\mathbb{C})\to T C^\infty(\mathbb{T}^d,\mathbb{C})$ ?

Yes, and it has a consequence.

Can we do the same job?

The 2-form $$\Omega_\psi(h,k)=\int \operatorname{Im} h\bar k \ dx$$ has a Liouville form
$$\Theta_\psi(h)= - \frac{1}{2}\int \operatorname{Im} h \bar\psi\ dx$$

Let's apply $L=1-a_1\Delta+a_2\Delta^2-\cdots \pm a_n \Delta^n$ to $\Theta$ with $a_1,\ldots, a_n \geq 0$ to define $$ \Theta^{L}_\psi(h)=\int \operatorname{Im} (1-a_1\Delta+a_2\Delta^2-\cdots \pm a_n \Delta^n) h \bar\psi\ dx$$

Then $\Omega^L\coloneqq d\Theta^L$ defines a symplectic form!

Do the same job

With $\Omega^L$ for $L=1-a_1\Delta-a_2\Delta^2-\cdots - a_n \Delta^n$ we get

$$i\partial_t \psi + (1-a_1\Delta-a_2\Delta^2-\cdots - a_n \Delta^n)^{-1}\Delta \psi =0$$

as the Hamiltonian flow of $$H(\psi)=\int\frac{1}{2} |\nabla\psi|^2 dx $$

Hamiltonian flows

Proposition

Family of equations

$$i\partial_t \psi + (1-a_1\Delta+a_2\Delta^2-\cdots \pm a_n \Delta^n)^{\textcolor{red}{-1}}\Delta \psi =0$$

for different choices of coefs $a_1,\ldots,a_n\geq 0$

Hamiltonian flows

Proposition

Family of equations

$$i\partial_t \psi + (1-a_1\Delta+a_2\Delta^2-\cdots \pm a_n \Delta^n)^{\textcolor{red}{-1}}\Delta \psi =0$$

for different choices of coefs $a_1,\ldots,a_n\geq 0$ are

the Hamiltonian systems for the same Hamiltonian

$$H(\psi)=\int\frac{1}{2} |\nabla\psi|^2 dx $$

but for different symplectic structures on $C^\infty(\mathbb{T}^d,\mathbb{C})$.

Hamiltonian flows

$$i\partial_t \psi + (1-a_1\Delta+a_2\Delta^2-\cdots \pm a_n \Delta^n)^{-1}\Delta \psi =0$$

are all explicitly solvable.

Hamiltonian flows

$i\partial_t \psi + \Delta \psi =0$

Schrödinger equation

$$i\partial_t \psi + (1-a_1\Delta+a_2\Delta^2-\cdots \pm a_n \Delta^n)^{-1}\Delta \psi =0$$

are all explicitly solvable.

Hamiltonian flows

$i\partial_t \psi + \Delta \psi =0$

$i\partial_t \psi + (1-a_1 \textcolor{blue}{\Delta})^{-1}\Delta \psi =0$

Schrödinger equation

somewhat blurred?

$$i\partial_t \psi + (1-a_1\Delta+a_2\Delta^2-\cdots \pm a_n \Delta^n)^{-1}\Delta \psi =0$$

are all explicitly solvable.

Hamiltonian flows

$i\partial_t \psi + \Delta \psi =0$

$i\partial_t \psi + (1-a_1 \textcolor{blue}{\Delta})^{-1}\Delta \psi =0$

$i\partial_t \psi + (1+a_2\textcolor{blue}{ \Delta^2})^{-1}\Delta \psi =0$

Schrödinger equation

somewhat blurred?

direction reversed!?

$$i\partial_t \psi + (1-a_1\Delta+a_2\Delta^2-\cdots \pm a_n \Delta^n)^{-1}\Delta \psi =0$$

are all explicitly solvable.

Why care?

$$i\partial_t \psi+ \sqrt{1-\Delta} \ \psi =0$$

Semi-relativistic Schrödinger equation

Why care?

$$i\partial_t \psi+ \sqrt{1-\Delta} \ \psi =0$$

Semi-relativistic Schrödinger equation

is usually obtained from the standard symplectic structure $\Omega$ and the modified Hamiltonian

$$\tilde H(\psi)=\sqrt{f(H(\psi)^2)+c^2}$$

with a certain function $f$ and light speed $c$.

Why care?

Can we get the semi-relativistic equation

without changing the Hamiltonian but changing the symplectic structure?

$$i\partial_t \psi+ \sqrt{1-\Delta} \ \psi =0$$

Yes.

And can be obtained as the limit of flows $\{V_H^n\}_n$ induced from structures $\{\Omega_n\}_n$,

Why care?

Yes.

And can be obtained as the limit of flows $\{V_H^n\}_n$ induced from structures $\{\Omega_n\}_n$,

$$\Omega^n(h,k)=\int \frac{|\xi|^2}{1+b_1|\xi|^2 - b_2 |\xi|^4 + \ldots \pm b_n |\xi|^{2n}} \operatorname{Im} \mathcal{F}h(\xi) \overline{\mathcal{F}k} (\xi) d\xi$$

with some coefficients $\{b_i\}_i$.

Why care?

Conclusion

A method to introduce different symplectic structures.

Conclusion

Consequence

Different dynamics form the same Hamiltonian
Same system from different settings $(\Omega_A, H_A)$ and $(\Omega_B, H_B)$.

A method to introduce different symplectic structures.

Conclusion

Consequence

Different dynamics form the same Hamiltonian
Same system from different settings $(\Omega_A, H_A)$ and $(\Omega_B, H_B)$.

A method to introduce different symplectic structures.

Potential applications?

Modeling many phenomena
Investigating many conserved quantities

Future work A

Do the same machinery to find more symplectic structures on other $\infty$-dim manifolds.

Future direction

Toward a paradigm for modeling dynamics by varying not only the Hamiltonian but the geometric (symplectic) structure of state spaces.

Future work

Our paper has a disclaimer

We do not guarantee any correctness of (even short-time behavior) dynamics in our simulation

Thanks!

- Space curves: preprint on arXiv 2407.19908

- Wave functions: in-preparation

Sadashige.Ishida@ist.ac.at

More symplectic structures

on the space of space curves

(and the space of wave functions)

Purpose of this talk

Introduction to myself

Introduction to myself

Introduction to myself

Introduction to myself

Introduction to myself

Introduction to myself

Introduction to myself

Introduction to myself

Overview

Joint with

Overview

Symplectic structure is a sandbox

for Hamiltonian dynamics

Symplectic structure is a sandbox

for Hamiltonian dynamics

Symplectic structure is a sandbox

for Hamiltonian dynamics

Symplectic structure is a sandbox

for Hamiltonian dynamics

Symplectic structure is a sandbox

for Hamiltonian dynamics

Symplectic structure is a sandbox

for Hamiltonian dynamics

Symplectic structure is a sandbox

for Hamiltonian dynamics

Symplectic structure is a sandbox

for Hamiltonian dynamics

Symplectic structure is a sandbox

for Hamiltonian dynamics

Why Hamiltonian dynamics?

Spaces with symplectic structures

and Hamiltonian dynamics

Spaces with symplectic structures

and Hamiltonian dynamics

Spaces with symplectic structures

and Hamiltonian dynamics

Spaces with symplectic structures

and Hamiltonian dynamics

The space of space curves

The space of space curves

The space of space curves

The space of space curves

The space of space curves

The space of space curves

The space of space curves

Canonical symplectic structure on \(\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)\)

Canonical symplectic structure on \(\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)\)

Canonical symplectic structure on \(\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)\)

Canonical symplectic structure on \(\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)\)

Canonical symplectic structure on \(\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)\)

Hamiltonian flow

Hamiltonian flow

More symplectic structures?

More symplectic structures?

More symplectic structures?

More symplectic structures?

More symplectic structures?

More symplectic structures?

Hint 1. Trend in shape analysis

Hint 1. Trend in shape analysis

Hint 1. Trend in shape analysis

Hint 1. Trend in shape analysis

Hint 1. Trend in shape analysis

Hint 1. Trend in shape analysis

Hint 1. Trend in shape analysis

Hint 2. Liouville form

Hint 2. Liouville form

Hint 1 + Hint 2

Hint 1 + Hint 2

Hint 1 + Hint 2

Hint 1 + Hint 2

Hint 1 + Hint 2

Hint 1 + Hint 2

Symplectic structure

induced by a conformal factor

Symplectic structure