Underline = Cmd+u
More symplectic structures
on the space of space curves
Joint with Martin Bauer & Peter Michor
September 2024 @ TU Wien
Sadashige Ishida (ISTA)

Introduction to myself
Sadashige, a PhD student @ ISTA (near Vienna)
Introduction to myself
Geometry & Dynamics in Math, Physics, CS
Sadashige, a PhD student @ ISTA (near Vienna)
Introduction to myself
Geometry & Dynamics in Math, Physics, CS
Sadashige, a PhD student @ ISTA (near Vienna)
Dynamics as \(\infty\)-dim geometry
e.g. fluids, optimal transport, shapes
Introduction to myself
Geometry & Dynamics in Math, Physics, CS
Sadashige, a PhD student @ ISTA (near Vienna)
Dynamics as \(\infty\)-dim geometry
e.g. fluids, optimal transport, shapes
+ their finite-dim approximations
a.k.a. discretization
Introduction to myself
Looking for a postgraduate/research fellow position starting late 2025
Dynamics as \(\infty\)-dim geometry
e.g. fluids, optimal transport, shapes
Geometry & Dynamics in Math, Physics, CS
+ their finite-dim approximations
a.k.a. discretization
Sadashige, a PhD student @ ISTA (near Vienna)
Overview
On the space of space curves, only one symplectic structure was known.
We found more.
Symplectic structure is a sandbox
for Hamiltonian dynamics
Space with
a symplectic structure \(\Omega\)
A function \(H\)
Dynamics \(V_H\)
Symplectic structure is a sandbox
for Hamiltonian dynamics
A symplectic structure \(\Omega\) is a 2-form on a manifold \(X\) s.t.
Symplectic structure is a sandbox
for Hamiltonian dynamics
A symplectic structure \(\Omega\) is a 2-form on a manifold \(X\) s.t.
- closed i.e. \(d\Omega=0\)
Symplectic structure is a sandbox
for Hamiltonian dynamics
A symplectic structure \(\Omega\) is a 2-form on a manifold \(X\) s.t.
- non-degenerate i.e. the map $$\flat: TX\to T^*X$$ $$ \qquad v\to \Omega(v, \cdot )$$ is injective
- closed i.e. \(d\Omega=0\)
Symplectic structure is a sandbox
for Hamiltonian dynamics
Symplectic structure is a sandbox
for Hamiltonian dynamics
For \(H \colon X\to \mathbb{R}\),
Hamiltonian vector field \(V_H\in \Gamma(TM)\) is the one
$$ dH = \Omega(V_H, \cdot). $$
Symplectic structure is a sandbox
for Hamiltonian dynamics
For \(H \colon X\to \mathbb{R}\),
Hamiltonian vector field \(V_H\in \Gamma(TM)\) is the one
$$ dH = \Omega(V_H, \cdot). $$
The Hamiltonian dynamics
$$\dot x=V_H(x).$$
Why Hamiltonian dynamics?
Has nice properties.
E.g.
- \(H\) is preserved in dynamics.
- If \(H\) is invariant under some group action, there is a conserved quantity.
Spaces with symplectic structures
and Hamiltonian dynamics
\(T^*M^n\)
\(T^*\operatorname{SDiff}(M)\)
Celestial mechanics
\(C^\infty(M,\mathbb{C})\)
Schrödinger equation
Incompressible fluids
Spaces with symplectic structures
and Hamiltonian dynamics
\(T^*M^n\)
\(T^*\operatorname{SDiff}(M)\)
\(C^\infty(M,\mathbb{C})\)
Schrödinger equation
Incompressible fluids
Space curves
Celestial mechanics
The space of space curves
$$\operatorname{Imm}(\mathbb{S}^1,\mathbb{R}^3)=\{ c\colon \mathbb{S}^1\to\mathbb{R}^3, \partial_\theta c\neq 0 \ \forall \theta\in\mathbb{S}^1 \}$$
Parametrized curves
The space of space curves
$$\operatorname{Imm}(\mathbb{S}^1,\mathbb{R}^3)=\{ c\colon \mathbb{S}^1\to\mathbb{R}^3, \partial_\theta c\neq 0 \ \forall \theta\in\mathbb{S}^1 \}$$
Parametrized curves
$$T_c\operatorname{Imm}(\mathbb{S}^1,\mathbb{R}^3)=C^\infty(\mathbb{S}^1,\mathbb{R}^3)$$
Tangent space

The space of space curves
$$\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)=\operatorname{Imm}(\mathbb{S}^1,\mathbb{R}^3)/\operatorname{Diff}^+(\mathbb{S}^1)$$
Unparametrized curves a.k.a. shape space
The space of space curves
$$\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)=\operatorname{Imm}(\mathbb{S}^1,\mathbb{R}^3)/\operatorname{Diff}^+(\mathbb{S}^1)$$
Unparametrized curves a.k.a. shape space
$$\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)$$
$$\operatorname{Imm}(\mathbb{S}^1,\mathbb{R}^3)$$
\[\Bigg\downarrow \pi\]
\[\curvearrowright\]
$$\operatorname{Diff}^+(\mathbb{S}^1)$$
The space of space curves
$$\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)=\operatorname{Imm}(\mathbb{S}^1,\mathbb{R}^3)/\operatorname{Diff}^+(\mathbb{S}^1)$$
Unparametrized curves a.k.a. shape space
Tangent space
$$T_{[c]}\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)=T_c\operatorname{Imm}(\mathbb{S}^1,\mathbb{R}^3)/\ker d\pi_c$$
$$\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)$$
$$\operatorname{Imm}(\mathbb{S}^1,\mathbb{R}^3)$$
\[\Bigg\downarrow \pi\]
\[\curvearrowright\]
$$\operatorname{Diff}^+(\mathbb{S}^1)$$
The space of space curves
$$\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)=\operatorname{Imm}(\mathbb{S}^1,\mathbb{R}^3)/\operatorname{Diff}^+(\mathbb{S}^1)$$
Unparametrized curves a.k.a. shape space
Tangent space
$$T_{[c]}\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)=T_c\operatorname{Imm}(\mathbb{S}^1,\mathbb{R}^3)/\ker d\pi_c$$
$$\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)$$
$$\operatorname{Imm}(\mathbb{S}^1,\mathbb{R}^3)$$
\[\Bigg\downarrow \pi\]
\[\curvearrowright\]
$$\operatorname{Diff}^+(\mathbb{S}^1)$$
\(\{a.\partial_\theta c \mid a\in C^\infty(\mathbb{S}^1)\}\)
curve tangent
The space of space curves
$$\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)=\operatorname{Imm}(\mathbb{S}^1,\mathbb{R}^3)/\operatorname{Diff}^+(\mathbb{S}^1)$$
Unparametrized curves a.k.a. shape space
Tangent space
$$T_{[c]}\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)=T_c\operatorname{Imm}(\mathbb{S}^1,\mathbb{R}^3)/\ker d\pi_c$$
$$\eqsim\{h \in T_c \operatorname{Imm}(\mathbb{S}^1,\mathbb{R}^3)\mid h\perp \partial_\theta c \}$$
$$\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)$$
$$\operatorname{Imm}(\mathbb{S}^1,\mathbb{R}^3)$$
\[\Bigg\downarrow \pi\]
\[\curvearrowright\]
$$\operatorname{Diff}^+(\mathbb{S}^1)$$
\(\{a.\partial_\theta c \mid a\in C^\infty(\mathbb{S}^1)\}\)
curve tangent
Symplectic structure
\[\Omega_c\colon T_c\operatorname{Imm}\times T_c\operatorname{Imm}\to \mathbb{R}\]
\[\Omega_c(h,k)=\int_{\mathbb{S}^1}\langle D_s c\times h, k\rangle ds\]
where
\[D_s = \frac{\partial_\theta }{|\partial_\theta c|}, \quad ds = |\partial_\theta c| d\theta \]
Closed (\(d\Omega=0\)),
Degenerate with
\(\ker \Omega_{[c]}= \ker d\pi_c= \{a. D_s c\mid a \in C^\infty(\mathbb{S}^1)\}\)
Symplectic?
On \(\operatorname{Imm}(\mathbb{S}^1,\mathbb{R}^3)\),
Canonical symplectic structure on \(\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)\)
The Marsden-Weinstein structure
\[\Omega_{[c]}\colon T_{[ c]}\operatorname{UImm}\times T_{[ c]}\operatorname{UImm}\to \mathbb{R},\]
Canonical symplectic structure on \(\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)\)
\[\Omega_{[c]}\colon T_{[ c]}\operatorname{UImm}\times T_{[ c]}\operatorname{UImm}\to \mathbb{R},\]
The Marsden-Weinstein structure
\[\Omega_{[c]}([h],[k])=\int_{\mathbb{S}^1}\langle D_s c\times h, k\rangle ds\]
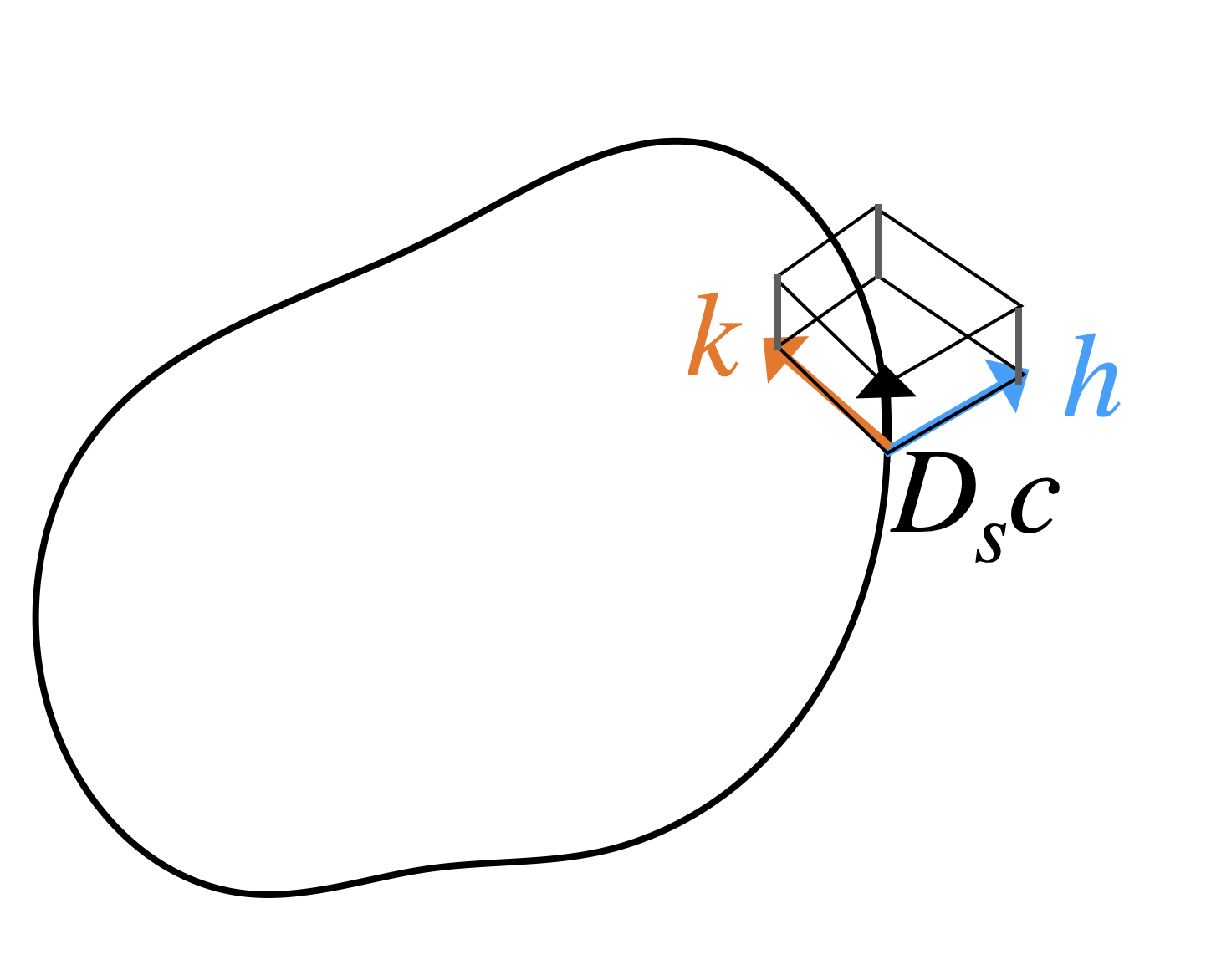
where
\[D_s = \frac{\partial_\theta }{|\partial_\theta c|}, \quad ds = |\partial_\theta c| d\theta \]
unit tangent
Canonical symplectic structure on \(\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)\)
\[\Omega_{[c]}\colon T_{[ c]}\operatorname{UImm}\times T_{[ c]}\operatorname{UImm}\to \mathbb{R},\]
Symplectic!
The Marsden-Weinstein structure
\[\Omega_{[c]}([h],[k])=\int_{\mathbb{S}^1}\langle D_s c\times h, k\rangle ds\]
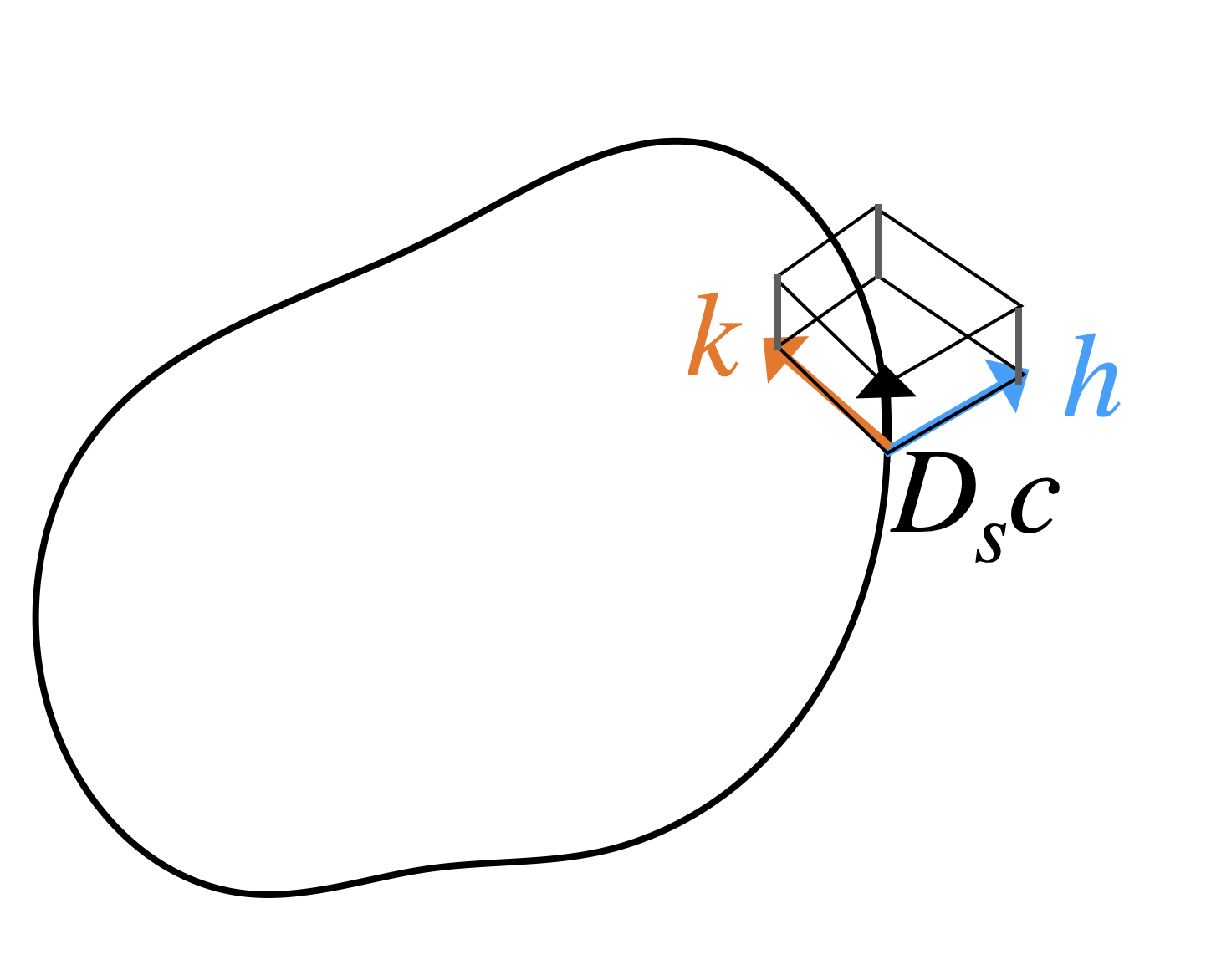
where
\[D_s = \frac{\partial_\theta }{|\partial_\theta c|}, \quad ds = |\partial_\theta c| d\theta \]
unit tangent
Canonical symplectic structure on \(\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)\)
\[\Omega_{[c]}\colon T_{[ c]}\operatorname{UImm}\times T_{[ c]}\operatorname{UImm}\to \mathbb{R},\]
Closed \(d\Omega=0\),
Symplectic!
The Marsden-Weinstein structure
\[\Omega_{[c]}([h],[k])=\int_{\mathbb{S}^1}\langle D_s c\times h, k\rangle ds\]
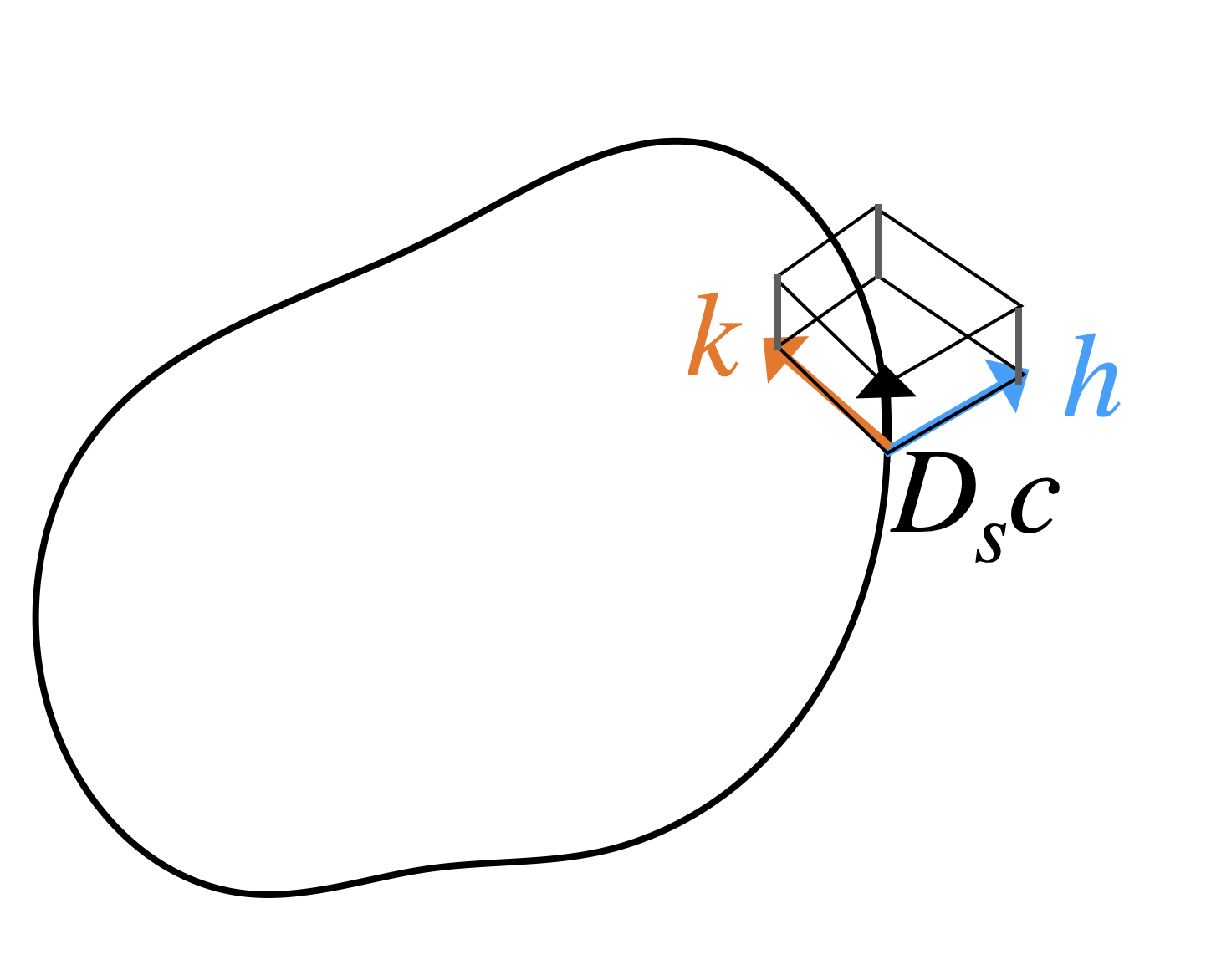
where
\[D_s = \frac{\partial_\theta }{|\partial_\theta c|}, \quad ds = |\partial_\theta c| d\theta \]
unit tangent
Canonical symplectic structure on \(\operatorname{UImm}(\mathbb{S}^1,\mathbb{R}^3)\)
\[\Omega_{[c]}\colon T_{[ c]}\operatorname{UImm}\times T_{[ c]}\operatorname{UImm}\to \mathbb{R},\]
Closed \(d\Omega=0\),
Symplectic!
The Marsden-Weinstein structure
\[\Omega_{[c]}([h],[k])=\int_{\mathbb{S}^1}\langle D_s c\times h, k\rangle ds\]
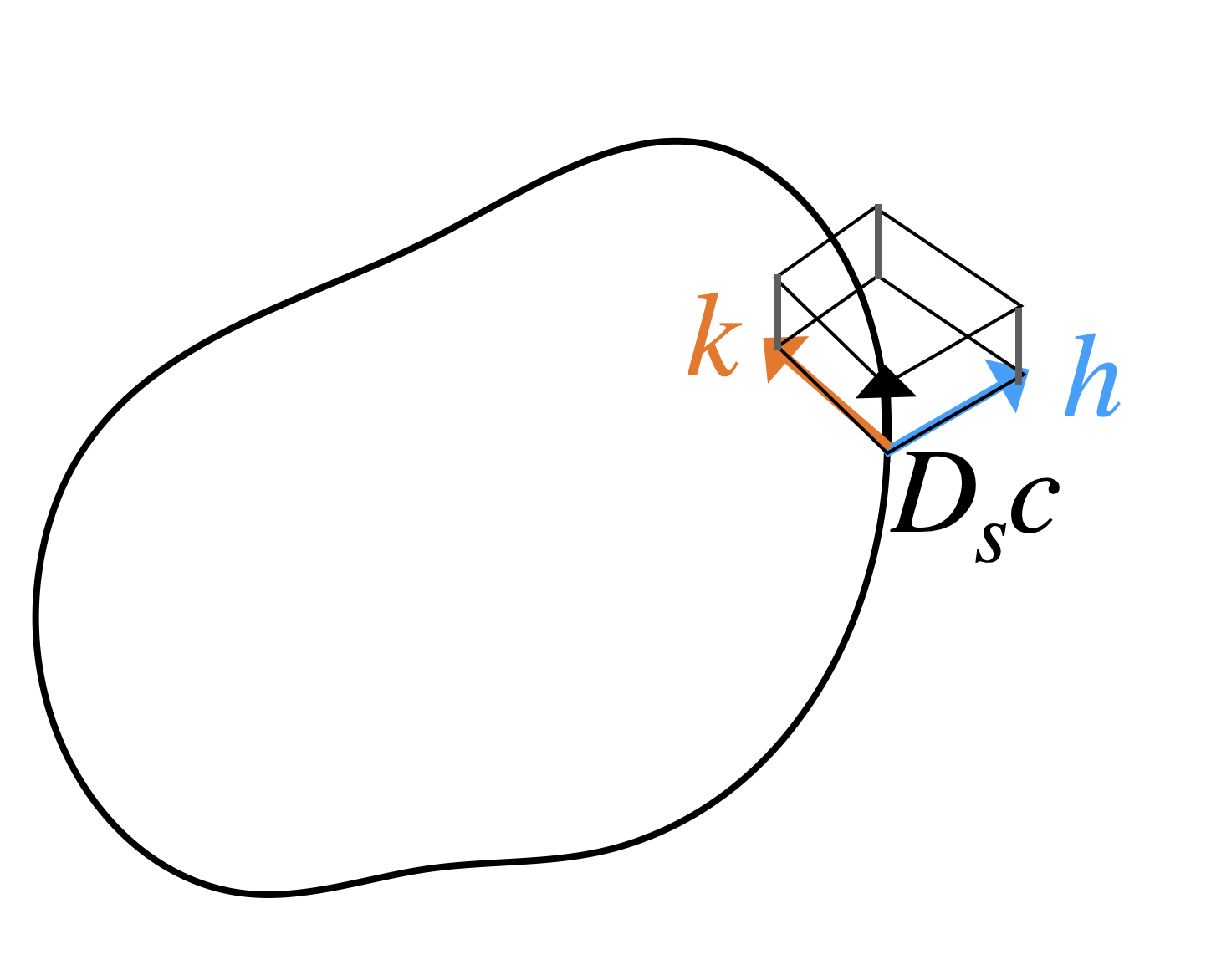
where
\[D_s = \frac{\partial_\theta }{|\partial_\theta c|}, \quad ds = |\partial_\theta c| d\theta \]
Non-degenerate \(\ker \Omega_{[c]}=[0]=\{a.D_s c \mid a \in C^\infty(\mathbb{S}^1)\}\)
unit tangent
Hamiltonian flow
E.g.
Hamiltonian \(H = \operatorname{Length}([c])\)
Binormal flow
Dynamics \(V_H=[D_s c \times D_s^2 c]\)
Hamiltonian flow
E.g.
Hamiltonian \(H = \operatorname{Length}([c])\)
Binormal flow
Dynamics \(V_H=[D_s c \times D_s^2 c]\)
A completely integrable system
More symplectic structures?
More symplectic structures?
Remember
A symplectic structure \(\Omega\) defines a Hamiltonian dynamics \(V_H\) via $$dH=\Omega(V_H,\cdot).$$
More symplectic structures?
A different \(\Omega\) defines different \(V_H\).
Remember
A symplectic structure \(\Omega\) defines a Hamiltonian dynamics \(V_H\) via $$dH=\Omega(V_H,\cdot).$$
More symplectic structures?
A different \(\Omega\) defines different \(V_H\).
But only one \(\Omega\) is known on \(\operatorname{UImm}\).
Remember
A symplectic structure \(\Omega\) defines a Hamiltonian dynamics \(V_H\) via $$dH=\Omega(V_H,\cdot).$$
More symplectic structures?
A different \(\Omega\) defines different \(V_H\).
We found more.
But only one \(\Omega\) is known on \(\operatorname{UImm}\).
Remember
A symplectic structure \(\Omega\) defines a Hamiltonian dynamics \(V_H\) via $$dH=\Omega(V_H,\cdot).$$
Hint 1. Trend in shape analysis
Hint 1. Trend in shape analysis
a Riemannian metric on \(\operatorname{Imm}\)
$$ g(h,k)=\int_{\mathbb{S}^1} \langle h,k\rangle ds$$
Hint 1. Trend in shape analysis
a Riemannian metric on \(\operatorname{Imm}\)
$$ g(h,k)=\int_{\mathbb{S}^1} \langle h,k\rangle ds$$
a suitable operator
$$L\colon T\operatorname{Imm}\to T\operatorname{Imm}. $$
Hint 1. Trend in shape analysis
a Riemannian metric on \(\operatorname{Imm}\)
$$ g(h,k)=\int_{\mathbb{S}^1} \langle h,k\rangle ds$$
New metric $$g^L(h,k)\coloneqq g(h,Lk) $$
a suitable operator
$$L\colon T\operatorname{Imm}\to T\operatorname{Imm}. $$
e.g. \(L_c=\operatorname{id}_c\),
$$g^{\operatorname{id}}_c(h,k)=\int_{\mathbb{S}^1} \langle h,k\rangle ds$$
Hint 1. Trend in shape analysis
e.g. \(L_c=\operatorname{id}_c\),
$$g^{\operatorname{id}}_c(h,k)=\int_{\mathbb{S}^1} \langle h,k\rangle ds$$
e.g. \(L_c=\lambda(c)\) with a conformal factor \(\lambda\colon \operatorname{Imm}\to \mathbb{R}_{>0}\)
$$g^{\lambda}_c(h,k)=\lambda(c)\int_{\mathbb{S}^1} \langle h,k\rangle ds$$
Hint 1. Trend in shape analysis
e.g. \(L_c=\operatorname{id}_c\),
$$g^{\operatorname{id}}_c(h,k)=\int_{\mathbb{S}^1} \langle h,k\rangle ds$$
e.g. Sobolev-type differential operator \(L_c=\operatorname{id}-D_s^2\)
$$g^{\operatorname{id}-D_s^2}_c(h,k)=\int_{\mathbb{S}^1} \langle h,k\rangle -\langle h, D_s^2 k \rangle ds = \int_{\mathbb{S}^1} \langle h,k\rangle + \langle D_s h, D_s k \rangle ds $$
Hint 1. Trend in shape analysis
e.g. \(L_c=\lambda(c)\) with a conformal factor \(\lambda\colon \operatorname{Imm}\to \mathbb{R}_{>0}\)
$$g^{\lambda}_c(h,k)=\lambda(c)\int_{\mathbb{S}^1} \langle h,k\rangle ds$$
Hint 2. Liouville form
\(\Omega\) is exact
i.e. there is a 1-form \(\Theta\) s.t. \(\Omega=d\Theta\).
Hint 2. Liouville form
\(\Omega\) is exact
\(\Theta\) is given by
$$\Theta_{[c]}([h])=\frac{1}{3}\int_{\mathbb{S}^1}\langle D_s c\times c, h\rangle ds=g^{\operatorname{id}}\left(\frac{1}{3}D_s c\times c, h\right).$$
i.e. there is a 1-form \(\Theta\) s.t. \(\Omega=d\Theta\).
Hint 1 + Hint 2
Let's define a 1-form
$$\Theta_{[c]}^{\color{blue}L}([h])\coloneqq g^{\color{blue}L}\left(\frac{1}{3}D_s c\times c, h\right)= \frac{1}{3} \int_{\mathbb{S}^1} \langle D_s c \times c, {\color{blue}L} h\rangle ds $$
Hint 1 + Hint 2
and a 2-form $$\Omega^L\coloneqq d\Theta^L$$
Let's define a 1-form
$$\Theta_{[c]}^{\color{blue}L}([h])\coloneqq g^{\color{blue}L}\left(\frac{1}{3}D_s c\times c, h\right)= \frac{1}{3} \int_{\mathbb{S}^1} \langle D_s c \times c, {\color{blue}L} h\rangle ds $$
$$\Omega^L\coloneqq d\Theta^L$$
Does \(\Omega^L\) define a symplectic structure on \(\operatorname{UImm}\)?.
Hint 1 + Hint 2
with \(\Theta_{[c]}^L([h])\coloneqq \frac{1}{3} \int_{\mathbb{S}^1} \langle D_s c \times c, L h\rangle ds \)
Closeness. OK because it is exact \(d\Omega^L=dd\Theta^L=0\)
$$\Omega^L\coloneqq d\Theta^L$$
Does \(\Omega^L\) define a symplectic structure on \(\operatorname{UImm}\)?.
Hint 1 + Hint 2
with \(\Theta_{[c]}^L([h])\coloneqq \frac{1}{3} \int_{\mathbb{S}^1} \langle D_s c \times c, L h\rangle ds \)
Closeness. OK because it is exact \(d\Omega^L=dd\Theta^L=0\)
$$\Omega^L\coloneqq d\Theta^L$$
Does \(\Omega^L\) define a symplectic structure on \(\operatorname{UImm}\)?.
Hint 1 + Hint 2
with \(\Theta_{[c]}^L([h])\coloneqq \frac{1}{3} \int_{\mathbb{S}^1} \langle D_s c \times c, L h\rangle ds \)
Non-degeneracy on \(\operatorname{UImm}\) ?
i.e. \(\ker \Omega_c^L = [0] = \{a. D_s c \mid a \in C^\infty(\mathbb{S}^1)\}\)
Closeness. OK because it is exact \(d\Omega^L=dd\Theta^L=0\)
$$\Omega^L\coloneqq d\Theta^L$$
Does \(\Omega^L\) define a symplectic structure on \(\operatorname{UImm}\)?.
Non-degeneracy on \(\operatorname{UImm}\) ?
i.e. \(\ker \Omega_c^L = [0] = \{a. D_s c \mid a \in C^\infty(\mathbb{S}^1)\}\)
Need to check case by case.
Hint 1 + Hint 2
with \(\Theta_{[c]}^L([h])\coloneqq \frac{1}{3} \int_{\mathbb{S}^1} \langle D_s c \times c, L h\rangle ds \)
Symplectic structure
induced by a conformal factor
$$\Omega^\lambda\coloneqq d\Theta^\lambda$$
Theorem
With a conformal factor \(\lambda\colon \operatorname{UImm}\to \mathbb{R}_{>0} \),
is a symplectic structure on \(\operatorname{UImm}\)
Symplectic structure
induced by a conformal factor
$$\Omega^\lambda\coloneqq d\Theta^\lambda$$
Theorem
With a conformal factor \(\lambda\colon \operatorname{UImm}\to \mathbb{R}_{>0} \),
is a symplectic structure on \(\operatorname{UImm}\)
if \(\Theta^\lambda\) is NOT invariant under scaling (\(c\to c+t c\) with \(t \in \mathbb{R}^\times\)).
Symplectic structure
induced by a conformal factor
$$\Omega^\lambda\coloneqq d\Theta^\lambda$$
Theorem
With a conformal factor \(\lambda\colon \operatorname{UImm}\to \mathbb{R}_{>0} \),
is a symplectic structure on \(\operatorname{UImm}\)
If \(\Theta^\lambda\) is invariant under scaling, \(\Omega^\lambda\) is NOT symplectic on \(\operatorname{UImm}\),
but becomes symplectic in another space! (Check out our paper)
if \(\Theta^\lambda\) is NOT invariant under scaling (\(c\to c+t c\) with \(t \in \mathbb{R}^\times\)).
Open problem
Is there a non-conformal \(L\) making \(\Omega^L\coloneqq d\Theta^L\) symplectic?
Open problem
Is there a non-conformal \(L\) making \(\Omega^L\coloneqq d\Theta^L\) symplectic?
Conjecture
Squared curvature \(L|_\theta=1+\kappa^2_c(\theta)\) defines a symplectic structure.
Open problem
Is there a non-conformal \(L\) making \(\Omega^L\coloneqq d\Theta^L\) symplectic?
Conjecture
Squared curvature \(L|_\theta=1+\kappa^2_c(\theta)\) defines a symplectic structure.
Result in preparation
Squared scale \(L|_\theta=|c(\theta)|^2\) defines a symplectic structure.
Simulation of Hamiltonian dynamics
Remember, different symplectic structures induce different dynamics from the same Hamiltonian.
(Marsden-Weinstein)
\(\Omega_c^{\operatorname{id}}\)
\(\Omega_c^{\operatorname{Length}(c)^{-1/10}}\)
\(\Omega_c^{\operatorname{Length}(c)^{2}}\)
Simulation of Hamiltonian dynamics
Hamiltonian dynamics \(V_H\) of total squared-scale $$H(c)=\int_{\mathbb{S}^1}|c|^2 ds$$
\(H\) is preserved in all of them.
Future work A
Do the same machinery to find more symplectic structures on other \(\infty\)-dim manifolds.
Future work
Future work
Our paper has a disclaimer
We do not guarantee any correctness of (even short-time behavior) dynamics in our simulation
Future work
Symplectic structure on the space of discrete space curves?
Toward a symplectic integrator for space curves
Our paper has a disclaimer
We do not guarantee any correctness of (even short-time behavior) dynamics in our simulation
Future work
Symplectic structure on the space of discrete space curves?
Toward a symplectic integrator for space curves
Looking for a collaborator!
Our paper has a disclaimer
We do not guarantee any correctness of (even short-time behavior) dynamics in our simulation
Thanks!
Preprint: arXiv 2407.19908
Sadashige.Ishida@ist.ac.at
