資料結構
Data Structure
講師


- 225賴柏宇
- 海之音、小海或其他類似的
- 初選 PC Debug 一小時沒過
- 表達能力差,不懂要問
- INFOR 36th 學術長
- 學弟加資訊社

目錄
補充
定義及概念
Definition
更加方便...
- 電腦組織、儲存資料的方式
- 優化特定操作
- 紀錄一些資訊,讓以後存取更加方便
- 每種狀況有對應的資料結構
- 「程式 = 演算法 + 資料結構」
- 目的性強,因此採目的導向講解
舉個例子
- 員工薪資紀錄:將字串對應到數字
- 應用字典樹加快存取
複習
暑假資讀 語法 & STL
前綴和/差分
- 前綴和:
- 取區間和
- 差分:
- 修改, 求值
樹狀結構
- Set/Map: 插入/刪除
- priority_queue: 插入/刪除最值
取最值
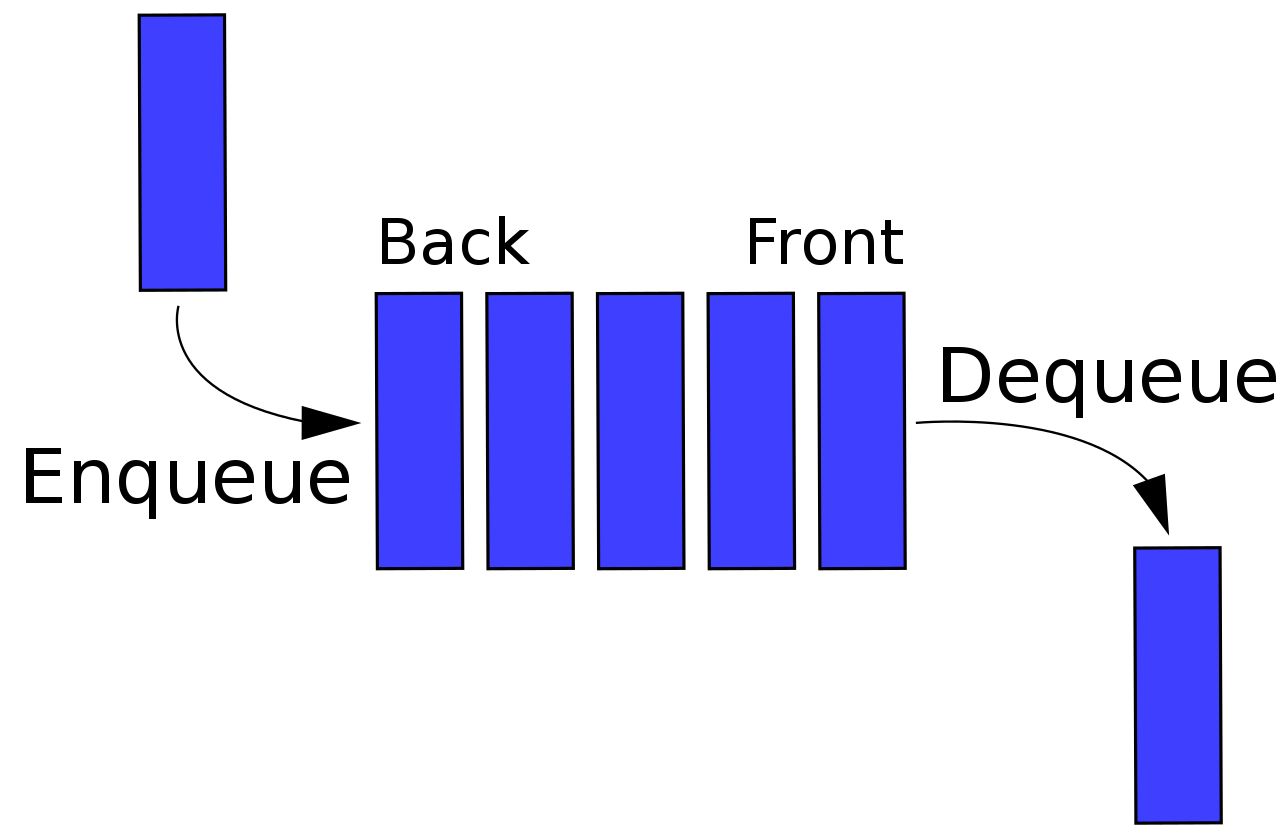
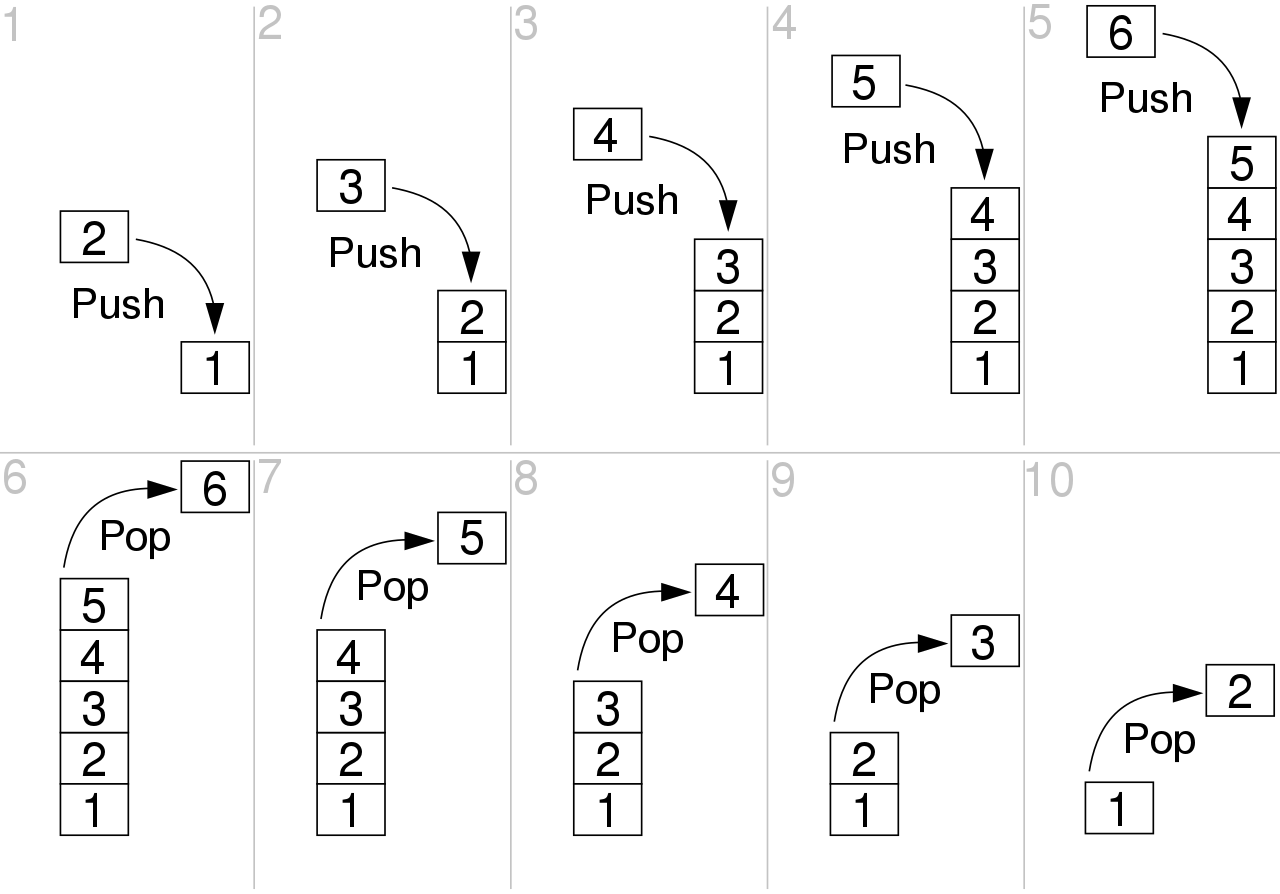
佇列類
- queue, stack: push, pop, front/top
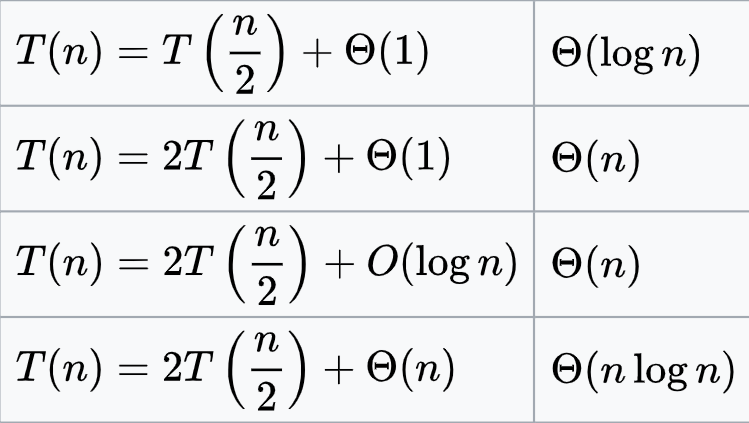
一些special case
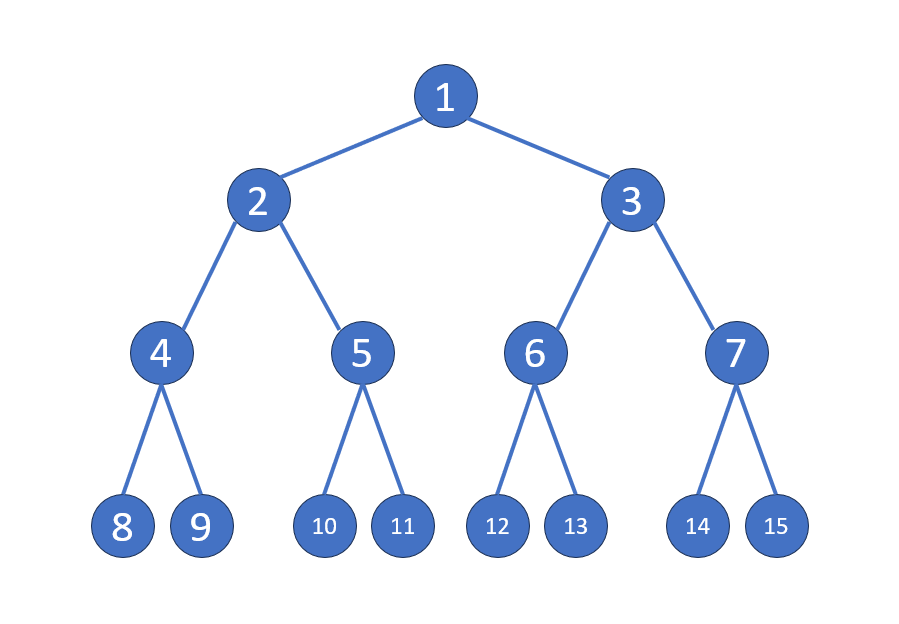
什麼是樹
根
葉子
父子關係
鄰接串列
Linked List
鄰接串列
- 用 struct 實作節點
- 節點包含:資料,左右節點的指標
- 記錄頭尾指標
- 不支援隨機存取
- 很少用到,但概念很重要
- 可實作 Queue, Stack ,但很笨
大概的扣
struct Linked_list {
struct node {
int data;
node *left, *right;
} *front = nullptr, *back = nullptr;
int size = 0;
}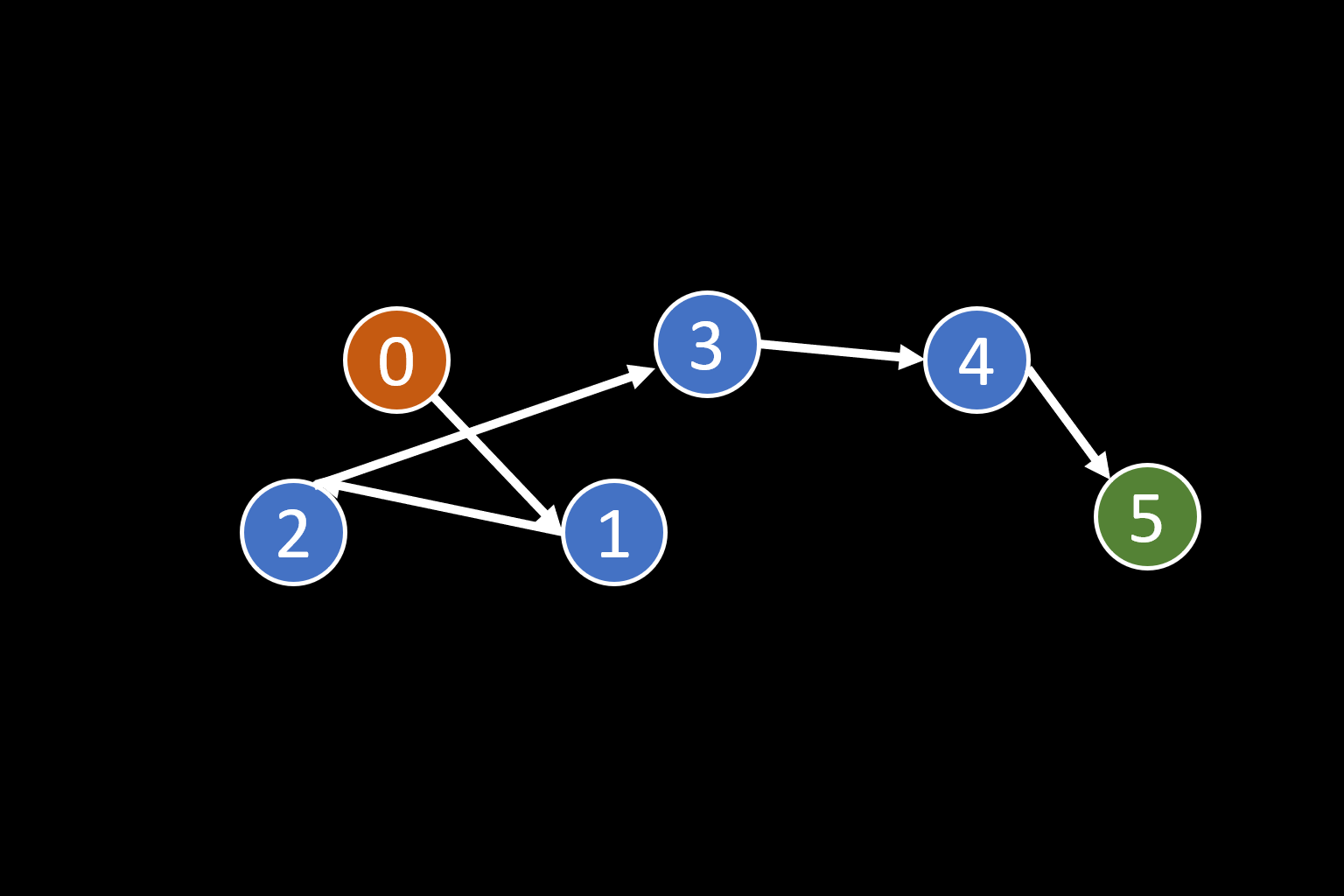
插入 借我偷下以前的圖
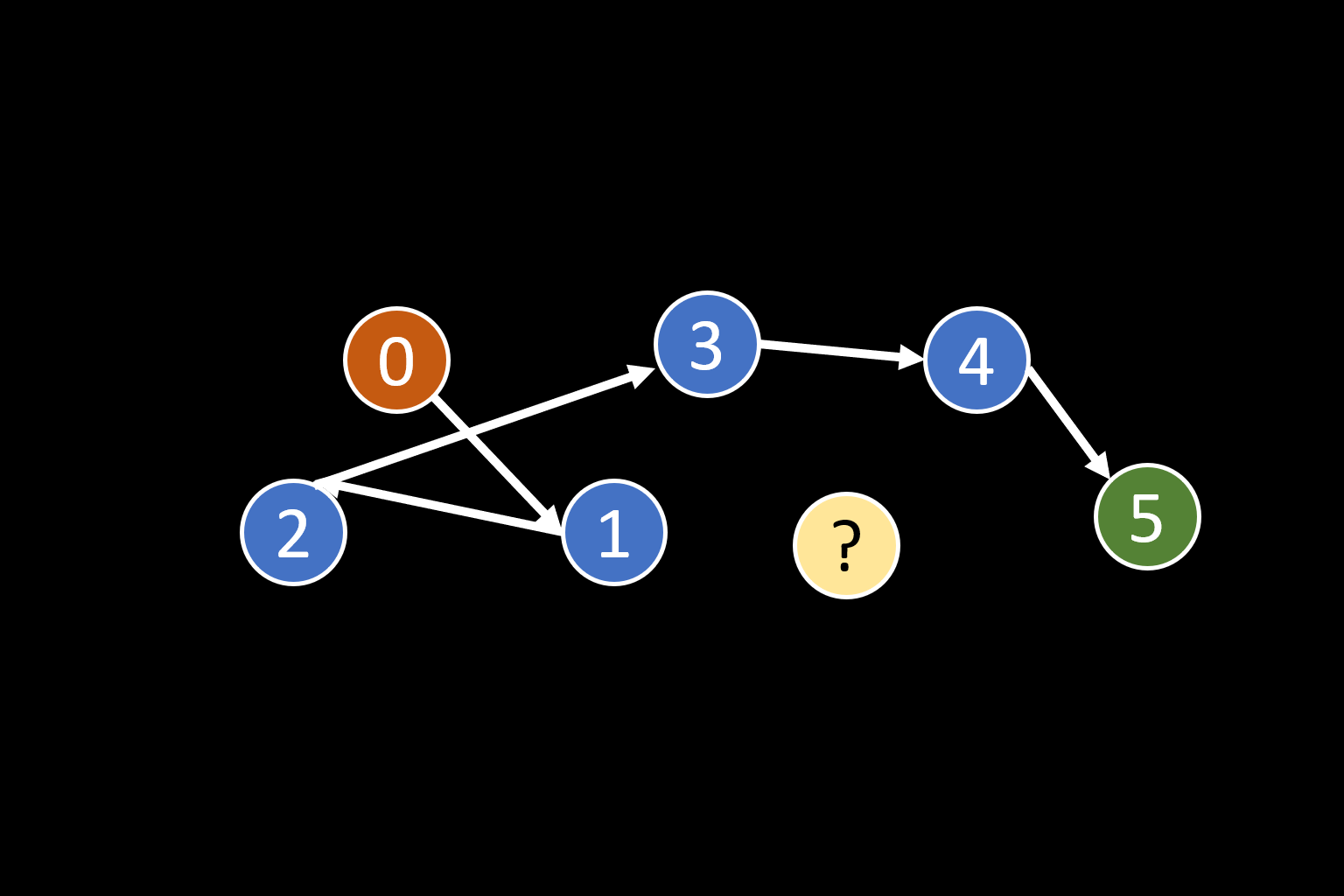
插入
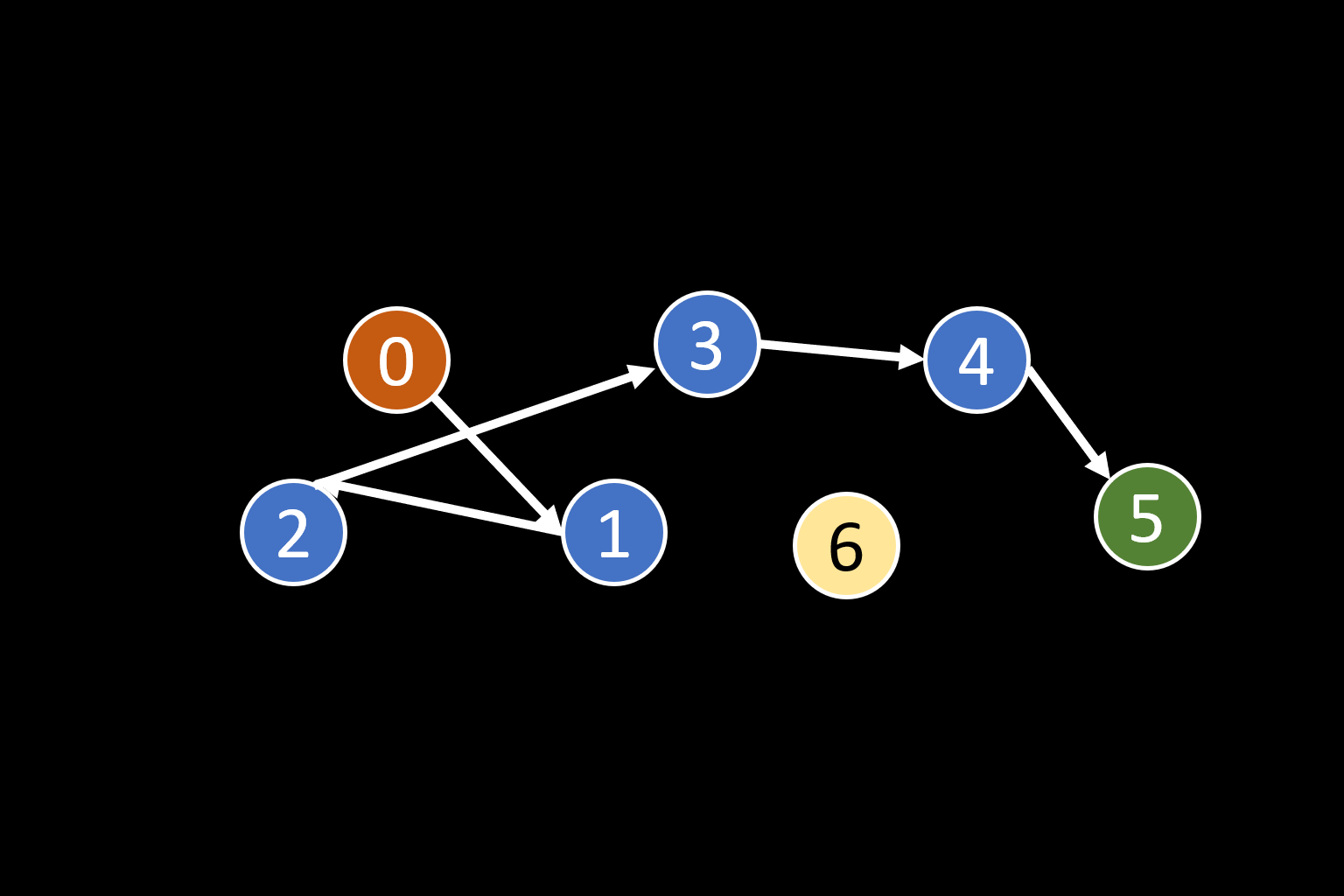
插入
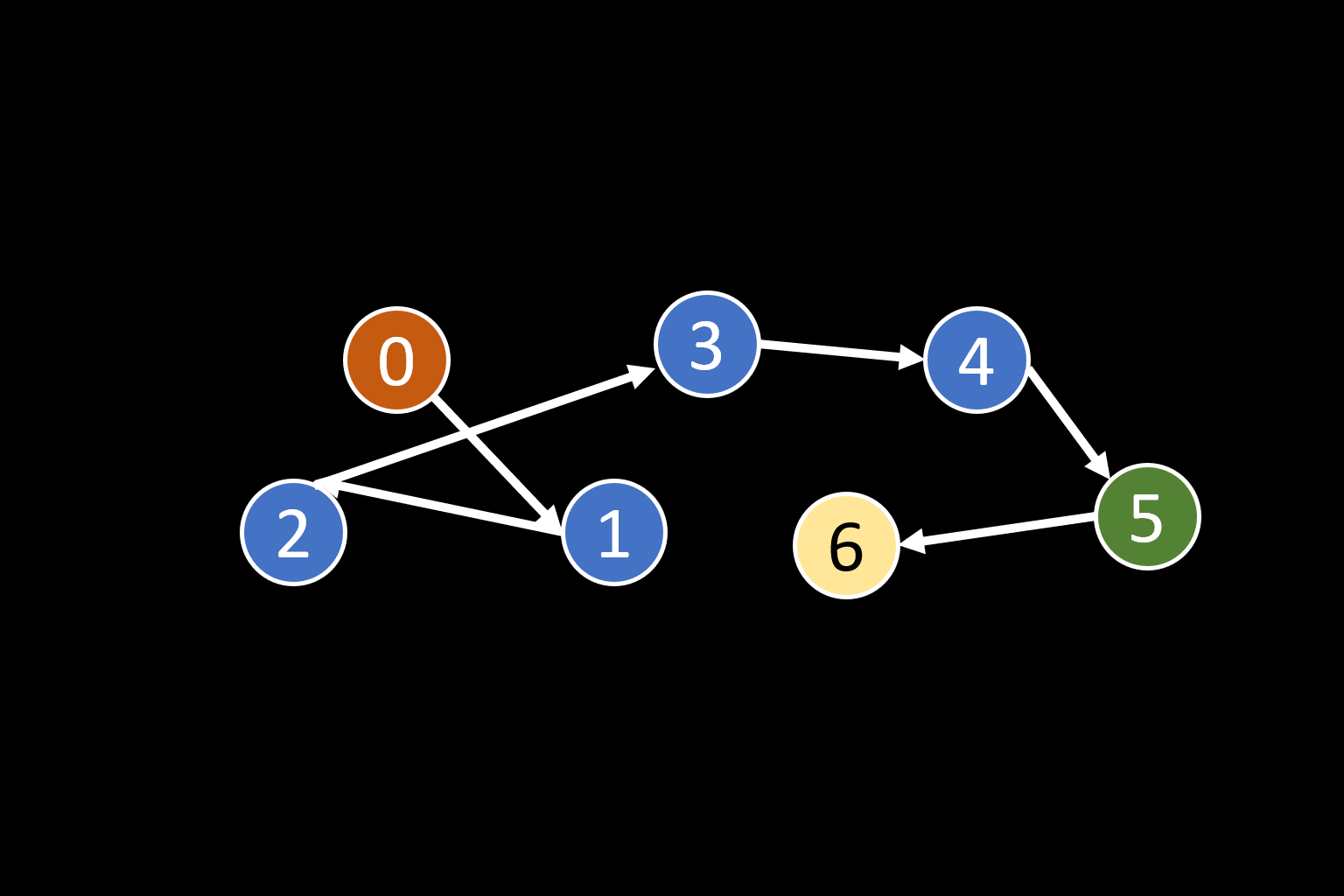
插入
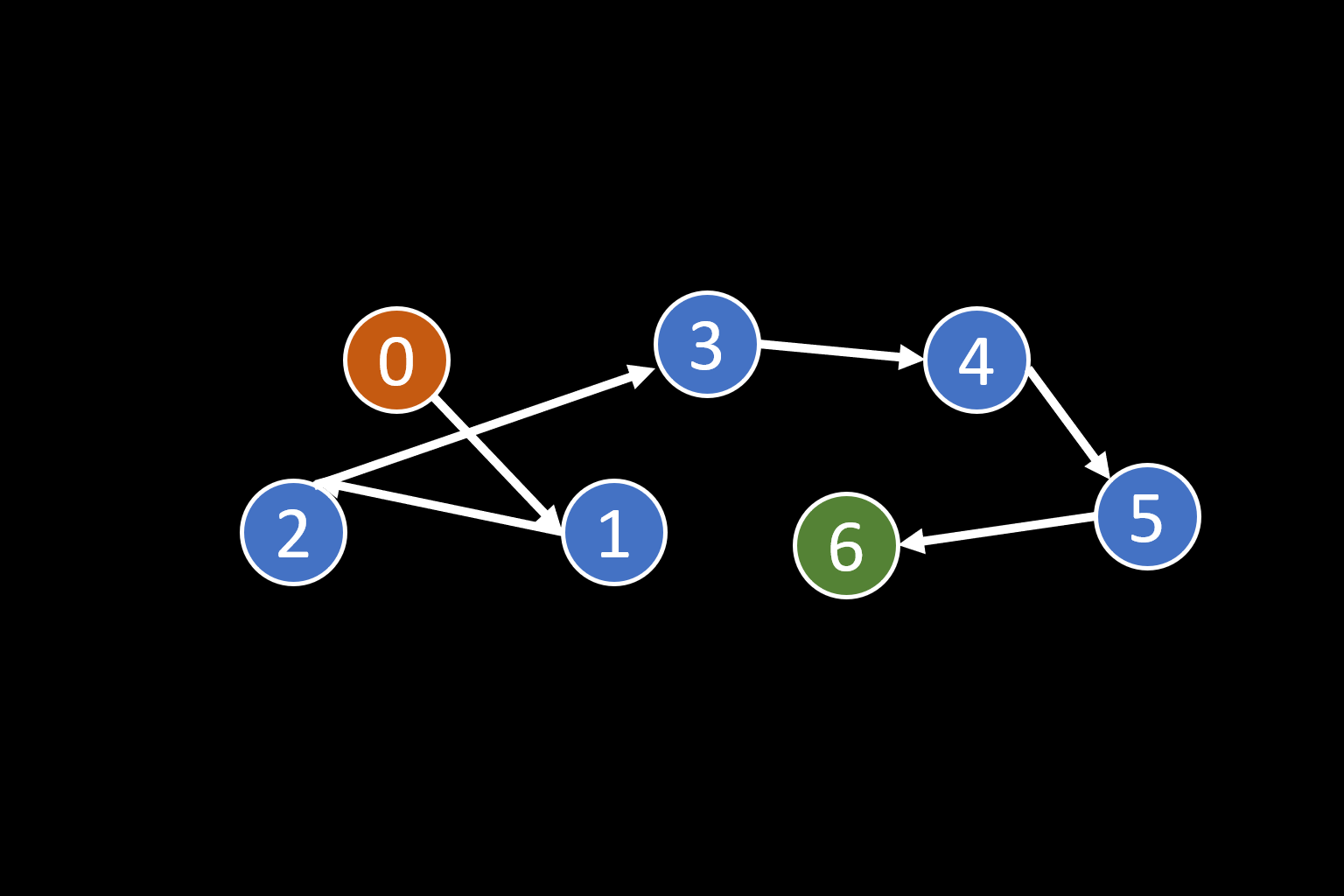
插入

刪除
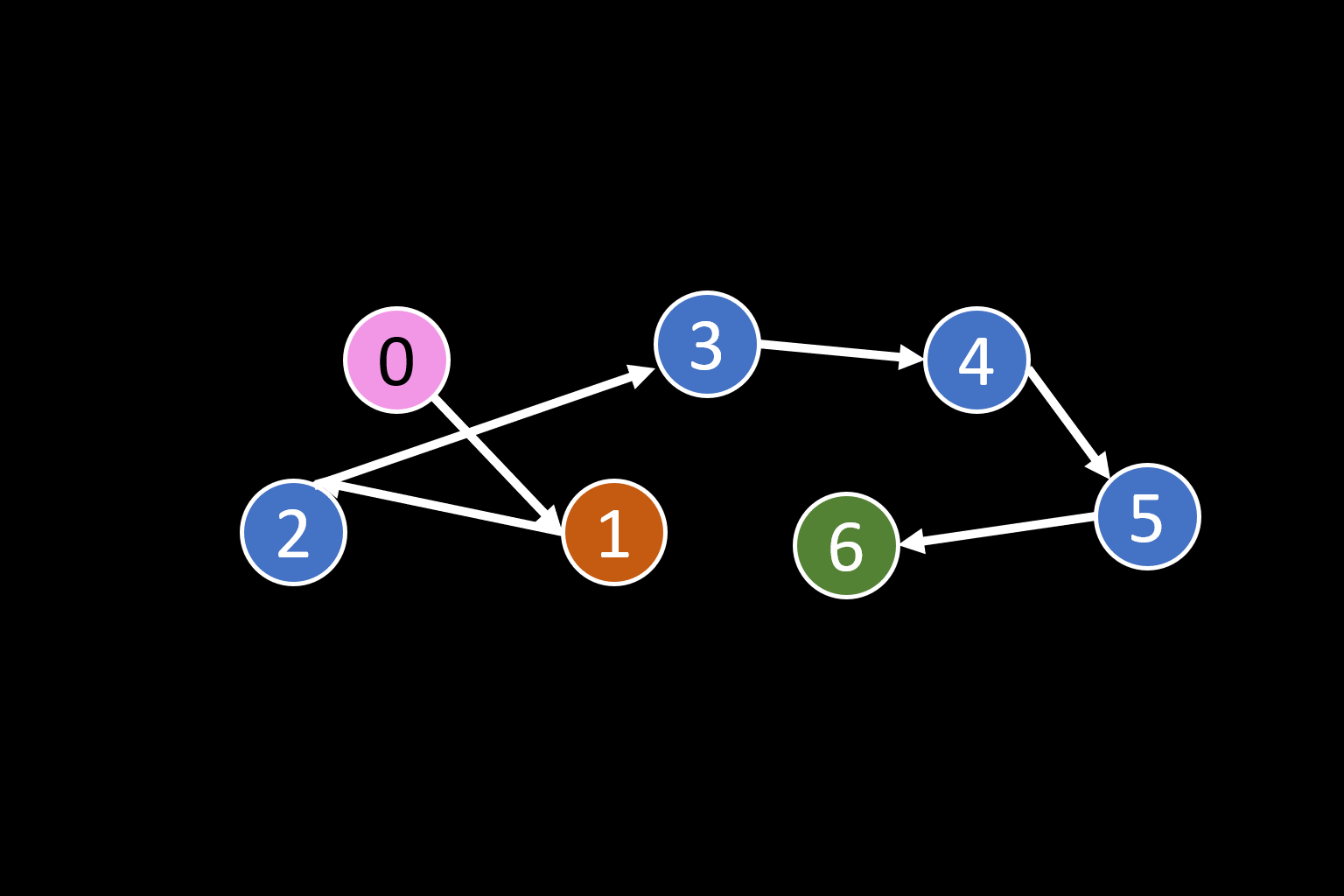
刪除
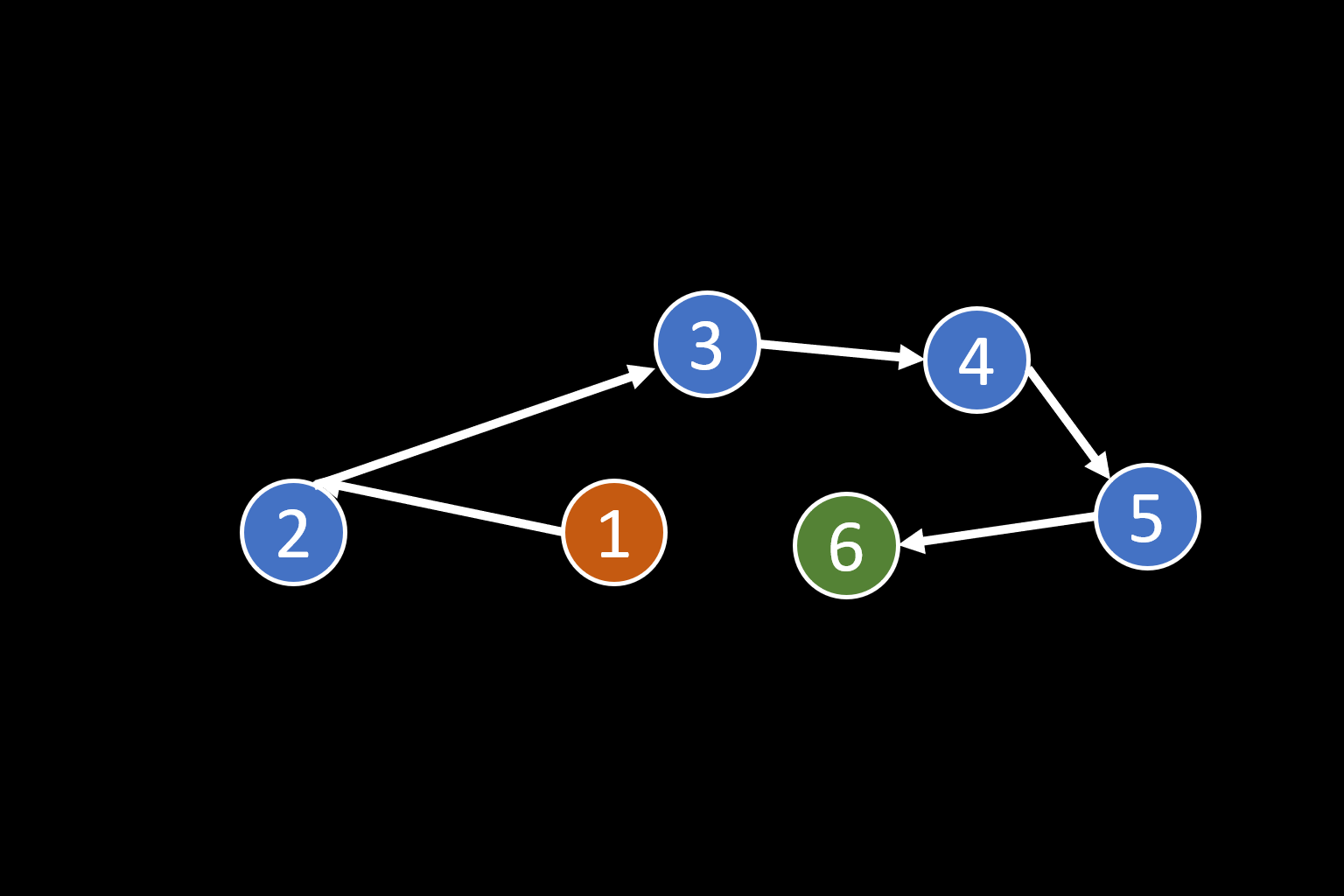
刪除
線段樹
Segment Tree
小目錄
線段樹
- 類似前綴和,維護「具結合律」的區間資料
- 支援修改
- 建樹
- 修改
- 查詢
實作
- 分治
- 將大區間拆成數個小區間,記錄區間答案
- 查詢時合併區間
- 看圖
實作
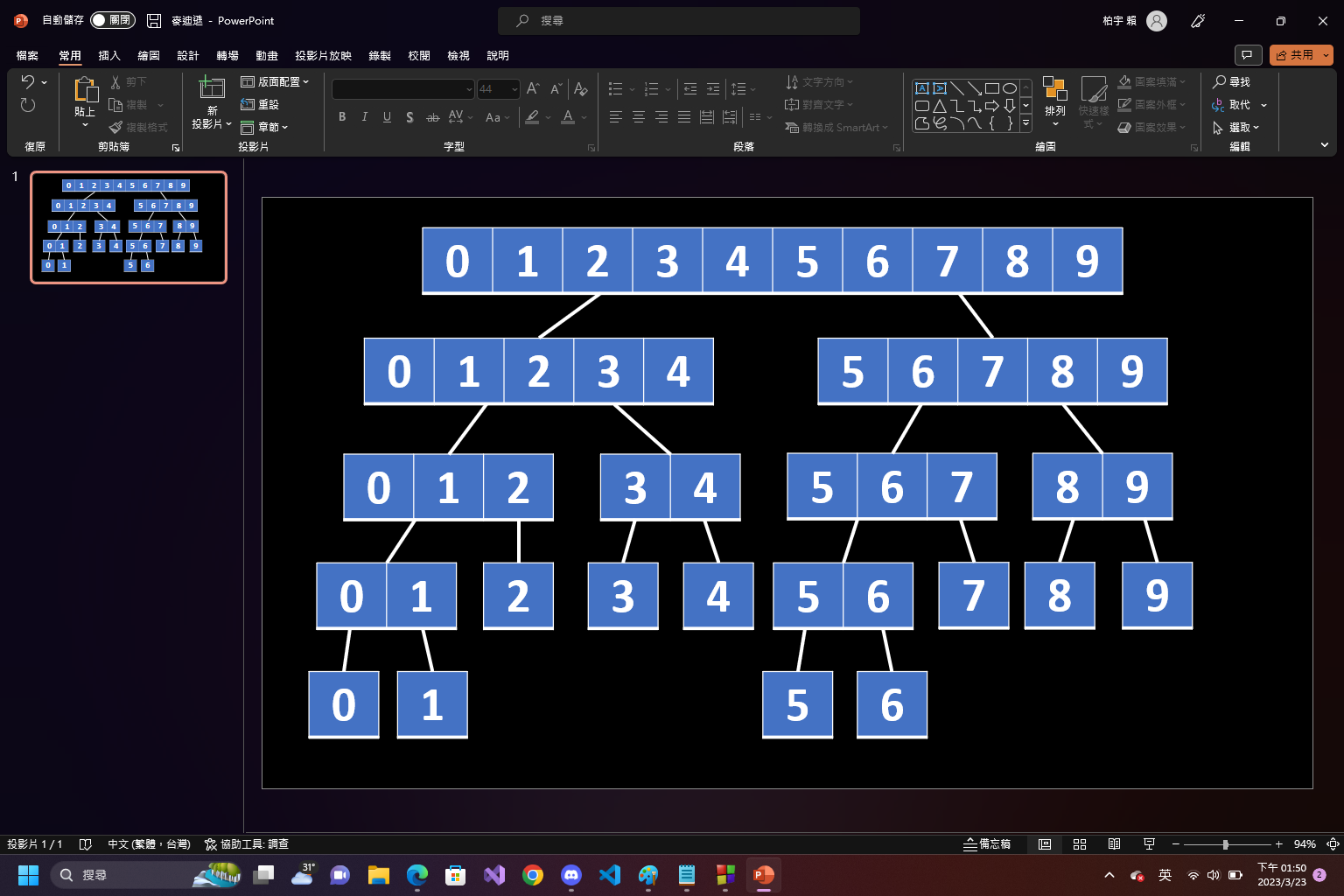
實作
- 每個長方形框框代表一段區間
- 一個節點記錄一個區間的答案
建樹
- 對於單次遞迴:
- 如果是葉子節點(區間大小為1):結束
- 否則:
- 建左子節點,遞迴左半區間
- 建右子節點,遞迴右半區間
- 合併左子節點、右子節點答案
- 這樣可以保證做父節點時,兩個子節點已經處理完了
實作樹形結構:類似鄰接串列
指標指向左子節點、右子節點
扣
struct Stree {
struct node {
int data;
node *lchild = nullptr, *rchild = nullptr;
} *root = nullptr;
int merge(int data1, int data2);
void build(int l, int r, node *cur) {
if (l == r - 1) return;
int m = (l + r) / 2; // 也可以是 (l + r + 1) / 2 ,個人喜歡這個
cur->lchild = new node, build(l, m, cur->lchild); // 遞迴左子樹
cur->rchild = new node, build(m, r, cur->rchild); // 遞迴右子樹
cur->data = merge(cur->lchild->data, cur->rchild->data);
return;
}
};
複雜度
設遞迴區間大小
設處理大小為 的區間需要 的時間
不難發現
區間查詢
- 將區間拆成子節點「有能力處理」的方式分割
- 分情況:
- 區間完全符合當前節點的區間,回傳
- 區間完全包含在左子節點的範圍內,往左遞迴
- 區間完全包含在右子節點的範圍內,往右遞迴
- 剩下情況將區間拆成兩個小區間遞迴
實作
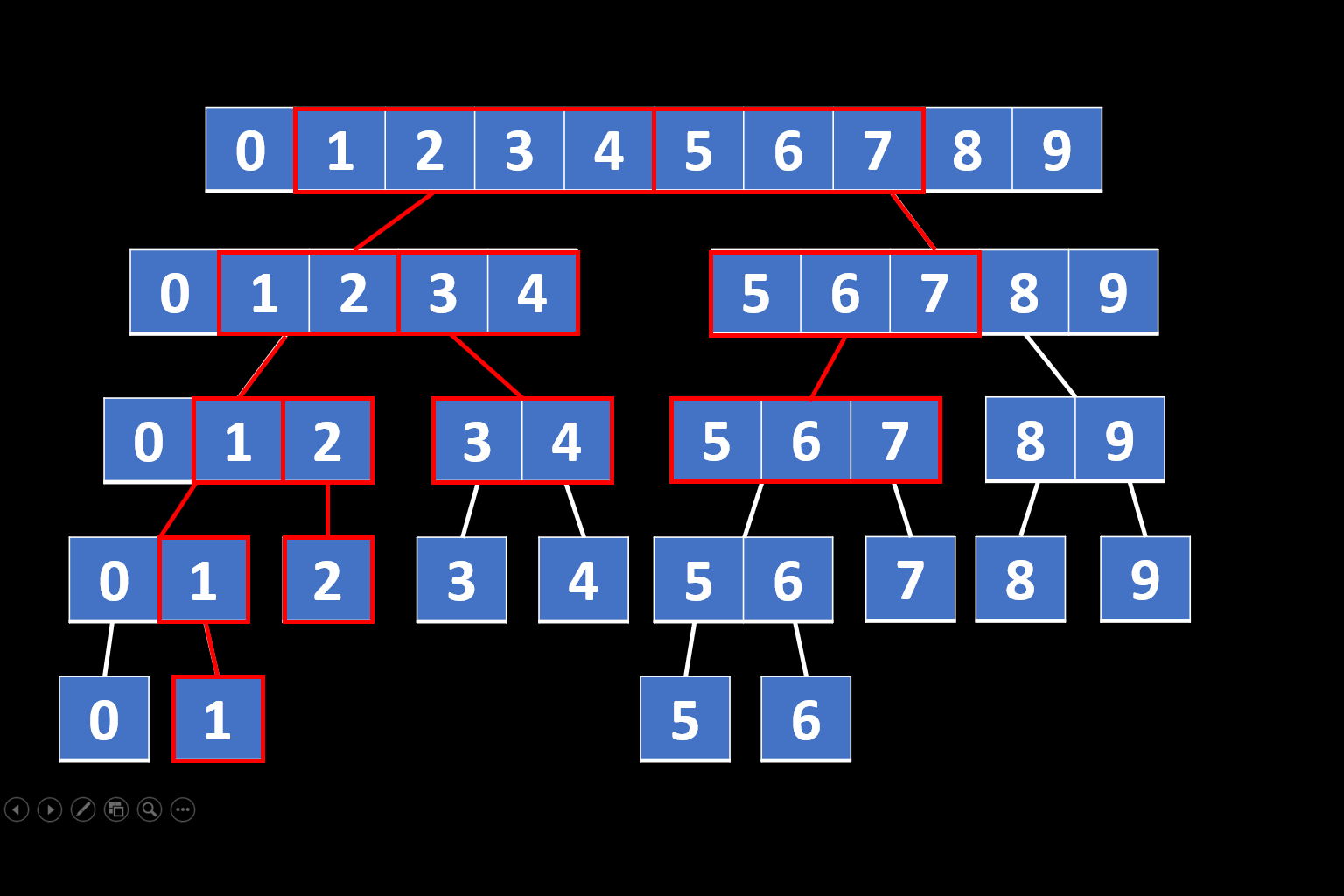
扣
struct Stree {
int query(int l, int r, int tl, int tr, node *cur) { // l, r 表示在樹裡面的區間,tl, tr 表示需要處理的區間
if (l == tl && r == tr) return cur->data;
int m = (l + r) / 2;
if (tr <= m) return query(l, m, tl, tr, cur->lchild); // 如果目標區間完全在左子節點範圍,向左遞迴
if (tl >= m) return query(m, r, tl, tr, cur->rchild); // 如果目標區間完全在右子節點範圍,向右遞迴
return merge(query(l, m, tl, m, cur->lchild),
query(m, r, m, tr, cur->rchild)); // 否則將當前區間切割,向左右遞迴
}
};
複雜度
- 觀察到被處理的區間在分裂成兩個區間後,兩個分裂後的區間至少左右界其中一界和線段樹的左右界是符合的
- 符合一界的區間再被分割,至少有一個完美的區間
- 因兩界都不符合又被分割的區間只會有一次
設處理目標區間對應到的線段樹區間大小為 ,且處理的目標區間至少有一界符合線段樹區間的左右界
設處理時間
處理兩界都不符合則時間 ,但只發生一次,總複雜度仍
單點修改
- 依範圍遞迴到葉節點,再沿路向上修改
struct Stree {
void modify(int l, int r, int pos, int new_data, node *cur) {
if (l == r - 1) {
cur->data = new_data;
return;
}
int m = (l + r) / 2;
if (pos < m) modify(l, m, pos, new_data, cur->lchild);
else modify(m, r, pos, new_data, cur->rchild);
cur->data = merge(cur->lchild->data, cur->rchild->data);
return;
}
};
範圍修改
- 如果套用很多次單點修改,複雜度最糟是
- 如果先一次修改完葉子節點,最糟也是
- 能不能不要直接修改到葉子節點?
懶標
- 懶懶地做
- 在一個節點加上標記,方便以後推答案
- 前提:可以由當前節點答案和標記推得新答案
- 記得更新父節點 (pull)
struct Stree {
int merge_data(int data1, int data2);
int merge_tags(int tag1, int tag2);
int pull(int l, int r, node* cur);
void modify(int l, int r, int tl, int tr, int tag, node *cur) {
if (l == tl && r == tr) {
cur->tag = merge_tags(tag, cur->tag);
return;
}
int m = (l + r) / 2;
if (tr <= m) modify(l, m, tl, tr, tag, cur->lchild);
else if (tl >= m) modify(m, r, tl, tr, tag, cur->rchild);
else modify(l, m, tl, m, tag, cur->lchild),
modify(m, r, m, tr, tag, cur->rchild);
pull(l, r, cur);
}
};
這樣查詢會是好的嗎?
懶標下推
- 讓懶標的影響能傳到子節點
- 將標記下傳
- 更新當前節點答案 (可以用pull)
- 將當前節點標記重置
- 查詢前下推
扣(附查詢)
struct Stree {
int merge_tag_data(int data, int tag, int l, int r);
void push(node *cur, int l, int r) {
cur->data = merge_tag_data(cur->data, cur->tag, l, r);
cur->lchild->tag = merge_tags(cur->tag, cur->lchild->tag);
cur->rchild->tag = merge_tags(cur->tag, cur->rchild->tag);
cur->tag = 0;
}
int query(int l, int r, int tl, int tr, node *cur) {
push(cur, l, r);
if (l == tl && r == tr) return cur->data;
int m = (l + r) / 2;
if (tr <= m) return query(l, m, tl, tr, cur->lchild);
if (tl >= m) return query(m, r, tl, tr, cur->rchild);
return merge_data(query(l, m, tl, m, cur->lchild),
query(m, r, m, tr, cur->rchild));
}
};
偽指標型線段樹
- new 常數很大,會被卡常
- 使用陣列的 index 代替指標
- cur->child 變成 tree[cur.child]
- 寫一個 new 函式,返回能用的空間的 index
陣列型線段樹
- 更簡化的偽指標
- 利用近完美二元樹結構
- 以 1 為根
- 左子節點為當前 index * 2
- 右子節點為當前 index * 2 + 1
- 陣列大小一般開 4 * data_size
陣列型線段樹

持久化線段樹
- 儲存每次修改過後的版本(用陣列存根)
- 對於沒有更動的節點,沿用原本的節點
- 基本上只能指標型或偽指標型
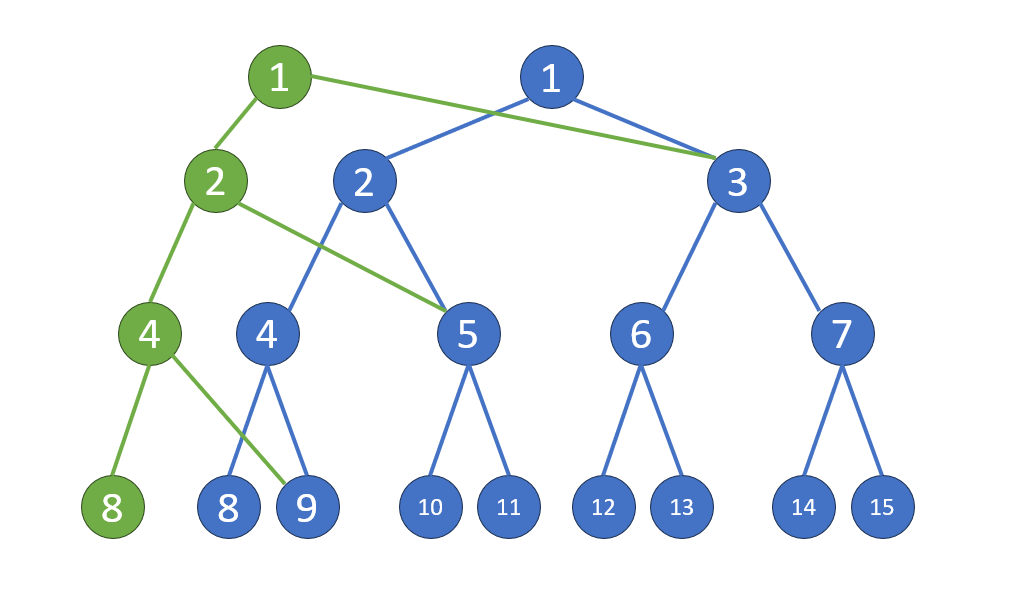
區間第K大問題
- 考慮開「值域線段樹」
- 針對每個值域區間記錄有多少數字
- 透過二分搜,我們可以知道某個數列的第 K 大值
以 {1, 2, 7} 找第 2 大為例:
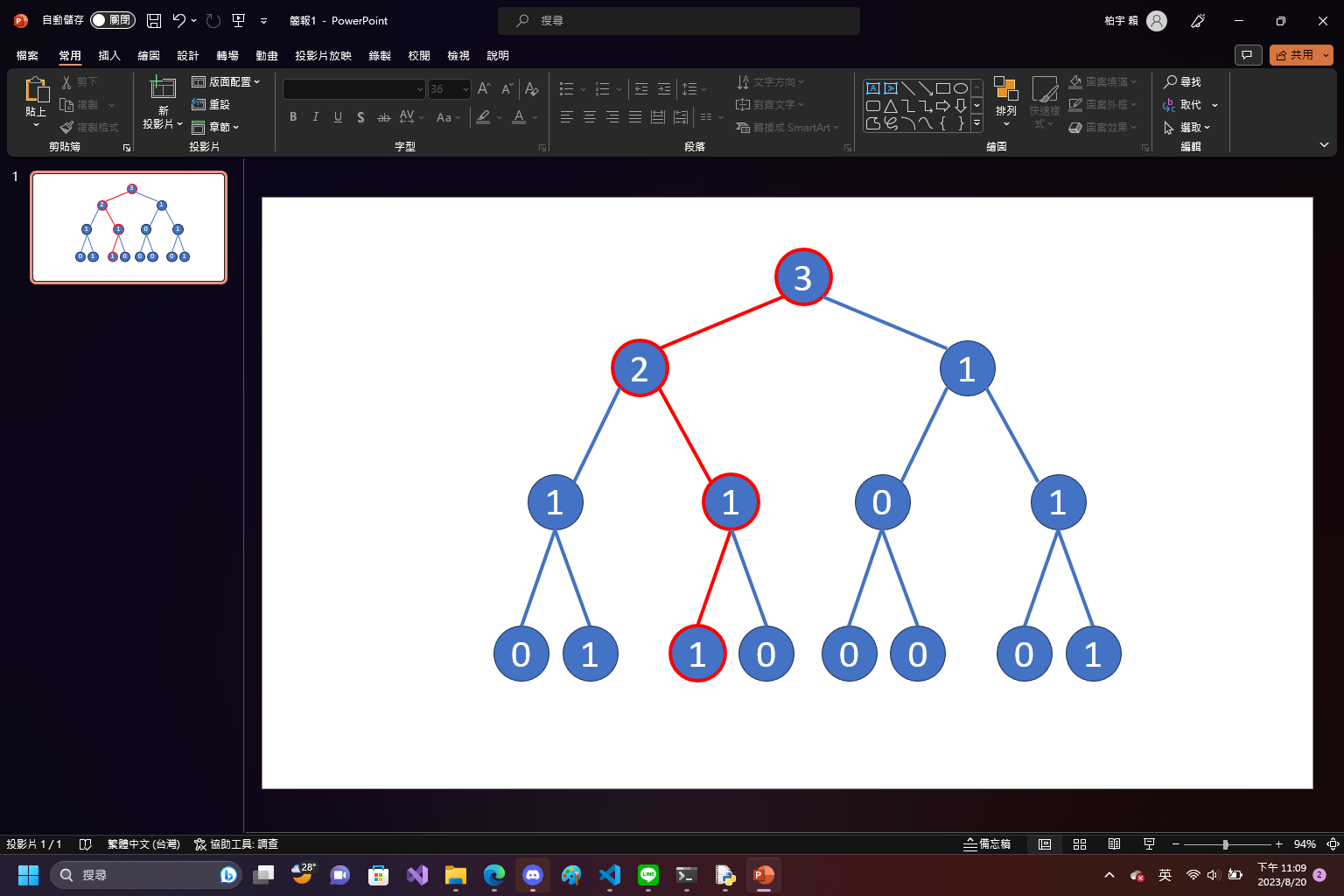
區間第K大問題
- 如果我們能維護每個子數列的線段樹就好了
- 暴力維護鐵定沒戲
- 利用持久化線段樹,從序列的一開始逐漸加入每個數的影響
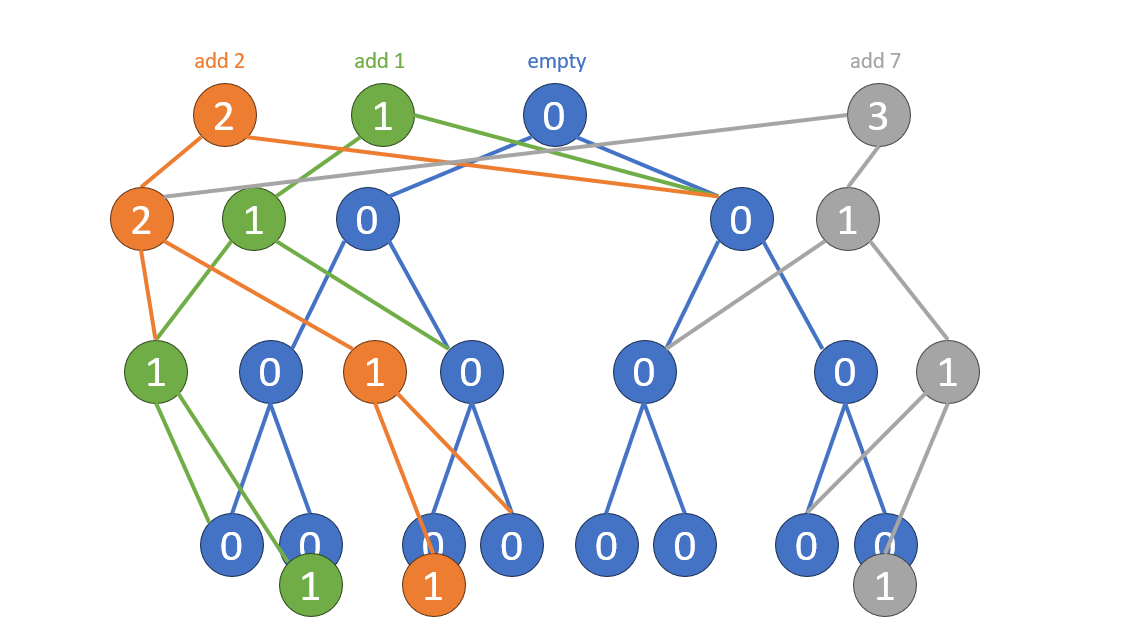
區間第K大問題
- 從查詢區間起點 -1 、終點分別查詢
- 當碰到節點時,兩個節點相減就是這個區間在對應線段樹上的答案

大概的扣
const int max_n = 2e5 + 1;
const int max_q = 2e5 + 1;
int n, q;
// 建議用偽指標寫,我用指標型只是因為我懶
struct Stree {
struct node {
int count = 0; // 在這個區間裡有多少數字
int l, r; // 這個區間維護的 l, r
node *lchild = nullptr, *rchild = nullptr;
} *root[max_n];
int cur_root = 0;
void build(node *cur) { // 建藍色部分
if (cur->l + 1 == cur->r) return;
int m = (cur->l + cur->r + 1) / 2;
cur->lchild = new node, cur->lchild->l = cur->l, cur->lchild->r = m;
build(cur->lchild);
cur->rchild = new node, cur->rchild->l = m, cur->rchild->r = cur->r;
build(cur->rchild);
}
node *new_root() {
return root[++cur_root] = new node;
}
void add_num(node *pre, node *cur, int num) {
cur->l = pre->l, cur->r = pre->r, cur->count = pre->count + 1;
if (cur->l + 1 == cur->r) return;
int m = (cur->l + cur->r + 1) / 2;
if (num < m) {
cur->lchild = new node, cur->rchild = pre->rchild;
add_num(pre->lchild, cur->lchild, num);
}
else {
cur->lchild = pre->lchild, cur->rchild = new node;
add_num(pre->rchild, cur->rchild, num);
}
}
} intv_cnt; // interval_count
void solve() {
int C; // 值域
// init n, q
int data[n];
// init data
intv_cnt.root[0] = new Stree::node;
intv_cnt.root[0]->l = 0, intv_cnt.root[0]->r = C;
intv_cnt.build(intv_cnt.root[0]);
for (int i = 0; i < n; i++) {
intv_cnt.add_num(intv_cnt.root[intv_cnt.cur_root], intv_cnt.new_root(), data[i]);
}
for (int i = 0; i < q; i++) {
int l, r, k;
// get l, r, k
--l, --r; // 我們要求的區間一般是左閉右閉,先讓 l 轉成要扣掉的部分
Stree::node *lcur = intv_cnt.root[l], *rcur = intv_cnt.root[r];
while (lcur->l + 1 != lcur->r) {
if (rcur->count - lcur->count <= k) lcur = lcur->lchild, rcur = rcur->rchild;
else lcur = lcur->rchild, rcur = rcur->rchild, k -= rcur->count - lcur->count;
}
// print lcur->l
}
}動態開點線段樹
- 基本上只能指標型或偽指標型
- 如果一次開全部會太大,就不要一次開出來,用到時再開
BIT
Binary Indexed Tree
只維護前綴?
- 只維護前綴的話,有漂亮性質能用
- 通靈得出以下結論
- 定義 為 在二進制時最右邊的 1 代表的數
- 定義
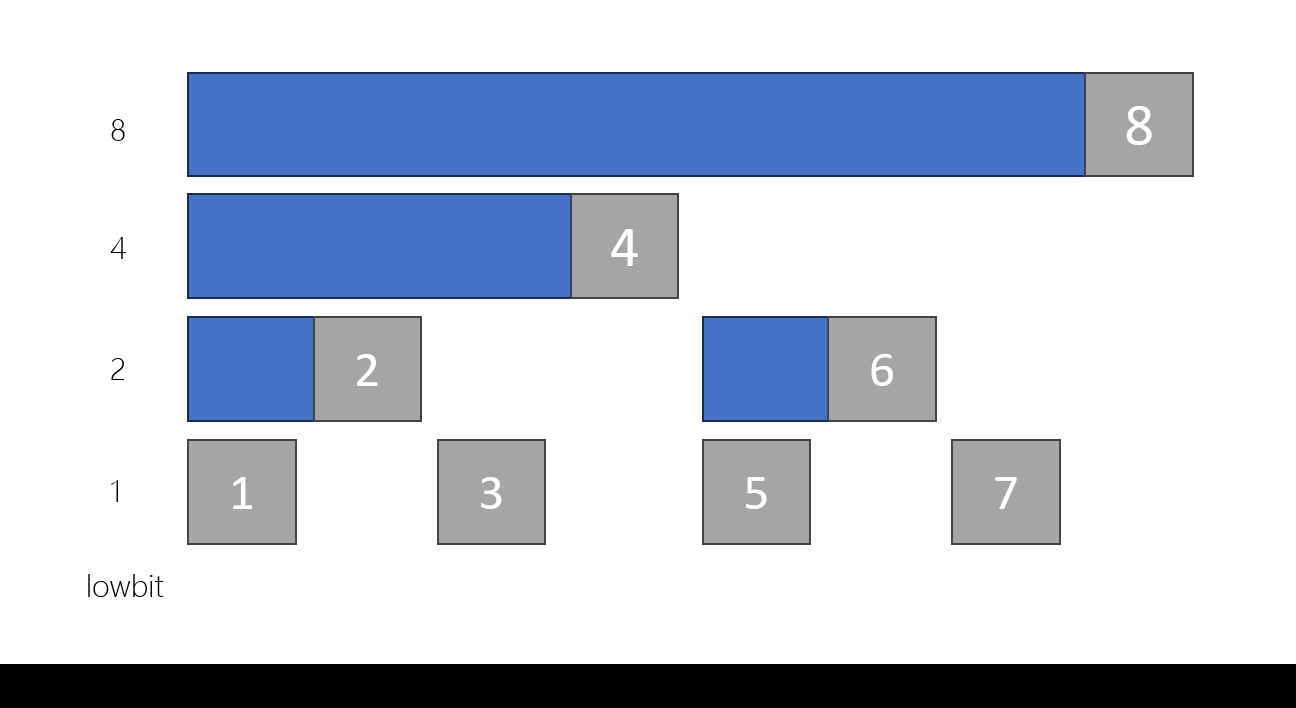
建樹
- 帶點 DP 的觀念,反正直接看扣
- lowbit(x) = x & -x 或者 x & (~x + 1)
struct BIT {
int tree[n + 1];
int lowbit(int n) {
return n & -n;
}
void build() {
for (int i = 1; i < n; i++) {
tree[i] += data[i];
if (i + lowbit(i) <= n) tree[i + lowbit(i)] += tree[i];
}
}
}查詢
- 每個數維護它的 lowbit 大小的區間,每次查完扣掉即可
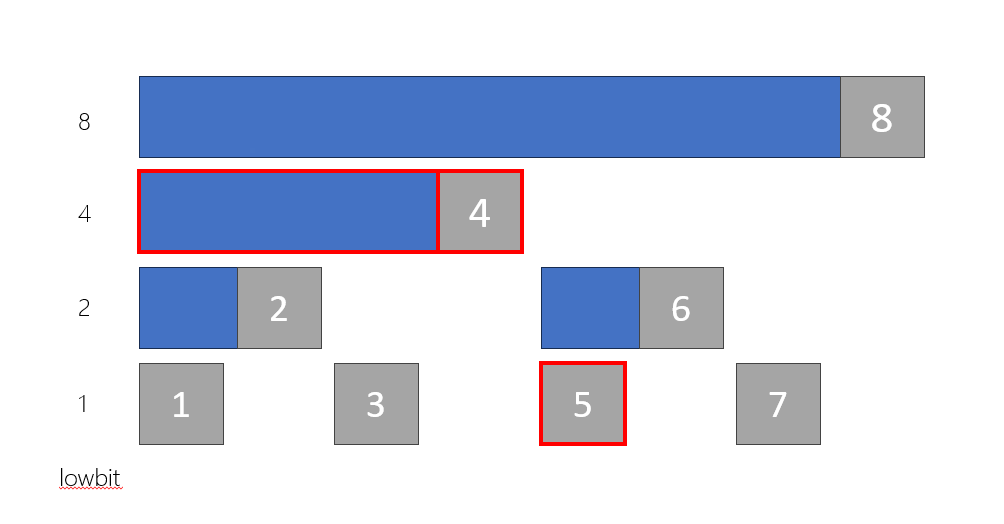
單點修改
看看建樹的扣,會發現會影響到的區間有
x + lowbit(x), x + lowbit(x) + lowbit(x + lowbit(x)) ...
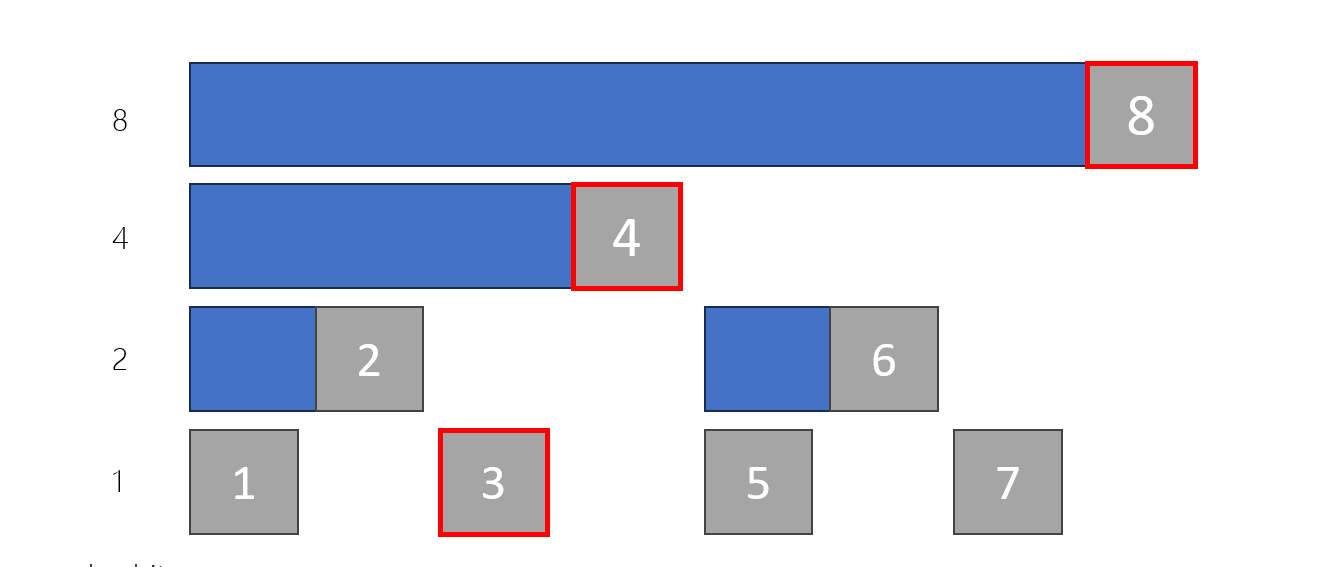
複雜度
- 建樹
- 查詢
- 修改
- 查詢修改都可以用二進位證
:阿那這樣為什麼不用線段樹
:它碼短 它常數小
全部的扣
真的很短
struct BIT {
int tree[max_n + 1];
void build() {
for (int i = 1; i <= n; i++) {
tree[i] += data[i];
if (i + (i & -i) <= n) tree[i + (i & -i)] += tree[i];
}
}
void modify(int pos, int diff) {
for (; pos <= n; pos += pos & -pos) tree[pos] += diff;
}
int query(int pos) {
int ans = 0;
for (; pos > 0; pos -= pos & -pos) ans += tree[pos];
return ans;
}
};BIT 找 LIS
- 對於 lis[x],維護值域內的數值 x 以下的 lis 長度
- 記得離散化
- 利用 BIT 維護 lis[x] 在值域的前綴最大值
- 用迴圈掃過數列,對於每個加入的值 x:
- 只能接在 < x 的值之後,所以我們查詢 BIT[x - 1]
- 接著用查完的值更新 BIT[x]
BIT 還能幹嘛?
- 熟悉 BIT 後,搭配離散化的值域可以替代很多普通你想不到的 DP 方式,尤其複雜度帶 log 的
- 常數夠小,只要複雜度是好的通常測資不太會卡
- 但是實作會比較久 (要寫離散化,但用 std 內建的東東會很好寫)
Project 參考題解
雖然我知道大家都用普通 DP
#include <stdio.h>
#include <algorithm>
#include <utility>
const int max_n = 2e5 + 1;
struct BIT {
long long tree[max_n << 1];
int size;
inline void modify(int pos, long long n) {
for (; pos <= size; pos += pos & -pos) tree[pos] = std::max(tree[pos], n);
}
inline long long query(int pos) {
if (!pos) return 0;
long long ans = 0;
for (; pos > 0; pos -= pos & -pos) ans = std::max(ans, tree[pos]);
return ans;
}
} max_money;
struct lisan {
int data[max_n << 1];
int size;
inline void init() {
std::sort(data, data + size);
size = std::unique(data, data + size) - data;
}
inline int operator[](int real) {
return std::lower_bound(data, data + size, real) - data;
}
} map;
bool cmp(const std::pair<std::pair<int, int>, int> _A, const std::pair<std::pair<int, int>, int> _B) {
return _A.first.first < _B.first.first;
}
std::pair<std::pair<int, int>, int> date[max_n];
#define begin_i (date[i].first.first)
#define end_i (date[i].first.second)
#define reward_i (date[i].second)
int main() {
int n;
scanf("%d", &n);
map.size = n << 1;
max_money.size = n << 1;
for (int i = 0; i < n; i++) {
scanf("%d%d%lld", &begin_i, &end_i, &reward_i);
map.data[i << 1] = begin_i;
map.data[i << 1 | 1] = end_i;
}
std::sort(date, date + n, cmp);
map.init();
for (int i = 0; i < n; i++) {
max_money.modify(map[end_i] + 1, max_money.query(map[begin_i]) + reward_i);
}
printf("%lld\n", max_money.query(n << 1));
}堆
Heap
優先權佇列
- 一個資料結構,支援取最值、插入、刪除
- STL - std::priority_queue
- 最值
- 插入
- 刪除

堆
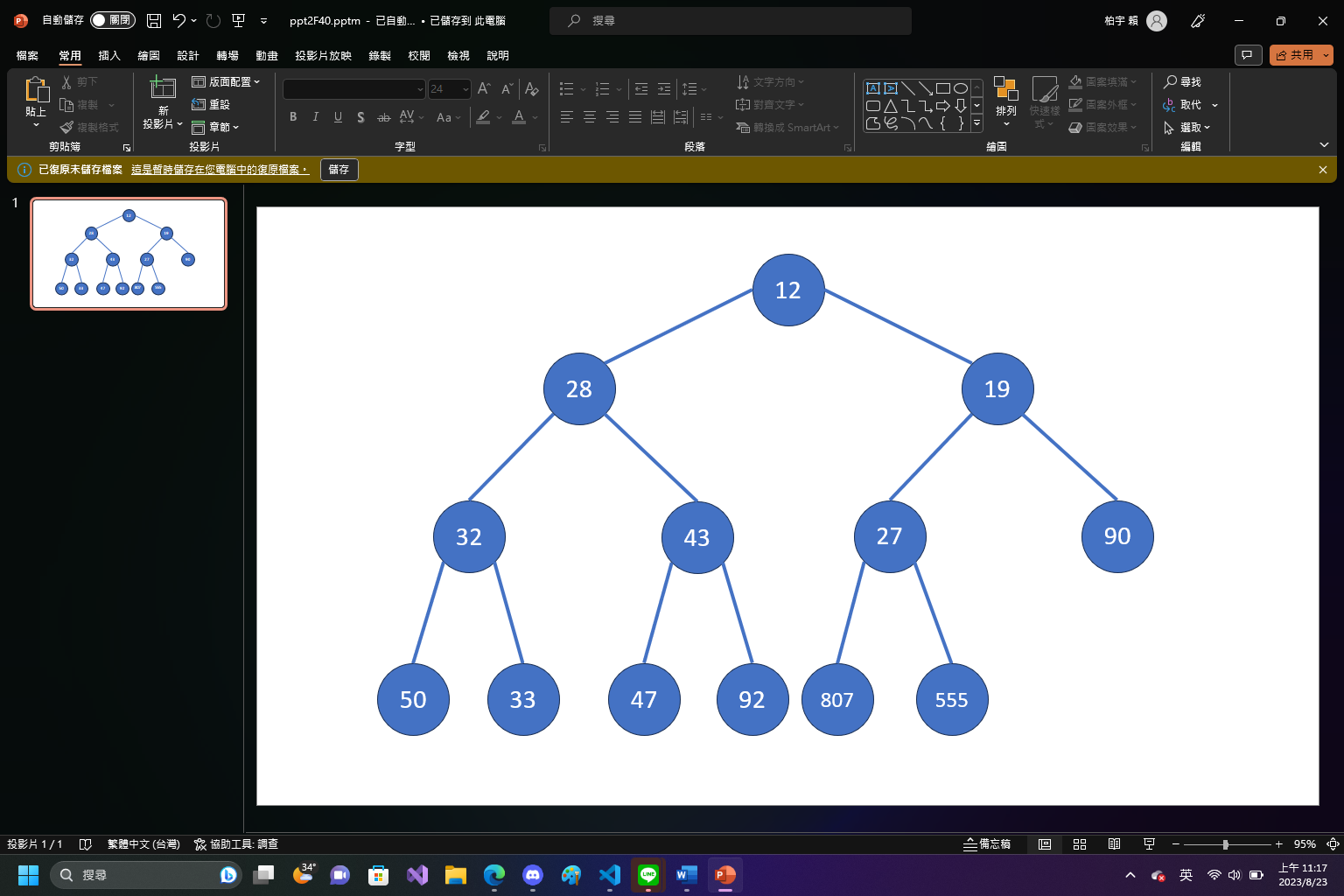
- 子節點的值總是比父節點小(最大堆:大)
- 完全樹,子節點總是由頂到底、由左到右填入
- 堆頂總是最小/最大值
堆
- 同樣以 1 為根,*2 左子節點、*2+1右子節點
- 實作(最小堆)
- shift down: 判斷節點是否合法,不合法則選擇和值較小的子節點交換
- shift up: 反過來,判斷它和父節點的關係
- build: 從最後一個元素向前跑,判斷與子節點的關係,有不符合就 shift down
- push: 從陣列最後加入元素,shift up
- pop: 將第一個元素替換成最後一個元素,shift down
shift down
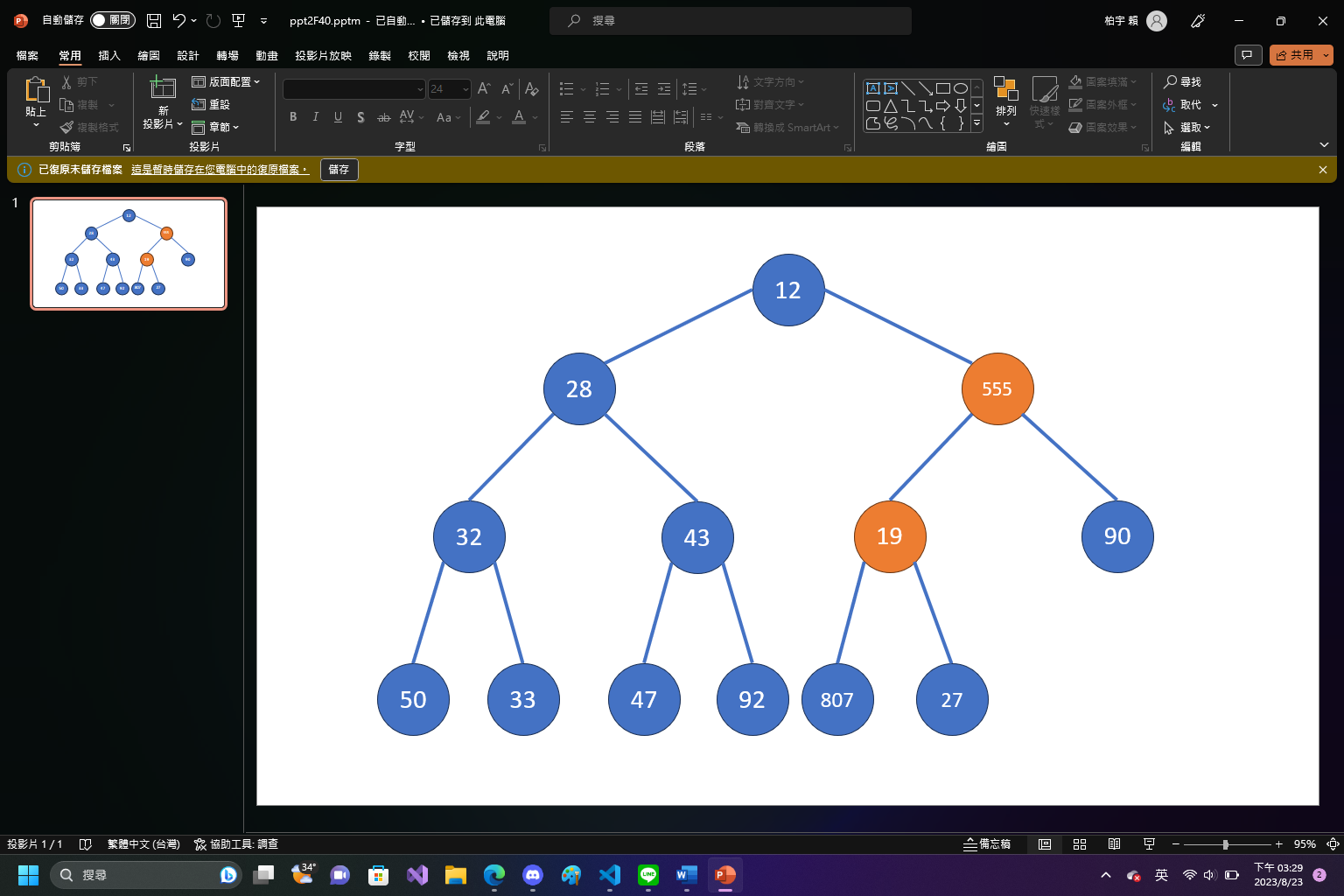
shift down
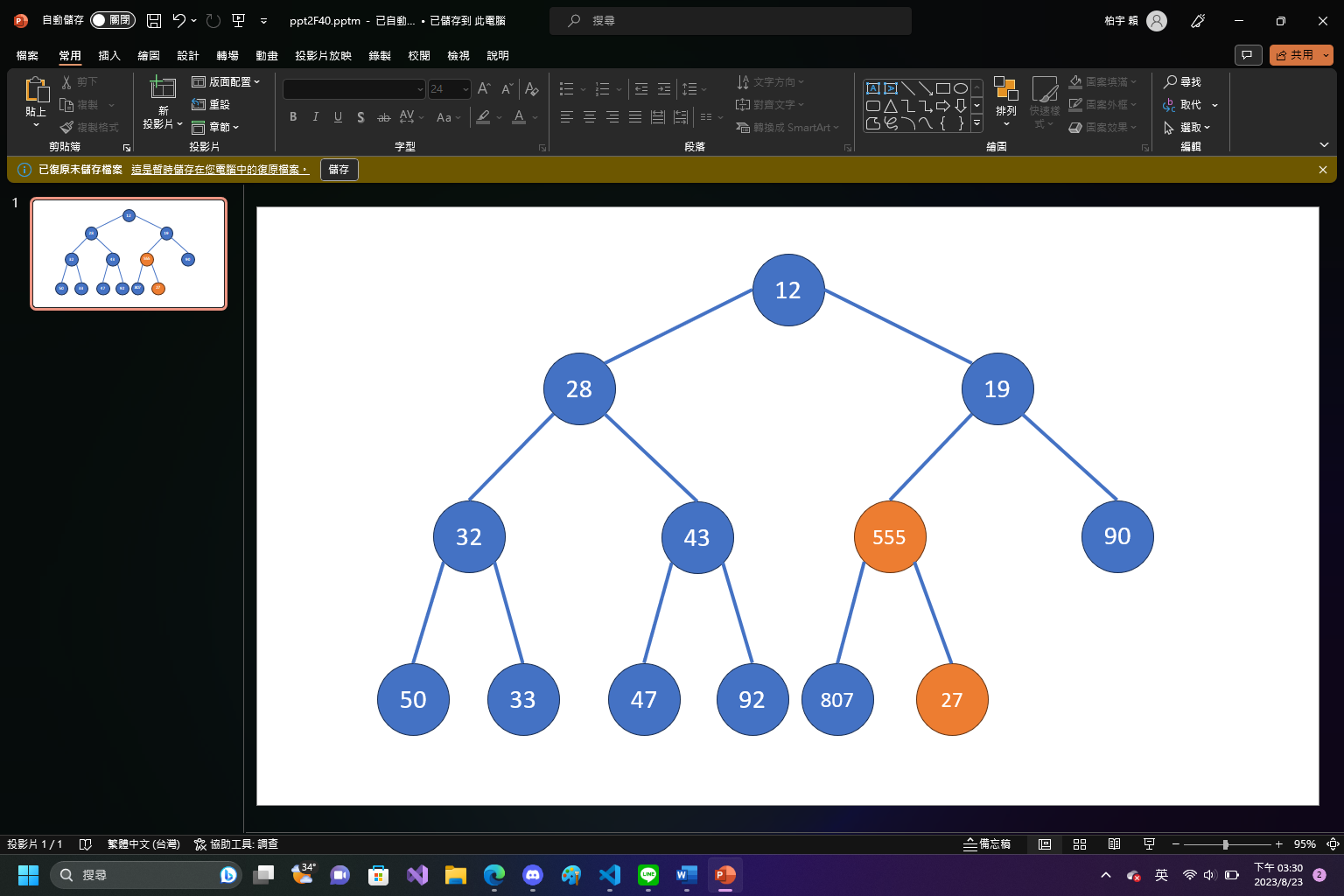
shift down
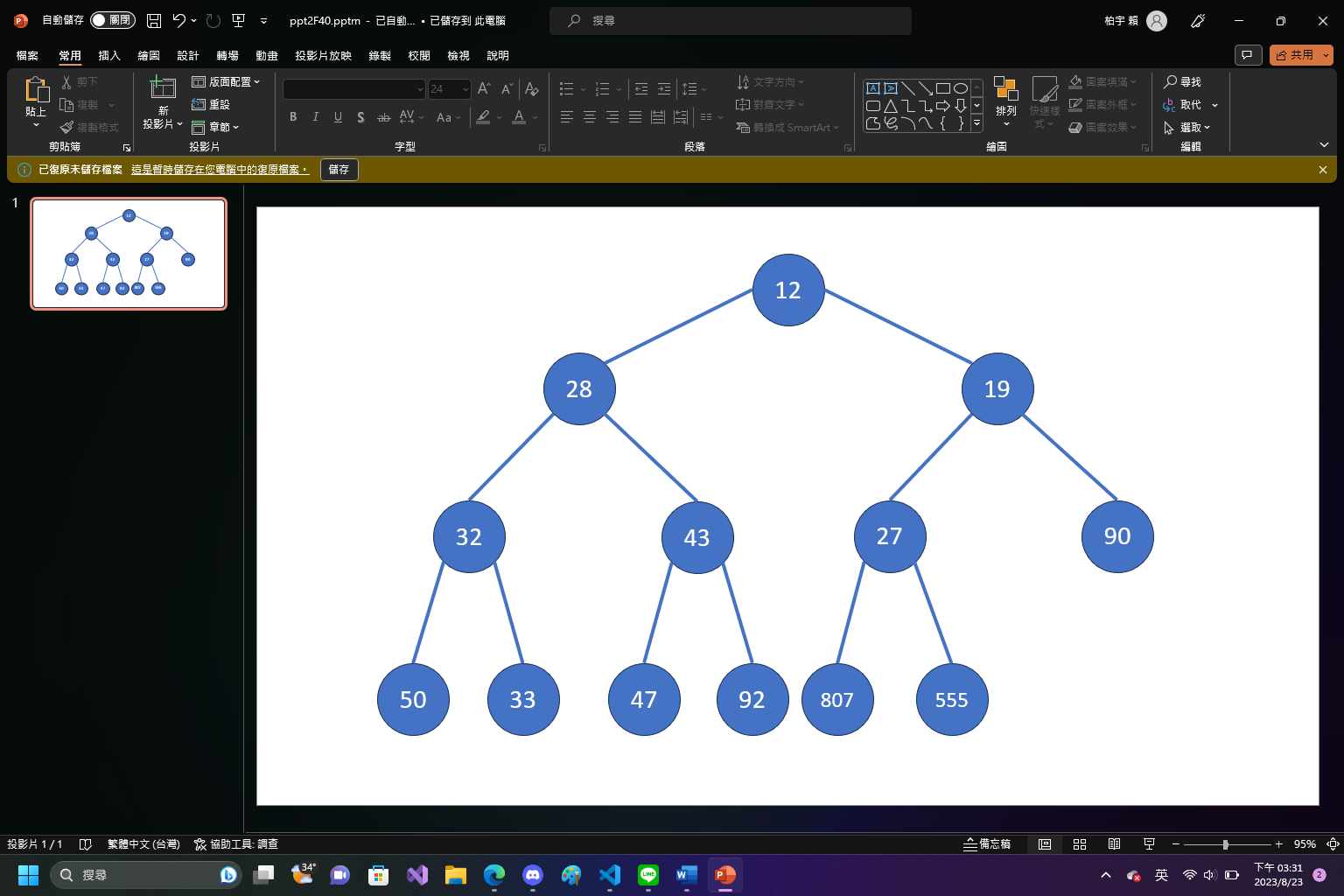
shift down
struct Heap {
int tree[max_n * 2 + 1];
int size = 0;
void shift_down(int pos) {
while(tree[pos] > tree[pos * 2] ||
tree[pos] > tree[pos * 2 + 1]) {
if (tree[pos * 2] < tree[pos * 2 + 1]) {
swap(tree[pos], tree[pos * 2]);
pos = pos * 2;
}
else {
swap(tree[pos], tree[pos * 2 + 1]);
pos = pos * 2 + 1;
}
}
}
};
tip:把不會用到的地方通通設成不會動到的值然後把陣列開大,方便處理邊界情況以及 Debug
也可以不把陣列開大,但值建議還是要設
build
struct Heap {
static const int INF = INT_MAX;
void init(int _size, int data[]) {
size = _size;
for (int i = 0; i < size; i++) tree[i + 1] = data[i];
for (int i = size; i <= max_n * 2; i++) tree[i] = INF;
}
void build() {
for (int i = size; i > 0; i--) shift_down(i);
}
};struct Heap {
void shift_up(int pos) {
while(pos > 1 && tree[pos / 2] > tree[pos])
swap(tree[pos/2], tree[pos]);
}
void push(int x) {
tree[++size] = x;
shift_up(size);
}
};
push & shift up
struct Heap {
void pop() {
tree[1] = tree[size];
tree[size] = INF;
--size;
shift_down(1);
}
int top() {
return tree[1];
}
};pop & top
一般來說比賽很少要手刻堆
所以你可以挑幾題 priotity queue 的題來做一做
但基本上沒必要 所以我沒放
二元搜尋樹/樹堆
Binary Search Tree / Treap
又是小目錄
Binary Search Tree, BST
- 二元:一個節點有兩個子節點
- 搜尋:可以搜尋
- 樹:結構是一顆樹
- 主要用途:std::set, std::map
- 查找某元素是否存在
- 插入某元素
- 刪除某元素
- 可以有對應值(map)
Binary Search Tree, BST
- 左子樹值小於父節點、右子樹值大於父節點
- 左子樹、右子樹也是一棵二元搜尋樹
- 一臉二分搜樣
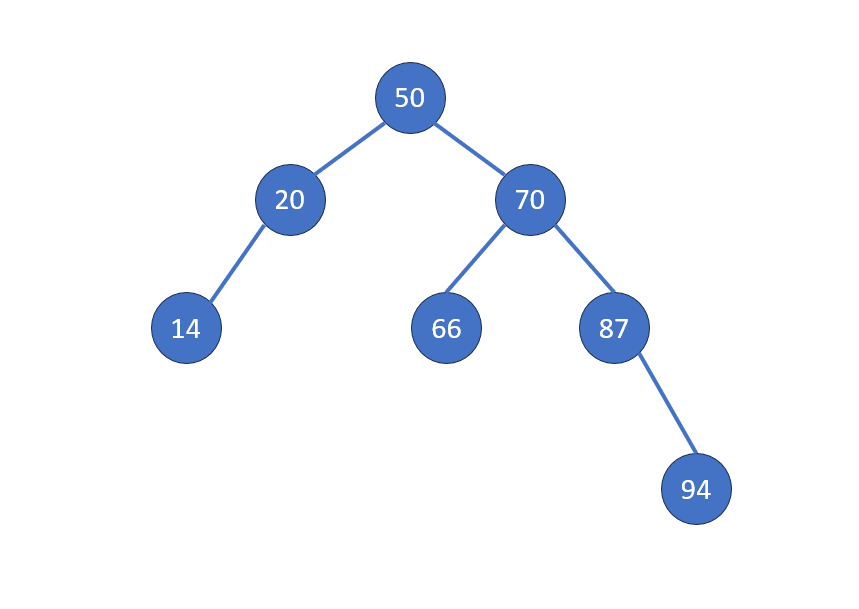
Binary Search Tree, BST
- 尋找:類二分搜
- 插入:類二分搜,建新節點

扣
struct BST {
struct node {
int val;
node *lchild = nullptr, *rchild = nullptr;
} *root = nullptr;
node *&find(int _val) {
if (!root) return root;
node *cur = root, *par = nullptr;
while (cur->val != _val) {
par = cur;
if (_val < cur->val) {
if (cur->lchild) cur = cur->lchild;
else return cur->lchild;
} else {
if (cur->rchild) cur = cur->rchild;
else return cur->rchild;
}
}
return (par->lchild->val == _val) ? par->lchild : par->rchild;
}
void insert(int _val) {
node *&target = find(_val);
if (!target) {
node *new_node = new node;
new_node->val = _val;
target = new_node;
}
}
};BST
- 刪除
- 想刪除的節點沒有子節點:直接刪除
- 一個子節點:將該子節點接上父節點
- 兩個子節點:找到右子樹最左節點/左子樹最右節點,替換值後按上述情形刪除
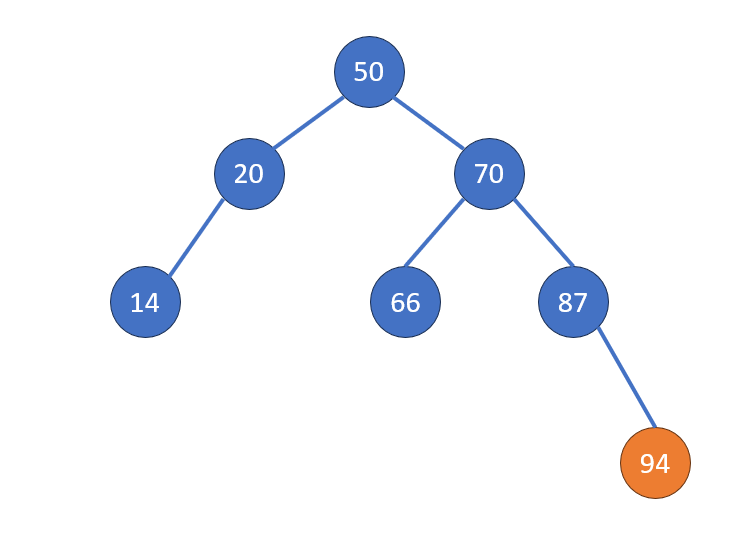
Case 1: 沒子節點
Case 1: 沒子節點
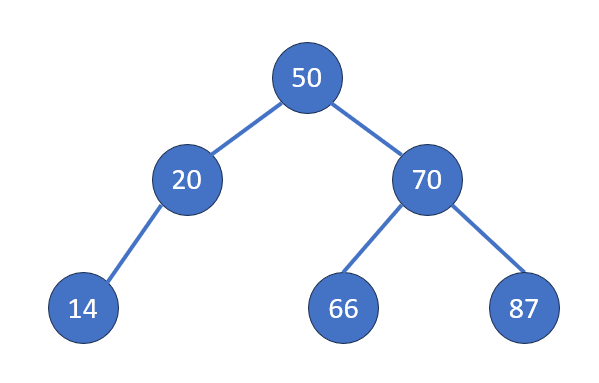
Case 2: 一個子節點
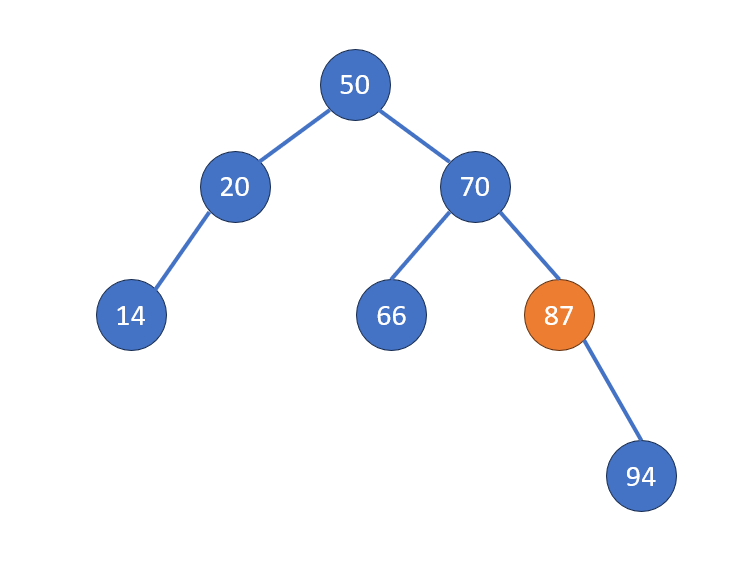
Case 2: 一個子節點
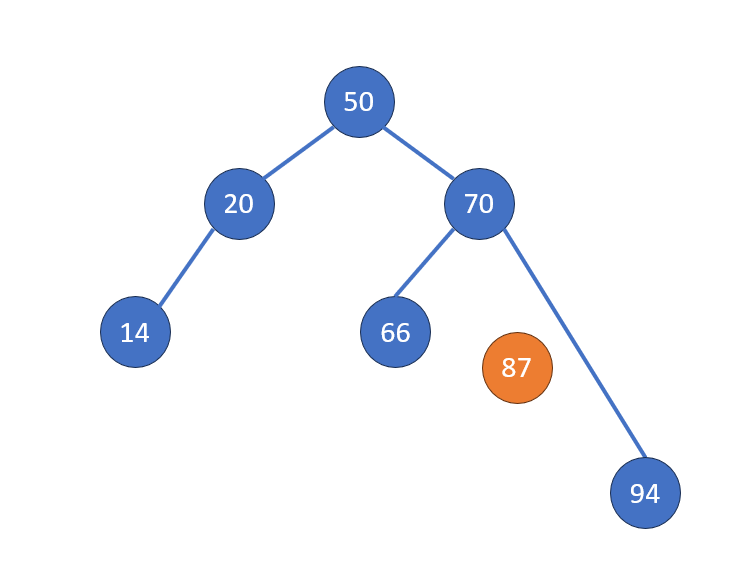
Case 2: 一個子節點
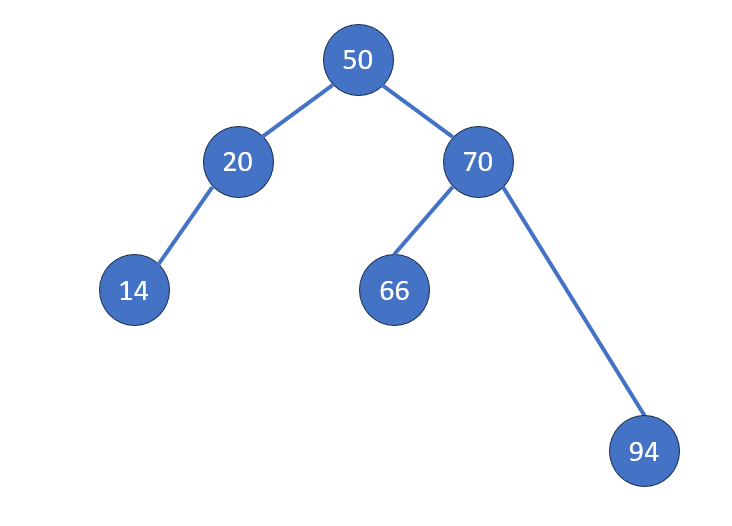
Case 3: 兩個子節點
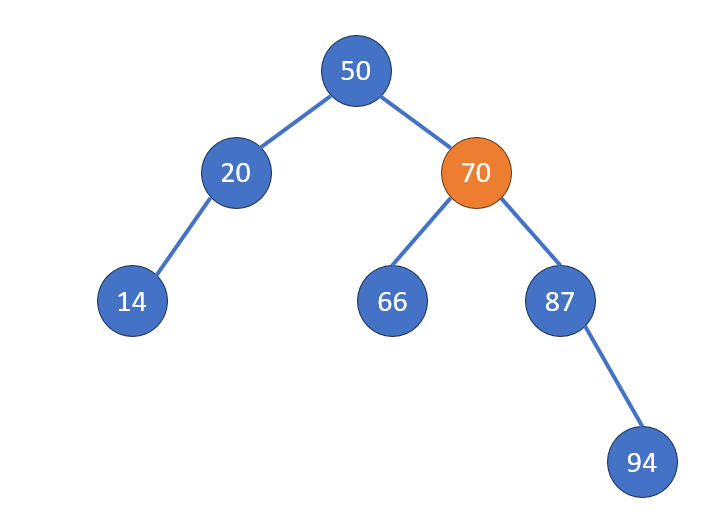
Case 3: 兩個子節點
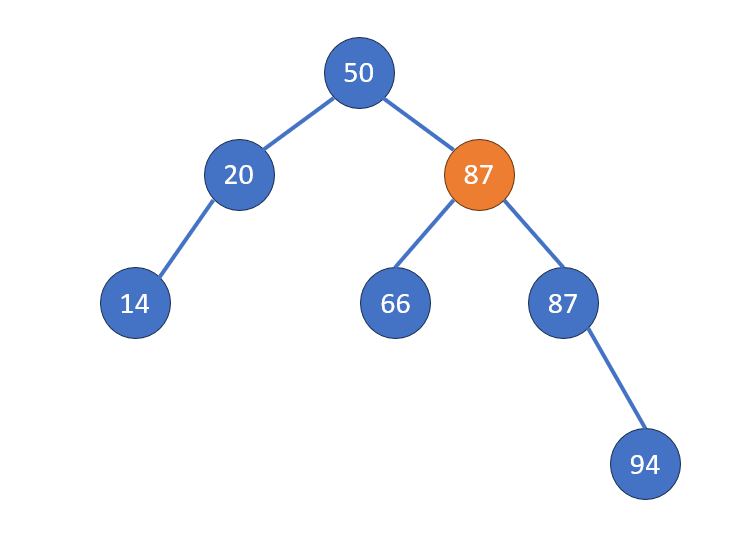
Case 3: 兩個子節點
轉化成一個子節點/沒有子節點的情況
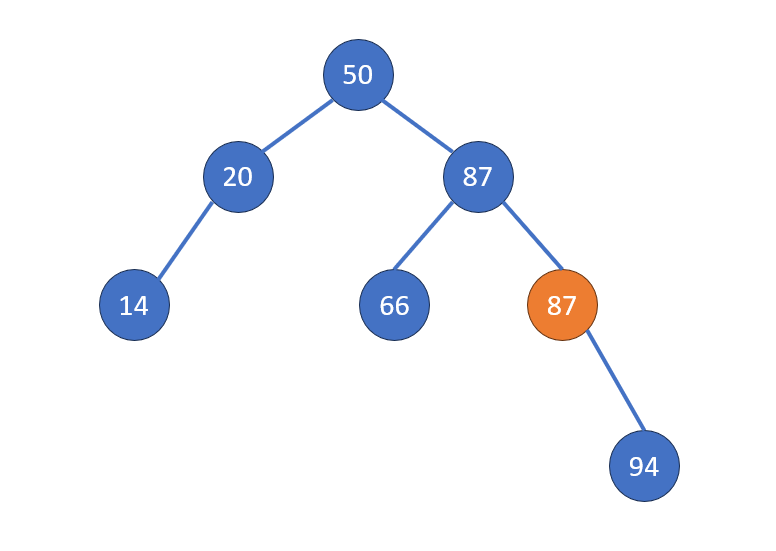
扣
tip: 當需要取用到不存在的節點資料時,可以實作NIL節點
struct BST {
void remove(int _val) {
node *&target = find(_val);
if (!target) return;
if (target->lchild && target->rchild) {
node *alt = target->rchild, *par = target;
while (alt->lchild) par = alt, alt = alt->lchild;
target->val = alt->val;
if (par == target) target->rchild = alt->rchild;
else par->lchild = alt->rchild;
delete alt;
return;
}
node *temp = target;
if (target->lchild) target = target->lchild;
else if (target->rchild) target = target->rchild;
delete temp;
return;
}
};複雜度?
因為是二分搜所以可以直接套
嗎?
退化
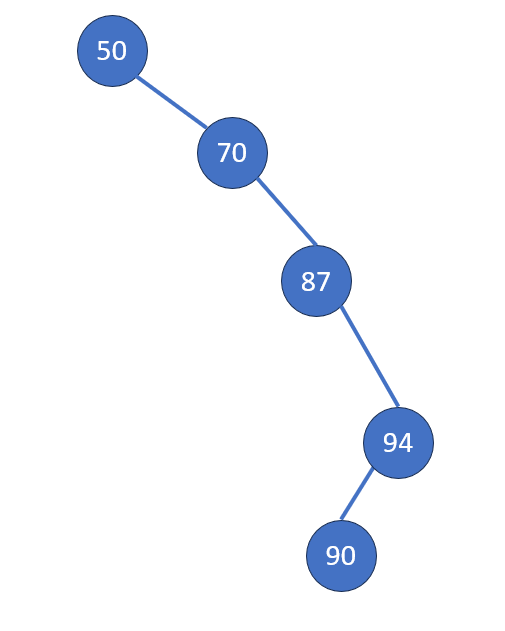
- 長成一條鍊時,複雜度是爛的
- 我們只維護「順序性」,不影響順序的操作都可以被接受
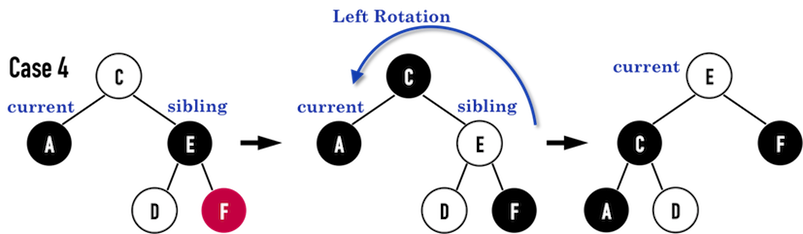
樹旋轉
- 不影響中序遍歷的順序
- 改變樹的形狀
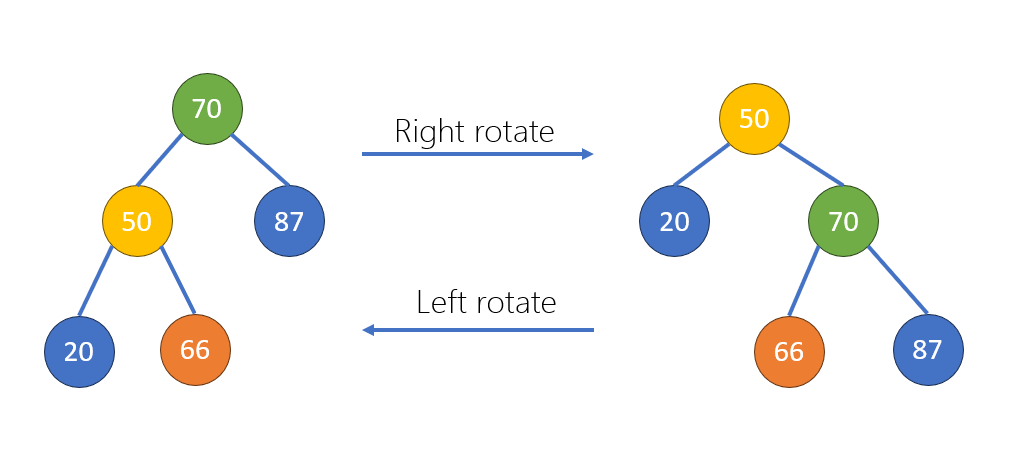
樹堆
- 在節點裡多存一個值 pri ,插入時給定隨機值
- pri 的性質類似堆,父節點比子節點小
- 同時維護二元搜尋樹、(最小)堆的性質
- 有違反就做對應旋轉
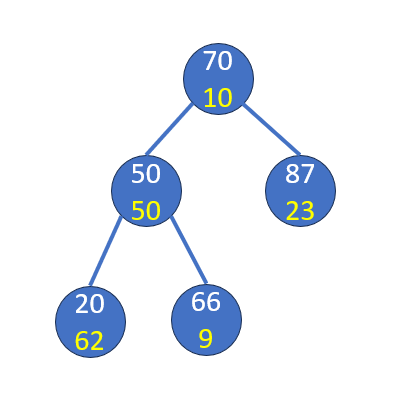
不合法樹堆(因插入66)
白:val
黃:pri
檢查插入和父節點
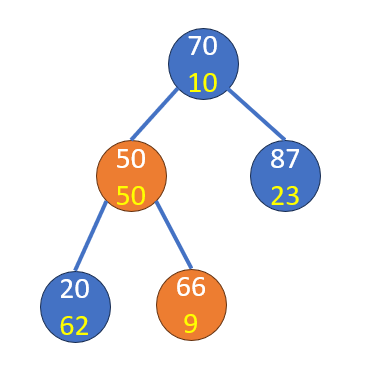
旋轉
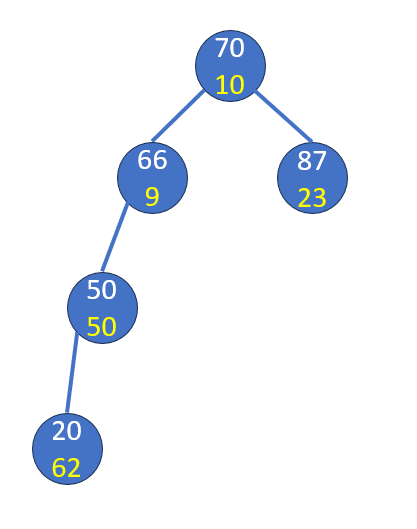
檢查新根和父節點
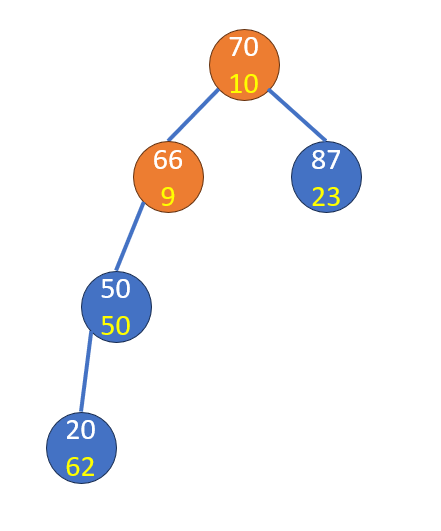
旋轉
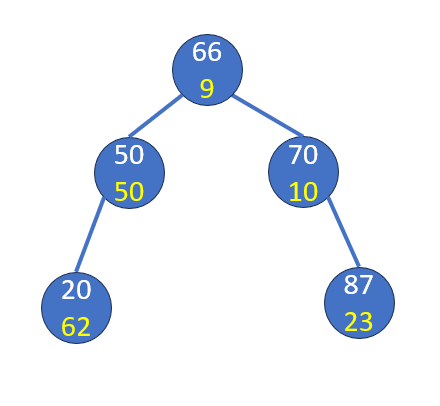
刪除
- 將兩子節點轉到只有單子節點/無子節點
- 每次選擇 pri 較大的那一方轉下去
複雜度
- 隨機取數,所以複雜度總是好的
- 用 stdlib 的 rand 常數很大,建議用 #include<random> 的
std::mt19937 mt_rand(std::random_device{}());
應用
- ordered set: 維護子樹大小
- find by order: 找尋第 k 大的值,用二分搜
- order of key: 找尋某值的排位,在搜尋時維護當前節點排名
- 需要維護 set/map 不能維護的怪東東
- 需要維護 __gnu_pbds::tree 不好寫的怪東東
參考題解
iscoj 陣列不能開太大,最好用 vector
有些部分是我在耍毒可以忽略
// 不能壓常哭哭
#include <stdlib.h>
#include <time.h>
#include <iostream>
#include <string>
#include <vector>
#define io std::ios_base::sync_with_stdio(0), cin.tie(0), cout.tie(0)
using std::cin;
using std::cout;
using std::string;
using std::vector;
using ll = long long;
const int max_n = 5e5 + 1;
const ll mod = 1e9 + 7;
const int INF = 2147483647;
// O(n) 做完後均攤是O(1)的,雖然我猜常數壓小點用O(log n)的快速冪也會過
vector<ll> pow27;
void init_pow() {
pow27[0] = 1LL;
for (int i = 1; i <= max_n; i++) pow27.push_back(pow27[i - 1] * 27 % mod);
}
// 樹堆,維護最小堆
struct Treap {
struct Node {
int pri, size = 1; // 權值,子樹大小
ll hash = 0;
char val = 0;
Node *lchild, *rchild;
};
inline static Node *NIL, *root;
Treap() {
NIL = new Node;
root = NIL;
NIL->size = 0;
NIL->pri = INF;
NIL->lchild = NIL;
NIL->rchild = NIL;
}
void update(Node *cur) {
if (cur != NIL) {
cur->size = cur->lchild->size + cur->rchild->size + 1;
cur->hash = (cur->lchild->hash + cur->val * pow27[cur->lchild->size] + cur->rchild->hash * pow27[cur->lchild->size + 1]) % mod;
}
return;
}
void lrotate(Node *&cur) {
Node *new_root = cur->rchild;
cur->rchild = cur->rchild->lchild;
update(cur);
new_root->lchild = cur;
cur = new_root;
update(cur);
}
void rrotate(Node *&cur) {
Node *new_root = cur->lchild;
cur->lchild = cur->lchild->rchild;
update(cur);
new_root->rchild = cur;
cur = new_root;
update(cur);
}
void insert(char val, int pos, Node *&cur = root) {
if (pos - cur->lchild->size - 1 >= 0) {
if (cur->rchild != NIL) insert(val, pos - cur->lchild->size - 1, cur->rchild);
else {
cur->rchild = new Node;
cur->rchild->pri = rand();
cur->rchild->hash = val - 'a' + 1;
cur->rchild->val = val - 'a' + 1;
cur->rchild->lchild = NIL;
cur->rchild->rchild = NIL;
}
} else {
if (cur->lchild != NIL) insert(val, pos, cur->lchild);
else {
cur->lchild = new Node;
cur->lchild->pri = rand();
cur->lchild->hash = val - 'a' + 1;
cur->lchild->val = val - 'a' + 1;
cur->lchild->lchild = NIL;
cur->lchild->rchild = NIL;
}
}
// 檢查樹平衡
// 可以保證,每次至多只有一邊是不合法的
// 如果左邊不合法,則右旋轉
if (cur->lchild->pri < cur->pri) rrotate(cur);
// 如果右邊不合法,則左旋轉
else if (cur->rchild->pri < cur->pri) lrotate(cur);
else update(cur);
return;
}
void update_to_leaf(Node *&cur) {
if (cur->lchild != NIL && cur->rchild != NIL) {
if (cur->lchild->pri < cur->rchild->pri) {
rrotate(cur);
update_to_leaf(cur->rchild);
} else {
lrotate(cur);
update_to_leaf(cur->lchild);
}
update(cur);
return;
} else if (cur->lchild != NIL) {
Node *new_root = cur->lchild;
delete cur;
cur = new_root;
return;
} else if (cur->rchild != NIL) {
Node *new_root = cur->rchild;
delete cur;
cur = new_root;
return;
} else {
delete cur;
cur = NIL;
return;
}
}
void remove(int pos, Node *&cur = root) {
// find
if (pos - cur->lchild->size - 1 == 0) {
update_to_leaf(cur);
update(cur);
return;
}
if (pos - cur->lchild->size - 1 > 0) remove(pos - cur->lchild->size - 1, cur->rchild);
else remove(pos, cur->lchild);
update(cur);
return;
}
} dynamic_string;
int main() {
io;
srand(time(NULL));
pow27.push_back(1LL);
init_pow();
string S;
cin >> S;
for (int i = 0; i < S.size(); i++) dynamic_string.insert(S[i], i);
int Q;
cin >> Q;
while (Q--) {
int type, x;
char c;
cin >> type;
if (type == 1) {
cin >> x >> c;
dynamic_string.insert(c, x);
} else if (type == 2) {
cin >> x;
dynamic_string.remove(x);
} else {
cout << dynamic_string.root->hash << '\n';
}
}
return 0;
}無旋式樹堆
- 減少碼量的東東
- 分裂與合併
- 常數比較大
- 好持久化
分裂
- 依照值 k 將樹堆分裂成兩個樹堆A, B
- 沿著「邊邊」分裂
- 遞迴式有:當前節點指標、分裂的界線值、接在 A 的參考、接在 B 的參考
- 如果當前值 <= k ,將當前節點歸在 A,向右遞迴
- 否則歸在 B,向左遞迴
合併
- 假設有兩個樹堆 A,B
- B 的值完全大於 A
- 遞迴下去,比較兩棵樹的 pri 值
- 比較大的接在比較小的下面,記得用符合二元搜尋樹性質的方式合併
這是扣
我開始後悔教旋轉式樹堆了
直觀但難寫得要死
struct BST {
struct node {
int val, pri;
node *lchild = nullptr, *rchild = nullptr;
} *root;
void pull(node *cur);
void split(node *cur, int k, node *&A, node *&B) {
if (!cur) {
A = B = nullptr;
return;
}
if (cur->val <= k) {
A = cur;
split(cur->rchild, k, A->rchild, B);
} else {
B = cur;
split(cur->lchild, k, A, B->lchild);
}
pull(cur);
}
node *merge(node *A, node *B) {
if (!A || !B) {
if (A) return A;
if (B) return B;
return nullptr;
}
if (A->pri < B->pri) {
A->rchild = merge(A->rchild, B);
pull(A);
return A;
} else {
B->lchild = merge(A, B->lchild);
pull(B);
return B;
}
}
};其他操作
- 插入值:以值分裂,合併三棵樹堆
- 刪除值:以值分裂,刪除中間的樹,合併左右兩棵樹
- 剩下操作基本相同
struct BST {
void insert(int k) {
node *L = nullptr, *R = nullptr;
node *new_node;
new_node->val = k, new_node->pri = rand();
split(root, k, L, R);
root = merge(merge(L, new_node), R);
}
void remove(int k) {
node *L = nullptr, *M = nullptr, *R = nullptr;
split(root, k - 1, L, M), split(M, k, M, R);
delete M;
root = merge(L, R);
}
};
扣
我真的恨透了我自己
再寫一次剛剛的樹堆題
稀疏表
Sparse Table
區間最小值
- 可以發現,用前綴並不能良好地維護區間最小值
- 觀察區間最小值具備的特性:
- 有重複的值並不影響結果
- 具有結合律
- 因此,可以藉由這特性弄出類似前綴的作用
區間最小值
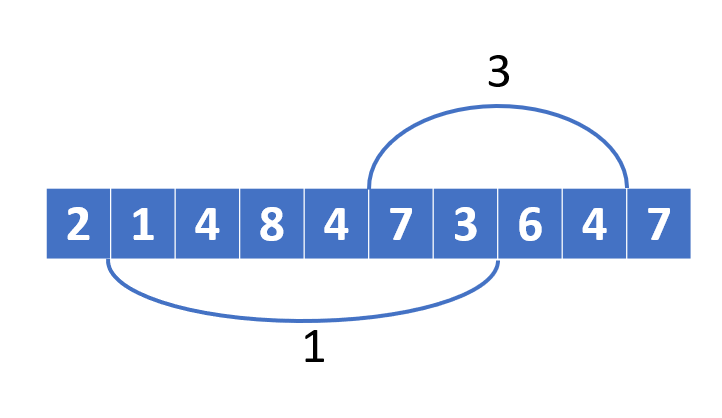
- 即便有重疊的區間,也不影響合併的答案
- [1, 6] 和 [5, 8] 有重疊 [5, 6],但可以直接合併兩個答案 1, 3 得到 [1, 8] 的答案
稀疏表
- 弄一堆大小區間,需要的時候取其中幾個合併就好
- 觀察到兩個大小為 的區間,可合併得一個大小為 的區間
- 以 記錄以 l 為開頭,大小 區間的答案
- 有
- 可以用 1 << i 代表
- 這種做法稱為倍增法,因為每次算出來的區間長度倍增
建表
- 初始化 i = 0 的答案,接著用迴圈從 i = 1 跑到 log n 的答案
- 複雜度
- 同樣,為了方便,用不到就設無限大
const int lg_n = std::__lg(n) + 1;
const int INF = 2147483647;
for (int i = 0; i < n; i++) scanf("%d", &sparse_table[0][i]);
for (int i = 1; i < lg_n; i++) {
int j = 0;
for (; j + (1 << (i - 1)) < n; j++)
sparse_table[i][j] = min(sparse_table[i - 1][j], sparse_table[i - 1][j + (1 << (i - 1))]);
for (; j < n; j++) sparse_table[i][j] = INF;
}取答案
- 取答案時找出 就可以用最接近 的兩塊湊出我們要的答案
- 即
- 程式中,我們利用 std::__lg 取得 lg 值,使用 clang 編譯器的請自行解決
- 總複雜度
- 用組語確認過 std::__lg 是好的
迭代式線段樹
Iterative Segment Tree
參考資料
zkw 線段樹和 Codeforces 上那一篇講的不一樣,我主要採用 Codeforces 上的版本,畢竟左閉右開而且好理解(大喜)
- 採用函式遞迴
- 碼量大
- 空間較大
- 常數較大
- 結構可變(好持久化)
- 函式參數多
- 不可直接取葉節點
- 幾乎不用位元運算
遞迴式線段樹
迭代式線段樹
- 使用迴圈
- 碼量小
- 空間較小
- 常數較小
- 結構固定(難持久化)
- 函式參數少
- 葉節點易掌握
- 須熟悉位元運算
特例 - 完美二元樹

- 除了葉節點以外每個節點都有兩個子節點
- 在這情況下沒有「分」治的必要,從葉節點更新就好了
節點相關運算
- 設 x 是當前節點
- x >> 1 父節點
- x << 1 左子節點
- x << 1 | 1 右子節點
- x & 1 是否為右子節點
- x ^ 1 兄弟節點
- 葉節點 = 原 index + 原大小
操作
- 建樹:用建堆的方式,從 i = size - 1 跑到 1,合併兩個子節點的答案
- 單點修改:從葉節點一路更新到根節點
範圍操作
- 由下向上取節點
- 如果要取的界線向上延伸會切過父節點,則這點要取:
- 左界:如果當前節點是右子節點
- 右界:如果當前節點是左子節點
- 考慮到使用左閉右開,因此程式裡跑的是右界 + 1 ,是右子節點時要取
- 取完後更新範圍
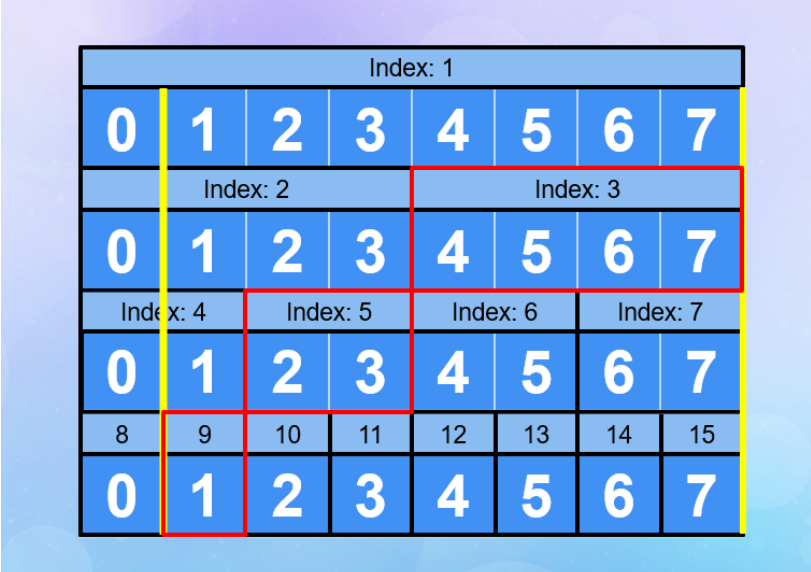
扣(以區間和為例)
懶標是類似的,但可以只開 size 大小,因為葉節點不用存懶標
struct Stree {
int size;
vector<int> tree;
void build(vector<int>& data) {
size = data.size();
tree.resize(size << 1);
for (int i = 0; i < size; i++) tree[i + size] = data[i];
for (int i = size - 1; i > 0; i--) tree[i] = tree[i << 1] + tree[i << 1 | 1];
}
void modify(int pos, int new_data) {
pos += size;
tree[pos] = new_data;
for (; pos > 0; pos >>= 1) tree[pos >> 1] = tree[pos] + tree[pos ^ 1];
}
int query(int l, int r) {
int ans = 0;
for (l += size, r += size; l < r; l >>= 1, r >>= 1) {
if (l & 1) ans += tree[l++];
if (r & 1) ans += tree[--r];
}
return ans;
}
};
懶標下推
- 在原版 zkw 中,使用「懶標永久化」的技巧
- 不巧地,某些題目不好懶標永久化
- 查詢前從根往下下推
push & pull
struct Stree {
int size;
vector<int> tree, tag;
void pull(int v) {
v += size;
for (int node_size = 1; v > 0; v >>= 1, node_size <<= 1) tree[v >> 1] = tree[v] + tag[v] * node_size + tree[v ^ 1] + tag[v ^ 1] * node_size;
}
void push(int v) {
for (int h = std::__lg(v + size); h >= 0; h--) {
tag[v >> h] += tag[v >> h >> 1];
tag[v >> h ^ 1] += tag[v >> h >> 1];
tag[v >> h >> 1] = 0;
}
pull(v);
}
};非完美二元樹?
- size 不總是二的冪次
- 你可以把他開滿,方便進行和結構有關的操作,但...
- 你知道嗎,有時候無腦砸他會是好的
- 對,完全不改 code 會是好的
- 結構變得很詭譎
- 我不會證明,但你大可相信他是好的 (?
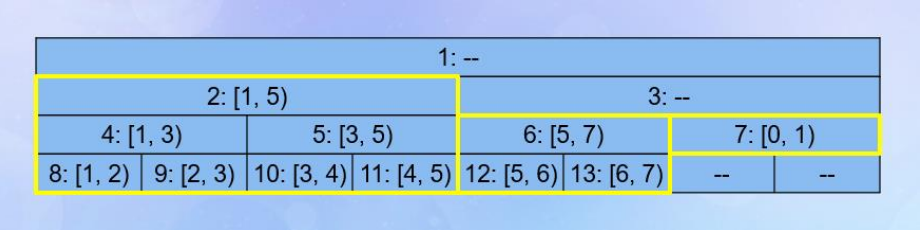
前面除了持久化和動態開點的題目都能用迭代式寫
雜湊表
Hash Table
想要更快...
- map, set 好慢,有沒有更快的作法?
- 如果是記錄數字,可以用陣列紀錄每個數字出現幾次
- 所以
- 也可以紀錄對應的值 (mapped)
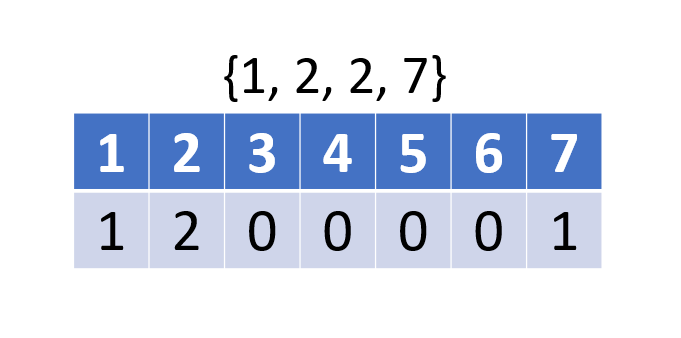
空間
- 空間要開數列最大 - 數列最小 + 1
- 如果值域很大 (1e9) 就爆掉了
- 將這個數 % 一個你喜歡的質數
- 鴿籠原理,會有不同值在同一個位置,稱為碰撞
解決碰撞
- 解法 1:拉鍊法
- 利用鄰接串列,值重複時將重複值串在下面
- 解法 2:找剩下空位
- 當這個位置不行,就利用一個函數改變 index,往下一個位置找
- 缺點:函數沒寫好時間複雜度會是爛的
Hash
- 對於不是數字的 key ,把他變成數字就對了
- 對於字串來說,可以用 27 進位制儲存
STL & PBDS
- #include<unordered_map>
- unordered_map
- #include<bits/extc++.h>
- __gnu_pbds::gp_hash_table<_key, _mapped, ...>
補充
紅黑樹
Red Black Tree
自平衡二元搜尋樹
- 當樹的結構過於不平衡時,使用樹旋轉平衡
- 定義不平衡的條件不同,造就不同種類的平衡樹
紅黑樹
- 綜合效能最高
- 實作特別麻煩
- 競程不會用到,別想了
- set, map 的基底資料結構
- 使用大量迭代代替遞迴
- __gnu_pbds::tree<_Key, _Mapped, ...> (默認紅黑樹模版)
#include <functional>
#include <utility>
#pragma GCC optimize(3)
/**
* @file rb_tree.cpp
* @brief This is a template of rb_tree.
* Use array instead of pointer.
* Can be used for map or set, multiset, etc.
* @author Sea of Voices, CKHS INFOR 36th.
* @date 2023/07/29
*/
using std::pair;
template <typename _Key, typename _Mapped, typename _Cmp = std::less<_Key>>
struct Rb_tree {
#define RED 1
#define BLACK 0
#define NIL 0
#define LEFT 0
#define RIGHT 1
private:
/**
* @brief Surely, the node of a tree.
* sub_size represents the size of left subtree + right subtree + 1
*/
struct Node {
public:
bool color = RED;
_Key key;
_Mapped value;
int parent = 0, lchild = 0, rchild = 0;
unsigned int sub_size = 1;
Node() {}
};
/**
* @brief Use array instead of using "new"
*/
struct _Alloc {
public:
inline static const int max_size = 200005, delete_size = 10;
inline static Node data[max_size];
inline static int space[delete_size];
int back = 1, stack_back = 0;
inline int new_node() {
return stack_back ? back++ : space[--stack_back];
}
inline int new_node(const _Key& _key, int _parent) {
if (!stack_back) {
data[back].key = _key;
data[back].parent = _parent;
return back++;
}
--stack_back;
data[space[stack_back]].key = _key;
data[space[stack_back]].parent = _parent;
return space[stack_back];
}
inline void relese_space(int _pos) {
data[_pos].parent = 0, data[_pos].lchild = 0, data[_pos].rchild = 0;
data[_pos].color = RED;
data[_pos].sub_size = 1;
space[stack_back++] = _pos;
return;
}
};
private:
inline static _Alloc alloc;
inline static int root = 0, _size = 0;
_Cmp cmp;
public:
/**
* @brief A simple iterator of the tree.
* Provides a bridge between other functions and value.
*/
struct iterator {
private:
int pos = 0;
public:
inline iterator() {}
inline iterator(int _pos) {
pos = _pos;
return;
}
_Mapped& operator*() {
return alloc.data[pos].value;
}
bool operator==(const iterator& it) {
return it.pos == pos;
}
bool operator!=(const iterator& it) {
return it.pos != pos;
}
iterator& operator++() {
#define Self alloc.data[pos]
#define is_lchild (alloc.data[alloc.data[pos].parent].lchild == pos)
if (pos == NIL) {
pos = root;
while (Self.lchild != NIL) pos = Self.lchild;
} else if (Self.rchild != NIL) {
pos = Self.rchild;
while (Self.lchild != NIL) pos = Self.lchild;
} else if (is_lchild) {
pos = Self.parent;
} else {
while (!is_lchild && pos != NIL) pos = Self.parent;
if (pos != NIL) pos = Self.parent;
}
return *this;
#undef Self
#undef is_lchild
}
iterator& operator=(const iterator& _it) {
pos = _it.pos;
}
};
public:
// default constructor
Rb_tree() {
alloc.data[0].color = BLACK;
alloc.data[0].sub_size = 0;
cmp = _Cmp{};
}
private:
/**
* @brief This function rotates a subtree.
* rotate_root stands for the root of the subtree,
* LEFT(0) stands for left rotation, RIGHT(1) stands
* for right rotation.
*/
inline void rotate(int rotate_root, bool direction) {
#define Parent alloc.data[alloc.data[rotate_root].parent]
#define Self alloc.data[rotate_root]
#define Rchild alloc.data[alloc.data[rotate_root].rchild]
#define Lchild alloc.data[alloc.data[rotate_root].lchild]
if (direction == LEFT) {
if (Self.parent != NIL) {
if (Parent.lchild == rotate_root) Parent.lchild = Self.rchild;
else Parent.rchild = Self.rchild;
} else root = Self.rchild;
Rchild.parent = Self.parent;
Self.parent = Self.rchild;
Self.rchild = Rchild.lchild;
if (Self.rchild != NIL) Rchild.parent = rotate_root;
Parent.lchild = rotate_root;
Self.sub_size = Lchild.sub_size + Rchild.sub_size + 1;
Parent.sub_size = Self.sub_size + alloc.data[Parent.rchild].sub_size + 1;
} else {
if (Self.parent != NIL) {
if (Parent.lchild == rotate_root) Parent.lchild = Self.lchild;
else Parent.rchild = Self.lchild;
} else root = Self.lchild;
Lchild.parent = Self.parent;
Self.parent = Self.lchild;
Self.lchild = Lchild.rchild;
if (Self.rchild != NIL) Lchild.parent = rotate_root;
Parent.rchild = rotate_root;
Self.sub_size = Lchild.sub_size + Rchild.sub_size + 1;
Parent.sub_size = Self.sub_size + alloc.data[Parent.lchild].sub_size + 1;
}
return;
#undef Parent
#undef Self
#undef Rchild
#undef Lchild
}
private:
/**
* @brief After inserting a node, update the shape of this tree.
*/
inline void update_node(int v) {
// update node
#define Self alloc.data[v]
#define Parent alloc.data[alloc.data[v].parent]
#define Grand_parent alloc.data[alloc.data[alloc.data[v].parent].parent]
#define is_parent_left_child (alloc.data[alloc.data[alloc.data[v].parent].parent].lchild == alloc.data[v].parent)
#define is_self_right_child (alloc.data[alloc.data[v].parent].rchild == v)
// update the size on the chain
for (int update_node = Self.parent; update_node != NIL; update_node = alloc.data[update_node].parent) ++alloc.data[update_node].sub_size;
while (v != root) {
// case 2: parent is black
if (Parent.color == BLACK) {
return;
}
// case 3: uncle is red
if (alloc.data[Grand_parent.lchild].color == RED && alloc.data[Grand_parent.rchild].color == RED) {
alloc.data[Grand_parent.lchild].color = BLACK;
alloc.data[Grand_parent.rchild].color = BLACK;
Grand_parent.color = RED;
v = Parent.parent;
continue; // back to case 1
}
// case 4: if it's a "zap" structure
if (is_parent_left_child == is_self_right_child) v = Self.parent, rotate(v, is_self_right_child ? RIGHT : LEFT);
// case 5: it's a chain
Parent.color = BLACK;
Grand_parent.color = RED;
rotate(Parent.parent, is_parent_left_child ? RIGHT : LEFT);
break;
}
if (v == root) Self.color = BLACK;
return;
#undef Self
#undef Parent
#undef Grand_parent
#undef is_parent_left_child
#undef is_self_right_child
}
private:
/**
* @brief This function insert a nod without change the value of it.
* Returns {pointer, success or not}
*/
inline pair<int, bool> _insert(const _Key& _key) {
if (!root) {
_size++;
root = alloc.new_node(_key, 0);
alloc.data[root].color = BLACK;
return {1, 1};
}
// binary search, insert
int v = root;
#define Self alloc.data[v]
while (v) {
if (Self.key == _key) return {v, 0};
if (cmp(_key, Self.key)) {
if (Self.lchild != NIL) v = Self.lchild;
else {
v = Self.lchild = alloc.new_node(_key, v);
break;
}
} else {
if (Self.rchild != NIL) v = Self.rchild;
else {
v = Self.rchild = alloc.new_node(_key, v);
break;
}
}
}
_size++;
return {v, 1};
#undef Self
}
public:
/**
* @brief Insert a key with value.
* If there exist a same key, it changes nothing but returns {irerator, 0}.
* Otherwise, it returns {iterator, 1}
*/
inline pair<iterator, bool> insert(const _Key& _key, const _Mapped& _val) {
pair<int, bool> result = _insert(_key);
alloc.data[result.first].value = _val;
if (result.second) update_node(result.first);
iterator result_it(result.first);
return {result_it, result.second};
}
/**
* @brief Returns the size of the tree.
*/
inline unsigned int size() {
return _size;
}
public:
/**
* @brief insert if there is no same key, update value if there exist a key.
*/
inline _Mapped& operator[](const _Key& _key) {
pair<int, bool> result = _insert(_key);
if (result.second) update_node(result.first);
return alloc.data[result.first].value;
}
public:
/**
* @brief Returns an iterator that point which is empty node, the end of the tree.
* Time complexity: O(1)
*/
inline iterator end() {
iterator result;
return result;
}
public:
/**
* @brief Returns an itrator that point at the start of the tree.
* It's the leftest node of the tree.
* WARNING, Different from STL, its time complexity is O(log n) (while STL is constant)
*/
inline iterator begin() {
iterator result;
return ++result;
}
public:
/**
* @brief Find with a key, and returns an iterator.
* Returns end() if it doesn't found anything.
*/
inline iterator find(const _Key& _key) {
#define Self alloc.data[v]
if (!root) return end();
int v = root;
while (v != NIL) {
if (_key == Self.key) break;
v = cmp(_key, Self.key) ? Self.lchild : Self.rchild;
}
iterator result(v);
return result;
#undef Self
}
private:
/**
* @brief This gives a way to erase a node without updating whole tree.
*/
int _erase(const _Key& _key) {
#define Target alloc.data[target]
#define Target_parent alloc.data[alloc.data[target].parent]
// find the target node
if (!root) return -1;
int target = root;
while (target != NIL) {
if (_key == Target.key) break;
target = cmp(_key, Target.key) ? Target.lchild : Target.rchild;
}
if (target == NIL) return -1;
--_size;
#define Self alloc.data[remove]
#define Parent alloc.data[alloc.data[remove].parent]
#define Lchild alloc.data[alloc.data[remove].lchild]
#define Rchild alloc.data[alloc.data[remove].rchild]
#define is_lchild (alloc.data[alloc.data[remove].parent].lchild == remove)
#define Empty alloc.data[0]
int remove = target;
if (Self.lchild != NIL && Self.rchild != NIL) {
remove = Self.rchild;
while (Self.lchild != NIL) remove = Self.lchild;
Target.key = Self.key;
Target.value = Self.value;
}
for (int v = remove; v != NIL; v = alloc.data[v].parent) --alloc.data[v].sub_size;
// focus on "Self"
if (Self.parent != NIL) {
if (is_lchild) Parent.lchild = Self.lchild != NIL ? Self.lchild : Self.rchild;
else Parent.rchild = Self.lchild != NIL ? Self.lchild : Self.rchild;
}
// delete the root
else {
root = Self.lchild != NIL ? Self.lchild : Self.rchild;
alloc.data[root].color = BLACK;
alloc.data[root].parent = NIL;
alloc.relese_space(remove);
return -1;
}
if (Self.lchild != NIL) Lchild.parent = Self.parent, Self.color = Lchild.color;
else if (Self.rchild != NIL) Rchild.parent = Self.parent, Self.color = Rchild.color;
else Empty.parent = Self.parent, alloc.relese_space(remove);
if (Self.color == RED || Lchild.color == RED || Rchild.color == RED) {
Lchild.color = BLACK;
Rchild.color = BLACK;
alloc.relese_space(remove);
return -1;
}
return remove;
#undef Self
#undef Parent
#undef Lchild
#undef Rchild
#undef is_lchild
#undef Empty
}
private:
/**
* @brief Update when a node is removed.
*/
void update_removed_node(int v) {
#define Self alloc.data[v]
#define Parent alloc.data[alloc.data[v].parent]
#define Lchild alloc.data[alloc.data[v].lchild]
#define Rchild alloc.data[alloc.data[v].rchild]
#define is_left (alloc.data[alloc.data[v].parent].lchild == v)
#define Empty alloc.data[0]
int remove = v;
while (v != root) {
if (is_left) {
#define Brother alloc.data[alloc.data[alloc.data[v].parent].rchild]
// case 1
if (Brother.color == RED) {
Parent.color = RED;
Brother.color = BLACK;
rotate(Self.parent, LEFT);
}
// case 2
if (alloc.data[Brother.lchild].color == BLACK && alloc.data[Brother.rchild].color == BLACK) {
v = Self.parent;
Rchild.color = RED;
if (Self.color == RED) {
Self.color = BLACK;
break;
}
continue;
}
// case 3
if (alloc.data[Brother.rchild].color == BLACK) {
alloc.data[Brother.lchild].color = RED;
rotate(Parent.rchild, RIGHT);
}
// case 4
Brother.color = Parent.color;
Parent.color = BLACK;
alloc.data[Brother.rchild].color = BLACK;
rotate(Self.parent, LEFT);
break;
}
#undef Brother
#define Brother alloc.data[alloc.data[alloc.data[v].parent].lchild]
else {
// case 1
if (Brother.color == RED) {
Parent.color = RED;
Brother.color = BLACK;
rotate(Self.parent, RIGHT);
}
// case 2
if (alloc.data[Brother.lchild].color == BLACK && alloc.data[Brother.rchild].color == BLACK) {
v = Self.parent;
Rchild.color = RED;
if (Self.color == RED) {
Self.color = BLACK;
break;
}
continue;
}
// case 3
if (alloc.data[Brother.lchild].color == BLACK) {
alloc.data[Brother.rchild].color = RED;
rotate(Parent.lchild, LEFT);
}
// case 4
Brother.color = Parent.color;
Parent.color = BLACK;
alloc.data[Brother.lchild].color = BLACK;
rotate(Self.parent, RIGHT);
break;
}
break;
}
alloc.relese_space(remove);
Empty.parent = NIL;
#undef Brother
#undef Self
#undef Parent
#undef Lchild
#undef Rchild
#undef is_left
#undef Empty
}
public:
/**
* @brief Removes a node from the tree.
*/
void erase(const _Key& _key) {
int result = _erase(_key);
if (result != -1) update_removed_node(result);
return;
}
public:
/**
* @brief Find a node with its order in this map.
* If cannot find the node, returns end().
*/
iterator find_by_order(int _order) {
#define Self alloc.data[v]
#define Lchild alloc.data[alloc.data[v].lchild]
int cur_order = 0;
int v = root;
while (v != NIL) {
if (cur_order + Lchild.sub_size == _order) break;
if (cur_order + Lchild.sub_size > _order) v = Self.lchild;
else cur_order += Lchild.sub_size + 1, v = Self.rchild;
}
iterator result(v);
return v;
#undef Self
#undef Lchild
}
public:
/**
* @brief Find a node with its key, return its order in this map.
*/
int order_of_key(const _Key& _key) {
#define Self alloc.data[v]
#define Lchild alloc.data[alloc.data[v].lchild]
int cur_order = 0;
int v = root;
while (v != NIL) {
if (_key == Self.key) return cur_order + Lchild.sub_size;
if (cmp(_key, Self.key)) {
if (Self.lchild != NIL) v = Self.lchild;
else return cur_order;
} else {
cur_order += Lchild.sub_size + 1;
if (Self.rchild != NIL) v = Self.rchild;
else return cur_order;
}
}
return -1;
#undef Self
#undef Lchild
}
#undef RED
#undef BLACK
#undef LEFT
#undef RIGHT
#undef NIL
};未完工的模版 (527行)
主要應該是刪除寫爛了
扣很醜,如果你真的有興趣可以來修修看
條件
- 每個節點非紅即黑
- 根是黑色
- 葉子是黑色 (葉子皆是NIL)
- 紅節點必有兩個黑色子節點
- 從根到任意葉子節點有相同數量的黑色節點
不難發現根到葉最長路徑不大於最短路徑的兩倍
可以證明樹高是 的
NIL
- 葉子節點,黑色,可以有一些資料
- 實作時通常指向同一個點,省空間
- 也可以不指向同個點,方便操作不用特判

插入
- 對於每次插入,我們插入一個紅色節點,因為加入黑節點很難調整
- 先依照二元搜尋樹的方式插入,再做後續調整
Case 1: 新的節點是根
- 可能違反「根是黑色」-> 改成紅色
- 對於每條到葉節點的路徑黑節點數量不動
- 不是紅色,不違反紅節點必有兩個黑子節點
- 做完了
Case 2: 父節點是黑色
- 紅節點有兩個黑節點並沒有失效
- 對於根到葉的路徑來說,並沒有增加黑色節點
- 做完了
Case 3: 叔父節點為紅色
- 違反紅節點有兩個黑節點
- 將祖父節點改為紅色,父節點和叔父節點改為黑色
- 對於這個子樹它不違反「紅節點有兩黑節點」,從根到葉節點的黑節點數量也不動
- 但祖父可能違反其他規則,因此將祖父視為新增節點從 case 1 處理
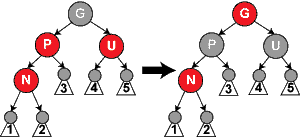
Case 4: ㄑ字形
- 對於父節點是左子節點的情況,新節點是右子節點;或者父節點是右子節點兒新節點是左子節點
- 對父節點進行一次旋轉,使它成為一直線,丟到 case 5 一起處理
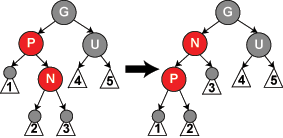
Case 5: 剩下的情況
- 注意到因為插入的是紅節點,根到葉的黑節點數量不變
- 解決紅節點必須有兩個黑子節點的問題,解決完就做完了
- 對祖父進行一次旋轉,設定顏色如下:
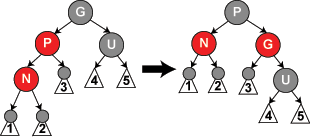
注意到可以使用迭代實現,不用遞迴
在節點裡要多記錄父節點的指標
善用酷酷的參考,你會寫得開心很多
還有可以發現樹旋轉必定 <= 2 次,所以常數很小
刪除
- 找到要刪除的節點
- 如果有兩個子節點,我們尋找左子樹最大節點/右子樹最小節點,將值複製過來
- 只複製值,所以對於另一個子樹來說不影響其他奇怪的性質
- 將問題簡化為「刪除僅一個子節點的節點(或沒有子節點)」的問題
- 因為只有一個子節點(或沒有子節點),如果是紅節點必定兩個子節點都是NIL,直接刪除不違反任何性質
- 只需討論黑節點的情況
前置作業
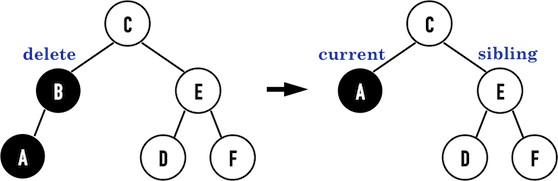
假定 current 是左子節點,如果是右節點操作要對稱過去
整體流程圖

Case 1: 兄弟節點是紅色
- 讓兄弟節點調整成黑色,進入 case 2, case 3 或 case 4
- 根到葉的黑節點數保持不變
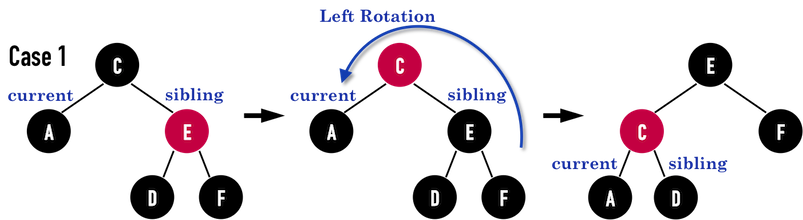
Case 2: 兄弟節點有二黑子節點
- 調整兄弟節點為紅
- 如果父節點為紅,把父節點調整為黑色就做完了
- 如果父節點為黑,將父節點設為新 current ,重頭判起
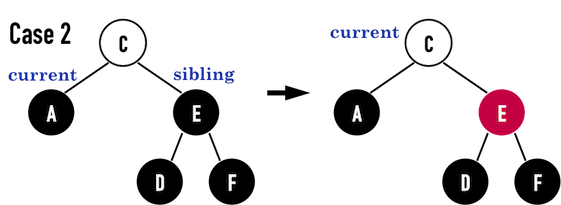
Case 3: 兄弟節點左子節點為紅
- 調整兄弟節點為紅、紅的子節點為黑
- 對兄弟進行一次右旋轉
- 進入 case 4
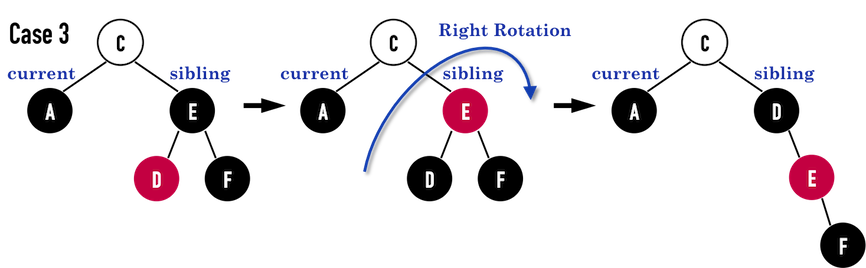
Case 4: 兄弟節點右子節點為紅
- 將兄弟塗成父節點的顏色
- 父節點塗成黑色
- 兄弟節點的右節點塗成黑色
- 對父節點進行一次左旋轉
- 調整後因為根到葉的黑節點數量都相同,就做完了