資料結構

Data Structure

講師

  • 225 賴柏宇
  • 海之音、小海或其他類似的
  • 美術能力見底
  • 表達能力差，不懂要問
  • INFOR 36th 學術長
  • 這頁是偷來的
  • 不會資結所以來當資結講師
# 前言

關於重做簡報

如果你對我之前發的資料結構簡報有印象那很正常，因為我之前在建中校內資讀有講這門課

為什麼要重做？很簡單，因為那不適合放課，講的東西太深，而且我覺得我那份簡報有點爛

當然，你可以將舊簡報當做一份資源使用，裡面有很多沒講的東西

還有一點是以前的簡報很醜，傷眼

  • 鄰接串列 (Linked List)

Index

  • 線段樹 I (Segment Tree)
  • BIT (Binary Indexed Tree)
  • 稀疏表 (Sparse Table)
  • 線段樹 II (Segment Tree)
  • 樹堆 (Treap)
  • 指標型線段樹 / 動態開點
  • 持久化線段樹
  • 迭代式線段樹
  • 線段樹優化建圖
  • 時間線段樹 ft. 迭代式線段樹

在資訊社講的

注意事項

講師表達能力不是很好，不懂要問

今天會大量用到遞迴、分治等等觀念

在我做這份簡報時另一位講師還沒做分治簡報，所以我就不丟連結了

分治 by BrineTW

資芽

定義及概念

Definition

"Data structures, not algorithms, are central to programming."

- Pike：Notes on Programming in C

定義 & 用途

  • 在電腦裡組織、儲存資料的方法
  • 針對特定操作優化
  • 儲存特定資訊，方便以後操作
  • 之前學的前綴和就帶有一點資料結構的概念
    • 記錄「前綴的和」，方便以後取「區間和」

原陣列

前綴和

1 2 3 4 5 6 7
1 3 6 10 15 21 28

例子

  • 記得 map 的用法嗎
    • 以「鍵值 (key-value)」配對取得資料
  • 底下它額外記錄了不少東西
  • 你不用管它背後如何實作的，反正它能在                時間內為你找到值就對了
O(log\ n)

品項

單價

蘋果

10

香蕉

13

芭樂

11

橘子

15

複習

Review

前綴和 (Prefix Sum)

  • 對於前綴和的每一格，它的值是從陣列頭加到那一格

原陣列

前綴和

1 2 3 4 5 6 7
1 3 6 10 15 21 28
  • 寫成數學式
prefix_{i+1} = prefix_i + a_{i+1}
  • 求區間和
prefix_{r} - prefix_{l-1},\ O(1)

差分 (Finite Difference)

  • 對於差分陣列的每一格，它的值是自己減前一格

原陣列

差分陣列

1 2 3 4 5 6 7
1 1 1 1 1 1 1
  • 寫成數學式
dif_{i} = a_i - a_{i-1}
  • 修改區間
dif_{l}+1,\ dif_{r+1}-1,\ O(1)
  • 求陣列值
O(n)

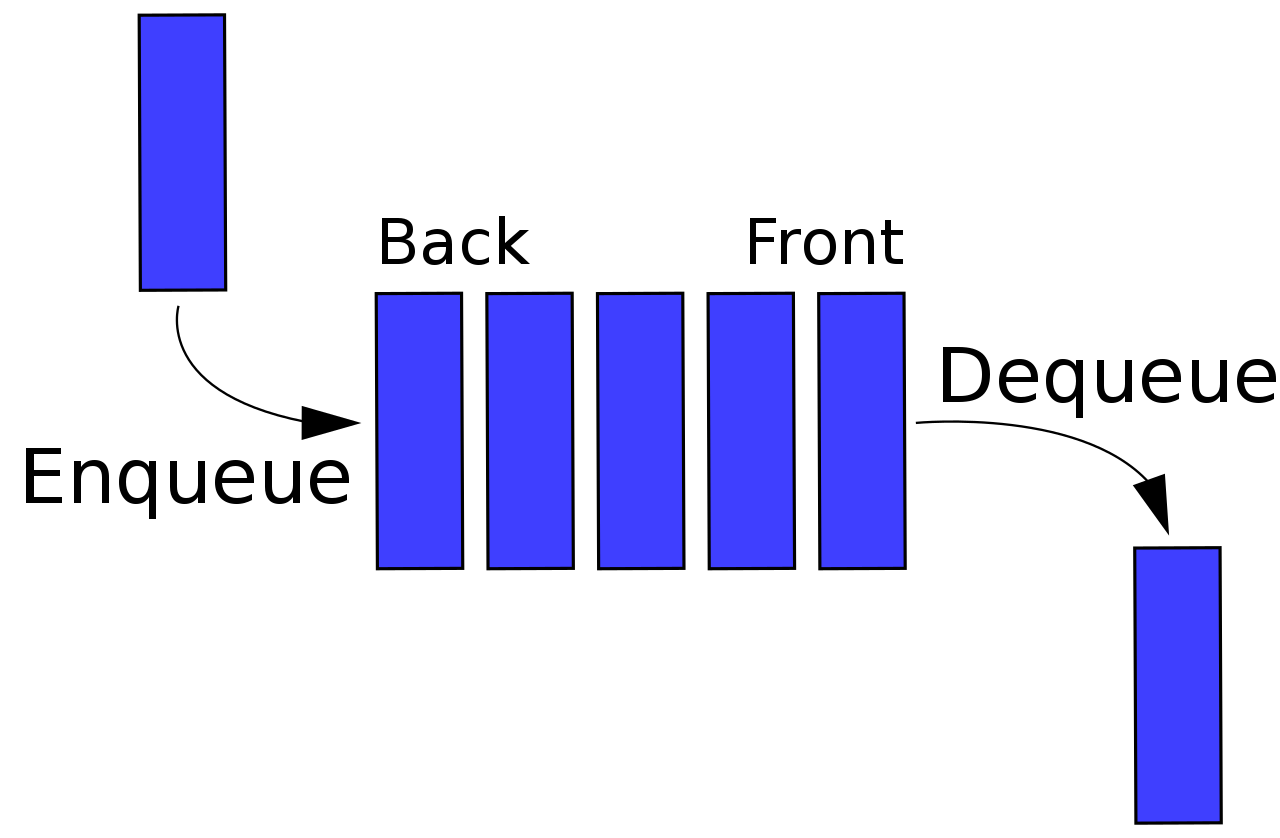
佇列 (Queue)

  • 一個隊伍，可以從後面入隊，前面出隊
  • 入隊
  • 出隊
  • 取隊伍頭
O(1)
O(1)
O(1)

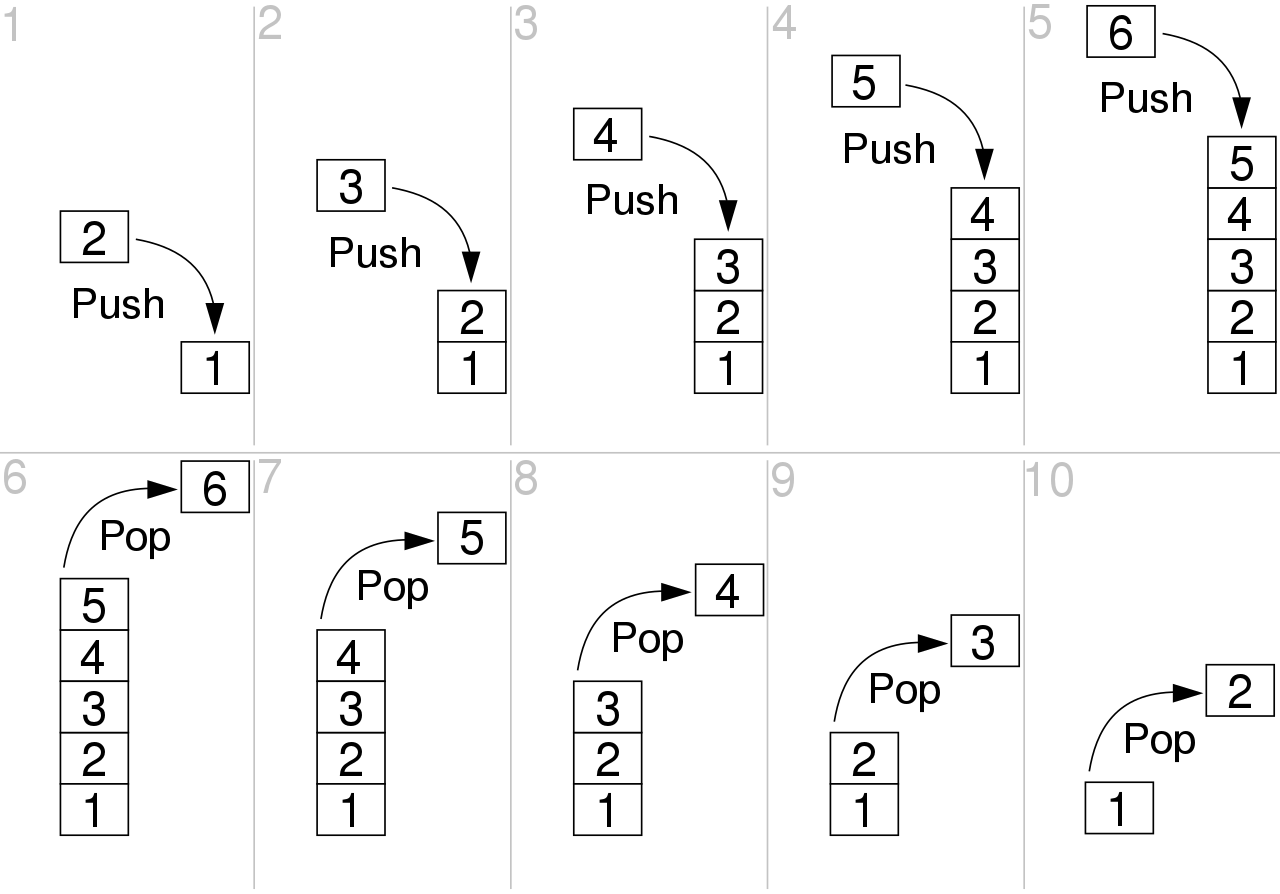
棧 (Stack)

  • 一堆書，可以從上面放書、上面拿書
  • 入堆
  • 出堆
  • 取堆頂
O(1)
O(1)
O(1)

優先權佇列 (Priority Queue)

  • 一堆數，堆頂總是最小 / 最大的數
  • 入堆
  • 出堆
  • 取堆頂
O(log\ n)
O(log\ n)
O(1)

Set / Map

  • Set: 記錄某個元素是否存在
    • 插入元素
    • 查詢元素
    • 刪除元素
  • Map: Key-Value 對應關係，複雜度同 Set
O(log\ n)
O(log\ n)
O(log\ n)

分治主定理 (Master Theorem)

  • 提供分治時計算複雜度的依據
  • 底下是一些比較常用的特例

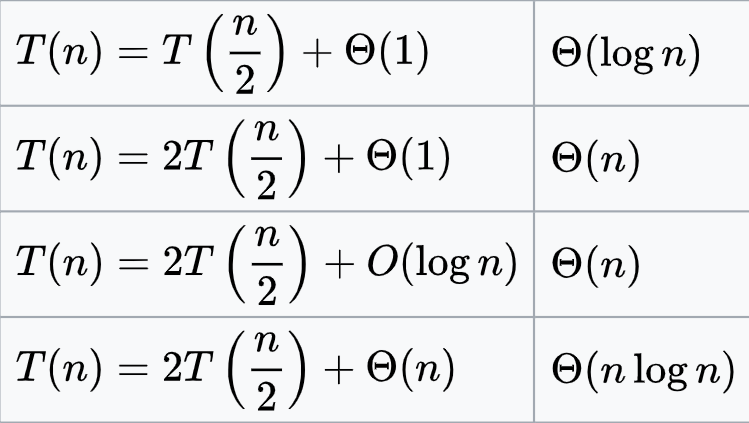
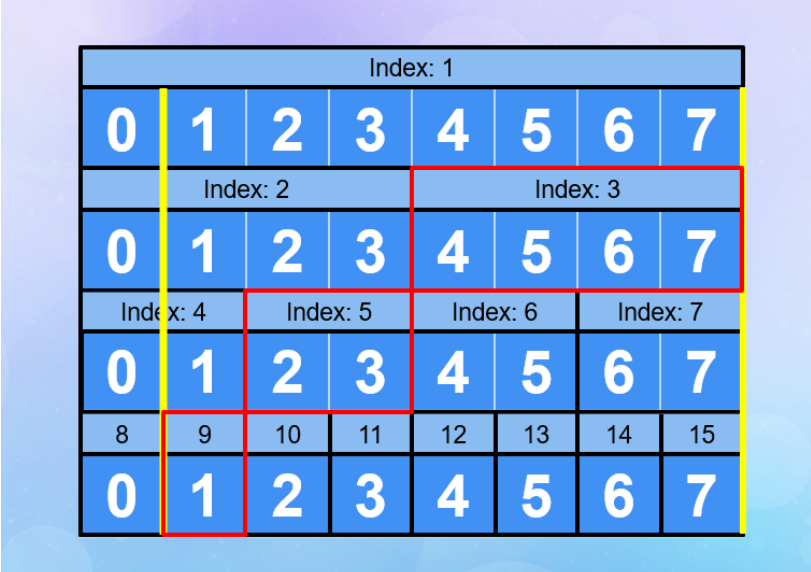
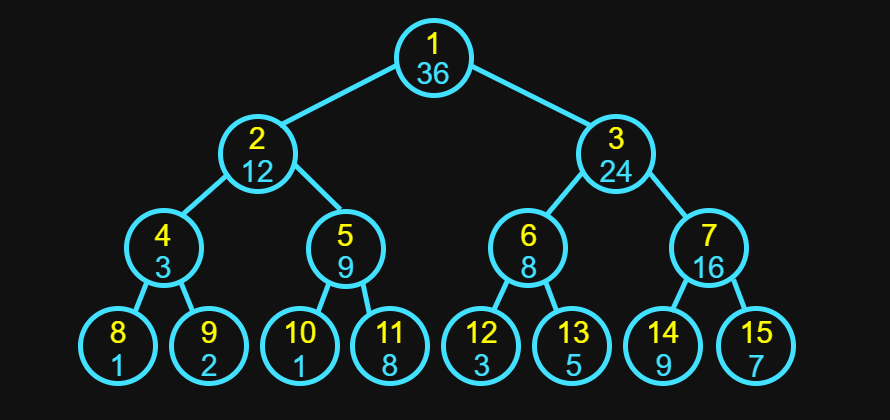
樹 (Tree)

  • 讓你們知道一下我等等可能會怎麼講東西而已

鄰接串列

Linked List

相對

  • 不在乎某個資料的絕對位置 (index)
  • 在乎資料與資料之間的相對關係
  • 百米短跑中，不在意實際位置，只在意自己前方有誰
  • 對於一個位置的資料來說，它只知道它的下一個是誰 / 前一個是誰

現在在哪不重要

重要的是前面 / 下一個是誰

指標？

  • 你看到那個指向另一個點的指針了嗎？
    • 如果你直覺敏銳，應該會覺得和指標有些關聯
    • 啊不是說指標不會用到？
  • 先別急，當然有替代方案，但我們要先講觀念

指針

  • 重要的是指針的觀念
  • 在一個點裡面，存指向下一個點的指標
  • 指標的觀念
    • 告訴我們記憶體的位置
    • 代表一個變數的位置
  • 你會發現有另一個東西功能很像
struct Node {
    int data;
    Node *next;
};

偽指標

  • C++ 中還有另一個可以指向變數的東西
  • 陣列 & 索引值 (Index)
  • 我們可以儲存指向下一個節點的 Index
struct Node {
    int data;
    int next;
};

Node linked_list[n];

next

索引

0

290

data

1

1

2

3

2

89

3

314

2

21

-1

好處

  • 前面提到資結可以優化特定操作，所以它的優勢是？
  • 什麼事只需要處理相鄰節點的？
  • 插入 / 刪除
  • 以刪除 1 節點為例

next

索引

0

290

data

1

1

2

3

2

89

3

314

2

21

-1

好處

  • 前面提到資結可以優化特定操作，所以它的優勢是？
  • 什麼事只需要處理相鄰節點的？
  • 插入 / 刪除
  • 以刪除 1 節點為例

next

索引

0

290

data

2

1

2

3

2

89

3

21

-1

314

2

壞處

  • 相對來說，它有一些壞處
  • 不能知道絕對位置了，會發生什麼？
  • 假設我想要取從頭數起第 3 個節點？

next

索引

0

290

data

2

1

2

3

2

89

3

21

-1

314

2

壞處

  • 相對來說，它有一些壞處
  • 不能知道絕對位置了，會發生什麼？
  • 假設我想要取從頭數起第 3 個節點？

next

索引

0

290

data

2

1

2

3

2

89

3

21

-1

314

2

壞處

  • 相對來說，它有一些壞處
  • 不能知道絕對位置了，會發生什麼？
  • 假設我想要取從頭數起第 3 個節點？

next

索引

0

290

data

2

1

2

3

2

89

3

21

-1

314

2

壞處

  • 相對來說，它有一些壞處
  • 不能知道絕對位置了，會發生什麼？
  • 假設我想要取從頭數起第 3 個節點？
  • 變成           了

next

索引

0

290

data

2

1

2

3

2

89

3

21

-1

314

2

O(n)

注意事項

  • 要記錄索引頭
  • 不然索引頭被刪掉時會無從進入這個串列

next

索引

0

290

data

1

1

2

3

2

89

3

314

2

21

-1

struct Linked_list {
    struct Node {
        int data = 0;
        int next = -1;
    };
    Node list[n];
    int front = 0;
    int back = 0;
    
    // 範例：從後面插入
    
    void push_back(int new_data) {
        List[back].next = back++;
        List[back].data = new_data;
    }
};
# EXAMPLE

範例

CONS

缺點

O(n) 搜尋

競程幾乎用不到

PROS & CONS

PROS

優點

如果真的使用指標，大小是可變的

如果有前後的 index 可以 O(1) 插入 / 刪除

O(1) 刪除頭 / 尾

對於相鄰節點處理方便

例題

其實 Linked List 沒有很重要

重要的只有雙指針和偽指標的觀念

題目看過去確定會解法就好了

線段樹 I

Segment Tree I

兼容

  • 前綴和有什麼特點？
    • O(1) 區間和
    • O(n) 修改
  • 差分有什麼特點？
    • O(1) 區間修改
    • O(n) 查詢˙
  • 兩種狀況好極端，有沒有兼容優點的方法？

改進

  • 我們可以從前綴和下手改進
    • 為何前綴和比較難修改？
    • 每個點交疊的區間太多，修改一個位置修改很多
  • 那麼，不要讓儲存的區間太大就好了
    • 不要太大？要多大？

前綴和

單一個數重疊的範圍太多

每疊到一條藍線就要修改一個值

線段樹？

# 線段樹示意圖

線段樹？

以藍線代表涵蓋範圍

0 1 2 3 4 5 6 7

原陣列 Index

# 線段樹示意圖

線段樹？

以藍線代表涵蓋範圍

0 1 2 3 4 5 6 7

原陣列 Index

# 線段樹示意圖

線段樹？

以藍線代表涵蓋範圍

0 1 2 3 4 5 6 7

原陣列 Index

# 線段樹示意圖

線段樹？

以藍線代表涵蓋範圍

0 1 2 3 4 5 6 7

原陣列 Index

# 線段樹示意圖

線段樹？

0 1 2 3 4 5 6 7

原陣列 Index

9 2 1 8 3 5 6 7

原陣列 data

# 線段樹示意圖

線段樹？

0 1 2 3 4 5 6 7

原陣列 Index

9 2 1 8 3 5 6 7

原陣列 data

9

2

1

8

3

5

6

7

# 線段樹示意圖

線段樹？

0 1 2 3 4 5 6 7

原陣列 Index

9 2 1 8 3 5 6 7

原陣列 data

9

2

1

8

3

5

6

7

11

9

8

13

# 線段樹示意圖

線段樹？

0 1 2 3 4 5 6 7

原陣列 Index

9 2 1 8 3 5 6 7

原陣列 data

9

2

1

8

3

5

6

7

11

9

8

13

20

21

# 線段樹示意圖

線段樹？

0 1 2 3 4 5 6 7

原陣列 Index

9 2 1 8 3 5 6 7

原陣列 data

9

2

1

8

3

5

6

7

11

9

8

13

20

21

41

# 線段樹示意圖

修改位置 6 為 9

0 1 2 3 4 5 6 7

原陣列 Index

9 2 1 8 3 5 6 7

原陣列 data

9

2

1

8

3

5

6

7

11

9

8

13

20

21

41

# 線段樹示意圖

修改位置 6 為 9

0 1 2 3 4 5 6 7

原陣列 Index

9 2 1 8 3 5 9 7

原陣列 data

9

2

1

8

3

5

6

7

11

9

8

13

20

21

41

# 線段樹示意圖

修改位置 6 為 9

0 1 2 3 4 5 6 7

原陣列 Index

9 2 1 8 3 5 9 7

原陣列 data

9

2

1

8

3

5

9

7

11

9

8

13

20

21

41

# 線段樹示意圖

修改位置 6 為 9

0 1 2 3 4 5 6 7

原陣列 Index

9 2 1 8 3 5 9 7

原陣列 data

9

2

1

8

3

5

9

7

11

9

8

16

20

21

41

# 線段樹示意圖

修改位置 6 為 9

0 1 2 3 4 5 6 7

原陣列 Index

9 2 1 8 3 5 9 7

原陣列 data

9

2

1

8

3

5

9

7

11

9

8

16

20

24

41

# 線段樹示意圖

修改位置 6 為 9

0 1 2 3 4 5 6 7

原陣列 Index

9 2 1 8 3 5 9 7

原陣列 data

9

2

1

8

3

5

9

7

11

9

8

16

20

24

44

# 線段樹示意圖

修改位置 0 為 1

0 1 2 3 4 5 6 7

原陣列 Index

9 2 1 8 3 5 9 7

原陣列 data

9

2

1

8

3

5

9

7

11

9

8

16

20

24

44

# 線段樹示意圖

修改位置 0 為 1

0 1 2 3 4 5 6 7

原陣列 Index

1 2 1 8 3 5 9 7

原陣列 data

9

2

1

8

3

5

9

7

11

9

8

16

20

24

44

# 線段樹示意圖

修改位置 0 為 1

0 1 2 3 4 5 6 7

原陣列 Index

1 2 1 8 3 5 9 7

原陣列 data

1

2

1

8

3

5

9

7

11

9

8

16

20

24

44

# 線段樹示意圖

修改位置 0 為 1

0 1 2 3 4 5 6 7

原陣列 Index

1 2 1 8 3 5 9 7

原陣列 data

1

2

1

8

3

5

9

7

3

9

8

16

20

24

44

# 線段樹示意圖

修改位置 0 為 1

0 1 2 3 4 5 6 7

原陣列 Index

1 2 1 8 3 5 9 7

原陣列 data

1

2

1

8

3

5

9

7

3

9

8

16

12

24

44

# 線段樹示意圖

修改位置 0 為 1

0 1 2 3 4 5 6 7

原陣列 Index

1 2 1 8 3 5 9 7

原陣列 data

1

2

1

8

3

5

9

7

3

9

8

16

12

24

36

# 線段樹示意圖

查詢位置 [0, 6] 的和

0 1 2 3 4 5 6 7

原陣列 Index

1 2 1 8 3 5 9 7

原陣列 data

1

2

1

8

3

5

9

7

3

9

8

16

12

24

36

改進

  • 所以，具體來說我們改進了多少？
  • 線段樹的層數 (高度) 是多少？
    • 下一層的大小會減半
    • 減半    次之後，大小為 1，代表原大小大約為
    • 所以高度

前綴和

單一個數重疊的範圍太多

每疊到一條藍線就要修改一個值

線段樹

2^k
O(log\ n)
k

做法

  • 預處理 (建樹)
  • (單點) 修改
  • (區間) 查詢

前綴和

單一個數重疊的範圍太多

每疊到一條藍線就要修改一個值

線段樹

建樹

  • 最大的問題是，如何儲存？
  • 你這時應該要想到前面的鄰接串列
    • 對於每個節點，記錄它左右子節點的編號
  • 有必要記錄嗎？
# 線段樹示意

幫它的圖瘦身下

1

2

1

8

3

5

9

7

3

9

8

16

12

24

36

# 線段樹示意

幫它的圖瘦身下

1

2

1

8

3

5

9

7

3

9

8

16

12

24

36

# 線段樹示意

給每個點編號

1

2

1

8

3

5

9

7

3

9

8

16

12

24

36

1

2

3

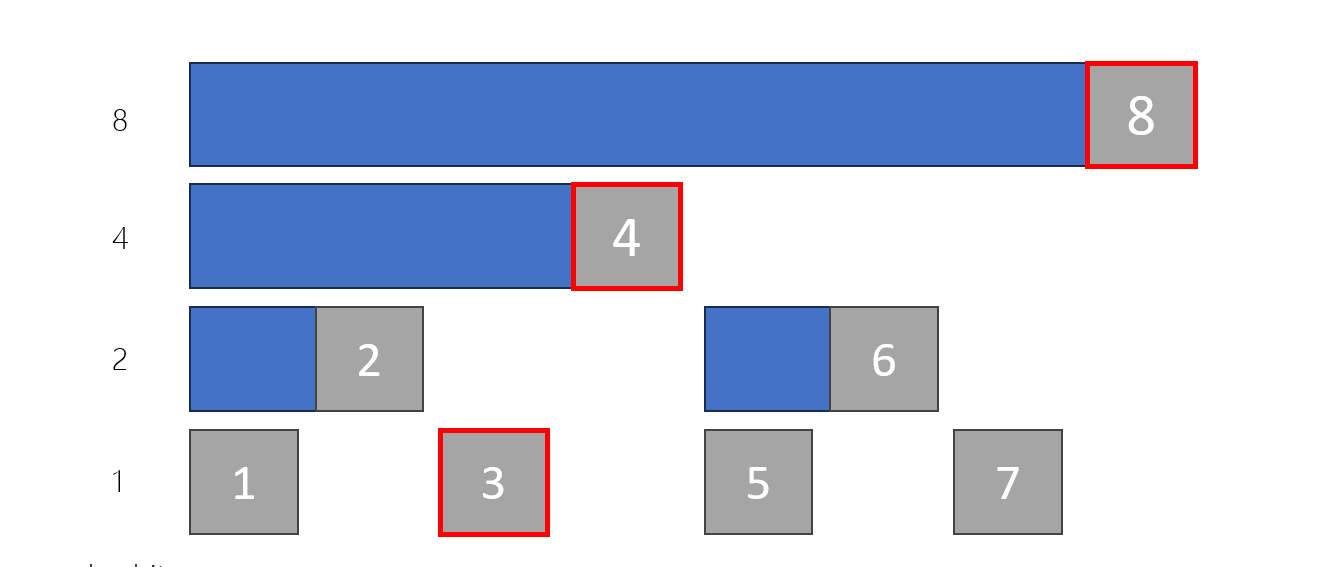
4

5

6

7

8

9

10

11

12

13

14

15

# 線段樹示意

左節點編號 = 當前節點 * 2      

右節點編號 = 當前節點 * 2 + 1

1

2

1

8

3

5

9

7

3

9

8

16

12

24

36

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

建樹

  • 目標：在每個節點對應到的 index 存入區間的答案
    • 以區間和來說，根結點應該存整個數列的和
  • 你會發現它的結構就一臉分治樣
  • 那就做分治吧
  • 如何分？如何治？

分治

  • 我們先來看看如何「治」
  • 假設有兩個子節點的答案
    • 一定要可以透過某種方式求得當前節點的答案
    • 以區間和為例，因為可以把子節點加起來
  • 接著是分
    • 沒有子節點答案什麼都做不了？
    • 那就別做，把任務拆小交給下面的人做就好
  • 當區間大小 = 1 時開始合併

1

2

3

時間複雜度

  • 假設要記錄一段長度為    的資料，花費          的時間
  • 每次將區間分割成兩半，分別需要 
  • 合併兩個區間的答案需要         的時間
  • 寫成遞迴式

 

  • 根據分治主定理，
n
T(n)
T(\frac{n}{2})
O(1)
T(n) = 2T(\frac{n}{2}) + O(1)
T(n) \in O(n)

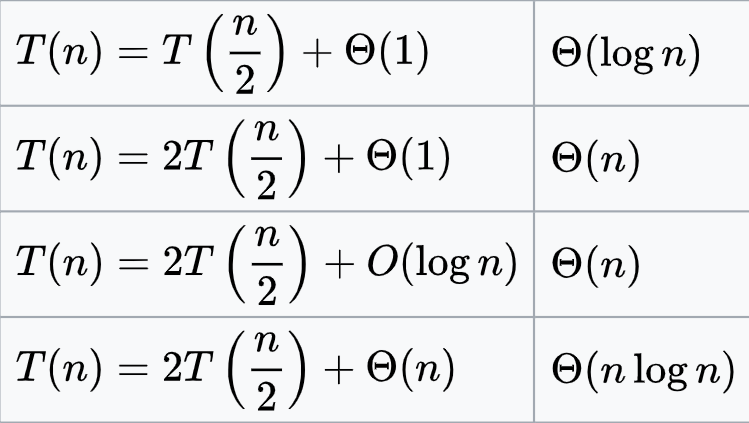
空間？

  • 線段樹不總是會填滿整個陣列，舉個例子：

1

2

3

3

6

21

4

5

9

6

15

1 2 3 4 5 6

空間？

  • 線段樹不總是會填滿整個陣列，舉個例子：

1

2

3

3

6

21

4

5

9

6

15

1

1 2 3 4 5 6

2

3

4

5

6

7

8

9

10

11

12

13

空間？

  • 線段樹不總是會填滿整個陣列，舉個例子：
  • 可以證明，最大的編號不會超過資料長度的 4 倍
struct Box {
    int length, width, height;
    Box(int l, int w, int h) {
        length = l, width = w, height = h;
    }
};
# Constructor

語法 - Constructor (建構式 / 建構子)

建構式會在宣告 Struct / Class 變數時觸發

可以當成一種特殊的函數來用

struct Box {
    int length, width, height;
    Box(int l, int w, int h) {
        length = l, width = w, height = h;
        cout << "Box generated: length(" << length << "), width(" << width << "), height(" << height << ")\n";
    }
};

int main() {
    Box box_a(1, 2, 3), box_b(4, 5, 6);
}
# Constructor

語法 - Constructor (建構式 / 建構子)

Output:

Box generated: length(1), width(2), height(3)
Box generated: length(4), width(5), height(6)
struct Stree {
    vector<int> tree;
    void build(int l, int r, int v, vector<int> &data) {
        if (r == l + 1) {
            tree[v] = data[l];
            return;
        }
        int m = (l + r + 1) / 2;
        build(l, m, v * 2, data);
        build(m, r, v * 2 + 1, data);
        tree[v] = tree[v * 2] + tree[v * 2 + 1];
    }
    Stree(vector<int> &data) {
        tree.resize(data.size() * 4);
        build(0, data.size(), 1, data);
    }
};
# Build Tree

建樹

一般來說，我習慣用左閉右開表示區間

並且在取中間線時會把卡在正中間的數丟到左邊

# 建樹

l = 0

r = 8

v = 1

0 1 2 3 4 5 6 7

原陣列 Index

遞迴參數

9 2 1 8 3 5 6 7 
# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

l = 0

r = 4

v = 2

9 2 1 8 3 5 6 7 
# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

l = 0

r = 4

v = 2

l = 0

r = 2

v = 4

9 2 1 8 3 5 6 7 
# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

l = 0

r = 4

v = 2

l = 0

r = 2

v = 4

l = 0

r = 1

v = 8

9 2 1 8 3 5 6 7 
# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

l = 0

r = 4

v = 2

l = 0

r = 2

v = 4

l = 0

r = 1

v = 8

9

8

9 2 1 8 3 5 6 7 
# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

l = 0

r = 4

v = 2

l = 0

r = 2

v = 4

9

8

9 2 1 8 3 5 6 7 
# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

l = 0

r = 4

v = 2

l = 0

r = 2

v = 4

l = 1

r = 2

v = 9

9

8

9 2 1 8 3 5 6 7 
# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

l = 0

r = 4

v = 2

l = 0

r = 2

v = 4

l = 1

r = 2

v = 9

9

8

2

9

9 2 1 8 3 5 6 7 
# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

l = 0

r = 4

v = 2

l = 0

r = 2

v = 4

9 2 1 8 3 5 6 7

9

8

2

9

11

4

# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

l = 0

r = 4

v = 2

9 2 1 8 3 5 6 7

9

8

2

9

11

4

# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

l = 0

r = 4

v = 2

9 2 1 8 3 5 6 7

9

8

2

9

11

4

l = 2

r = 4

v = 5

# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

l = 0

r = 4

v = 2

9 2 1 8 3 5 6 7

9

8

2

9

11

4

l = 2

r = 4

v = 5

l = 2

r = 3

v = 10

# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

l = 0

r = 4

v = 2

9 2 1 8 3 5 6 7

9

8

2

9

11

4

l = 2

r = 4

v = 5

l = 2

r = 3

v = 10

1

10

# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

l = 0

r = 4

v = 2

9 2 1 8 3 5 6 7

9

8

2

9

11

4

l = 2

r = 4

v = 5

1

10

# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

l = 0

r = 4

v = 2

9 2 1 8 3 5 6 7

9

8

2

9

11

4

l = 2

r = 4

v = 5

1

10

l = 3

r = 4

v = 11

# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

l = 0

r = 4

v = 2

9 2 1 8 3 5 6 7

9

8

2

9

11

4

l = 2

r = 4

v = 5

1

10

l = 3

r = 4

v = 11

8

11

# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

l = 0

r = 4

v = 2

9 2 1 8 3 5 6 7

9

8

2

9

11

4

l = 2

r = 4

v = 5

1

10

8

11

9

5

# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

l = 0

r = 4

v = 2

9 2 1 8 3 5 6 7

9

8

2

9

11

4

1

10

8

11

9

5

20

2

# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

9 2 1 8 3 5 6 7

9

8

2

9

11

4

1

10

8

11

9

5

20

2

# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

9 2 1 8 3 5 6 7

9

8

2

9

11

4

1

10

8

11

9

5

20

2

l = 4

r = 8

v = 3

# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

9 2 1 8 3 5 6 7

9

8

2

9

11

4

1

10

8

11

9

5

20

2

l = 4

r = 8

v = 3

l = 4

r = 6

v = 6

# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

9 2 1 8 3 5 6 7

9

8

2

9

11

4

1

10

8

11

9

5

20

2

l = 4

r = 8

v = 3

l = 4

r = 6

v = 6

l = 4

r = 5

v = 12

# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

9 2 1 8 3 5 6 7

9

8

2

9

11

4

1

10

8

11

9

5

20

2

l = 4

r = 8

v = 3

l = 4

r = 6

v = 6

l = 4

r = 5

v = 12

3

12

# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

9 2 1 8 3 5 6 7

9

8

2

9

11

4

1

10

8

11

9

5

20

2

l = 4

r = 8

v = 3

l = 4

r = 6

v = 6

3

12

# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

9 2 1 8 3 5 6 7

9

8

2

9

11

4

1

10

8

11

9

5

20

2

l = 4

r = 8

v = 3

l = 4

r = 6

v = 6

3

12

l = 5

r = 6

v = 13

# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

9 2 1 8 3 5 6 7

9

8

2

9

11

4

1

10

8

11

9

5

20

2

l = 4

r = 8

v = 3

l = 4

r = 6

v = 6

3

12

l = 5

r = 6

v = 13

5

13

# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

9 2 1 8 3 5 6 7

9

8

2

9

11

4

1

10

8

11

9

5

20

2

l = 4

r = 8

v = 3

l = 4

r = 6

v = 6

3

12

5

13

8

6

# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

9 2 1 8 3 5 6 7

9

8

2

9

11

4

1

10

8

11

9

5

20

2

l = 4

r = 8

v = 3

3

12

5

13

8

6

# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

9 2 1 8 3 5 6 7

9

8

2

9

11

4

1

10

8

11

9

5

20

2

l = 4

r = 8

v = 3

3

12

5

13

8

6

l = 6

r = 8

v = 7

# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

9 2 1 8 3 5 6 7

9

8

2

9

11

4

1

10

8

11

9

5

20

2

l = 4

r = 8

v = 3

3

12

5

13

8

6

l = 6

r = 8

v = 7

l = 6

r = 7

v = 14

# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

9 2 1 8 3 5 6 7

9

8

2

9

11

4

1

10

8

11

9

5

20

2

l = 4

r = 8

v = 3

3

12

5

13

8

6

l = 6

r = 8

v = 7

l = 6

r = 7

v = 14

6

14

# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

9 2 1 8 3 5 6 7

9

8

2

9

11

4

1

10

8

11

9

5

20

2

l = 4

r = 8

v = 3

3

12

5

13

8

6

l = 6

r = 8

v = 7

6

14

# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

9 2 1 8 3 5 6 7

9

8

2

9

11

4

1

10

8

11

9

5

20

2

l = 4

r = 8

v = 3

3

12

5

13

8

6

l = 6

r = 8

v = 7

6

14

l = 7

r = 8

v = 15

# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

9 2 1 8 3 5 6 7

9

8

2

9

11

4

1

10

8

11

9

5

20

2

l = 4

r = 8

v = 3

3

12

5

13

8

6

l = 6

r = 8

v = 7

6

14

l = 7

r = 8

v = 15

7

15

# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

9 2 1 8 3 5 6 7

9

8

2

9

11

4

1

10

8

11

9

5

20

2

l = 4

r = 8

v = 3

3

12

5

13

8

6

6

14

7

15

13

7

l = 6

r = 8

v = 7

# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

9 2 1 8 3 5 6 7

9

8

2

9

11

4

1

10

8

11

9

5

20

2

l = 4

r = 8

v = 3

3

12

5

13

8

6

6

14

7

15

13

7

21

3

# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

l = 0

r = 8

v = 1

遞迴參數

9 2 1 8 3 5 6 7

9

8

2

9

11

4

1

10

8

11

9

5

20

2

3

12

5

13

8

6

6

14

7

15

13

7

21

3

41

1

# 建樹
0 1 2 3 4 5 6 7

原陣列 Index

遞迴參數

9 2 1 8 3 5 6 7

9

8

2

9

11

4

1

10

8

11

9

5

20

2

3

12

5

13

8

6

6

14

7

15

13

7

21

3

41

1

實際輸出看看

struct Stree {
    vector<int> tree;
    void build(int l, int r, int v, vector<int> &data) {
        cout << "Building: (" << l << ", " << r << ", " << v << ")\n";
        if (r == l + 1) {
            cout << "Leaf: (" << l << ", " << r << ", " << v << ")\n";
            tree[v] = data[l];
            return;
        }
        int m = (l + r + 1) / 2;
        build(l, m, v * 2, data);
        build(m, r, v * 2 + 1, data);
        tree[v] = tree[v * 2] + tree[v * 2 + 1];
        cout << "Finish: (" << l << ", " << r << ", " << v << ")\n";
        
    }
    void print() {
        for (int i = 0; i < tree.size(); i++) cout << tree[i] << ' ';
        cout << '\n';
    }
    Stree(vector<int> &data) {
        tree.resize(data.size() * 4);
        build(0, data.size(), 1, data);
        print();
    }
};

int main () {
    vector<int> data = {9, 2, 1, 8};
    Stree sum(data);
}
# 實際輸出
Building: (0, 4, 1)
Building: (0, 2, 2)
Building: (0, 1, 4)
Leaf: (0, 1, 4)
Building: (1, 2, 5)
Leaf: (1, 2, 5)
Finish: (0, 2, 2)
Building: (2, 4, 3)
Building: (2, 3, 6)
Leaf: (2, 3, 6)
Building: (3, 4, 7)
Leaf: (3, 4, 7)
Finish: (2, 4, 3)
Finish: (0, 4, 1)
0 20 11 9 9 2 1 8 0 0 0 0 0 0 0 0

修改

  • 先討論單點修改
  • 把所有包含對應位置的節點修改一遍

9

2

1

8

3

5

9

7

11

9

8

16

20

24

44

實作

  • 如果要修改的範圍在左半區間，往左邊遞迴
  • 反之往右邊遞迴

9

2

1

8

3

5

9

7

11

9

8

16

20

24

44

實作

  • 如果要修改的範圍在左半區間，往左邊遞迴
  • 反之往右邊遞迴

9

2

1

8

3

5

9

7

11

9

8

16

20

24

44

實作

  • 如果要修改的範圍在左半區間，往左邊遞迴
  • 反之往右邊遞迴

9

2

1

8

3

5

9

7

11

9

8

16

20

24

44

實作

  • 如果要修改的範圍在左半區間，往左邊遞迴
  • 反之往右邊遞迴

9

2

1

8

3

5

9

7

11

9

8

16

20

24

44

實作

  • 如果要修改的範圍在左半區間，往左邊遞迴
  • 反之往右邊遞迴

9

2

1

8

3

5

9

7

11

9

8

16

20

24

44

struct Stree {
    void modify(int l, int r, int v, int pos, int new_val) {
        if (r == l + 1) {
            tree[v] = new_val;
            return;
        }
        int m = (l + r + 1) / 2;
        if (pos < m) modify(l, m, v * 2, pos, new_val);
        else modify(m, r, v * 2 + 1, pos, new_val);
        tree[v] = tree[v * 2] + tree[v * 2 + 1];
        return;
    }
};
# Modify

修改

修改葉節點後，要更新當前節點的值

實際輸出看看

struct Stree {
    vector<int> tree;
    void build(int l, int r, int v, vector<int> &data) {
        if (r == l + 1) {
            tree[v] = data[l];
            return;
        }
        int m = (l + r + 1) / 2;
        build(l, m, v * 2, data);
        build(m, r, v * 2 + 1, data);
        tree[v] = tree[v * 2] + tree[v * 2 + 1];
        
    }
    void print() {
        for (int i = 0; i < tree.size(); i++) cout << tree[i] << ' ';
        cout << '\n';
    }
    Stree(vector<int> &data) {
        tree.resize(data.size() * 4);
        build(0, data.size(), 1, data);
        print();
    }
    void modify(int l, int r, int v, int pos, int new_val) {
        cout << "modify: " << l << ' ' << r << ' ' << v << '\n';
        if (r == l + 1) {
            tree[v] = new_val;
            return;
        }
        int m = (l + r + 1) / 2;
        if (pos < m) modify(l, m, v * 2, pos, new_val);
        else modify(m, r, v * 2 + 1, pos, new_val);
        tree[v] = tree[v * 2] + tree[v * 2 + 1];
        return;
    }
};

int main () {
    vector<int> data = {9, 2, 1, 8, 3, 5, 6, 7};
    Stree sum(data);
    sum.modify(0, data.size(), 1, 6, 106);
    sum.print();
}
# 實際輸出
0 41 20 21 11 9 8 13 9 2 1 8 3 5 6 7 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 
modify: 0 8 1
modify: 4 8 3
modify: 6 8 7
modify: 6 7 14
0 141 20 121 11 9 8 113 9 2 1 8 3 5 106 7 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

查詢

  • 現在，我們要查詢原陣列一段區間的結果

1

2

1

8

3

5

9

7

3

9

8

16

12

24

36

查詢

  • 一樣用分治的概念，把大問題拆成小問題
  • 怎麼分？
  • 定義一個函式
  • 對線段樹上的一個區間，求出它一段子區間的答案
  • 舉個例子
    • 對根節點代表區間 [0, 8) 來說，求出 [1, 5) 的和

分割問題

  • 接著，想辦法把大問題拆小
    • 如果在當前節點沒辦法解決的事，丟給下面處理
    • 分情況拆區間！

Case 1: 剛好覆蓋

節點區間

目標區間

Case 2: 左半邊

Case 3: 右半邊

Case 4: 中間

Case 1: 目標區間 = 節點區間

  • 這個情況很簡單，直接回傳當前節點的值就好了
  • 遞迴到當前節點時節點左右界分別等於目標左右界

Case 1: 剛好覆蓋

節點區間

目標區間

Case 2: 左半邊

Case 3: 右半邊

Case 4: 中間

Case 2: 目標區間在節點區間左半

  • 目標區間完全包含在節點區間的左半邊內
  • 丟給左子節點（左半區間）處理
  • 目標區間的右界比節點中線還左邊

Case 1: 剛好覆蓋

節點區間

目標區間

Case 2: 左半邊

Case 3: 右半邊

Case 4: 中間

Case 3: 目標區間在節點區間右半

  • 比照 Case 2 辦理
  • 目標左界比中線還右邊

Case 1: 剛好覆蓋

節點區間

目標區間

Case 2: 左半邊

Case 3: 右半邊

Case 4: 中間

Case 4: 目標區間橫跨中線

  • 把目標區間以節點中線拆成兩部分
  • 這樣就可以丟給左子節點和右子節點處理了

Case 1: 剛好覆蓋

節點區間

目標區間

Case 2: 左半邊

Case 3: 右半邊

Case 4: 中間

合併結果

  • 算完以後回傳結果的時候順便把結果合併就做完了
  • 如果只有一邊節點的答案那就只採用一邊的節點

複雜度？

  • 查詢的複雜度比較不好想
  • 可以看這裡（我之前做的簡報）
  • 講結論，複雜度
O(log\ n)
struct Stree {
    int query(int vl, int vr, int v, int tl, int tr) {
        if (vl == tl && vr == tr) return tree[v];
        int vm = (vl + vr + 1) / 2;
        if (tr <= vm) return query(vl, vm, v * 2, tl, tr);
        if (tl >= vm) return query(vm, vr, v * 2 + 1, tl, tr);
        return query(vl, vm, v * 2, tl, vm) + query(vm, vr, v * 2 + 1, vm, tr);
    }
};
# Query

查詢

要特別注意特判時因為寫左閉右開所以都要加等於

以及特判的順序要對

實際輸出看看

# 實際輸出
node: [0, 8), target: [0, 7)
node: [0, 4), target: [0, 4)
use node: (0, 4)
node: [4, 8), target: [4, 7)
node: [4, 6), target: [4, 6)
use node: (4, 6)
node: [6, 8), target: [6, 7)
node: [6, 7), target: [6, 7)
use node: (6, 7)
34
struct Stree {
    vector<int> tree;
    void build(int l, int r, int v, vector<int> &data) {
        if (r == l + 1) {
            tree[v] = data[l];
            return;
        }
        int m = (l + r + 1) / 2;
        build(l, m, v * 2, data);
        build(m, r, v * 2 + 1, data);
        tree[v] = tree[v * 2] + tree[v * 2 + 1];
    }
    Stree(vector<int> &data) {
        tree.resize(data.size() * 4);
        build(0, data.size(), 1, data);
    }
    int query(int vl, int vr, int v, int tl, int tr) {
        cout << "node: [" << vl << ", " << vr << "), "
             << "target: [" << tl << ", " << tr << ")\n";
        if (vl == tl && vr == tr) {
            cout << "use node: (" << vl << ", " << vr << ")\n";
            return tree[v];
        }
        int vm = (vl + vr + 1) / 2;
        if (tr <= vm) return query(vl, vm, v * 2, tl, tr);
        if (tl >= vm) return query(vm, vr, v * 2 + 1, tl, tr);
        return query(vl, vm, v * 2, tl, vm) + query(vm, vr, v * 2 + 1, vm, tr);
    }
};

int main() {
    vector<int> data = {9, 2, 1, 8, 3, 5, 6, 7};
    Stree sum(data);
    cout << sum.query(0, data.size(), 1, 0, 7);
}

例題

因為還沒講到線段樹最重要的功能

所以題單就先這樣

然後只要符合結合律的運算都可以用線段樹維護

線段樹 II

Segment Tree II

範圍...修改？

  • 單點修改：把某個位置的數據修改
  • 範圍查詢：查詢某個範圍內合併的結果
  • 範圍...修改？
    • 把一段範圍的數通通加上 d
    • 把一段範圍的數通通設成 x

怎麼做

  • 思考一下，如果我們對範圍內的每個點都做單點修改
    • 每點修改需要               ，最糟情況要
    • 糟糕透頂，不如重新建樹
  • 可以想到範圍查詢的做法也是
    • 怎麼套用？
    • 範圍查詢需要一個節點的答案
    • 對應到修改，怎麼直接對一整個節點修改？
O(log\ n)
O(n\ log\ n)
O(log\ n)

怎麼做

  • 以區間和為例，如果要讓一個節點的區間全部 +d
    • 節點值會 +(d * 節點大小)
    • 這樣就結束了嗎？
  • 如果今天要查詢這個節點的子節點？
    • 沒救，我們一定得多記錄些什麼

怎麼做

  • 不如打個標記，說明我要修改這個節點
  • 如果需要查詢更下方的節點時就有依據
    • push: 將標記傳給下面的節點，並更新當前節點
    • pull: 利用子節點更新當前節點的值
  • 這種作法實際上就是拖延修改的時間，所以稱為懶標
# 線段樹示意

原線段樹

1

2

1

8

3

5

9

7

3

9

8

16

12

24

36

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

val

tag

# 線段樹示意

[1, 5) 加上 3

1

2

1

8

3

5

9

7

3

9

8

16

12

24

36

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

val

tag

# 線段樹示意

[1, 5) 加上 3

1

2

1

8

3

5

9

7

3

9

8

16

12

24

36

0

0

0

0

3

0

0

0

3

0

0

3

0

0

0

val

tag

# 線段樹示意

[1, 5) 加上 3

1

2

1

8

3

5

9

7

6

9

11

16

21

27

48

0

0

0

0

3

0

0

0

3

0

0

3

0

0

0

val

tag

# 線段樹示意

查詢 [4, 6)

1

2

1

8

3

5

9

7

6

9

11

16

21

27

48

0

0

0

0

3

0

0

0

3

0

0

3

0

0

0

val

tag

# 線段樹示意

查詢 [4, 6)

1

2

1

8

3

5

9

7

6

15

11

16

21

27

48

0

0

0

0

0

0

0

0

3

3

3

3

0

0

0

val

tag

# 線段樹示意

查詢 [4, 6)

1

2

1

11

3

5

9

7

6

15

11

16

21

27

48

0

0

0

0

0

0

0

0

3

3

0

3

0

0

0

val

tag

# 線段樹示意

查詢 [4, 6)

1

2

1

11

3

5

9

7

6

15

11

16

21

27

48

0

0

0

0

0

0

0

0

3

3

0

3

0

0

0

val

tag

# 線段樹示意

查詢 [4, 6)

1

2

1

11

6

5

9

7

6

15

11

16

21

27

48

0

0

0

0

0

0

0

0

3

3

0

0

0

0

0

val

tag

# Modify

範圍修改 & 查詢

非常類似於 query

多記錄 tag

struct Stree {
    vector<int> tree, tag;

    void push(int target, int l, int r) {
        int lchild = target << 1, rchild = target << 1 | 1;
        tree[target] += tag[target] * (r - l);
        tag[lchild] += tag[target];
        tag[rchild] += tag[target];
        tag[target] = 0;
    }

    void pull(int target, int l, int r) {
        int m = l + r + 1 >> 1;
        int lchild = target << 1, rchild = target << 1 | 1;
        int lchild_val = tree[lchild] + tag[lchild] * (m - l);
        int rchild_val = tree[rchild] + tag[rchild] * (r - m);
        tree[target] = lchild_val + rchild_val;
    }

    void modify(int vl, int vr, int v, int tl, int tr, int d) {
        if (vl == tl && vr == tr) {
            tag[v] += d;
            return;
        }

        int vm = vl + vr + 1 >> 1;
        if (tr <= vm) modify(vl, vm, v << 1, tl, tr, d);
        else if (tl >= vm) modify(vm, vr, v << 1 | 1, tl, tr, d);
        else modify(vl, vm, v << 1, tl, vm, d), modify(vm, vr, v << 1 | 1, vm, tr, d);

        pull(v, vl, vr);
    }

    int query(int vl, int vr, int v, int tl, int tr, int d) {
        push(v, vl, vr);
        if (vl == tl && vr == tr) return tree[v] + tag[v] * (vr - vl);
        int vm = vl + vr + 1 >> 1;
        if (tr <= vm) return query(vl, vm, v << 1, tl, tr, d);
        if (tl >= vm) return query(vm, vr, v << 1 | 1, tl, tr, d);
        return query(vl, vm, v << 1, tl, vm, d) + query(vm, vr, v << 1 | 1, vm, tr, d);
    }
};

例題

BIT

Binary Indexed Tree

特化

  • 線段樹的好處是方便查詢區間問題，複雜度也不差
  • 然而，有時候一直寫線段樹碼量偏大，常數也大
    • 迭代式線段樹
  • 如果我們只維護前綴，有些漂亮性質能用
  • 你猜怎麼著？又是二進位

Lowbit

  • 先介紹一個東西叫做 Lowbit
    • 二進位的情況下最後一位 1 所代表的數

14 = 1110(2)

lowbit(6) = 10(2) = 2

11 = 1011(2)

lowbit(11) = 1(2) = 1

8 = 1000(2)

lowbit(8) = 1000(2) = 8

12 = 1100(2)

lowbit(12) = 100(2) = 4

Lowbit

  • 求法？
  • 考慮位元運算：
    • lowbit(x) = x & (~x + 1)
    • ~x + 1 = -x (C語言儲存機制)
  • 為什麼？
 x     = oooo10000
~x     = xxxx01111
~x + 1 = xxxx10000

其中 o, x 表示相反的位元

利用 & 運算可以確保前面都是 0

並且後面保持不變

BIT

  • 回到 BIT，有了剛剛提到的 lowbit 有什麼用？
    • 可以更方便地將數字用二進位拆開？
    • 就這樣嗎？
  • 觀察到一件事，所有自然數都可以用二進位拆開
  • 區間大小也可以！

BIT

  • 所以，對於第 x 項的前綴：
    • x = 1 = 1
    • x = 2 = 2
    • x = 3 = 2 + 1
    • x = 4 = 4
    • x = 5 = 4 + 1
    • x = 6 = 4 + 2
    • x = 7 = 4 + 2 + 1

BIT

  • 透過觀察，發現可以在對應位置儲存它「新的範圍」
    • 對於 1 來說，它只有 [1, 1]
    • 2 相對於 1，[1, 2] 是新的範圍
    • 3 相對於 2，[3, 3] 是新的範圍
    • 4 相對於 3，[1, 4] 是新的範圍
    • 5 相對於 4，[5, 5] 是新的範圍
    • 6 相對於 5，[5, 6] 是新的範圍
    • 7 相對於 6，[7, 7] 是新的範圍

1

2

3

4

5

6

7

BIT

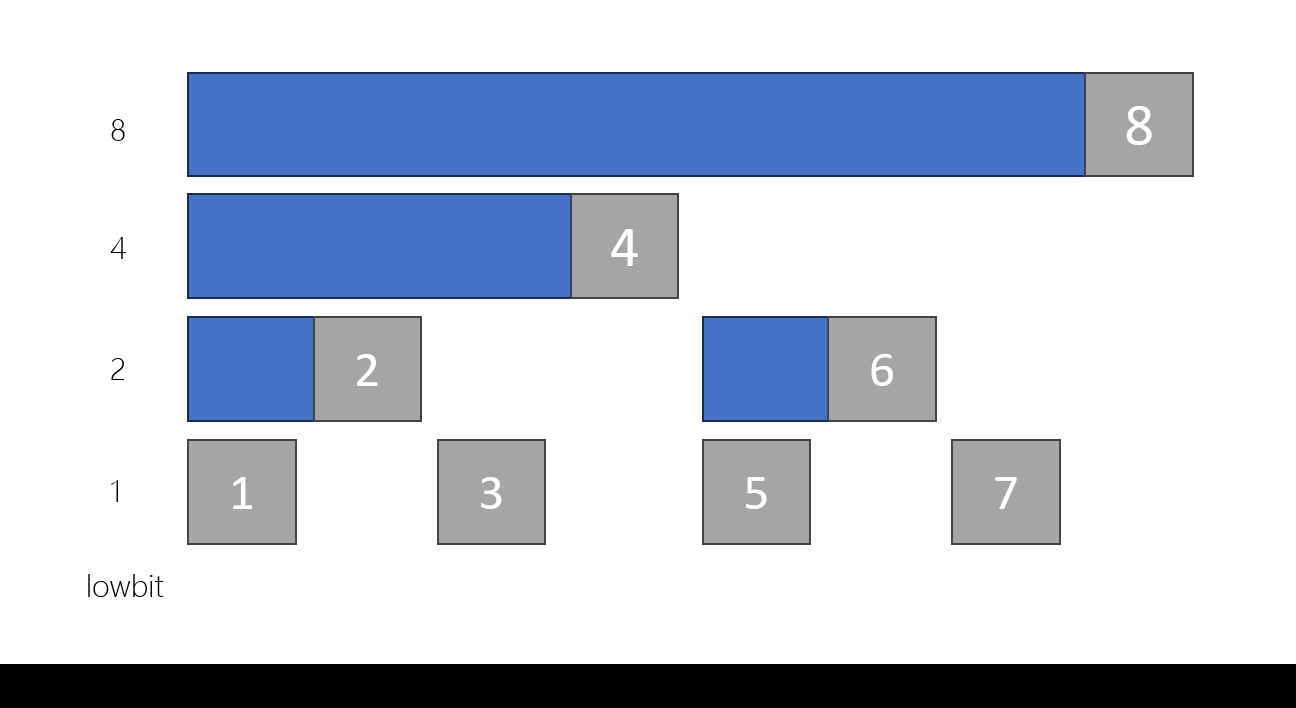
  • 同時，你會發現它一定是涵蓋的區塊中最後面那個
  • 大小是 lowbit
  • 所以，對於某個 x 來說
    • 儲存 [x - lowbit(x) + 1, x]
    • 好像滿漂亮的？
    • 有什麼用？

1

2

3

4

5

6

7

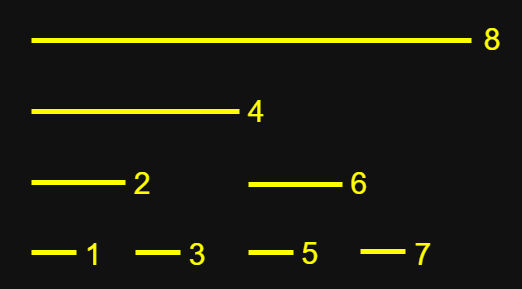
建樹

  • 關於為什麼是樹請看動畫
  • 下面兩張是 BIT

1

2

3

4

5

6

7

8

建樹

  • 這是線段樹

建樹

  • 這是線段樹減肥

建樹

  • 我相信你看出來了

建樹

  • 所以，我們要怎麼建？
  • 直接按照定義的話複雜度會是
  • 不是很爛，但線段樹是          耶，有辦法改進嗎？
  • 注意到每個區間可以由其他不重疊的小區間疊起來
    • 我們可以在做那些小區間時把值加到大區間中
    • 怎麼判斷小區間要加到哪？
O(n\ log\ n)
O(n)

建樹

  • 一個大區間應該會包含哪些小區間？
  • 因為區間大小都是 2 的冪次，考慮一種拆法：
    • 1000 = 111 + 1 = 100 + 10 + 1 + 1
    • 10000 = 1111 + 1 = 1000 + 100 + 10 + 1 + 1
  • 其中，最後的 1 代表原始陣列裡那格的數

1  2  3  4  5  6  7  8

1  2  3  4

建樹

  • 你會發現，x + lowbit(x) 相當於大區間的 index
  • 所以，我們用迴圈從左邊跑到右邊
    • 如果 x + lowbit(x) 不超過資料大小
    • BIT[x + lowbit(x)] += BIT[x]
  • 複雜度顯然

1  2  3  4  5  6  7  8

1  2  3  4

O(n)
#include <time.h>
#include <iostream>
#define iofast ios_base::sync_with_stdio(0), cin.tie(0)
using namespace std;
int main() {
    clock_t time1, time2, time3;
    time1 = clock();
    for (int i = 0; i < 10000; i++)
        cout << "Hello\n";
	time2 = clock();
    iofast;
    for (int i = 0; i < 10000; i++)
        cout << "Hello\n";
    time3 = clock();
    cout << time2 - time1 << ' ' << time3 - time2;
}
# Define

語法 - Define

將空格前面的東西替換成後面的東西

#define lowbit(x) (x & -x)
struct BIT {
    vector<int> tree;
    int size;
    BIT(const vector<int> &data) {
        size = data.size() - 1;
        tree.resize(size + 1, 0);
        for (int i = 1; i <= size; i++) {
            tree[i] += data[i];
            if (i + lowbit(i) <= size)
                tree[i + lowbit(i)] += tree[i];
        }
    }
};
# Build

建樹

你會發現，實際上有用的只有三行，超級短

實際輸出看看

#include <iostream>
#include <vector>
#define lowbit(x) (x & -x)
using std::cout;
using std::vector;

struct BIT {
    vector<int> tree;
    int size;
    // 資料預設 1 - base
    BIT(const vector<int> &data) {
        size = data.size() - 1;
        tree.resize(size + 1, 0);
        for (int i = 1; i <= size; i++) {
            tree[i] += data[i];
            if (i + lowbit(i) <= size)
                tree[i + lowbit(i)] += tree[i];
        }
    }
    void print() {
        for (int i = 1; i <= size; i++)
            cout << tree[i] << " ";
    }
};

int main() {
    BIT sum(vector<int>{0, 1, 2, 3, 4, 5, 6, 7, 8});
    sum.print();
}

# 實際輸出
1 3 3 10 5 11 7 36

修改

  • 線段樹能修改，BIT 當然也要能
  • 有了建樹的經驗，修改就簡單了
  • 一個資料點在建樹時會影響到哪些樹上節點？
    • 在建樹時除了直接影響到 x + lowbit(x) 以外？
    • 下個節點也會繼續影響到下一個節點
    • x, x + lowbit(x), (x + lowbit(x)) + lowbit(x + lowbit(x))...
  • 每次加的數都至少 * 2，複雜度
O(log\ n)
#define lowbit(x) (x & -x)
struct BIT {
    void modify(int pos, int d) {
        for (; pos <= size; pos += lowbit(pos))
            tree[pos] += d;
    }
};
# Modify

修改

又是兩行解決

實際輸出看看

#include <iostream>
#include <vector>
#define lowbit(x) (x & -x)
using std::cout;
using std::vector;

struct BIT {
    vector<int> tree;
    int size;
    // 資料預設 1 - base
    BIT(const vector<int> &data) {
        size = data.size() - 1;
        tree.resize(size + 1, 0);
        for (int i = 1; i <= size; i++) {
            tree[i] += data[i];
            if (i + lowbit(i) <= size)
                tree[i + lowbit(i)] += tree[i];
        }
    }
    void print() {
        for (int i = 1; i <= size; i++)
            cout << tree[i] << " ";
    }
    void modify(int pos, int d) {
        for (; pos <= size; pos += lowbit(pos))
            tree[pos] += d;
    }
};

int main() {
    BIT sum(vector<int>{0, 1, 2, 3, 4, 5, 6, 7, 8});
    sum.modify(1, 100);
    sum.print();
}

# 實際輸出
1
2
4
8
101 103 3 110 5 11 7 136

查詢

  • 我們照著一開始的定義做
  • BIT[x] 存的是 [x - lowbit(x) + 1, x]
  • 所以將 x 扣掉 lowbit(x) 就可以取得更前面的值
  • 二進位數有                個 1，所以複雜度
O(log\ n)
O(log\ n)
#define lowbit(x) (x & -x)
struct BIT {
    int query(int pos) {
        int ans = 0;
        for (; pos > 0; pos -= lowbit(pos))
            ans += tree[pos];
        return ans;
    }
};
# Query

查詢

又是兩行解決

實際輸出看看

#include <iostream>
#include <vector>
#define lowbit(x) (x & -x)
using std::cout;
using std::vector;

struct BIT {
    vector<int> tree;
    int size;
    // 資料預設 1 - base
    BIT(const vector<int> &data) {
        size = data.size() - 1;
        tree.resize(size + 1, 0);
        for (int i = 1; i <= size; i++) {
            tree[i] += data[i];
            if (i + lowbit(i) <= size)
                tree[i + lowbit(i)] += tree[i];
        }
    }
    int query(int pos) {
        int ans = 0;
        for (; pos > 0; pos -= lowbit(pos)) {
            ans += tree[pos];
            cout << pos << "\n";
        }
        return ans;
    }
};

int main() {
    BIT sum(vector<int>{0, 1, 2, 3, 4, 5, 6, 7, 8});
    cout << sum.query(7);
}

# 實際輸出
7
6
4
28

例題

關於 BIT...

  • 基本上可以把 BIT 的扣大概記下來，畢竟不長
  • BIT 的優點包括：
    • 常數小
    • 好寫
    • 碼短
  • 所以雖然他的所有功能都可以用線段樹辦到，但該用 BIT 還是得用 BIT

其他功能

  • BIT 搭配離散化還可以做很多有關位置的操作
  • 離散化：當實際值不重要，只和相對大小有關的事
    • 將資料排序，以某個數的 index 作為代表
  • 舉例來說，LIS

其他功能

  • 我們用 LIS[x] 代表以數字 x 當結尾時的 LIS 長度
  • 利用 BIT，我們可以記錄 0 ~ x 中 LIS 最大值
  • 用迴圈跑過離散化過後的數字，加入新數字的影響
    • 新的數字 n 只能接在 < n 的數後面
    • 利用 BIT[n - 1] 更新
  • 套資結的好處是寫起來很無腦
  • 很多時候比純 DP 作法好想
# Example

範例

#include <stdio.h>
 
#include <algorithm>
#include <functional>
const int max_n = 2e5 + 1;
struct BIT {
	int data[max_n];
	int size;
	inline int query(int pos) {
		int ans = 0;
		for (; pos > 0; pos -= pos & -pos) ans = std::max(ans, data[pos]);
		return ans;
	}
	inline void modify(int pos, int alt) {
		for (; pos <= size; pos += pos & -pos) data[pos] = std::max(alt, data[pos]);
	}
} LIS;
int num[max_n], map[max_n];
int main() {
	int n;
	scanf("%d", &n);
	for (int i = 0; i < n; i++) scanf("%d", num + i), map[i] = num[i];
	std::sort(map, map + n);
	LIS.size = std::unique(map, map + n) - map;
	for (int i = 0; i < n; i++) {
		int mapped = std::lower_bound(map, map + LIS.size, num[i]) - map + 1;
		LIS.modify(mapped, LIS.query(mapped - 1) + 1);
	}
	printf("%d", LIS.query(LIS.size));
	return 0;
}

例題

稀疏表

Sparse Table

區間極值問題

  • 先從最常見的用途講起
  • 雖然線段樹可以很好地維護區間極值，但
    • 查詢複雜度                有時太慢了
    • 常數大
    • 碼量大
  • 有沒有查詢更快，常數更小的作法？
O(log\ n)

區間極值問題

  • 先想想區間極值的特性
    • 滿足結合律和交換律
    • 假設極值函數      ，則
      • 也就是說
  • 也就是說，即使重複算到同樣的東西，答案也是好的
M
M(x, x) = x
min(x, x) = x,\ max(x, x) = x

區間極值問題

  • 圖解
  • [1, 6] 和 [5, 8] 有重疊 [5, 6]
  • 合併兩個區間的答案 1, 3 仍可得到 [1, 8] 的最小值 1

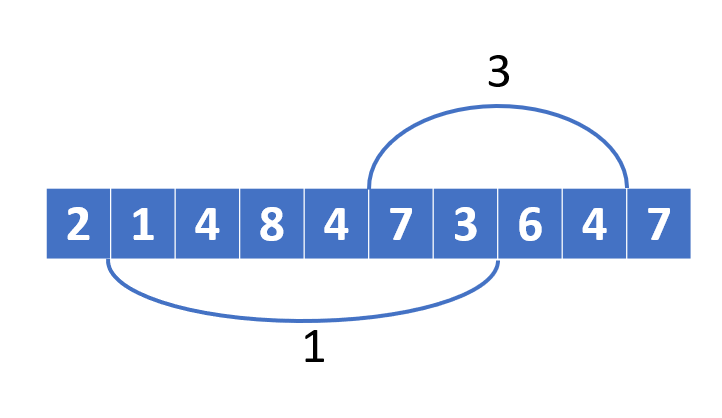
區間極值問題

  • 那這樣我們弄一堆大 / 小區間，有需要時合併就好了
    • 區間要多大？
    • 要存多少東西？
    • 要怎麼預先知道大區間的答案？

倍增法

  • 如果要將兩個大小相同的區間合併
    • 小區間至少要 >= 目標區間的一半
  • 如果每次取答案都要合併兩個大小相同的區間
    • 小區間大小至少要有 1, 2, 4, 8, 16...
  • 這就是倍增法的初始想法

倍增法

  • 我們以            表示區間大小為   ，區間左界   的答案
    • 舉個例子：             表示            的答案
  • 觀察到兩個大小為     的區間可合併成大小為        的
  • 所以我們有
  • 照這個想法把表打好
sp[i][l]
i
l
sp[3][5]
[5,\ 13)
2^i
2^{i+1}
sp[i+1][l] = M(sp[i][l],\ sp[i][l + 2^i])

倍增法

3 2 4 1 6 5

i = 0

倍增法

2
3 2 4 1 6 5

i = 1

倍增法

2 2
3 2 4 1 6 5

i = 1

倍增法

2 2 1
3 2 4 1 6 5

i = 1

倍增法

2 2 1 1
3 2 4 1 6 5

i = 1

倍增法

2 2 1 1 5
3 2 4 1 6 5

i = 1

倍增法

1
2 2 1 1 5
3 2 4 1 6 5

i = 2

倍增法

1 1
2 2 1 1 5
3 2 4 1 6 5

i = 2

倍增法

1 1 1
2 2 1 1 5
3 2 4 1 6 5

i = 2

# Build

建表

struct SparseTable {
    vector<vector<int>> sp;
    int size, lg_size;

    SparseTable(const vector<int> &data, int _size)
        : size(_size), lg_size(std::__lg(_size)), sp(lg_size + 1, vector<int>(_size, 0)) {
        sp[0] = data;

        for (int i = 1; i <= lg_size; i++)
            for (int l = 0; l + (1 << i - 1) < size; l++)
                sp[i][l] = min(sp[i - 1][l], sp[i - 1][l + (1 << i - 1)]);
    }
};

使用 std::__lg O(1) 取得以 2 為底的 log 值

1 << i 就是 2 的 i 次方

實際輸出看看

struct SparseTable {
    vector<vector<int>> sp;
    int size, lg_size;

    SparseTable(const vector<int> &data, int _size)
        : size(_size), lg_size(std::__lg(_size)), sp(lg_size + 1, vector<int>(_size, 0)) {
        sp[0] = data;

        for (int i = 1; i <= lg_size; i++)
            for (int l = 0; l + (1 << i - 1) < size; l++)
                sp[i][l] = min(sp[i - 1][l], sp[i - 1][l + (1 << i - 1)]);
    }

    void print() {
        for (int i = 0; i <= lg_size; i++) {
            for (int l = 0; l < size; l++) {
                cout << sp[i][l] << " ";
            }
            cout << "\n";
        }
    }
};

int main() {
    SparseTable min_val({3, 2, 1, 4, 5, 6}, 6);
    min_val.print();
}

# 實際輸出
3 2 1 4 5 6 
2 1 1 4 5 0 
1 1 1 0 0 0

查詢

  • 知道怎麼打表後查詢就簡單了
  • 需要兩個 >= 一半目標區間大小的區間合併
1 1 1
2 2 1 1 5
3 2 4 1 6 5

查詢 [1, 6) 需要兩個大小為 4 的區間

查詢

  • 知道怎麼打表後查詢就簡單了
  • 需要兩個 >= 一半目標區間大小的區間合併
1 1 1
2 2 1 1 5
3 2 4 1 6 5

查詢 [2, 5) 需要兩個大小為 2 的區間

查詢

  • 區間大小 = 右界 - 左界
  • 用來合併的區間須大於等於一半：用 std::__lg 取得 
  •  
\lfloor log_2(x) \rfloor
ans_{[l, r)} = M(sp[i][l], sp[i][r - 2 ^ i]),\ i = \lfloor log_2(r - l) \rfloor
# Query

查詢

struct SparseTable {
    int query(int l, int r) {
        int i = std::__lg(r - l);
        return min(sp[i][l], sp[i][r - (1 << i)]);
    }
    
    // 或
    int operator()(int l, int r) {
        int i = std::__lg(r - l);
        return min(sp[i][l], sp[i][r - (1 << i)]);
    }
};

如果有聽課可以重載 () 運算子

修改

  • 聽起來不錯，但是這樣要怎麼修改？
    • 很簡單，稀疏表沒辦法改，要改的東西太多了

例題

樹堆

Treap

樹 + 堆

  • 樹堆是由兩種資料結構複合而來的
  • 二元搜尋樹 (Tree)
  • 堆 (Heap)

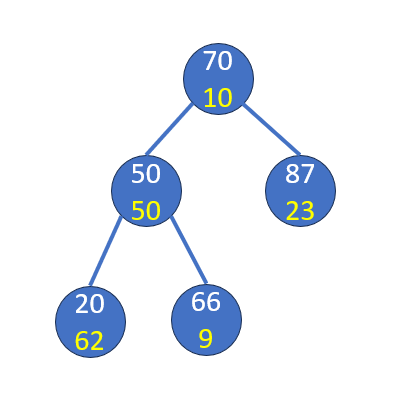
二元搜尋樹

  • Binary Search Tree
  • 望文生義：
    • 二元 (Binary)：每個節點至多有兩個子節點
    • 搜尋 (Search)：可以搜尋
    • 樹 (Tree)：這個資料結構是一種樹

二元搜尋樹

  • 它的特性很像二分搜
    • 左子節點值 < 父節點
    • 右子節點值 > 父節點
  • 二子節點也都是二元搜尋樹

31

17

23

53

67

47

73

59

二元搜尋樹

  • 這樣有什麼用？
  • 可以插入 / 刪除元素，並且查找是否存在
    • 從根節點比較，如果比較小就往左走
    • 否則往右走，直到該位置為空
  • 平常用的 set / map 也是一種二元搜尋樹

二元搜尋樹

  • 實作：最好用指標啦
  • 如果要用偽指標不是不行，要實作分配空間的東西

缺陷

  • 分析複雜度：
    • 理想的情況下，除了葉節點以外都有兩個子節點
    • 樹高大約  
    • 因此插入、刪除一般的情況是  
  • 最差情況呢？
log\ n
O(log\ n)

缺陷

  • 最差情況長這樣：
  • 變成一條鍊時最差是
  • 要怎麼解決這問題？ 

53

67

73

31

O(n)

改善

  • 既然變成鍊會出問題，那就不要讓它變成鍊！
  • 如何維持樹的形狀？
    • ​透過維護某些條件我們可以知道樹的變形程度
  • 知道樹的變形程度後怎麼修正形狀？
    • 旋轉
    • 分裂、合併
  • 其中，旋轉碼量太大不適合競程

堆

  • 要維護什麼條件來修正？
  • 運用堆的性質
    • 子節點比父節點大

5

7

73

13

16

19

79

59

樹 + 堆

  • 我們在每個節點多維護一個隨機值
  •       遵守堆的規則
  • 透過隨機值維護樹的結構
  • 原本二元搜尋樹查找用的稱作
  • 透過這兩個條件約束，可以保證樹的形狀唯一
    • 因為       值隨機，所以結構大致上隨機
pri
pri
key
pri

樹 + 堆

37

61

73

3

21

43

63

12

47

36

2

10

7

74

91

24

49

29

69

88

key

pri

分裂和合併

  • 分裂和合併可以修正樹的結構
  • 分裂：將一棵樹堆按照值域分成兩棵樹堆
  • 合併：將兩棵值域不重疊的樹堆合併

分裂

  • 把               的節點分到樹堆 A，否則分去樹堆 B
  • 把底下的樹堆以 49 為界分裂：
key \leq x

37

3

21

43

12

47

36

2

10

7

74

91

24

29

49

61

73

63

69

88

分裂

  • 把               的節點分到樹堆 A，否則分去樹堆 B
  • 把底下的樹堆以 49 為界分裂：
key \leq x

37

3

21

43

12

47

36

2

10

7

74

91

24

29

49

61

73

63

69

88

樹堆 A

樹堆 B

分裂

  • 沿著邊界遞迴
  • 從根開始判斷當前的點應該歸入 A 還是 B
    • 如果當前點歸入 A，表示左子節點一定在 A
    • 如果當前點歸入 B，表示右子節點一定在 B
  • 要記錄節點丟入 A / B 後應該要接在哪
  • 往另一邊遞迴判斷就好

分裂

37

61

73

3

21

43

63

12

47

36

2

10

7

74

91

24

49

29

69

88

k = 62

key <= 62 ，此節點歸給 A，向右遞迴

分裂

37

61

73

3

21

43

63

12

47

36

2

10

7

74

91

24

49

29

69

88

k = 62

key <= 62 ，此節點歸給 A，向右遞迴

分裂

37

61

73

3

21

43

63

12

47

36

2

10

7

74

91

24

49

29

69

88

k = 62

key > 62 ，此節點歸給 B，向左遞迴

分裂

37

61

73

3

21

43

63

12

47

36

2

10

7

74

91

24

49

29

69

88

k = 62

key <= 62 ，此節點歸給 A，向右遞迴

分裂

37

61

73

3

21

43

63

12

47

36

2

10

7

74

91

24

49

29

69

88

k = 62

當前節點為空，終止遞迴並將 A, B 連接處設為空

# Build

分裂

const int max_size = 1e6;

struct Treap {
    struct Node {
        int key, pri;
        int lchild = -1, rchild = -1;
        int val;

        Node(int _key, int _val)
            : key(_key), val(_val) {}
    };

    Node tree[max_size];
    int root_pt = -1;

    void split(int v, int k, int &A, int &B) {
        if (v == -1) {
            A = B = -1;
            return;
        }
        if (tree[v].key <= k) {
            A = v;
            split(tree[v].rchild, k, tree[v].rchild, B);
        }
        else {
            B = v;
            split(tree[v].lchild, k, A, tree[v].lchild);
        }
    }
};

注意節點為空時的做法

合併

  • 合併時需要注意        值
    • 分裂時一定是向下走，       只會越來越大
  • 合併後回傳合併後的根
  • 合併時必須保證 B 樹的所有        > A 樹
    • 只有 A 最右邊的節點 & B 最左邊的節點會受影響
    • 在遞迴下去的時候順便用       排序
pri
pri
key
pri

合併

37

43

47

7

9

29

保證 B Treap 的        大於 A

B 的節點一定接在 A 的右側

只需要關心 A 右側的節點，反之亦然

key

A

B

53

44

49

61

73

63

69

88

5

10

8

91

3

74

10

2

14

17

25

27

90

29

合併

37

43

47

7

9

29

保證 B Treap 的        大於 A

B 的節點一定接在 A 的右側

只需要關心 A 右側的節點，反之亦然

key

A

B

53

44

49

61

73

63

69

88

5

10

8

91

3

74

10

2

14

17

25

27

90

29

合併

37

43

47

7

9

29

保證 B Treap 的        大於 A

B 的節點一定接在 A 的右側

只需要關心 A 右側的節點，反之亦然

key

A

B

10

2

17

25

90

29

10

2

47

7

37

29

9

43

90

29

17

25

依照        的大小將節點排序

pri

37

29

90

29

17

25

9

43

47

7

10

2

37

29

90

29

17

25

9

43

47

7

10

2

37

29

90

29

10

2

47

7

9

43

17

25

10

2

5

10

8

91

3

74

37

29

90

29

47

7

9

43

17

25

49

61

73

63

69

88

53

44

14

27

合併

  • 實作利用歸併排序時的合併
  • 每次挑選比較小的那一方放進序列
  • 後面接剩下部分排序結果的頭
# Query

合併

struct Treap {
    int merge(int A, int B) {
        if (A == -1 || B == -1) return A == -1 ? B : A;
        if (tree[A].pri < tree[B].pri) {
            tree[A].rchild = merge(tree[A].rchild, B);
            return A;
        }
        else {
            tree[B].lchild = merge(A, tree[B].lchild);
            return B;
        }
    }
};

插入 & 刪除

  • 講了這麼多還沒講插入 & 刪除
  • 其實很簡單
    • 插入
      • 將樹堆依值域分裂成兩堆
      • 創要插入的新節點
      • 合併左邊堆、新節點、右邊堆
    • 刪除就是插入反過來
# Query

插入

struct Treap {
    int back = 0;  // 能用的空間的最後
    int new_node(int key, int val) {
        tree[back].val = val;
        tree[back].key = key;
        tree[back].pri = rand();
        return back++;
    }
    void insert(int key, int val) {
        if (root_pt = -1) {
            root_pt = new_node(key, val);
            return;
        }
        int insert_node_pt = new_node(key, val);
        int A, B;
        split(root_pt, key, A, B);
        root_pt = merge(merge(A, insert_node_pt), B);
    }
};

more

  • 除了依照值域分裂以外，這東西還可以
    • 結合樹 DP 玩出更多花樣
    • 選擇元素插入位置
    • 替代部分線段樹的功能
    • 各種奇葩操作...

例題

Made with Slides.com