Artificial Neural Network, ANN
手刻神經網路
INFOR 36th. @小海_夢想特急_夢城前



講師
- 225 賴柏宇
- 海之音、小海或其他類似的
- 美術能力見底
- 表達能力差,不懂要問
- INFOR 36th 學術長
這頁是偷來的- 不會 NN 所以來當 NN 講師

- 神經網路的概念
- 矩陣及向量
- 前向傳播
- 微積分的概念 - 斜率及極限
- 偏微分的概念 - 梯度
- 反向傳播
Index
神經網路的概念
Concept
- 實際上神經網路的功能相當於一個函數:
- 吃一連串的參數,輸出一連串的結果
- 舉圖像辨識來說:
函數擬合
神經網路
像素點 1
像素點 2
像素點 3
...
像素點 n
目標 1
目標 2
目標 3
...
目標 m
- 目標:
- 找到一個函數,使得指定輸入對到指定輸出
- 舉個例子:
- 假設 f(x) = ax + b
- x = 1 時 y = 2
- x = 2 時 y = 6
- 求 f(x)
- 把這個概念推廣,只是輸入輸出複雜得多
函數擬合
- 這樣做有什麼好處?
- 訓練過程中找到特徵
- 將無窮的可能性用有限的參數接近答案
函數擬合
矩陣及向量
Matrix and Vector
- 所以接下來的問題就是:
- 如何處理一串數字?
- 利用矩陣和向量
- 向量可以視為矩陣的特例
數值化
\begin {bmatrix}
x_{11} & x_{12} & x_{13} \\
x_{21} & x_{22} & x_{23}
\end {bmatrix}
\begin{bmatrix}
x_1 \\
x_2 \\
x_3
\end{bmatrix}
- 定議矩陣的加法:
- 每一個對應的位置相加
數值化
\begin {bmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end {bmatrix}
+
\begin {bmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end {bmatrix}
=
\begin {bmatrix}
2 & 4 & 6 \\
8 & 10 & 12 \\
14 & 16 & 18
\end {bmatrix}
- 定義矩陣的乘法
數值化
\begin {bmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end {bmatrix}
\begin {bmatrix}
1\ \ \ & 2\ \ \ & 3\\
4\ \ \ & 5\ \ \ & 6\\
7\ \ \ & 8\ \ \ & 9
\end {bmatrix}
\begin {bmatrix}
30 & 36 & 42 \\
66 & 81 & 96 \\
102 & 126 & 150
\end {bmatrix}
=
- 定義矩陣的乘法
數值化
\begin {bmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end {bmatrix}
\begin {bmatrix}
1\ \ \ & 2\ \ \ & 3\\
4\ \ \ & 5\ \ \ & 6\\
7\ \ \ & 8\ \ \ & 9
\end {bmatrix}
\begin {bmatrix}
30 & 36 & 42 \\
66 & 81 & 96 \\
102 & 126 & 150
\end {bmatrix}
- 定義矩陣的乘法
數值化
\begin {bmatrix}
1 & 2 & 3
\end {bmatrix}
\begin {bmatrix}
1\\
4\\
7
\end {bmatrix}
\begin {bmatrix}
30
\end {bmatrix}
= 1 \times 1 + 2 \times 4 + 3 \times 7
- 矩陣的轉置
數值化
\begin {bmatrix}
1 & 2 & 3
\end {bmatrix}^T
=
\begin {bmatrix}
1 \\
2 \\
3
\end {bmatrix}
- 特例:矩陣乘向量
- 你會發現這就是一種函數
線性變換
\begin {bmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end {bmatrix}
\begin {bmatrix}
a\\
b\\
c
\end {bmatrix}
\begin {bmatrix}
1a + 2b + 3c \\
4a + 5b + 6c \\
7a + 8b + 9c
\end {bmatrix}
=
- 具結合律、分配律
- 不具交換律
線性變換
A
x
Ax
=
- 具結合律、分配律
- 不具交換律
線性變換
(AB)x = A(Bx) = ABx \\
A(x + y) = Ax + Ay
- NumPy 是目前主流、基本、核心的數學相關套件之一
- 學機器學習基本上躲不掉這東西
- 提供高效、與底層語言兼容的資料型態
- 方便與底層語言串接
NumPy
- 為什麼 NumPy 很高效?
- Python 的資料存儲型態包括:
- 資料本身
- 資料型態以及相關方法
- List 是由 array of pointers 組成
- NumPy 提供的 array 是真正的 array
NumPy
安裝 Python
- Linux users (Debian, Ubuntu...):
sudo apt-get install python3
- Windows users:
你很糟糕,快去裝 Linux
- MacOS users:
- 輸入後照指示做
/bin/bash -c "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/HEAD/install.sh)"brew install python3安裝 Python
- 確認一下是否安裝成功
- 如果跳出版本就表示你裝對了
python3 --version安裝 NumPy
- 如果你裝到 Python 的老版本請自行安裝 pip
pip install numpy使用 NumPy
- 使用 numpy 前記得引入 numpy
- 之後要使用 numpy 底下的東西就是 np.something
import numpy as np導入 numpy 模組,稱為 np
使用 NumPy
- 宣告陣列(矩陣)
import numpy as np
# 使用 python 的 list 宣告陣列
arr = np.array(
[[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]
)
# 宣告一個全是 0 的陣列
arr1 = np.zeros((2, 3))
# 宣告一個隨機填充的陣列
arr2 = np.random.random((2, 3))
print(arr, arr1, arr2, sep = '\n')使用 NumPy
- 可以選擇類型
import numpy as np
# 宣告一個 fp16 的陣列
arr = np.array(
[[1, 2, 3],
[4, 5, 6],
[7, 8, 9]],
dtype = np.float16
)
print(arr)使用 NumPy
- 加減法
import numpy as np
arr = np.array(
[[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]
)
print(arr + arr, arr - arr, sep = '\n')使用 NumPy
- 轉置
import numpy as np
arr = np.array(
[[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]
)
print(arr.T)使用 NumPy
- 矩陣乘法
import numpy as np
arr = np.array(
[[1, 2, 3],
[4, 5, 6]]
)
print(arr.dot(arr.T), arr.T.dot(arr), sep = '\n')C++
- 論為什麼你應該使用 NumPy
- 註:這沒經過優化,搞不好比 NumPy 還慢
#include <cassert>
#include <cmath>
#include <concepts>
#include <functional>
#include <iostream>
#include <random>
#include <utility>
#include <vector>
template <typename Tp>
concept addable = requires(Tp a, Tp b) {
a + b;
};
template <typename Tp>
concept minusable = requires(Tp a, Tp b) {
a - b;
};
template <typename Tp>
concept multiplyable = requires(Tp a, Tp b) {
a * b;
};
template <typename Tp>
requires addable<Tp> && minusable<Tp> && multiplyable<Tp>
class Matrix {
std::vector<std::vector<Tp>> data;
int R, C;
public:
Matrix() = default;
Matrix(const Matrix<Tp> &) = default;
Matrix(Matrix<Tp> &&) = default;
Matrix &operator=(const Matrix<Tp> &) = default;
Matrix &operator=(Matrix<Tp> &&) = default;
Matrix(int _R)
: R(_R), C(1), data(_R, std::vector<Tp>(1)) {}
Matrix(int _R, std::function<Tp()> &&generator)
: R(_R), C(1), data(_R, std::vector<Tp>(1)) {
for (int i = 0; i < _R; i++)
data[i][0] = generator();
}
Matrix(int _R, std::function<Tp(int)> &&generator)
: R(_R), C(1), data(_R, std::vector<Tp>(1)) {
for (int i = 0; i < _R; i++)
data[i][0] = generator(i);
}
Matrix(int _R, int _C)
: R(_R), C(_C), data(_R, std::vector<Tp>(_C)) {}
Matrix(int _R, int _C, std::function<Tp()> &&generator)
: R(_R), C(_C), data(_R, std::vector<Tp>(_C)) {
for (int i = 0; i < _R; i++)
for (int j = 0; j < _C; j++)
data[i][j] = generator();
}
Matrix(int _R, int _C, std::function<Tp(int, int)> &&generator)
: R(_R), C(_C), data(_R, std::vector<Tp>(_C)) {
for (int i = 0; i < _R; i++)
for (int j = 0; j < _C; j++)
data[i][j] = generator(i, j);
}
Matrix(std::vector<std::vector<Tp>> &&_data) {
assert(_data.size() > 0);
R = _data.size();
assert(_data[0].size() > 0);
C = _data[0].size();
data = std::forward<std::vector<std::vector<Tp>>>(_data);
}
Matrix(const std::vector<Tp> &_data) {
assert(_data.size() > 0);
R = _data.size(), C = 1;
data.resize(R, std::vector<Tp>(1));
for (int i = 0; i < R; i++)
data[i][0] = _data[i];
}
public:
inline Tp &operator()(int _r, int _c) {
return data[_r][_c];
}
inline const Tp &operator()(int _r, int _c) const {
return data[_r][_c];
}
Matrix operator+(const Matrix &another) const {
assert(R == another.R && C == another.C);
Matrix result(R, C);
for (int i = 0; i < R; i++)
for (int j = 0; j < C; j++)
result(i, j) = data[i][j] + another(i, j);
return result;
}
Matrix &operator+=(const Matrix &another) {
assert(R == another.R && C == another.C);
for (int i = 0; i < R; i++)
for (int j = 0; j < C; j++)
data[i][j] += another(i, j);
return (*this);
}
Matrix operator-(const Matrix &another) const {
assert(R == another.R && C == another.C);
Matrix result(R, C);
for (int i = 0; i < R; i++)
for (int j = 0; j < C; j++)
result(i, j) = data[i][j] - another(i, j);
return result;
}
Matrix &operator-=(const Matrix &another) {
assert(R == another.R && C == another.C);
for (int i = 0; i < R; i++)
for (int j = 0; j < C; j++)
data[i][j] -= another(i, j);
return (*this);
}
Matrix operator*(Tp k) const {
Matrix result(*this);
for (int i = 0; i < R; i++)
for (int j = 0; j < C; j++)
result(i, j) = data[i][j] * k;
return result;
}
Matrix &operator*=(Tp k) {
for (int i = 0; i < R; i++)
for (int j = 0; j < C; j++)
data[i][j] *= k;
return (*this);
}
Matrix operator*(const Matrix another) const {
assert(C == another.R);
Matrix result(R, another.C);
for (int r = 0; r < R; r++)
for (int c = 0; c < another.C; c++)
for (int i = 0; i < C; i++)
result(r, c) += data[r][i] * another(i, c);
return result;
}
public:
std::pair<int, int> size() {
return {R, C};
}
friend std::ostream &operator<<(std::ostream &out, Matrix<Tp> target) {
out << "[\n";
for (int i = 0; i < target.R; i++) {
out << " [";
for (int j = 0; j < target.C; j++)
out << target.data[i][j] << " ";
out << "\b]\n";
}
out << "]";
return out;
}
Matrix T() {
Matrix<Tp> result(C, R);
for (int i = 0; i < C; i++)
for (int j = 0; j < R; j++)
result(i, j) = data[j][i];
return result;
}
};前向傳播
Forward
- 只用矩陣乘法和加法有什麼限制?
- 實際上,矩陣是「線性的」
線性變換
- 舉幾個直觀的例子來說:
- 拋物線有辦法用直線表示嗎?
- 並且,所謂線性變換:
- 也就是說,無論經過多少次線性變換都等價於只進行一次線性變換
線性變換
C(Ax + b) + d = (AC)x + (Cb + d)
- 所以,我們會在這裡面加入一些非線性要素
- 常用的非線性函數有:
非線性變換
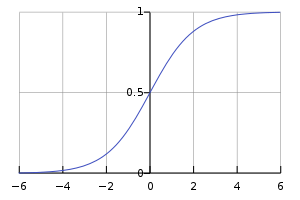
Sigmoid
tanh
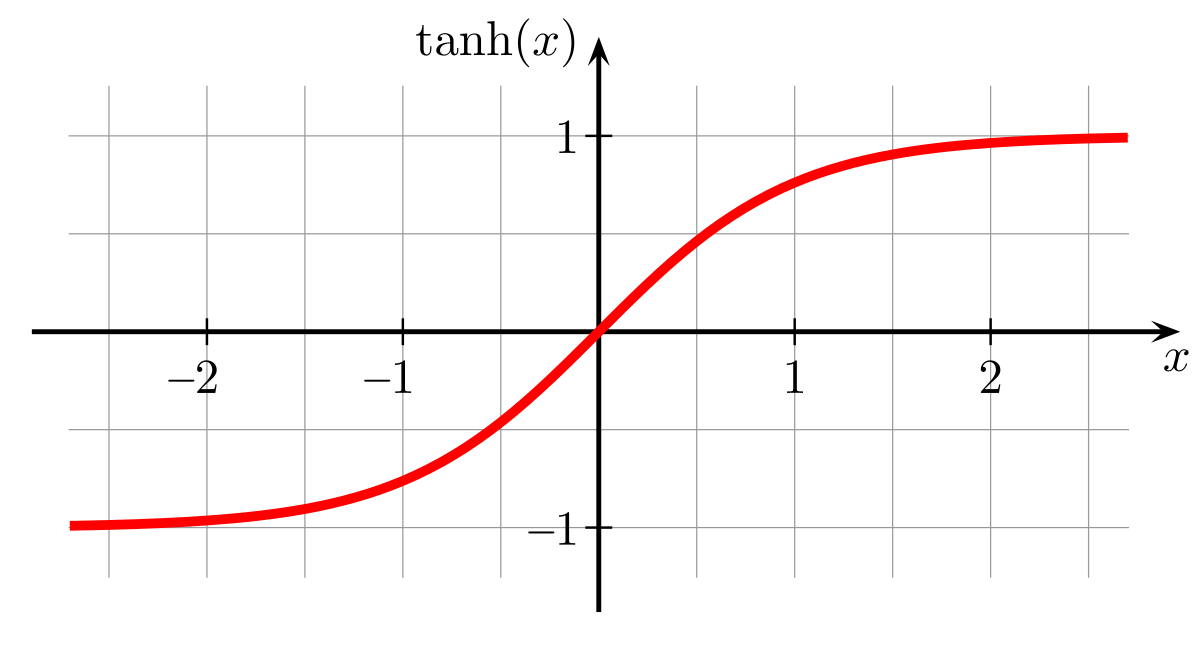
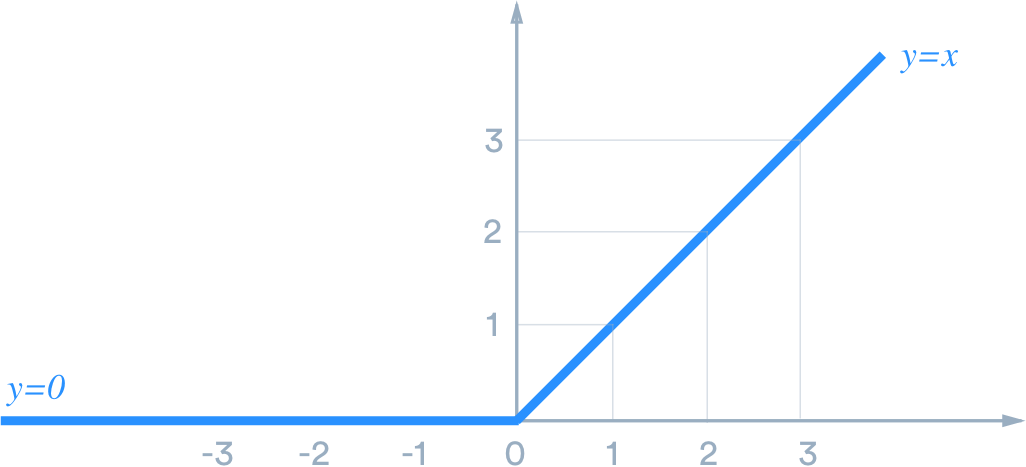
ReLU
- 我們稱這些函數為激勵函數 (Activation Function)
- 定義 是將向量中元素進行非線性變換
- 這樣,我們的函數應該會變得類似
- 其中,W 為權重 (Weight),b 為 bias
非線性變換
\sigma(x)
f(x) = \sigma (Wx+b)
圖像化
x_1
x_2
x_3
z_1
z_2
= W_{11}x_1 + W_{12}x_2 + W_{13}x_3 + b_1
= W_{21}x_1 + W_{22}x_2 + W_{23}x_3 + b_2
z = Wx+b
圖像化
x_1
x_2
x_3
\sigma(z_1)
\sigma(z_2)
然而,只有一層的話經常複雜度不夠
聰明的你肯定能想到怎麼做吧
圖像化
然而,只有一層的話經常複雜度不夠
聰明的你肯定能想到怎麼做吧
x_1
x_2
x_3
x'_1
x'_2
x''_1
x''_2
x''_1
x''_2
...
圖像化
以前一層激活後的輸出作為後一層的輸入
看起來就像在把資料往前傳
x_1
x_2
x_3
x'_1
x'_2
x''_1
x''_2
x''_1
x''_2
...
實作
import numpy as np
class NeuralNetwork:
def __init__(self, topo: list[int], act, dact):
self.weight = [np.zeros((0, 0), dtype = np.float16)]
self.bias = [np.zeros((topo[0], 1), dtype = np.float16)]
self.value = [np.zeros((topo[0], 1), dtype = np.float16)]
self.zeta = [np.zeros((topo[0], 1), dtype = np.float16)]
self.act = act
self.dact = dact
self.topo = topo
self.num_layers = len(topo)
for i in range(self.num_layers - 1):
self.weight.append(np.random.randn(topo[i + 1], topo[i]))
self.bias.append(np.random.randn(topo[i + 1], 1))
self.value.append(np.zeros((topo[i + 1], 1), dtype = np.float16))
self.zeta.append(np.zeros((topo[i + 1], 1), dtype = np.float16))
def forward(self, input: np.ndarray) -> None:
self.value[0] = input
for i in range(self.num_layers - 1):
self.zeta[i + 1] = np.dot(self.weight[i + 1], self.value[i]) + self.bias[i + 1]
self.value[i + 1] = self.act(self.zeta[i + 1])C++
class NeuralNetwork {
std::vector<Matrix<float>> weight, bias, value, zeta;
std::vector<int> topo;
std::function<float(float)> act_func;
unsigned size;
public:
NeuralNetwork() = delete;
NeuralNetwork(const NeuralNetwork &) = default;
NeuralNetwork(NeuralNetwork &&) = default;
NeuralNetwork(std::vector<int> &&_topo, std::function<float(float)> _act_func)
: topo(std::forward<std::vector<int>>(_topo)), act_func(std::forward<std::function<float(float)>>(_act_func)), size(topo.size()) {
std::default_random_engine random_engine(std::random_device{}());
std::normal_distribution<float> distributor(-1.0, 1.0);
auto random = [&]() -> float { return distributor(random_engine); };
weight.resize(size), bias.resize(size), value.resize(size), zeta.resize(size);
bias[0] = zeta[0] = value[0] = Matrix<float>(topo[0]);
for (int i = 1; i < size; i++) {
weight[i] = Matrix<float>(topo[i], topo[i - 1], random);
zeta[i] = value[i] = bias[i] = Matrix<float>(topo[i], random);
}
}
public:
std::vector<float> forward(std::vector<float> &&input) {
auto activate = [&](int value_index) -> void {
Matrix<float> &x = value[value_index], &z = zeta[value_index];
for (int i = 0; i < topo[value_index]; i++) x(i, 0) = z(i, 0);
};
value[0] = std::forward<std::vector<float>>(input);
for (int i = 1; i < size; i++) {
zeta[i] = weight[i] * value[i - 1] + bias[i];
activate(i);
}
std::vector<float> result(topo[size - 1]);
for (int i = 0; i < topo[size - 1]; i++)
result[i] = value[size - 1](i, 0);
return result;
}
};極限 & 斜率
Calculus
- 很多人開玩笑說「生活哪裡用得到微積分」
- 微積分確實很有用,但不是體現在日常生活中
- 微積分可以用來
- 處理連續及非連續的性質
- 處理極限的情況(極大、極小、極接近)
- 代數學和幾何學的結合
- ...
微積分的用途
- 讓我們從非常不嚴謹但直觀的觀點切入
- 斜率:傾斜的程度
斜率
x
y
f(x) = x + 1
f(x) = \frac 1 2 x
f(x) = -x
- 以 f(x) = mx + b 來說,傾斜程度只和 m 有關
- 我們定這個值為斜率
斜率
x
y
f(x) = x + 1
f(x) = \frac 1 2 x
f(x) = -x
- 在幾何意義上來說,這個值代表
- 意思是 y 的改變量和 x 的改變量的比值
斜率
x
y
f(x) = x + 1
f(x) = \frac 1 2 x
f(x) = -x
\frac{\Delta y}{\Delta x}
- 在幾何意義上來說,這個值代表
- 意思是 y 的改變量和 x 的改變量的比值
斜率
\frac{\Delta y}{\Delta x}
m = 1: 當 x 增加 1 時 y 增加 1
m = 2: 當 x 增加 1 時 y 增加 2
\Delta x
\Delta y
- 當然這個值可以是負的,線會是左上 - 右下
斜率
m = 1: 當 x 增加 1 時 y 增加 -1
- 讓我們從非常不嚴謹但直觀的觀點切入
- 所謂極限,就是非常極端的情況
- 非常接近某數
- 非常大
- 非常小
- ...
極限
- 剛剛討論斜率只討論直線的狀況
- 曲線也有斜率:切線斜率
- 切線也有一個切點,所以稱那是該點的斜率
極限 & 斜率
切線斜率 = -0.23
- 問題來了,切線斜率怎麼求?
- 結合極限的概念去想
極限 & 斜率
- 兩點一線
極限 & 斜率
- 兩點一線
極限 & 斜率
- 兩點一線
極限 & 斜率
- 兩點一線 -> 接近一點一線
極限 & 斜率
- 兩點一線的求法
極限 & 斜率
(x, f(x))
(x + h, f(x + h))
m = \frac {f(x + h) - f(x)}{h}
- 接近一點一線
極限 & 斜率
m = \frac {f(x + h) - f(x)}{h},\ h \rightarrow 0
- 換個專業一點的寫法
極限 & 斜率
m = \lim_{h\rightarrow0} \frac {f(x + h) - f(x)}{h}
- 以 為例
極限 & 斜率
\lim_{h\rightarrow0} \frac {f(x + h) - f(x)}{h}
= \lim_{h\rightarrow0} \frac{(a(x + h) + b) - (ax + b)}{h}
= \lim_{h\rightarrow0} \frac{ah}{h}
= \lim_{h\rightarrow0} a
= a
f(x) = ax + b
- 以 為例
f(x) = ax^2 + bx + c
\lim_{h\rightarrow0} (\frac {f(x + h) - f(x)}{h})
= \lim_{h\rightarrow0} (\frac{(a(x + h)^2 + b(x + h) + c) - (ax^2 + bx + c)}{h})
= \lim_{h\rightarrow0} (\frac{2axh + ah^2 + bh}{h})
= \lim_{h\rightarrow0} (2ax + ah + b)
= 2ax + b
- 也是一種 的函數
- 把原函數轉成 對該點斜率的函數稱為微分
- 微分可以記成 或者
極限 & 斜率
a, 2ax + b
x
x
f(x)
f'(x)
\frac{d}{dx} f(x)
- 一般的微分如果都照定義做太麻煩,以下是幾個通則:
微分
\frac{d}{dx} x^n = nx^{n-1}
\frac{d}{dx} (f(x) + g(x)) = \frac{d}{dx} f(x) + \frac{d}{dx} g(x)
\frac{d}{dx} e^x = e^x
\frac{d}{dx} f(g(x)) = \frac{d}{dg} f(g) \frac{d}{dx} g(x)
(fg)' = f'g + fg'
(\frac g h)' = \frac {g'h - gh'}{h^2}
偏微分
Partial Derivative
- 然而,微分只能處理單變數的函數
- 偏微分能幫助我們處理更多變數的東西
- 偏微分處理的東西會像是
- 多變數打到單變數上
- 向量 -> 純量
偏微分
f(x, y, z) = xyz
- 既然一般的微分只有單變數,那就只看一個
- 其他的變數怎麼辦?
- 當常數啊
偏微分
\frac{\partial}{\partial x} (x + y)^2 = \frac{\partial}{\partial x} x^2 + 2xy + y^2 = 2x + 2y
\frac{\partial}{\partial x} xy = y
- 接著我們把所有變量合成一個向量稱為梯度
梯度
\begin {bmatrix}
\frac {\partial f}{\partial x} \\
\\
\frac {\partial f}{\partial y} \\
\\
\frac {\partial f}{\partial z}
\end {bmatrix}
f(x, y, z)
的梯度:
- 梯度具有什麼幾何意義呢?
- 我們從最基本的單變數,也就是斜率看起
梯度
- 斜率為正,放到 x 軸上相當於是正向
梯度
- 斜率為負,放到 x 軸上相當於是負向
- 發現了嗎?它永遠指向比較高的那側
梯度
- 而梯度相當於是多個維度疊合在一起
- 所以,梯度其實就是指向高處的向量
梯度
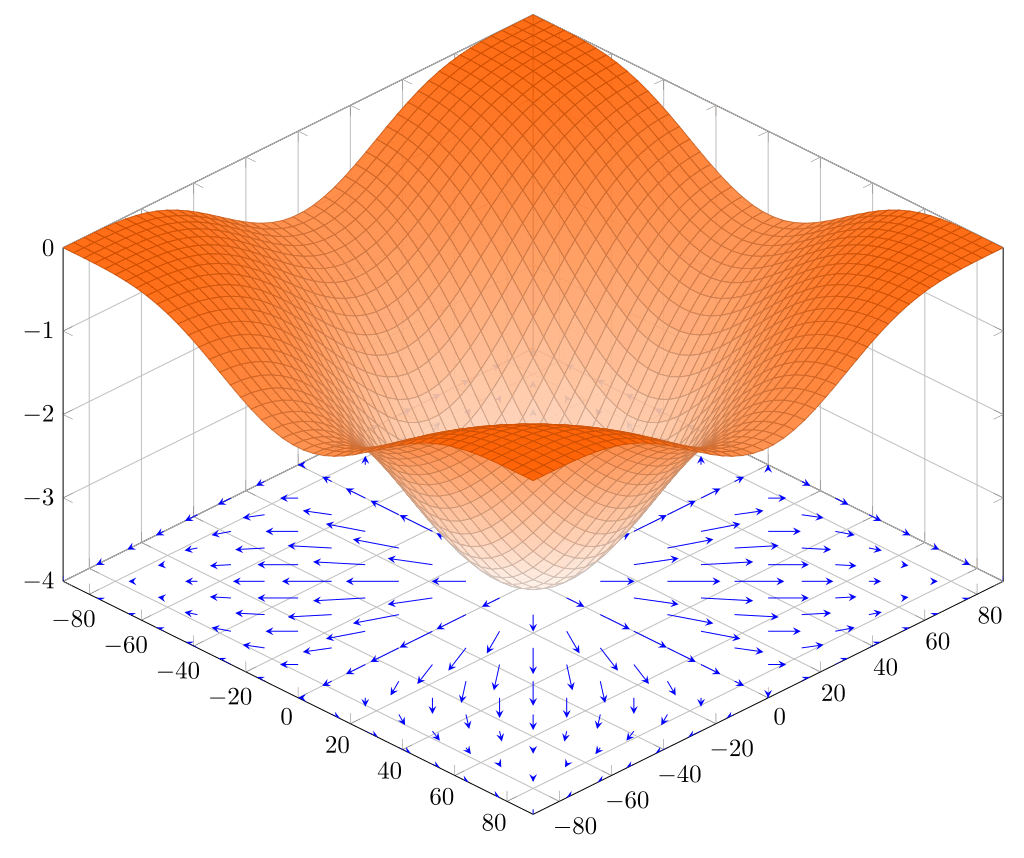
反向傳播
Backward
- 前向傳播時提到這樣做理論上應該可以很好地貼合各類函數
- 然而,我們沒提到要怎麼貼合
- 總不可能手動調參數吧?
擬合
- 於是,我們要介紹訓練的方法:反向傳播
- 利用已知的輸入和輸出調整參數
擬合
- Loss Function 是當前的輸出和期望的差距
- 舉個例子
- 預期輸出是(0, 1),實際輸出是(0, 1)
- 損失函數為 0
- 預期輸出是(0, 1),實際輸出是 (1, 1)
- 損失函數 > 0
損失函數
- 損失函數可以用距離平方表示
- 注意這只是其中一種損失函數
- 假設預期輸出 實際輸出
- 損失
損失函數
(y_1, y_2, y_3...y_n)
(x_1, x_2, x_3...x_n)
L = \sum^n_{i=1} (y_i - x_i)^2 = (y_1 - x_1)^2 + (y_2 - x_2)^2...(y_n - x_n)^2
*在實務上我們通常會在前面乘上 1/2
- 現在的目標是要減小這個損失
- 我們要怎麼連結參數和損失?
- 把損失試著表示成參數的函數!
- 然後呢?
損失函數
L =\frac{1}{2} \sum^n_{i=1} (y_i - x_i)^2
L = f(args)
- 前面提到,梯度是指向高處的向量
- 我們的目標是減少損失
- 往梯度的反方向走!
梯度下降
args
L
- 前面提到,梯度是指向高處的向量
- 我們的目標是減少損失
- 往梯度的反方向走!
梯度下降
args
L
- 問題來了,怎麼把損失表示成參數相關的函數
損失函數
- 好像有點太複雜,我們先關注 W 中的其中一個數吧
x^1_1
x^1_2
x^1_3
\sigma(z_1)
\sigma(z_2)
\begin {bmatrix}
W^1_1 \\
W^1_2 \\
\end {bmatrix}
=\sigma (W^1_{11}x^1_1 + W^1_{12}x^1_2 + W^1_{13}x^1_3 + b_1)
=\sigma (W^1_{21}x^1_1 + W^1_{22}x^1_2 + W^1_{23}x^1_3 + b_2)
損失函數
L = \frac 1 2 \sum^n_{i = 0} (y_i - x_i)^2
\frac{\partial}{\partial W^1_{rc}} L = \frac{\partial}{\partial W^1_{rc}} \frac 1 2 \sum^n_{i = 0} (y_i - x_i)^2
=\frac 1 2 (\frac{\partial}{\partial x_r} \sum^n_{i = 0} (y_i - x_i)^2) (\frac{\partial}{\partial W^1_{rc}} x_r)
=\frac 1 2 (2x_r - 2y_r)(\frac{\partial}{\partial W^1_{rc}} x_r)
= (x_r - y_r)(\frac{\partial}{\partial W^1_{rc}} \sigma(z_r))
損失函數
\frac{\partial}{\partial W^1_{rc}} L = \frac{\partial}{\partial W^1_{rc}} \frac 1 2 \sum^n_{i = 0} (y_i - x_i)^2
=(x_r - y_r)(\frac{\partial}{\partial W^1_{rc}} \sigma(z_r))
=(x_r - y_r)(\frac{\partial}{\partial z_r} \sigma(z_r))(\frac{\partial}{\partial W^1_{rc}} z_r)
=(x_r - y_r)\sigma'(z_r)(\frac{\partial}{\partial W^1_{rc}} (W^1_rx^1 + b^1_r))
=(x_r - y_r)\sigma'(z_r)(\frac{\partial}{\partial W^1_{rc}} (W^1_{r1}x^1_1 + W^1_{r2}x^1_2 + ... + W^1_{rc}x^1_c + ... W^1_{rm}x^1_m + b^1_r))
=(x_r - y_r)\sigma'(z_r)x^1_c
損失函數
- b 是類似的,但是在最後這步有點不同
=(x_r - y_r)\sigma'(z_r)
\frac{\partial}{\partial b^1_r} L
=(x_r - y_r)\sigma'(z_r)(\frac{\partial}{\partial b^1_r} (W^1_{r1}x^1_1 + W^1_{r2}x^1_2 + ... + W^1_{rc}x^1_c + ... W^1_{rm}x^1_m + b^1_r))
損失函數
- 結論:
W^1_{rc} \leftarrow W^1_{rc} - k(x_r - y_r)\sigma'(z_r)x^1_c
b^1_r \leftarrow b^1_r - k(x_r - y_r)\sigma'(z_r)
- 再加上一些通靈其實可以得出更簡潔的結論
W^1 \leftarrow W^1 - r\ dW, dW = (x - y)\sigma'(z)(x^1)^T
其中 k 是常數,稱為學習率
b^1 \leftarrow b^1 - r\ db, db = (x - y)\sigma'(z)
反向傳播
- 但這樣只有更新一層的參數
- 我們再把前一層的參數打開吧
- 過程有點麻煩,講結論
\frac{\partial}{\partial W^2_{hc}} L = \sum^n_{i = 1} \sigma'(z_i)W^1_{ih}(x^1_h - y^1_h)\sigma'(z^1_h)x^2_c
- 這樣計算複雜度不會太高嗎?
- 會,所以我們才要用反向傳播
反向傳播
- 用比較不嚴謹的寫法會像是
\frac{\partial L}{\partial W^{l-1}} = \frac{\partial L}{\partial x^{l-1}}\frac{\partial x^{l-1}}{\partial z^{l-1}}\frac{\partial z^{l-1}}{\partial W^{l-1}}
= \frac{\partial L}{\partial x^{l-1}}\sigma'(z^{l-1})x^{l-1}
- 而前面的 就是剛剛難計算的那部份,可以拆成
\frac{\partial L}{\partial x^{l-1}}
\frac{\partial L}{\partial x^{l-1}} = \frac{\partial L}{\partial x^l} \frac{\partial x^l}{\partial z^{l-1}} \frac{\partial z^{l-1}}{\partial x^{l-1}}
= \frac{\partial L}{\partial x^l} \sigma'(z^l)W^l
上標代表它在第幾層
反向傳播
\frac{\partial L}{\partial x^{l - 1}} = \frac{\partial L}{\partial x^l} \sigma'(z^l)W^l
- 不難發現有遞迴關係
- 我們從最後一層算回去的時候順便幫前一層算這東西
反向傳播
\frac{\partial L}{\partial W^{l-1}} = \frac{\partial L}{\partial x^{l-1}}\frac{\partial x^{l-1}}{\partial z^{l-1}}\frac{\partial z^{l-1}}{\partial W^{l-1}}
- 不難發現有遞迴關係
- 我們從最後一層算回去的時候順便幫前一層算
- 利用 dx 更新 W 和 B
\frac{\partial L}{\partial b^{l-1}} = \frac{\partial L}{\partial x^{l-1}}\frac{\partial x^{l-1}}{\partial z^{l-1}}\frac{\partial z^{l-1}}{\partial b^{l-1}}
= \frac{\partial L}{\partial x^{l-1}}\sigma'(z^{l-1})x^{l-1}
= \frac{\partial L}{\partial x^{l-1}}\sigma'(z^{l-1})
\frac{\partial L}{\partial x^{l - 1}}
反向傳播
Python 實作要小心 Vector 和 Matrix 上的差別
import numpy as np
class NeuralNetwork:
def __init__(self, topo: list[int], act, dact):
self.weight = [np.zeros((0, 0), dtype = np.float16)]
self.bias = [np.zeros((topo[0], 1), dtype = np.float16)]
self.value = [np.zeros((topo[0], 1), dtype = np.float16)]
self.zeta = [np.zeros((topo[0], 1), dtype = np.float16)]
self.act = act
self.dact = dact
self.topo = topo
self.num_layers = len(topo)
for i in range(self.num_layers - 1):
self.weight.append(np.random.randn(topo[i + 1], topo[i]))
self.bias.append(np.random.randn(topo[i + 1], 1))
self.value.append(np.zeros((topo[i + 1], 1), dtype = np.float16))
self.zeta.append(np.zeros((topo[i + 1], 1), dtype = np.float16))
def forward(self, input: np.ndarray) -> None:
self.value[0] = input
for i in range(self.num_layers - 1):
self.zeta[i + 1] = np.dot(self.weight[i + 1], self.value[i]) + self.bias[i + 1]
self.value[i + 1] = self.act(self.zeta[i + 1])
def backward(self, label: np.ndarray, learning_rate) -> None:
dx = self.value[-1] - label
for i in range(self.num_layers - 1, 0, -1):
db = dx * self.dact(self.zeta[i])
dW = np.dot(db, self.value[i - 1].T)
dx = np.dot(self.weight[i].T, db)
self.weight[i] -= learning_rate * dW
self.bias[i] -= learning_rate * db
def predict(self, input: np.ndarray) -> np.ndarray:
self.forward(input)
return self.value[-1]
def fit(self, input: np.ndarray, label: np.ndarray, learning_rate) -> None:
self.forward(input)
self.backward(label, learning_rate)反向傳播
C++ 實作一切都自己來,自己肯定比較了解
class NeuralNetwork {
std::vector<Matrix<float>> weight, bias, value, zeta;
std::vector<int> topo;
std::function<float(float)> act_func, dact_func;
unsigned size;
public:
NeuralNetwork() = delete;
NeuralNetwork(const NeuralNetwork &) = default;
NeuralNetwork(NeuralNetwork &&) = default;
NeuralNetwork(std::vector<int> &&_topo, std::function<float(float)> _act_func, std::function<float(float)> _dact_func)
: topo(std::forward<std::vector<int>>(_topo)), act_func(std::forward<std::function<float(float)>>(_act_func)), dact_func(std::forward<std::function<float(float)>>(_dact_func)), size(topo.size()) {
std::default_random_engine random_engine(std::random_device{}());
std::normal_distribution<float> distributor(-1.0, 1.0);
auto random = [&]() -> float { return distributor(random_engine); };
weight.resize(size), bias.resize(size), value.resize(size), zeta.resize(size);
weight[0] = bias[0] = zeta[0] = value[0] = Matrix<float>(topo[0]);
for (int i = 1; i < size; i++) {
weight[i] = Matrix<float>(topo[i], topo[i - 1], random);
zeta[i] = value[i] = bias[i] = Matrix<float>(topo[i], random);
}
}
private:
void forward(const std::vector<float> &input) {
auto activate = [&](int value_index) -> void {
Matrix<float> &x = value[value_index], &z = zeta[value_index];
for (int i = 0; i < topo[value_index]; i++) x(i, 0) = act_func(z(i, 0));
};
value[0] = input;
for (int i = 1; i < size; i++) {
zeta[i] = weight[i] * value[i - 1] + bias[i];
activate(i);
}
}
void backward(const std::vector<float> &output, float learning_rate) {
Matrix<float> label(output);
Matrix<float> dx = value[size - 1] - label;
for (int i = size - 1; i > 0; i--) {
Matrix<float> db(dx);
for (int j = 0; i < topo[j]; j++)
db(j, 0) *= dact_func(zeta[i](j, 0));
Matrix<float> dW(db * value[i - 1].T());
dx = weight[i].T() * db;
weight[i] -= dW * learning_rate;
bias[i] -= db * learning_rate;
}
}
public:
std::vector<float> predict(const std::vector<float> &input) {
forward(input);
std::vector<float> result(topo[size - 1]);
for (int i = 0; i < topo[size - 1]; i++)
result[i] = value[size - 1](i, 0);
return result;
}
void fit(const std::vector<float> &input, const std::vector<float> &output, double learning_rate) {
forward(input);
backward(output, learning_rate);
}
};XOR 測試
XOR 是簡單的非線性問題
可以拿來驗證神經網路具有非線性函數的擬合
import numpy as np
class NeuralNetwork:
def __init__(self, topo: list[int], act, dact):
self.weight = [np.zeros((0, 0), dtype = np.float16)]
self.bias = [np.zeros((topo[0], 1), dtype = np.float16)]
self.value = [np.zeros((topo[0], 1), dtype = np.float16)]
self.zeta = [np.zeros((topo[0], 1), dtype = np.float16)]
self.act = act
self.dact = dact
self.topo = topo
self.num_layers = len(topo)
for i in range(self.num_layers - 1):
self.weight.append(np.random.randn(topo[i + 1], topo[i]))
self.bias.append(np.random.randn(topo[i + 1], 1))
self.value.append(np.zeros((topo[i + 1], 1), dtype = np.float16))
self.zeta.append(np.zeros((topo[i + 1], 1), dtype = np.float16))
def forward(self, input: np.ndarray) -> None:
self.value[0] = input
for i in range(self.num_layers - 1):
self.zeta[i + 1] = np.dot(self.weight[i + 1], self.value[i]) + self.bias[i + 1]
self.value[i + 1] = self.act(self.zeta[i + 1])
def backward(self, label: np.ndarray, learning_rate) -> None:
dx = self.value[-1] - label
for i in range(self.num_layers - 1, 0, -1):
db = dx * self.dact(self.zeta[i])
dW = np.dot(db, self.value[i - 1].T)
dx = np.dot(self.weight[i].T, db)
self.weight[i] -= learning_rate * dW
self.bias[i] -= learning_rate * db
def predict(self, input: np.ndarray) -> np.ndarray:
self.forward(input)
return self.value[-1]
def fit(self, input: np.ndarray, label: np.ndarray, learning_rate) -> None:
self.forward(input)
self.backward(label, learning_rate)
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def dsigmoid(x):
return sigmoid(x) * (1 - sigmoid(x))
nn = NeuralNetwork([2, 3, 1], sigmoid, dsigmoid)
for i in range(1000):
nn.fit(np.array([[0], [0]]), np.array([[0]]), 2)
nn.fit(np.array([[0], [1]]), np.array([[1]]), 2)
nn.fit(np.array([[1], [0]]), np.array([[1]]), 2)
nn.fit(np.array([[1], [1]]), np.array([[0]]), 2)
print(nn.predict(np.array([[0], [0]])))
print(nn.predict(np.array([[0], [1]])))
print(nn.predict(np.array([[1], [0]])))
print(nn.predict(np.array([[1], [1]])))XOR 測試
XOR 是簡單的非線性問題
可以拿來驗證神經網路具有非線性函數的擬合
#include <cassert>
#include <cmath>
#include <concepts>
#include <functional>
#include <iostream>
#include <random>
#include <utility>
#include <vector>
template <typename Tp>
concept addable = requires(Tp a, Tp b) {
a + b;
};
template <typename Tp>
concept minusable = requires(Tp a, Tp b) {
a + b;
};
template <typename Tp>
concept multiplyable = requires(Tp a, Tp b) {
a * b;
};
template <typename Tp>
requires addable<Tp> && minusable<Tp> && multiplyable<Tp>
class Matrix {
std::vector<std::vector<Tp>> data;
int R, C;
public:
Matrix() = default;
Matrix(const Matrix<Tp> &) = default;
Matrix(Matrix<Tp> &&) = default;
Matrix &operator=(const Matrix<Tp> &) = default;
Matrix &operator=(Matrix<Tp> &&) = default;
Matrix(int _R)
: R(_R), C(1), data(_R, std::vector<Tp>(1)) {}
Matrix(int _R, std::function<Tp()> &&generator)
: R(_R), C(1), data(_R, std::vector<Tp>(1)) {
for (int i = 0; i < _R; i++)
data[i][0] = generator();
}
Matrix(int _R, std::function<Tp(int)> &&generator)
: R(_R), C(1), data(_R, std::vector<Tp>(1)) {
for (int i = 0; i < _R; i++)
data[i][0] = generator(i);
}
Matrix(int _R, int _C)
: R(_R), C(_C), data(_R, std::vector<Tp>(_C)) {}
Matrix(int _R, int _C, std::function<Tp()> &&generator)
: R(_R), C(_C), data(_R, std::vector<Tp>(_C)) {
for (int i = 0; i < _R; i++)
for (int j = 0; j < _C; j++)
(*this)(i, j) = generator();
}
Matrix(int _R, int _C, std::function<Tp(int, int)> &&generator)
: R(_R), C(_C), data(_R, std::vector<Tp>(_C)) {
for (int i = 0; i < _R; i++)
for (int j = 0; j < _C; j++)
(*this)(i, j) = generator(i, j);
}
Matrix(std::vector<std::vector<Tp>> &&_data) {
assert(_data.size() > 0);
R = _data.size();
assert(_data[0].size() > 0);
C = _data[0].size();
data = std::forward<std::vector<std::vector<Tp>>>(_data);
}
Matrix(const std::vector<Tp> &_data) {
assert(_data.size() > 0);
R = _data.size(), C = 1;
data.resize(R, std::vector<Tp>(1));
for (int i = 0; i < R; i++)
data[i][0] = _data[i];
}
public:
inline Tp &operator()(int _r, int _c) {
return data[_r][_c];
}
inline const Tp &operator()(int _r, int _c) const {
return data[_r][_c];
}
Matrix operator+(const Matrix &another) const {
assert(R == another.R && C == another.C);
Matrix result(R, C);
for (int i = 0; i < R; i++)
for (int j = 0; j < C; j++)
result(i, j) = (*this)(i, j) + another(i, j);
return result;
}
Matrix &operator+=(const Matrix &another) {
assert(R == another.R && C == another.C);
for (int i = 0; i < R; i++)
for (int j = 0; j < C; j++)
(*this)(i, j) += another(i, j);
return (*this);
}
Matrix operator-(const Matrix &another) const {
assert(R == another.R && C == another.C);
Matrix result(R, C);
for (int i = 0; i < R; i++)
for (int j = 0; j < C; j++)
result(i, j) = (*this)(i, j) - another(i, j);
return result;
}
Matrix &operator-=(const Matrix &another) {
assert(R == another.R && C == another.C);
for (int i = 0; i < R; i++)
for (int j = 0; j < C; j++)
(*this)(i, j) -= another(i, j);
return (*this);
}
Matrix operator*(Tp k) const {
Matrix result(*this);
for (int i = 0; i < R; i++)
for (int j = 0; j < C; j++)
result(i, j) *= k;
return result;
}
Matrix &operator*=(Tp k) {
for (int i = 0; i < R; i++)
for (int j = 0; j < C; j++)
(*this)(i, j) *= k;
return (*this);
}
Matrix operator*(const Matrix another) const {
assert(C == another.R);
Matrix result(R, another.C);
for (int r = 0; r < R; r++)
for (int c = 0; c < another.C; c++)
for (int i = 0; i < C; i++)
result(r, c) += (*this)(r, i) * another(i, c);
return result;
}
public:
std::pair<int, int> size() {
return {R, C};
}
friend std::ostream &operator<<(std::ostream &out, const Matrix<Tp> &target) {
out << "[\n";
for (int i = 0; i < target.R; i++) {
out << " [";
for (int j = 0; j < target.C; j++)
out << target.data[i][j] << " ";
out << "\b]\n";
}
out << "]";
return out;
}
Matrix T() {
Matrix<Tp> result(C, R);
for (int i = 0; i < C; i++)
for (int j = 0; j < R; j++)
result(i, j) = (*this)(j, i);
return result;
}
};
class NeuralNetwork {
std::vector<Matrix<float>> weight, bias, value, zeta;
std::vector<int> topo;
std::function<float(float)> act_func, dact_func;
unsigned size;
public:
NeuralNetwork() = delete;
NeuralNetwork(const NeuralNetwork &) = default;
NeuralNetwork(NeuralNetwork &&) = default;
NeuralNetwork(std::vector<int> &&_topo, std::function<float(float)> _act_func, std::function<float(float)> _dact_func)
: topo(std::forward<std::vector<int>>(_topo)), act_func(std::forward<std::function<float(float)>>(_act_func)), dact_func(std::forward<std::function<float(float)>>(_dact_func)), size(topo.size()) {
std::default_random_engine random_engine(std::random_device{}());
std::normal_distribution<float> distributor(-1.0, 1.0);
auto random = [&]() -> float { return distributor(random_engine); };
weight.resize(size), bias.resize(size), value.resize(size), zeta.resize(size);
weight[0] = bias[0] = zeta[0] = value[0] = Matrix<float>(topo[0]);
for (int i = 1; i < size; i++) {
weight[i] = Matrix<float>(topo[i], topo[i - 1], random);
zeta[i] = value[i] = bias[i] = Matrix<float>(topo[i], random);
}
}
private:
void forward(const std::vector<float> &input) {
auto activate = [&](int value_index) -> void {
Matrix<float> &x = value[value_index], &z = zeta[value_index];
for (int i = 0; i < topo[value_index]; i++) x(i, 0) = act_func(z(i, 0));
};
value[0] = input;
for (int i = 1; i < size; i++) {
zeta[i] = weight[i] * value[i - 1] + bias[i];
activate(i);
}
}
void backward(const std::vector<float> &output, float learning_rate) {
Matrix<float> label(output);
Matrix<float> dx = value[size - 1] - label;
for (int i = size - 1; i > 0; i--) {
Matrix<float> db(dx);
for (int j = 0; i < topo[j]; j++)
db(j, 0) *= dact_func(zeta[i](j, 0));
Matrix<float> dW(db * value[i - 1].T());
dx = weight[i].T() * db;
weight[i] -= dW * learning_rate;
bias[i] -= db * learning_rate;
}
}
public:
std::vector<float> predict(const std::vector<float> &input) {
forward(input);
std::vector<float> result(topo[size - 1]);
for (int i = 0; i < topo[size - 1]; i++)
result[i] = value[size - 1](i, 0);
return result;
}
void fit(const std::vector<float> &input, const std::vector<float> &output, double learning_rate) {
forward(input);
backward(output, learning_rate);
}
};
int main() {
auto sigmoid = [](float x) -> float { return 1.0 / (1 + exp(-x)); };
auto dsigmoid = [sigmoid](float x) -> float { return sigmoid(x) * (1 - sigmoid(x)); };
NeuralNetwork nn({2, 3, 1}, sigmoid, dsigmoid);
for (int i = 0; i < 1000; i++) {
nn.fit({0, 0}, {0}, 0.5);
nn.fit({0, 1}, {1}, 0.5);
nn.fit({1, 0}, {1}, 0.5);
nn.fit({1, 1}, {0}, 0.5);
}
std::cout << nn.predict({0, 0})[0] << "\n";
std::cout << nn.predict({0, 1})[0] << "\n";
std::cout << nn.predict({1, 0})[0] << "\n";
std::cout << nn.predict({1, 1})[0] << "\n";
}