Algoritmia y Programación 1

Uninorte

M.Sc. Sebastian David Ariza Coll.

Contenido

Descripción del curso
Profesor (sobre mí)
Estudiantes (sobre ustedes)
Objetivo general del curso
Contenido del curso
Calificaciones
Textos de referencia

Descripción del curso

Nombre: Algoritmia y Programación I

NRC:

Créditos: 3

Profesor (sobre mí)

Ing. Sebastian David Ariza Coll, M.Sc.

Ingeniero de Datos en Gases del Caribe

Temas de investigación:

Inteligencia artificial (Machine Learning)
Weather Forecasting
Data Assimilation

Email: sdariza@uninorte.edu.co

Objetivo general del curso

Desarrollar la lógica y el pensamiento analítico y sistémico para resolver problemas básicos de ingeniería mediante el diseño de algoritmos y su codificación en un lenguaje de programación.

Contenido I

Introducción a la teoría de algoritmos

¿Qué es un algoritmo?
Algoritmos de la vida diaria.
Pasos para la elaboración de un algoritmo.
Conceptos básicos:
- Variables, tipos de datos, operadores.

El uso del celular está restringido.

Introducción a la teoría de algoritmos

¿Algoritmo?

Durante la infancia, desarrollamos las bases de nuestra estructura lógica mediante interacciones con el entorno. Una vez establecida esta lógica, la utilizamos para llevar a cabo procesos cotidianos, tanto conscientes como inconscientes, desde operaciones matemáticas hasta actividades como hablar, leer y caminar.

Asimismo, estos procesos están formalizados en algoritmos, representaciones conscientes de la lógica que nos guían en nuestras acciones. Los algoritmos nos permiten describir los procesos de manera que cualquier persona, incluso sin conocimiento previo, pueda llevarlos a cabo con éxito.

¿Qué es un algoritmo?

Definición formal: "Un algoritmo es un conjunto de pasos lógicos sin ambigüedad que permiten la realización de un proceso en un tiempo finito".

Por ejemplo: tome la operación aritmética formal de la suma. Suponga que desea sumar dos número. ¿Qué cree que debe hacer?

Lo anterior parece un proceso lógico, ¿cierto? Tenga presente que todos los algoritmos lo son. Una vez formalizado el proceso lógico para la realización de una tarea, este puede ser entendido en forma fácil por cualquier persona.

Sin embargo el proceso para la formulación de la lógica es lo que resulta inicialmente difícil en el aprendizaje de los algoritmos.

Algoritmos en la vida diaria

Suponga que usted está frente a una escalera y desea ascender hasta llegar al final. ¿Qué haría usted? Es decir, ¿cuál es el proceso lógico que debe realizar para alcanzar su objetivo?

La forma detallada de analizar todos los eventos es lo que conforma un algoritmo.

Algoritmos en la vida diaria

Tomemos otro ejemplo, suponga ahora que usted desea beber un vaso con agua. ¿Cuál sería el algoritmo?

Algoritmos en la vida diaria

Del ejemplo anterior, note que el solo hecho de dirigirse a la nevera es un proceso mucho más complejo que el de subir una escalera. Ya que el desplazamiento dependerá de cuán alejado se esté de la nevera y hayan más obstáculos que nos separen de ella.

Un algoritmo consta de 3 secciones principales

Entrada: introducción de datos para ser transformado
Proceso: conjunto de operaciones a realizar para dar solución a un problema.
Salida: Resultados obtenidos a través del proceso.

Entrada

Proceso

Salida

Algoritmos en la vida diaria

Ejercicios propuestos

Escriba los algoritmos necesarios para realizar los siguientes procesos:

Cambiar la llanta a un automóvil.
Escribir la letra E en un papel.
Preparar una limonada.
Calcular 10 elevado a 10.
Cenar.
Seleccionar un lugar a dónde ir.

Pasos para la elaboración de un algoritmo

La elaboración de un algoritmo es un proceso sistemático que implica varios pasos clave para asegurar que el resultado final sea claro, eficiente y efectivo.

Definición del problema.
Análisis del problema.
Diseño del algoritmo.
Desarrollo del algoritmo.
Cumplir con los requisitos clave.

Tipos de datos

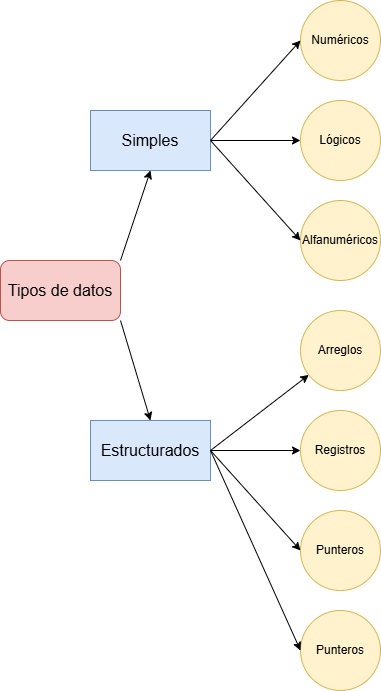
Variables

Almacenador de datos que pueden cambiar o no durante el transcurso del algoritmo.
Se identifican por su nombre y guardan un dato de los descritos en el anterior slide.
El nombre debe ser representativo a lo almacenado y se sugiere que los nombres no sean extensos.

Variables

Cada vez que se necesite realizar un proceso es necesario conocer:

¿Cuál es el proceso?
Los datos que se necesitan para la realización de dicho proceso.
¿Qué se debe obtener de estos datos? (Finalidad)

Sin embargo todos estos elementos son almacenados en memoria. Similar a nosotros, los sistemas de computación poseen una memoria electrónica, lugar en el cual pueden almacenar sus procesos, datos e información generada.

Imagínese esa memoria como una serie de casillas, cada una de las cuales tiene asociada una posición de la memoria.

Debido a que usted está en la capacidad de cambiar el valor almacenado dentro de cada casilla en cualquier momento, a estas casillas se les denomina variables. Con lo que una variable es una posición de memoria en el computador en el cual puede almacenar un dato o una información.


50

30
20

'casa'

vec[1] = 1
vec[2] = 10
vec[3] =2

'0'

Variables

Para facilitar el manejo de estas variables, a cada una de ellas se les asocia un nombre o identificador, el cual tiene unas reglas que se detallan a continuación:

Deben comenzar con una letra
La primera letra debe ser seguida por letras o dígitos, cero o más veces.
El caracter " " no es ni letra ni dígito, por lo que no puede formar parte de ningún nombre de variable. Es decir el nombre de una variable necesariamente debe ser una sola palabra.

Ejemplos:

Nombre de variable	Validez
A
A123C
A BVC
NUM-X
sw

Ejercicios propuestos

Determine cuál de los siguientes elementos son o no nombres válidos para variables

Nombre de variable	Validez
123AXT
LadoX
--XYX
A*VA
NUM

Estructuras algorítmicas secuenciales

Primitiva Inicio - Fin

Inicio

... Proceso lógico

Fin

Primitiva de asignación o adjudicación de datos

variable <-- valor

<--

Primitiva de entra y salida

LEA v1, V2, V3, ... , Vn
ESCRIBA  valor_a_escribir

Inicio: comienzo de ejecución.

Fin: El conjunto de pasos lógicos ha terminado.

Indica que el valor va a ser almacenado en la variable

LEA: nos permite almacenar datos del teclado en las variables.

Escriba: nos permite mostrar el valor almacenado en las variables

Pseudocódigo - Primitivas básicas

Entrada

Proceso

Salida

LEA

ESCRIBA

Diagrama Entrada, Proceso y salida - Primitivas básicas

¿Qué datos necesito?

¿Qué procedimiento debo seguir?

¿Qué resultados son los esperados?

Entrada

Proceso

Salida

LEA

ESCRIBA

Un estudiante desea conocer el diagrama de entrada, proceso y salida para poder calcular su promedio en las 4 evaluaciones realizadas de una asignatura.

\frac{nota1 + nota2 + nota3 + nota4}{4}

nota1

nota2

nota3

nota4

promedio

Diagrama - Primitivas básicas

Entrada

Proceso

Salida

LEA

ESCRIBA

El estudiante ahora desea conocer el diagrama de entrada, proceso y salida para poder calcular el área de un cuadrado.

Diagrama - Primitivas básicas

Operadores

Aritméticos: Permiten la realización de operaciones matemáticas con los valores de las variables y de las constantes.

Símbolo	Nombre del operador aritmético
+	Suma
-	Resta
*	Multiplicación
/	División
Mod ó %	Módulo (Residuo de la división)
/ ó div	División parte entera
** ó ^	Exponenciación

7/2 = 3.5 \\ 12 \% 7 = 5\\ 1+1=2\\ 4-5 = -1\\ 6 //1 5= 0

Ejemplos

Son elementos que relacionan los datos de una o más variables y/o constantes. Es decir, los operadores permiten hacer cálculos con los datos. Estos pueden ser: aritméticos, de relación y lógicos.

Precedencia de operadores aritméticos

Todas las expresiones entre paréntesis se realizan primero. Además, las expresiones con paréntesis anidados se deben realizar de adentro hacia afuera. Es decir, el paréntesis más interno se ejecuta primero.
Dentro de una misma expresión, los operadores se evalúan en el siguiente orden:

Paréntesis.
Exponenciación.
Multiplicación, división, mod, div.
Suma y Resta.

Las operaciones en una misma expresión con igual nivel de prioridad se evalúan de izquierda a derecha.

Ejemplos

Realice un algoritmo para calcular la suma de dos números reales.
Realice un algoritmo para leer un número cualquiera y calcule su cuadrado.
Realice un algoritmo para calcular el área y perímetro de un cuadrado en metros cuadrados, dada la longitud de su lado en cm.
Realice un algoritmo para leer el nombre, la edad, el número de horas trabajadas, el número de horas extras y el valor de la hora de un empleado. Asimismo, calcule cuánto se le debe pagar, si la hora extra tiene un recargo de un 20% de la hora normal.
Realice un algoritmo para calcular el promedio de 3 números enteros.
Realice un algoritmo para calcular el área de un círculo.

Operadores relacionales

Símbolo	Significado del operador relacional
>	Mayor que (estrictamente)
<	Menor que (estrictamente)
>=	Mayor o igual que
<=	Menor o igual que
<>	Es diferente
=	Es igual a

a <-- 10
b <-- 20
c <-- 34

¿Cuál de las siguientes operaciones es correcta?

a + b > 100

a - b < c

a - b = c

a * b <> c

a (a div 10) * 10 >= 100

Lógica

Tendencia innata de las personas a razonar de manera lógica.
Esquema mental que ayuda a determinar si un razonamiento es válido o no.
Análisis de las técnicas y principios necesarios para diferenciar entre razonamientos correctos e incorrectos.

Se utilizan en las instrucciones condicionales que dan como resultado verdadero o falso.

Los operadores lógicos son: AND, OR, y NOT, y su prioridad es: NOT, AND, OR.

Operadores lógicos

Lógica proposicional - Matemática

Estudio de las técnicas empleadas para verificar si un razonamiento es acertado o erróneo.

¿Qué es una proposición?

Es una afirmación que puede ser verdadera o falsa.

Ejemplos de proposiciones

2 es mayor que 3.
Hoy no lloverá.
9 es un número entero impar.
La semana tiene 7 días.
Todos los carros son automáticos.

Ejemplos que NO son proposiciones

Llama al doctor.
La camisa amarilla.
Vete.
¿Cómo estás?

Por simplicidad, las proposiciones son representadas por letras

tales como: p, q, v, s, t, ...

Proposiciones

p: Llueve

q: Iré al concierto

Operadores lógicos

Negación (NO): !, ~, /, ¬, `
Conjunción (y):
Disyunción (o):
Entonces (condicional):
Si y solo si (Bicondicional):

\lor

\land

\rightarrow

\iff

Ejemplos - Negación

p: Iré al bloque J.

q: Iré a la U.

r: 9 es un número entero impar.

s: La semana tiene 7 días.

t: Mañana es festivo.

l: No está lloviendo

¬p:

¬q:

!r:

~s:

¬t:

l ¿?

¬p, también se lee como es falso que p

Ejemplos - Conjunción:

p: Iré al bloque J.

q: Iré a la U.

r: 9 es un número entero impar.

s: La semana tiene 7 días.

t: Mañana es festivo.

l: No está lloviendo

\land

Ejemplos - Disyunción:

p: Iré al bloque J.

q: Iré a la U.

r: 9 es un número entero impar.

s: La semana tiene 7 días.

t: Mañana es festivo.

l: No está lloviendo

\lor

Tablas de verdad - Conjunción

p: Iré al bloque J.

q: Iré a la U.

p	q	p q
verdadero	Verdadero
Verdadero	Falso
Falso	Verdadero
Falso	Falso

Conclusión:

\land

Tablas de verdad - Disyunción

p: Iré al bloque J.

q: Iré a la U.

p	q	p q
verdadero	Verdadero
Verdadero	Falso
Falso	Verdadero
Falso	Falso

\lor

Conclusión:

Ejemplos operadores lógicos

a <-- 10
b <-- 20
c <-- 34
(a < b) and (b < c)

----------------------------

x <-- True
y <-- False

NOT (x or y) and x

----------------------------

En algunos lenguajes de programación es incorrecto definir intervalos de esta manera: a < b < c.

Lo correcto es usar operadores lógicos como conector de dos expresiones: a <b and b <c

Primitiva para bloques condicionales NO repetitivos

SI (condición es verdadera) ENTONCES
	Instrucción 1
    Instrucción 2
	Instrucción 3
	...
	Instrucción n
SINO
	Instrucción 1
    Instrucción 2
	Instrucción 3
	...
	Instrucción m
Fin

Primitiva bloque condicional modificada (Dependiendo de)

DD expresión HAGA
	VALOR1: BLOQUE DE INSTRUCCIÓN 1
	VALOR2: BLOQUE DE INSTRUCCIÓN 2    
    ...
	VALORn: BLOQUE DE INSTRUCCIÓN n
	Ow:
    	Bloque de instrucciones
    
FIN-DD

Ejercicio

En un centro de copiado, se puede realizar impresiones y/o fotocopias de documentos. Cada impresión tiene un costo de $300 pesos. Al valor total de las impresiones se le debe sumar un impuesto como sigue:

Realice un algoritmo para calcular el valor a pagar de un usuario.

Valor total	%
Desde 3000 hasta 10000	2%
Desde 10001 hasta 20000	5%
Desde 20001 hasta 30000	10%
Mayor a 30000	15%

Ejercicio

La nota definitiva de AYP1 depende 4 notas según lo siguiente

Nota	%
1	30%
2	25%
3	30%
4	15%

Realice un algoritmo para calcular la nota definitiva de un estudiante.

Bloques condicionales repetitivos

Primitivas procesos repetitivos

MQ (condición) HAGA
	Instrucción 1
	Instrucción 2
    ...
	Instrucción n
FIN-MQ

Primitiva mientras que

Lógicamente esta primitiva verifica la condición que controla el ciclo y las instrucciones encerradas dentro de la estructura son ejecutadas MIENTRAS QUE la condición se cumpla, o sea mientras el valor lógico de esta sea verdadero.

Ejercicio

Imprima los números enteros del 1 al n

Ejercicio

Imprima todos los números pares del 1 al n

Ejercicio

Imprima todos los números del 1 al n que sean múltiplos de 5

Ejercicio

Imprima todos los dígitos de un número entero de derecha a izquierda

Ejercicio

La nota definitiva de AYP1 depende 4 notas según lo siguiente

Nota	%
1	30%
2	25%
3	30%
4	15%

Realice un algoritmo para que dado n estudiantes se calcule su respectiva nota final.

Ejercicio

Realice un algoritmo para convertir un número entero de base x a base y.

Donde: 1<x<11, 1<y<11

Ejercicio

Realice un algoritmo para gestionar las ganancias en el centro de copiado.

Valor total	%
Desde 3000 hasta 10000	2%
Desde 10001 hasta 20000	5%
Desde 20001 hasta 30000	10%
Mayor a 30000	15%

Ejercicio

Determine si un número es primo

Primitiva cíclica con base en un contador

Esta primitiva cíclica trabaja con base en una variable contador, la cual va a cambiar dentro de un rango posible de valores que es especificado como parte de la estructura.

Además se conoce el número de veces que esta se ejecuta.

PARA (contador <-- <V.inicial>, <V.final>, <inc>) HAGA
	Instrucción 1
	Instrucción 2
    ...
	Instrucción n
FIN-PARA

Primitiva Haga Hasta

A diferencia con el MQ, las instrucciones dentro del ciclo se ejecutan mínimo 1 vez.

HH
	Instrucción 1
	Instrucción 2
    ...
	Instrucción n
FIN-HH(condición)

Arreglos unidimensionales

Variables arreglo

En las secciones anteriores se ha venido trabajando con base en variables que solo pueden almacenar un valor. Las variables arreglos tienen como característica principal el hecho que pueden almacenar un gran número posibles de valores, con la única restricción que todos ellos deben ser necesariamente del mismo tipo.

Para diferenciar cada uno de los valores que estén almacenados en una variable arreglo, estos son numerados y su posición es indicada mediante un índice como parte del nombre de la variable.

Manejo de vectores

Dependiendo del número de subíndices asociados a las variables arreglo, estas se clasifican en uni, bi, o n-dimensional.

Los arreglos de una dimensión son comúnmente llamados Vectores, los cuales a nivel interno, se encuentran en una secuencia lineal de variables simples, por lo que también se les llama Arreglos lineales. A estos arreglos se les referencia colocando el nombre del vector, seguido de un par de paréntesis donde está guardado el índice que designa la variable del arreglo a referenciar.

Es decir, su sintaxis es:

Vec(i) ó Vec[i]

Donde:

Vec: es el nombre del vector.

i: variable que referencia la posición i-ésima del vector.

34	565	453	13	4	892	88	86	23	3

Representación visual

1 2 3 4 5 6 7 8 9 10

Se tiene un vector con:

10 elementos
Es de tipo entero
El nombre es a
i referencia la posición sobre a

Lectura de un vector unidimensional

INICIO
	ENTERO vec = []
	LEA N
        PARA(i = 0, N-1, 1) HAGA
            LEA vec(i)
        FIN-PARA
FIN

Escritura de un vector unidimensional

INICIO
	ENTERO vec = []
	LEA N
        PARA(i = 0, N-1, 1) HAGA
            LEA vec(i)
        FIN-PARA
        
        PARA(i = 0, N-1, 1) HAGA
            ESCRIBA vec(i)
        FIN-PARA
FIN

Ejercicios

- Lea un vector de n elementos e indique el valor de la suma de todos los valores del mismo.

- Sea un vector "v" de n elementos, desarrolle un algoritmo que encuentre el mayor elemento.

- Sea un vector "x" de n elementos, desarrolle un algoritmo que lo ordene de forma ascendente: https://www.chrislaux.com/miscsort

- Sean 2 vectores "a" y "b", desarrolle un algoritmo que calcule la operación a + b si es posible.

- Sean 2 vectores "a" y "b" de dimensión n, realice un algoritmo que calcule

- Desarrolle un programa que acepte la entrada de un vector con N elementos. Luego, realice una inversión de todos los elementos de tal manera que el primer elemento pase a ser el último, el último se convierta en el primero, el segundo elemento se coloque en la posición penúltima, y así sucesivamente hasta completar la reordenación de todos los elementos.

- Haga un algoritmo para almacenar en un vector x los factores primos de un n dado.

a \cdot b

Ejercicio propuesto

En una carrera de 12 caballos enumerados del 1 al 12 se registran en un vector c todas las vueltas de la carrera realizada por cada uno de los caballos, en un vector t (paralelo al c) se registran los tiempos en segundos para cada carrera registrada en c en el mismo orden con que se ingresan en c. Realice un pseudocódigo para determinar:

1. ¿Qué caballo fue el ganador de las carreras?

2. ¿Cuál es el tiempo promedio para el ganador de las carreras?

3. Indique para los 10 primeros puestos el número del caballo y el tiempo promedio de sus carreras.

4. ¿Cuál fue el promedio de los tiempos en general?

Ejercicio propuesto

Dado un vector v con n elementos, realice un algoritmo para eliminar el elemento x si existe.

Suponga que el vector NO tiene elementos repetidos

3	4	5	23	45	245	2	1	10

1	2	3	4	5	6	7	8	9

Vector de entrada

3	4	5	23	45	245	1	10

1	2	3	4	5	6	7	8

Vector resultante, si x = 2