Compiladores

Compilador

Compilador

Programa objeto

Errores generados

Programa fuente

  • Compilador: programa que toma como entrada un programa escrito en lenguaje fuente, y lo traduce en un programa objeto equivalente.

 

Durante este proceso, el compilador informa al usuario si hay errores en el programa fuente para su respectivo ajuste.

Estructura del lenguaje fuente

Preprocesador

Contexto de un compilador

Programa fuente

Compilador

Programa objeto en lenguaje ensamblador

Ensamblador

Código de máquina relocalizable

Editor de carga y enlace

Código de máquina absoluto

Biblioteca, archivos objetos relocalizables

Fases del compilador

  • Etapa de análisis
    • Análisis lineal o léxico o lexicográfico.
    • Análisis sintáctico o Jerárquico.
    • Análisis semántico.
  • Etapa de Síntesis
    • Generación de código intermedio.
    • Optimización de código.
    • Generación de código objeto

Fases del compilador

  • Etapa de análisis
    • Análisis lineal o léxico o lexicográfico:
      • La cadena de caracteres que constituye el programa fuente se lee de izquierda a derecha y de arriba hacia abajo.
      • Los caracteres leídos se agrupan en componentes léxicos (tokens) que son secuencia de caracteres con un significado colectivo.
      • La secuencia de caracteres que forman un token se denomina lexema del token.
      • Se eliminan los espacios en blanco, tabulaciones, y comentarios.

Fases del compilador

  • Etapa de análisis
    • Análisis sintáctico o Jerárquico:
      • ​Los componentes léxicos (tokens) se agrupan jerárquicamente en colecciones anidadas con un significado colectivo.
      • Se construye un árbol sintáctico. Si NO se logra construir el árbol, se presenta un error sintáctico.
      • Se utilizan reglas recursivas para la construcción jerárquica.

Fases del compilador

  • Etapa de análisis
    • Análisis semántico:
      • ​Se realizan revisiones para asegurar que los componentes de un programa se ajustan de un modo significativo.
      • Se lleva a cabo la verificación de tipos en el uso de datos y variables.

Fases del compilador

  • Etapa de síntesis
    • Generación de código intermedio:
      • ​Representación intermedia del programa fuente.
      • Se realizará mediante código de tres direcciones, cada posición de memoria actúa como un registro.​
      • Código de tres direcciones:
        1. Cada instrucción tiene máximo 3 operadores.
        2. Tiene máximo 1 operador, además de la asignación.
        3. Se generan nombres temporales para guardar cálculos.
        4. Algunas instrucciones tienen menos de 3 operandos.

Fases del compilador

  • Etapa de síntesis
    • Optimización de código:
      • ​Mejora el código intermedio, de tal forma que el código se ejecute más rápido.
      • Una forma de mejorarlo es utilizando una instrucción para cada operador en le representación de árbol después del análisis semántico.
      • Todas las instrucciones quedan en formato de código de 3 direcciones.

Fases del compilador

  • Etapa de síntesis
    • Generación de código objeto:
      • ​Generar código de máquina relocalizable o código ensambaldor.

Análisis léxico

  • Primera fase de un compilador.
  • Proceso en el que se leen los caracteres de entrada suminstrados por un programa fuente y elabora una secuencia de componentes léxicos que toma el analizador sintáctico para hacer el análisis

¿Qué es un análisis léxico?

Analizador Léxico

Analizador sintáctico

Tabla de símbolos

Programa fuente

Ejemplo

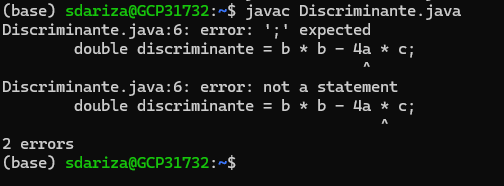
Programa fuente

Cáculo del descriminante de una ecuación cuadrática

Errores léxicos:

Componetes Léxicos, Patrones y Lexemas

Componente Léxico Lexemas de ejemplos Descripción del patrón o regla
za1d, xyw_1, user1
45, 4243, 353
+
-
if
for
<

Especificación de Componentes Léxicos

  • Alfabeto
    • Conjunto finito de símbolos
    • Denotado por 
\Sigma

Ejemplos

\Sigma_1 = \left\{0,1\right\}
\Sigma_2 = \left\{0,1,2,3, \cdots, 9\right\}
\Sigma_3 = \left\{a, b, c, \cdots, z\right\}

Especificación de Componentes Léxicos

  • Cadena
    • Secuencia finita de símbolos tomados de un alfabeto 

Ejemplos

\Sigma_1 = \left\{0,1\right\} s_1 = ``1010" \quad s_2 = ``101010" \quad s_3 = ``01010"
\Sigma_2 = \left\{0,1,2,3, \cdots, 9\right\} \quad t_1 = ``2411" \quad t_2 = ``1135010" \quad t_3 = ``99120"
\Sigma_3 = \left\{a, b, c, \cdots, z\right\} \quad f_1=``asc" \quad f_2 = ``hola"
\Sigma

Especificación de Componentes Léxicos

  • Longitud de una cadena |s|
    • Número de apariciones de símbolos en una cadena

Ejemplos

s_1 = ``1010" \quad |s_1| = 4\\ t_3 = ``99120" \quad |t_3| = 5\\ f_1=``asc" \quad |f_1| = 3

Especificación de Componentes Léxicos

  • Cadena vacía
    • Representada por   , es una cadena especial de longitud cero. Es decir: 
\epsilon
|\epsilon| = 0

Especificación de Componentes Léxicos

  • Concatenación de dos cadenas
    • p y q son cadenas definidas en los alfabetos       y        o sobre el mismo alfabeto    . La concatenación    , es la cadena que resulta al añadir q a p.
\Sigma_1
\Sigma_2
\Sigma
pq
p =``hello" \quad q = ``world" \quad pq = ``helloworld"
|pq| = |x| + |y|

Especificación de Componentes Léxicos

  • Elemento Identidad de Concatenación
    • La cadena vacía es el elemento identidad de la concatenación.
p =``hello" \rightarrow p\epsilon = ``hello" = \epsilon p

Especificación de Componentes Léxicos

  • Concatenación como producto:
    • La concatenación se puede considerar como el producto de cadenas.

Especificación de Componentes Léxicos

  • Exponenciación de cadenas:
    • ​Si p es una cadena definida sobre un alfabeto. Entonces pp, ppp, pppp, etc. También lo estarán.
pp = p^2 \quad ppp = p^3, pppp = p^4
\rightarrow \underbrace{ppp \cdots p}_{\text{n-veces}} = p^n, n \in \mathbb{N}
\rightarrow p^0=\epsilon \rightarrow p^n = p ^ {n-1} p = pp ^ {n-1}
|p^n| = n |p|

Si p es una cadena definida en 

\Sigma_1

y q es una cadena definida en

\Sigma_2

o ambas cadenas están definidas en 

a qué será igual
\Sigma
\Sigma_1
|p^nq^m|/n \text{ y } m \in \mathbb{N}

Especificación de Componentes Léxicos

  • Partes de cadenas:​
    • ​Prefijo:
      • Cadena obtenida al retirar cero más símbolos desde la derecha de cualquier cadena.
         
p=``Compilador" \rightarrow

Especificación de Componentes Léxicos

  • Partes de cadenas:​
    • Sufijo:
      • Cadena obtenida al retirar cero más símbolos desde la izquierda de cualquier cadena.
         
p=``Compilador" \rightarrow

Especificación de Componentes Léxicos

  • Partes de cadenas:​
    • Subcadena:
      • ​Cadena resultante de eliminar un prefijo y un sufijo de la cadena.
      • Todo prefijo y sufijo es una subcadena, pero NO toda subcadena es un prefijo o sufijo.
p=``Compilador" \rightarrow

Especificación de Componentes Léxicos

  • Partes de cadenas:​
    • Prefijo, sufijo, subcadena propios de p:
      • ​Cualquier cadena s, donde s no es vacía. Además, s es un prefijo, sufijo o subcadena de p, donde p es diferente de s.
p=``Compilador" \rightarrow

Especificación de Componentes Léxicos

  • Partes de cadenas:​
    • Subsecuencia:​
      • ​Cualquier cadena formada por la eliminación de cero o más símbolos no necesariamente contiguos de una cadena.
p=``Compilador" \rightarrow

Especificación de Componentes Léxicos

  • Lenguaje
    • ​Cualquier conjunto de cadenas de un alfabeto

Ejemplos

L_1 = \left\{\right\}
L_2 = \left\{ \epsilon \right\}
L_3 = \left\{00, 01, 10, 1001, 1111\right\}

Especificación de Componentes Léxicos

  • Operaciones sobre lenguajes:​
    • Unión​
      • ​L y M son lenguajes, su unión se define:
L = \left\{a,b,c,d, \cdots, z\right\}\\ M = \left\{0,1,2,3, \cdots, 9\right\}\\ \rightarrow L \cup M =\left\{0,1,2,3, \cdots, 9, a,b,c,d, \cdots, z\right\}
L \cup M= \left\{x/ x \in L \vee x \in M\right\}

Ejemplo: sean

Especificación de Componentes Léxicos

  • Operaciones sobre lenguajes:​
    • Concatenación
      • ​L y M son lenguajes, su concatenación se define:
L = \left\{a,b,c,d, \cdots, z\right\}\\ M = \left\{0,1,2,3, \cdots, 9\right\}\\ \rightarrow LM =\left\{a0, a1, a2 ,\cdots, a9, b0, b1, b2 ,\cdots, b9, \cdots, z0, z1, z2 ,\cdots, z9\right\}
L M= \left\{xy/ x \in L \wedge y \in M\right\}

Ejemplo: sean

Especificación de Componentes Léxicos

  • Operaciones sobre lenguajes:​
    • Exponenciación
      • ​L es un lenguaje, su exponenciación se define:
L = \left\{a,b,c,d, \cdots, z\right\}\\ \rightarrow LL =\left\{aa, ab, ac ,\cdots, az, ba, bb, bc ,\cdots, bz, \cdots, za, zb, zc ,\cdots, zz\right\}\\ \rightarrow LL =\left\{a^2, ab, ac ,\cdots, az, ba, b^2, bc ,\cdots, bz, \cdots, za, zb, zc ,\cdots, z^2\right\}
L L= \left\{xy/ x \in L \wedge y \in L\right\} = L ^2 \\ \rightarrow L ^0 = \{\epsilon\}\\ \rightarrow L ^n = L^{n-1}L = LL^{n-1} / n \in \mathbb{N}\\

Ejemplo: sea

Especificación de Componentes Léxicos

  • Operaciones sobre lenguajes:​
    • Cerradura de Kleene
      • ​L es un lenguaje, su cerradura de Kleene se define:
L = \left\{a,b,c,d, \cdots, z\right\}\\ \rightarrow L^* = L^0 \cup L^1 \cup L^2 \cup \cdots \cup L^\infty\\ \rightarrow L^* = \left\{ \epsilon, a,b,c,d, \cdots, z ,a^2, ab, ac ,\cdots, az, ba, b^2, bc ,\cdots, bz, \cdots, za, zb, zc ,\cdots, z^2, \cdots \right\}
L ^ * = \bigcup_{i=0}^\infty L^i = L^0 \cup L^1 \cup L^2 \cup \cdots \cup L^\infty\\

Ejemplo: sea

Especificación de Componentes Léxicos

  • Operaciones sobre lenguajes:​
    • Cerradura positiva de Kleene
      • ​L es un lenguaje, su cerradura positiva de Kleene se define:
L = \left\{a,b,c,d, \cdots, z\right\}\\ \rightarrow L^+ = L^1 \cup L^2 \cup \cdots \cup L^\infty\\ \rightarrow L^+ = \left\{a,b,c,d, \cdots, z ,a^2, ab, ac ,\cdots, az, ba, b^2, bc ,\cdots, bz, \cdots, za, zb, zc ,\cdots, z^2, \cdots \right\}
L ^ + = \bigcup_{i=1}^\infty L^i = L^1 \cup L^2 \cup \cdots \cup L^\infty\\

Ejemplo: sea

Especificación de Componentes Léxicos

L ^ + = \bigcup_{i=1}^\infty L^i = L^1 \cup L^2 \cup \cdots \cup L^\infty\\

Quiz

L ^ * = \bigcup_{i=0}^\infty L^i = L^0 \cup L^1 \cup L^2 \cup \cdots \cup L^\infty\\

Calcular:

  • La equivalencia de 
  • La equivalencia de 

Si L es un lenguaje y además:

L ^ +
L ^ *

en función de

en función de

L ^ +
L ^ *

Especificación de Componentes Léxicos

  • De lo visto anteriormente:​
    • Ejercicios:
      1. ​​Sea p = "holaatodos" calcule |p|
      2. Indique 2 prefijos propios de "complicado"
      3. Sean                              y                   calcule 
        •  
        •  
        •  
      4. Sean                               y                                 calcule
        •  
        •  
        •  
        • ​​
        •  
        •  
L = \left\{a,e,i,o,u\right\}\\
A = \left\{0,1\right\}\\
L = \left\{a, b, c, \cdots , z\right\}\\
M = \left\{0,1, 2, \cdots, 9\right\}\\
LM^2
ML^*
L(L \cup M)
L(L \cup M)^*
M(L \cup M)^3
M^+
LA
AL
A \cup L

Especificación de Componentes Léxicos

\Sigma
r
L(r)
  • Expresiones regulares 
    • Norma o regla definida sobre un alfabeto    y a partir de la cual se generan las cadenas de un lenguaje L.
    • Si    es una expresión regular definida sobre    , entonces L(r) es el lenguaje generado por   
r
r

Especificación de Componentes Léxicos

  • Expresiones regulares 
    • Construcción:
      • Se van construyendo a partir de expresiones regulares más simples usando un método inductivo, de esta manera:

Caso Base:

  1.     es una expresión regular que representa al lenguaje
  2. Si     es un símbolo del      , entonces     es una expresión regular que designa al lenguaje 
\epsilon
\{\epsilon\}
a
\Sigma
a
\{a\}

Especificación de Componentes Léxicos

  • Expresiones regulares 
    • Construcción:
\boldsymbol{r}
\boldsymbol{s}
\Sigma_1

Suposición:

Si     y     son e.r. definidas en los alfabetos       y       , o definidas e el mismo      ; y además generan los lenguajes          y           , se induce que:

Paso inductivo:​

3.        es una e.r que genera 

4.       es una e.r que genera 

5.       es una e.r que genera 

\Sigma_2
\Sigma
\boldsymbol{L(r)}
\boldsymbol{L(s)}
r|s
L(r|s) = L(r) \cup L(s)
rs
L(rs) = L(r)L(s)
r^{*}
L(r^{*}) = (L(r))^{*}

Especificación de Componentes Léxicos

  • Expresiones regulares 
    • Construcción:

Ejemplos:

  1. Construye una e.r que genere los números binarios
  2. Construye una e.r que genere los números binarios pares.
  3. Construye una e.r que genere los números binarios impares.
  4. Para un                      , construye una e.r que genere las cadenas que finalicen en        , sin importar el prefijo de inicio. Ejemplo:
\Sigma = \{a, b\}
abb
abb, bbababaabb, abaabb, \dots

Especificación de Componentes Léxicos

  • Definiciones regulares

Una definición regular es darle nombre a una expresión regular con el fin de, por notación y facilidad, usarla en otra expresión regular.

Dado un alfabeto     , una definición regular (d.r.) es una secuencia de definiciones de  la forma:

\Sigma
d_1 \rightarrow r_1 \\ d_2 \rightarrow r_2 \\ \vdots \\ d_n \rightarrow r_n \\
d_i
r_i

: nombre distinto

: es una e.r. con los simbolos de 

\Sigma \cup \{d_1, d_2, \dots, d_{i-1}\}

Especificación de Componentes Léxicos

  1. Uno o más casos:
     
  2. Cero o un caso:
     
  3. Selección de un carácter del conjunto:
  • Definiciones regulares 
    • Abreviaturas de la notación
a^*a = aa^* = a^+
a|\epsilon = \epsilon |a = a?
𝑎|𝑏|𝑐|…|𝑧=[𝑎−𝑧] \\ 0|1|…|9=[0−9] \\ 𝑎|𝑏|𝑐|(…|𝑧|𝐴)|𝐵|𝐶|…|𝑍=[𝑎−𝑧𝐴−𝑍] \\ 𝑎|𝑏|𝑐|(…|𝑧|0)|1|2|…|9=[𝑎−𝑧0−9]

Especificación de Componentes Léxicos

  • Definiciones regulares 

Ejemplos:

Construye definiciones regulares para:

  1. Variables de un programa.
  2. Los números reales positivos.
  3. La identificación de un archivo, que consta de un nombre alfanumérico de cualquier longitud; seguido  por una extensión que contiene un punto(.), y máximo tres caracteres alfanuméricos.

Autómatas finitos

¿Que son autómatas finitos?

Cadena x

Autómata Finito

(Reconocedor)

Si

 

No

Reconocedor de un lenguaje: Programa que toma como entrada una cadena x y responde “si” si x es una frase que pertenece al lenguaje, y “no”, si no lo es.

A partir de una e.r., se construye un reconocedor utilizando un diagrama de transiciones llamado autómata finito

Autómatas finitos

  • Tipos de autómatas finitos

Tipo Memoria Complejidad Reconocimiento
Determinístico Menos Más complejos Más rápido
No determinístico Más Menos complejos Más lento

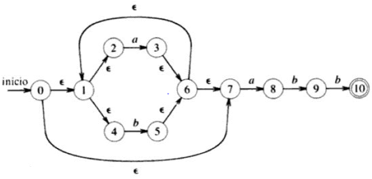
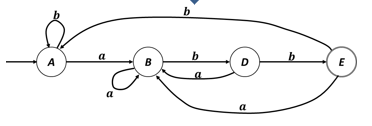
Autómata Finito Determinístico

Autómata Finito No Determinístico

Autómatas finitos

Autómata finito no determinístico (AFN)

Modelo matemático formado por una quíntupla

N = \{S, \Sigma, s_0, F, mueve(\delta)\}
  1.     : un conjunto de estados.
  2.     : un conjunto de símbolos de entrada (alfabeto).
  3.     : el estado de inicio o inicial.
  4.     : un conjunto de estados de finalización o de reconocimiento.
  5.                   : una función de transición que transforma pares estado-símbolos en conjuntos de estados.
S
\Sigma
s_0
F
mueve(\delta)
s_0 \in S
F \subseteq S

Autómatas finitos

Autómata finito no determinístico (AFN)

  • Función de transición mueve

Dado un conjunto S, el conjunto             se denomina Potencia de S y es el conjunto formado por todos los subconjuntos de S.

\mathcal{P}(S)
mueve: S \times \Sigma \rightarrow \mathcal{P}(S)
mueve(s,a) = S', S' \text{ está en } \mathcal{P}(S)

Ejemplo:

A = \{a,b,c\}
\mathcal{P}(S) = \{\emptyset, A, \{a\}, \{b\}, \{c\}, \{a,b\}, \{a,c\}, \{b,c\} \}
|A| = 3; |\mathcal{P}(S)| = 2^{|A|} = 8

Autómatas finitos

Autómata finito no determinístico (AFN)

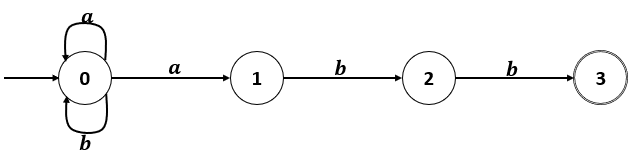
Se puede representar mediante un grafo dirigido etiquetado, llamado grafo de transiciones.

Ejemplo:

\text{Expresión regular: } (a|b)^* abb

Autómatas finitos

Autómata finito no determinístico (AFN)

Componentes del autómata

S = \{0,1,2,3\}
\Sigma = \{a,b\}
s_0 = 0
F=\{3\}
mueve(0,a) = \{0,1 \}
mueve(0,b) = \{0 \}
mueve(1,a) = \{\}
mueve(1,b) = \{2\}
mueve(2,a) = \{ \}
mueve(2,b) = \{3 \}
mueve(3,a) = \{\}
mueve(3,b) = \{\}

Autómatas finitos

Autómata finito no determinístico (AFN)

Tabla de Transiciones

Estado a b
0 {0,1} {0}
1 {} {2}
2 {} {3}
3 {} {}

Autómatas finitos

Autómata finito no determinístico (AFN)

Reconocimiento o Aceptación

Un AFN acepta una cadena de entrada x, si y solo si, existe algún camino en el grafo de transiciones, desde el estado de inicio hacia algún estado de aceptación, de tal forma que las etiquetas de las aristas a lo largo del camino deletreen a x.

El camino se realiza mediante transiciones llamadas movimientos.

Autómatas finitos

Autómata finito no determinístico (AFN)

Reconocimiento o Aceptación

Ejemplo:

Reconoce las cadenas 

abb,ababb,ababa

Autómatas finitos

Autómata finito Determinístico (AFD)

Modelo matemático formado por una quíntupla

D = \{S, \Sigma, s_0, F, mueve(\delta)\}
  1.     : un conjunto de estados.
  2.     : un conjunto de símbolos de entrada (alfabeto).
  3.     : el estado de inicio o inicial.
  4.     : un conjunto de estados de finalización o de reconocimiento.
  5.                   : una función de transición que transforma pares estado-símbolos en conjuntos de estados.
S
\Sigma
s_0
F
mueve(\delta)
s_0 \in S
F \subseteq S

Autómatas finitos

Autómata finito Determinístico (AFD)

  • Función de transición mueve

A diferencia del AFN, en el AFD, la función de transición mueve genera un solo estado de S, NO un conjunto.

El AFD se le considera un caso especial del AFN.

mueve: S \times \Sigma \rightarrow S
mueve(s,a) = s', s' \text{ está en } S

Autómatas finitos

Autómata finito Determinístico (AFD)

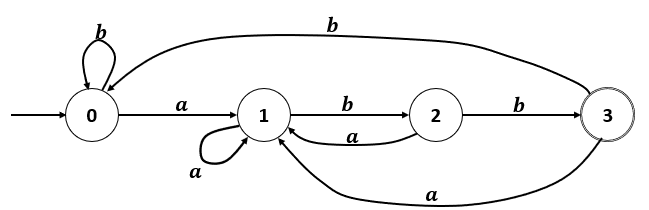
Se puede representar también mediante un  grafo de transiciones.

Ejemplo:

\text{Expresión regular: } (a|b)^* abb

Autómatas finitos

Autómata finito Determinístico (AFD)

Componentes del autómata

S = \{0,1,2,3\}
\Sigma = \{a,b\}
s_0 = 0
F=\{3\}
mueve(0,a) = 1
mueve(0,b) = 0
mueve(1,a) =1
mueve(1,b) = 2
mueve(2,a) = 1
mueve(2,b) =3
mueve(3,a) = 1
mueve(3,b) = 0

Autómatas finitos

Autómata finito Determinístico (AFD)

Tabla de Transiciones

Estado a b
0 1 0
1 1 2
2 1 3
3 1 0

Autómatas finitos

Autómata finito Determinístico (AFD)

Reconocimiento o Aceptación

El camino se realiza mediante transiciones llamadas movimientos.

Ejemplo:

Reconoce las cadenas 

abb,ababb,ababa

Autómatas finitos

Diferencias entre AFN y AFD

1. En un AFD, para cada estado s hay como máximo una arista etiquetada con un símbolo de entrada a que sale de s.

2. En un AFN puede haber aristas etiquetadas con la entrada    .

(a|b)^* abb

AFN

AFD

\epsilon

Autómatas finitos

Paso de una expresión regular a un AFN

Entrada: Una expresión regular     definida en un alfabeto    .

Salida: Un AFN      que acepte el lenguaje
 

  • Método de Thompson
r
\Sigma
N
L(r) = L(N)

Autómatas finitos

Paso de una expresión regular a un AFN

Caso Base:

  • Método de Thompson
\epsilon

1. Para la e.r    , el AFN es el siguiente:

a

1. Para la e.r    , el AFN es el siguiente:

\epsilon

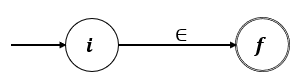
Este AFN reconoce {  }

a

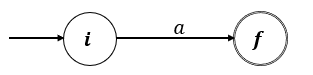
Este AFN reconoce {  }

Autómatas finitos

Paso de una expresión regular a un AFN

Suposición:

  • Método de Thompson
N(r)

Si           y           son AFNs para las e.r    y    respectivamente; además          y          son los lenguajes que reconocen respectivamente estas e.r.

N(s)
s
r
L(r)
L(s)

Reconoce a

Reconoce a

L(r)
L(s)

Autómatas finitos

Paso de una expresión regular a un AFN

Paso inductivo:

  • Método de Thompson

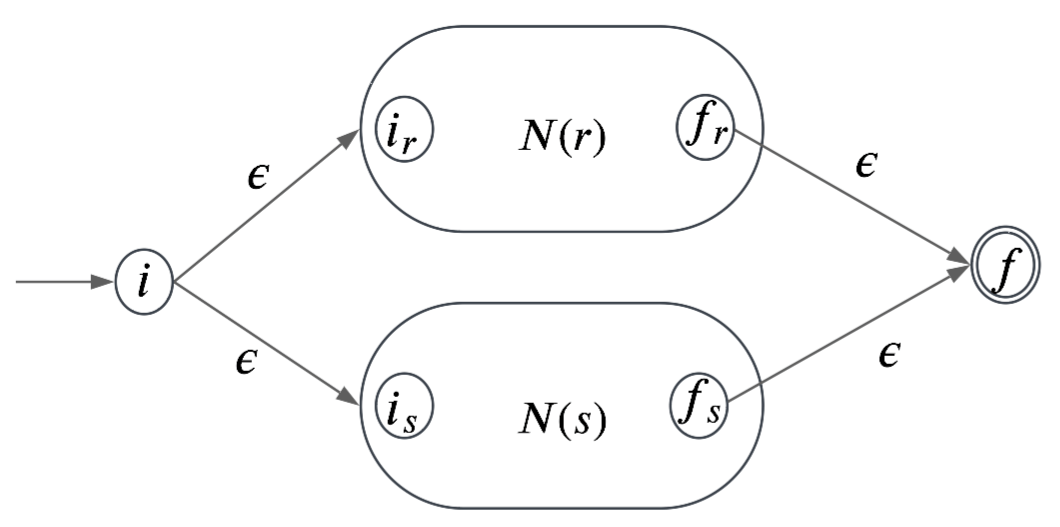
3. Para la e.r      , el AFN es el siguiente: 

r|s

Reconoce a

L(r|s) = L(r) \cup L(s)

Autómatas finitos

Paso de una expresión regular a un AFN

Paso inductivo:

  • Método de Thompson

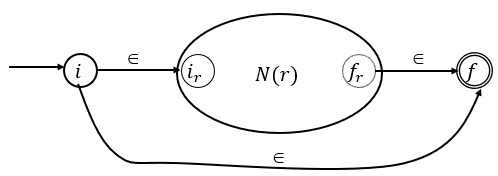
4. Para la e.r      , el AFN es el siguiente: 

rs

Reconoce a

L(rs) = L(r)L(s)

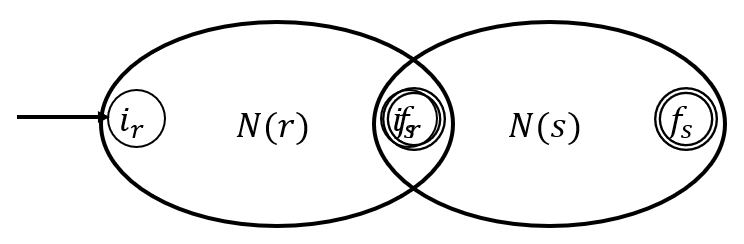
Autómatas finitos

Paso de una expresión regular a un AFN

Paso inductivo:

  • Método de Thompson

7. Para la e.r      , el AFN es el siguiente: 

r?

Reconoce a

L(r?) = L(r)?

Autómatas finitos

Paso de una expresión regular a un AFN

Paso inductivo:

  • Método de Thompson

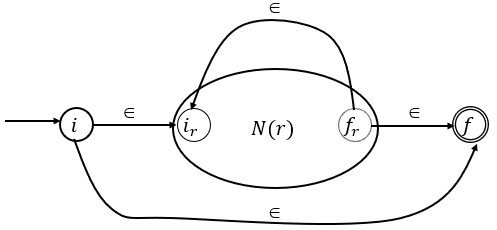
5. Para la e.r      , el AFN es el siguiente: 

r^*

Reconoce a

L(r^*) = (L(r))^* = L^*(r)

Autómatas finitos

Paso de una expresión regular a un AFN

Paso inductivo:

  • Método de Thompson

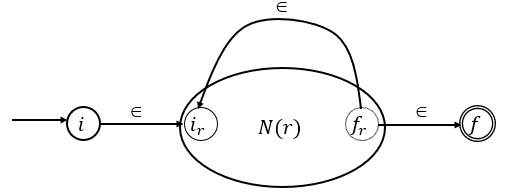
6. Para la e.r      , el AFN es el siguiente: 

r^+

Reconoce a

L(r^+) = (L(r))^+ = L^+(r)

Autómatas finitos

Paso de una expresión regular a un AFN

Ejemplos:

  • Método de Thompson

Construir el AFN para las expresiones regulares:

1. (a|b)^* abb
2. a(a|b)^* bb

Autómatas finitos

Paso de una expresión regular a un AFN

Ejemplos:

  • Método de Thompson

1. AFN para

(a|b)^* abb

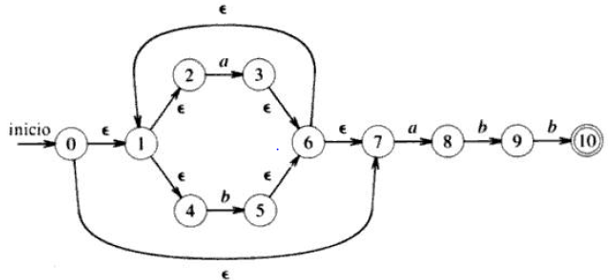
Autómatas finitos

Entrada: Un AFN      que acepte el lenguaje
 

Salida: Un AFD      no óptimo que acepte el mismo lenguaje.
 

  • Método de Subconjuntos
D
N
L(N)

Paso de un AFN a un AFD-No Óptimo

Autómatas finitos

Paso de un AFN a un AFD-No Óptimo

Operaciones sobre los estados del AFN.

cerradura- (s): Conjunto de estados del AFN alcanzables desde el estado     del AFN con transiciones     solamente.

Ejemplo:

  • Método de Subconjuntos
s
\epsilon
\epsilon
T = cerradura-\epsilon(0) = \{0,1,2,4,7\}

Autómatas finitos

Paso de un AFN a un AFD-No Óptimo

Operaciones sobre los estados del AFN.

mueve          :Conjunto de estados del AFN hacia los cuales hay una transición con el símbolo de entrada     desde algún estado    en      del AFN.

Ejemplo:

  • Método de Subconjuntos
a
(T,a)
T = cerradura-\epsilon(0) = \{0,1,2,4,7\}
s
T
A = mueve(T,a) = \{3,8\}
B = mueve(T,b) = \{5\}

Autómatas finitos

Paso de un AFN a un AFD-No Óptimo

  • Método de Subconjuntos
A = mueve(T,a) = \{3,8\}
B = mueve(T,b) = \{5\}

Operaciones sobre los estados del AFN.

cerradura- (T): Conjunto de estados del AFN alcanzables desde algún estado     del AFN con transiciones     solamente.

Ejemplo:

s
\epsilon
\epsilon
C = cerradura-\epsilon (A) = \{3,6,1,7,2,4,8\}
D = cerradura-\epsilon (B) = \{5,6,1,7,2,4\}

Autómatas finitos

Paso de un AFN a un AFD-No Óptimo

  • Método de Subconjuntos

Algoritmo de Subconjuntos

// Al inicio, cerradura-ε(s0) es el único estado dentro de estadosD y no está marcado
MIENTRAS QUE(haya un estado no marcado T en estadosD) HACER:
	marcar T;
    PARA cada símbolo de entrada a HACER:
    	U = cerradura-ε(mueve(T,a));
        SI U no está en estadosD:
        	añadir U como estado no marcado a estadosD;
        FIN-SI
        tranD[T,a] = U;
    FIN-PARA
FIN-MIENTRASQUE
Estado Símbolo(a) Símbolo(b)

tranD

Estado
Marca

estadosD

Paso de un AFN a un AFD-No Óptimo

  • Método de Subconjuntos

Algoritmo de Subconjuntos

// Al inicio, cerradura-ε(s0) es el único estado dentro de estadosD y no está marcado
MIENTRAS QUE(haya un estado no marcado T en estadosD) HACER:
	marcar T;
    PARA cada símbolo de entrada a HACER:
    	U = cerradura-ε(mueve(T,a));
        SI U no está en estadosD:
        	añadir U como estado no marcado a estadosD;
        FIN-SI
        tranD[T,a] = U;
    FIN-PARA
FIN-MIENTRASQUE
Estado Símbolo(a) Símbolo(b)

tranD

Estado
Marca

estadosD

// Al inicio, cerradura-ε(s0) es el único estado dentro de estadosD y no está marcado
MIENTRAS QUE(haya un estado no marcado T en estadosD) HACER:
	marcar T;
    PARA cada símbolo de entrada a HACER:
    	U = cerradura-ε(mueve(T,a));
        SI U no está en estadosD:
        	añadir U como estado no marcado a estadosD;
        FIN-SI
        tranD[T,a] = U;
    FIN-PARA
FIN-MIENTRASQUE
Estado Símbolo(a) Símbolo(b)
A B C
B B D
C B C
D B E
*E B C

tranD

Estado A B C D E
Marca - - - - -

estadosD

Ejemplo: Hallar el AFD de:

\begin{aligned} \mathbf{A} &= \textit{cerradura}-\epsilon(0) = \textcolor{blue}{\{0,1,2,4,7\}} \\ \mathbf{B} &= \textit{cerradura}-\epsilon(\textbf{mueve(A,a)}) = \textit{cerradura}-\epsilon \textbf{(\{3,8\})} = \textcolor{blue}{\{1,2,3,4,6,7,8\}} \\ \mathbf{C} &= \textit{cerradura}-\epsilon(\textbf{mueve(A,b)}) = \textit{cerradura}-\epsilon \textbf{(\{5\})} = \textcolor{blue}{\{1,2,4,5,6,7\}} \\ B &= \textit{cerradura}-\epsilon(\textbf{mueve(B,a)}) = \textit{cerradura}-\epsilon(\{3,8\}) \\ \mathbf{D} &= \textit{cerradura}-\epsilon(\textbf{mueve(B,b)}) = \textit{cerradura}-\epsilon \textbf{(\{5,9\})} = \textcolor{blue}{\{1,2,4,5,6,7,9\}} \\ B &= \textit{cerradura}-\epsilon(\textbf{mueve(C,a)}) = \textit{cerradura}-\epsilon(\{3,8\}) \\ C &= \textit{cerradura}-\epsilon(\textbf{mueve(C,b)}) = \textit{cerradura}-\epsilon(\{5\}) \\ B &= \textit{cerradura}-\epsilon(\textbf{mueve(D,a)}) = \textit{cerradura}-\epsilon(\{3,8\}) \\ \mathbf{E} &= \textit{cerradura}-\epsilon(\textbf{mueve(D,b)}) = \textit{cerradura}-\epsilon \textbf{(\{5,10\})} = \textcolor{blue}{\{1,2,4,5,6,7,10\}} \\ B &= \textit{cerradura}-\epsilon(\textbf{mueve(E,a)}) = \textit{cerradura}-\epsilon(\{3,8\}) \\ C &= \textit{cerradura}-\epsilon(\textbf{mueve(E,b)}) = \textit{cerradura}-\epsilon(\{5\}) \end{aligned}
Estado Símbolo(a) Símbolo(b)
A B C
B B D
C B C
D B E
*E B C

tranD

\begin{aligned} \mathbf{A} &= \textit{cerradura}-\epsilon(0) = \textcolor{blue}{\{0,1,2,4,7\}} \\ \mathbf{B} &= \textit{cerradura}-\epsilon(\textbf{mueve(A,a)}) = \textit{cerradura}-\epsilon \textbf{(\{3,8\})} = \textcolor{blue}{\{1,2,3,4,6,7,8\}} \\ \mathbf{C} &= \textit{cerradura}-\epsilon(\textbf{mueve(A,b)}) = \textit{cerradura}-\epsilon \textbf{(\{5\})} = \textcolor{blue}{\{1,2,4,5,6,7\}} \\ \mathbf{D} &= \textit{cerradura}-\epsilon(\textbf{mueve(B,b)}) = \textit{cerradura}-\epsilon \textbf{(\{5,9\})} = \textcolor{blue}{\{1,2,4,5,6,7,9\}} \\ \mathbf{E} &= \textit{cerradura}-\epsilon(\textbf{mueve(D,b)}) = \textit{cerradura}-\epsilon \textbf{(\{5,10\})} = \textcolor{blue}{\{1,2,4,5,6,7,10\}} \\ \end{aligned}

AFN

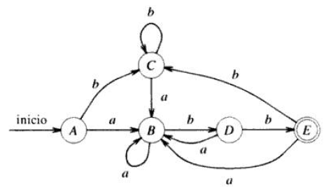
AFD-No Óptimo

Autómatas finitos

Paso de un AFN a un AFD-No Óptimo

  • Método de Subconjuntos

Algoritmo de Subconjuntos

Autómatas finitos

Entrada: Un AFD      No Óptimo que acepte el lenguaje
 

Salida: Un AFD      Óptimo que acepte el mismo lenguaje.
 

  • Método de Estados Significativos
D
D
L(D)

Paso de un AFD-No Óptimo a un AFD Óptimo

Autómatas finitos

Estado Significativo: Es un estado de un AFN que tiene transiciones de salida diferentes de    .

El                             , si     es significativo para algún     en     .

Ejemplo: En el AFN, cuáles son los estados significativos?

  • Método de Estados Significativos

Paso de un AFD-No Óptimo a un AFD Óptimo

\epsilon
mueve(s,a) \neq \emptyset
s
a
\Sigma

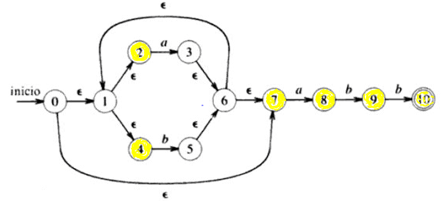
Estados Significativos={2,4,7,8,9,10}

Autómatas finitos

Identificamos los estados significativos para cada subconjunto encontrado en el método anterior y si dos subconjuntos tienen los mismos estados significativos, estos se pueden resumir en un único estado.

  • Método de Estados Significativos

Paso de un AFD-No Óptimo a un AFD Óptimo

\begin{aligned} \mathbf{A} &= \textit{cerradura}-\epsilon(0) = \textcolor{blue}{\{0,1,\textcolor{red}{2,4,7}\}} \\ \mathbf{B} &= \textit{cerradura}-\epsilon(\textbf{mueve(A,a)}) = \textit{cerradura}-\epsilon \textbf{(\{3,8\})} = \textcolor{blue}{\{1,\textcolor{red}{2},3,\textcolor{red}{4},6,\textcolor{red}{7,8}\}} \\ \mathbf{C} &= \textit{cerradura}-\epsilon(\textbf{mueve(A,b)}) = \textit{cerradura}-\epsilon \textbf{(\{5\})} = \textcolor{blue}{\{1,\textcolor{red}{2,4},5,6,\textcolor{red}{7}\}} \\ \mathbf{D} &= \textit{cerradura}-\epsilon(\textbf{mueve(B,b)}) = \textit{cerradura}-\epsilon \textbf{(\{5,9\})} = \textcolor{blue}{\{1,\textcolor{red}{2,4},5,6,\textcolor{red}{7,9}\}} \\ \mathbf{E} &= \textit{cerradura}-\epsilon(\textbf{mueve(D,b)}) = \textit{cerradura}-\epsilon \textbf{(\{5,10\})} = \textcolor{blue}{\{1,\textcolor{red}{2,4},5,6,\textcolor{red}{7},\textcolor{orange}{10}\}} \\ \end{aligned}
Estado a b
A B C
B B D
C B C
D B E
*E B C

Ejemplo:

Est_Sig(A)={2,4,7}

Est_Sig(B)={2,4,7,8}

Est_Sig(C)={2,4,7}

Est_Sig(D)={2,4,7,9}

Est_Sig(E)={2,4,7,10}

Estado a b
A B A
B B D
D B E
*E B A

tranD

Autómatas finitos

AFD Óptimo con Estados Significativos

  • Método de Estados Significativos

Paso de un AFD-No Óptimo a un AFD Óptimo

Estado a b
A B A
B B D
D B E
*E B A

tranD

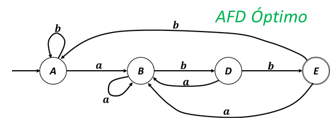
Autómatas finitos

  1. Construir un árbol sintáctico T para la e.r aumentada r#.
     
  2. Construir las funciones anulable, primerapos, ultimapos y siguientepos haciendo recorridos de abajo-arriba en T.
     
  3. Construir el conjunto de estados de D (estadosD) y la tabla de transiciones para D (tranD)
  • Método del Árbol Sintáctico

Paso de una e.r a un AFD Óptimo

Autómatas finitos

Al construir el AFN en el método de Thompson, se genera un estado significativo cuando un símbolo del alfabeto aparece en la e.r.

El AFN solo tiene un estado de aceptación, pero este estado no es significativo porque no tiene transiciones de salida.

Por esto se concatena un marcador # a la e.r. r, y se le da al estado de aceptación de r una transición con el símbolo #, convirtiéndolo en estado significativo del AFN para r#.

  • Método del Árbol Sintáctico

Paso de una e.r a un AFD Óptimo

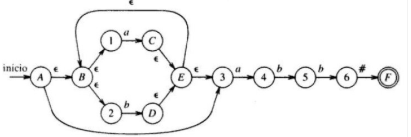
En la imagen, los estados significativos se representan en numeros. Cuando se realiza el reconocimiento, y la construcción está completa, cualquier estado del AFN con una transición en # debe ser estado de aceptación.​

Autómatas finitos

Una e.r aumentada r#, se representa mediante un árbol sintáctico con los siguientes tipos de nodos:

  • Método del Árbol Sintáctico

Paso de una e.r a un AFD Óptimo

Autómatas finitos

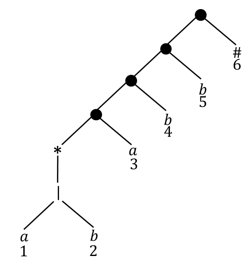
A cada hoja no etiquetada con    se le asocia una posición, que es un entero.

Un símbolo repetido en una e.r. tiene varias posiciones.

La posición de cada símbolo se puede identificar con la etiqueta del estado significativo en el AFN, como se observa en la figura. 

  • Método del Árbol Sintáctico

Paso de una e.r a un AFD Óptimo

\epsilon
r\# = (a|b)^* abb\#

1   2     3 4 5  6

Autómatas finitos

Ejemplo:

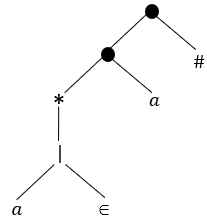
Para la e.r.               , construye el árbol sintáctico, y señala las posiciones tanto en la e.r como en el árbol. 

  • Método del Árbol Sintáctico

Paso de una e.r a un AFD Óptimo

(a|\epsilon)^* a

1           2  3

r\# = (a|\epsilon)^* a \#

1

2

3

Autómatas finitos

Funciones:

anulable(𝑛): Función booleana sobre un nodo 𝑛. El anulable será Verdadero si al aplicarlo sobre el nodo 𝑛, existe la posibilidad de generar la cadena vacía    en algún momento; o Falso si nunca la genera.

Ejemplo:

El anulable de las siguientes expresiones es: 

  • Método del Árbol Sintáctico

Paso de una e.r a un AFD Óptimo

\epsilon

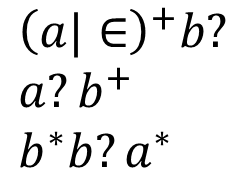
Verdadero: Es posible que la e.r genere la cadena vacía.

Falso: No es posible que sea vacía ya que b se repite 1 o mas veces

Verdadero: Es posible que la e.r genere la cadena vacía.

Autómatas finitos

Funciones:

𝑝𝑟𝑖𝑚𝑒𝑟𝑎𝑝𝑜𝑠(𝑛): Función sobre un nodo 𝑛 que devuelve el conjunto de posiciones que pueden concordar con el primer símbolo de una cadena generada por la sub-expresión regular con raíz en 𝑛.

Ejemplo:

El primerapos de las siguientes expresiones es: 

  • Método del Árbol Sintáctico

Paso de una e.r a un AFD Óptimo

(a|b)^* abb
primerapos = \{1, 2, 3 \}
a? b^+ ab^*
primerapos = \{1, 2\}
b^* b? a^*
primerapos = \{1, 2, 3\}

1     2         3  4   5 

 1       2       3  4   

 1     2      3  

ab^+ (a|b)^*
primerapos = \{1\}

 1  2           3     4  

Autómatas finitos

Funciones:

𝑢𝑙𝑡𝑖𝑚𝑎𝑝𝑜𝑠(𝑛): Función sobre un nodo 𝑛 que devuelve el conjunto de posiciones que pueden concordar con el último símbolo de una cadena generada por la sub-expresión regular con raíz en 𝑛.

Ejemplo:

El ultimapos de las siguientes expresiones es: 

  • Método del Árbol Sintáctico

Paso de una e.r a un AFD Óptimo

(a|b)^* abb
ultimapos = \{5\}
a? b^+ ab^*
ultimapos = \{3, 4\}
b^* b? a^*
ultimapos = \{1, 2, 3\}

1     2         3  4   5 

 1       2       3  4   

 1     2      3  

ab^+ (a|b)^*
ultimapos = \{2,3,4\}

 1  2           3     4  

Autómatas finitos

Reglas para resolver las funciones en los nodos

  • Método del Árbol Sintáctico

Paso de una e.r a un AFD Óptimo

Autómatas finitos

Reglas para resolver las funciones en los nodos

  • Método del Árbol Sintáctico

Paso de una e.r a un AFD Óptimo

Autómatas finitos

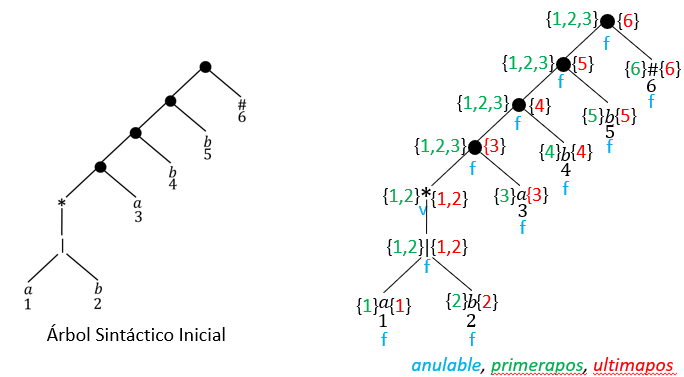
Ejemplo: 

𝑎𝑛𝑢𝑙𝑎𝑏𝑙𝑒, 𝑝𝑟𝑖𝑚𝑒𝑟𝑎𝑝𝑜𝑠 𝑦 𝑢𝑙𝑡𝑖𝑚𝑎𝑝𝑜𝑠 para

 

  • Método del Árbol Sintáctico

Paso de una e.r a un AFD Óptimo

(a|b)^* abb\#

Autómatas finitos

Cálculo del siguientepos:

  1. Si 𝑛 es un nodo-cat con hijo izquierdo      e hijo derecho     , 𝑖 es una posición dentro de 𝑢𝑙𝑡𝑖𝑚𝑎𝑝𝑜𝑠(   ), entonces todas las posiciones de 𝑝𝑟𝑖𝑚𝑒𝑟𝑎𝑝𝑜𝑠(   ) están en el 𝑠𝑖𝑔𝑢𝑖𝑒𝑛𝑡𝑒𝑝𝑜𝑠(𝑖).
  • Método del Árbol Sintáctico

Paso de una e.r a un AFD Óptimo

c_1
c_1
c_2
c_2
c_1 \cdot c_2
pp(c_1)
pp(c_2)
up(c_1)
up(c_2)
\{i, j, \dots\}
\{k, l, \dots\}

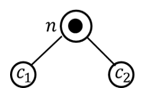
𝑠𝑖𝑔𝑢𝑖𝑒𝑛𝑡𝑒𝑝𝑜𝑠(𝑖) contiene a

𝑠𝑖𝑔𝑢𝑖𝑒𝑛𝑡𝑒𝑝𝑜𝑠(j) contiene a

\{k, l, \dots\}
\{k, l, \dots\}

Autómatas finitos

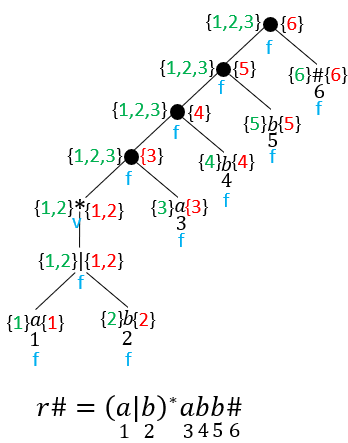
Cálculo del siguientepos:

  • Método del Árbol Sintáctico

Paso de una e.r a un AFD Óptimo

Dado que ya se calcularon el 𝑝𝑟𝑖𝑚𝑒𝑟𝑎𝑝𝑜𝑠 y 𝑢𝑙𝑡𝑖𝑚𝑎𝑝𝑜𝑠 en el árbol sintáctico para cada nodo, se calcula 𝑠𝑖𝑔𝑢𝑖𝑒𝑛𝑡𝑒𝑝𝑜𝑠 haciendo un recorrido de abajo hacia arriba en el árbol.

Posición 𝑖 𝒔𝒊𝒈𝒖𝒊𝒆𝒏𝒕𝒆𝒑𝒐𝒔(𝒊)
1 {1,2,3}
2 {1,2,3}
3 {4}
4 {5}
5 {6}
6 {}

Autómatas finitos

  • Método del Árbol Sintáctico

Paso de una e.r a un AFD Óptimo

// Al inicio, el único estado no marcado en estadosD es primerapos(raiz), donde raiz es la raiz del árbol para (r)#
MIENTRAS QUE(haya un estado no marcado T en estadosD) HACER:
	marcar T;
    PARA cada símbolo de entrada a HACER:
		//sea U el conjunto de posiciones que están en siguientepos(p), para alguna posición en T, tal que el símbolo en la posición p es a;
        SI U no está vaciao y no está en estadosD:
        	añadir U como estado no marcado a estadosD;
        FIN-SI
        tranD[T,a] = U;
    FIN-PARA
FIN-MIENTRASQUE
Estado Símbolo(a) Símbolo(b)

tranD

Estado
Marca

estadosD

Autómatas finitos

  • Método del Árbol Sintáctico

Paso de una e.r a un AFD Óptimo

// Al inicio, el único estado no marcado en estadosD es primerapos(raiz), donde raiz es la raiz del árbol para (r)#
MIENTRAS QUE(haya un estado no marcado T en estadosD) HACER:
	marcar T;
    PARA cada símbolo de entrada a HACER:
		//sea U el conjunto de posiciones que están en siguientepos(p), para alguna posición en T, tal que el símbolo en la posición p es a;
        SI U no está vaciao y no está en estadosD:
        	añadir U como estado no marcado a estadosD;
        FIN-SI
        tranD[T,a] = U;
    FIN-PARA
FIN-MIENTRASQUE
\begin{aligned} \mathbf{\textcolor{green}{A}} &= \textit{ppos}(raiz) = \{ \textcolor{blue}{1,2,3}\} \\ T &= A; a = a; U = \mathbf{B} = \textit{spos}(1) \cup \textit{spos}(3) = \{ \textcolor{blue}{1,2,3,4}\} \\ T &= A; a = b; U = \mathbf{A} = \textit{spos}(2) = \{ \textcolor{blue}{1,2,3}\} \\ T &= B; a = a; U = \mathbf{B} = \textit{spos}(1) \cup \textit{spos}(3) \\ T &= B; a = b; U = \mathbf{C} = \textit{spos}(2) \cup \textit{spos}(4) = \{ \textcolor{blue}{1,2,3,5}\} \\ T &= C; a = a; U = \mathbf{B} = \textit{spos}(1) \cup \textit{spos}(3) \\ T &= C; a = b; U = \mathbf{\textcolor{red}{D}} = \textit{spos}(2) \cup \textit{spos}(5) = \{ \textcolor{blue}{1,2,3,6}\} \\ T &= D; a = a; U = \mathbf{B} = \textit{spos}(1) \cup \textit{spos}(3) \\ T &= D; a = b; U = \mathbf{A} = \textit{spos}(2) \end{aligned}

El estado de inicio del AFD corresponde con la ppos(raiz).

El estado de finalización del AFD contiene la posición de #.

𝑖 𝒔𝒑𝒐𝒔(𝒊)
1 {1,2,3}
2 {1,2,3}
3 {4}
4 {5}
5 {6}
6 {}
Estado a b
A B A
B B C
C B D
*D B A

tranD

Autómatas finitos

  • Método del Árbol Sintáctico

Paso de una e.r a un AFD Óptimo

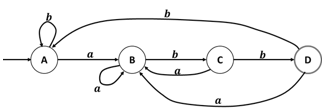
Estado a b
A B A
B B C
C B D
*D B A

tranD

Autómatas finitos

  • Lema de Ardem

Conversión de un AFD a una E.R.

Sistemas de Ecuaciones en E.R.

Ecuación en expresiones regulares: Ecuación lineal donde variables y coeficientes toman la forma de expresiones regulares.

X = rX|s

Entrada: Autómata finito                                   , con 

Salida: Sistema de ecuaciones donde en     determina el lenguaje del AFD.

Método:

  1. Por cada estado     , introducir una variable    .
  2. Si     está en F, luego añadir en la parte derecha de la 𝑖-ésima ecuación el término ∈; es decir,     =∈.
  3. Si                       entonces en la parte derecha de la 𝑖-ésima ecuación aparece el término       ; es decir,                 , con    en              .
D = \{\Sigma, S, s_0, F, \delta \}
S = \{s_0,s_1,s_2,\dots, s_n \}
s_0
s_i
s_i
s_i
s_i
\delta (s_i, a) = s_j
as_j
s_i = as_j
a
\Sigma \cup \{\epsilon\}

Autómatas finitos

  • Lema de Ardem

Conversión de un AFD a una E.R.

Sea                       una ecuación en expresiones regulares, luego                   es una solución para la ecuación. Es única si ∈ es generada por 𝑟.

X = rX|s
  • Dado un sistema de ecuaciones en expresiones regulares, la resolución viene tras aplicar el método de Gauss utilizando el Lema de Arden para reducir.
     
  • Útil para obtener una e.r. a partir de un A.F. o una gramática regular.
     

 

X = r^*s
  • Sistema de ecuaciones en E.R

Autómatas finitos

  • Lema de Ardem

Conversión de un AFD a una E.R.

Ejemplo 1:

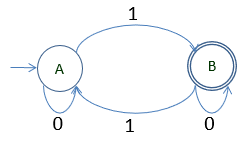
A=1B | 0A             (1)
B=1A | 0B | ∈      (2)
Resolviendo
De (1): Aplicando Ardem
A=0*1B                   (1’)
Remplazando (1’) en (2)
B=10*1B | 0B | ∈
B= (10*1| 0)B | ∈
B= (10*1 | 0)* ∈   Aplicando Ardem
B= (10*1 | 0)*        (2’)
Remplazando. (2’) en (1’)
A=0*1 (10*1 | 0)* Expr. Regular Final

Autómatas finitos

  • Lema de Ardem

Conversión de un AFD a una E.R.

Ejemplo 2:

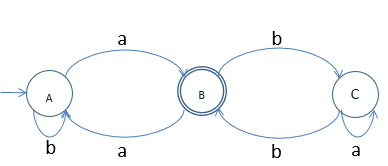
A= bA | aB                 (1)
B= bC | aA | ∈          (2)
C=aC  | bB                  (3)
Resolviendo
De (1): Por Ardem
A=b*aB                       (1’)
De (3): Por Ardem
C=a*bB                       (3’)
Rempl (1’) y (3’) en (2)
B=ba*bB | ab*aB | ∈
B=(ba*b | ab*a ) B | ∈
B= (ba*b | ab*a )* ∈   Por Ardem
B= (ba*b | ab*a )*      (2’)
Rempl en (1’)
A=b*a (ba*b | ab*a )*   Exp. Regular

Análisis léxico

Flex

¿Qué es Flex?

  • Generador de analizadores léxico - Scanners
  • Genera código fuente en C
  • Distibuido bajo licencia BSD.
  • Source: https://flex.sourceforge.net

Especificación Flex

Flex

lex.yy.c

yylex()

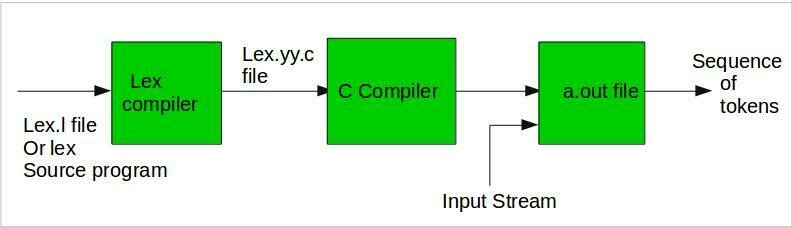
¿Cómo se utiliza Flex?

Especificación del analizador léxico

  • Entrada de Flex: Especificación del analizador léxico
  • Consta de 3 Secciones:
    • Deficiones
    • %%
      Reglas
      %%
    • Código de usuario
  • Texto encerrado entre %{ y %} se copiará a la salida
  • Comentarios encerrados entre /* y */

Deficiones

  • Son declaraciones de nombres asociados a expresiones regulares.
    • <name> <r.e>
  • Posteriormente se usará el nombre entre {}
  • Ejemplo:
    • digito [0-9]
    • letraMinuscula [a-z]

Reglas

  • Una de las más importantes, ya que se establece las patrones a reconcer en el fichero de entrada 
  • Contiene reglas de la forma:
    • <patrón> <acción>
      • Donde:
        • <patrón>: expresión regular.
        • <acción>: código C que se ejecutará.
  • Ejemplo:
    • {digito} {ECHO;}

Ejemplo Completo

digito [0-9]
%%
{digito} {ECHO;}
{digito}+ {ECHO;}
%%
main(){
  yylex();
}

Expresiones regulares

r.e Reconocimiento
x caracter x
. Cualquier carácter excepto nueva línea
[abc] una 'a' o una 'b' o una 'c'
[ab-p] una 'a' o una 'b' o cualquier letra entre b y p
[^A-Z] Caracteres negados: Cualquier carácter excepto una letra mayúscula.
r* Cero o más ocurrencias de la e.r r
r+ Una o más ocurrencias de la e.r r
r|s r o s (unión)
sr e.r s seguida de la e.r r (concatenación)

Expresiones regulares

r.e Reconocimiento
r? Cero o una ocurrencia de r
r{3,6} De 3 a 6 ocurrencias de r
{nombre} e.r de la definición "nombre"
\x x: 'a', 'b', 'f', 'n', 'r', 't', o 'v' : ANSI-C. Ow: x
"[xyz]"\fo" Cadena literalmente: [xyz]"\fo
<<EOF>> Fin del fichero

Ejemplos

  • Expresión regular Flex para:
    • Un dígito:
      • [0-9]  {printf("He reconocido un dígito")}
    • Un número natural:
      • [0-9]+ {printf("He reconocido un número natural")}
    • La palabra "for"
      • for {printf("He reconocido la palabrea for")}

Ejemplo Completo

digito [0-9]
nentero {digito}+
nreal {nentero}\.{digito}*
%%
{digito} {ECHO;}
{nentero} {ECHO;}
{nreal} {ECHO;}
. {printf("<<error>>");}
<<EOF>> {yyterminate();}
%%
main(){
  yylex();
}

Análisis Sintáctico

Análisis Sintáctico

Analizador Léxico

Analizador sintáctico

Tabla de símbolos

Programa fuente

Resto de

Etapa Inicial

Árbol de análisis sintáctico

Analizador Sintáctico: Segunda fase de un compilador. Obtiene una cadena de componentes léxicos del Analizador Léxico, y verifica si la cadena puede ser generada por la gramática del lenguaje fuente. Informa de los errores sintácticos que se presenten.

Los lenguajes de programación poseen una estructura inherentemente recursiva que se define gracias a las Gramáticas Independientes del Contexto (GIC).

Las GIC son un modelo matemático formado por una cuadrupla:

Gramáticas Independientes del Contexto

G = \{T,N,S,P\}

1. 𝑻: Terminales: Símbolos básicos con los que se  forman las cadenas. Componente léxico es sinónimo de terminal.
2. 𝑵: No terminales: Son variables sintácticas que denotan conjuntos de cadenas. Estos definen conjuntos de cadenas que ayudan a definir el lenguaje generado por la GIC.
3. 𝑺: Símbolo Inicial: Es un No terminal, y define a un conjunto de cadenas que representan al lenguaje generado por la GIC.
4. 𝑷: Producciones: Especifican cómo se combinan los Terminales y los No Terminales para formar cadenas. Cada producción consta de dos partes:
Cabecera: Es un No Terminal, seguido por una flecha
Cuerpo: Cadena de Terminales y No Terminales.
Ejemplo: 𝐴→𝛼 es una producción.

Gramáticas Independientes del Contexto

Ejemplo de GIC: Gramática de Operadores Aritméticos

Gramáticas Independientes del Contexto

\begin{aligned} E &\rightarrow E + E \\ E &\rightarrow E - E \\ E &\rightarrow E * E \\ E &\rightarrow E / E \\ E &\rightarrow (E) \\ E &\rightarrow id \end{aligned}
G = \{T,N,S,P\}
T = \{+,-,*,/,(,),id\}
N = \{E\}
S = \{E\}

P son las producciones que se encuentran en el lado izquierdo.

Escritura abreviada

E \rightarrow E + E | E - E | E * E | E / E | (E) | id

Ejemplo de GIC: Gramática de Operadores Aritméticos

Gramáticas Independientes del Contexto

\begin{aligned} E &\rightarrow E + T \\ E &\rightarrow E - T \\ E &\rightarrow T \\ T &\rightarrow T * F \\ T &\rightarrow T/F\\ T &\rightarrow F \\ F &\rightarrow (E) \\ F &\rightarrow id \\ \end{aligned}
G = \{T,N,S,P\}
T = \{+,-,*,/,(,),id\}
N = \{E, T, F\}
S = \{E\}

P son las producciones que se encuentran en el lado izquierdo.

Escritura abreviada

\begin{aligned} E &\rightarrow E + T | E - T | T \\ T &\rightarrow T * F | T/F| F \\ F &\rightarrow (E) | id \end{aligned}

Ejemplo de GIC:

Gramáticas Independientes del Contexto

\begin{aligned} S &\rightarrow (L) | a \\ L &\rightarrow L,S | S \\ \end{aligned}
G = \{T,N,S,P\}
T = \{(,),a, ,\}
N = \{S, L\}
S = \{S\}

P son las producciones que se encuentran en el lado izquierdo.

Por convención:

  • Los No Terminales se escriben con letras mayúsculas
  • El Símbolo Inicial(S) es el primer no Terminal que aparece en las producciones

Derivaciones
Una GIC 𝐺 define un lenguaje 𝐿(𝐺).
Las derivaciones establecen el proceso mediante el cual la GIC define un lenguaje.
Se considera cada producción como una regla de escritura, donde el No terminal a la izquierda es sustituido por la cadena del lado derecho de la producción.

 

Gramáticas Independientes del Contexto

Derivaciones
Ejemplo:

 

Derivar la cadena:

Gramáticas Independientes del Contexto

E \rightarrow E + E | E - E | E * E | E / E | (E) | id
id * id + id
E \Rightarrow E + E \Rightarrow E * E + E \Rightarrow id * E + E\\ \Rightarrow id * id + E \Rightarrow id * id + id

A estas sustituciones se les llama derivación de la cadena

Derivaciones
Reglas y Notaciones:

Dada una GIC 𝐺 con símbolo inicial 𝑆, se utiliza la relación     para definir 𝐿(𝐺), el lenguaje generado por 𝐺.
1. Las cadenas en 𝐿(𝐺) pueden contener sólo símbolos terminales de 𝐺; es decir, si 𝜔 está en 𝐿(𝐺), luego 𝜔 es generada por    .
2. 𝜔 está en 𝐿(𝐺) sí, y solo sí, 𝑆    𝜔.

 

 

Gramáticas Independientes del Contexto

T^*
\overset{*}{\Rightarrow}
\overset{+}{\Rightarrow}

Derivaciones
Reglas y Notaciones:

3. A la cadena 𝜔 se le llama frase de 𝐺.
4. A un lenguaje generado por una GIC, se le denomina lenguaje independiente del contexto (LIC).
5. Dos GIC que generan el mismo lenguaje, se les denomina GIC’s equivalentes. Es decir, si 𝐿(𝐺) = 𝐿(𝐺′), luego 𝐺≅𝐺′.
6. Si 𝑆    𝛼, donde 𝛼 puede contener no terminales, luego 𝛼 es una forma de frase de 𝐺.
7. Una frase es una forma de frase sin no terminales.

Gramáticas Independientes del Contexto

\overset{*}{\Rightarrow}

Derivaciones
Ejemplo:

 

Gramáticas Independientes del Contexto

E \rightarrow E + E | E - E | E * E | E / E | (E) | id
E \Rightarrow \textcolor{green}{ E + E} \Rightarrow \textcolor{green}{ E * E + E } \Rightarrow \textcolor{green}{ id * E + E}\\ \Rightarrow \textcolor{green}{id * id + E} \Rightarrow \textcolor{blue}{id * id + id}

En la siguiente derivación:

\textcolor{blue}{id * id + id}

es una frase de la GIC.

\textcolor{green}{ E + E}, \textcolor{green}{ E * E + E }, \textcolor{green}{ id * E + E}, \textcolor{green}{id * id + E},\textcolor{blue}{id * id + id}

son formas de frase de la GIC.

Derivaciones
Tipos de derivaciones

 

Gramáticas Independientes del Contexto

E \rightarrow E + E | E - E | E * E | E / E | (E) | id
E \Rightarrow E + E \Rightarrow E * E + E \Rightarrow id * E + E \\ \Rightarrow id * id + E \Rightarrow id * id + id

Derivación 1: Más Izquierda

E \Rightarrow E * E \Rightarrow id * E \Rightarrow id * E + E \\ \Rightarrow id * id + E \Rightarrow id * id + id

Derivación 2: Más Izquierda

Derivaciones
Tipos de derivaciones

 

Gramáticas Independientes del Contexto

E \rightarrow E + E | E - E | E * E | E / E | (E) | id
E \Rightarrow E + E \Rightarrow E + id \Rightarrow E * E + id \\ \Rightarrow E * id + id \Rightarrow id * id + id

Derivación 3: Más Derecha

E \Rightarrow E * E \Rightarrow E *E + E \Rightarrow E * E + id \\ \Rightarrow E * id + id \Rightarrow id * id + id

Derivación 4: Más Derecha

Derivaciones
Tipos de derivaciones

Derivación Más Izquierda

Gramáticas Independientes del Contexto

Se realiza la sustitución del no terminal que se encuentra más a la izquierda de cualquier forma de frase.

 

𝑤𝐴𝛾     𝑤𝛿𝛾, donde 𝑤 está formada solo de terminales, 𝐴→𝛿 es  la producción aplicada y 𝛾 es una cadena de símbolos gramaticales.


Aquí 𝑤𝛿𝛾 es una forma de frase izquierda de la GIC.

 

\Rightarrow

Derivaciones
Tipos de derivaciones

Derivación Más Derecha

Gramáticas Independientes del Contexto

Se realiza la sustitución del no terminal que se encuentra más a la derecha de cualquier forma de frase.

 

𝛾𝐴𝑤    𝛾𝛿𝑤, donde 𝑤 está formada solo de terminales, 𝐴→𝛿 es  la producción aplicada y 𝛾 es una cadena de símbolos gramaticales.


Aquí 𝛾𝛿𝑤 es una forma de frase derecha de la GIC.

 

 

\Rightarrow

Derivaciones
Ambigüedad

Una GIC que genera una cadena con más de una derivación del mismo tipo, se considera ambigua.

 

Analizar ambigüedad de la primera y segunda GIC de Operadores Aritméticos

Gramáticas Independientes del Contexto

Derivaciones
Árbol de análisis sintáctico

Gramáticas Independientes del Contexto

Es una representación gráfica de una derivación que no muestra la elección relativa al orden de sustitución.

Cada nodo interior del árbol se etiqueta con algún no terminal A.

Los hijos de este nodo interior A, se etiquetan, de izquierda a derecha, con los símbolos del lado derecho de la producción por la cual se sustituyó esta A en la derivación.

Las hojas del árbol en cualquier momento se pueden leer de izquierda a derecha y forman una forma de frase, llamada frontera del árbol.

Derivaciones
Árbol de análisis sintáctico

Gramáticas Independientes del Contexto

E
E
E
+
E
E
*
id
id
id
E \Rightarrow E + E \Rightarrow E * E + E \Rightarrow id * E + E \\ \Rightarrow id * id + E \Rightarrow id * id + id

Ejemplo: Derivación 1: Más Izquierda

Arbol de análisis sintáctico

Derivación final

Derivaciones
Árbol de análisis sintáctico

Gramáticas Independientes del Contexto

E \Rightarrow E * E \Rightarrow id * E \Rightarrow id * E + E \Rightarrow id * id + E \Rightarrow id * id + id

Ejercicio: Dada la GIC, construye los AAS correspondientes

Derivación 2: Más Izquierda

E \Rightarrow E + E \Rightarrow E + id \Rightarrow E * E + id \Rightarrow E * id + id \Rightarrow id * id + id

Derivación 3: Más Derecha

E \Rightarrow E * E \Rightarrow E *E + E \Rightarrow E * E + id \Rightarrow E * id + id \Rightarrow id * id + id

Derivación 4: Más Derecha

Escritura de una Gramática
Expresiones regulares a GIC

Gramáticas Independientes del Contexto

Toda e.r se puede escribir como una GIC. Con las siguientes reglas:

  1. Construir un Autómata Finito.
  2. Para cada estado del    AF, crear un símbolo no terminal      .
    a) Si             , se agrega la producción
    b) Si              , se agrega la producción
    c) Si    está en F(estado de finalización), se agrega
    d) Si    es el estado de inicio del AF, luego       es el símbolo de inicio de la GIC.
i
A_i
\delta (i,a)
\delta (i,\in)
i
A_i \rightarrow aA_j
A_i \rightarrow A_j
A_i \rightarrow \in
i
A_i
\delta (i,a)

: Si existe un movimiento que sale del estado i con el símbolo a

Escritura de una Gramática
Expresiones regulares a GIC

Gramáticas Independientes del Contexto

Ejemplo: Convertir a una GIC la e.r                    a partir de AFD óptimo

(a|b)^* abb
A \rightarrow aB|bA \\ B \rightarrow aB|bC \\ C \rightarrow aB|bD \\ D \rightarrow aB|bA| \in

Escritura de una Gramática
Eliminación de Recursividad Izquierda

Gramáticas Independientes del Contexto

Una GIC es recursiva por izquierda si tiene un no terminal 𝐴 tal que existe una derivación 𝐴    𝐴𝛼 para alguna cadena 𝛼. Es decir que el no terminal tiene producciones con el mismo no terminal a la izquierda.


Los analizadores sintácticos descendentes no pueden manejar gramáticas recursivas por la izquierda.

\overset{+}{\Rightarrow}

Escritura de una Gramática
Eliminación de Recursividad Izquierda

Gramáticas Independientes del Contexto

Método Simple:

Dada la GIC                             , la GIC        sin recursividad:

G: A \rightarrow A \alpha | \beta
G'
A \rightarrow \beta A' \\ A' \rightarrow \alpha A'|\in

Ejemplo: Dada la GIC, eliminar la recursividad

S \rightarrow (L) |a \\ L \rightarrow L,S|S
S \rightarrow (L) |a \\ L \rightarrow SL' \\ L' \rightarrow ,SL'|\in

Escritura de una Gramática
Eliminación de Recursividad Izquierda

Gramáticas Independientes del Contexto

Método Compuesto:

Dada la GIC                                                                            , la GIC       sin recursividad es:

G: A \rightarrow A \alpha_1 | A \alpha_2 | \dots | A \alpha_n |\beta_1 |\beta_2 | \dots |\beta_m
G'
A \rightarrow A(\alpha_1 | \alpha_2 | \dots |\alpha_n) | (\beta_1 |\beta_2 | \dots |\beta_m)

Si                                                                          , entonces                      , se convierte en el caso simple y se elimina igual que ese método:

\alpha =\alpha_1 | \alpha_2 | \dots |\alpha_n \text{ y } \beta = \beta_1 |\beta_2 | \dots |\beta_m
A \rightarrow A \alpha|\beta
A \rightarrow \beta A' \\ A' \rightarrow \alpha A'|\in

Escritura de una Gramática
Eliminación de Recursividad Izquierda

Gramáticas Independientes del Contexto

Método Compuesto:

Ejemplo: Eliminar recursividad

\begin{aligned} E &\rightarrow E + T| E - T|T \\ T &\rightarrow T * F|T/F|F \\ F &\rightarrow (E) | id \end{aligned}
\begin{aligned} E &\rightarrow E(+T|-T)|T \\ T &\rightarrow T(* F|/F)|F \\ F &\rightarrow (E) | id \end{aligned}
\begin{aligned} E &\rightarrow TE' \\ E' &\rightarrow +TE'|-TE'|\in \\ T &\rightarrow FT' \\ T' &\rightarrow *FT'|/FT'|\in \\ F &\rightarrow (E) | id \end{aligned}

Escritura de una Gramática
Factorización por Izquierda

Gramáticas Independientes del Contexto

Es otra transformación necesaria de una GIC para utilizarla en un Analizador Sintáctico Descendente.

Dada la GIC                                                  

 

Método:

Se transforma en la GIC equivalente:

A \rightarrow \alpha \beta_1 | \alpha \beta_2 | \dots | \alpha \beta_n | \gamma
\begin{aligned} A &\rightarrow \alpha A'|\gamma \\ A &\rightarrow \beta_1 | \beta_2 | \dots | \beta_n \end{aligned}

Escritura de una Gramática
Factorización por Izquierda

Gramáticas Independientes del Contexto

Ejemplo: Dada la GIC, realiza la factorización izquierda

\begin{aligned} P &\rightarrow iEtP|iEtPeP|a \\ E &\rightarrow b \end{aligned}
\begin{aligned} P &\rightarrow iEtPP'|a \\ P &\rightarrow \in | eP \\ E &\rightarrow b \end{aligned}
Made with Slides.com