Integrating discrete choice models with MATSim scoring

Sebastian Hörl

25 March 2021

ABMTRANS 2021

Discrete choice models vs. MATSim

Discrete choice model

Choice-making in MATSim

=

Discrete choice models vs. MATSim

Discrete choice model

Choice-making in MATSim

=

?

Discrete choice modeling

Discrete choice modeling

Discrete choice modeling

Discrete choice modeling

  • Definition of utility v for a choice situation i with travel characteristics X and utility parameters beta
     
  • Observed choice in each situation i

 

 

  • Concept of utility
    maximization
v_k(X_i) = \beta^T \cdot X_k
y_i \in \{ 1, ..., K \}
\beta
y_i = \text{arg max}_k \{ v_k(X_i|\beta) \} \ \ \forall i

Find               such that

Discrete choice modeling

  • Definition of utility v for a choice situation i with travel characteristics X and utility parameters beta
     
  • Observed choice in each situation i

 

 

  • Concept of utility
    maximization

    Problem: Usually cannot be solved!
v_k(X_i) = \beta^T \cdot X_k
y_i \in \{ 1, ..., K \}
\beta
y_i = \text{arg max}_k \{ v_k(X_i|\beta) \} \ \ \forall i

Find               such that

Discrete choice modeling

  • Random utility model adds
    stochastic component to the
    systematic utility
     
  • Random utility maximization (RUM)
u_{k,i} = v_{k,i} + \sigma \epsilon_{k,i}
E[\epsilon_{k,i}] = 0
\sigma \geq 0
k^*_i = \text{arg max}_k \{ u_{k,i} \}
k^*_i = \{ k \ | \ (u_{k,i} \geq u_{1,i}) \land \ (u_{k,i} \geq u_{2,i}) \land ... \}

Discrete choice modeling

  • If we choose the error to be EV / Gumbel-distributed ...
     
  • ... there is a closed form expression of the choice probabity!

     
  • Two alternatives:
    Binary logit model
     
  • More alternatives:
    Multinomial logit model
\epsilon_{k,i} \sim \text{EV}
u_k = v_k + \sigma \epsilon_k
P[k] = \frac{\exp(\sigma^{-1} v_k)}{\sum_{k'}\exp(\sigma^{-1} v_{k'})}

Discrete choice modeling

  • Closed-form expression allows to derive maximum likelihood estimate
P[k] = \frac{\exp(\sigma^{-1} v_k)}{\sum_{k'}\exp(\sigma^{-1} v_{k'})}
\mathcal{L}(\beta) = \prod_i P[y_i|X_i,\beta]
l(\beta) = \sum_i \log P[y_i|X_i,\beta]
\beta^* = \text{arg max}_{\beta} \sum_i \log P[y_i|X_i,\beta]

Discrete choice modeling

  • Models can be estimated from survey data, also for non-existant modes!

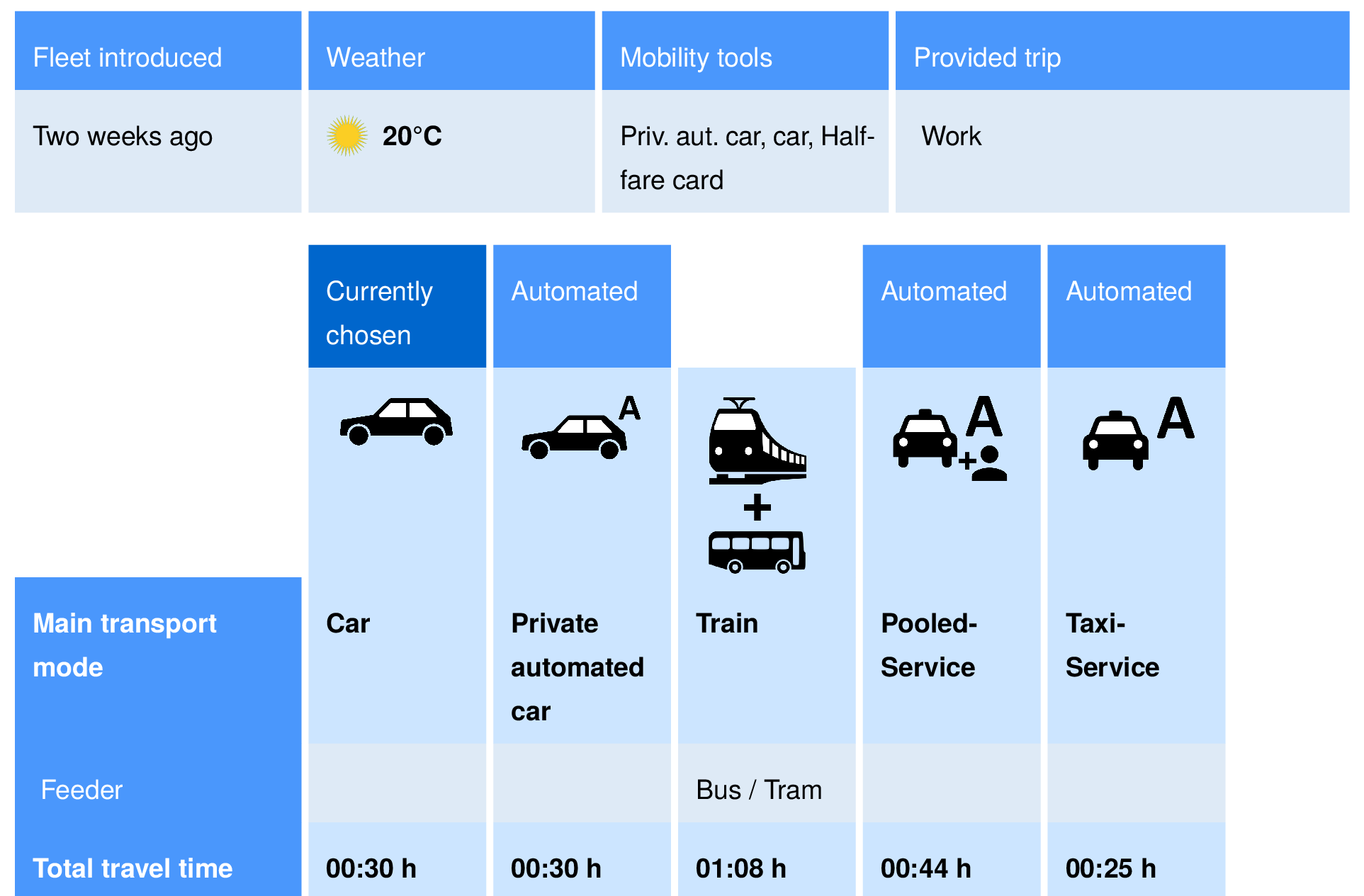
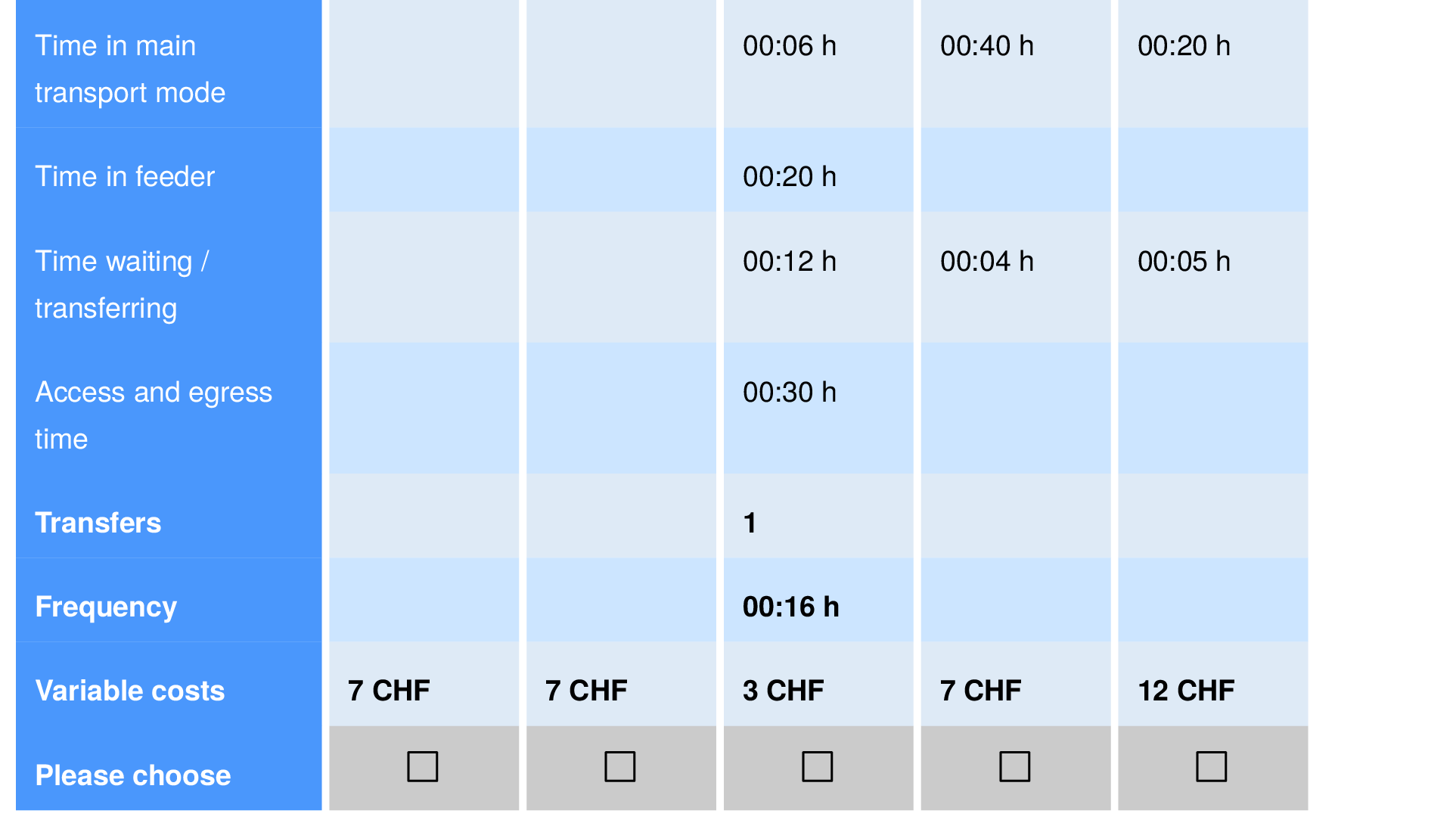
Discrete choice modeling

Discrete choice modeling

Discrete choice modeling: Simulation

  • Given X, we have two options for predicting or simulating a choice

     
  • Probability-based, sampling one alternative

     
  • Maximization-based, sampling one error term
k^* \sim P[k] = \frac{\exp(\sigma^{-1} v_k)}{\sum_{k'}\exp(\sigma^{-1} v_{k'})}
\epsilon_{k} \sim \text{EV}
u_k = v_k + \sigma \epsilon_k
k^* = \text{max} \{ u_k \}

Discrete choice modeling

Summary
 

  • Utility maximization principle
     
  • Utilities affected by error / taste component to reflect uncertainty / noise in the data
     
  • Generalization to non-existant modes is possible
     
  • But: Solve very specific problem (e.g. mode choice)

Choice data

Utility model

Estimation

Simulation

Scoring-based choice making in MATSim

Mobility simualtion

Scoring

Replanning

  • Daily plans of agents are simulated and scored in parallel
    • Performing activities brings positive score
    • Travling brings negative score
       
  • After, some agents replan
    • Either they choose from plans they have seen before (selection)
    • Or they make random modification on an existing plan (innovation)

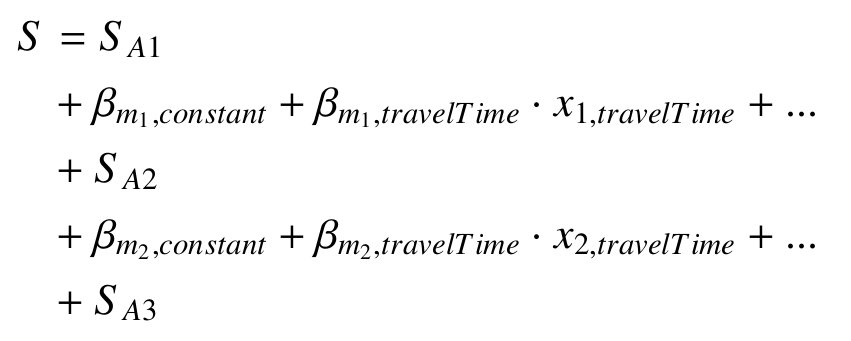
Scoring-based choice making in MATSim

MATSim

Comparison

New parameters

  • We can make the simulation fit to reality by calibration








     

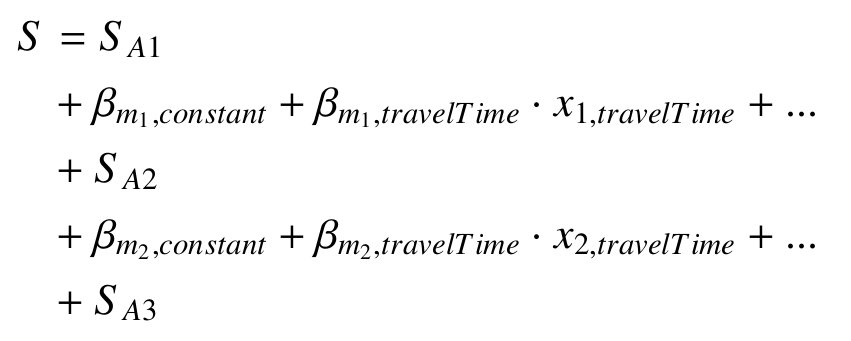
New parameters

  • We can only fit simulation to baseline / historical cases
  • We can only construct future scenarios of new modes of transport

Scoring-based choice making in MATSim

Summary
 

  • Score maximization
     
  • Complex activity chain possible
     
  • Offers large flexibility
     
  • But how to incorporate consistently future modes?

Scoring-based choice making in MATSim

Summary
 

  • Score maximization
     
  • Complex activity chain possible
     
  • Offers large flexibility
     
  • But how to incorporate consistently future modes?

Is it possible to make use of a discrete choice model in MATSim?

Scoring-based choice making in MATSim

  • Integrating discrete choice models directly as a replanning strategy
    • Available as discrete_mode_choice contrib (next presentation)
    • As DMC, very specific use case: Mode choice!
    • Not clear how to interact with other choice dimensions
    • Pragmatic solution
       
  • Making use of scoring to resemble a DMC
    • This presetation!
    • More theoretical analysis
    • May lead to better insights  and
      compatibility in the future

Choice process in detail

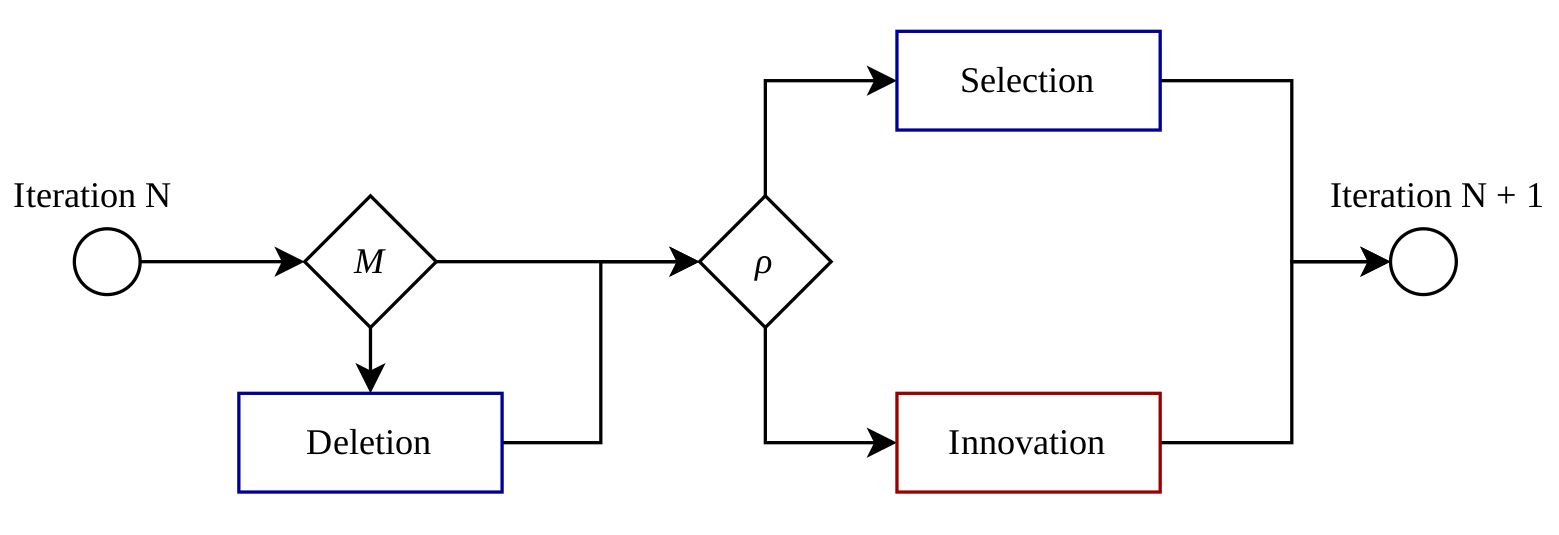
  • M: Maximum memory size
  • ρ: Innovation rate

Choice process in detail

  • Selection and deletion steer plans in memory towards higher scores
  • Innovation explores all the potential plans

Hypotheses

  • If we run this process infinitely, the memory of each agent should become populated with the same plan with maximum score
     
  • Whenever an agent performs innovation, there is one non-optimal plan generated in memory
     
  • The selection process resembles score (utility) maximization except for some cases where we have innovation

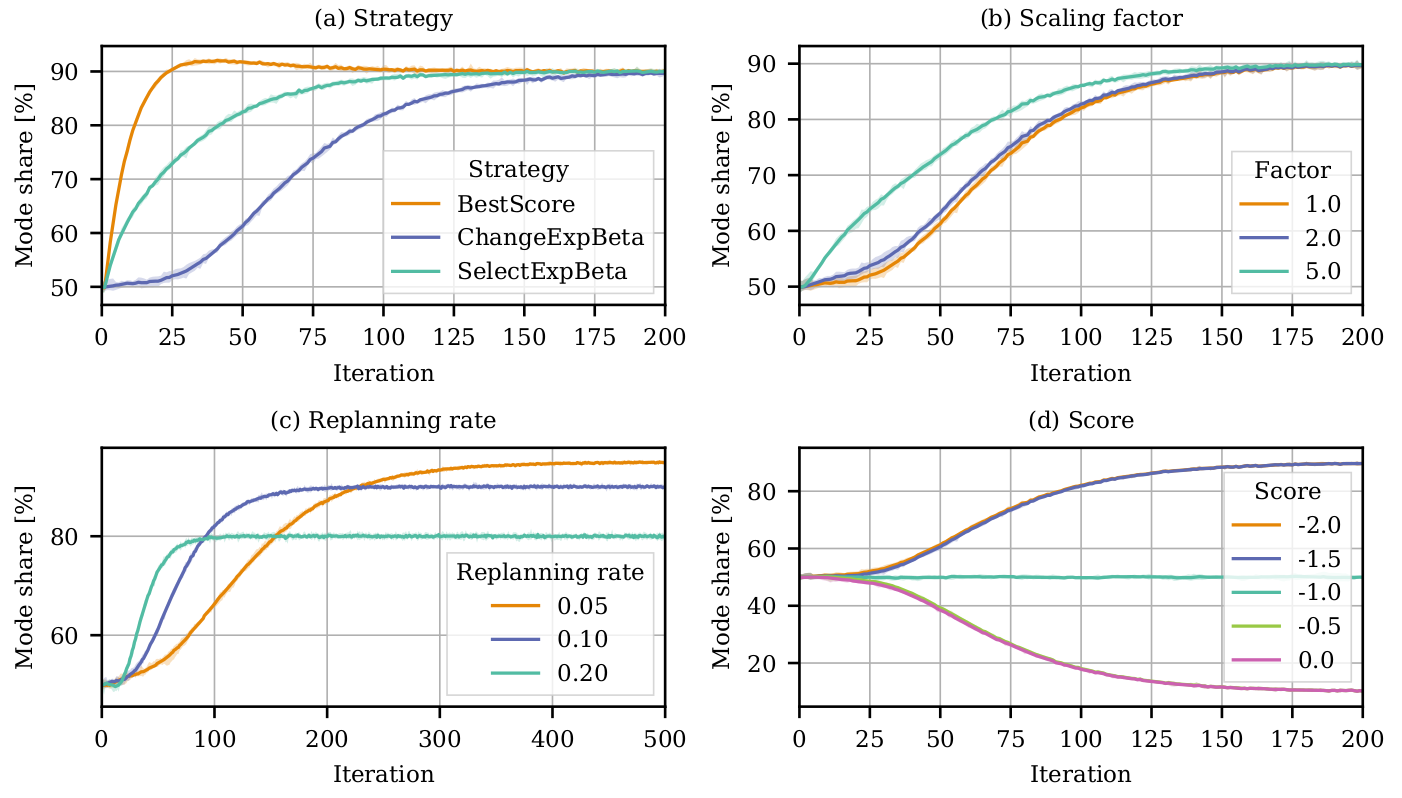
Experimental setup

  • 10,000 agents; one leg each
  • Two modes (A and B; e.g., car vs. pt)

    Defaults
     
  • Mode A leads to score -1 for the plan
  • Mode B leads to score -2 for the plan
  • Memory of size 3
  • Innovation rate 10%

    Tests
  • Choice strategy
  • Innovation rate
  • Change of score for mode B

A/B

Experimental results

Frozen errors

  • MATSim is score maximizing
  • But it is affected by innovation
     
  • We can use frozen errors to simulate the error terms we have in the discrete choice model
     
  • Has been used for location choice, but not from a generic perspective
     
  • Idea: For each combination of (Person, Trip Index, Mode), we need to determinstically create an error term
e = f(Person, Trip, Mode)

Cryptographic hash functions

  • Cryptographic hash functions are used, e.g. to encode passwords



     
  • In binary representation

flower123

H(\cdot)

abd5142fab24ef15

01001001

H(\cdot)

00110110001000101011001010

Fixed size, depending on hash function, e.g. SHA-512

Cryptographic hash functions

  • Avalanche effect: "If one bit in the input changes, at least 50% of bits in the output must change"
     
  • This leads to the fact that if the input is changed (systematically), we get a (approx.) uniformly distributed output over the value range of the hash function!

01001001

H(\cdot)

00110110001000101011001010

abc

abd

abe

...

H(\cdot)
h \sim Uniform

Cryptographic hash functions

  • The error term stays fix for each combination, but over all trips in the population, the term is uniformly distributed!
     
  • We can use Inverse Transform Sampling to create any distribution using the inverse CDF

01001001

H(\cdot)

00110110001000101011001010

(Person, Trip, Mode)

H(\cdot)
e(P,T,M) \sim Uniform
x = F^{-1}(u)

F can be Gumbel, Normal, ...

Implementation

  • Straight-forward implementation as additive scoring function

Experiments

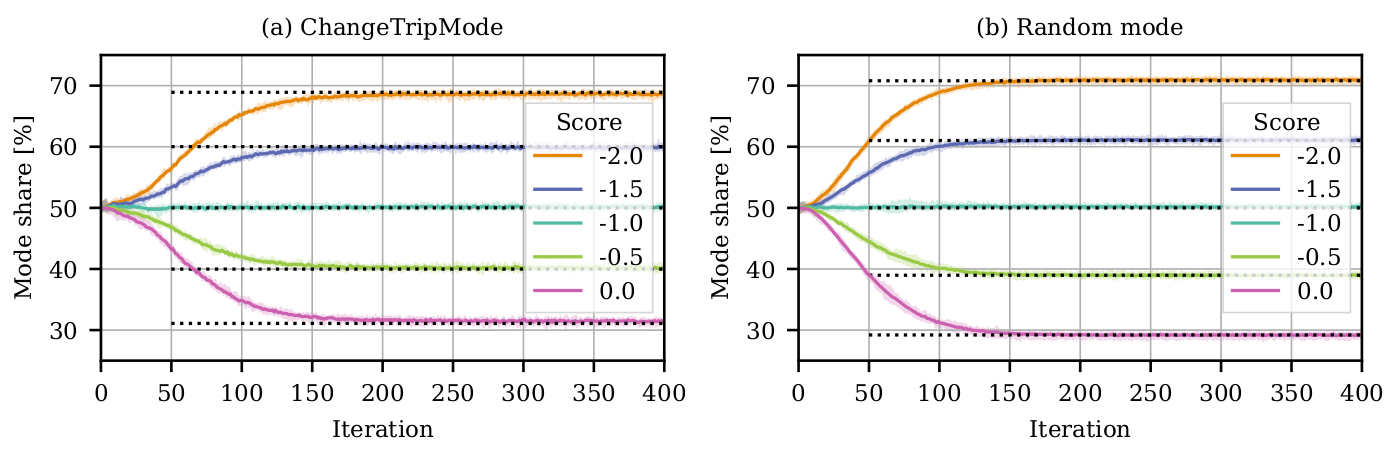
  • Model is now sensitive to score!
  • However, we would expect
P(A) = \frac{\exp(-1)}{\exp(-1) + \exp(-2)} = 73\%

Experiments

  • Choice probability is affected by innovation strategy!

    Random mode



    ChangeTripMode

 

 

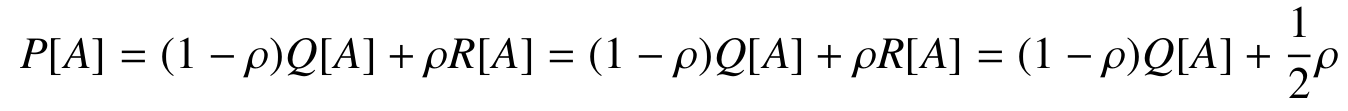
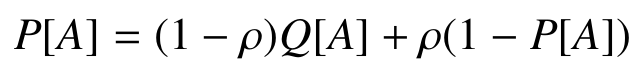
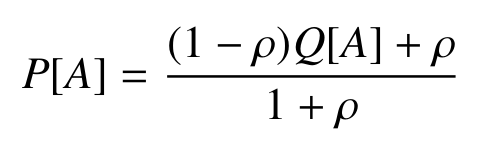
Experiments

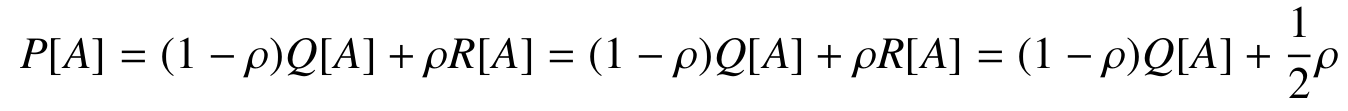
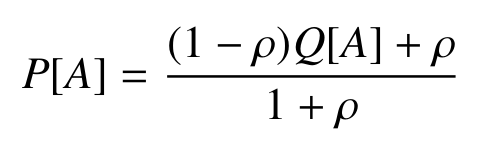
Conclusion

  • On a conceptual level choice model parameters cannot be translated directly into scoring parameters
     
  • MATSim as a utility maximizer can replicate the dynamics of an estimated discrete choice model
     
  • We can systematically quantify the differences in a toy example
     
  • Outlook
    • What does this mean for stability of the simulation?
    • What to do with innovation turn-off?
    • How to generalize to other choice dimensions?

Thank you!

Questions ?

Contact: sebastian.horl@irt-systemx.fr

Slides: https://slides.com/sebastianhorl/abmtrans21-scoring