Integrating discrete choice models with MATSim scoring
Sebastian Hörl
25 March 2021
ABMTRANS 2021
Discrete choice models vs. MATSim
Discrete choice model
Choice-making in MATSim
=
Discrete choice models vs. MATSim
Discrete choice model
Choice-making in MATSim
=
?
Discrete choice modeling
Discrete choice modeling
Discrete choice modeling
Discrete choice modeling
- Definition of utility v for a choice situation i with travel characteristics X and utility parameters beta
- Observed choice in each situation i
- Concept of utility
maximization
v_k(X_i) = \beta^T \cdot X_k
y_i \in \{ 1, ..., K \}
\beta
y_i = \text{arg max}_k \{ v_k(X_i|\beta) \} \ \
\forall i
Find such that
Discrete choice modeling
- Definition of utility v for a choice situation i with travel characteristics X and utility parameters beta
- Observed choice in each situation i
- Concept of utility
maximization
Problem: Usually cannot be solved!
v_k(X_i) = \beta^T \cdot X_k
y_i \in \{ 1, ..., K \}
\beta
y_i = \text{arg max}_k \{ v_k(X_i|\beta) \} \ \
\forall i
Find such that
Discrete choice modeling
- Random utility model adds
stochastic component to the
systematic utility
- Random utility maximization (RUM)
u_{k,i} = v_{k,i} + \sigma \epsilon_{k,i}
E[\epsilon_{k,i}] = 0
\sigma \geq 0
k^*_i = \text{arg max}_k \{ u_{k,i} \}
k^*_i = \{ k \ | \ (u_{k,i} \geq u_{1,i}) \land \ (u_{k,i} \geq u_{2,i}) \land ... \}
Discrete choice modeling
- If we choose the error to be EV / Gumbel-distributed ...
- ... there is a closed form expression of the choice probabity!
- Two alternatives:
Binary logit model
- More alternatives:
Multinomial logit model
\epsilon_{k,i} \sim \text{EV}
u_k = v_k + \sigma \epsilon_k
P[k] = \frac{\exp(\sigma^{-1} v_k)}{\sum_{k'}\exp(\sigma^{-1} v_{k'})}
Discrete choice modeling
- Closed-form expression allows to derive maximum likelihood estimate
P[k] = \frac{\exp(\sigma^{-1} v_k)}{\sum_{k'}\exp(\sigma^{-1} v_{k'})}
\mathcal{L}(\beta) = \prod_i P[y_i|X_i,\beta]
l(\beta) = \sum_i \log P[y_i|X_i,\beta]
\beta^* = \text{arg max}_{\beta} \sum_i \log P[y_i|X_i,\beta]
Discrete choice modeling
- Models can be estimated from survey data, also for non-existant modes!
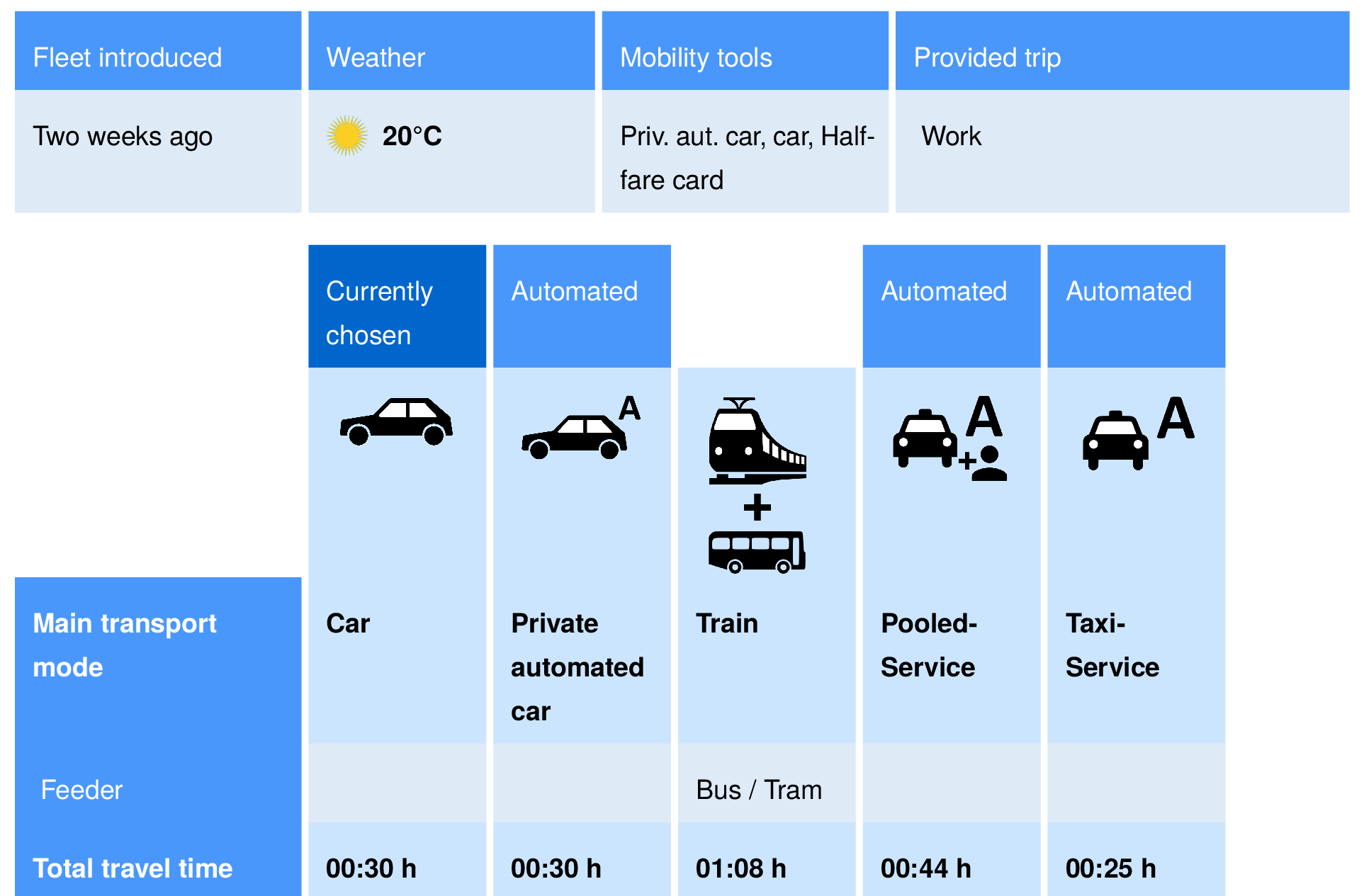
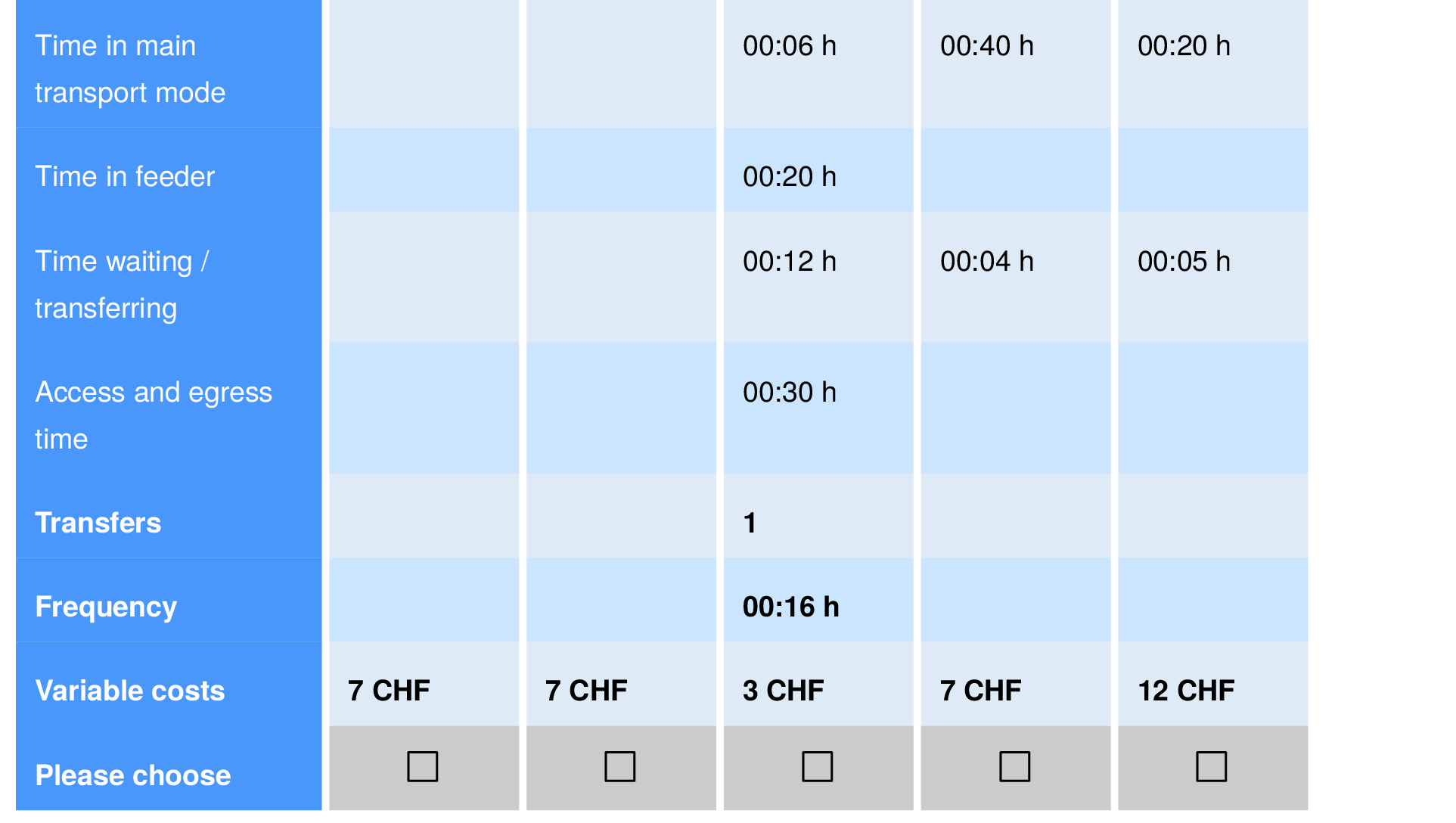
Discrete choice modeling
Discrete choice modeling
Discrete choice modeling: Simulation
- Given X, we have two options for predicting or simulating a choice
- Probability-based, sampling one alternative
- Maximization-based, sampling one error term
k^* \sim P[k] = \frac{\exp(\sigma^{-1} v_k)}{\sum_{k'}\exp(\sigma^{-1} v_{k'})}
\epsilon_{k} \sim \text{EV}
u_k = v_k + \sigma \epsilon_k
k^* = \text{max} \{ u_k \}
Discrete choice modeling
Summary
- Utility maximization principle
- Utilities affected by error / taste component to reflect uncertainty / noise in the data
- Generalization to non-existant modes is possible
- But: Solve very specific problem (e.g. mode choice)
Choice data
Utility model
Estimation
Simulation
Scoring-based choice making in MATSim
Mobility simualtion
Scoring
Replanning
- Daily plans of agents are simulated and scored in parallel
- Performing activities brings positive score
- Travling brings negative score
- After, some agents replan
- Either they choose from plans they have seen before (selection)
- Or they make random modification on an existing plan (innovation)
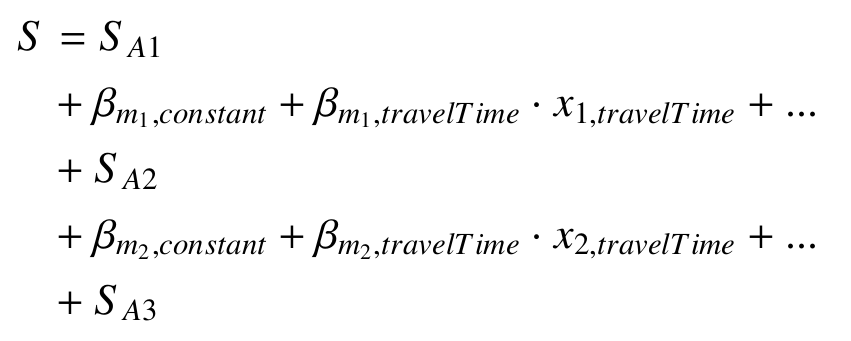
Scoring-based choice making in MATSim
MATSim
Comparison
New parameters
- We can make the simulation fit to reality by calibration
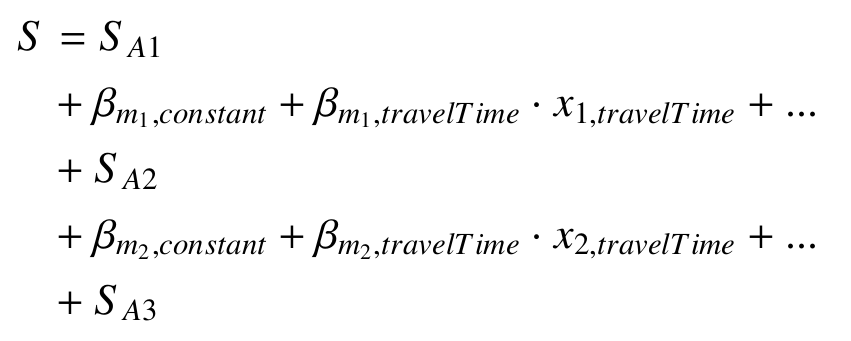
New parameters
- We can only fit simulation to baseline / historical cases
- We can only construct future scenarios of new modes of transport
Scoring-based choice making in MATSim
Summary
- Score maximization
- Complex activity chain possible
- Offers large flexibility
- But how to incorporate consistently future modes?
Scoring-based choice making in MATSim
Summary
-
Score maximization
- Complex activity chain possible
- Offers large flexibility
- But how to incorporate consistently future modes?
Is it possible to make use of a discrete choice model in MATSim?
Scoring-based choice making in MATSim
-
Integrating discrete choice models directly as a replanning strategy
- Available as discrete_mode_choice contrib (next presentation)
- As DMC, very specific use case: Mode choice!
- Not clear how to interact with other choice dimensions
-
Pragmatic solution
-
Making use of scoring to resemble a DMC
- This presetation!
- More theoretical analysis
- May lead to better insights and
compatibility in the future
Choice process in detail
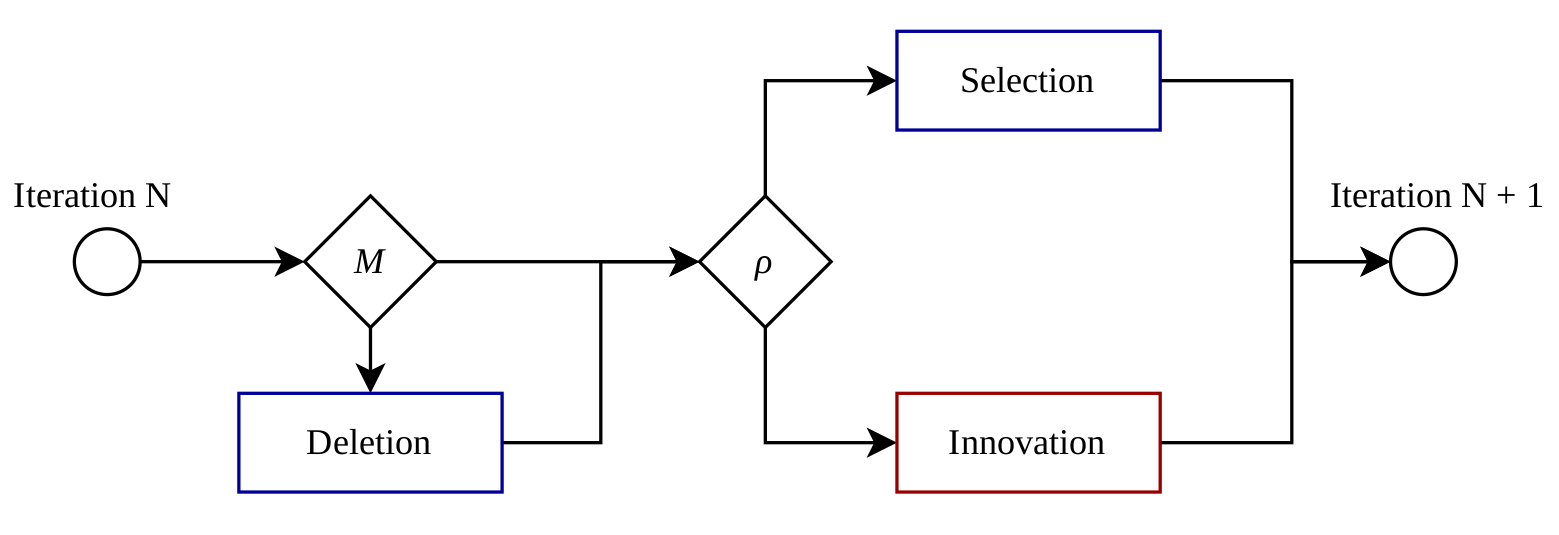
- M: Maximum memory size
- ρ: Innovation rate
Choice process in detail
- Selection and deletion steer plans in memory towards higher scores
- Innovation explores all the potential plans
Hypotheses
-
If we run this process infinitely, the memory of each agent should become populated with the same plan with maximum score
-
Whenever an agent performs innovation, there is one non-optimal plan generated in memory
- The selection process resembles score (utility) maximization except for some cases where we have innovation
Experimental setup
- 10,000 agents; one leg each
- Two modes (A and B; e.g., car vs. pt)
Defaults
- Mode A leads to score -1 for the plan
- Mode B leads to score -2 for the plan
- Memory of size 3
- Innovation rate 10%
Tests - Choice strategy
- Innovation rate
- Change of score for mode B
A/B
Experimental results
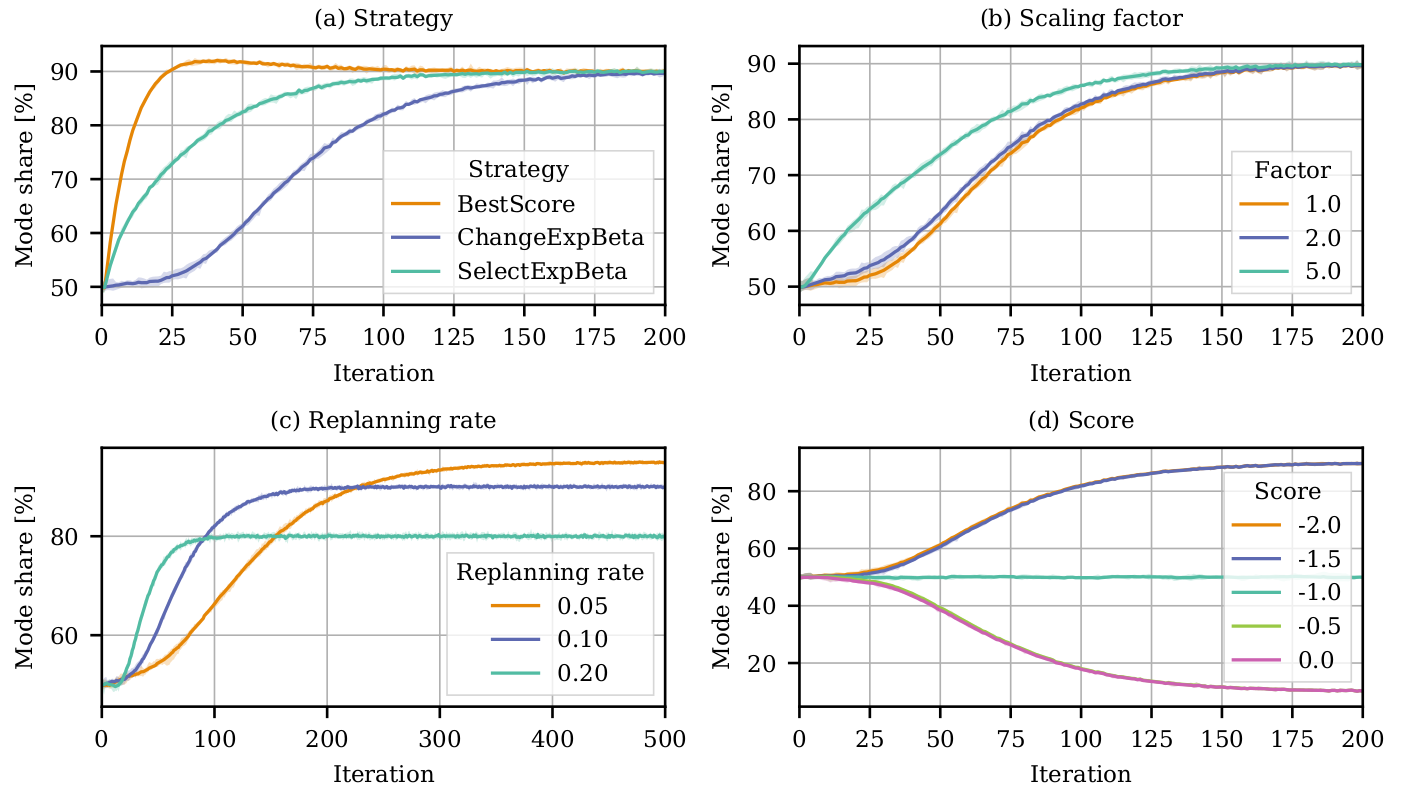
Frozen errors
- MATSim is score maximizing
- But it is affected by innovation
- We can use frozen errors to simulate the error terms we have in the discrete choice model
- Has been used for location choice, but not from a generic perspective
- Idea: For each combination of (Person, Trip Index, Mode), we need to determinstically create an error term
e = f(Person, Trip, Mode)
Cryptographic hash functions
- Cryptographic hash functions are used, e.g. to encode passwords
- In binary representation
flower123
H(\cdot)
abd5142fab24ef15
01001001
H(\cdot)
00110110001000101011001010
Fixed size, depending on hash function, e.g. SHA-512
Cryptographic hash functions
- Avalanche effect: "If one bit in the input changes, at least 50% of bits in the output must change"
- This leads to the fact that if the input is changed (systematically), we get a (approx.) uniformly distributed output over the value range of the hash function!
01001001
H(\cdot)
00110110001000101011001010
abc
abd
abe
...
H(\cdot)
h \sim Uniform
Cryptographic hash functions
- The error term stays fix for each combination, but over all trips in the population, the term is uniformly distributed!
- We can use Inverse Transform Sampling to create any distribution using the inverse CDF
01001001
H(\cdot)
00110110001000101011001010
(Person, Trip, Mode)
H(\cdot)
e(P,T,M) \sim Uniform
x = F^{-1}(u)
F can be Gumbel, Normal, ...
Implementation
- Straight-forward implementation as additive scoring function
Experiments
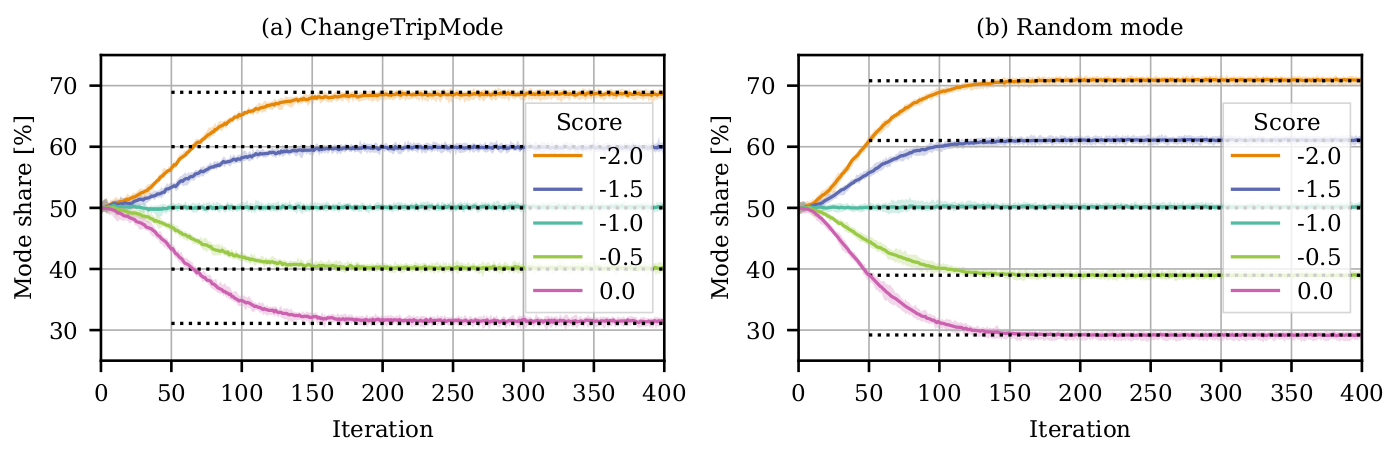
- Model is now sensitive to score!
- However, we would expect
P(A) = \frac{\exp(-1)}{\exp(-1) + \exp(-2)} = 73\%
Experiments
- Choice probability is affected by innovation strategy!
Random mode
ChangeTripMode
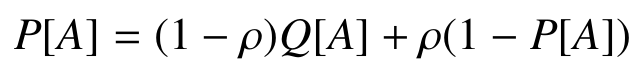
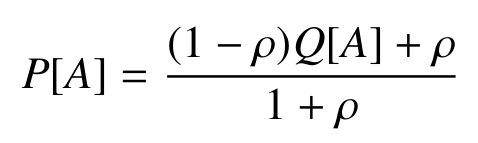
Experiments
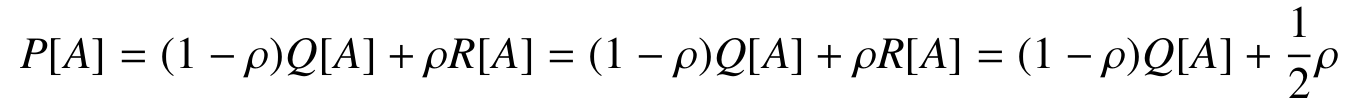
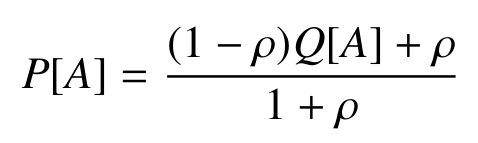
Conclusion
- On a conceptual level choice model parameters cannot be translated directly into scoring parameters
- MATSim as a utility maximizer can replicate the dynamics of an estimated discrete choice model
- We can systematically quantify the differences in a toy example
- Outlook
- What does this mean for stability of the simulation?
- What to do with innovation turn-off?
- How to generalize to other choice dimensions?
Thank you!
Questions ?
Contact: sebastian.horl@irt-systemx.fr
Integrating discrete choice models with MATSim scoring
By Sebastian Hörl
Integrating discrete choice models with MATSim scoring
ABMTRANS 2021, 25 March 2021
