Representation of mobility demand in agent-based transport simulation
Sebastian Hörl
22 November 2024
ENPC
http://www.loc.gov/pictures/item/2016800172/
The street in 1900
The street today
https://commons.wikimedia.org/wiki/File:Atlanta_75.85.jpg
- Autonomous Mobility
- Mobility as a Service
- Mobility on Demand
- Electrification
- Aerial Mobility
Julius Bär / Farner
The street of tomorrow?
Julius Bär / Farner
I. Transport simulation
Classic transport planning
- Zones
- Flows
- Peak hours
- User groups
Aggregated
Agent-based models
0:00 - 8:00
08:30 - 17:00
17:30 - 0:00
0:00 - 9:00
10:00 - 17:30
17:45 - 21:00
22:00 - 0:00
- Discrete locations
- Individual travelers
- Individual behaviour
- Whole day analysis
Disaggregated
Icons on this and following slides: https://fontawesome.com
MATSim
- Flexible, extensible and well-tested open-source transport simulation framework
- Used by many research groups and companies all over the world
- Extensions for parking behaviour, signal control, location choice, freight, ...
matsim-org/matsim-libs
MATSim
Synthetic demand
MATSim
Mobility simulation
Synthetic demand
MATSim
Decision-making
10:00 - 17:30
17:45 - 21:00
22:00 - 0:00
Mobility simulation
Synthetic demand
MATSim
Decision-making
Mobility simulation
Synthetic demand
MATSim
Decision-making
Mobility simulation
Analysis
Synthetic demand
https://pixabay.com/en/zurich-historic-center-churches-933732/
II. AMoD in Zurich
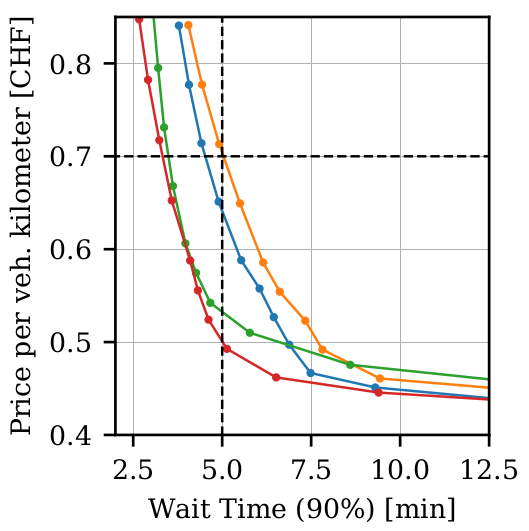
Cost structures?
User preferences?
System impact?
Cost Calculator for automated mobility
Stated preference survey
MATSim simulation
1
2
3
What do we know about automated taxis?
What do we know about automated taxis?
Bösch, P.M., F. Becker, H. Becker and K.W. Axhausen (2018) Cost-based analysis of autonomous mobility services, Transport Policy, 64, 76-91
What do we know about automated taxis?
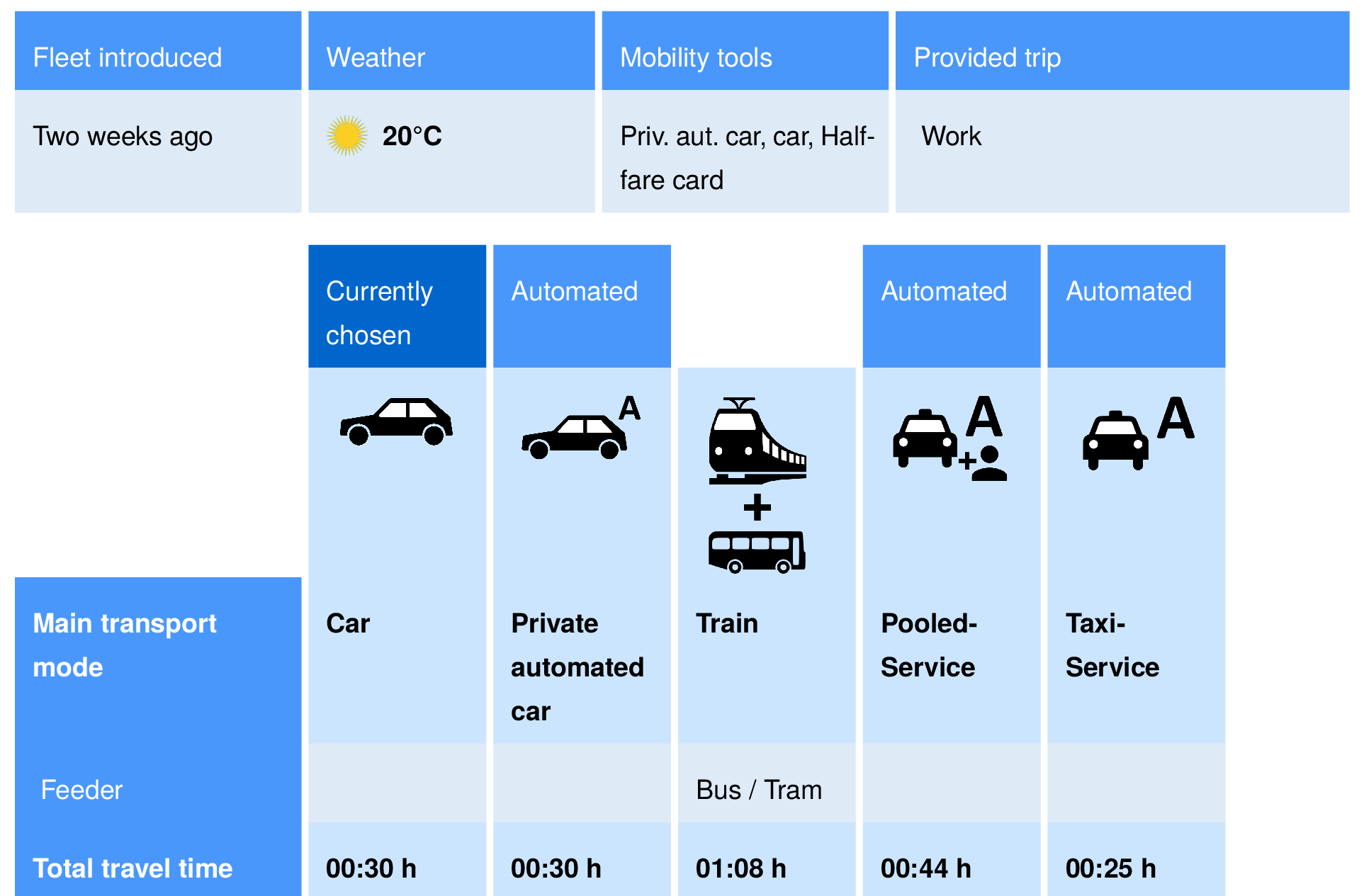
Felix Becker, Institute for Transport Planning and Systems, ETH Zurich.
VTTS
13 CHF/h
AMoD
Taxi
19 CHF/h
Conventional
Car
12 CHF/h
Public
Transport
AMoD
Car by Adrien Coquet from the Noun Project
Bus by Simon Farkas from the Noun Project
Wait by ibrandify from the Noun Project
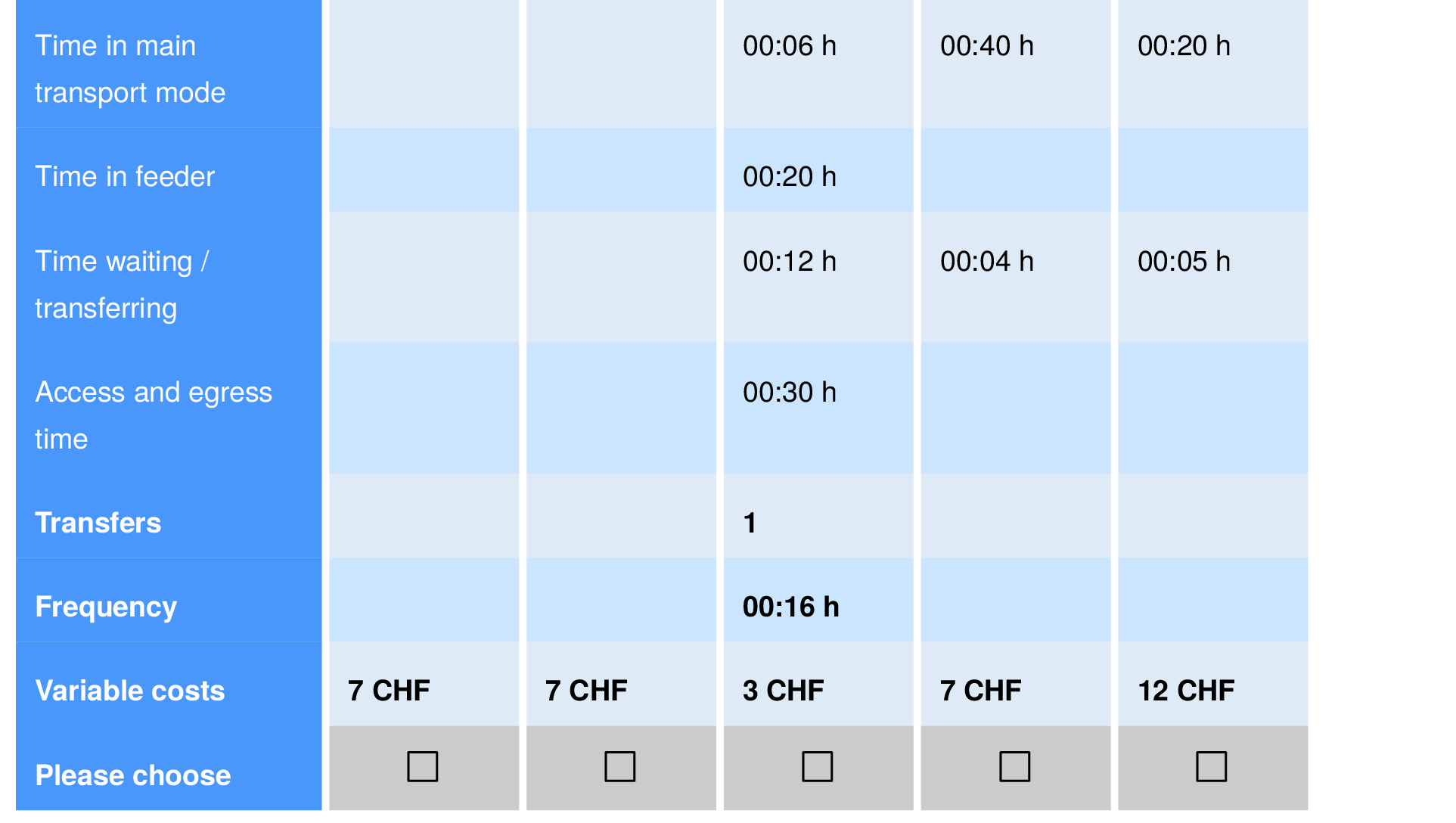
VTTS
13 CHF/h
AMoD
Taxi
19 CHF/h
Conventional
Car
12 CHF/h
Public
Transport
21 CHF/h
32 CHF/h
AMoD
Car by Adrien Coquet from the Noun Project
Bus by Simon Farkas from the Noun Project
Wait by ibrandify from the Noun Project
Model structure
Cost calculator
Plan modification
Discrete Mode Choice Extension
Mobility simulation
Prediction
Price
Trips
- Utilization
- Empty distance, ...
- Travel times
- Wait times, ...
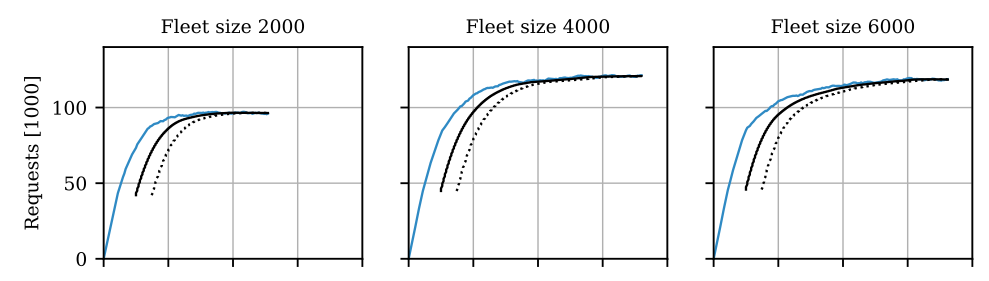
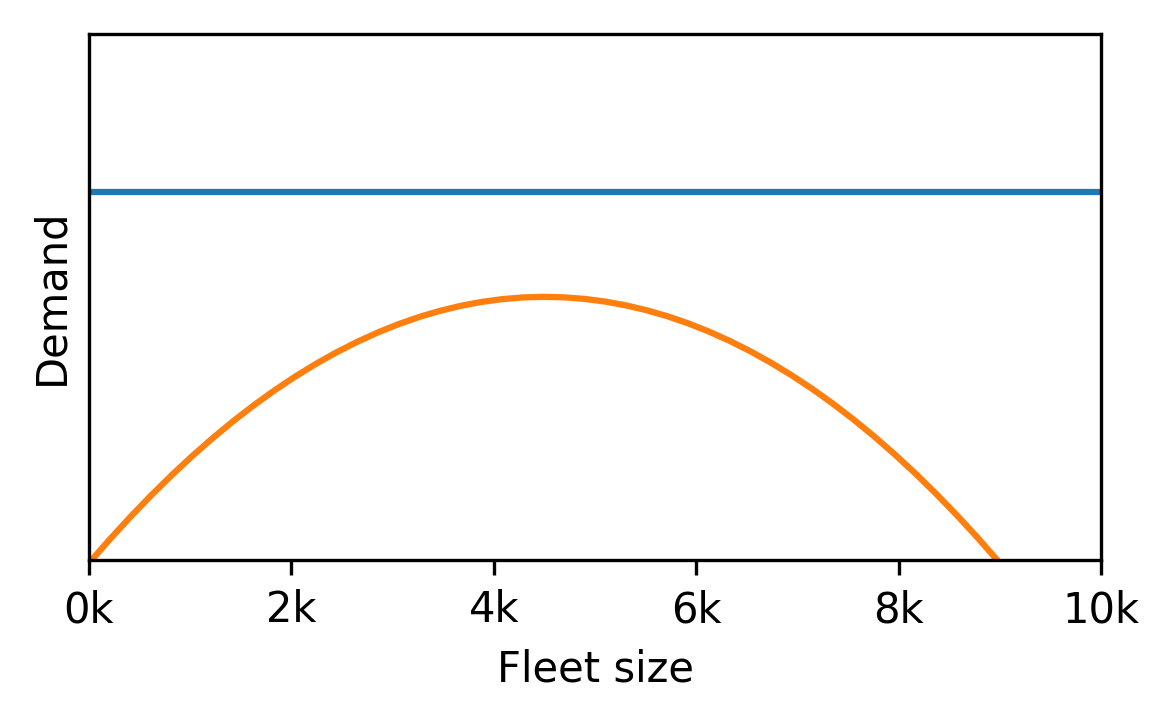
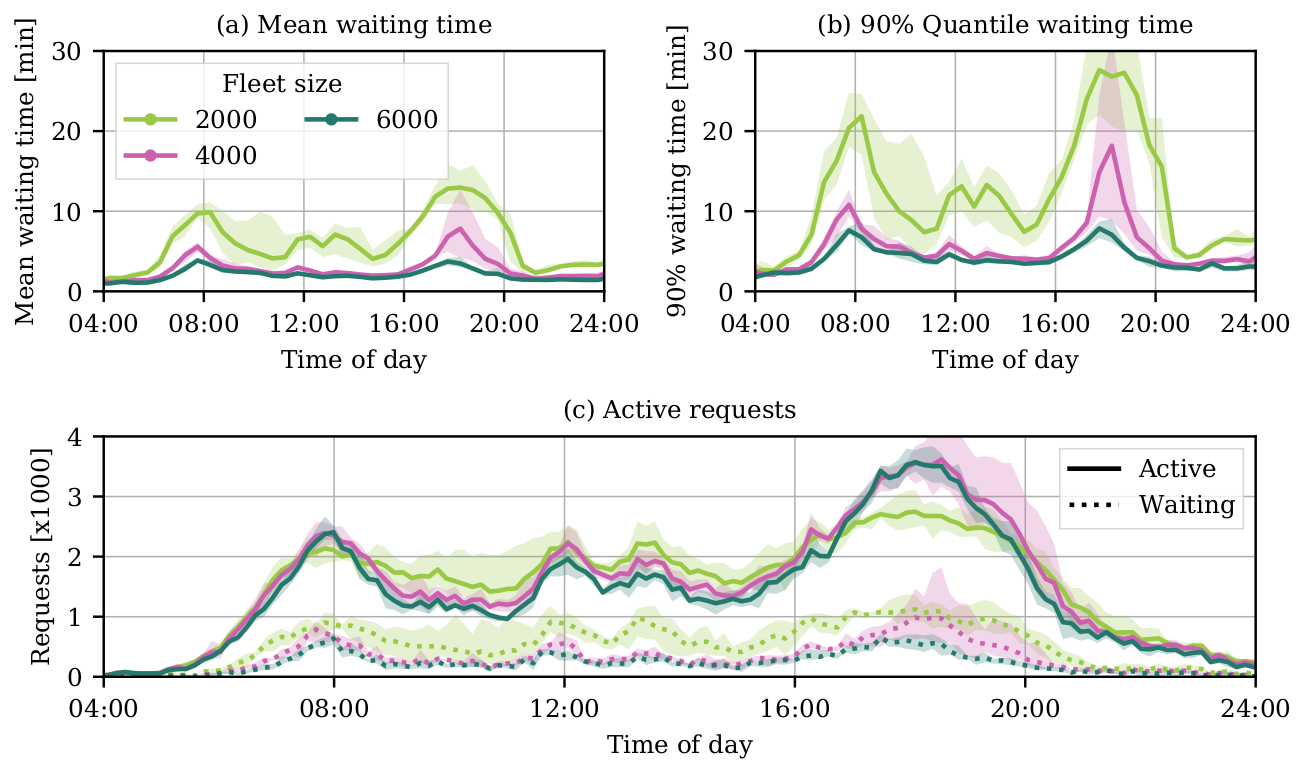
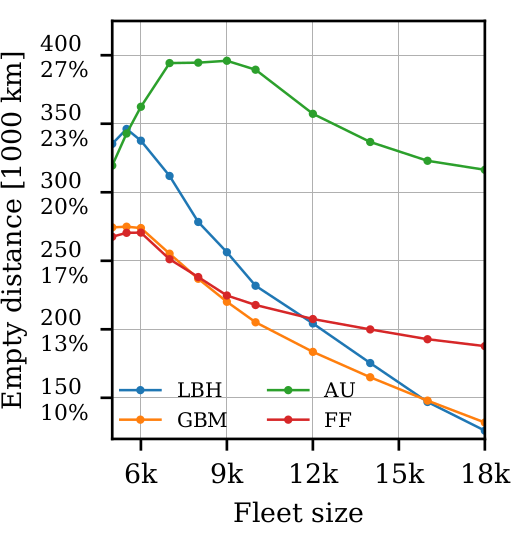
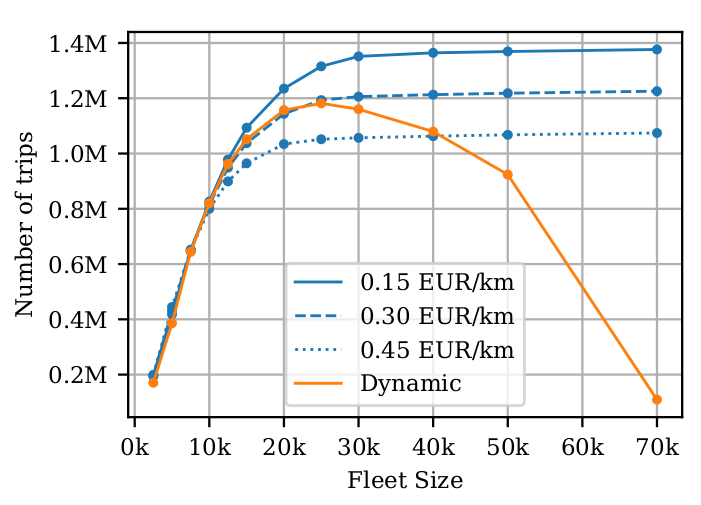
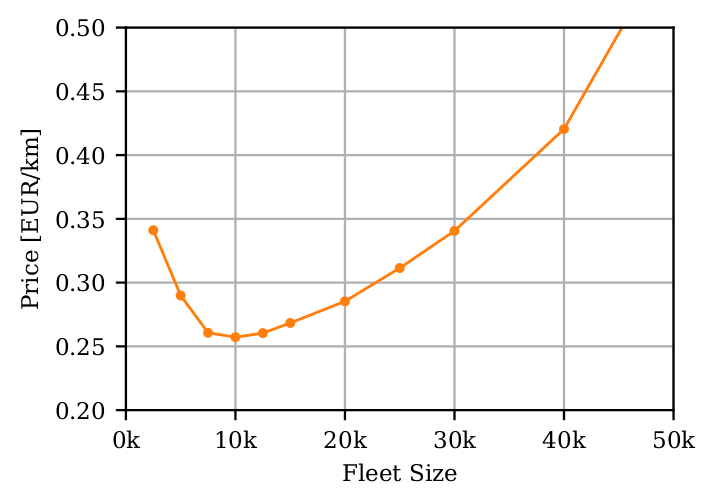
Fleet sizing with dynamic demand
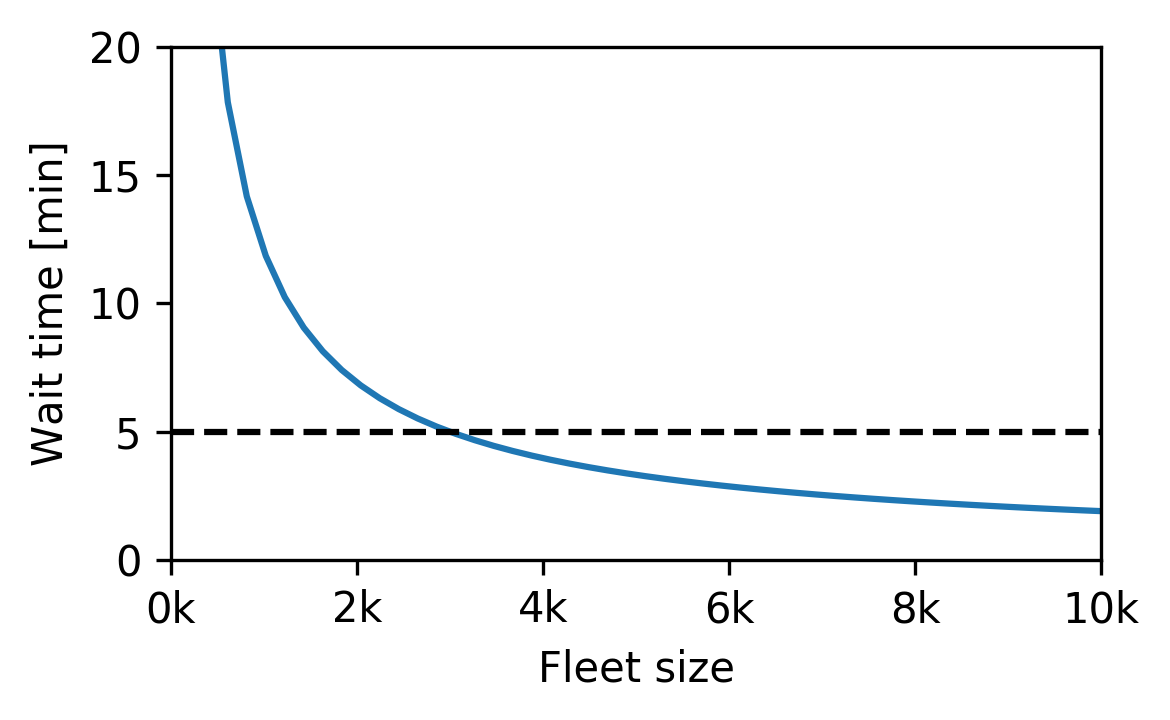
Fleet sizing with dynamic demand
Fleet sizing with dynamic demand
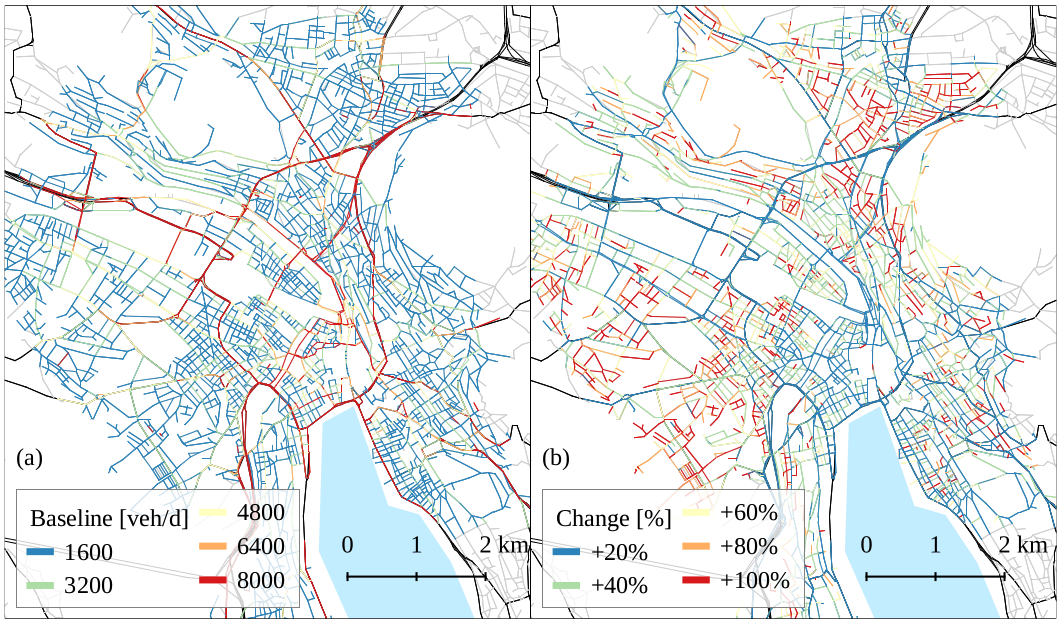
Visualisation
Automated taxi
Pickup
Dropoff
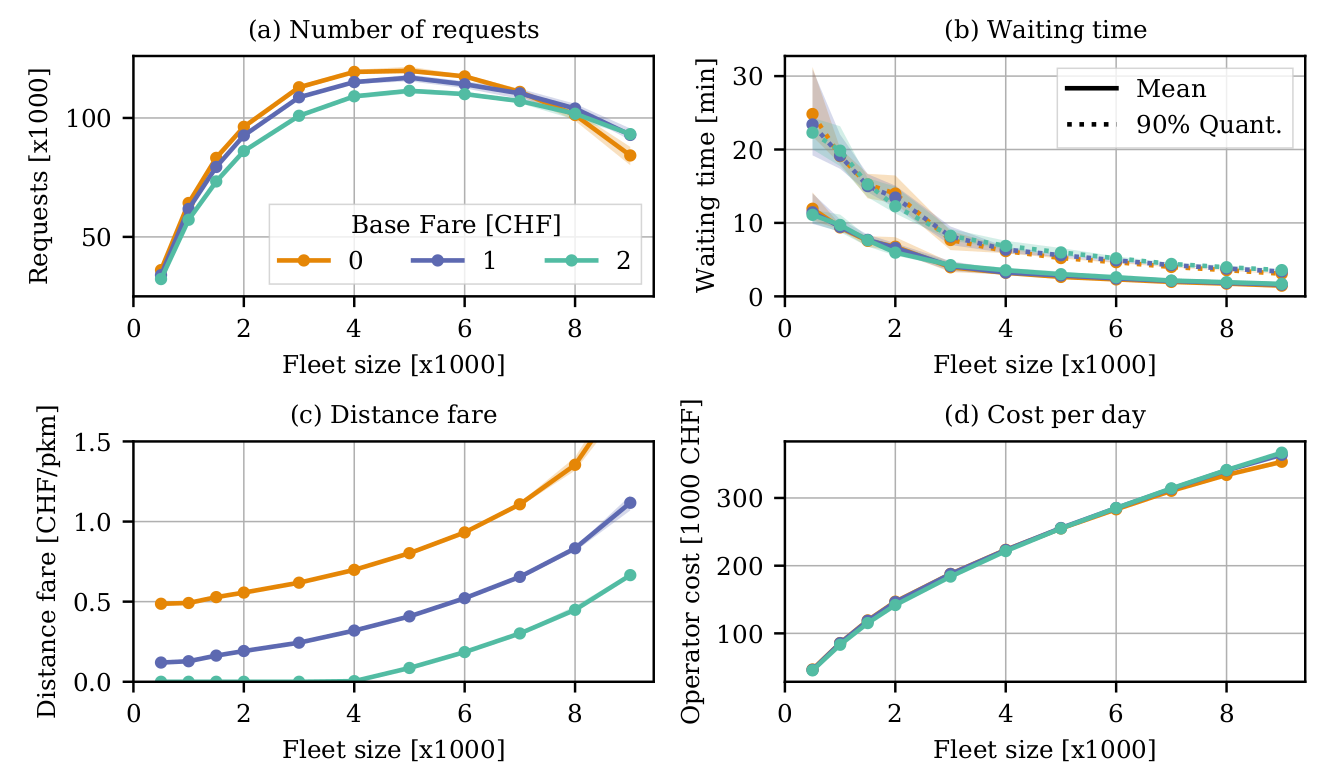
Hörl, S., F. Becker and K.W. Axhausen (2020) Automated Mobility on Demand: A comprehensive simulation study of cost, behaviour and system impact for Zurich
Hörl, S., F. Becker and K.W. Axhausen (2020) Automated Mobility on Demand: A comprehensive simulation study of cost, behaviour and system impact for Zurich
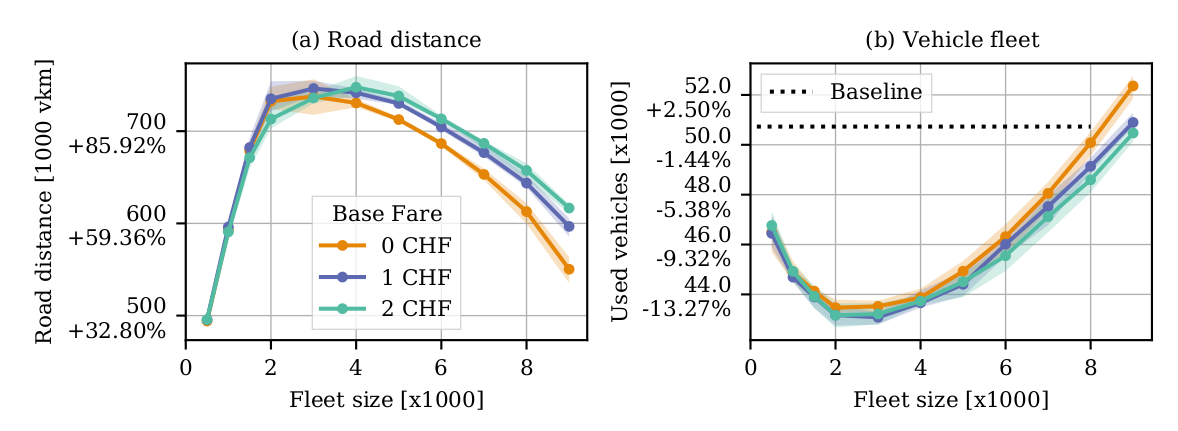
13% reduction in vehicles
100% increase in VKT
Hörl, S., F. Becker and K.W. Axhausen (2020) Automated Mobility on Demand: A comprehensive simulation study of cost, behaviour and system impact for Zurich
100% increase in VKT
Hörl, S., F. Becker and K.W. Axhausen (2020) Automated Mobility on Demand: A comprehensive simulation study of cost, behaviour and system impact for Zurich
Other aspects
Hörl, S., C. Ruch, F. Becker, E. Frazzoli and K.W. Axhausen (2019) Fleet operational policies for automated mobility: a simulation assessment for Zurich, Transportation Research: Part C, 102, 20-32.
Fleet control
Operational constraints
Spatial constraints
Intermodality
Pooling
III. Demand data
https://pixabay.com/en/paris-eiffel-tower-night-city-view-3296269/
Macroscopic four-step model
Generation
Distribution
Mode choice
Assignment
-
Classic way of demand modeling
- Four steps making use of different data sources
- From static to more dynamic mobility decisions
- Multiple possible feedback loops (most common example here)
Macroscopic four-step model
Generation
Distribution
Mode choice
Assignment
- Where do trips appear?
- What is the destination of the trips?
- What transport mode is used?
- What congestion is caused?
Macroscopic four-step model
Generation
Distribution
Mode choice
Assignment
Travel demand
Travel supply
- Characterizes the need for mobility in the population for economic activity, leisure, ...
- Means that allow for mobility
- Road infrastructure, rail network, ...
Macroscopic four-step model
Generation
Distribution
Mode choice
Assignment
Travel demand
Travel supply
- Characterizes the need for mobility in the population for economic activity, leisure, ...
- Means that allow for mobility
- Road infrastructure, rail network, ...
Equilibrium
- Given limited capacity,
how is the system used?
I) Trip Generation
-
Goal: Define statistically where trips starts, i.e. where they are "generated" or produced
- Focus on peak hours in 4S, e.g. morning peak and focus on commuting activity
- Either making use of direct data (e.g. from surveys) or based on population data, land use information, ...
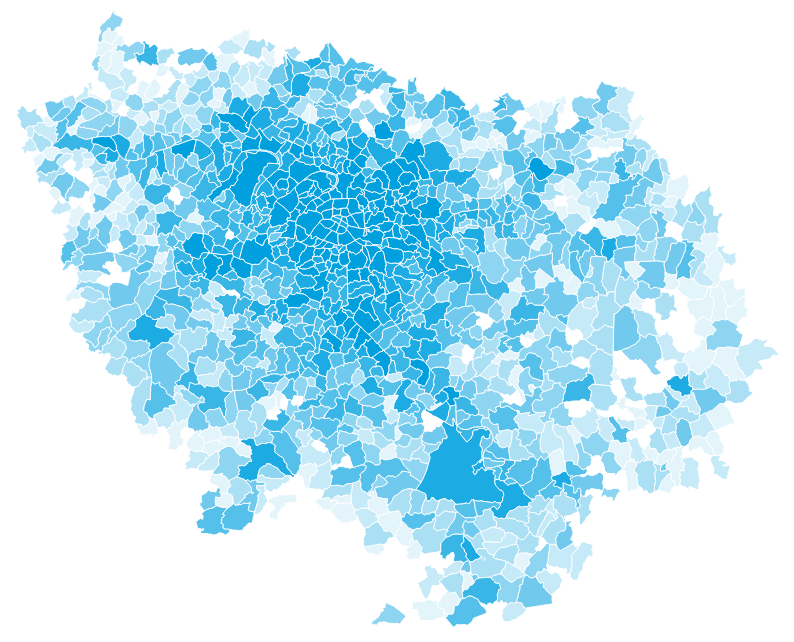
Number of inabitants in Île-de-France
I) Trip Generation
- May be per homogeneous user group, e.g.
- Single-person households
- Multi-persons households
without children - Multi-person households
with children -
Households with retired persons
- Possible to use statistical models
Os,g=f(Xs)
O_{s,g} = f(X_s)
Generated trips
in zone s in group g
Trip generation model
Model inputs
I) Trip Generation
- Example: Linear model based on socioprofessional category (CS):
- Employee
- Worker
- Retired
-
...
- Do we have reference number of trips for some of the zones? Then we can create a model from this formula! Example: Ordinary Least Squares (OLS)
f(X)=∑CSλCS⋅xCS
f(X) = \sum_{CS} \lambda_{CS} \cdot x_{CS}
Model parameters (linear factors)
Census data (inhabitants)
minΛ∑s(f(Xs∣Λ)−O^s)2
\text{min}_\Lambda \sum_s (f(X_s|\Lambda) - \hat O_s)^2
Reference data
II) Trip Distribution
- Goal: Given the produced trips with their origin zone, define where they end = distribute the trips over a set of potential destination
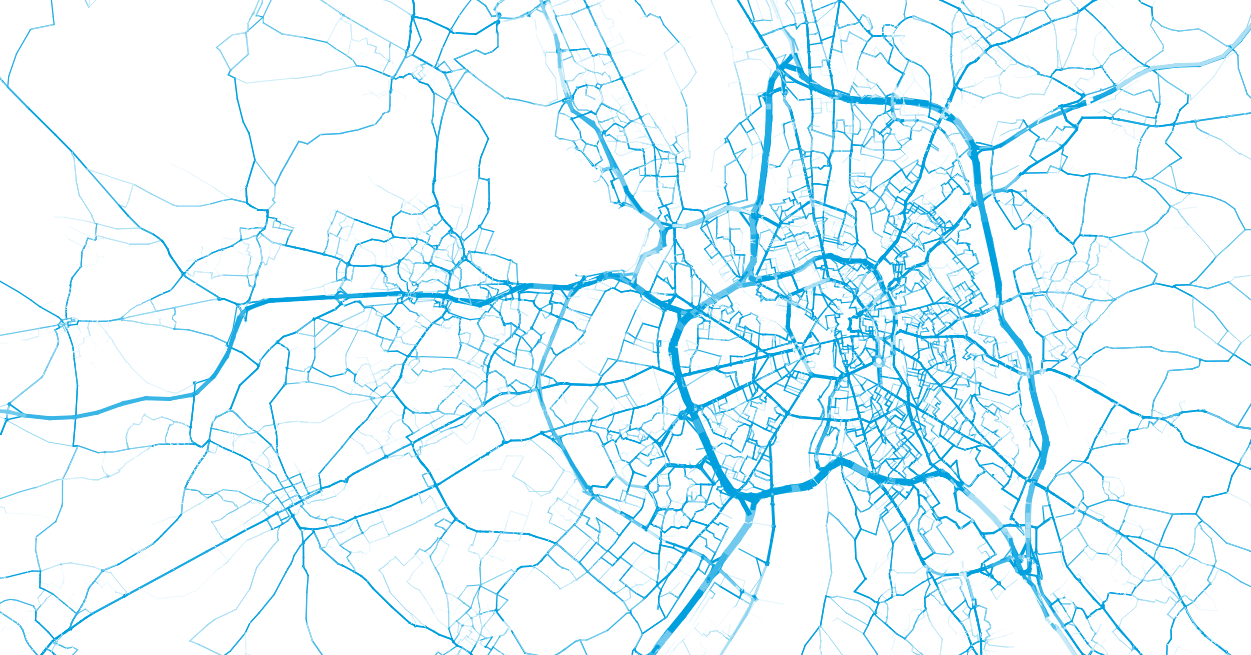
Number of daily commutes arriving from 13th arrondissement
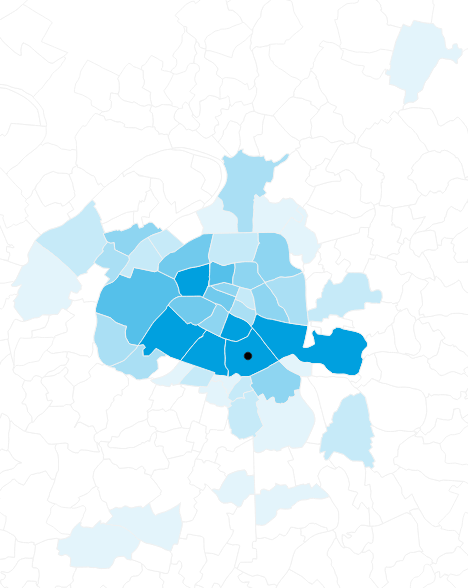
II) Trip Distribution
- Based on trip generation, we want to predict the number of trips going from zone s to zone t
- Various ways to model flows between zones
- Gravity model
- Discrete choice model
-
Maximum entropy
- Can be formulated per group g.
Fs,t=f(Xs,Xt)
F_{s,t} = f(X_s, X_t)
Flow between s and t
Model
| O1 | ... | ... | On | |
|---|---|---|---|---|
| D1 | ||||
| ... | Fst | |||
| ... | ||||
| Dn |
Os
O_s
Dt
D_t
III) Mode choice
-
Goal: Given the infrastructure and the generated OD trips, which mode of transport should be used for them.
- Expressed as mode share: How many percent of the trips on a OD relation are performed with mode m?
P[m]
P[m]
m∈{car,pt,...}
m \in \{ car, pt, ... \}
∑mP[m]=1
\sum_m P[m] = 1
P[m]≥0
P[m] \geq 0
III) Mode choice
-
Utility maximization is important concept in transport planning: Given a set of choices (modes, destinations, ...) we can assign a utility v to each alternative k.
- We assume rational decision makers that always want to choose the alternative with the highest utility.
- Homo oeconomicus
vk=βTX
v_k = \beta^T X
k∗=arg maxk{v1,...,vk,...vK}
k^* = \text{arg max}_k \{ v_1, ..., v_k, ... v_K \}
- Example: Choice between two public transport connections
vk=βtravelTime⋅xk,travelTime+βinterchanges⋅xk,interchanges
v_k = \beta_\text{travelTime} \cdot x_{k, \text{travelTime}} + \beta_\text{interchanges} \cdot x_{k, \text{interchanges}}
Connection A
xA,travelTime=20 min
x_{A, \text{travelTime}} = 20\ \text{min}
Connection B
xB,travelTime=30 min
x_{B, \text{travelTime}} = 30\ \text{min}
xB,interchanges=0
x_{B, \text{interchanges}} = 0
xA,interchanges=1
x_{A, \text{interchanges}} = 1
-0.6
-1.0
-0.6 * 20 - 1.0 * 1 = -13
-0.6 * 30 - 1.0 * 0 = -19
Connection A is better alternative.
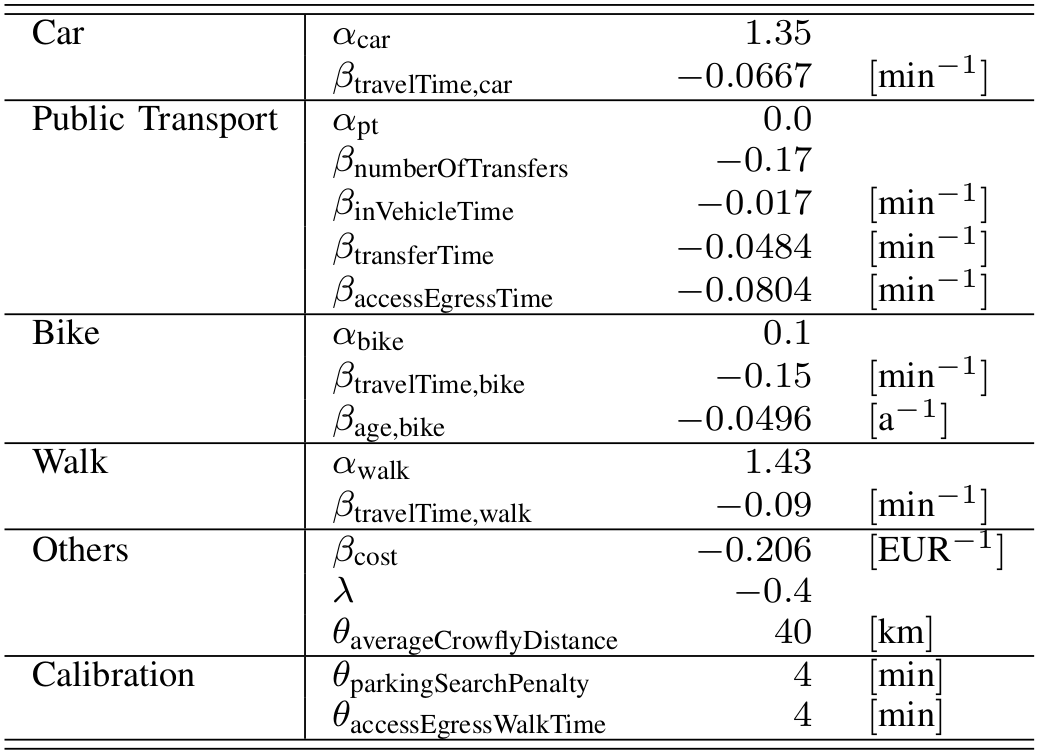
III) Mode choice
III) Mode choice
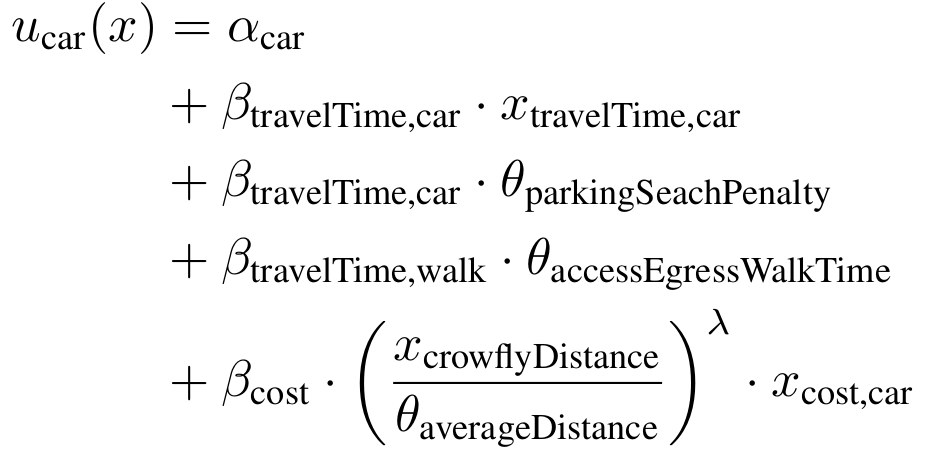
- Example: Mode choice model
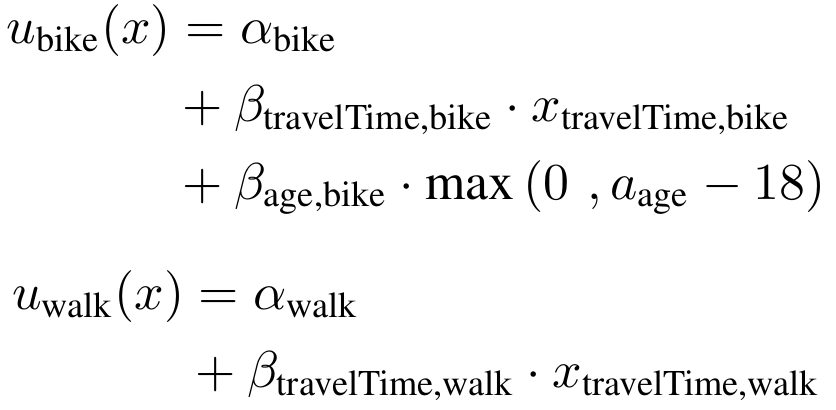
( IV: Assignment )
- Last step of 4S model
- What are resulting flows on the roads?
- What are the resulting travel times?
( IV: Assignment )
- Example: Two routes
- Travellers on Route A:
- Travellers on Route B:
- Total travellers from S to E:
- Travel time route A (normal road):
- Travel time route B (highway):
- Wardrop principle: Travellers tend to minimize their travel time.
S
E
Route A
Route B
nA
n_{A}
nB
n_{B}
N=nA+nB
N = n_{A} + n_{B}
tA(nA)=500+nA⋅2
t_A(n_A) = 500 + n_A \cdot 2
tB(nB)=1000+nB⋅1
t_B(n_B) = 1000 + n_B \cdot 1
How many people use each road? What are the travel times?
( IV: Assignment )
S
E
Route A
- Example: Two routes
- If travel time on A is shorter than B, people would switch to B, and vice versa. Hence, travel times, must be in equilibirum!
- This gives
- If travel time on A is shorter than B, people would switch to B, and vice versa. Hence, travel times, must be in equilibirum!
N=nA+nB
N = n_{A} + n_{B}
tA(nA)=500+nA⋅2
t_A(n_A) = 500 + n_A \cdot 2
tB(nB)=1000+nB⋅1
t_B(n_B) = 1000 + n_B \cdot 1
tA(nA)=tB(nB)
t_A(n_A) = t_B(n_B)
500+2⋅nA=1000+1⋅nB
500 + 2 \cdot n_A = 1000 + 1 \cdot n_B
nA=N−nB
n_A = N - n_B
(*)
from (**)
(**)
Route B
( IV: Assignment )
S
E
Route A
- Example: Two routes
- If travel time on A is shorter than B, people would switch to B, and vice versa. Hence, travel times, must be in equilibirum!
- This gives
- If travel time on A is shorter than B, people would switch to B, and vice versa. Hence, travel times, must be in equilibirum!
N=nA+nB
N = n_{A} + n_{B}
tA(nA)=500+nA⋅2
t_A(n_A) = 500 + n_A \cdot 2
tB(nB)=1000+nB⋅1
t_B(n_B) = 1000 + n_B \cdot 1
tA(nA)=tB(nB)
t_A(n_A) = t_B(n_B)
500+2⋅nA=1000+1⋅nB
500 + 2 \cdot n_A = 1000 + 1 \cdot n_B
nA=N−nB
n_A = N - n_B
(*)
from (**)
(**)
Route B
N = 1000
( IV: Assignment )
S
E
Route A
- Example: Two routes
- If travel time on A is shorter than B, people would switch to B, and vice versa. Hence, travel times, must be in equilibirum!
- This gives
- If travel time on A is shorter than B, people would switch to B, and vice versa. Hence, travel times, must be in equilibirum!
N=nA+nB
N = n_{A} + n_{B}
tA(nA)=500+nA⋅2
t_A(n_A) = 500 + n_A \cdot 2
tB(nB)=1000+nB⋅1
t_B(n_B) = 1000 + n_B \cdot 1
tA(nA)=tB(nB)
t_A(n_A) = t_B(n_B)
500+2⋅nA=1000+1⋅nB
500 + 2 \cdot n_A = 1000 + 1 \cdot n_B
nA=N−nB
n_A = N - n_B
(*)
from (**)
(**)
Route B
nA=433.33
n_A = 433.33
nB=566.66
n_B = 566.66
tA=tB=1366.66
t_A = t_B = 1366.66
N = 1000
( IV: Assignment )
- What about many different routes between two points?
- What about many different start/end points in a network?
- Wardrop defined general formulation, leading to a game-theoretic Nash equilibrium
minx∑a∫0xata(xa)dx
\text{min}_x \sum_a \int_0^{x_a} t_a(x_a) \text{d}x
∑kfkrs=qrs ∀r,s
\sum_k f_k^{rs} = q_{rs} \ \ \ \forall r, s
xa=∑r∑s∑kδk,arsfkrs ∀a
x_a = \sum_r \sum_s \sum_k \delta^{rs}_{k,a} f_k^{rs} \ \ \ \forall a
fkrs≥0
f_k^{rs} \geq 0
xa≥0
x_a \geq 0
s.t.
s.t.
How to disaggregate the demand?
Population census (RP)
Income data (FiLoSoFi)
Synthetic travel demand
Population census (RP)
Income data (FiLoSoFi)
Commuting data (RP-MOB)
Synthetic travel demand
Population census (RP)
Income data (FiLoSoFi)
Commuting data (RP-MOB)
Household travel survey (EDGT)
0:00 - 8:00
08:30 - 17:00
17:30 - 0:00
0:00 - 9:00
10:00 - 17:30
17:45 - 21:00
22:00 - 0:00
Synthetic travel demand
Population census (RP)
Income data (FiLoSoFi)
Commuting data (RP-MOB)
Household travel survey (EDGT)
Enterprise census (SIRENE)
Address database (BD-TOPO)
Synthetic travel demand
Population census (RP)
Income data (FiLoSoFi)
Commuting data (RP-MOB)
Household travel survey (EDGT)
Enterprise census (SIRENE)
Address database (BD-TOPO)
Person ID
Age
Gender
Home (X,Y)
1
43
male
(65345, ...)
2
24
female
(65345, ...)
3
9
female
(65345, ...)
Synthetic travel demand
Population census (RP)
Income data (FiLoSoFi)
Commuting data (RP-MOB)
Household travel survey (EDGT)
Enterprise census (SIRENE)
Address database (BD-TOPO)
Person ID
Activity
Start
End
Loc.
523
home
08:00
(x,y)
523
work
08:55
18:12
(x,y)
523
shop
19:10
19:25
(x,y)
523
home
19:40
(x,y)
Synthetic travel demand
Population census (RP)
Income data (FiLoSoFi)
Commuting data (RP-MOB)
Household travel survey (EDGT)
Enterprise census (SIRENE)
OpenStreetMap
GTFS (SYTRAL / SNCF)
Address database (BD-TOPO)
Synthetic travel demand
Population census (RP)
Income data (FiLoSoFi)
Commuting data (RP-MOB)
Household travel survey (EDGT)
Enterprise census (SIRENE)
OpenStreetMap
GTFS (SYTRAL / SNCF)
Address database (BD-TOPO)
Synthetic travel demand
Population census (RP)
Income data (FiLoSoFi)
Commuting data (RP-MOB)
National HTS (ENTD)
Enterprise census (SIRENE)
OpenStreetMap
GTFS (SYTRAL / SNCF)
Address database (BD-TOPO)
Synthetic travel demand
EDGT
Population census (RP)
Income data (FiLoSoFi)
Commuting data (RP-MOB)
Enterprise census (SIRENE)
OpenStreetMap
GTFS (SYTRAL / SNCF)
Address database (BD-TOPO)
Synthetic travel demand
Open
Data
Open
Software
+
=
Reproducible research
Integrated testing
National HTS (ENTD)
EDGT
Population census (RP)
Income data (FiLoSoFi)
Commuting data (RP-MOB)
Enterprise census (SIRENE)
OpenStreetMap
GTFS (SYTRAL / SNCF)
Address database (BD-TOPO)
Synthetic travel demand
Open
Data
Open
Software
+
=
Reproducible research
Integrated testing
National HTS (ENTD)
EDGT
Current use cases
Nantes
- Noise modeling
Current use cases
Lille
- Park & ride applications
- Road pricing
Current use cases
Toulouse
- Placement and use of shared offices
Current use cases
Rennes
- Micromobility simulation
Current use cases
Paris / Île-de-France
- Scenario development for sustainable urban transformation
- New mobility services
Mahdi Zargayouna (GRETTIA / Univ. Gustave Eiffel)
Nicolas Coulombel (LVMT / ENPC)
Current use cases
Paris / Île-de-France
- Cycling simulation
Current use cases
Paris / Île-de-France
- Simulation of dynamic mobility services
- Fleet control through reinforcement learning
Current use cases
Lyon (IRT SystemX)
- Low-emission first/last mile logistics
Current use cases
Current use cases
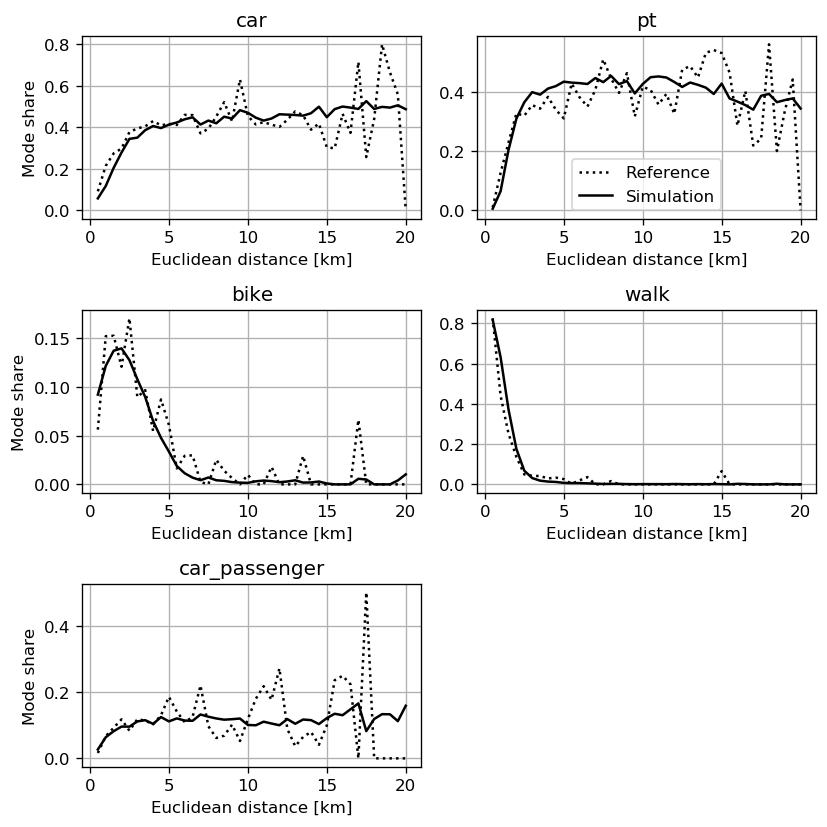
Balac, M., Hörl, S. (2021) Synthetic population for the state of California based on open-data: examples of San Francisco Bay area and San Diego County, presented at 100th Annual Meeting of the Transportation Research Board, Washington, D.C.
Sallard, A., Balac, M., Hörl, S. (2021) Synthetic travel demand for the Greater São Paulo Metropolitan Region, based on open data, Under Review
Sao Paulo, San Francisco Bay area, Los Angeles five-county area, Switzerland, Montreal, Quebec City, Jakarta, Casablanca, ...
Emissions in Paris
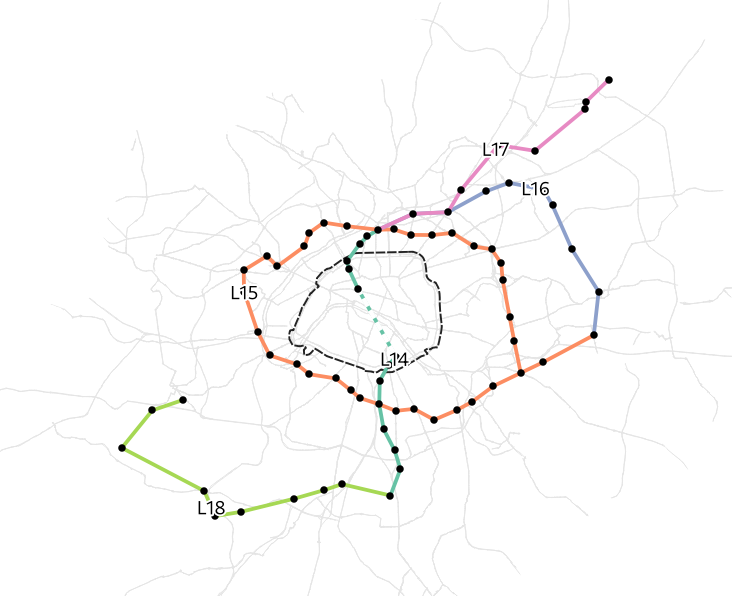
Grand Paris Express
Automated taxis in Paris
Automated taxis in Paris
IV. Logistics
LEAD Project
Low-emission Adaptive last-mile logistics supporting on-demand economy through Digital Twins
- H2020 Project from 2020 to 2023
- Six living labs with different innovative logistics concepts
- Lyon, The Hague, Madrid, Budapest, Porto, Oslo
- One partner for implementation and one for research each
- Development of a generic modeling library for last-mile logistics scenario simulation and analysis
Lyon Living Lab
- Peninsula Confluence between Saône and Rhône
- Interesting use case as there are limited access points
- Implementation of an urban consolidation center (UCC) to collect the flow of goods and organize last-mile distribution
- using cargo-bikes
- using electric robots
- and others
- Analysis and modeling through
- Flow estimation through cameras
- Simulation of future scenarios
- Focus on parcel deliveries due to data availability
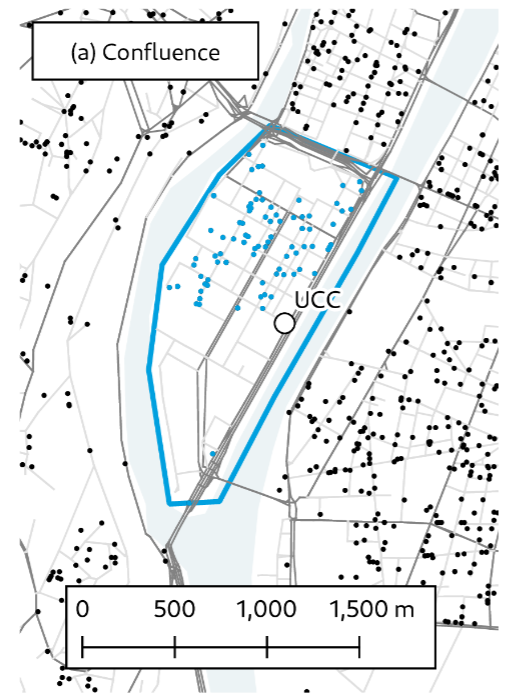
Modeling methodology
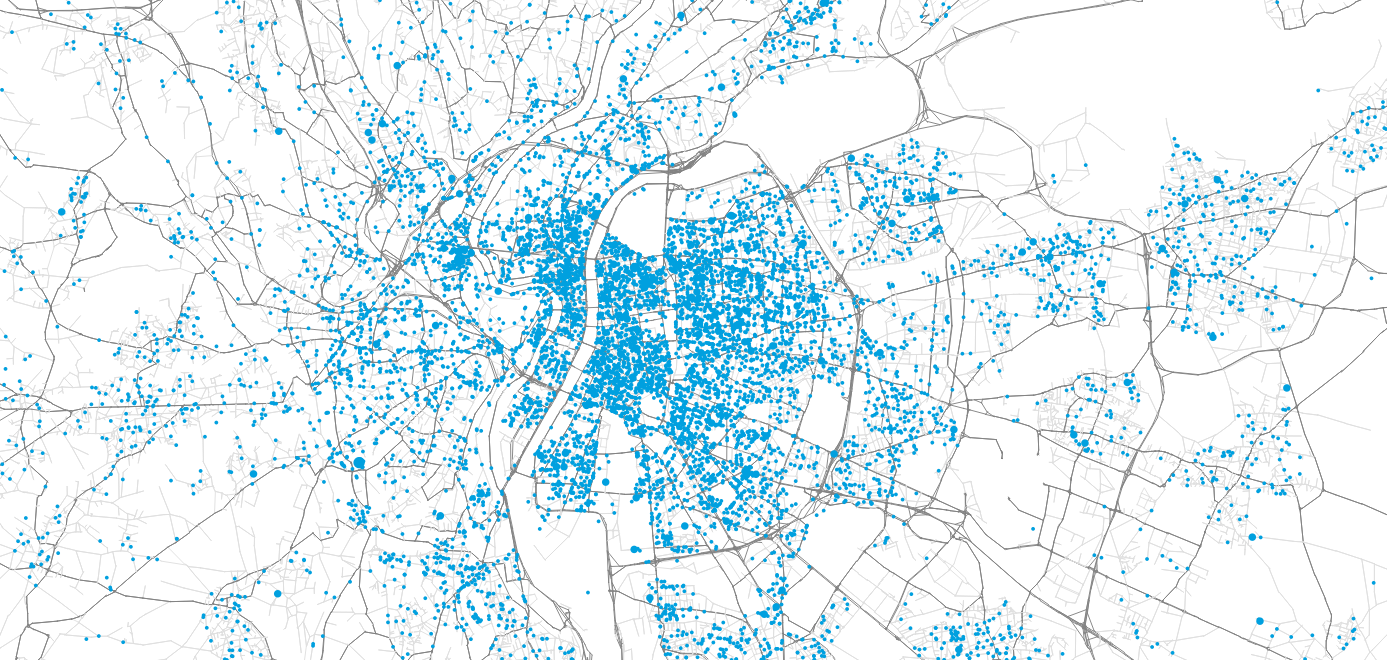
Agent-based simulation of Lyon
Demand in parcel deliveries
Distribution by operators
KPI Calculation
- Main question: What is the impact on traffic and population of implementing an Urban Consolidation Center in Confluence?
- Focus on B2C parcel deliveries due to data availability
Methodology: Parcel demand
Synthetic population
+
Synthetic population
Out-of-home purchase survey
Achats découplés des ménages
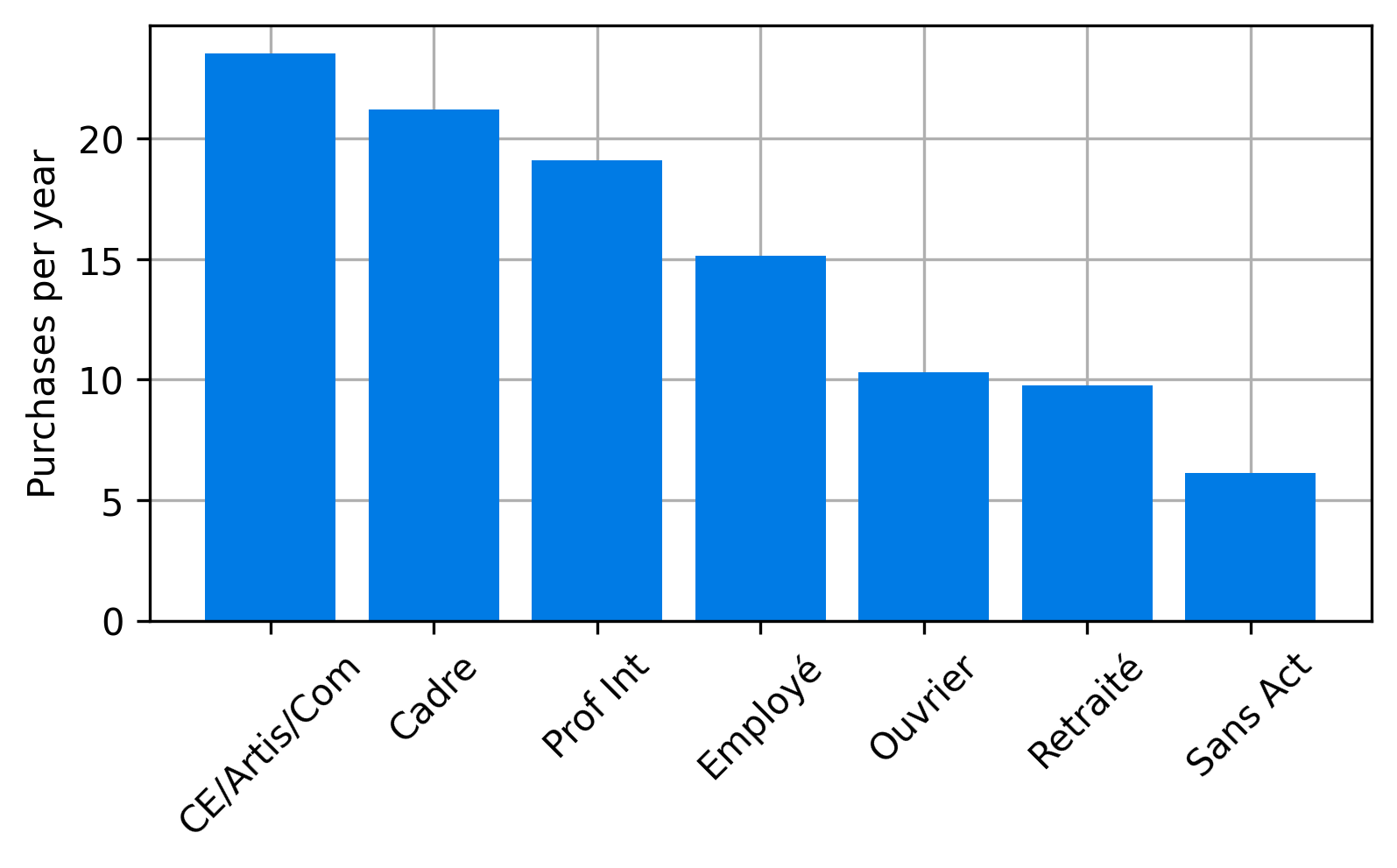
Based on sociodemographic attributes of the households, parcels are generated for the city on an average day.
Gardrat, M., 2019. Méthodologie d’enquête: le découplage de l’achat et de la récupération des marchandises par les ménages. LAET, Lyon, France.
Methodology: Parcel demand
Synthetic population
+
Synthetic population
Out-of-home purchase survey
Achats découplés des ménages
Based on sociodemographic attributes of the households, parcels are generated for the city on an average day.
Gardrat, M., 2019. Méthodologie d’enquête: le découplage de l’achat et de la récupération des marchandises par les ménages. LAET, Lyon, France.
Methodology: Parcel demand
Synthetic population
+
Synthetic population
Out-of-home purchase survey
Achats découplés des ménages
Based on sociodemographic attributes of the households, parcels are generated for the city on an average day.
Gardrat, M., 2019. Méthodologie d’enquête: le découplage de l’achat et de la récupération des marchandises par les ménages. LAET, Lyon, France.
Methodology: Parcel demand
Synthetic population
+
Synthetic population
Out-of-home purchase survey
Achats découplés des ménages
Based on sociodemographic attributes of the households, parcels are generated for the city on an average day.
Gardrat, M., 2019. Méthodologie d’enquête: le découplage de l’achat et de la récupération des marchandises par les ménages. LAET, Lyon, France.
Methodology: Parcel demand
Synthetic population
Gardrat, M., 2019. Méthodologie d’enquête: le découplage de l’achat et de la récupération des marchandises par les ménages. LAET, Lyon, France.
+
Synthetic population
Out-of-home purchase survey
Achats découplés des ménages
Based on sociodemographic attributes of the households, parcels are generated for the city on an average day.
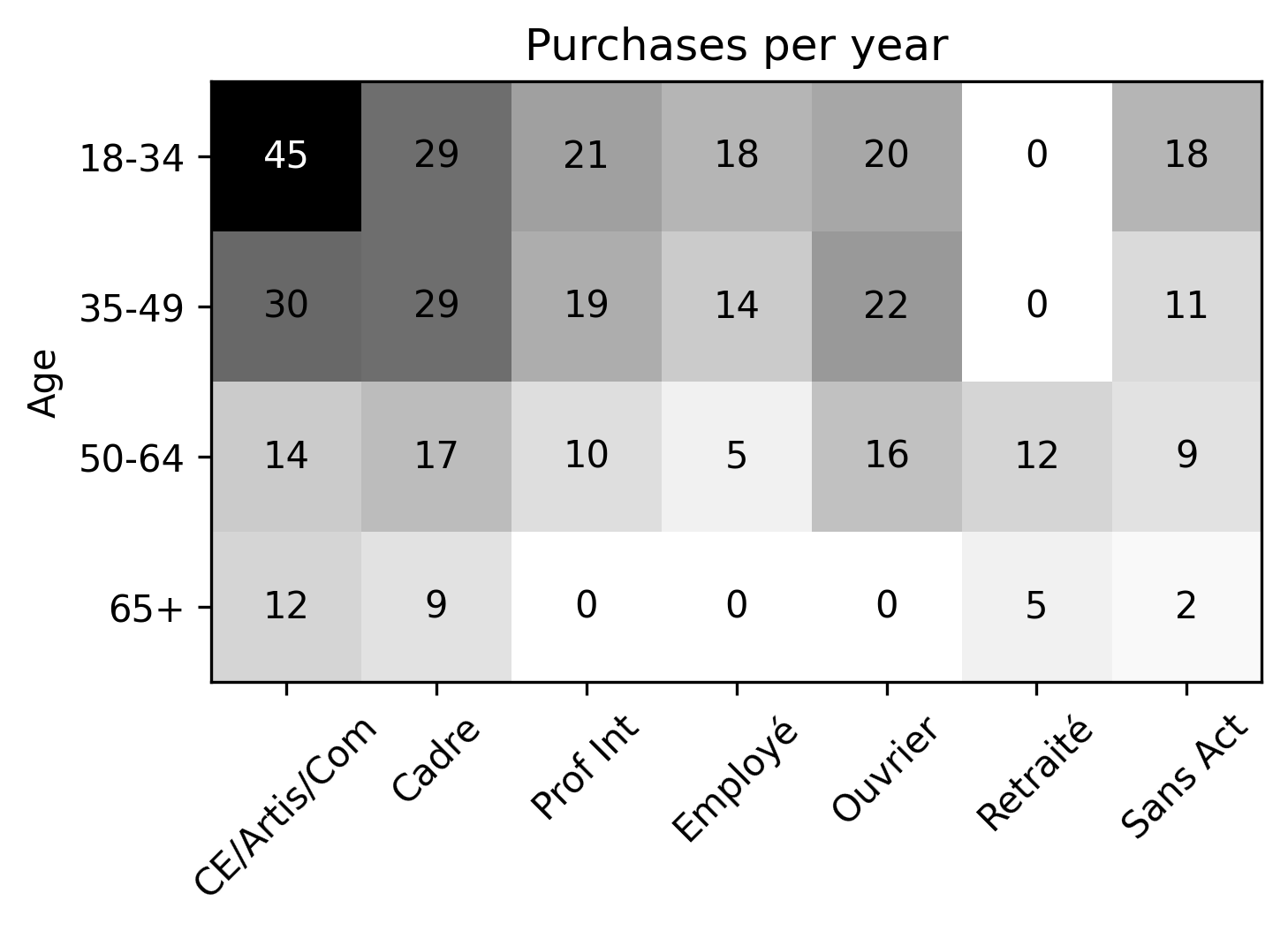
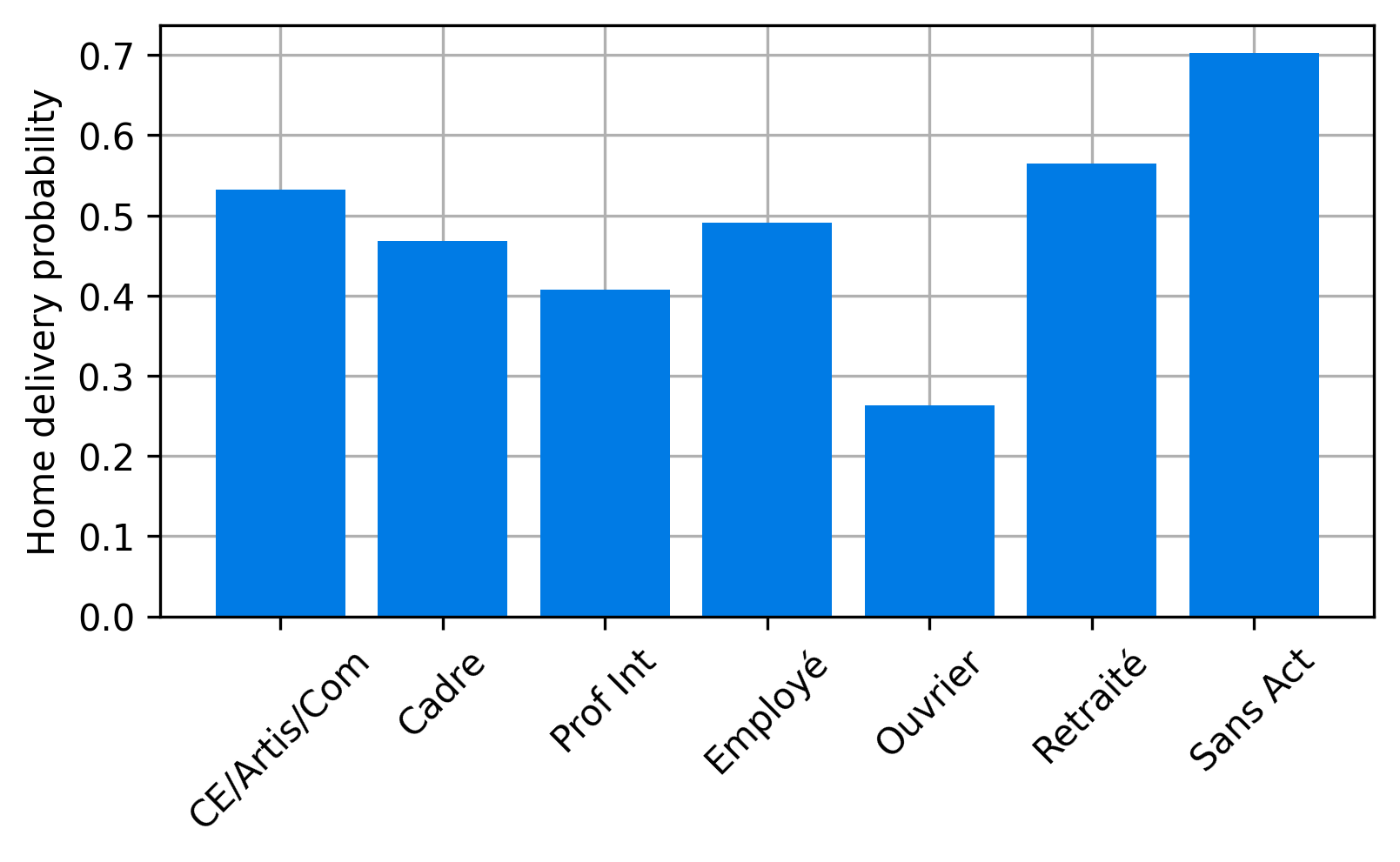
Iterative proportional fitting (IFP)
- Based on synthetic population, find average number of purchases delivered to a household defined by socioprofesional class, age of the reference person and household size per day.
μa,h,s=ds⋅365wa,h,s
\mu_{a,h,s} = d_{s} \cdot \frac{w_{a,h,s}}{365}
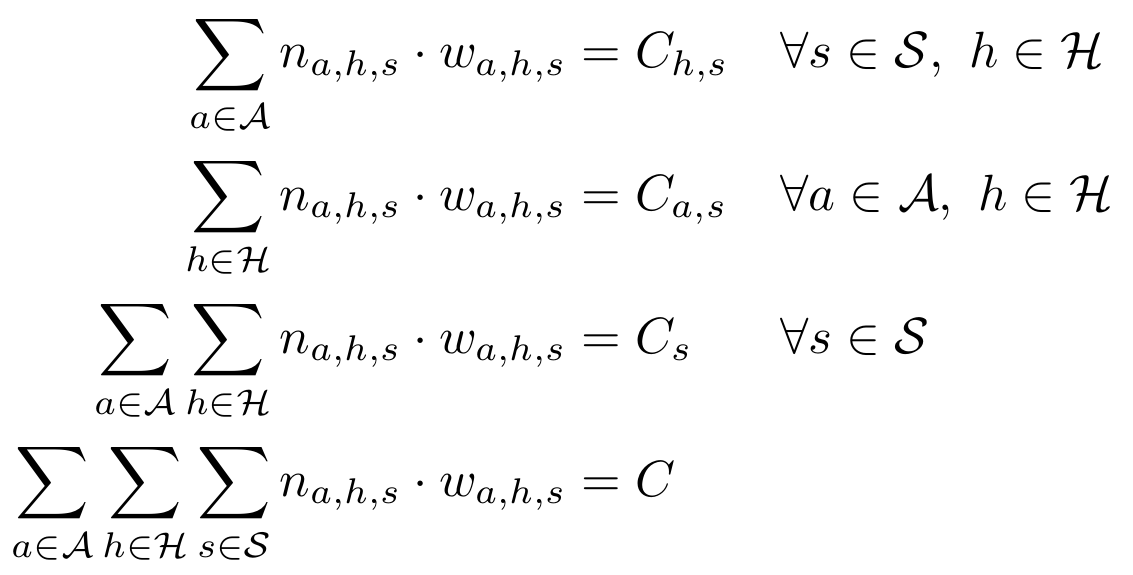
Methodology: Parcel demand
Synthetic population
Gardrat, M., 2019. Méthodologie d’enquête: le découplage de l’achat et de la récupération des marchandises par les ménages. LAET, Lyon, France.
+
Synthetic population
Out-of-home purchase survey
Achats découplés des ménages
Based on sociodemographic attributes of the households, parcels are generated for the city on an average day.
Maximum entropy approach
- We now the average number of parcels, but we do not now the distribution of the number of parcels for a household on an average day.
- We know it must be non-negative, and we know the mean.
- Without additional data, we assume maximum entropy distribution, which is Exponential in this case.
F(N≤n)=Pois(μ)
F(N \leq n) = \text{Pois}(\mu)
Methodology: Parcel demand
Synthetic population
Gardrat, M., 2019. Méthodologie d’enquête: le découplage de l’achat et de la récupération des marchandises par les ménages. LAET, Lyon, France.
+
Synthetic population
Out-of-home purchase survey
Achats découplés des ménages
Based on sociodemographic attributes of the households, parcels are generated for the city on an average day.
Methodology: Parcel demand
Synthetic population
Gardrat, M., 2019. Méthodologie d’enquête: le découplage de l’achat et de la récupération des marchandises par les ménages. LAET, Lyon, France.
+
Synthetic population
Out-of-home purchase survey
Achats découplés des ménages
Based on sociodemographic attributes of the households, parcels are generated for the city on an average day.
Methodology: Parcel demand
Synthetic population
Gardrat, M., 2019. Méthodologie d’enquête: le découplage de l’achat et de la récupération des marchandises par les ménages. LAET, Lyon, France.
+
Synthetic population
Out-of-home purchase survey
Achats découplés des ménages
Based on sociodemographic attributes of the households, parcels are generated for the city on an average day.
Methodology: Parcel demand
Synthetic population
Gardrat, M., 2019. Méthodologie d’enquête: le découplage de l’achat et de la récupération des marchandises par les ménages. LAET, Lyon, France.
+
Synthetic population
Out-of-home purchase survey
Achats découplés des ménages
Based on sociodemographic attributes of the households, parcels are generated for the city on an average day.
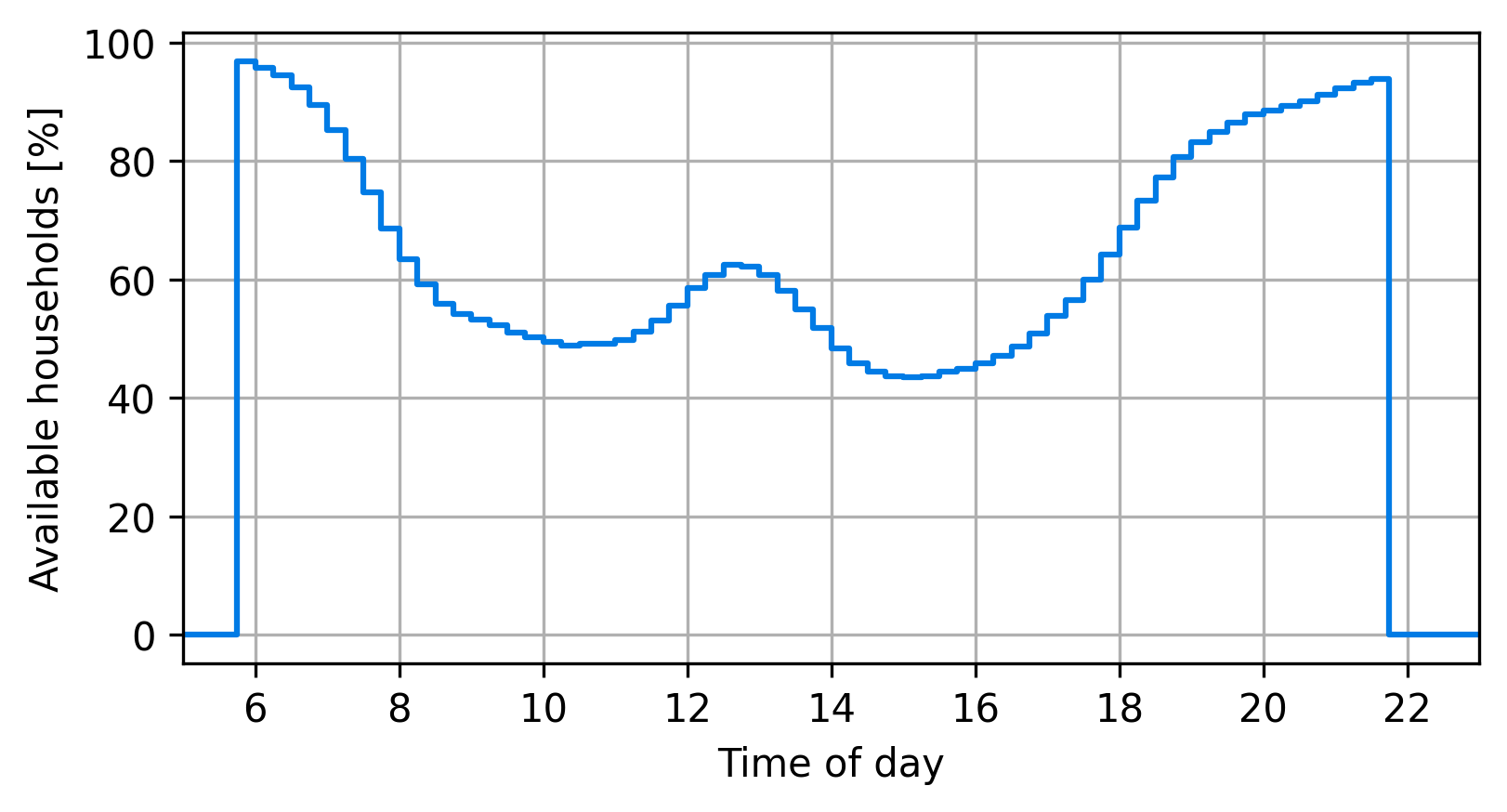
Presence of household members
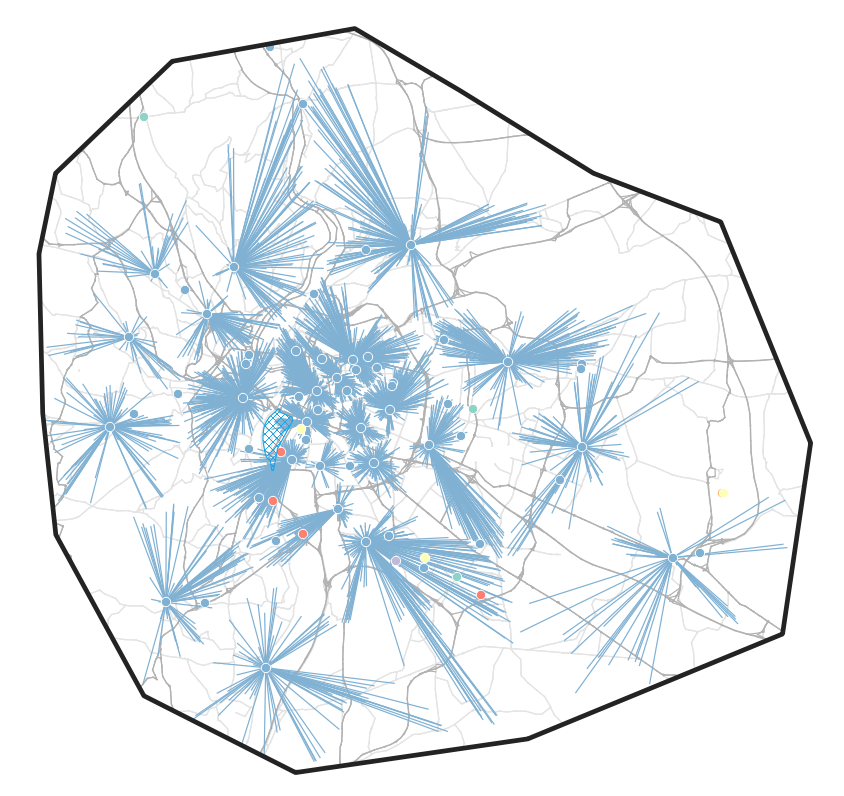
Methodology: Route optimization
Using a heursitic routing solver, an optimal distribution scheme per distribution center is obtained to arrive at a lower bound estimate for the distance covered for the deliveries.
JSprit
First case study
Hörl, S. and J. Puchinger (2021) From synthetic population to parcel demand: Modeling pipeline and case study for last-mile deliveries in Lyon, Working paper.
Solve VRP-TW based on generated parcels and household presence
JSprit
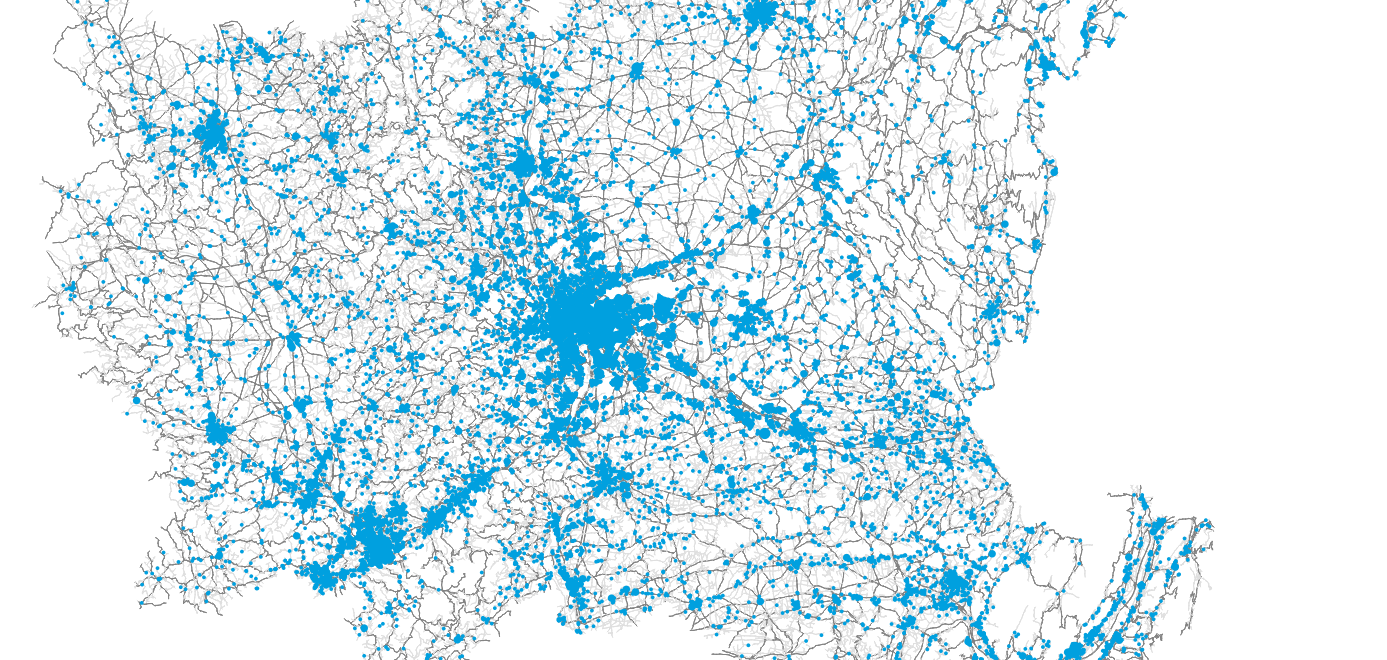
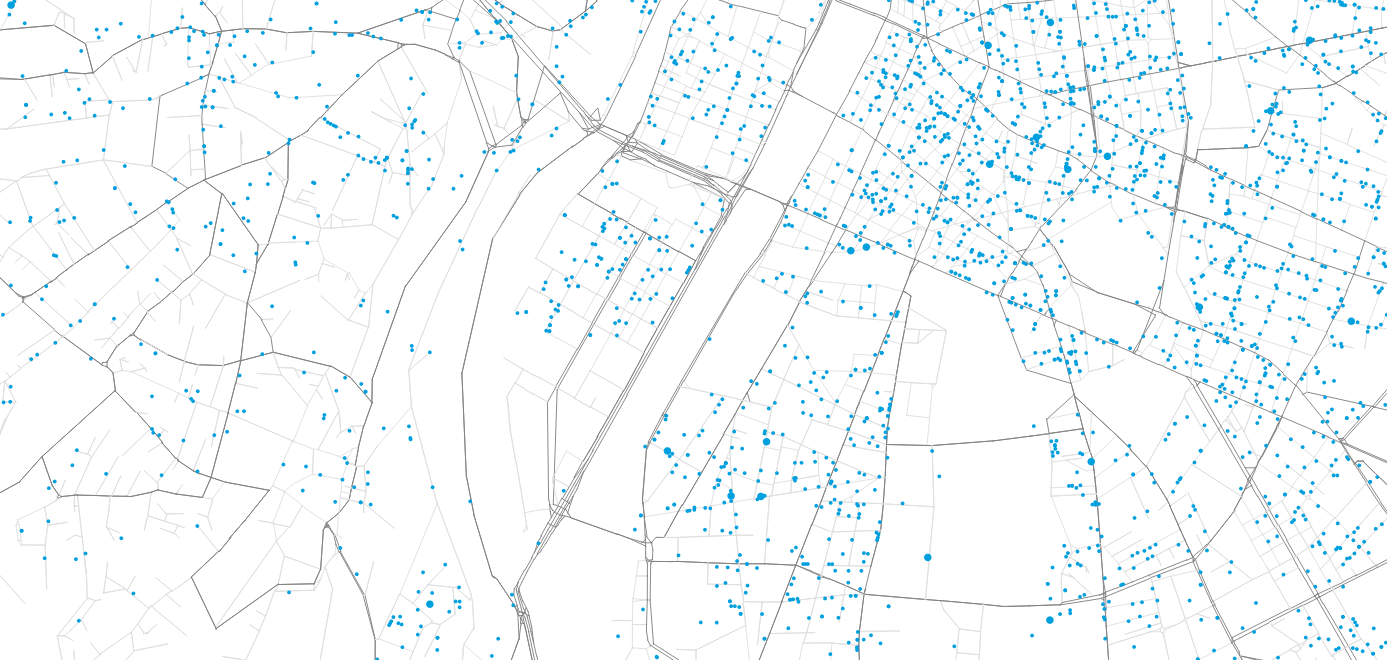
Scaling up: City-wide baseline
Using shares of customer preference, parcels are assigned to operators and the closest distribution centers.
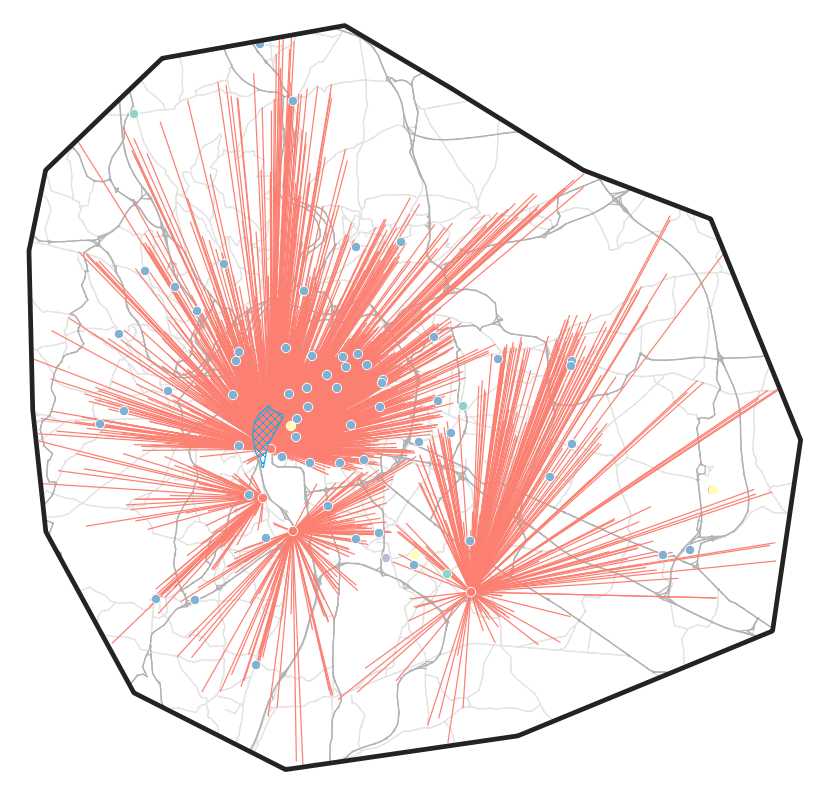
SIRENE: Delivery centers
Scaling up: City-wide baseline
Using shares of customer preference, parcels are assigned to operators and the closest distribution centers.
SIRENE: Delivery centers
Scaling up: City-wide baseline
Using shares of customer preference, parcels are assigned to operators and the closest distribution centers.
SIRENE: Delivery centers
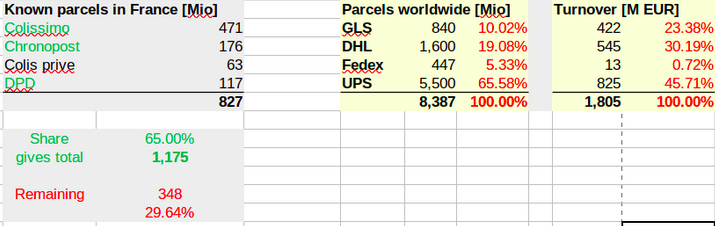
Scaling up: City-wide baseline
Using shares of customer preference, parcels are assigned to operators and the closest distribution centers.
SIRENE: Delivery centers
Methodology: Supply side
Vehicle routing and fleet composition problem
- Minimize total cost of delivering all parcels for each center
- Distance cost influenced by fuel / electricity cost
- Fixed cost (per day) influenced by salaries and vehicle cost
- Derive
- Distances driven and related emissions
- Fleet composition for each center
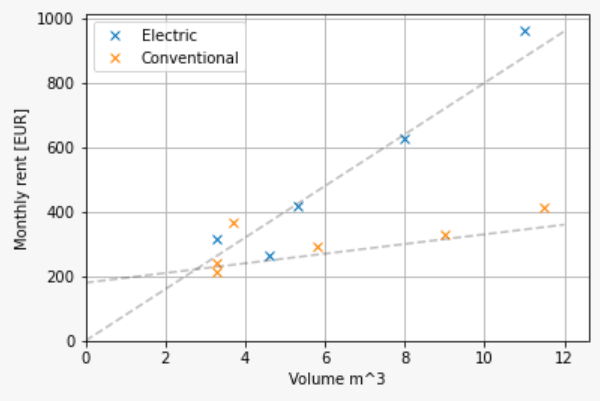
Novel approximation method
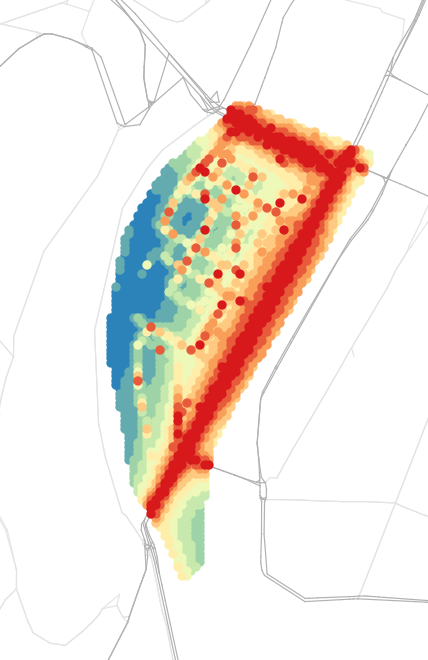
Visualisation platform
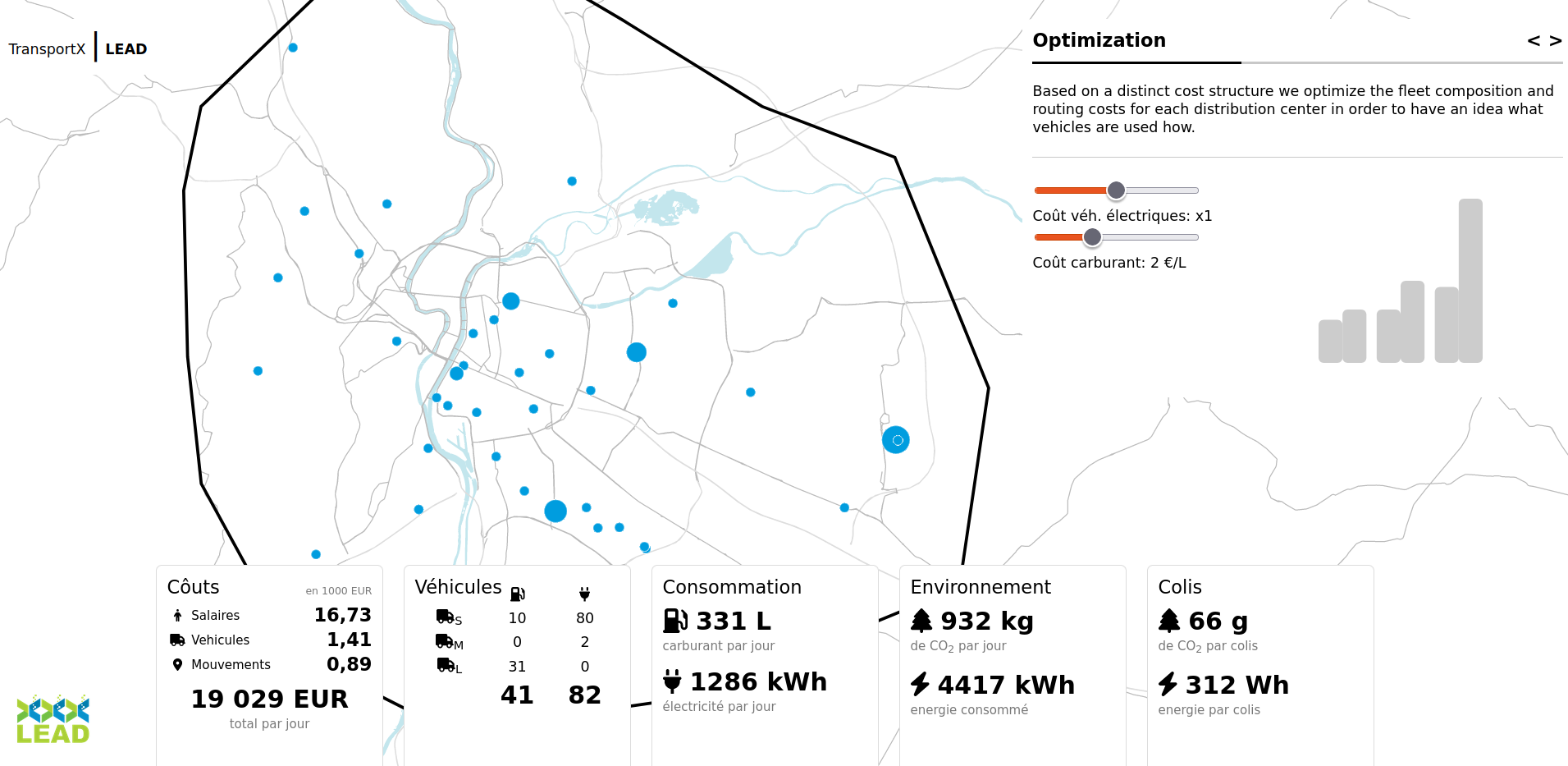
UCC platform
Questions?
Representation of mobility demand in agent-based transport simulation Sebastian Hörl 22 November 2024 ENPC
Representation of mobility demand in ABMS
By Sebastian Hörl
Representation of mobility demand in ABMS
ENPC, 22 November 2024
- 215
