Maths around
Rubik's cube

A bit of history
Ernő Rubik
"Searching to find a good task for my students." 1974
Professor of architecture in Hungary
Industrialized in 1979 by Ideal Toys




Impossible configurations with the Rubik's cube
Disclaimer
This is not a math lesson! Some vocabulary and notations are "internal" to this presentation.

Kinds of pieces
- 8 corners: 3 faces
- 12 sides: 2 faces
- 6 center: 1 faces

Centers don't move

Let's number the moving pieces
1
2
3
4
5
6
7
8
9
10
10
11
12
13
14
15
We will only care about positioning the pieces in the presentation, not the orientation (e.g. red/blue faces of the piece n° 2)

1
2
3
4
5
6
7
8
| 3 | 2 | 1 |
| 4 | 8 | |
| 5 | 6 | 7 |
| 1 | 8 | 7 |
| 2 | 6 | |
| 3 | 4 | 5 |
This is called a permutation.
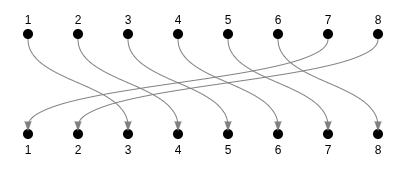

1
2
3
4
5
6
7
8


M
M
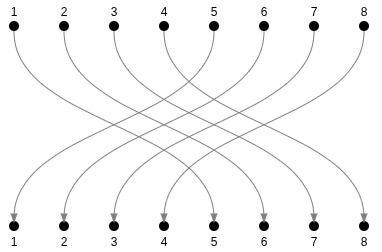
MM
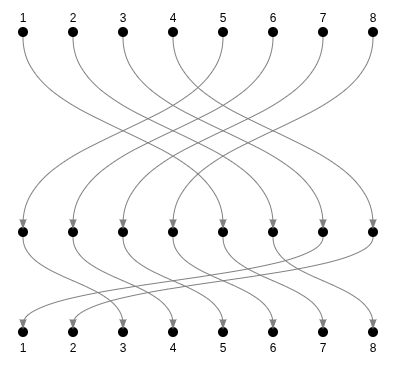
M
MMM
M

MMMM
Chaining permutations...
Creates another permutation!
🤯
RIGHT
LEFT
UP
FRONT
BACK

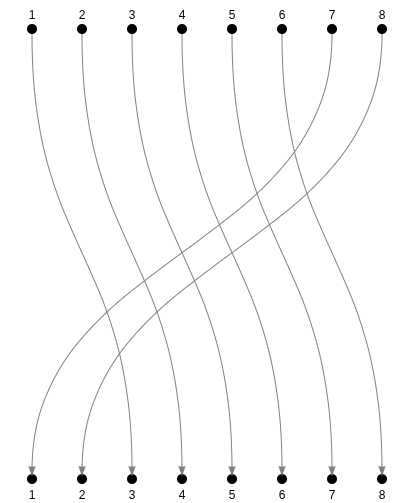
Can we decompose this in simpler chunks?

1
2
3
4
5
6
7
8
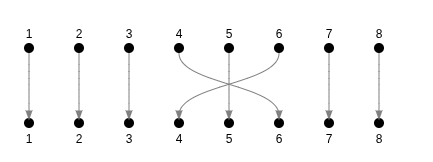
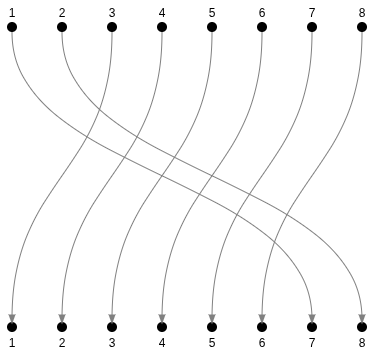
Only 2 numbers are inverted, so we call this... an inversion
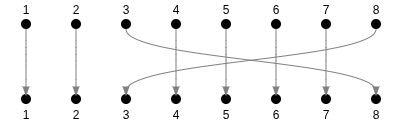
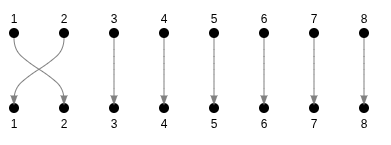
Other examples:

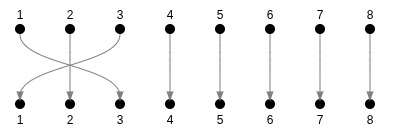
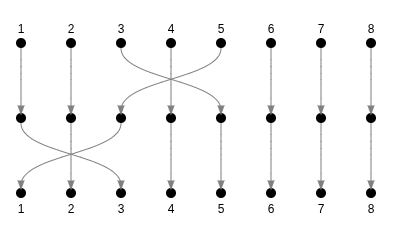
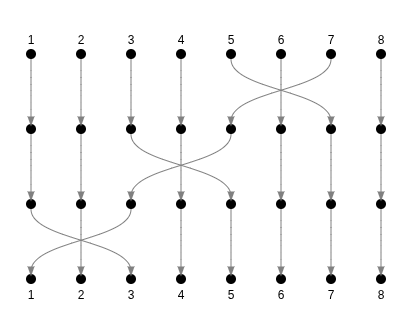
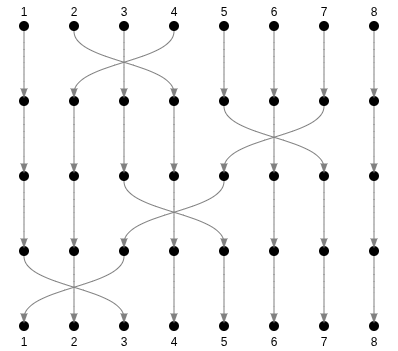
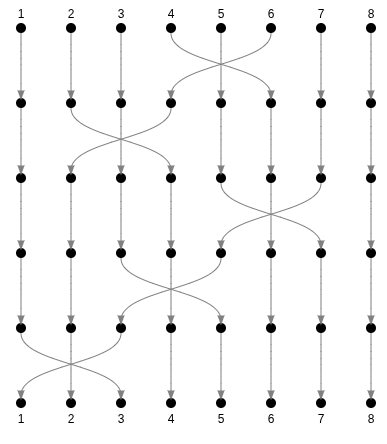
6 inversions
RIGHT

RIGHT

UP
1 9 7 8 12 13 10 11
1 9 7 8 12 13 10 11
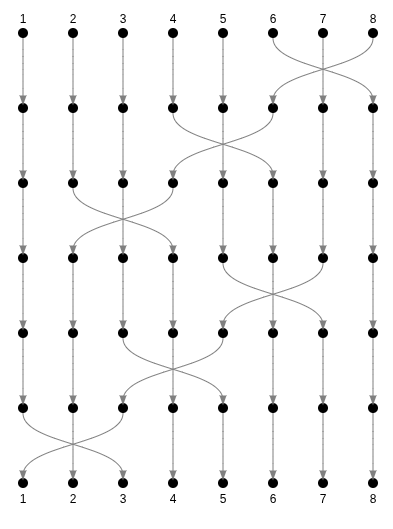
All basic movements decompose into 6 inversions
RIGHT
LEFT



$$ 6 + 6 = 12 $$ inversions
RIGHT
UP


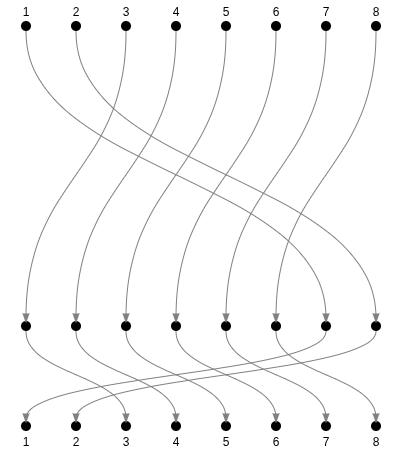
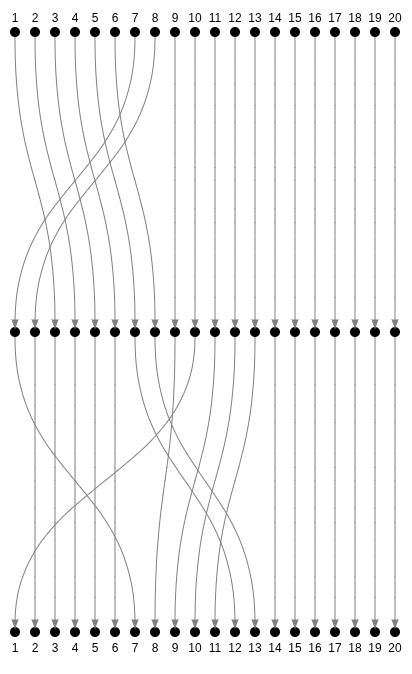
Can you guess the number of inversions?
10 inversions !
Some inversions "cancelled". However, those cancellations can only happen by pair.
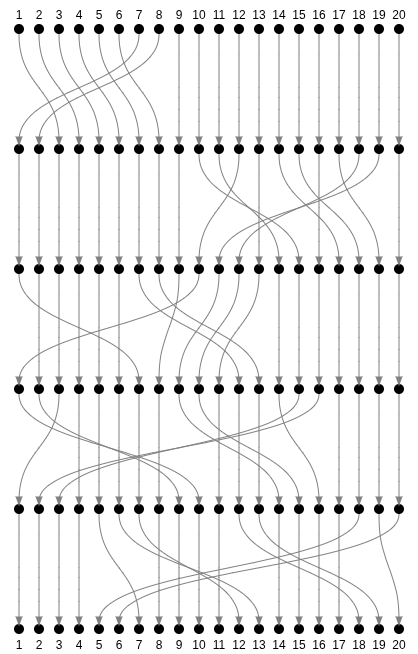
Basic movements have an even number of inversions (6)
Chaining movements add the number of inversions of each movement minus some even number.
Hence, all "legal" chaining of movements will have even number of inversions.
Theorem

Can we solve this cube?
The permutation consists of a single inversion
1 is odd.
Hence, you cannot find a "legal" movement reverting this permutation
Questions ?