Joint embedding of structure and features via graph convolutional networks
Sébastien Lerique, Jacobo Levy-Abitbol, Márton Karsai
IXXI, École Normale Supérieure de Lyon
a walk through
What are "node embeddings"
DeepWalk, LINE, node2vec, ...
Preserve different properties:
- pairwise distances
- communities
- structural position
Easily answer questions like:
- who is similar to X
- who is X likely to connect to
Twitter users can...


... be tightly connected
... relate through similar interests
... write in similar styles
graph node2vec: \(d_n(u_i, u_j)\)
average user word2vec: \(d_w(u_i, u_j)\)
Questions
-
Create a task-independent representation of network + features
-
What is the dependency between network structure and feature structure
-
Can we capture that dependency in a representation



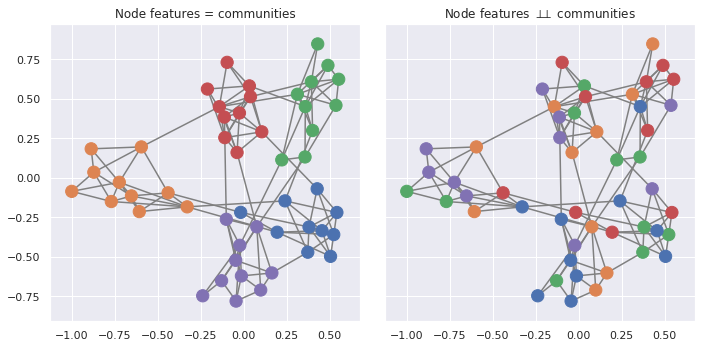
network—feature dependencies
network—feature independence
Use deep learning to create embeddings



Introduction
Network embeddings → Twitter → network-feature dependencies
Building blocks
Neural networks + Graph convolutions + Auto-encoders
Capture dependencies
by arranging the building blocks together
Neural networks

x
y
green
red

\(H^{(l+1)} = \sigma(H^{(l)}W^{(l)})\)
\(H^{(0)} = X\)
\(H^{(L)} = Z\)
Inspired by colah's blog
Graph-convolutional neural networks



\(H^{(l+1)} = \sigma(H^{(l)}W^{(l)})\)
\(H^{(0)} = X\)
\(H^{(L)} = Z\)
\(H^{(l+1)} = \sigma(\color{DarkRed}{\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}}H^{(l)}W^{(l)})\)
\(H^{(0)} = X\)
\(H^{(L)} = Z\)
\(\color{DarkGreen}{\tilde{A} = A + I}\)
\(\color{DarkGreen}{\tilde{D}_{ii} = \sum_j \tilde{A}_{ij}}\)

Kipf & Welling (2016)

Semi-supervised graph-convolution learning
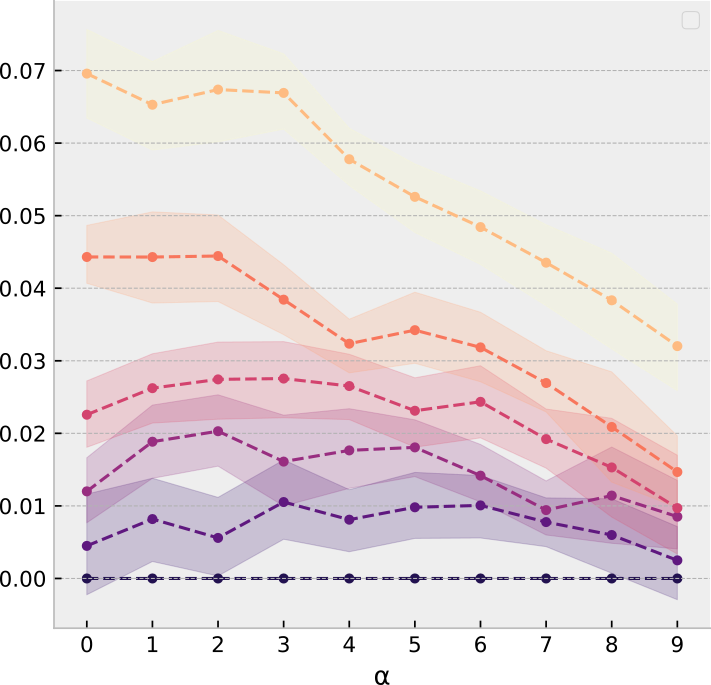
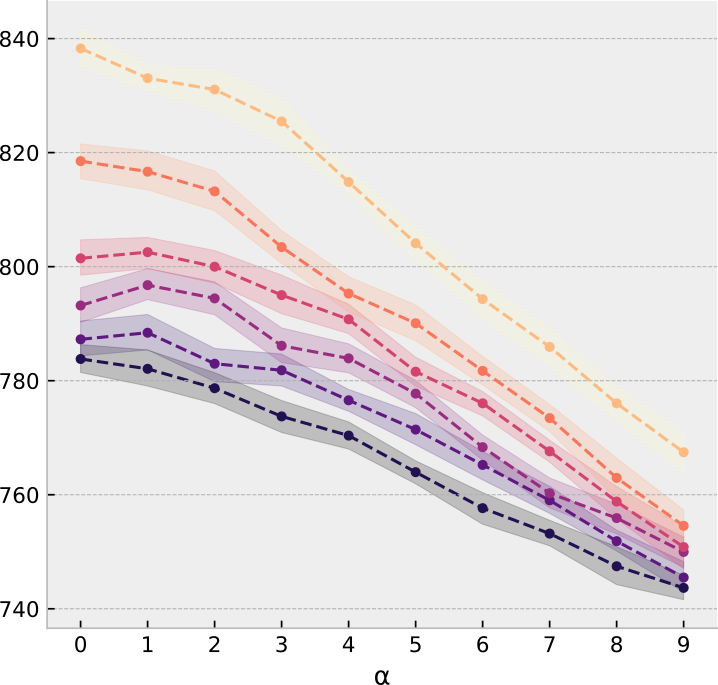
Four well-marked communities of size 10, small noise

More semi-supervised GCN netflix
Overlapping communities of size 12, small noise
Two feature communities in a near-clique, small noise
Five well-marked communities of size 20, moderate noise

(Variational) Auto-encoders

From blog.keras.io
- Bottleneck compression → creates embeddings
- Flexible training objectives
- Free encoder/decoder architectures
high dimension
high dimension
low dimension
Example — auto-encoding MNIST digits

MNIST Examples by Josef Steppan (CC-BY-SA 4.0)
60,000 training images
28x28 pixels
784 dims
784 dims
2D

From blog.keras.io
GCN + Variational auto-encoders = 🎉💖🎉

Socio-economic status
Language style
Topics
Socio-economic status
Language style
Topics

Compressed & combined representation of nodes + network
Kipf & Welling (2016)


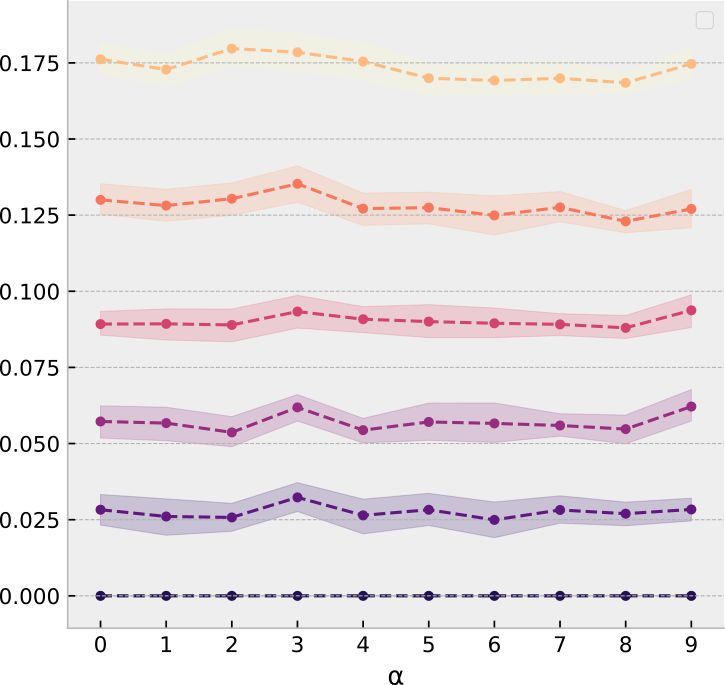
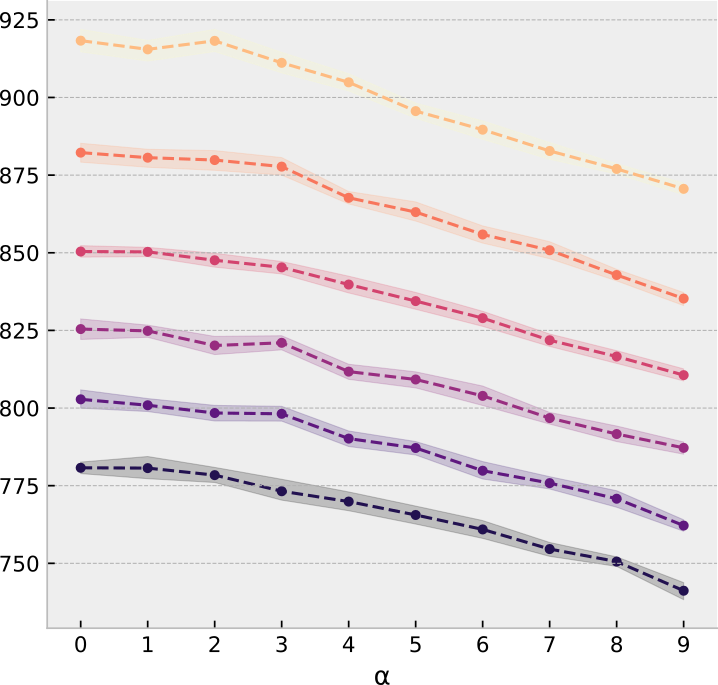
GCN+VAE learning
Five well-marked communities of size 10, moderate label noise


Introduction
Network embeddings → Twitter → network-feature dependencies
Building blocks
Neural networks + Graph convolutions + Auto-encoders
Capture dependencies
by arranging the building blocks together
Example network-feature dependencies
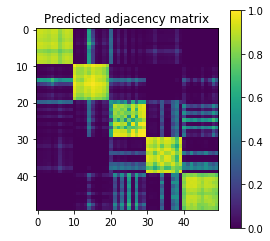
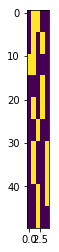
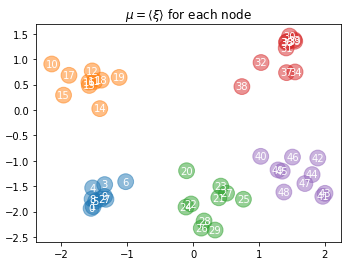
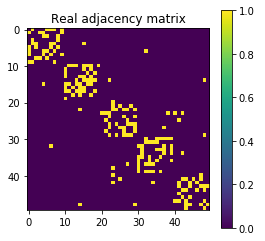
Features finer than network communities
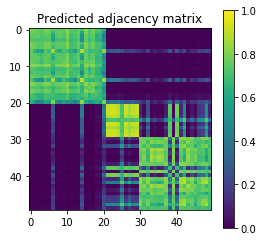
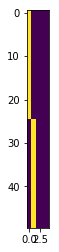
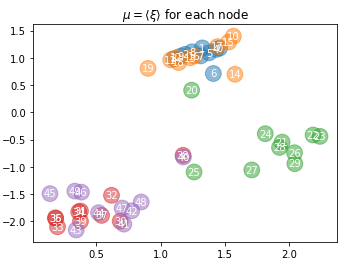
Features coarser than network communities
Allocating network/feature embedding dims
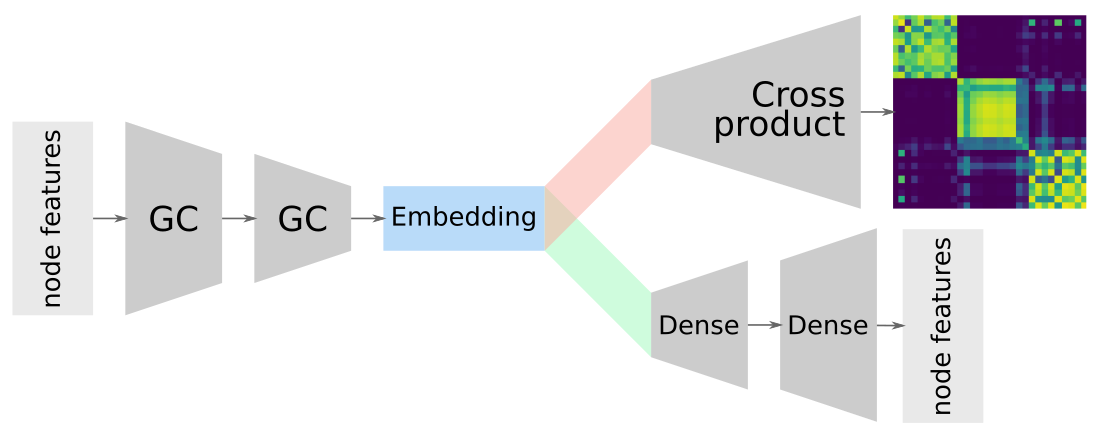
Advantages of overlapping embeddings
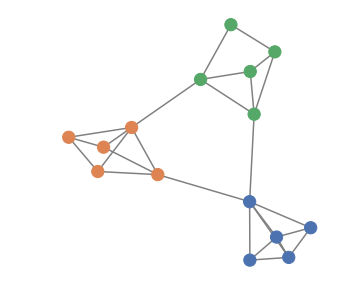
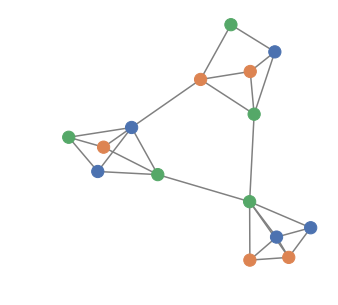

No correlation
Full correlation


Full overlap
Medium overlap
No overlap



Overlapping model
Reference model