Joint embedding of structure and features via graph convolutional networks
Sébastien Lerique, Jacobo Levy-Abitbol, Márton Karsai
IXXI, École Normale Supérieure de Lyon
a walk through
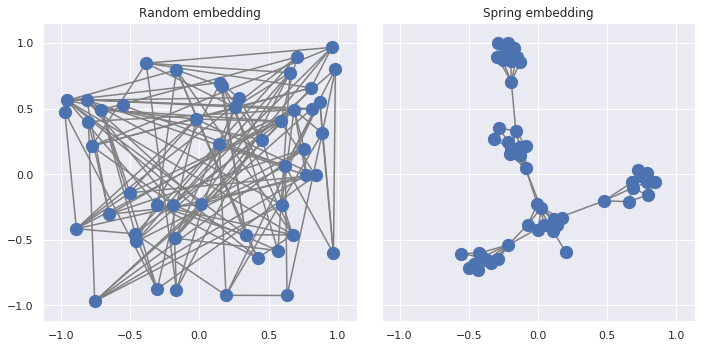
What are "node embeddings"
DeepWalk, LINE, node2vec, ...
Preserve different properties:
- pairwise distances
- communities
- structural position
Easily answer questions like:
- who is similar to X
- who is X likely to connect to
Twitter users can...


... be tightly connected
... relate through similar interests
... write in similar styles
graph node2vec: \(d_n(u_i, u_j)\)
average user word2vec: \(d_w(u_i, u_j)\)
Questions
-
Create a task-independent representation of network + features
-
What is the dependency between network structure and feature structure
-
Can we capture that dependency in a representation



network—feature dependencies
network—feature independence
Use deep learning to create embeddings



Introduction
Network embeddings → Twitter → network-feature dependencies
Building blocks
Neural networks + Graph convolutions + Auto-encoders
Capture dependencies
by arranging the building blocks together
Neural networks

x
y
green
red

\(H^{(l+1)} = \sigma(H^{(l)}W^{(l)})\)
\(H^{(0)} = X\)
\(H^{(L)} = Z\)
Inspired by colah's blog
Graph-convolutional neural networks



\(H^{(l+1)} = \sigma(H^{(l)}W^{(l)})\)
\(H^{(0)} = X\)
\(H^{(L)} = Z\)
\(H^{(l+1)} = \sigma(\color{DarkRed}{\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}}H^{(l)}W^{(l)})\)
\(H^{(0)} = X\)
\(H^{(L)} = Z\)
\(\color{DarkGreen}{\tilde{A} = A + I}\)
\(\color{DarkGreen}{\tilde{D}_{ii} = \sum_j \tilde{A}_{ij}}\)

Kipf & Welling (2016)

Semi-supervised graph-convolution learning
Four well-marked communities of size 10, small noise

More semi-supervised GCN netflix
Overlapping communities of size 12, small noise
Two feature communities in a near-clique, small noise
Five well-marked communities of size 20, moderate noise

(Variational) Auto-encoders

From blog.keras.io
- Bottleneck compression → creates embeddings
- Flexible training objectives
- Free encoder/decoder architectures
high dimension
high dimension
low dimension
Example — auto-encoding MNIST digits

MNIST Examples by Josef Steppan (CC-BY-SA 4.0)
60,000 training images
28x28 pixels
784 dims
784 dims
2D

From blog.keras.io
GCN + Variational auto-encoders = 🎉💖🎉

Socio-economic status
Language style
Topics
Socio-economic status
Language style
Topics

Compressed & combined representation of nodes + network
Kipf & Welling (2016)


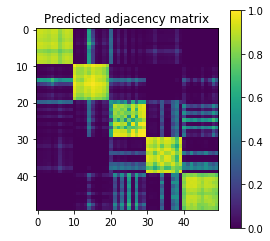
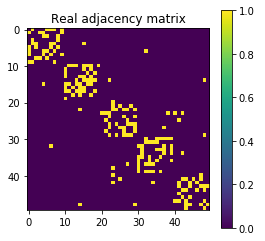
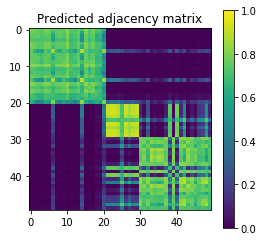
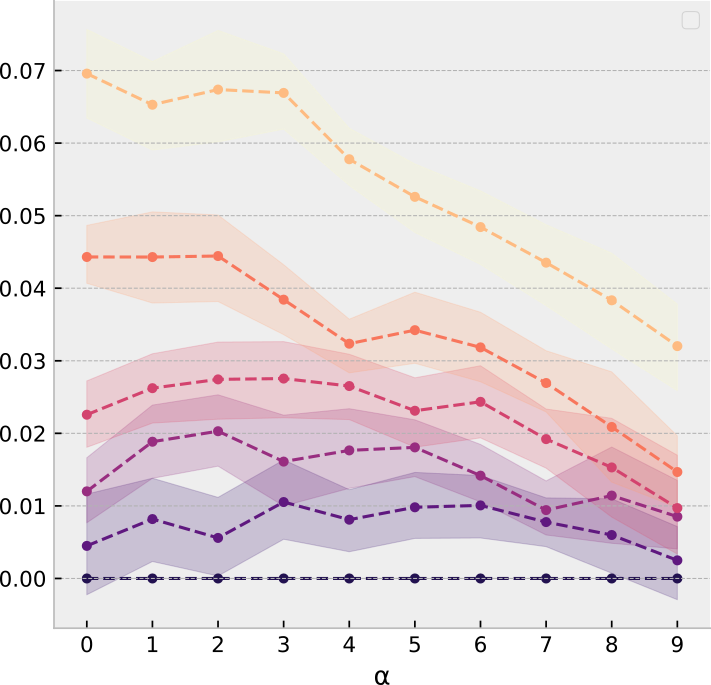
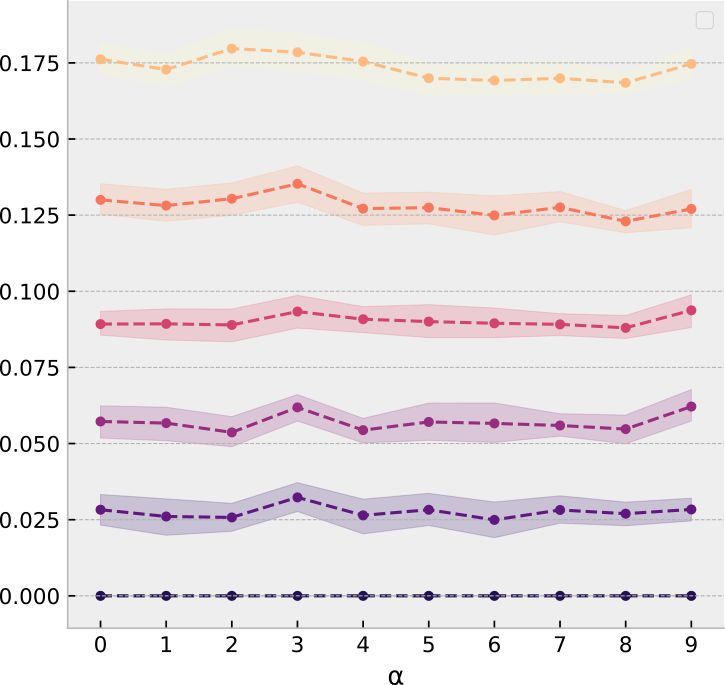
GCN+VAE learning
Five well-marked communities of size 10, moderate label noise


Introduction
Network embeddings → Twitter → network-feature dependencies
Building blocks
Neural networks + Graph convolutions + Auto-encoders
Capture dependencies
by arranging the building blocks together
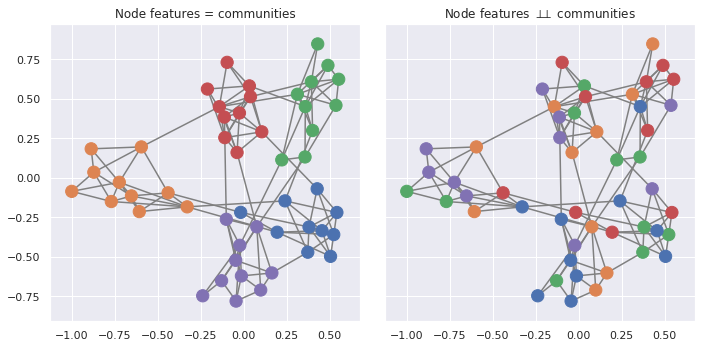
Example network-feature dependencies
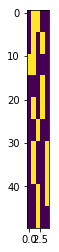
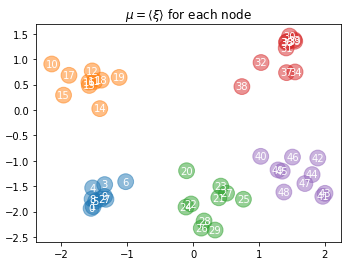
Features finer than network communities
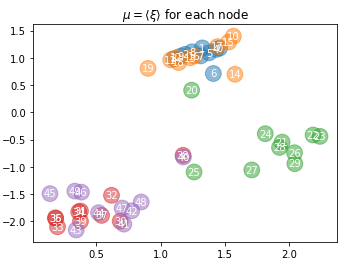
Features coarser than network communities
Allocating network/feature embedding dims
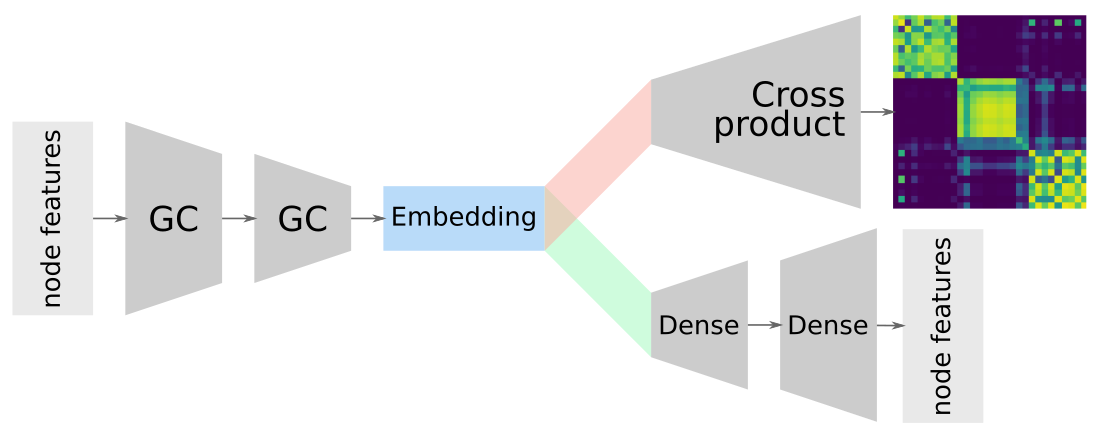
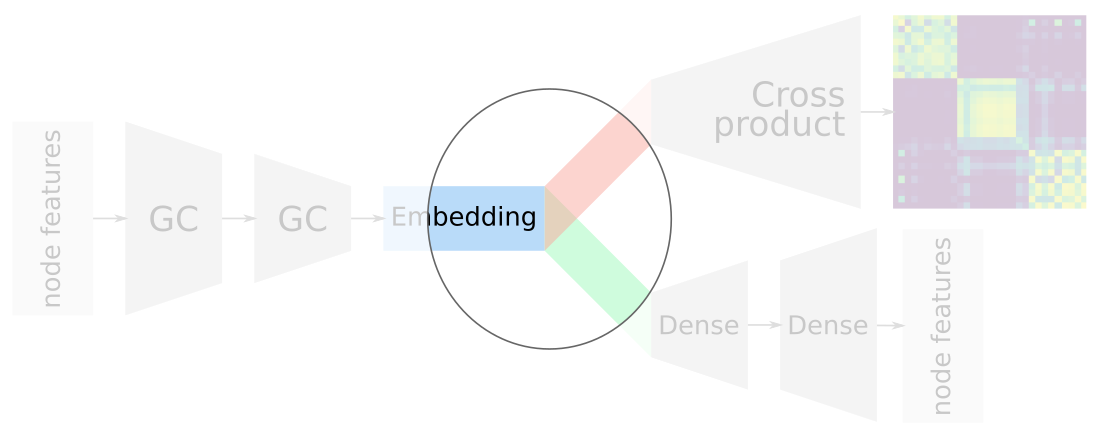
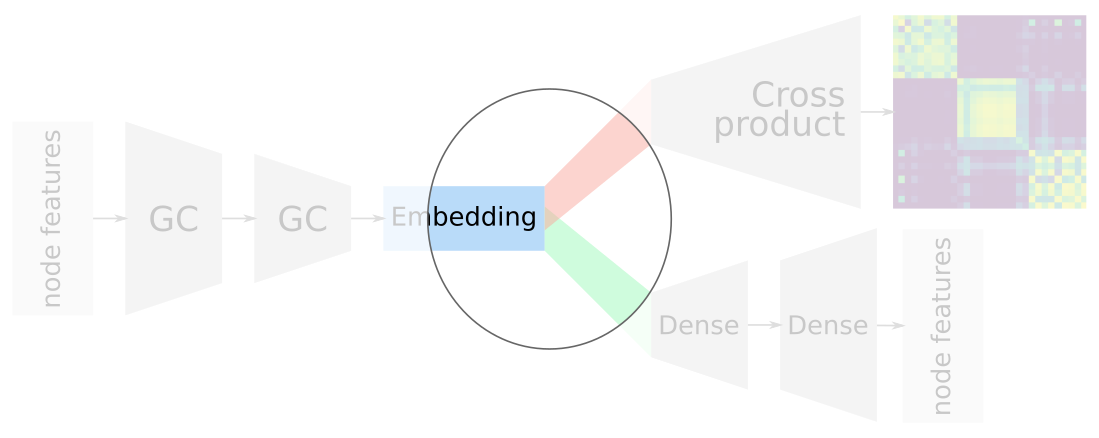
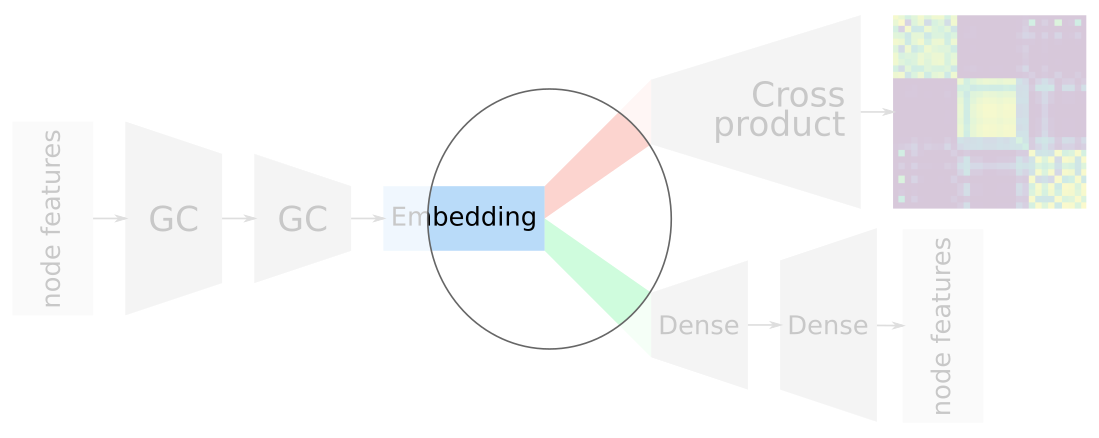
Advantages of overlapping embeddings
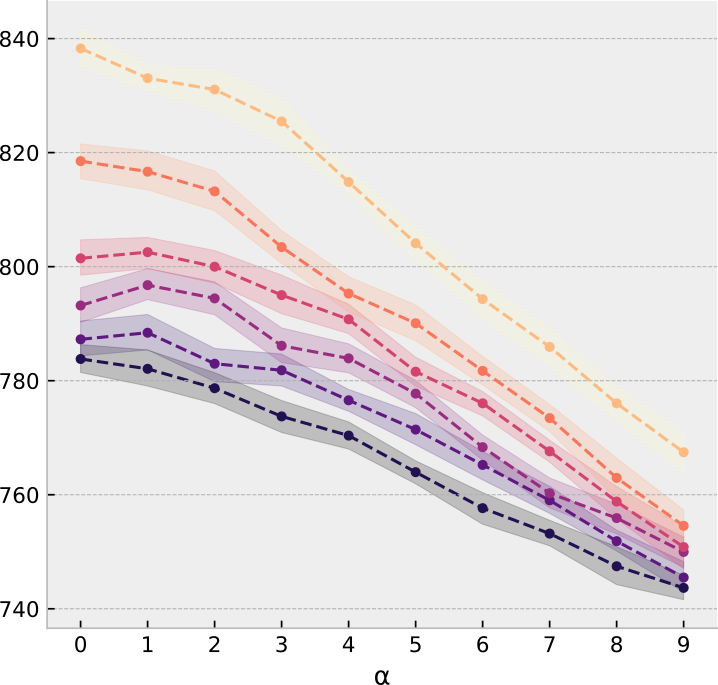
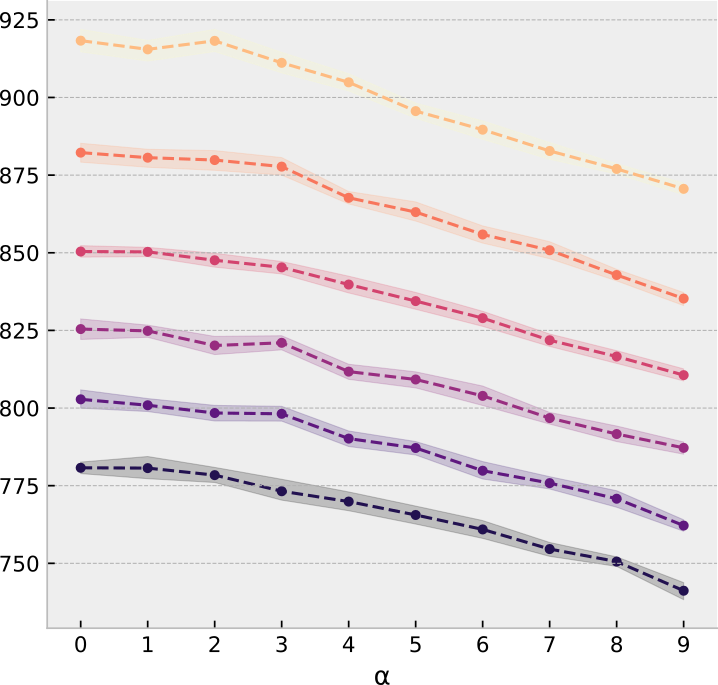
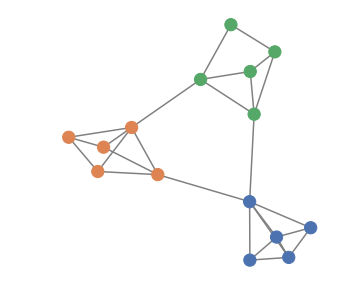
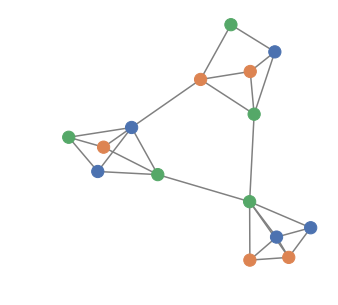

No correlation
Full correlation


Full overlap
Medium overlap
No overlap



Overlapping model
Reference model
Joint embedding of structure and features via graph convolutional networks
By Sébastien Lerique
Joint embedding of structure and features via graph convolutional networks
- 1,665



