ODENet
(Ordinary Neural Differential Equation)
自己紹介
京都大学 理学部1回生 村井誠司
機械学習、学習歴は約1〜2年程。
機械学習に関しての使用言語はpython
keras,pytorch,(scikit-learn)のライブラリを使いますが、
最近はもっぱらpytorchです。(githubにpytorch実装が多いので)
大学のレポートに追われております。
ODE(常微分方程式)について
常微分方程式
(Ordinary Differential Equation)
- 変数が本質的に1つである微分方程式のこと
この場合だと解は
一例
ODEsolver
常微分方程式をとくアルゴリズム
- オイラー法
- ルンゲクッタ法
- 差分法
- etc...
オイラー法
一次近似の解法
ルンゲクッタ法
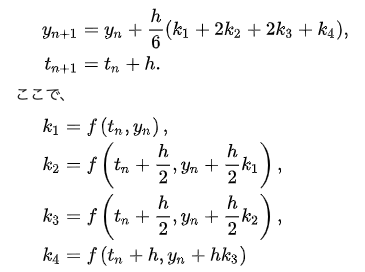
四次近似の解法
ODENetとは
2018年、カナダのトロント大学が発表したモデル
Ricky T. Q. Chen et.al., Neural Ordinary Differential Equations, NIPS 2018
同年、NeurIPS(Neural Information Processing system)
の最優秀論文に輝いた。
これから説明するが、離散的レイヤーという概念から離れた新しいもの(post-Deeplearningに近い)であるのでとても納得
連続的なNeuralNet
今までの離散的なレイヤーではなく空間的連続な関数をみる
つまり、今までのレイヤー、パラメータなどを連続関数の連続パラメータ1つに統合して考える。誤差逆伝播もODEを解くことを考える。
一例をあげるとレイヤー\(n\)、パラメータ\(\theta_i\)に対して
\(f_n:\theta_n \rightarrow \theta_{n+1}\)とすると
\[\theta = (f_n \circ f_{n-1} \circ ... \circ f_1)(\theta_0)\]
と定義するイメージである。
ResNet
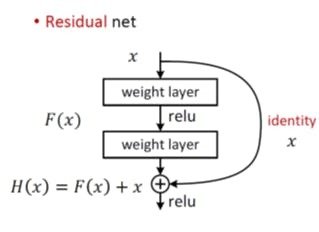
ResNetはレイヤーをreluで変換した後に、差分を学習させる
数式で書くと
この形は\(h_t\)が非常に小さい時の関数\(f\)の一次近似と同様の形をしている
つまり、連続関数として推論ができそう
一般化すると
\[h_{t+1} = h_t + f(h_t,\theta_t)\]
ODENet
任意の時間\(t\)において
\[\frac{dh(t,\theta)}{dx} = f(h(t),t,\theta)\]
が成り立つような推論モデルである
(\(f\)は任意の写像、\(\theta\)はハイパーパラメータ)
レイヤーという言葉を使わなかったのは、ODENetでは複数レイヤーを連続関数に置き換えたものであるから
連続の場合は\(h\)と\(\theta\)は一つの定数である。
連続化する利点
- Memory Efficiency(メモリ効率化)
- Adaptive computation(適応可能な計算量)
- Parameter efficiency (パラメータの効率化)
- Scalable and invertible normalizing flows(NFの変数変換が可能)
- Continuous time-series models(時系列モデルの連続化)
メモリ効率化
レイヤーの間の演算を計算グラフとして保持して、forward,back propagationを行なっていた。
多くの場合、ここが計算量のボトルネックとなっている
離散的なモデル
連続的なモデル
更新がODESolverで解くことができ、誤差伝播も特殊な方法を用いることでODESolverで求められる
つまり、計算グラフを保持する必要がない
適応可能な計算量
ODENetはODESolverで更新、誤差伝播を行う
つまりODESolverを変えることによって、同一モデルでありながら、計算量が可変である。
例えば、
trainは精度よりも時間、validationは時間より精度を重視
ということができる。
パラメータの効率化
離散的なモデルの場合、パラメータは各層にそれぞれ与えてあるので、レイヤーが増えれば増えるだけパラメータは増加する。
連続的なモデルの場合、パラメータは離散的な場合のレイヤー全て統合した時のパラメータと考えられるため、数を減らすことができる。(メモリ効率化とも言える)
Normalizing Flowへの適用
(私がNormalizing flowをよく知っていないが)
Normalizing Flowとは近似事後分布を精度よく求める方法であり
\(\bold{z}_n = (f_1 \circ f_2 \circ ... \circ f_n) (\bold{z_0} )\)
ただし\(\bold{z}_i\)は確率分布、\(f_i\)は確率分布の写像である
連続関数としてみると、正規化の計算が容易になる
時系列データモデル
RNN(Recurrent Neural Network)では時系列データを離散化しなければならない。
連続的なモデルであれば任意の時間の推論ができるため、離散的なモデルよりはるかに自然にモデリングすることができる。
学習と誤差伝播
学習
微分方程式\[\frac{dh(t,\theta)}{dt} = f(h(t),t,\theta)\]
学習するための始点の時間を\(t_0\)、終点の時間を\(t_1\)とすると、両辺を積分することによって
\[h(t_1,\theta)= \int_{t_0}^{t_1}f(h(t),t,\theta) dt\]
となる
これを学習したい点\(t\)でODESolverを解けば良い
ディープラーニングでは損失関数を元に誤差を逆伝播させてパラメータを調節していく。
それはODENetでも同じ。
しかし、普通にやると結局計算グラフを保持しないといけない。
adjoint-methodを用いる
adjoint method
名前の由来は随伴行列(adjoint matrix)を使うことから。
損失関数の誤差伝播を計算グラフの逆を辿るのではなく、ODEを解くことで行っていく。
\[L(\bold{z}(t_1)) =\\ L\left(\int_{t_0}^{t_1}f(\bold{z}(t),t,\theta)dt\right) = L(\textit{ODESolver}(\bold{z}_0,f,t_0,t_1,\theta)) \]
adjoint method
まず損失関数を\(L\)とすると、
\[L(\bold{z}(t_1)) =\\ L\left(\int_{t_0}^{t_1}f(\bold{z}(t),t,\theta)dt\right) = L(\textit{ODESolver}(\bold{z}(t),f,t_0,t_1,\theta))\]
求めたいのは損失勾配であるので計算グラフを辿る、もしくは効率の良い計算をして各変数に対して損失勾配を計算する。
これに関してadjoint
\[\bold{a} (t) = \frac{\partial L}{\partial\bold{z}(t) }\]
を考える.これは連鎖律(chain rule)により
\[\frac{\partial \bold{a}(t)}{\partial t} = -\bold{a}(t)^T \frac{\partial f(\bold{z}(t),t,\theta)}{\partial \bold{z}} \]
という関係が成り立っているので
\[\frac{\partial L}{\partial\bold{z}(t) } =-\int_{t_0}^{t_1}\bold{a}(t)^T \frac{\partial f(\bold{z}(t),t,\theta)}{\partial \bold{z}} \]
となる。同様のことを\(\theta\)と\(t\)でも行う
計算で損失勾配を求められた。
つまり、計算グラフの保持は必要ではない。
↓
メモリ効率化が図れる
図解
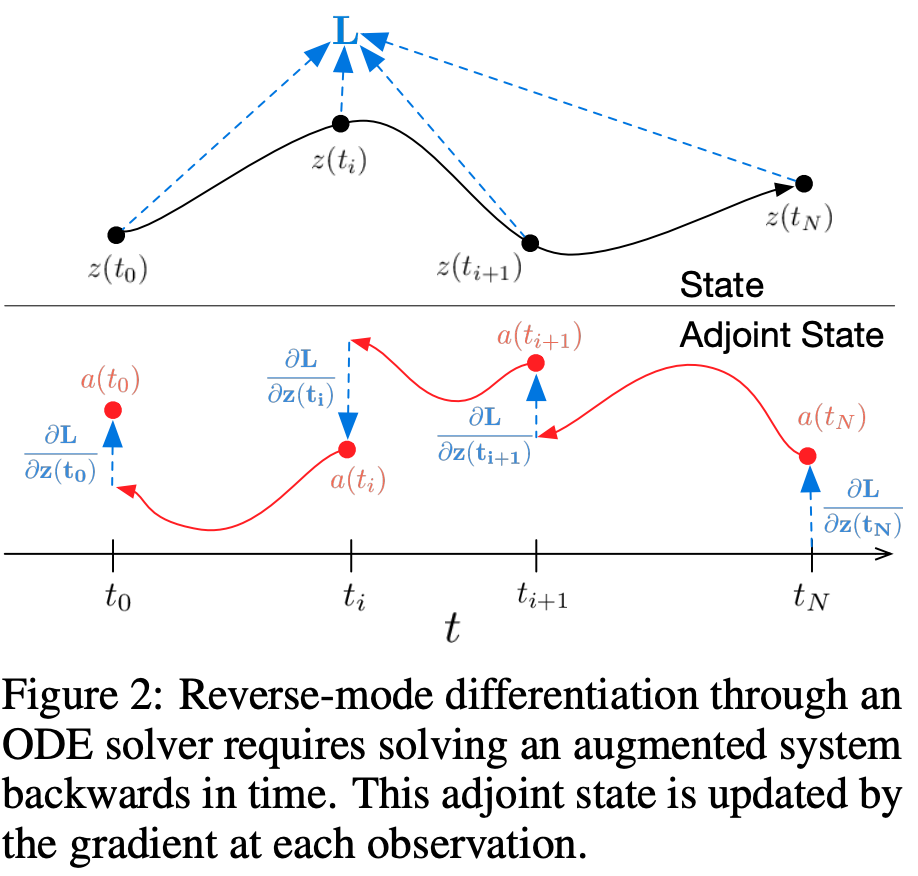
- \(t_i (0 \leq i \leq N)\)の点で学習
- 各点でbackward
擬似コード

終点\(t_1\)から始点\(t_0\)への損失の勾配が各変数それぞれ返るようなコードになっている
github
精度や計算量について
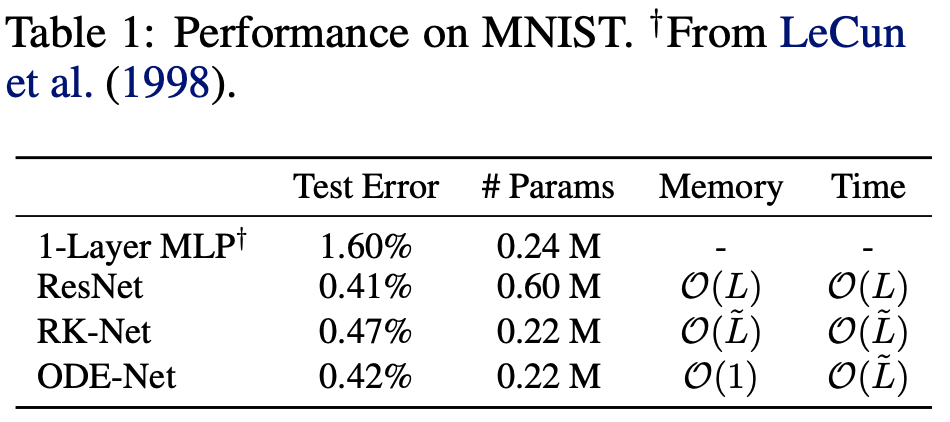
MNISTによる比較
1-Layer MLPはパラメータ数を同一に
ResNetは精度を同一にしている。
RK-netはルンゲクッタ法によるもの
\(\tilde{L}\)はODEの計算回数
同一精度ながら
メモリ効率が上がっている
(パラメータの減少とパラメータ保存の不必要性)
エラーコントロール
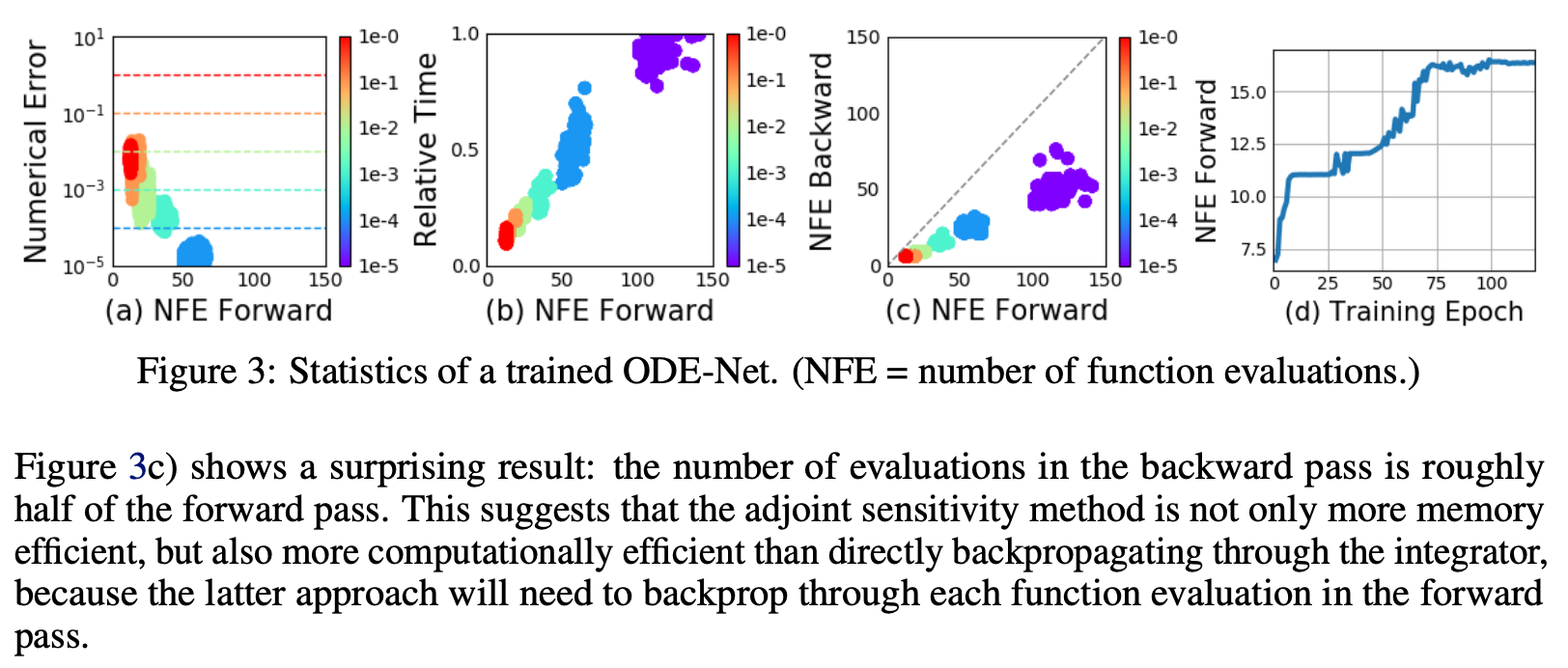
(a): forward回数と誤差
(b): forward回数と相対的経過時間
(c): forward回数とbackwardの回数
(d): epoch数とforward回数
色の変化はtolerance(学習率みたいなもの)
エラーコントロール

(a)からtoleranceと誤差はトレードオフであることがわかる
(b)から(当然ながら)計算時間は上昇する
(c)も計算時間は上昇。backpropagateの回数は半分だが、おそらくadjoint methodの効果であろう(論文も半信半疑)
(d)からepochが進むほど複雑化している(forwardが増える)
Continuous Normalizing Flow
Normalizing flowに関してある全単射\(f\)がサンプルの写像である時\(p\)を確率分布として、
\[\bold{z}_{1} = f(\bold{z}_0) \Longrightarrow \log p(\bold{z}_0) - \log\left|\mathrm{det}\frac{\partial f}{\partial \bold{z}_0}\right|\]
これが\(\frac{d\bold{z}}{dt} = f(z(t),t)\)かつ\(\bold{z}(t)\)と\(t\)でリプシッツ条件を満たす時
\[\frac{\partial \log p(\bold{z}(t))}{\partial t} = -\mathrm{tr}\left(\frac{df}{d\bold{z}(t)}\right)\]
となり、計算量がrankの3乗からrankの1乗になる。
加えてトレースは線形関数なため、NFによる写像\(f_1,f_2,...,f_n\)の合成関数の正規化は
\[\frac{\partial \log p(\bold{z}(t))}{\partial t} = \sum_{n=1}^{M}\mathrm{tr}\left(\frac{df_n}{d\bold{z}(t)}\right)\]
となり、計算が容易となる。
これによりNormalizing Flowの深さ\(n\)を増やしても計算量が莫大になることがない!
実行例
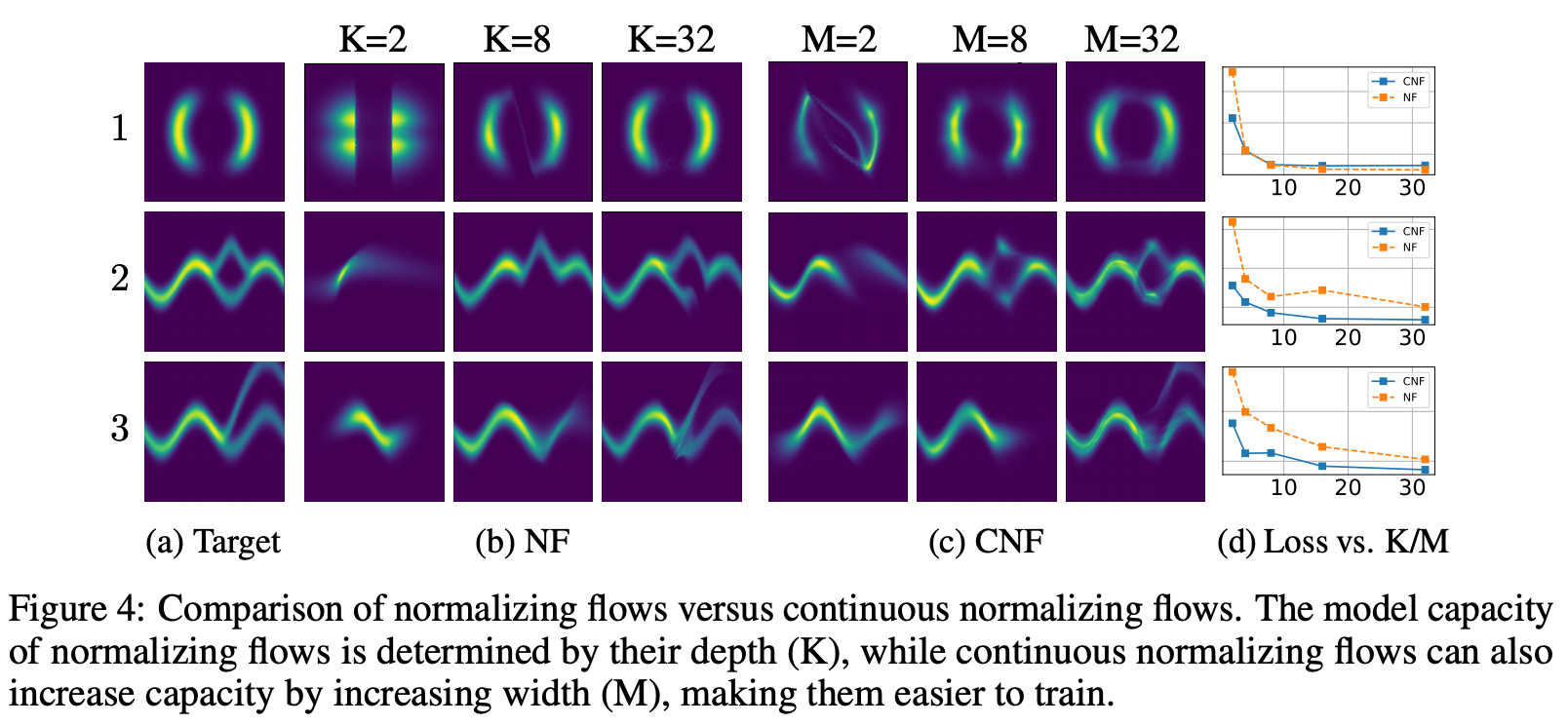
Target分布になるように学習。
CNFが今回の連続化モデル(continuous normalizing flow)
Lossは確実にCNFが低く算出されている。
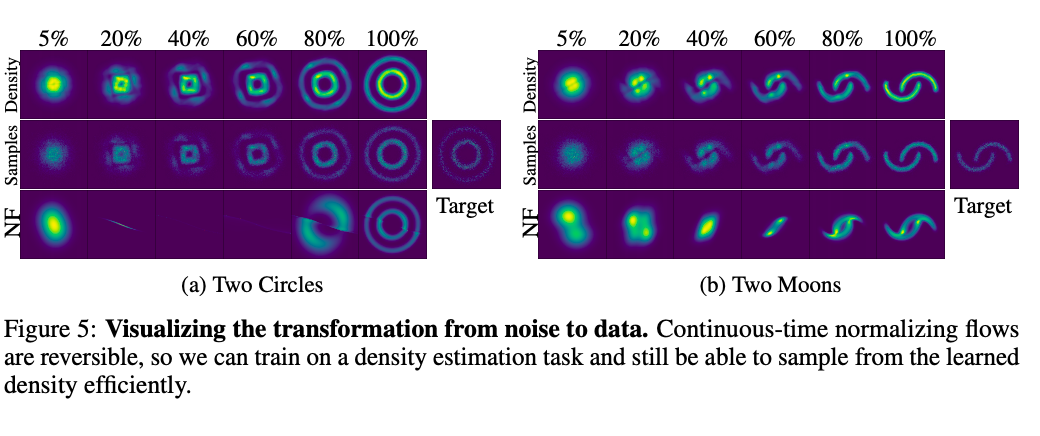
Target分布になるように学習。
それぞれノイズから視覚的に学習する様子を表している
CNFは可逆であるので、学習した密度から効率的にサンプリングできる
時系列モデル
概要
RNNでは離散的なため、観測されない時間が存在する。
----timestampなどをしてきた。
連続化すると時間の連続性が自然に反映されると考えられている。
論文では時系列による生成モデルが紹介されている。
A generative latent function time-series model
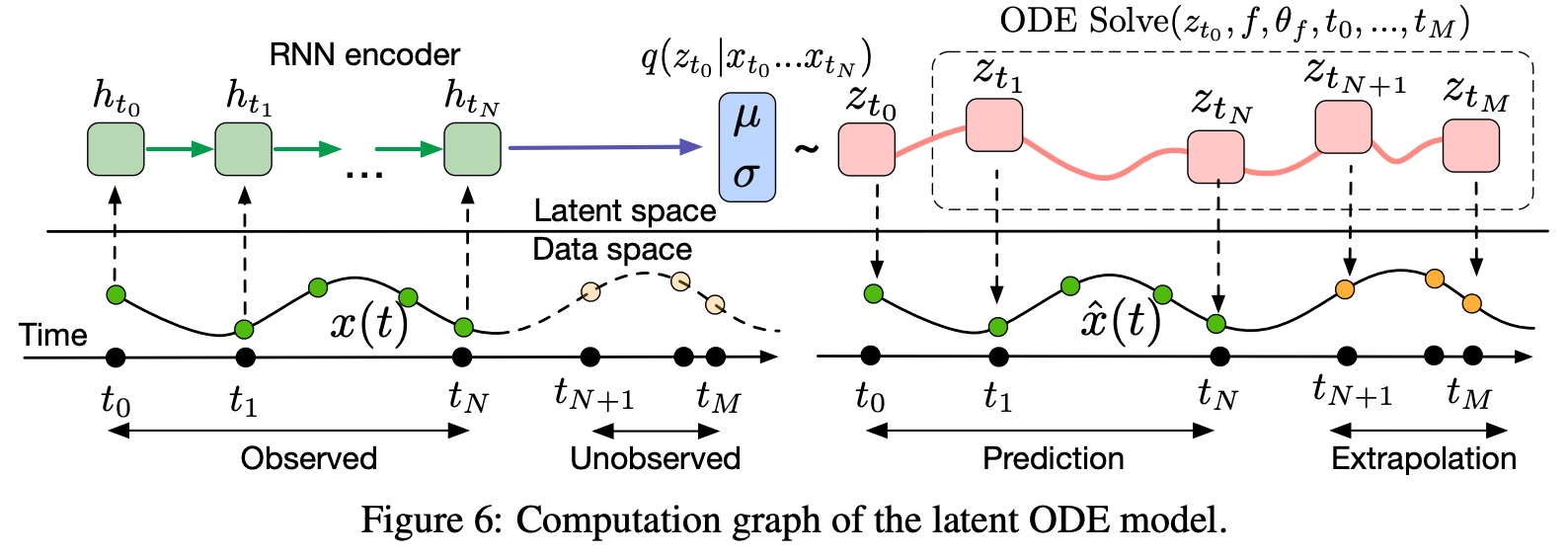
VAEmodelとなっている。
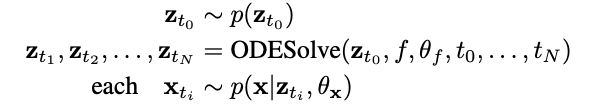
実行例
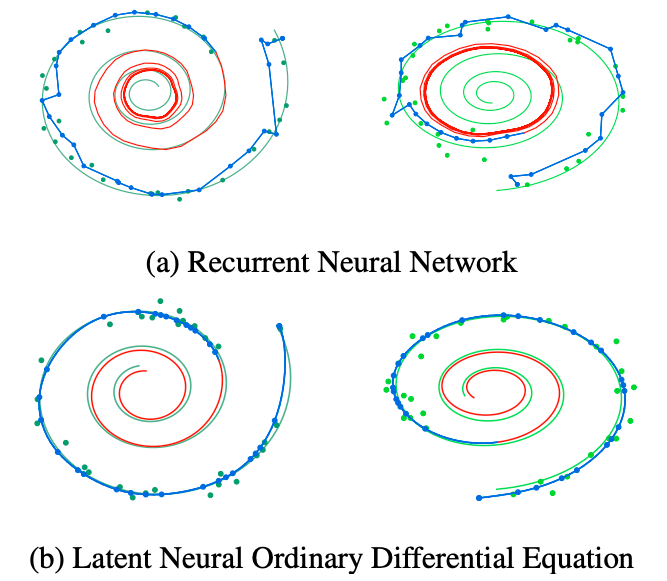
- 上が従来のRNNによるもの
- 下が新しいモデル
予測元は時間によってきまる軌道になっている
結論
- メモリ効率化と計算量調節が行える
- 時系列モデルや確率分布の変数変換に強い
- (関数の連続性や収束などは数学的に証明しやすいので従来のモデルの勾配消失だったり統計的に正しいものを数学的に証明でき...そう)
2018年論文なため研究最中ではあるが、これから注目されると考えられる