Estimation of Mixture Distributions
Dr. Sergey Kosov
Contents
- Introduction
- Properties of Gaussian Distribution
- Gaussian Mixture Model
- Properties of The Gaussian Mixture Model
- Training The Gaussian Mixture Model
University of Applied Sciences
Würzburg - Schweinfurt


20.07.2021
Introduction
Introduction
Introduction
Assumes that the PDF of random variables have normal (Gaussian) distribution
$$\mathcal{N}(\vec{y};~\vec{\mu}, \Sigma) = \frac{1}{(2\pi)^{m/2}} \frac{1}{|\Sigma|^{1/2}}\exp{\left(-\frac{1}{2}(y-\mu)^\top\Sigma^{-1}(y-\mu)\right)}$$
+ Models the conditional dependencies of all features \(f_i(y)\) via covariance matrix \(\Sigma\)
- Can't model complex non-Gaussian distributions
Gaussian PDF

Mixture PDF
Today: Gaussian Mixture Model
Assumes that the PDF of random variables can be modeled by a linear combination of multiple Gaussians $$\sum_i\mathcal{N}_i(\vec{y};~\vec{\mu}_i, \Sigma_i)$$
+ Can model complex non-Gaussian distributions
+ One of the most accurate methods among generative approaches

Expected Value
The average value of a random function \(f(x)\) under a probability distribution \(p(x)\) is called the expectation of \(f(x)\) and denoted through \(E[f(x)]\):
- Discrete case
$$E[f(x)]=\sum p(x)f(x)$$
- Continuous case
$$E[f(x)]=\int\limits^{\infty}_{-\infty}p(x)f(x)dx$$
Variance
The variance of a random function \(f(x)\) is the expected value of the squared deviation from the mean of \(f(x)\),
here mean \(\mu=E[f(x)]\)
$$Var[f(x)]=E[(f(x)-E[f(x)])^2]$$
- The expression for the variance can be expanded as follows
$$E[(f(x)-E[f(x)])^2]=E[f(x)^2]-E[f(x)]^2$$
Properties of
The Gaussian
Distribution
1. Expected Value
If a random variable \(y\) has normal distribution:
- \(p(y)=\mathcal{N}(y;~\mu, \sigma)\)
- \(f(y)=y\)
2. Variance
Gaussian Mixture Model
Mixture of Gaussians
- The Gaussian distribution is the most commonly found in nature, it suffers from the lack of generality
- It has obvious limitations when it comes to approximating complex distributions. Whereas a linear
superposition of number of Gaussians is free from these limitations and in most cases can give us a
better characterisation of a data set
- Such superpositions, formed by taking linear combinations of more basic distributions such as
Gaussians, can be formulated as probabilistic models known as mixture distributions
- By using a sufficient number of Gaussians, and by adjusting their means and covariances as well as the
coefficients in the linear combination, almost any continuous density can be approximated to arbitrary
accuracy
We therefore consider a superposition of \(G\) Gaussian densities of the form:
$$\mathcal{P}(\vec{y}) = \sum^{G}_{k=1}\omega_k\mathcal{N}_k(\vec{y};~\vec{\mu}_k,\Sigma_k)$$
which is called a mixture of Gaussians.
Each Gaussian density \(\mathcal{N}_k(\vec{y};~\vec{\mu}_k,\Sigma_k)\) is called a mixture component of the mixture and has its own mean \(\vec{\mu}_k\) and covariance \(\Sigma_k\)
The weights \(\omega_k\) are called mixture coefficients
Examples
The Gaussian mixture distribution in 1D formed by 3 Gaussians
$$\mathcal{P}(y)=\omega_1\mathcal{N}_1+\omega_2\mathcal{N}_2 + \omega_3\mathcal{N}_3$$
Source: Christopher M. Bishop's textbook “Pattern Recognition & Machine Learning”
Examples
The Gaussian mixture distribution in 2D formed by 4 Gaussians
$$\mathcal{P}(\vec{y})=\omega_1\mathcal{N}_1+\omega_2\mathcal{N}_2 + \omega_3\mathcal{N}_3+\omega_4\mathcal{N}_4$$
Properties of
The Gaussian Mixture Model
Mixture Coefficients
If we integrate both sides of equation
\(\mathcal{P}(\vec{y}) = \sum^{G}_{k=1}\omega_k\mathcal{N}_k(\vec{y};~\vec{\mu}_k,\Sigma_k)\) with respect to \(\vec{y}\), and note that both \(\mathcal{P}(\vec{y})\) and the individual Gaussian components are normalised, we obtain \(\sum^{G}_{k=1}\omega_k=1\).
Also, given that \(\mathcal{N}_k(\vec{y};~\vec{\mu}_k, \Sigma_k)\ge0\), a sufficient condition for the requirement \(\mathcal{P}(\vec{y})\ge0\) is that \(\omega_k\ge0, \forall k \in [1; G]\). Combining this with the condition above we obtain \(0\le\omega_k\le1\).
Mixture Coefficients
We therefore see that the mixture coefficients satisfy the requirements to be probabilities, and so, could be considered as as the prior probabilities of picking the k-th component.
The densities \(\mathcal{N}_k(\vec{y};~\vec{\mu}_k, \Sigma_k)\), in its turn, could be considered as the probabilities of \(\vec{y}\) conditioned on \(k\): \(p(\vec{y}~|~k)\).
From Bayes' theorem we can write:
$$p(\vec{y}~|~k)\propto p(\vec{y})\cdot p(\vec{y}~|~k) = \omega_k\mathcal{N}_k(\vec{y};~\vec{\mu}_k,\Sigma_k)$$
Training
The Gaussian Mixture Model
Estimation of Mixture Distributions
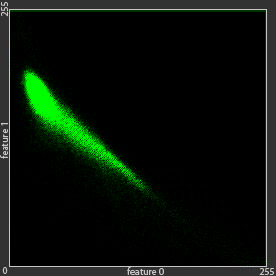
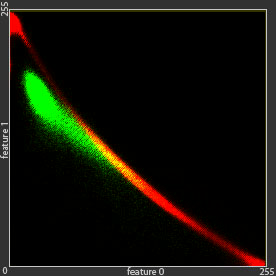
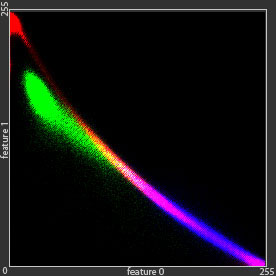
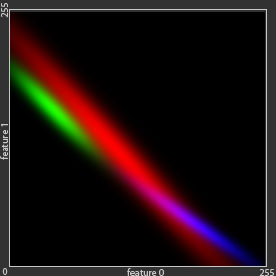
The green dot are an example of given data that cannot be modelled using single Gaussian distribution, because it has two clusters or summits.
To model green dots distributions, we can use linear combination of Gaussian distributions , which is much better than single Gaussian distribution.

Estimation of Mixture Distributions
is the estimation of mixture coefficients \(\omega_k\) and parameters of the mixture components \(\vec{\mu}_k\), \(\Sigma_k\) from training dataset
Brute Force Approach
Split the training samples into some number \(K\) of clusters using for example a non-probabilistic technique called the K-means algorithm.
Estimation of Mixture Distributions
is the estimation of mixture coefficients \(\omega_k\) and parameters of the mixture components \(\vec{\mu}_k\), \(\Sigma_k\) from training dataset
Expectation Maximization Algorithm
alternates between performing an expectation (E) step and a maximization (M) step:
-
E: based on the current estimate for the parameters, determines an estimate for the posterior probability that a specific cluster was responsible for creating each sample point
- M: based on a maximum likelihood estimation of the parameters, using the results of the E step as weights for the contribution of each observation to the determination of the parameters of a specific cluster
Expectation maximization algorithm takes several iterations in order to reach (approximate) convergence and each cycle requires heavy computation.
It requires the simultaneous storage and processing of all the training samples and the prior definition of the number \(G\) of Gaussians in the mixture model.
Estimation of Mixture Distributions
is the estimation of mixture coefficients \(\omega_k\) and parameters of the mixture components \(\vec{\mu}_k\), \(\Sigma_k\) from training dataset
Sequential Method
is used to overcome the limitations of the expectation maximization algorithm.
Two assumptions on training sample points
- The maximum possible distance between sample points in feature space is known
- the sequence of input sample points has a random order, since the algorithm is sensible to the ordering of incoming samples (guarantees a uniform distribution of the mixture components’ centers \(\vec{\mu}_k\) in feature space).
Sequential methods allow data points to be processed one at a time and then discarded and are important for online applications, and also where large data sets are involved so that batch processing of all data points at once is infeasible.
Additional Reading
EM-Algorithm
Arthur P. Dempster, Nan M. Laird, and Donald B. Rubin. “Maximum likelihood from incomplete data via the EM algorithm.” In: Journal of the Royal Statistical Society: Series B 39.1 (1977), pp. 1–38
C++ Implementation Code
OpenCV library: cv::ml::EM Class Reference
Sequential Algorithm
Sergey G. Kosov, Franz Rottensteiner and Christian Heipke: "Sequential Gaussian Mixture Models for Two-Level Conditional Random Fields", In: Proceedings of the 35th German Conference on Pattern Recognition (GCPR). Vol. 8142. Lecture Notes in Computer Science. Springer, 2013, pp. 153–163
C++ Implementation Code
DGM library: DGM::CTrainNodeGMM Class Reference
Multivariate Gaussian Implementation: CKDGauss.h CKDGauss.cpp
Estimation of the GMMparameters (learning): CTrainNodeGMM.h CTrainNodeGMM.cpp