Lesson 6

Texturing and Solids

Contents

  1. Introduction
  2. Surface Parametrisation
  3. Bump Mapping
  4. Displacement Mapping
  5. Environmental Mapping
  6. Procedural Textures

Introduction

What is Texture ?

Texture is the perceived surface quality. In CG texture is a 2D multi-channel image overlaid on the surface of a 3D solid to give it color or illusion of relief. Being the property of the geometry, textures play essential role in modeling BRDFs and thus they are managed entirely by the shaders. The quality of a textured surface is determined by the number of pixels per texture element (textel).

in OpenRT, textures are described by class rt::CTexture : public cv::Mat

Introduction

What is Texture ?

Image Texture

Image texture is a bitmap image usually stored in a common image file format. The quality of textured surface is determined by the number of pixels per telex. The resolution of image texture play a major role, which affects the overall impression of the quality of graphics in 3D-application.

Introduction

What is Texture ?

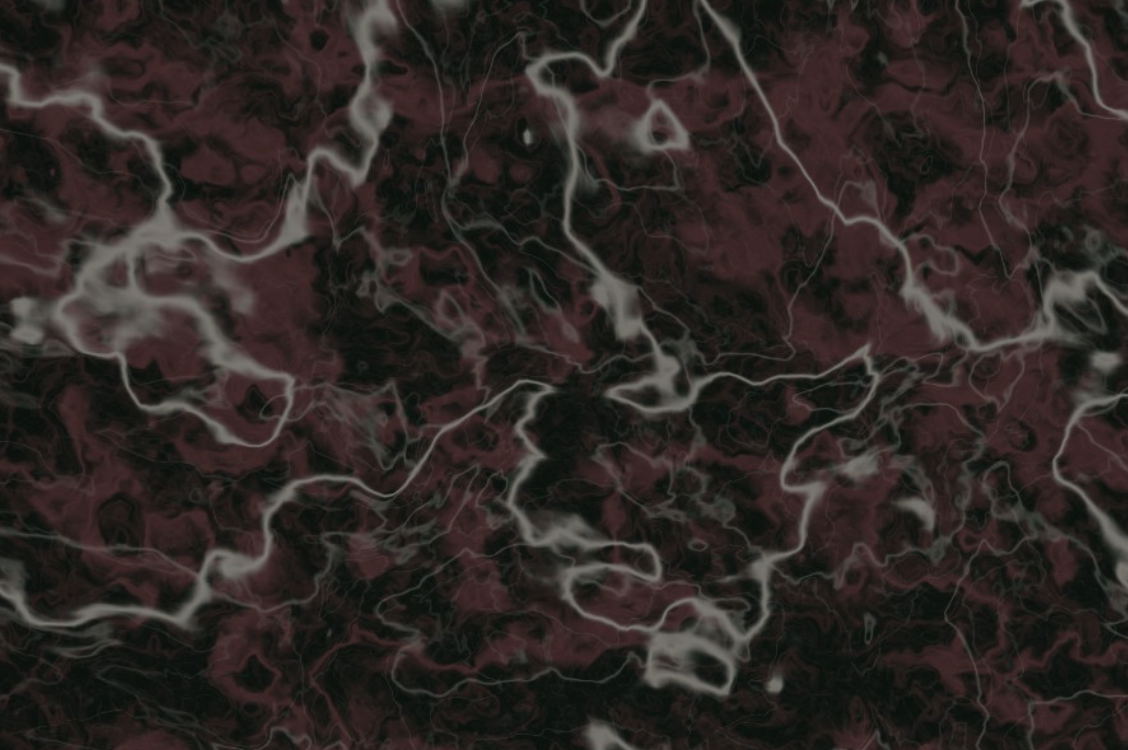
Procedural Texture

Procedural texture is created using a mathematical description (i.e. an algorithm) rather than directly stored data. The advantage of this approach is low storage cost, unlimited texture resolution and easy texture mapping. Procedural textures are used to model surface of natural elements such as clouds, marble, granite, metal, stone, and others.

Introduction

Texture-Modulated Quantities

Radiance at a point \(\vec{p}\)

  • Color (RGB)
  • Diffuse coefficient \(k_d\) 
  • Specular coefficient \(k_s\)
  • Opacity \(\alpha\)

 

Deviation of normal vector at a point \(\vec{p}\)

Bump mapping or Normal mapping

  • If vectors \(\vec{a}\) and \(\vec{b}\) are tangent to the surface at point \(\vec{p}\) and together with normal \(\vec{n}\) form an orthogonal basis, then deviate the normal by \((\Delta_1, \Delta_2)\) from the texture:  \(\vec{n} = \vec{n} + \Delta_1\cdot\vec{a} + \Delta_2\cdot\vec{b}  \)

 

Geometry Displacement

Displacement mapping

  • Displace every point \(\vec{p}\) along its normal \(\vec{n}\) by the value of \(\Delta\) given in the texture:
    \(\vec{p} = \vec{p} + \Delta\cdot\vec{n}\)

 

Distant Illumination

Environmental mapping or Reflection mapping

(r,g,b,k_d,k_s,\alpha)\in CV\_8UC6
(\Delta_1, \Delta_2)\in CV\_8UC2
\Delta\in CV\_8UC1

Introduction

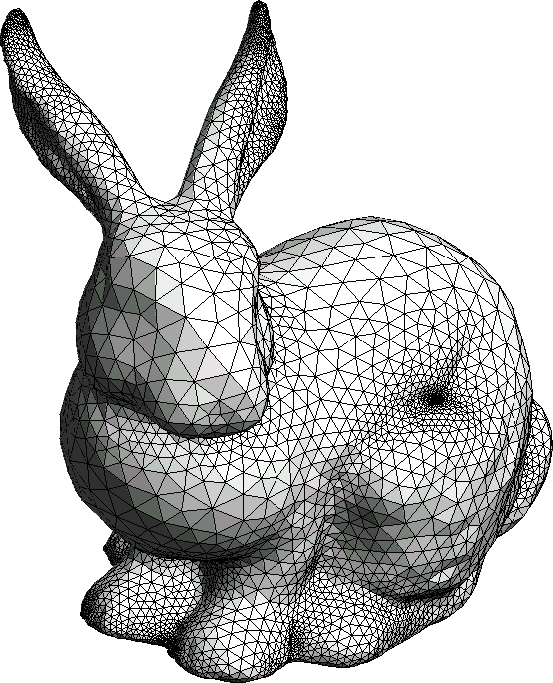
Solid is a rigid geometrical construction which consists out of multiple primitives, usually triangles. Primitives are combined into solids in order to make application of geometrical transformations and texturing easier.

in OpenRT, solids are described by class rt::CSolid

What is Solid?

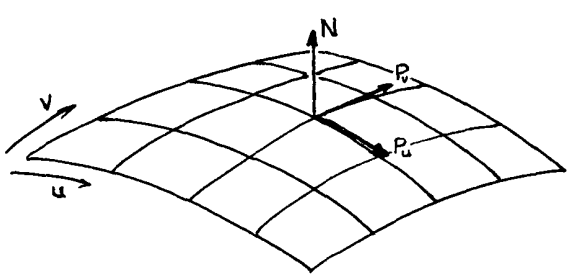
Surface Parametrization

The bidirectional reflectance distribution function:

 

$$ f_r(\vec{p},\omega_o,\omega_i) = \frac{dL_o(\vec{p},\omega_o)}{dE(\vec{p},\omega_i)},$$

 

where \(\vec{p}\equiv\vec{p}(x, y, z)\) is a 3 dimentional point on solid's surface

From 3D hit-point to 2D texture coordinates

Texture is about modeling point - dependent characteristics of BRDF

Parametrization

To map a two-dimensional texture to three-dimensional surface for every 3D point \(\vec{p}(x,y,z)\) a corresponding 2D point \(\vec{q}(u,v)\) in texture must be found. 

$$f:(x,y,z)\rightarrow (u,v), $$

 

where usually

 

$$u,v\in[0; 1]$$

Surface Parametrization

From 3D hit-point to 2D texture coordinates

Parametrization

To map a two-dimensional texture to three-dimensional surface for every 3D point \(\vec{p}(x,y,z)\) a corresponding 2D point \(\vec{q}(u,v)\) in texture must be found. 

$$f:(x,y,z)\rightarrow (u,v), $$

 

where usually

 

$$u,v\in[0; 1]$$

When ray - primitive intersection is found, the hit-point \(\vec{p} = \vec{o} + t\cdot\vec{d}\) is encoded into the ray structure, thus parametrization can be implemented for every primitive in a method

Vec2f rt::IPrim::getTextureCoords(const Ray& ray) const = 0;

Surface Parametrization

Primitive: Sphere

\vec{p}(x,y,z)
\theta
\varphi

Cartesian to Spherical

 

$$r=\sqrt{x^2+y^2+z^2}$$

 

$$\varphi=\arctan_2\frac{y}{x}$$

 

$$\theta=\arccos\frac{z}{r}$$

 

(read more about \(\arctan_2\) function)

y
z
x

Spherical to Texture

 

Since \(\varphi\in[-\pi; \pi]\) and \(\theta\in[0;\pi]\)

 

$$u=\frac{\pi+\varphi}{2\pi}$$

 

$$v=\frac{\theta}{\pi}$$

Vec2f CPrimSphere::getTextureCoords(const Ray& ray) const
{
    Vec3f hitPoint = ray.hitPoint() - m_origin;
    float theta = acosf(hitPoint.val[1] / m_radius);	  // [0; Pif]

    float phi = atan2(hitPoint.val[2], hitPoint.val[0]);  // [-Pif; Pif]
    if (isnan(phi)) phi = 0;

    return Vec2f((Pif + phi) / (2 * Pif), theta / Pif);
}

Surface Parametrization

Primitive: Triangle

Möller-Trumbore intersection algorithm

in addition to intersection distance \(t\) implicitly calculates the barycentric intersection coordinates \((u,v)\in[0; 1]\), which may be used directly as the texel coordinates

  1. On construction provide additionally texture coordinates for all 3 triangle vertices
  2. Store barycentric coordinates in the ray structure together with \(t\) value
Vec2f CPrimTriangle::getTextureCoords(const Ray& ray) const {
    return (1.0f - ray.u - ray.v) * m_ta 
           + ray.u * m_tb 
           + ray.v * m_tc;
}
\vec{a}(u_a,v_a)
\vec{p}(u,v)
\vec{o}
struct Ray {
    Vec3f        org;	// Ray origin
    Vec3f        dir;	// Ray direction
    double       t;     // Current/maximum hit distance
    const IPrim* hit;	// Pointer to currently closest primitive 
    float        u;     // Barycentric u coordinate
    float        v;     // Barycentric v coordinate
} ray;
t
\vec{b}(u_b,v_b)
\vec{c}(u_c,v_c)
see source code

Surface Parametrization

Solid: Quad

Quadrilateral Solid

Quadrilateral solid \((a,b,c,d)\) consists out of two triangles \(a,b,c)\) and \((a,c,d)\). 

  1. On construction provide texture coordinates for all 4 quadrilateral vertices
  2. There is no ray-quad intersection check, only 2 ray-triangle intersection checks
\vec{a}(u_a,v_a)
\vec{b}(u_b,v_b)
\vec{c}(u_c,v_c)
\vec{p}(u,v)
\vec{o}
t
\vec{d}(u_d,v_d)
see CSolidQuad source code

Surface Parametrization

Solid: Cylinder

\vec{p}(x,y,z)
\varphi

Cartesian to Cylindrical

 

$$r=\sqrt{x^2+y^2}$$

 

$$\varphi=\arctan_2\frac{y}{x}$$

 

$$h=h$$

 

(read more about \(\arctan_2\) function)

y
z
x

Spherical to Texture

 

Since \(\varphi\in[-\pi; \pi]\) and \(h\in[0;H]\)

 

$$u=\frac{\pi+\varphi}{2\pi}$$

 

$$v=\frac{h}{H}$$

h
H

Surface Parametrization

Solid: Cylinder

\vec{p}(x,y,z)
\varphi
z
x
h
H
a
b
c
d

If a cylinder has \(n\) sides and every side \(s\) of a cylinder is modeled with a quad \((a,b,c,d)\), it is straightforward to calculate the 3D vertex positions as well as 2D texture coordinates:

 

$$u_a = \frac{s+1}{n};   v_a = 1$$

$$u_b = \frac{s}{n};   v_b = 1$$

$$u_c = \frac{s}{n};   v_c = 0$$

$$u_d = \frac{s+1}{n};   v_d = 0$$ 

see CSolidCylinder source code

Surface Parametrization

Complex Solids

Inverse mapping for arbitrary 3D surfaces is too complex

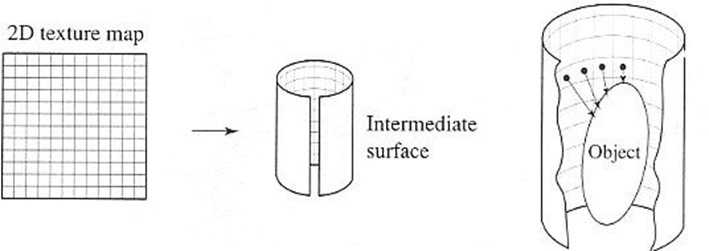
Two-Stage Texture Mapping

is an approximation technique to generate texture coordinates for every vertex of a complex-shaped solid

  • Stage 1: Mapping from a texture space to a more simple intermediate 3D surface which is a reasonable approximation of the destination surface (e.g., cylinder, sphere, box or plane) 
  • Stage 2: Mapping from a the intermediate surface to the destination object surface

Surface Parametrization

Complex Solids

Inverse mapping for arbitrary 3D surfaces is too complex

Example

Texturing a vase with different intermediate surfaces:

Plane

Strong distortion where object surface normal is orthogonal to the intermediate plane normal

Cylinder

Reasonably uniform mapping (symmetry!)

Sphere

Problems with concave regions

Bump Mapping / Normal Mapping

Bump Mapping

2D texture map looks unrealistically smooth across different material, especially at low viewing angle

 

Fool the human viewer:

  • Perception of shape is determined by shading, which is determined by surface normal
  • Use texture map to perturb the surface normal per fragment
  • Does not actually alter the geometry of the surface
  • Shade each fragment using the perturbed normal as if the surface were a different shape

Sphere with diffuse texture

Swirly bump map

Sphere with diffuse texture and bump map

Bump Mapping

Treat the texture as a single-valued height function (height map)

  • Grayscale image (CV_8UC1) stores height: black - high area; white - low (or vice versa)
  • Difference in heights determines how much to perturb \(\vec{n}\) in the \((u, v)\) directions of a parametric surface

\[\frac{\partial b}{\partial u}=\frac{h_{x+1,y}-h_{x-1,y}}{dx}\] 

\[\frac{\partial b}{\partial v}=\frac{h_{x,y+1}-h_{x,y-1}}{dy}\]

  • compute a new, perturbed normal from \((b_u, b_v)\)

Bump Mapping

Computing Perturbed Normal

\vec{n}=\vec{p}_u\times\vec{p}_v
\vec{p}_u=\frac{\partial}{\partial u}\vec{p}(u,v), \vec{p}_v=\frac{\partial}{\partial v}\vec{p}(u,v)
\vec{p}'=\vec{p}(u,v)+b(u,v)\vec{n}
\vec{p}_u'=\frac{\partial}{\partial u}\left( \vec{p}(u,v)+b(u,v)\vec{n} \right)=\vec{p}_u+b_u\vec{n}+b(u,v)\vec{n}_u=\vec{p}_u+b_u\vec{n}
\vec{p}_v'=\frac{\partial}{\partial v}\left( \vec{p}(u,v)+b(u,v)\vec{n} \right)=\vec{p}_v+b_v\vec{n}+b(u,v)\vec{n}_v=\vec{p}_v+b_v\vec{n}

perturbed surface

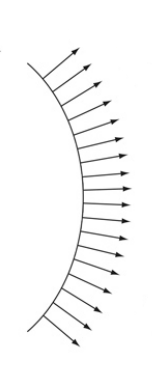
\(\vec{p}\)

\(\vec{n}\)

\(\vec{p}\)

\(\vec{p}'\)

Bump Mapping

Computing Perturbed Normal

\vec{n}'=\vec{p}_u'\times\vec{p}_v'
\vec{p}_u'=\vec{p}_u+b_u\vec{n}
\vec{p}_v'=\vec{p}_v+b_v\vec{n}

\(\vec{p}\)

\(\vec{n}\)

\(\vec{p}\)

\(\vec{p}'\)

\vec{n}'=(\vec{p}_u+b_u\vec{n})\times(\vec{p}_v+b_v\vec{n})
=\vec{p}_u\times\vec{p}_v+b_u(\vec{n}\times\vec{p}_v)+b_v(\vec{p}_u\times\vec{n})+b_ub_v(\vec{n}\times\vec{n})

\(\vec{p}'\)

\(\vec{n}'\)

=\vec{n}+b_u(\vec{n}\times\vec{p}_v)-b_v(\vec{n}\times\vec{p}_u)

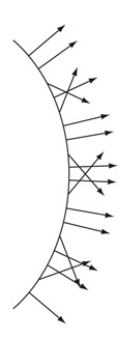
\(\vec{p}\)

\(\vec{n}'\)

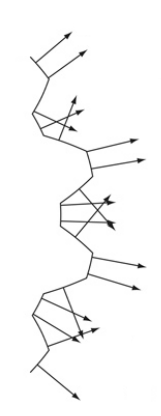
Bump Mapping

Bump Mapping VS Normal Mapping

Computing \(\vec{n}’\) requires the height samples from 4 neighbours

  • Each sample by itself doesn’t perturb the normal
  • An all-white height map renders exactly the same as an all-black height map

 

Instead of encoding only the height of a point, a normal map encodes the normal of the desired surface, in the tangent space of the surface at the point

  • Can be obtained from:
    • a high-resolution 3D model
    • photos (http://zarria.net/nrmphoto/nrmphoto.html)
    • a height-map (with more complex offline computation of perturbed normals)
    • filtered color texture (Photoshop, Blender, Gimp, etc. with plugin)

Bump Mapping

Bump Mapping VS Normal Mapping

height map

normal map

\[(n_x,n_y,n_z)=(r,g,b)\]

Interpret the RGB values per texel as the perturbed normal, not height value

Displacement Mapping

Displacement Mapping

Interpret texel as offset vector to actually displace fragments:

 

\[\vec{p'} = \vec{p} + h(u,v)\vec{n}\]

  • Correct silhouettes and shadows

  • Complex geometry at virtually no memory cost

  • Must be done during modelling stage, e.g. before ray-geometry intersection

Displacement Mapping

Interpret texel as offset vector to actually displace fragments:

 

\[\vec{p'} = \vec{p} + h(u,v)\vec{n}\]

  • Correct silhouettes and shadows

  • Complex geometry at virtually no memory cost

  • Must be done during modelling stage, e.g. before ray-geometry intersection

Fractal Landscapes

Procedural generation of geometry

Displacement Mapping

Fractal Landscapes

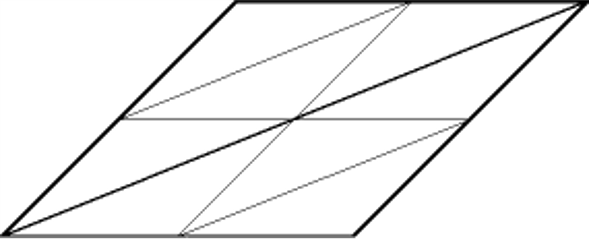
Coarse triangle mesh approximation

1:4 triangle subdivision

  • Vertex insertion at edge-midpoints

 

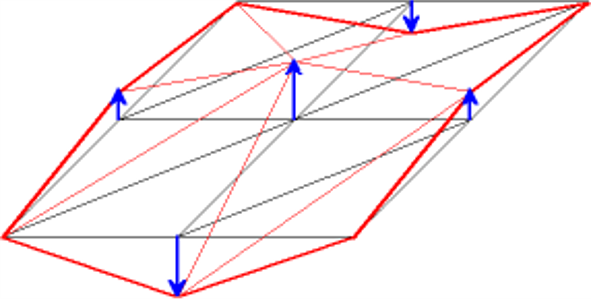
New vertex perturbation

  • Displacement along normal
  • Random amplitude
  • Perturbation scale depends on subdivision level
    • Decreasing power spectrum
    • Parameter for model roughness

 

Recursive subdivision

  • Level of detail determined by number of subdivisions

Displacement Mapping

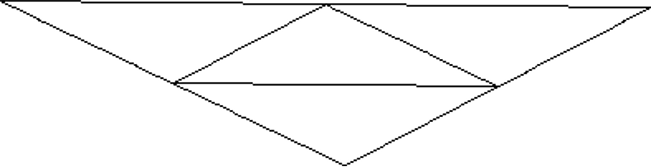
Fractal Landscapes

Fields of Application

  • Base mesh

  • Repeated subdivision &  vertex displacement

  • Water surface

  • Fog

  • …

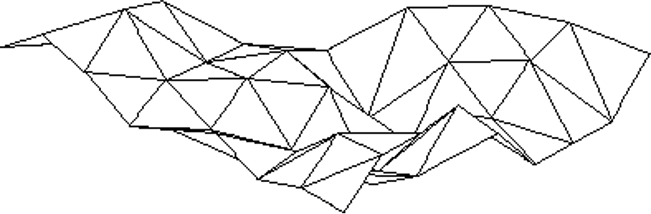
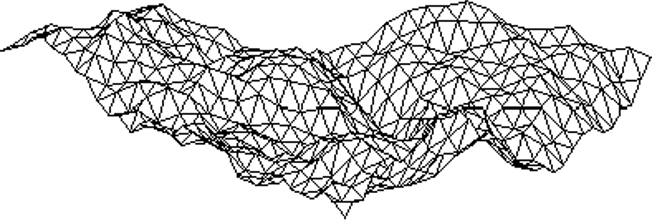
Displacement Mapping

Bump Mapping VS Displacement Mapping

bump mapping

displacement mapping

Displacement Mapping

Bump Mapping VS Displacement Mapping

Environmental Mapping

(a.k.a Reflection Mapping)

Environmental Mapping

(a.k.a Reflection Mapping)

The key to depicting a shiny-looking material is to provide something for it to reflect

  • Proper reflection requires ray tracing, expensive
  • Can be simulated with a pre-rendered environment, stored as a texture
  • Imagine object is enclosed in an infinitely large sphere or cube
  • Rays are bounced off object into environment to determine color

Reflection Mapping
=
Environmental Mapping
*
surface color
 

Environmental Mapping

Steps:

  • Load environment map as a texture and apply it to environmental sphere
  • Do not consider primary ray - environmental sphere intersections
  • For each ray-prim intersection point \(\vec{p}\), compute normal to the prim \(\vec{n}(\vec{p})\)
  • Compute the corresponding reflection vector \[\vec{r} =\vec{d}- 2\vec{n}\left(\vec{n}\cdot\vec{d}\right)\]
  • Re-trace the reflection ray \(\left(\vec{p}, \vec{r}(\vec{p},\vec{n})\right)\)
  • Once reflection ray hits the environmental sphere return corresponding texel from the environmental map

\(\vec{n}\)

\(\vec{p}\)

\(\vec{r}\)

primary ray

environmental sphere

omitted intersection point

really visible point

Environmental Mapping

Examples

Terminator 2 motion picture 1991

Environmental Mapping

Examples

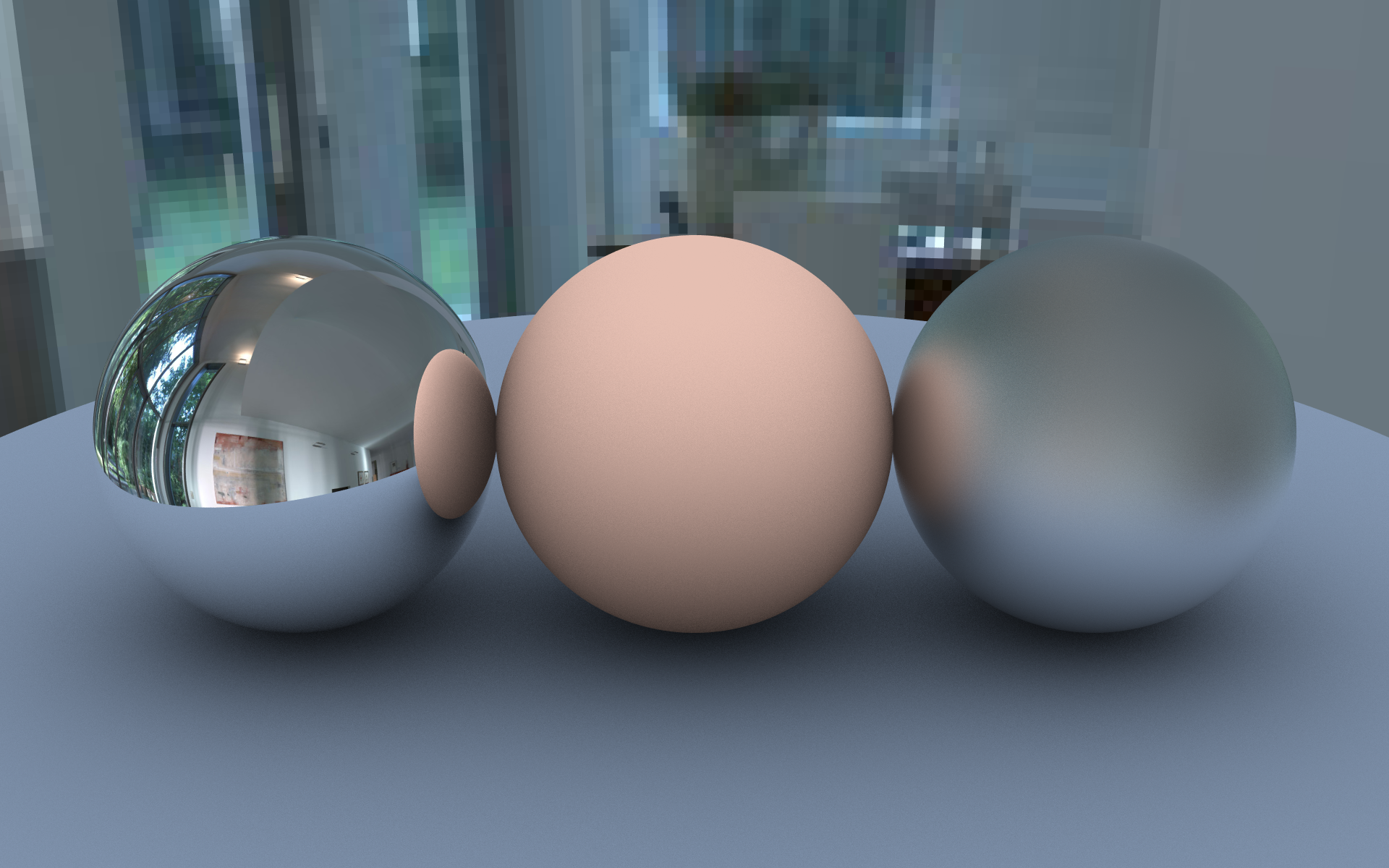
OpenRT mirror balls 2021

Environmental Mapping

1280 x 573 pixels size environmental map

Methods to Create Environmental Maps

Environmental Mapping

Gazing balls

  • Historical method from 1982 / 83
  • I.e. photo of a reflecting sphere (gazing ball)

Methods to Create Environmental Maps

Environmental Mapping

360° Cameras / Panorama stitching apps

  • Insta 360°, Facebook Surround 360°, etc.
  • Microsoft Photosynth app, etc.

CGI Environmental Camera (e.g. OpenRT rt::CCameraEnvironment)

Methods to Create Environmental Maps

Procedural Textures

Procedural Textures

3D Textures

  • Create a 3D parallelisation \((u,v,w) \) for the texture
  • Map this onto the object
  • The easiest parametrization is to use the model-space coordinate system to index into a 3D texture \((u,v,w) = (x, y, z)\)
  • Like carving the object from the material

2D mapping

3D carving

3D Procedural Textures

Instead of using the texture coordinates as an index, use them to compute a function that defines the texture 

 

\[f(u,v,w)\]

Procedural Textures

Example

Instead of an image, use a function

Vec3f CTextureProcedural::getVoxel(const Vec3f& uvw) const
{
    float u = uvw.val[0];	// hitpoint.x
    float v = uvw.val[1];	// hitpoint.y
    float w = uvw.val[2];	// hitpoint.z

    float k = 100;
    float intencity = (1 +  sinf(k * u) * cosf(k * v)) / 2;
	
    Vec3f color = Vec3f::all(intencity);

    return color;
}

Procedural Textures

Pros and Cons

Advantages over image texture

Disadvantages

  • Infinite resolution and size
  • More compact than texture maps
  • No need to parameterise surface
  • No worries about distortion and deformation
  • Objects appear sculpted out of solid substance
  • Can animate textures
  • Difficult to match existing texture
  • Not always predictable
  • More difficult to code and debug
  • Perhaps slower
  • Aliasing can be a problem 

Procedural Textures

Simple Procedural Textures

Stripe

Rings

Color each point one or the other color depending on where \(floor(z)\) (or \(floor(x)\) or \(floor(y)\)) is even or odd

Color each point one or the other color depending on whether the \(floor(\) distancefrom object center along two coordinates\()\) is even or odd

Procedural Textures

Wood Texture

Classify texture space into cylindrical shells 

\[f(u,v,w) = (u^2+v^2)\]

Outer rings closer together, which simulates the growth rate of real trees.

Color look-up table

  • woodmap(0)
  • woodmap(1)

= brown earlywood

= tan latewood

Wood texture

  • wood(u,v,w)=woodmap((u*u + v*v) % 1)

Procedural Textures

Wood Texture

Wood texture

  • wood(u,v,w)=woodmap((u*u + v*v) % 1)

Adding noise

Add noise to cylinders to warp wood

  • wood(u,v,w)=woodmap((u*u + v*v) % 1 + noise(u,v,w))

\[noise(u,v,w)=\alpha\cdot noise(f_xu+\phi_x,f_yv+\phi_y,f_zw+\phi_z)\]

  • Frequency (\(f\)): coarse vs. fine detail, number and thickness of noise peaks
  • Phase (\(\phi\)): location of noise peaks
  • Amplitude (\(\alpha\)): controls distortion due to noise effect 

Procedural Textures

Wood Texture

Without noise

With noise

Procedural Textures

Perlin Noise

\(noise(u,v,w)\): pseudo-random number generator with the following characteristics:

  • Memoryless
  • Repeatable
  • Isotropic
  • Band limited (coherent): difference in values is a function of distance
  • No obvious periodicity
  • Translation and rotation invariant (but not scale invariant)
  • Known range \([-1, 1]\)
    • scale to \([0,1]\) using \(\frac{1 + noise()}{2}\)
    • \(|noise()|\) creates dark veins at zero crossings

white noise

Perlin noise

Abs(Perlin noise)

Procedural Textures

Turbulence

Fractal

Sum multiple calls to noise:

 

\[turbulance(u,v,w)=\sum^{octaves}_{i=1}\frac{1}{2^if}noise(2^if\cdot(u,v,w))\]

 

each additional term adds finer detail, with diminishing return  

1-8 octaves of turbulence

Procedural Textures

Marble Texture

Use a sine function to create the stripes:

 

\[marble(u,v,w)=sin\left(f\cdot u+\alpha\cdot turbulance(u,v,w)\right)\]

  • The frequency (\(f\)) of the sine function controls the number and thickness of the veins
  • The amplitude (\(\alpha\)) of the turbulence controls the distortion of the veins
Made with Slides.com