Contact Sampling for
Contact Rich Manipulation

28 April 2023
 

By Shao Yuan Chew Chia

Joint work with: Terry Suh, Pang Tao, Sizhe Li

Contact Sampling Problem

Given a goal state \(x_g\) and current state \(x\) of the object,

how should you position the robot \(q\) to best reach \(x_g\),

through subsequent commands \(u\)

\(x_g\)

\(x\)

\(q\)

\(u\)

Why this problem?

Address the discrete question of where/how to make contact

\(x_g\)

\(x\)

\(q_{1}\)

\(q_{2}\)

Why this problem?

Address the discrete question of where/how to make contact

\(x_g\)

\(x\)

\(q_{1}\)

\(q_{2}\)

General Problem Area

Motion planning for high dimensional contact-rich manipulation

Classes of Methods Trajectory Optimization Sampling based motion planning Learning based methods
Examples Continuous trajectory optimization
 Rapidly exploring Random Tree (RRT) Reinforcement Learning,
Behavior cloning
How contact sampling can help Provide good initial guesses Increase state space coverage of "extend" step Improve sample efficiency

Improving Trajectory Optimization

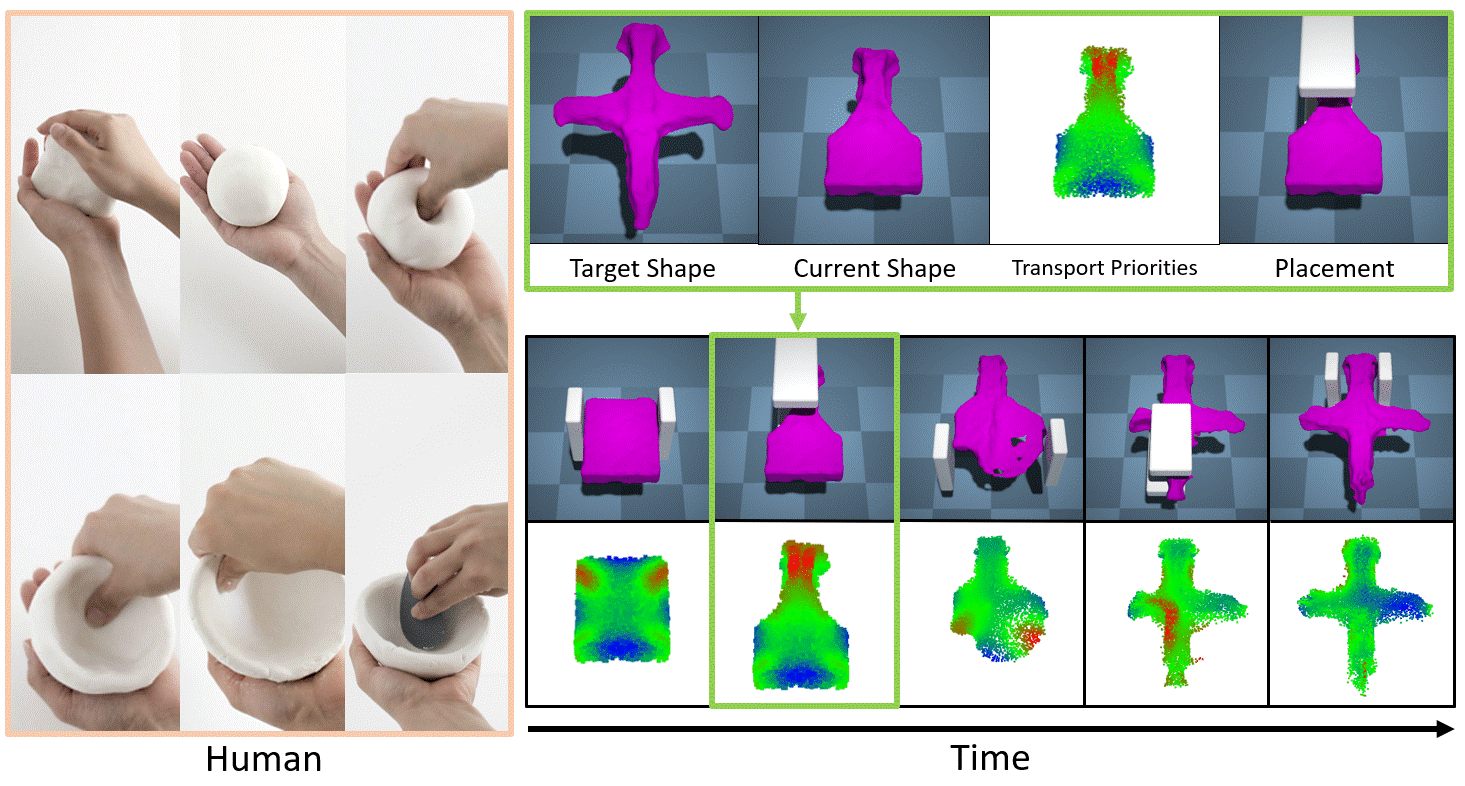
Uses optimal transport to define a heuristic for which particles need to move the most

Improving RRT

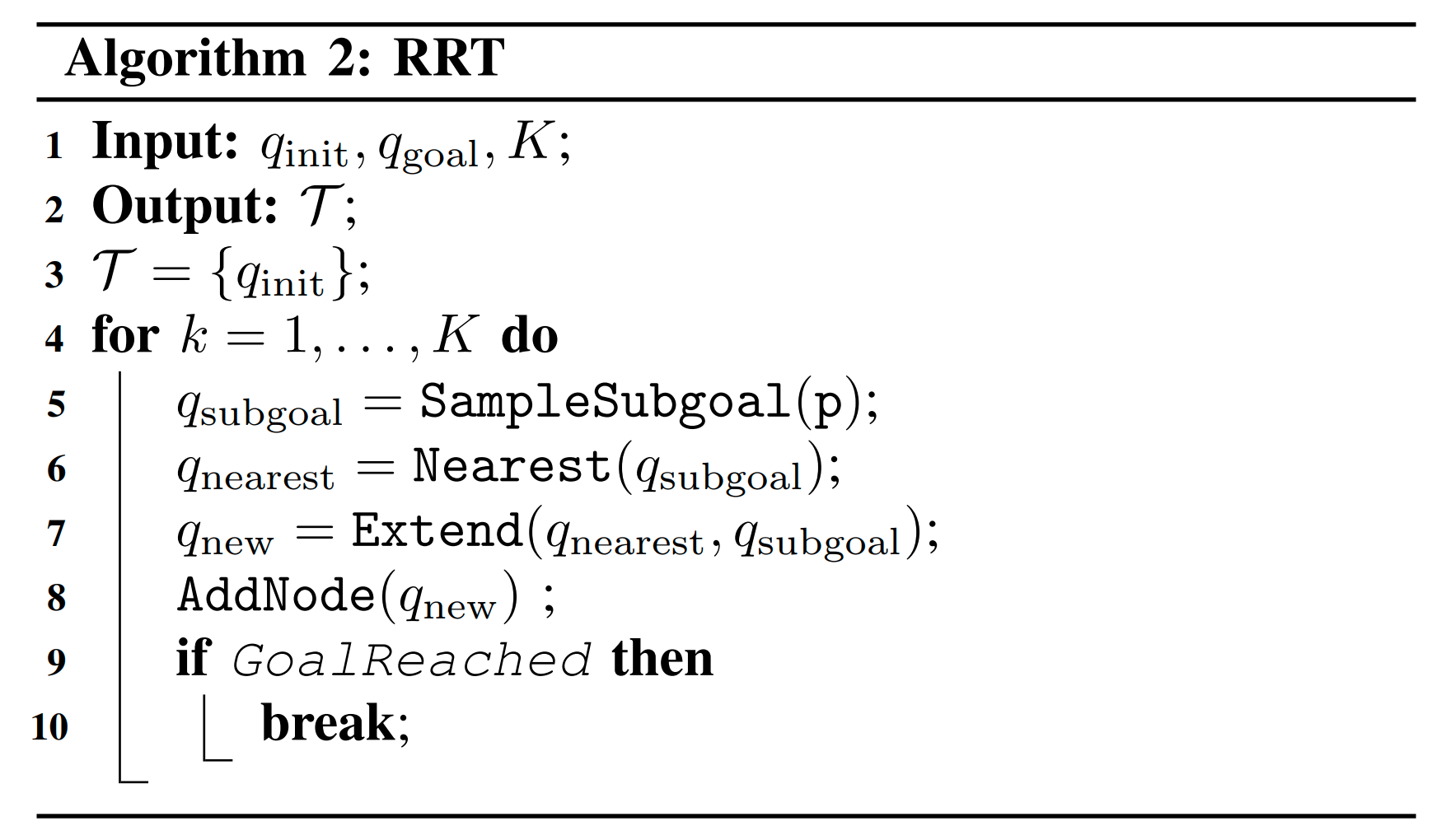
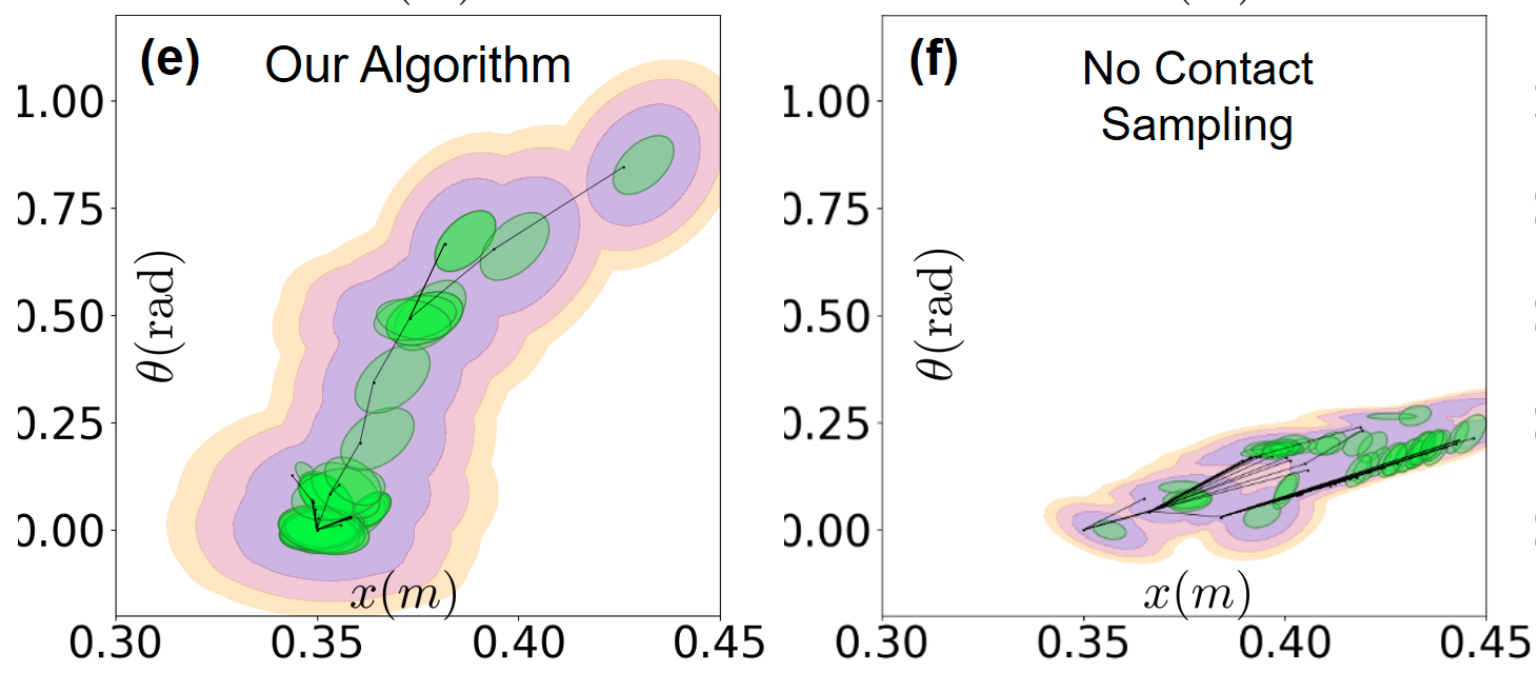
Contact Sampling Problem

Given a goal state \(x_g\) and current state \(x\) of the object,

how should you position the robot \(q\) to best reach \(x_g\),

through subsequent commands \(u\)

\(x_g\)

\(x\)

\(q\)

\(u\)

Contact Sampling Problem

Given a goal state \(x_g\) and current state \(x\) of the object,

how should you position the robot \(q\) to best reach \(x_g\),

through subsequent commands \(u\)

\(x_g\)

\(x\)

\(q\)

\(u\)

Long horizon question

Modified Problem

Given a goal state \(x_g\) and current state \(x\) of the object,

find the robot position \(q\), that would in one subsequent command \(u\), minimize the object's distance to the goal,

\(x_g\)

\(x\)

\(q\)

\(u\)

\min_{q\in\mathcal{A}(x)} d( x_g, f(x,q,u))

Assumptions

  • Discrete time

  • Quasistatic dynamics

  • Absolute position commands

s_{next} = f(x, q, u)
s = \begin{bmatrix}x\\ q\end{bmatrix}

Solution Sketch

Input: \(x\), \(x_g\)

Output: \(N\) best \(q\)'s

  • Sample \(M\) initial admissible positions of the robot \(q_0\)
    • Rejection sample via collision checker
    • Uniform distribution over workspace
  • Do gradient descent to evolve the initial positions
    • At each step, project \(q\) back into admissible set
  • Return \(N\) best \(q\)'s

Key Challenge

contact dynamics lead to the cost landscape being flat 

\min_{q\in\mathcal{A}(x)} d( x_g, f(x,q,u))

Solution 1:

Randomized Smoothing of the cost

\min_{q\in\mathcal{A}(x)} d( x_g, f(x,q,u))
\min_{q\in\mathcal{A}(x)} \mathbb{E}_w \left[d(x_g, f(x, q, q+w))\right] \qquad w\sim\mathcal{N}(0,\sigma^2)

Cost landscape: Randomized Smoothing (Warm up 1)

  • [x,y,theta]
     
  • x_init
    [0,0,0] (Blue)
  • x_goal
    [2,0,0] (Green)
  • x_init
    [0,0,0]
    (Blue)
  • x_goal
    [-1.5,-1.5,1] (Green)

Cost landscape: Randomized Smoothing (Warm up 2)

Cost landscape: Randomized Smoothing (Distance from Goal)

\(x_g\) = [0.3, 0, 0]

\(x_g\) = [2, 0, 0]

Cost landscape: Randomized Smoothing (Action Standard Deviation, Goal Near)

std = 0.01

std = 0.1

Cost landscape: Randomized Smoothing (Action Standard Deviation, Goal Far)

std = 0.01

std = 0.1

Cost landscape: Randomized Smoothing (Action Standard Deviation Animations)

std = [0.01 , ... , 1]

Cost landscape: Randomized Smoothing
Sample Aggregation Function

Min

Mean

Max

Non-Physical Behavior of Anitescu Convex Relaxation

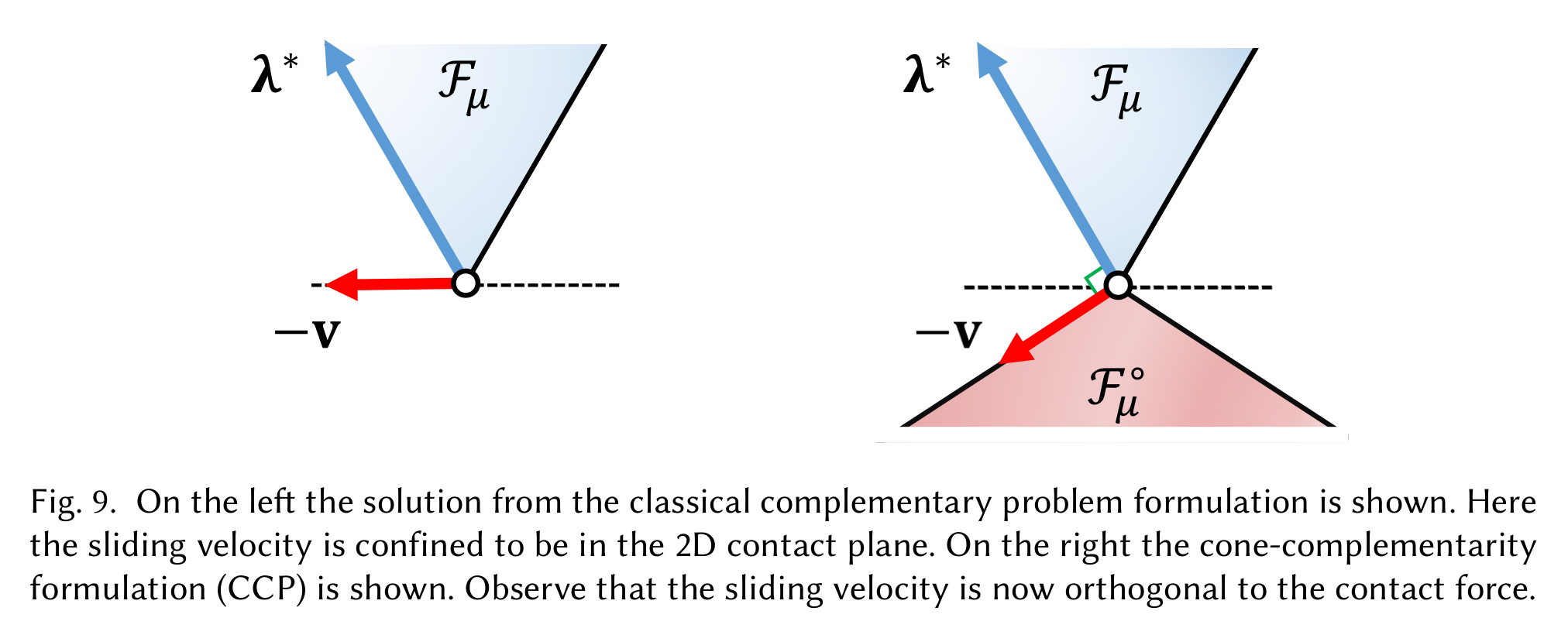
Andrews, S., Erleben, K., & Ferguson, Z. (2022). Contact and friction simulation for computer graphics. In ACM SIGGRAPH 2022 Courses (pp. 1-172).

Non-Physical Behavior of Anitescu Convex Relaxation
Effect on Cost Landcape (std = 0.5)

Incremental steps = 10

Incremental steps = 5

Incremental steps = 1

Non-Physical Behavior of Anitescu Convex Relaxation
Effect on Cost Landcape (std = 0.1)

Incremental steps = 10

Incremental steps = 5

Incremental steps = 1

Zeroth Order Batch Gradient

Randomized Smoothing of
cost

Gradient Computation

We want to solve

\min_{q} \mathbb{E}_w \left[d(x_g, f(x, q, q+w))\right] \qquad w\sim\mathcal{N} (0,\sigma_{w}^2\mathbf{I})

To use zeroth-order methods, we can instead choose a surrogate objective

\min_{q} \mathbb{E}_{v,w} \left[d(x_g, f(x, q+v, q+v+w))\right]
w\sim\mathcal{N}(0,\sigma_{w}^2\mathbf{I}) \text{ and } v\sim\mathcal{N}(0,\sigma_v^2\mathbf{I})

Gradient Computation

\nabla_q \mathbb{E}_{v,w} \left[d(x_g, f(x, q+v, q+v+w))\right]
= \mathbb{E}_{v,w} \left[\frac{v}{\sigma^2_v}\left[d(f(x, q +v, q+v+w),x_g)- \mu^*\right] \right]
\mu^* = {E}_{v,w} \left[d(x_g, f(x, q+v, q+v+w))\right]

where

which has the unbiased estimator of the sample mean, i.e.

\mu_{\rho}(q) = \frac{1}{N}\sum^N_{i=1} v_i\left[d(f(x, q + v_i, q + v_i + w_i), x_g)\right]

Gradient Computation

\nabla_q \mathbb{E}_{v,w} \left[d(x_g, f(x, q+v, q+v+w))\right]
= \mathbb{E}_{v,w} \left[\frac{v}{\sigma^2_v}\left[d(f(x, q +v, q+v+w),x_g)- \mu^*\right] \right]

Thus the natural estimator of the gradient is

\frac{1}{\sigma_v^2}\frac{1}{N}\sum^N_{i=1} v_i\left[d(f(x, q + v_i, q + v_i + w_i), x_g) - \mu_{\rho}(q)\right]

Zeroth Order Batch Gradient

\(x_g\) = [2,0,0], q_std = 0.1, u_std = 0.1, h=0.01

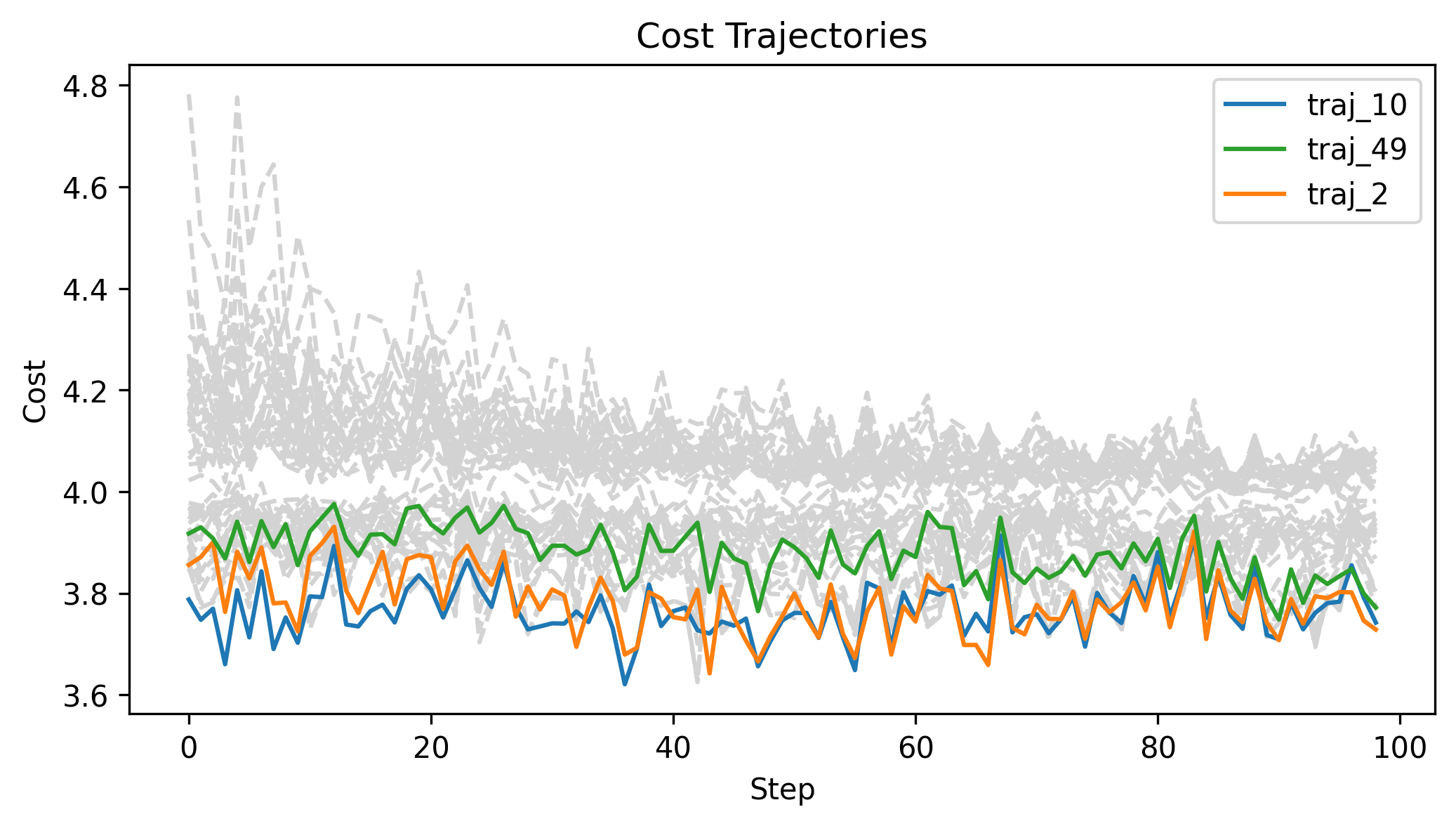
Zeroth Order Batch Gradient

\(x_g\) = [2,0,0], q_std = 0.1, u_std = 0.1, h=0.01

Zeroth Order Batch Gradient

\(x_g\) = [-1.5,-1.5,1], q_std = 0.1, u_std = 0.1, h=0.01

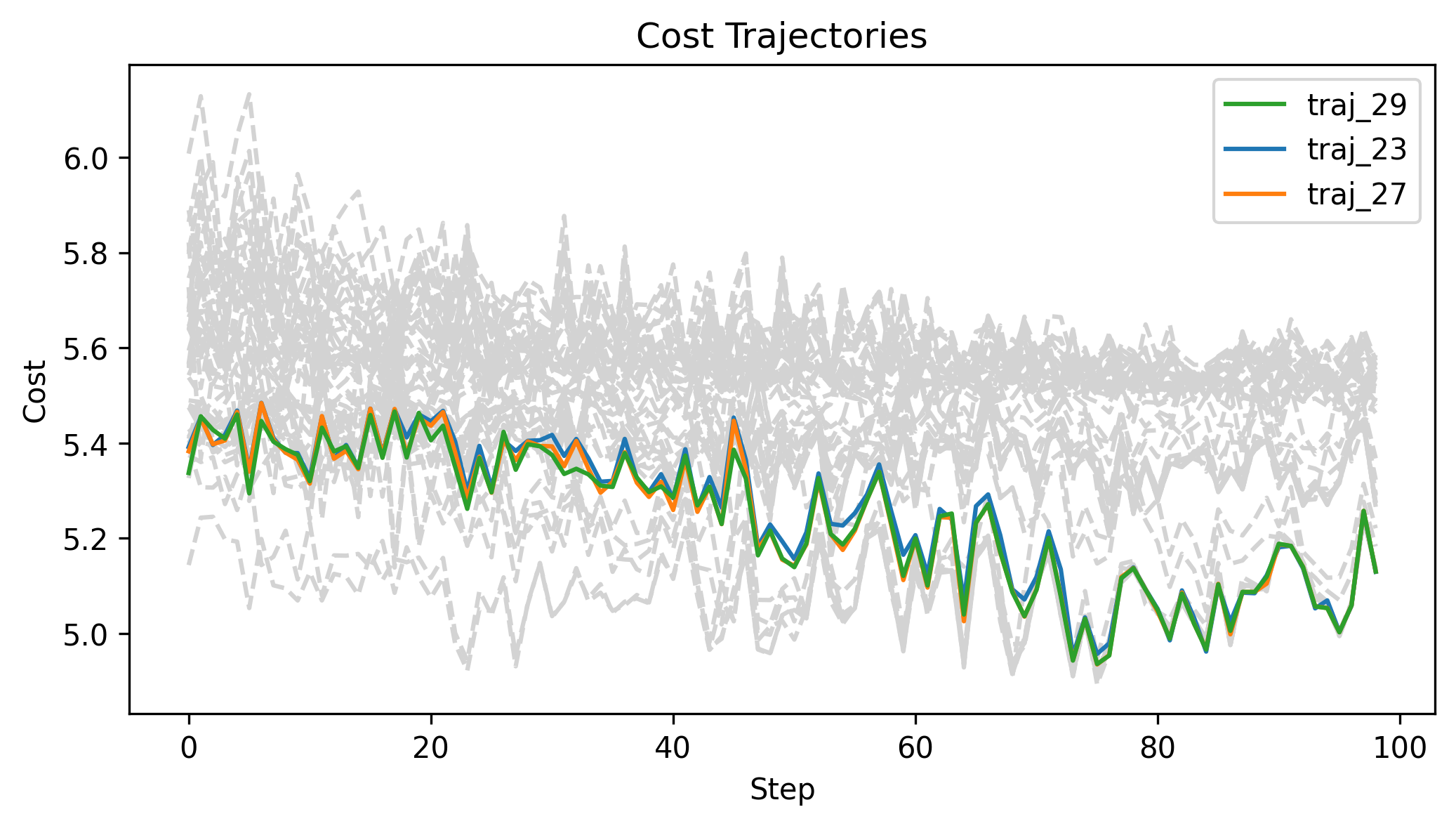
Zeroth Order Batch Gradient

\(x_g\) = [-1.5,-1.5,1], q_std = 0.1, u_std = 0.1, h=0.01

Zeroth Order Batch Gradient

\(x_g\) = [-1.5,-1.5,1], q_std = 0.1, u_std = 0.1, h=0.01

Zeroth Order Batch Gradient

\(x_g\) = [2,0,0], q_std = 0.1, h=0.01

u_std = 0.1

u_std = 0.3

u_std = 0.5

Zeroth Order Batch Gradient

\(x_g\) = [2,0,0], u_std = 0.3, h=0.01

q_std = 0.05

q_std = 0.1

q_std = 0.3

Zeroth Order Batch Gradient

\(x_g\) = [2,0,0], u_std = 0.3, h=0.05

q_std = 0.05

q_std = 0.1

q_std = 0.3

Solution 2:

Analytic Smoothing of
Contact Dynamics

Cost Landscape: Analytic Smoothing of Contact Dynamics

\(x_g\) = [2,0,0]

Log barrier weight = 1000

(0.001N at 1m)

Log barrier weight = 100

(0.01N at 1m)

Log barrier weight = 10

(0.1N at 1m)

Cost Landscape: Analytic Smoothing of Contact Dynamics

\(x_g\) = [0.3,0,0]

Log barrier weight = 1000

(0.001N at 1m)

Log barrier weight = 100

(0.01N at 1m)

Log barrier weight = 10

(0.1N at 1m)

Cost Landscape: Analytic Smoothing of Contact Dynamics

\(x_g\) = [-1.5,-1.5,1]

Log barrier weight = 1000

(0.001N at 1m)

Log barrier weight = 100

(0.01N at 1m)

Log barrier weight = 10

(0.1N at 1m)

First Order Batch Gradient

Analytic Smoothing of
Contact Dynamics

Gradient Computation

x' = f_x(x, q, u)
s' = f(x, q, u)
x' = f^{\rho}_x(x, q, u)

Full state dynamics

Just next object state

Just next object state, but analytically smoothed dynamics

Gradient Computation

We want to calculate

Analytically smoothed dynamics that takes a relative position command \(u_r\) and only returns \(x\)

\nabla_q d(f^{\rho r}_x(x, q, u_r), x_g)
u(q, u_r) \coloneqq q + u_r
f^{\rho}_x(x, q, u(q,u_r)) = f^{\rho r}_x(x, q, u_r)

Absolute position command as a function of robot position and relative position command

Gradient Computation

\nabla_q d(f^{\rho r}_x(x, q, u_r), x_g)
= \frac{\partial}{\partial q} x'^\top\bigg|_{x'=f^{\rho r}_x(\bar{x}, \bar{q}, \bar{u_r})}\frac{\partial }{\partial x'} d(x_g, x')\bigg|_{x'=f^{\rho r}_x(\bar{x}, \bar{q}, \bar{u_r})}

Gradient Computation

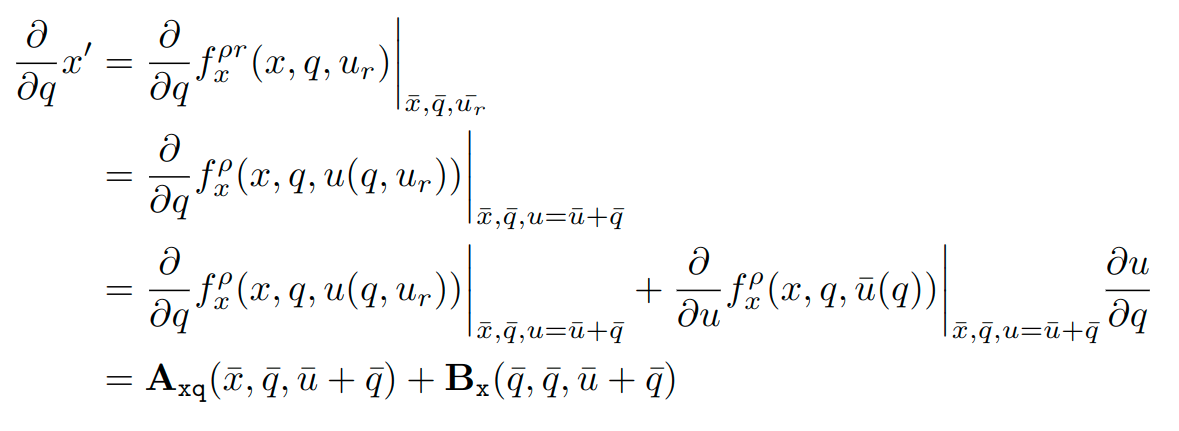
Gradient Computation

\frac{\partial }{\partial x'} d(x_g, x') = -2 \mathbf{Q} (x_g - x')
d(x_g,x')=(x_g - x')^\top \mathbf{Q} (x_g - x')

Weighted L2 Norm Cost

Gradient Computation

= -2 [\mathbf{A}_{\mathtt{xq}}(\bar{x},\bar{q},\bar{u}+\bar{q}) + \mathbf{B}_{\mathtt{x}}(\bar{q},\bar{q},\bar{u}+\bar{q})]\mathbf{Q} (x_g - x')
\nabla_q d(f^{\rho r}_x(x, q, u_r), x_g)
= \frac{\partial}{\partial q} x'^\top\bigg|_{x'=f^{\rho r}_x(\bar{x}, \bar{q}, \bar{u_r})}\frac{\partial }{\partial x'} d(x_g, x')\bigg|_{x'=f^{\rho r}_x(\bar{x}, \bar{q}, \bar{u_r})}

First Order Batch Gradient

\(x_g\) = [-1.5,-1.5,1], log barrier weight = 100, h = 0.01

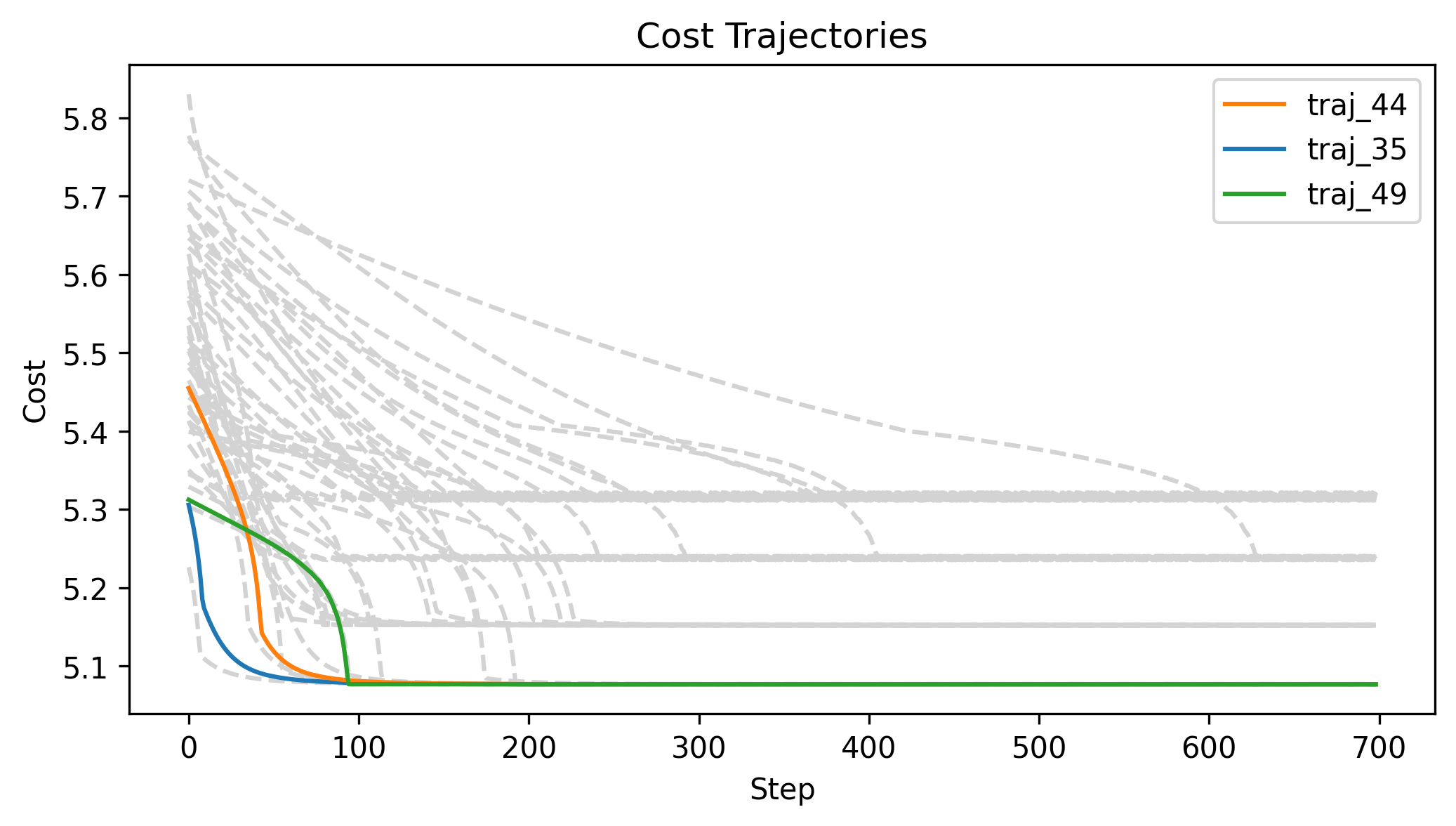
First Order Batch Gradient

\(x_g\) = [-1.5,-1.5,1], log barrier weight = 100, h = 0.01

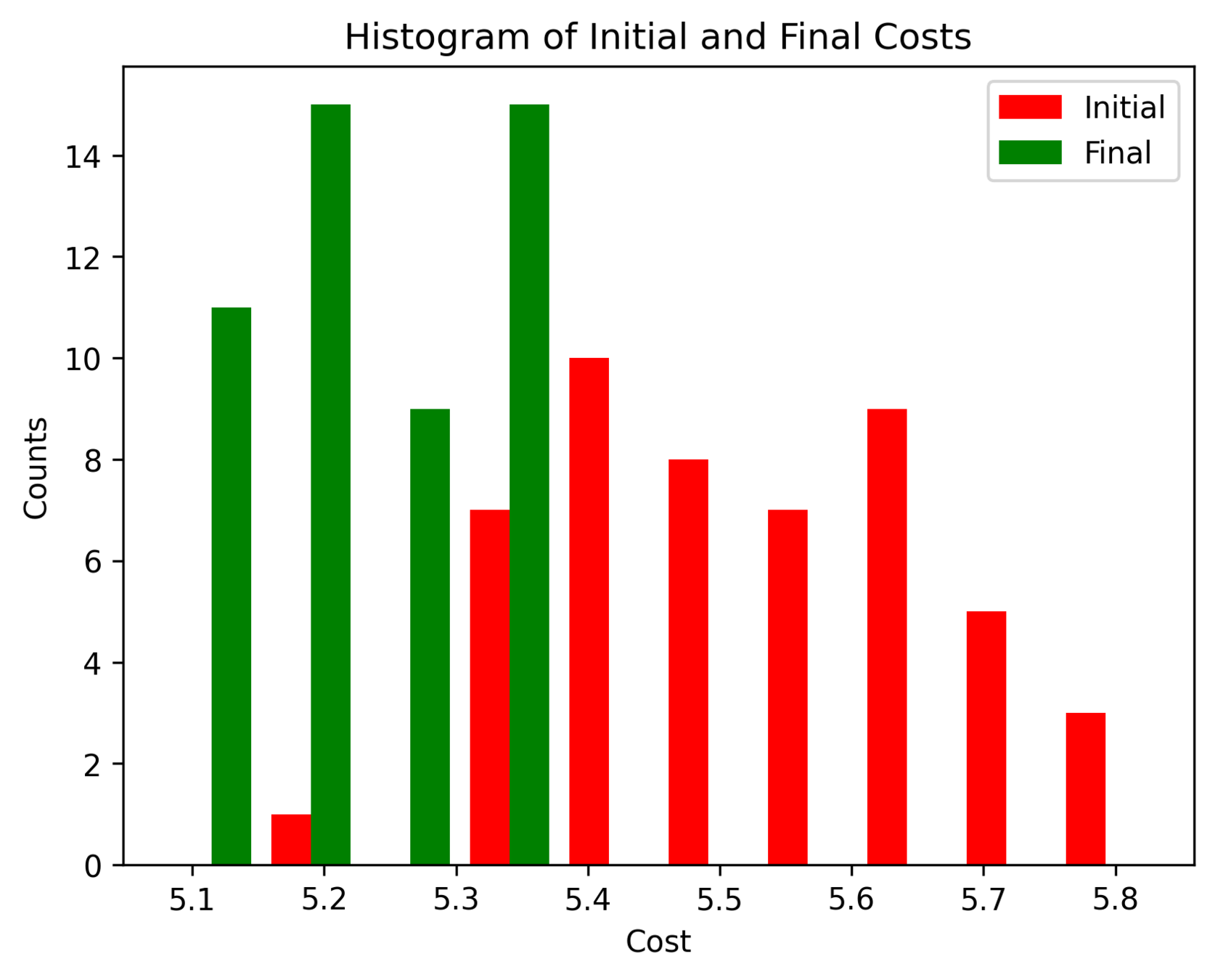
First Order Batch Gradient

\(x_g\) = [-1.5,-1.5,1], log barrier weight = 100, h = 0.01

First Order Batch Gradient

\(x_g\) = [-1.5,-1.5,1]

Log barrier weight = 1000

(0.001N at 1m)

Log barrier weight = 100

(0.01N at 1m)

Log barrier weight = 10

(0.1N at 1m)

First Order Batch Gradient

\(x_g\) = [2, 0, 0]

Log barrier weight = 1000

(0.001N at 1m)

Log barrier weight = 100

(0.01N at 1m)

Log barrier weight = 10

(0.1N at 1m)

First Order Batch Gradient \(x_g\) = [2, 0, 0]

Log barrier weight = 1000

(0.001N at 1m)

Log barrier weight = 100

(0.01N at 1m)

Log barrier weight = 10

(0.1N at 1m)

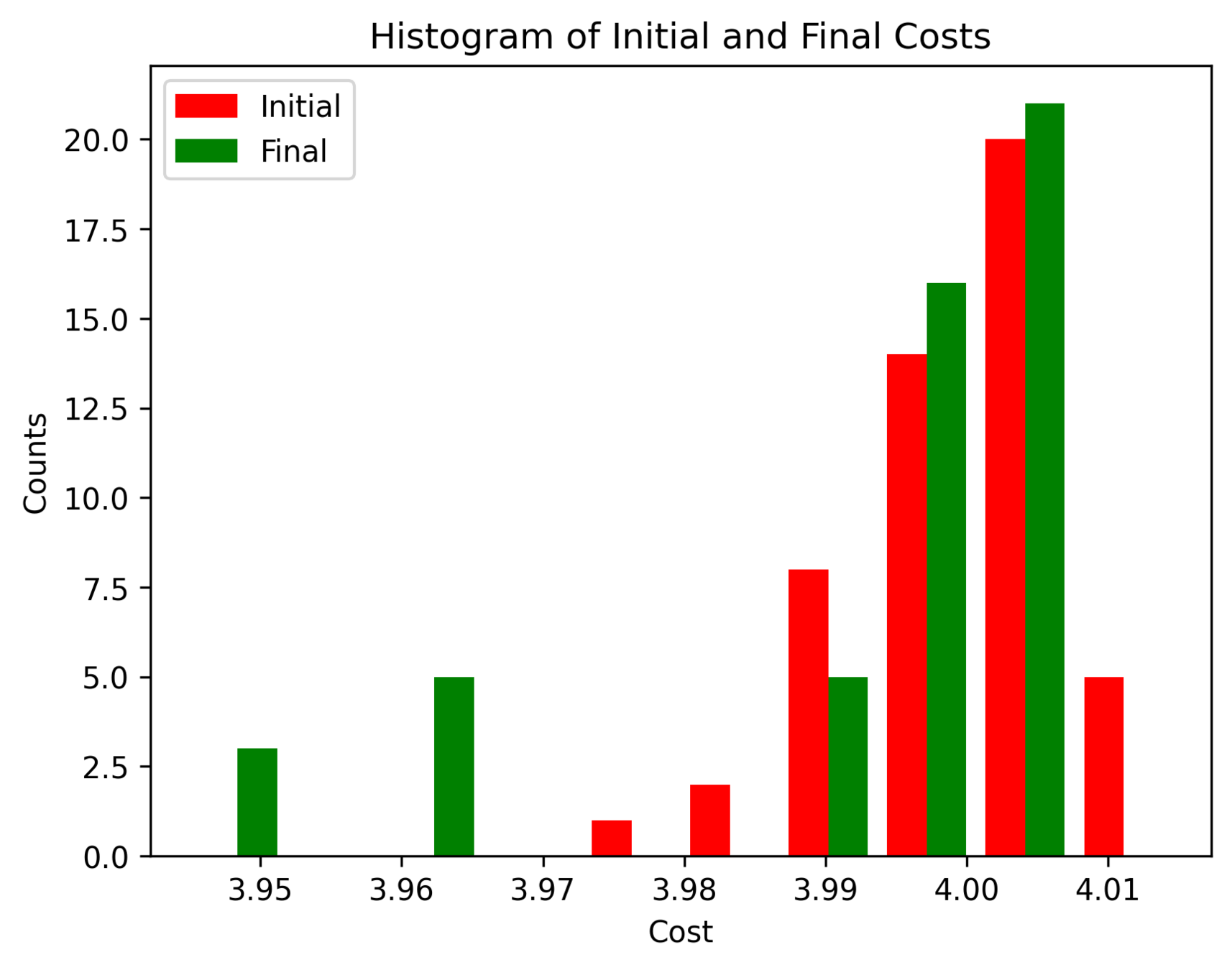
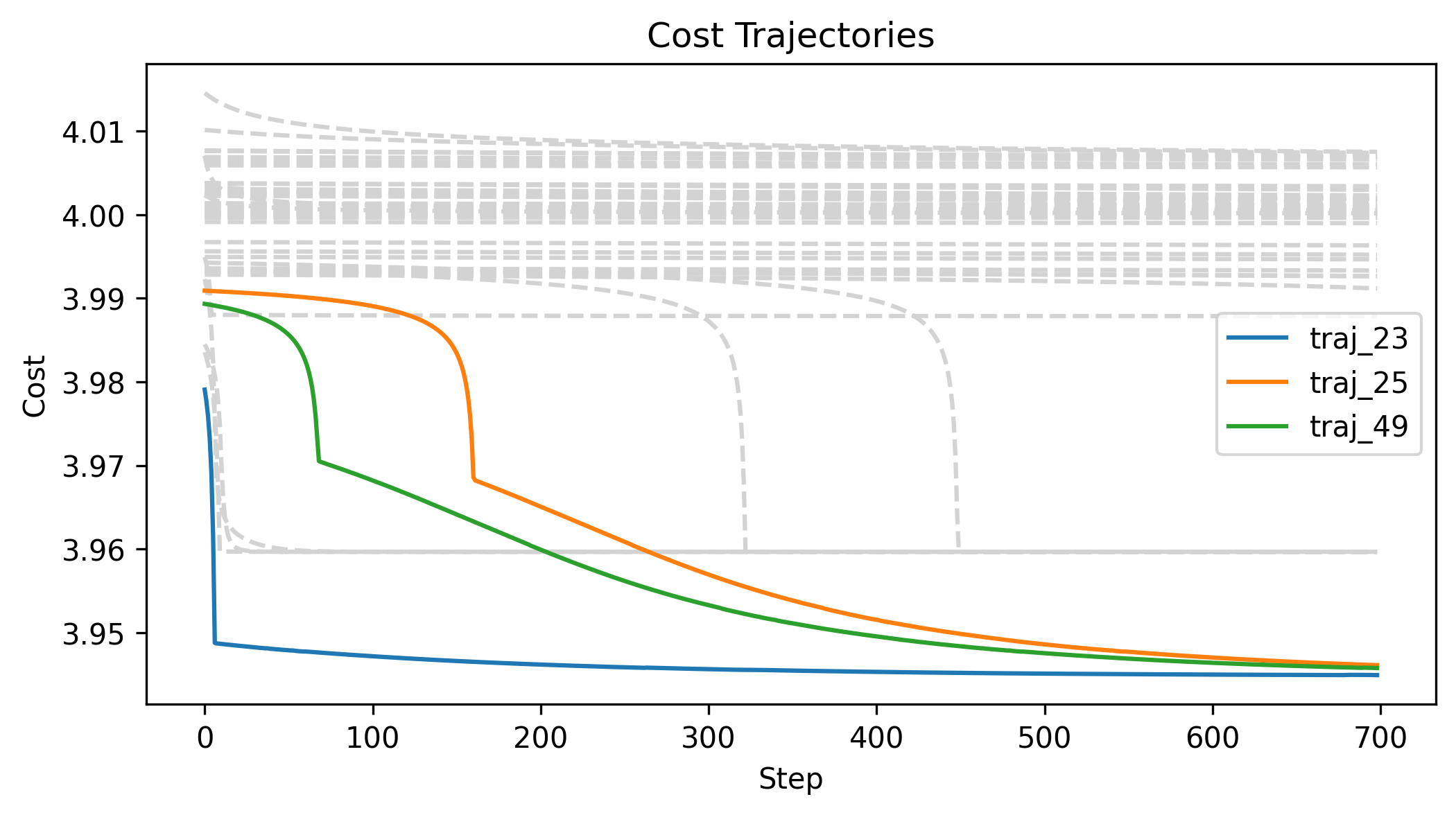
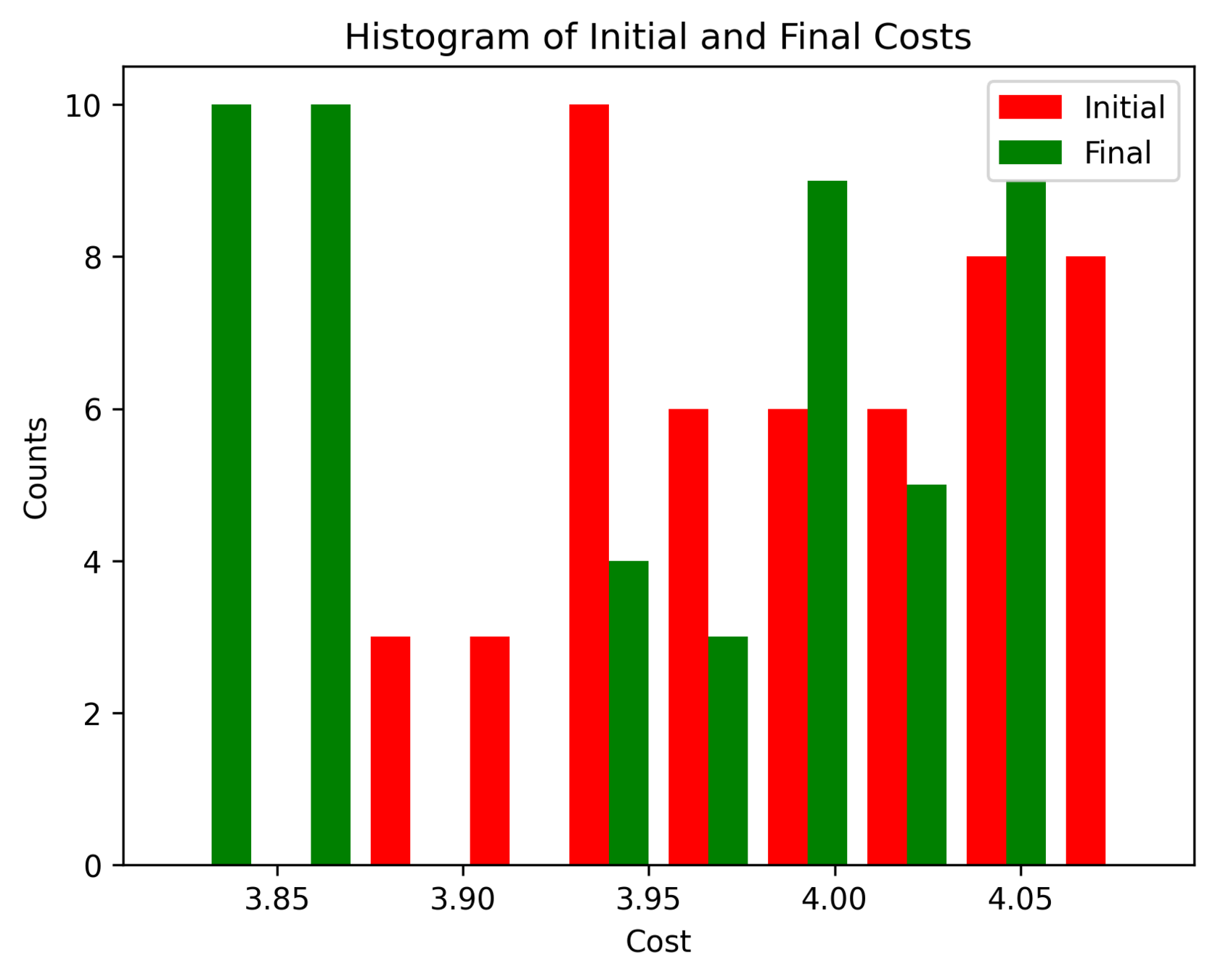
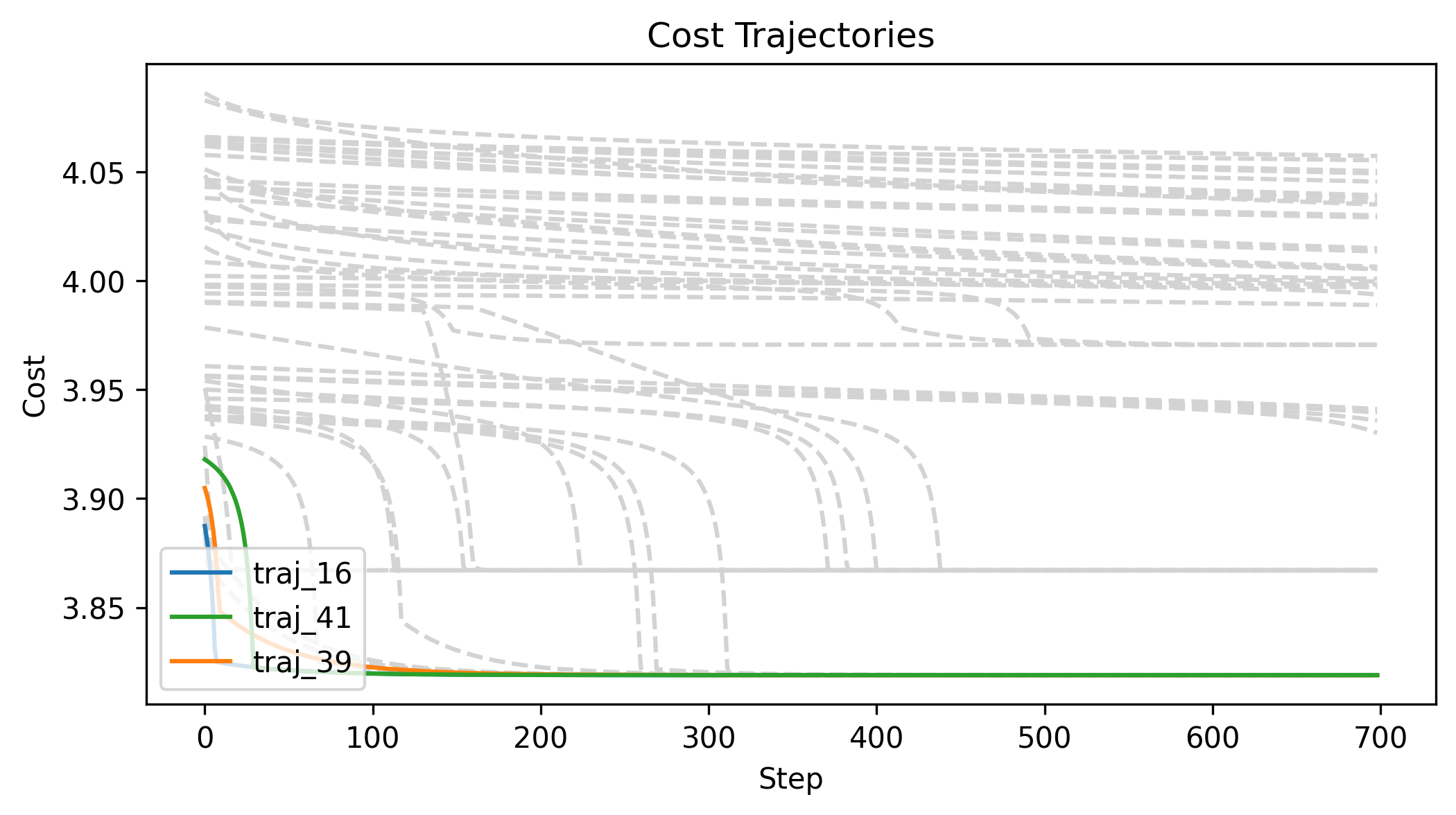
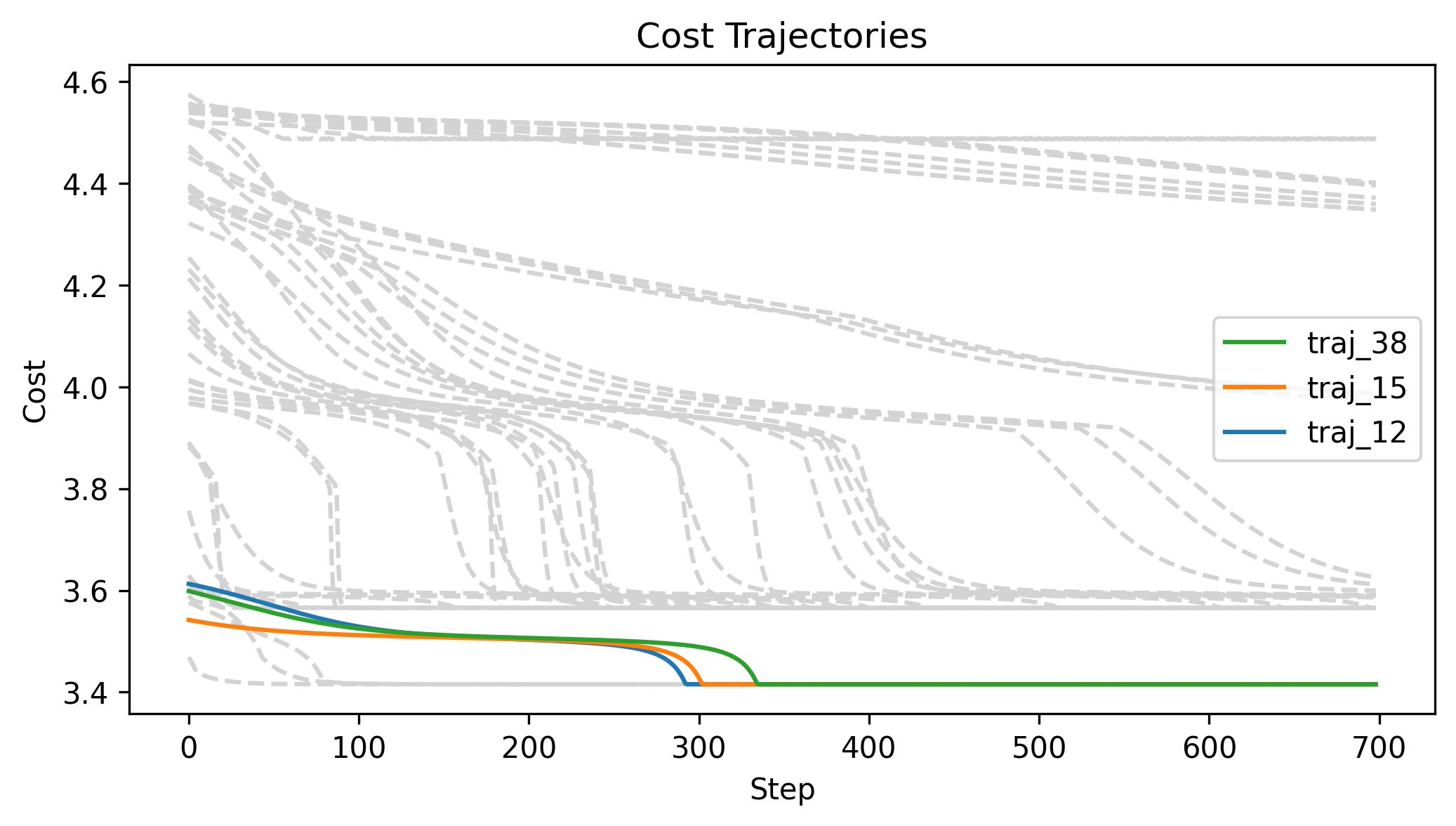
First Order Batch Gradient

\(x_g\) = [0.3, 0, 0]

Log barrier weight = 1000

(0.001N at 1m)

Log barrier weight = 100

(0.01N at 1m)

Log barrier weight = 10

(0.1N at 1m)

Next Steps

  • Understand what's going on in the corners
  • Try variance schedule/annealing
  • Explore randomized smoothing min?
  • Try it on more complex rigid body manipulators (Planar hand, Allegro hand)
  • Try it on deformable objects (Plasticine Lab)
  • Integrate into RRT
Made with Slides.com