Discrete-time Control Contraction Metrics (DCCM)
for Quasistatic Planar Pushing
using Smoothed Dynamics
MIT 2.152[J] Nonlinear Control
16 May 2023
By Shao Yuan Chew Chia
Harvard College
Control though Contact
It's important


Challenges:
-
Non-smooth contact dynamics
-
Underactuated system
Current Methods
Explicit enumeration of contact modes
Russ Tedrake. Underactuated Robotics: Algorithms for Walking, Running, Swimming, Flying, and Manipulation (Course Notes for MIT 6.832). Downloaded on May 14 from https://underactuated.csail.mit.edu/
Current Methods
Smoothing of contact dynamics
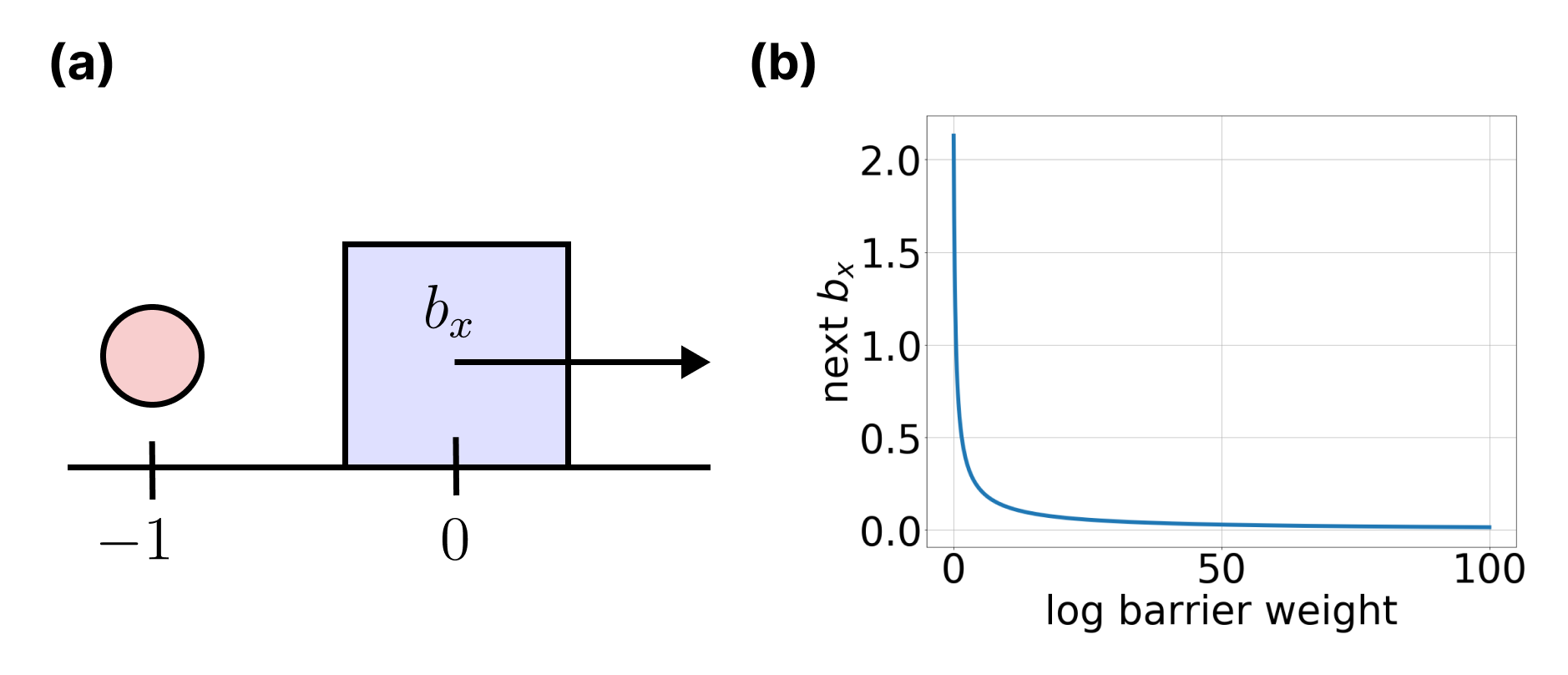
Our Approach
Smoothing of contact dynamics
+
Control Contraction Metrics
Control Contraction Metrics
Differential version of a Control Lyapunov Function
I. R. Manchester and J.-J. E. Slotine, “Control Contraction Metrics: Convex and Intrinsic Criteria for Nonlinear Feedback Design,” IEEE Transactions on Automatic Control, vol. 62, no. 6, pp. 3046–3053, Jun. 2017, ISSN:1558-2523. DOI: 10.1109/TAC.2017.2668380.
Control Contraction Metrics
Advantages
-
Certificates of stability and convergence rates
-
Trajectory independent controllers
-
Convex synthesis of the controller
-
Faster online computation of the control law
Problem Setup
Dynamics:
- Discrete-time
- Analytically smoothed
- Nonlinear
- Control Affine

Theory of DCCM
dynamics
differential dynamics
Jacobians
differential state feedback control law
Theory of DCCM
differential squared distance in the positive definite metric \(M\)
at the next time step...
contraction condition
Theory of DCCM (Online)
Riemannian length
Riemannian energy
geodesic
tracking controller
Methods: DCCM Synthesis
Sums of Squares (SOS) Programming
contraction condition
where \(W := M^{-1}\) and \(L := KW\)
Methods: DCCM Synthesis
Sums of Squares (SOS) Programming
is SOS
relaxation slack variable
coefficients of \(L\) and \(W\)
enforced over samples
Methods: DCCM Synthesis
Sums of Squares (SOS) Programming
matrix of polynomials
polynomial expression
monomial basis
Methods: DCCM Synthesis
Sampling strategy

Methods: Online Computation
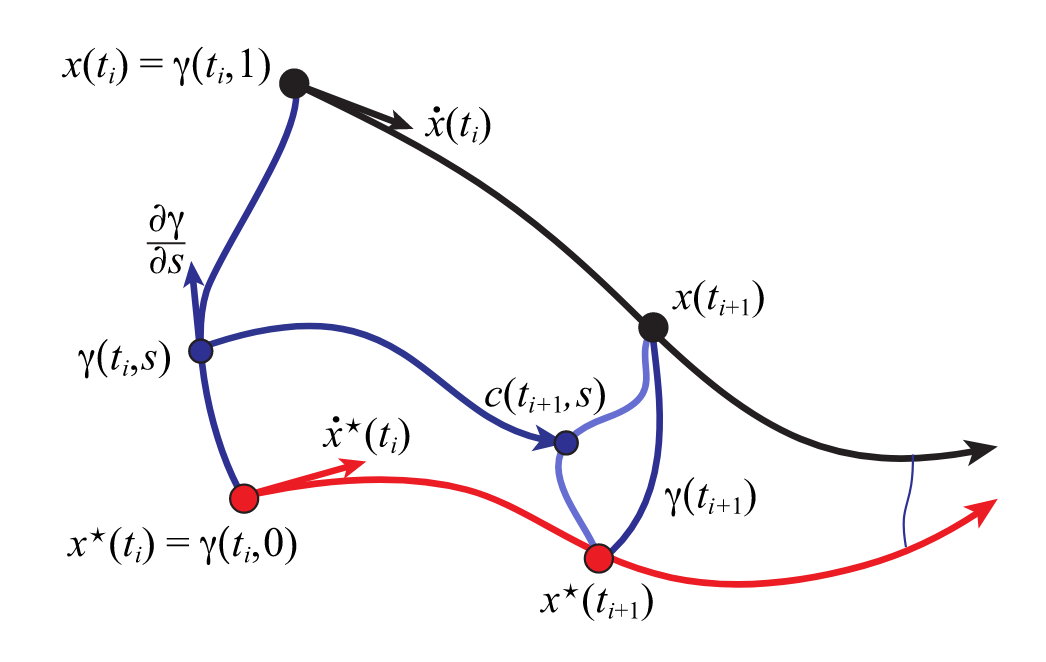
Finding the geodesic
geodesic energy
start and end of geodesic
continuity
Methods: Online Computations
Finding the geodesic
geodesic energy
even out length of segments
\( M = W^{-1}\)
Methods: Online Computations
Tracking controller
Results
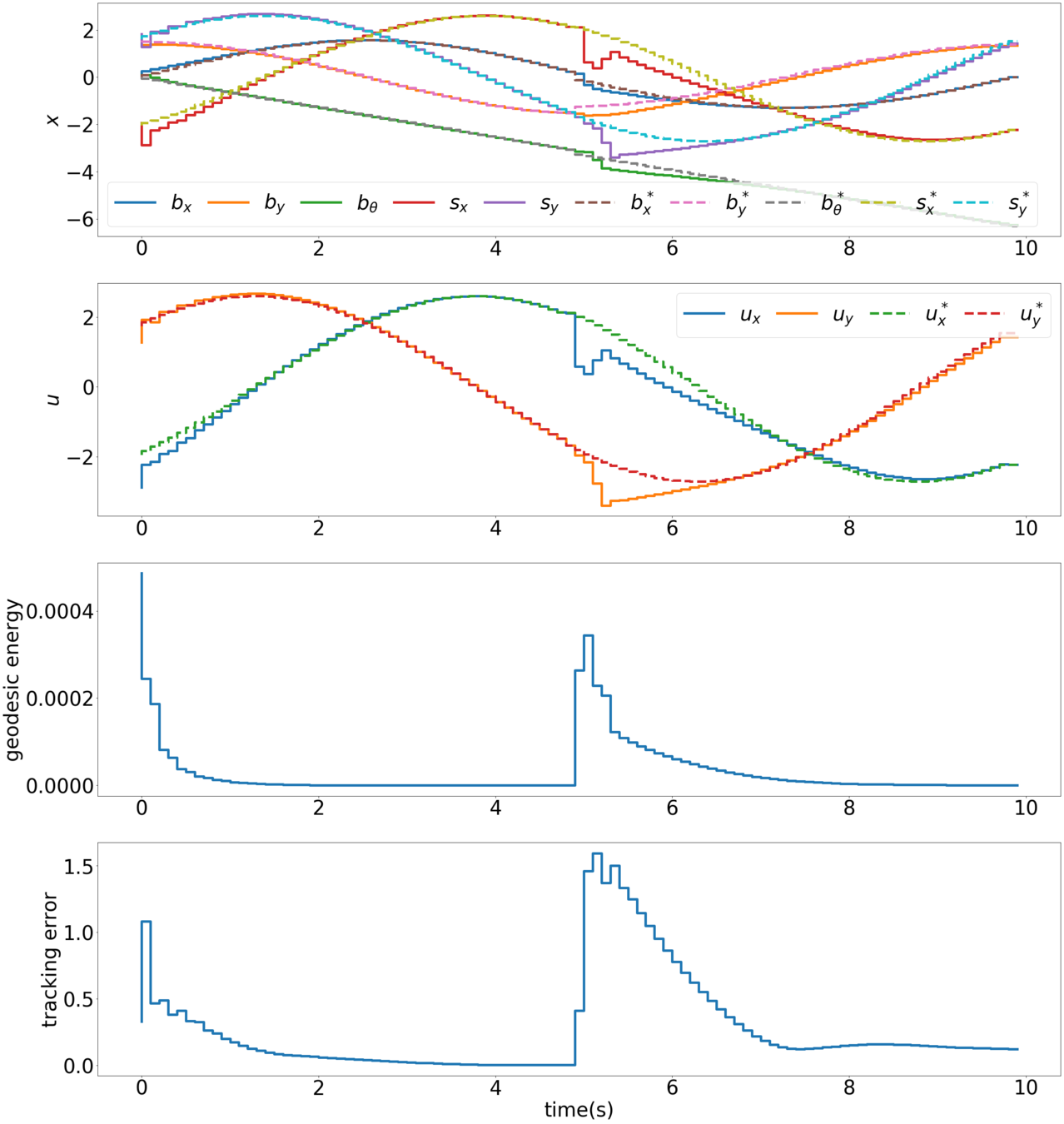
Overview

Results
Controller performance

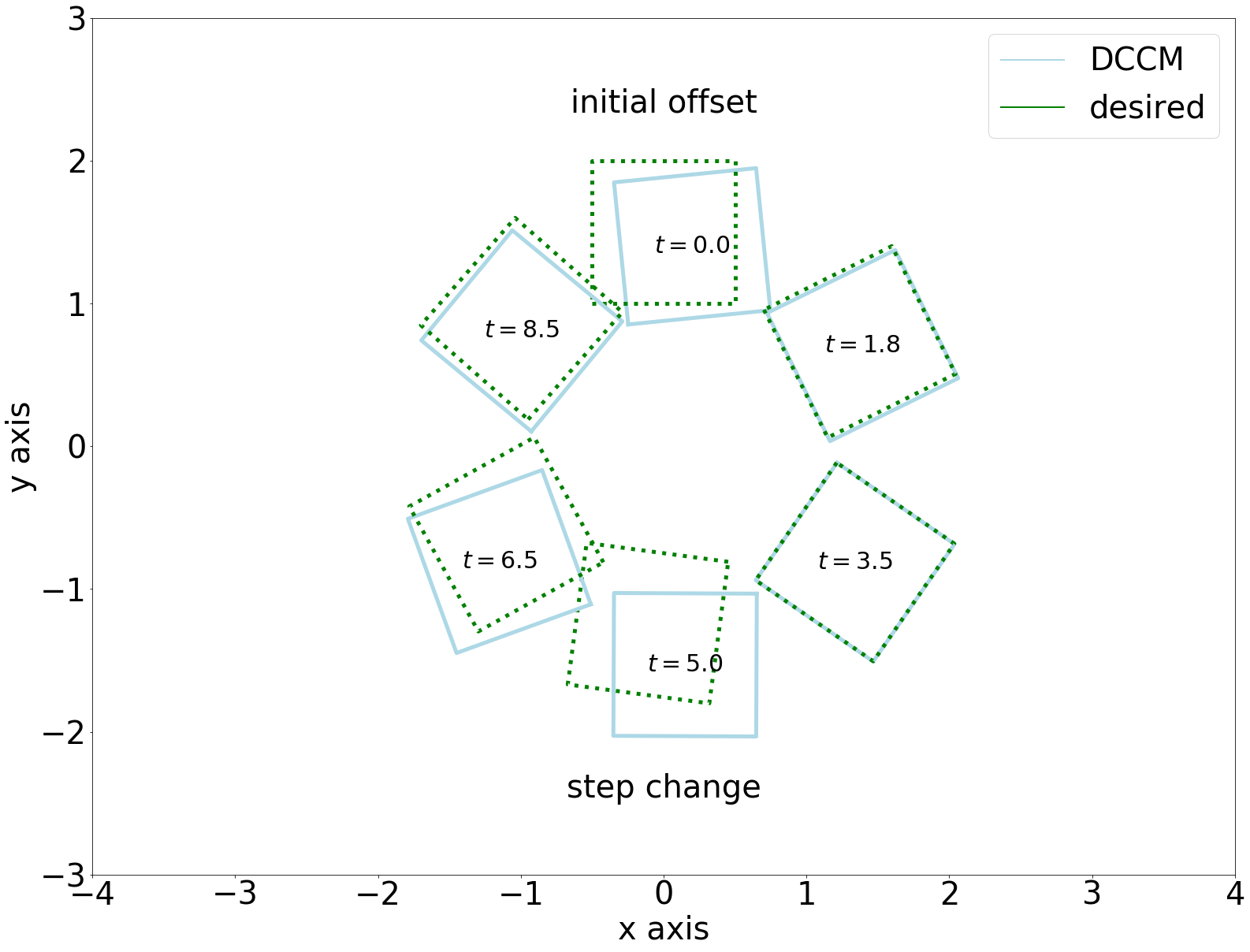
Results
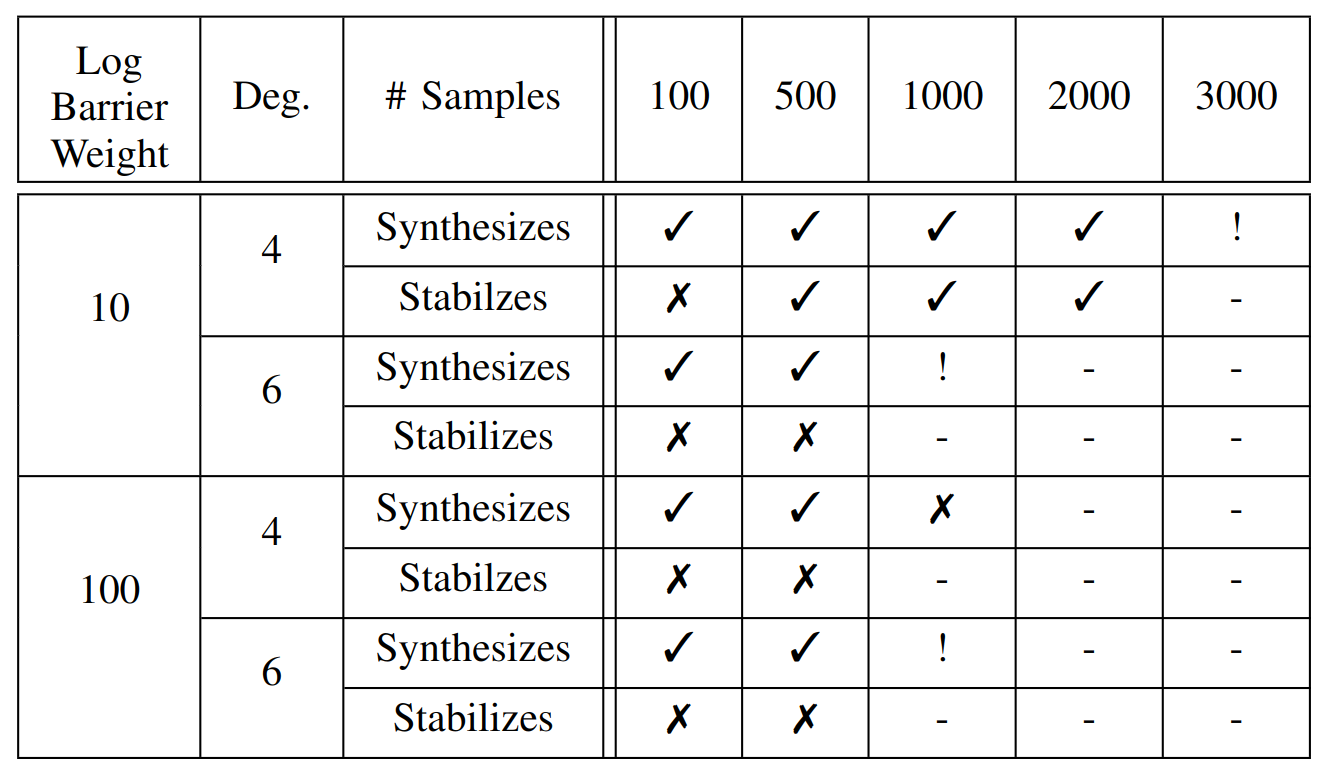
Effect of number of samples on performance

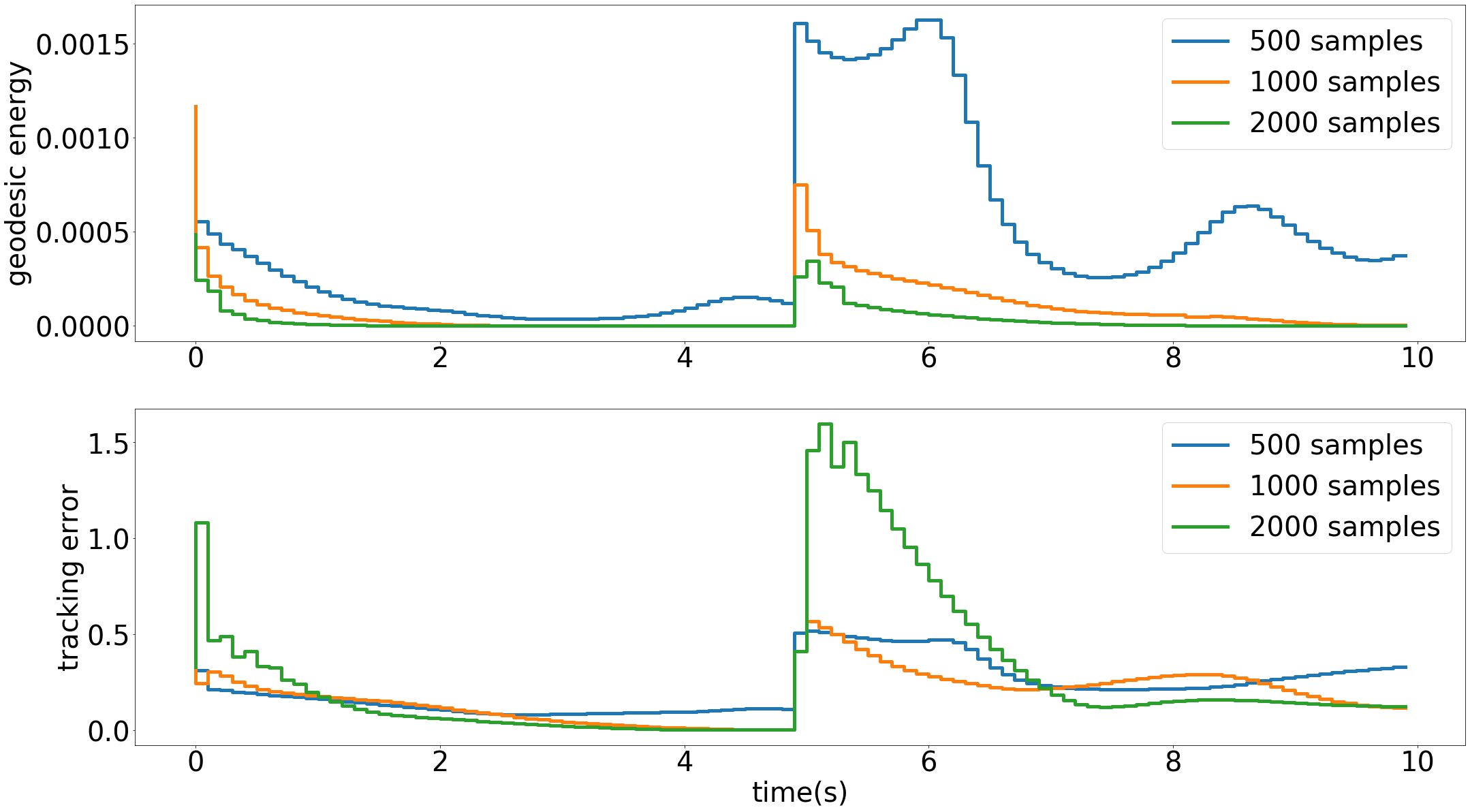
Results
Unexplained issues
- Discretization of the geodesic
- Optimization program failed when \(N > 1\)
- Choosing \(\beta\)
- Synthesizing DCCM with \(\beta > 0.3\) failed
- DCCM with \(\beta = 0.3\) did not stabilize the system while \(\beta = 0.1\) did
Results
Computation time
| Task | Parameters | Time |
|---|---|---|
| Synthesis | Deg 4, 500 Samples | 18 min |
| Synthesis | Deg 6, 500 Samples | 3 hr 20 min |
| Synthesis | Deg 4, 2000 Samples | 1 hr |
| Geodesic | Deg 4, 1 Segment | 1.54 s |
| Geodesic | Deg 6, 1 Segment | 3.81 s |
Linux machine with 31.3GB of RAM, an with an Intel Core i7-6700 CPU @ 3.40GHz x 8 processor.
Conclusion and Future Work
Success:
- Synthesized stabilizing DCCM with highly smoothed dynamics for planar pushing
Yet to be achieved:
- Certificates of stability and convergence rates
- Error due to sparse sampling
- Error due to exact vs smoothed dynamics
- Trajectory independent controller
- Synthesis of controller for contact dynamics with less smoothing
- Learn the metric [13], [14]
- Faster computation of the control law
- Warm starting techniques
- Pseudospectral approaches [15]
Other possible directions: stabilizing to submanifold [8]
References
[1] T. Pang, H. J. T. Suh, L. Yang, and R. Tedrake. (Feb. 27,
2023). Global Planning for Contact-Rich Manipulation
via Local Smoothing of Quasi-dynamic Contact Mod-
els. Comment: The first two authors contributed equally
to this work. arXiv: 2206 . 10787 [cs], [Online].
Available: http : / / arxiv. org / abs / 2206 . 10787 (visited
on 03/15/2023), preprint.
[2] D. E. Stewart and M. Anitescu, “Optimal control of
systems with discontinuous differential equations,” Nu-
merische Mathematik, vol. 114, no. 4, pp. 653–695,
Feb. 1, 2010, ISSN: 0945-3245. DOI: 10.1007/s00211-
009 - 0262 - 2. [Online]. Available: https : / / doi . org / 10 .
1007/s00211-009-0262-2 (visited on 05/12/2023).
[3] F. R. Hogan and A. Rodriguez. (Nov. 24, 2016). Feed-
back Control of the Pusher-Slider System: A Story of
Hybrid and Underactuated Contact Dynamics. arXiv:
1611.08268 [cs], [Online]. Available: http://arxiv.org/
abs/1611.08268 (visited on 05/12/2023), preprint.
[4] J.-P. Sleiman, J. Carius, R. Grandia, M. Wer-
melinger, and M. Hutter, “Contact-Implicit Trajectory
Optimization for Dynamic Object Manipulation,” in
2019 IEEE/RSJ International Conference on Intelligent
Robots and Systems (IROS), Comment: 8 Pages, 10
Figures. Submitted to the International Conference on
Intelligent Robots and Systems (IROS), 2019, Nov.
2019, pp. 6814–6821. DOI: 10 . 1109 / IROS40897 .
2019 . 8968194. arXiv: 2103 . 01104 [cs]. [Online].
Available: http : / / arxiv. org / abs / 2103 . 01104 (visited
on 03/17/2023).
[5] K. Nakatsuru, W. Wan, and K. Harada. (Feb. 25, 2023).
Implicit Contact-Rich Manipulation Planning for a Ma-
nipulator with Insufficient Payload. arXiv: 2302.13212
[cs], [Online]. Available: http://arxiv.org/abs/2302.
13212 (visited on 03/17/2023), preprint.
[6] M. Posa, C. Cantu, and R. Tedrake, “A direct method
for trajectory optimization of rigid bodies through
contact,” International Journal of Robotics Research,
vol. 33, no. 1, pp. 69–81, Jan. 1, 2014, ISSN: 0278-3649.
DOI: 10.1177/0278364913506757. [Online]. Available:
https://doi.org/10.1177/0278364913506757 (visited on
03/17/2023).
[7] R. Tedrake, I. R. Manchester, M. Tobenkin, and
J. W. Roberts, “LQR-trees: Feedback Motion Plan-
ning via Sums-of-Squares Verification,” The Interna-
tional Journal of Robotics Research, vol. 29, no. 8,
pp. 1038–1052, Jul. 1, 2010, ISSN: 0278-3649. DOI:
10.1177/0278364910369189. [Online]. Available: https:
/ / doi . org / 10 . 1177 / 0278364910369189 (visited on
05/13/2023).
[8] I. R. Manchester and J.-J. E. Slotine, “Control Contrac-
tion Metrics: Convex and Intrinsic Criteria for Nonlin-
ear Feedback Design,” IEEE Transactions on Automatic
Control, vol. 62, no. 6, pp. 3046–3053, Jun. 2017, ISSN:
1558-2523. DOI: 10.1109/TAC.2017.2668380.
References
[9] I. R. Manchester, J. Z. Tang, and J.-J. E. Slotine, “Unify-
ing Robot Trajectory Tracking with Control Contraction
Metrics,” in Robotics Research: Volume 2, ser. Springer
Proceedings in Advanced Robotics, A. Bicchi and W.
Burgard, Eds., Cham: Springer International Publishing,
2018, pp. 403–418, ISBN: 978-3-319-60916-4. DOI: 10.
1007 / 978 - 3 - 319 - 60916 - 4 23. [Online]. Available:
https://doi.org/10.1007/978-3-319-60916-4 23 (visited
on 05/05/2023).
[10] S. Singh, A. Majumdar, J.-J. Slotine, and M. Pavone,
“Robust Online Motion Planning via Contraction The-
ory and Convex Optimization,” May 29, 2017. DOI: 10.
1109/ICRA.2017.7989693.
[11] L. Wei, R. Mccloy, and J. Bao, “Control Contraction
Metric Synthesis for Discrete-time Nonlinear Systems,”
IFAC-PapersOnLine, 16th IFAC Symposium on Ad-
vanced Control of Chemical Processes ADCHEM 2021,
vol. 54, no. 3, pp. 661–666, Jan. 1, 2021, ISSN: 2405-
8963. DOI: 10 . 1016 / j . ifacol . 2021 . 08 . 317. [Online].
Available: https : / / www . sciencedirect . com / science /
article/pii/S2405896321010910 (visited on 04/16/2023).
[12] Russ Tedrake and the Drake Development Team. (2019). Drake:
Model-Based Design and Verification for Robotics,
[Online]. Available: https://drake.mit.edu/ (visited on
05/10/2023).
[13] S. Singh, V. Sindhwani, J.-J. E. Slotine, and M. Pavone.
(Jul. 31, 2018). Learning Stabilizable Dynamical Sys-
tems via Control Contraction Metrics, arXiv.org, [On-
line]. Available: https : / / arxiv. org / abs / 1808 . 00113v2
(visited on 05/04/2023).
[14] G. Chou, N. Ozay, and D. Berenson, “Model Er-
ror Propagation via Learned Contraction Metrics for
Safe Feedback Motion Planning of Unknown Sys-
tems,” Dec. 14, 2021, pp. 3576–3583. DOI: 10.1109/
CDC45484.2021.9683354.
[15] K. Leung and I. R. Manchester. (Nov. 4, 2017). Non-
linear Stabilization via Control Contraction Metrics:
A Pseudospectral Approach for Computing Geodesics.
arXiv: 1607 . 04340 [cs], [Online]. Available: http :
/ / arxiv. org / abs / 1607 . 04340 (visited on 05/06/2023),
preprint.
Images:
- https://news.clearancejobs.com/wp-content/uploads/2021/08/1150x732-2021-08-23T065258.010.jpg
- https://cdn.shopify.com/s/files/1/0091/4056/8111/products/PRUB007_Medium_Moving_Box_18__x_18__x_16_2000x.jpg?v=1565898544