Heat-records
Yesterday's temp
Given \(T_{ijk}\):
-- \(T' = \max_k T_{ijk}[j == `0612`]\)
→ \(T'\) is a vector of length \(i\); it is also the data we see in the right
-- \(h = T'[i == `2022` ]\)
→ \(h\) is the highlight

Let data be a 3D tensor \(T_{ijk}\); \(i\) for year; \(j\) for date; \(k\) for the # of records per day; it could also be seen as a 2D matrix when we drop \(k\) and \(\max_k\)
Last 4 weeks' temp
Given \(T_{ijk}\):
-- \(T' = \max_k T_{ijk}[`0509` \leq j \leq `0612`]\)
-- \(h = T'[i == `2022` ]\)
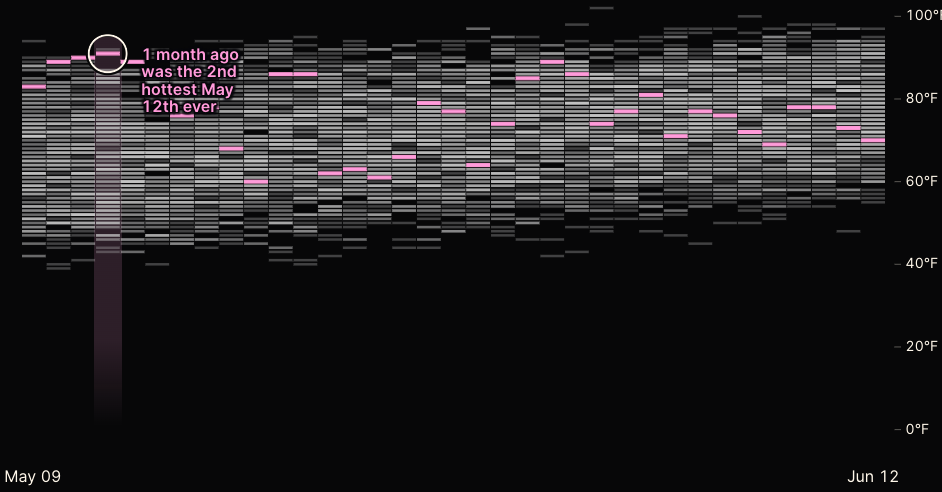
extended \(j\) from scalar to interval;
changed highlight color from blue to pink (which, doesn't quite make sense, seeing that they map to the same h)
Record high for the last 4 weeks
Given \(T_{ijk}\):
-- \(T' = \max_k T_{ijk}[`0509` \leq j \leq `0612`]\)
-- \(h = \max_i T'\)

changed highlight;
left one pink highlight for the temperature record that is closest to the historical record
Record high for the year
Given \(T_{ijk}\):
-- \(T' = h = \max_{i, k} T_{ijk}\)
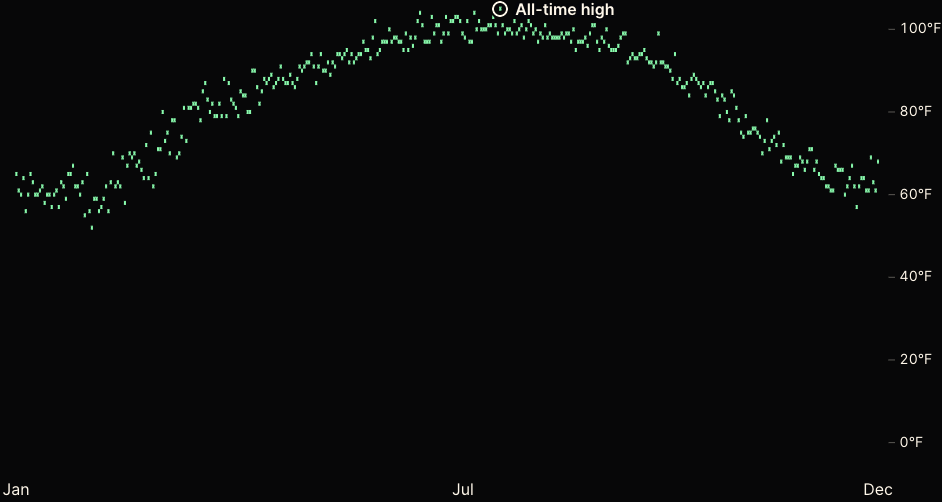
The transition was in fact (1) \(\max_k T_{ijk}[`0509`\leq j \leq `0612`]\) to \(\max_{i, k} T_{ijk} [`0509` \leq j \leq `0612`]\) and then
(2) dropping the date selection / filter \(\max_{i, k} T_{ijk}\)
change in underlying data: matrix → (highlight) vector