Does learning require memorization?

Presented by Sheng Long, Liren Shan, Lixu Wang 

By Vitaly Feldman

Overview

  • Introduction 
  • What is memorization? 
  • When is memorization necessary for learning? 
  • Conclusion 

Introduction

  • The phenomenon
    • Deep Neural Networks fit well even random
      labels
  • Why do we care? 
    • Gap between modern ML practices and theory is interesting 
    • Learning algorithms that memorize may impose privacy risks 

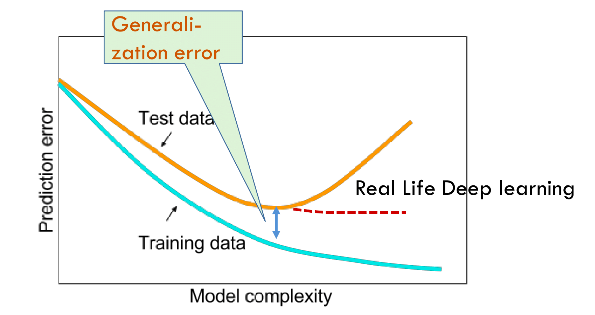
Generalization, from Desh Raj

Example

  • Why do differential privacy (DP) algorithms fall short of their non-private counterparts?
  • What examples are DP algorithms more likely to misclassify?

digits from MNIST dataset 

Intuitive explanation

DP cannot achieve the same accuracy as non-private learning because it cannot memorize the tail of the mixture distribution. 

... so far it seems that learning does require memorization.

\(\to\) When does learning require memorization?

What is memorization?

  • Standard case: model obtained by training dataset \(S\) with \((x,y)\) predicts \(y\) on \(x\)
  • Informally,  
    • model obtained by training dataset \(S\) without \((x,y)\) is unlikely to predict \(y\) given \(x\)

The unstructured model 

  • Data domain \(X\) with size \(N\); Label domain \(Y\);
  • True labeling function \(f: X \to Y \) drawn from a distribution over functions \(\mathcal{F}\);
  • The individual frequency of each point in \(X\) is unknown.
  • Frequency of each point is drawn i.i.d. from a known prior: \(\pi = (\pi_1, ..., \pi_N)\); Normalized to a distribution \(D\) over \(X\); (denoted by \(D \sim \mathcal{D}_\pi\))
  • Sample set \(S \sim (D,f)^n\)

 

 

The unstructured model 

  • Data domain \(X\) with size \(N\); Label domain \(Y\);
  • True labeling function \(f \sim \mathcal{F}\);
  • Frequency of each point is drawn i.i.d. from a known prior: \(\pi = (\pi_1, ..., \pi_N)\); Normalized to a distribution \(D\) over \(X\); (denoted by \(D \sim \mathcal{D}_\pi\))
  • Sample set \(S \sim (D,f)^n\)

 

Goal: Find algorithm \(\mathcal{A}\) to minimize the generalization error given a sample set \(Z\), defined as 

\(\)

 

where \(\texttt{err}_{D,f}(\mathcal{A}) = \mathbb{E}_{(x,y) \sim (D,f),h\sim \mathcal{A}(Z)} [h(x)\neq y]\)

\bar{\tt err}(\pi, \mathcal{F}, \mathcal{A} | S = Z) = \mathbb{E}_{(D,f)|Z}[\texttt{err}_{D,f}(\mathcal{A})]

The generalization error

Theorem 2.3(informal): Given a frequency prior \(\pi\), and a distribution \(\mathcal{F}\) over labeling function, we have for every algorithm \(\mathcal{A}\) and every dataset \(Z \in (X,Y)^n\),

 

 

where \(\texttt{errn}_Z(\mathcal{A},\ell) = \mathbb{E}_{h\sim \mathcal{A}}[\texttt{errn}_Z(h,\ell)]\)

and \(\texttt{errn}_Z(h,\ell)\) is the sum of empirical error rates for data points that appear exactly \(\ell\) times in \(Z\).

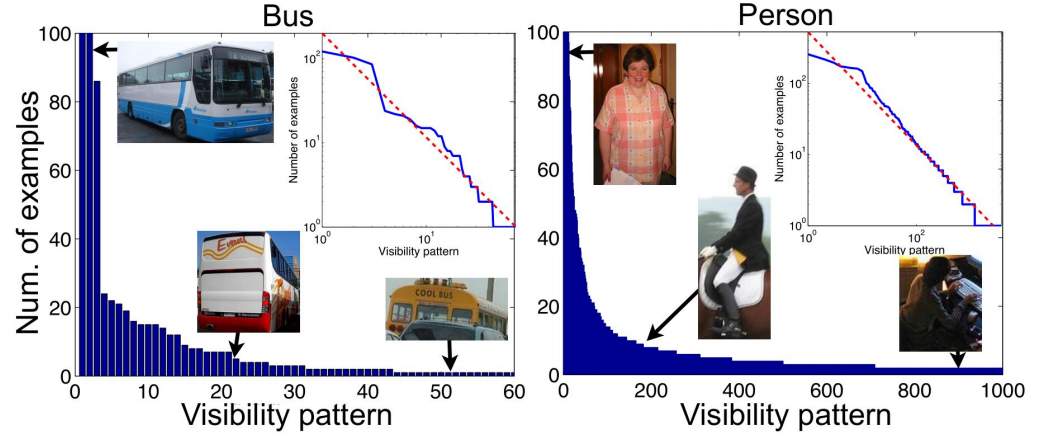
\bar{\texttt{err}(\pi,\mathcal{F},\mathcal{A}|Z)} \geq \texttt{opt}(\pi,\mathcal{F} | Z) + \sum_{\ell \in [n]} \tau_\ell \cdot \texttt{errn}_Z(\mathcal{A},\ell)

The impact of priors 

  • Singleton sample -- appear only once in the dataset, usually in the tail of the frequency priors.
  • The impact of singleton samples in the error:
    • \(\bar{\tt err}(\pi, \mathcal{F}, \mathcal{A}) \ge {\tt opt}(\pi, \mathcal{F}) + \tau_1\mathbb{E}[{\tt errn}_S(\mathcal{A},1)]\)
    • Lemma 2.6. \(\tau_1 \ge \frac{1}{7n} \cdot {\tt weight}\left(\pi, \left[\frac{1}{3n}, \frac{1}{n}\right]\right)\)
    • In long-tailed cases, the proportion of singleton samples is significant. (\(n, {\tt weight}\left(\pi, \left[0, \frac{1}{n}\right]\right)\))
  • The excess error is significant if and only if the frequency prior is long-tailed.

The joint-population model 

  • Unlabeled data distribution \(X\): a mixture of distributions \(M_1, ..., M_N\). (with disjoint support);
  • The marginal distribution \(M_i\) is unstructured only with a frequency prior: \(\pi = (\pi_1, ..., \pi_N)\);
  • Label priors \(\mathcal{F}\) which consists of a series of labeling functions \(f \sim \mathcal{F}\);

Theorem 3.2. The generalization error of learning algorithm \(\mathcal{A}\)

\bar{\tt err}(\pi, \mathcal{F}, \mathcal{A}) \ge {\tt opt}(\pi, \mathcal{F}) + \underset{D \sim D_{\pi}^{[N]}, f \sim \mathcal{F}, S \sim (M_D, L_f)^n }{\mathbb{E}} \left[ \underset{ \mathcal{l} \in [n]}{\sum} \lambda_{\mathcal{l}} \tau_{\mathcal{l}} \cdot {\tt errn}_S (\mathcal{A}, l) \right]
{\tt mem} (\mathcal{A}, S, i) := \Pr_{h\sim \mathcal{A}(S)} [h(x_i)=y_i] - \Pr_{h\sim \mathcal{A}(S ^{\setminus i})} [h(x_i)=y_i]

The memorization

  • Formal definition: For a dataset \(S=(x_i, y_i)_{i \in [n]}\)

where \(S^{\setminus i}\) denotes the dataset that is \(S\) with \((x_i, y_i)\) removed.

The impact of memorization

  • The relation between memorization and empirical error.
    • Lemma 4.2. \(\frac{1}{n}\underset{S \sim P^n}\mathbb{E}\left[\sum_{i \in [n]}{\tt mem}(\mathcal{A}, S, i)\right] = \underset{S \sim P^n}\mathbb{E}[{\tt err}_S(\mathcal{A}, S)] - \underset{S_{\prime} \sim P^{n-1}}\mathbb{E}[{\tt err}_{S^{\prime}}(\mathcal{A}, S^{\prime})]\) , where \({\tt err}_S(\mathcal{A}, S)\) is the expected empirical error of \(\mathcal{A}\) on \(S\).
  • The relation between the generalization error and the memorization of singleton samples.
    • Lemma 4.3. \({\tt errn}_S(\mathcal{A}, 1) = \sum_{i \in [n], x_i \in X_{S\#1}}\Pr_{h \sim \mathcal{A}(S^{\setminus i})}[h(x_i) \neq y_i] - {\tt mem}(\mathcal{A}, S, i)\)

Conclusions

  • Provide a formal and theoretical model that demonstrates memorization is necessary for achieving close-to-optimal generalization error. 
  • Focus on long-tail distribution.
  • Discuss the security concern of the memorization.

Thank you for listening!

Questions? 

Made with Slides.com