
Intro to Machine Learning


Lecture 6: Neural Networks
Shen Shen
March 8, 2024
(many slides adapted from Phillip Isola and Tamara Broderick)
Outline
- Recap and neural networks motivation
- Neural Networks
- A single neuron
- A single layer
- Many layers
- Design choices (activation functions, loss functions choices)
- Forward pass
- Backward pass (back-propogation)
e.g. linear regression represented as a computation graph
- Each data point incurs a loss of \((w^Tx^{(i)} + w_0 - y^{(i)})^2 \)
- Repeat for each data point, sum up the individual losses
- Gradient of the total loss gives us the "signal" on how to optimize for \(w, w_0\)

learnable parameters (weights)



- Each data point incurs a loss of \(- \left(y^{(i)} \log g^{(i)}+\left(1-y^{(i)}\right) \log \left(1-g^{(i)}\right)\right)\)
- Repeat for each data point, sum up the individual losses
- Gradient of the total loss gives us the "signal" on how to optimize for \(w, w_0\)

learnable parameters (weights)



e.g. linear logistic regression (linear classification) represented as a computation graph
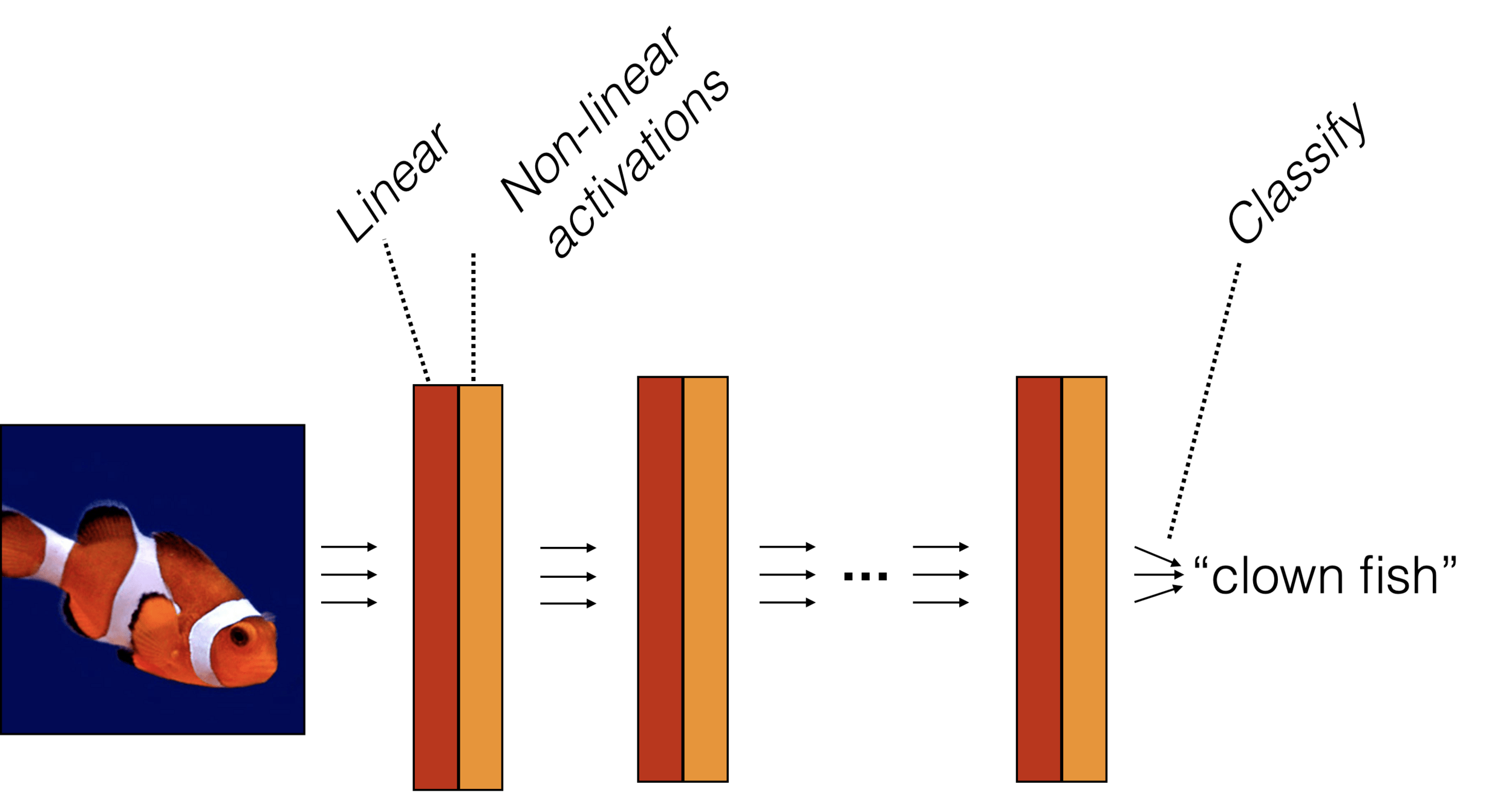
We saw that, one way of getting complex input-output behavior is
to leverage nonlinear transformations

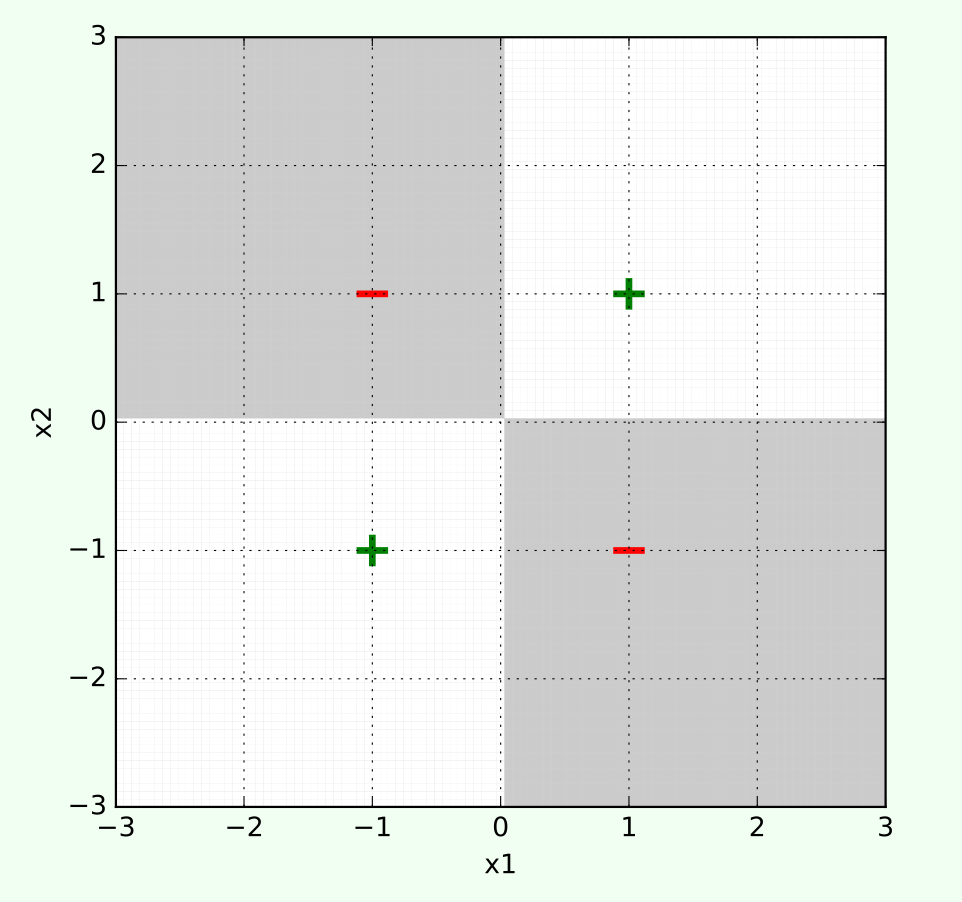
transform
e.g. use for decision boundary
👆 importantly, linear in \(\phi\), non-linear in \(x\)
Today (2nd cool idea): "stacking" helps too!
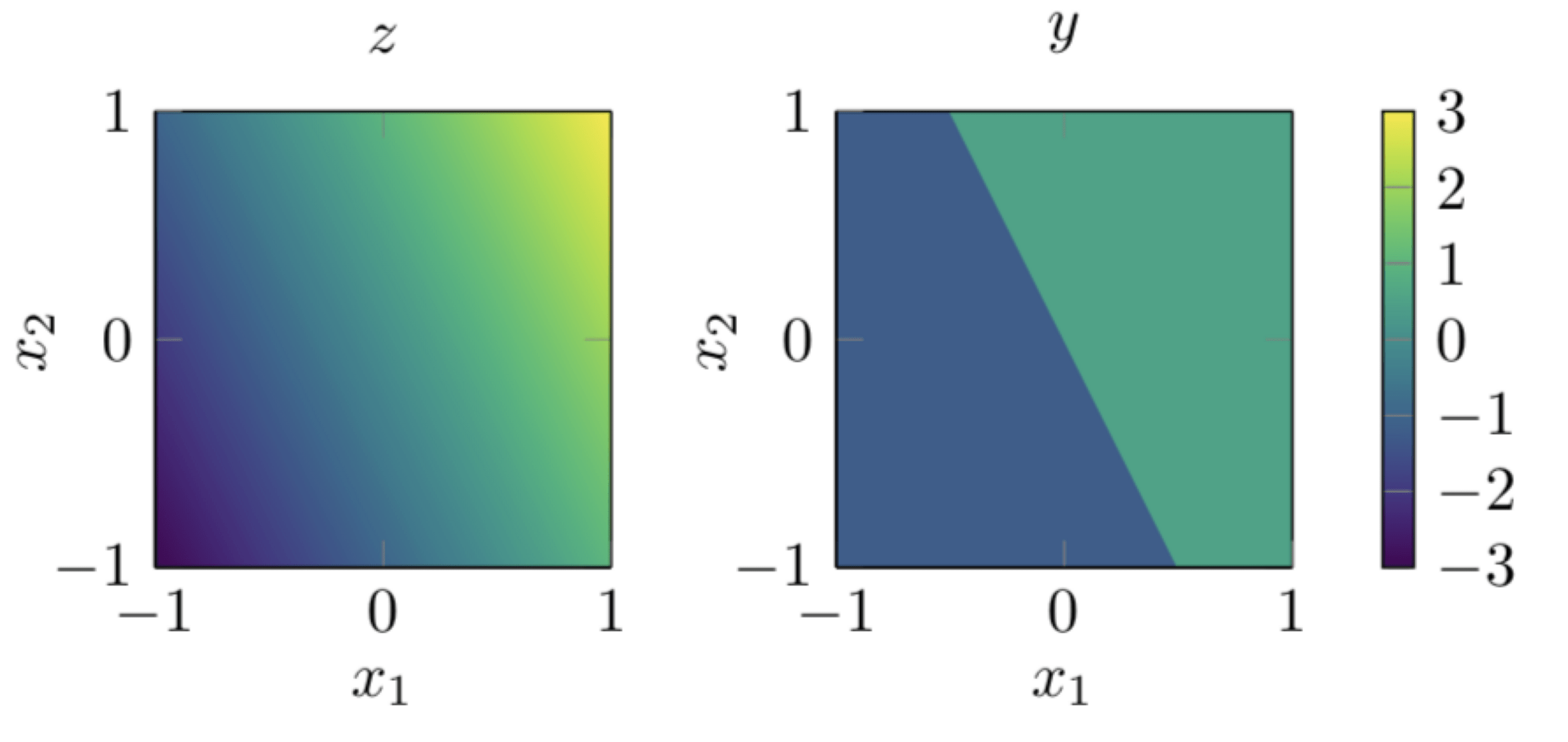
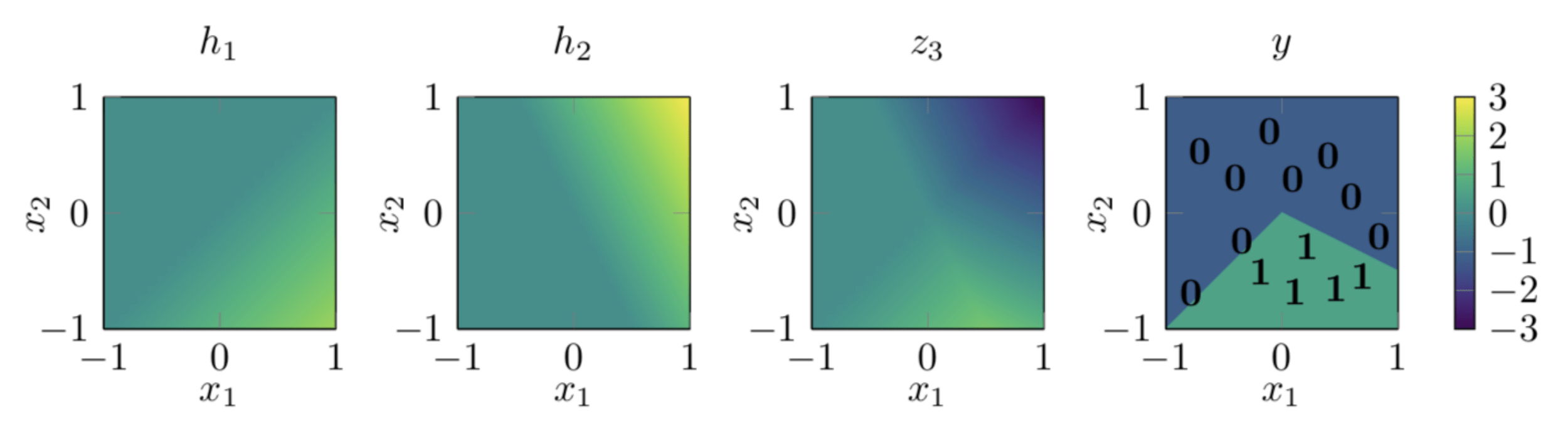

So, two epiphanies:
- nonlinearity empowers linear tools
- stacking helps
(👋 heads-up: all neural network graphs focus on a single data point for simple illustration.)
Outline
- Recap and neural networks motivation
- Neural Networks
- A single neuron
- A single layer
- Many layers
- Design choices (activation functions, loss functions choices)
- Forward pass
- Backward pass (back-propogation)
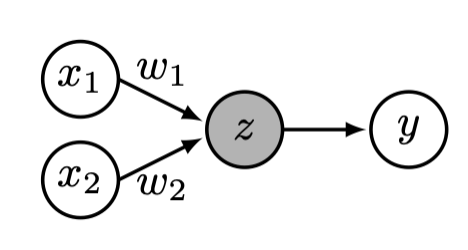
A single neuron is
- the basic operating "unit" in a neural network.
- the basic "node" when a neural network is viewed as computational graph.
- neuron , a function, maps a vector input \(x \in \mathbb{R}^m\) to a scalar output
- inside the neuron, circles do function evaluation/computation
- \(f\): we engineers choose
- \(w\): learnable parameters
- \(x\): \(m\)-dimensional input (a single data point)
- \(w\): weights (i.e. parameters)
- \(z\): pre-activation scalar output
- \(f\): activation function
- \(a\): post-activation scalar output




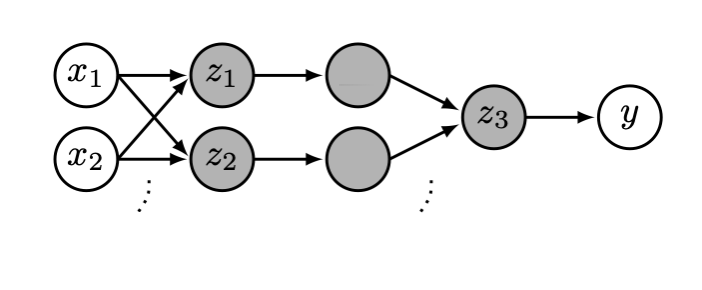
A single layer is
- made of many individual neurons.
- (# of neurons) = (layer output dimension).
- typically, all neurons in one layer use the same activation \(f\) (if not; uglier/messier algebra)
- typically, no "cross-wire" between neurons. e.g. \(z_1\) doesn't influence \(a_2\). in other words, a layer has the same activation applied element-wise. (softmax is an exception to this, details later.)
- typically, fully connected. i.e. there's an edge connecting \(x_i\) to \(z_j,\) for all \(i \in \{1,2,3, \dots , m\}; j \in \{1,2,\dots, n\}\). in other words, all \(x_i\) influence all \(a_j.\)



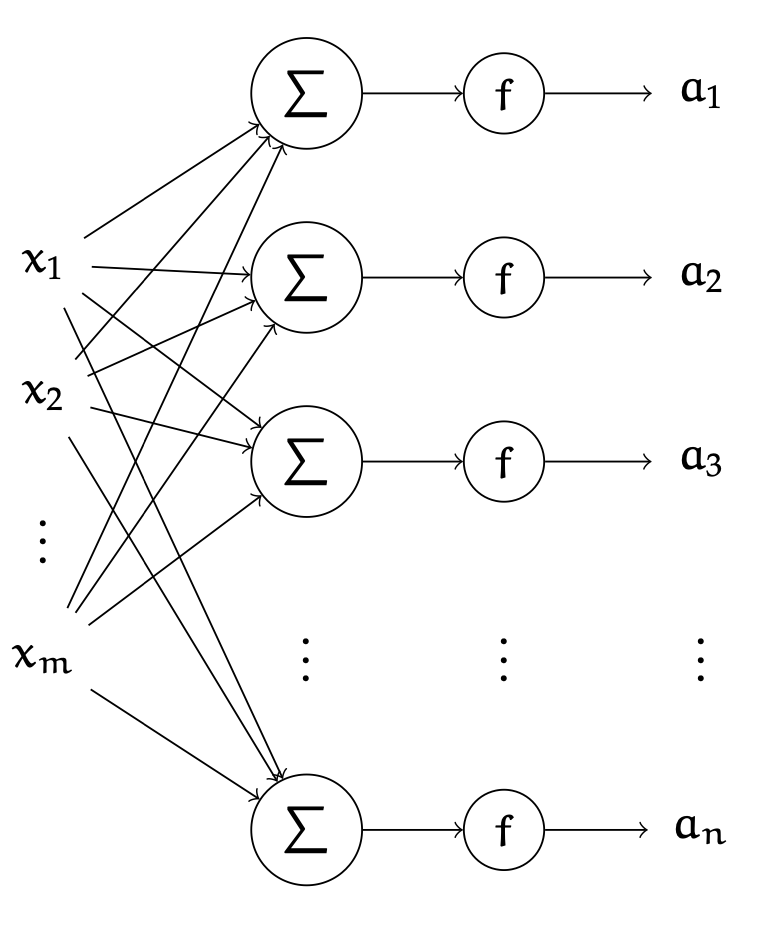
layer
learnable weights





















learnable weights
layer
linear combo
activations
input
A (feed-forward) neural network is
Activation function \(f\) choices
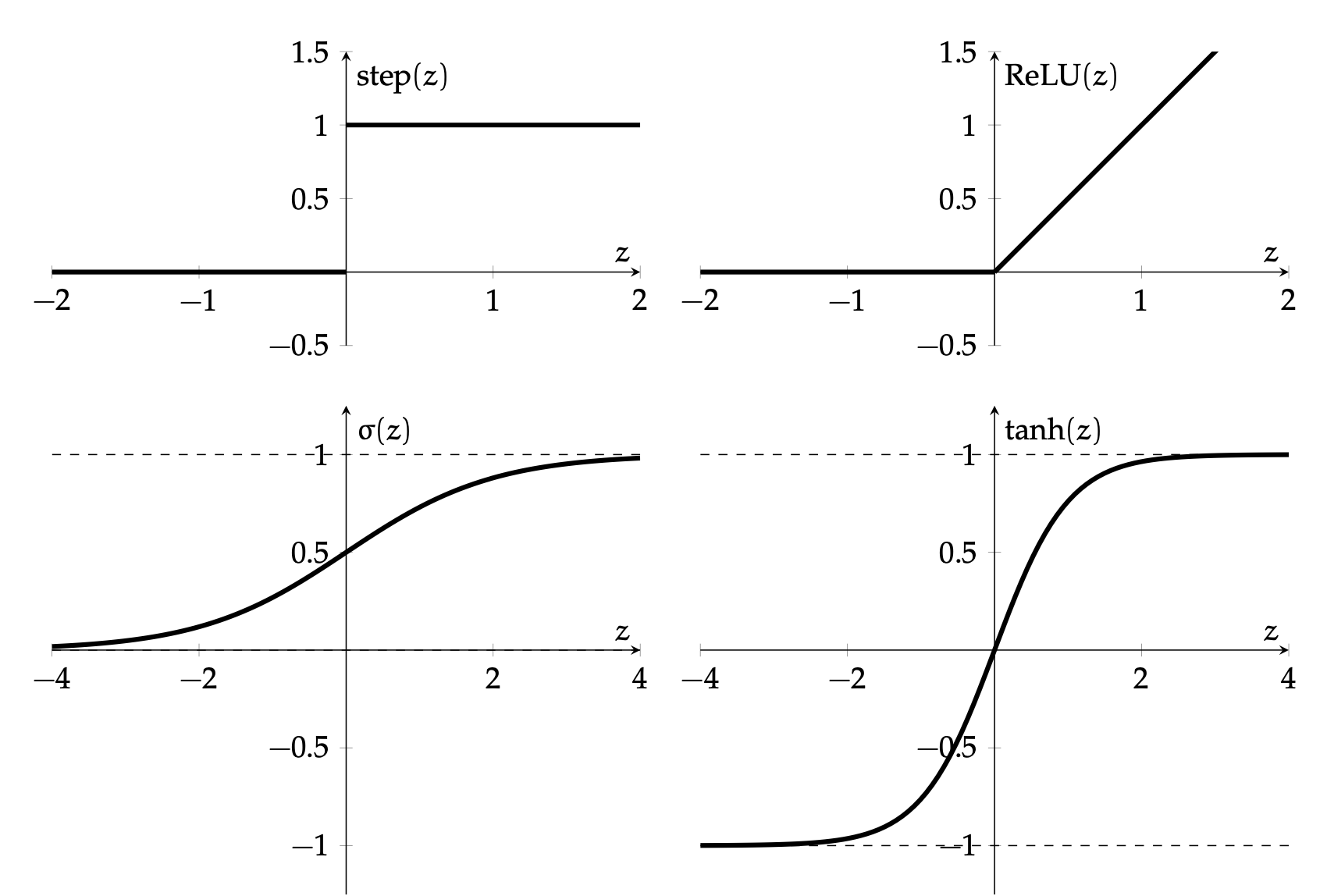
\(\sigma\) used to be popular
- firing rate of neuron
- \(\sigma^{\prime}(z)=\sigma(z) \cdot(1-\sigma(z))\)
ReLU is the de-facto activation choice nowadays
- Default choice in hidden layers.
- Pro: very efficient to implement, choose to let the gradient be:
- Drawback: if strongly in negative region, unit can be "dead" (no gradient).
- Inspired variants like elu, leaky-relu.
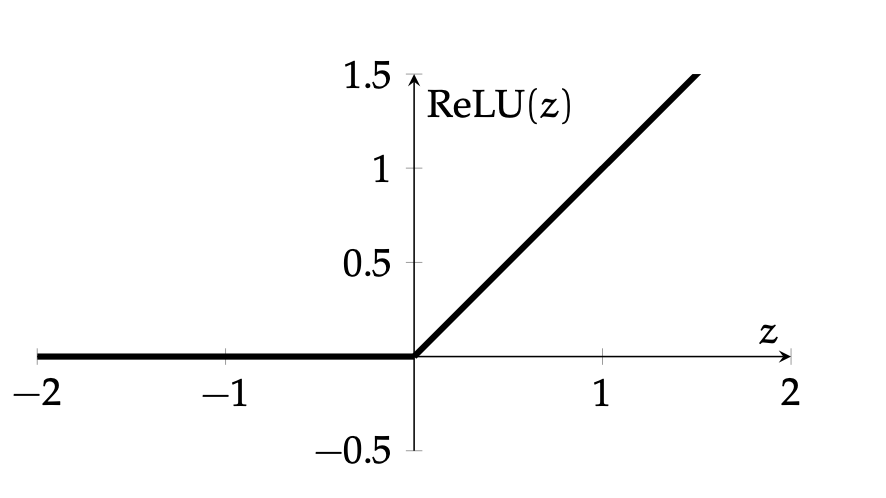



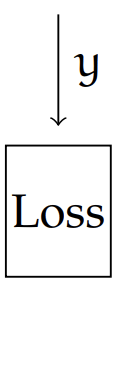
The last layer, the output layer, is special
- activation and loss depends on problem at hand
- we've seen e.g. regression (one unit in last layer, squared loss).

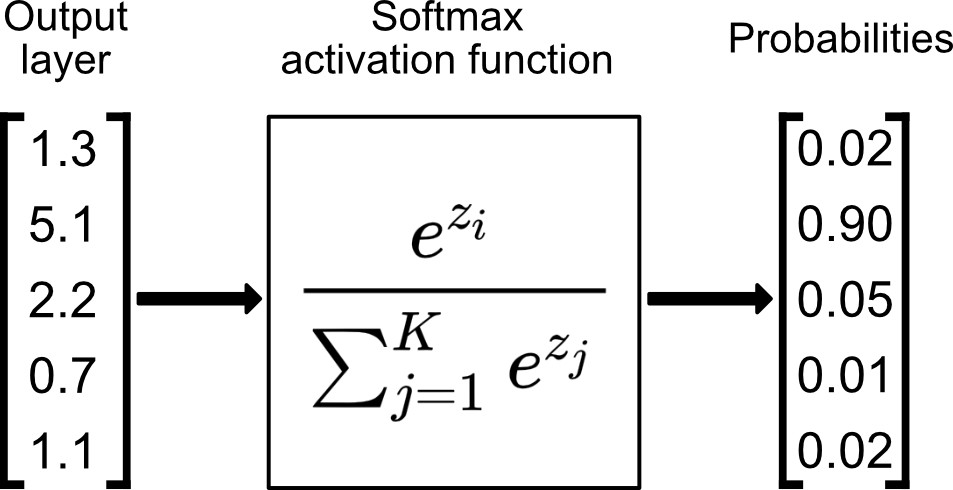
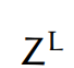
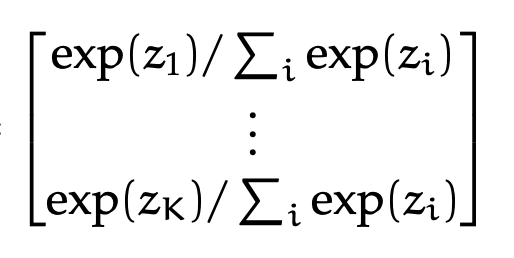
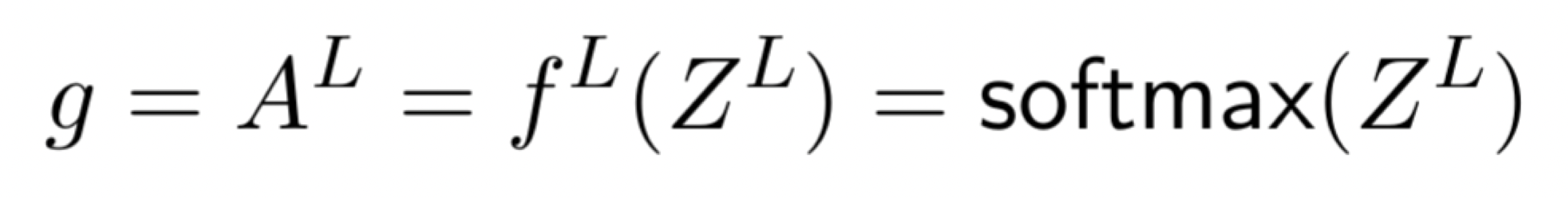
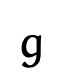
(output layer)
e.g., say \(K=5\) classes
More complicated example: predict one class out of \(K\) possibilities
then last layer: \(K\) nuerons, softmax activation


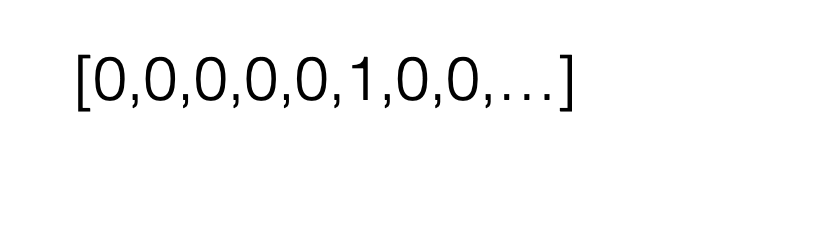




Outline
- Recap and neural networks motivation
- Neural Networks
- A single neuron
- A single layer
- Many layers
- Design choices (activation functions, loss functions choices)
- Forward pass
- Backward pass (back-propogation)
How do we optimize
\(J(\mathbf{W})=\sum_{i=1} \mathcal{L}\left(f_L\left(\ldots f_2\left(f_1\left(\mathbf{x}^{(i)}, \mathbf{W}_1\right), \mathbf{W}_2\right), \ldots \mathbf{W}_L\right), \mathbf{y}^{(i)}\right)\) though?

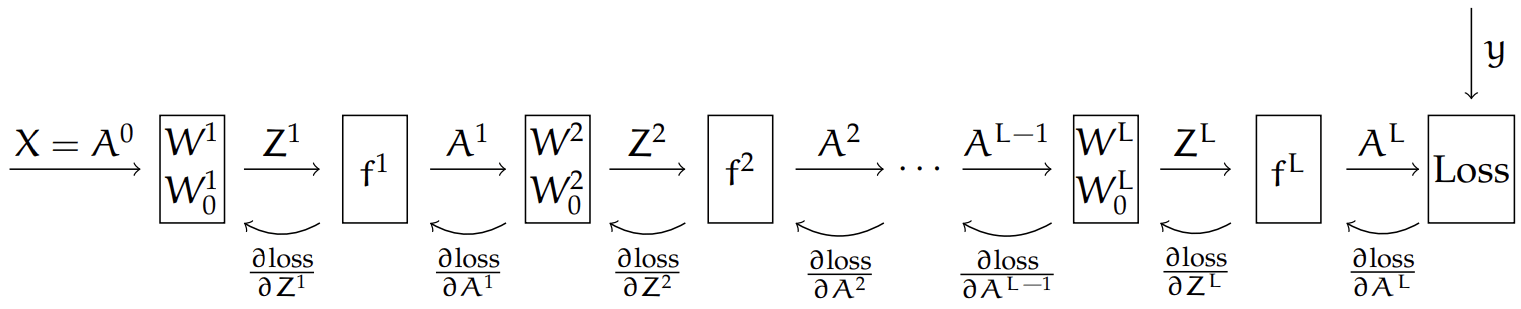

Backprop = gradient descent & the chain rule
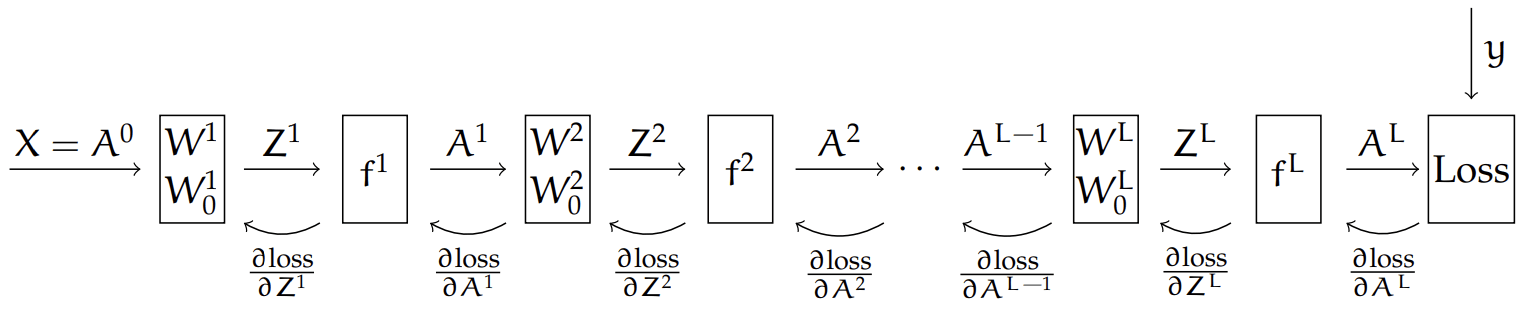
Recall that, the chain rule says:
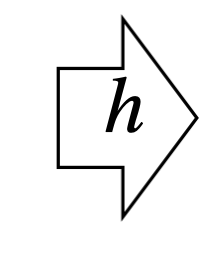
For the composed function: \(h(\mathbf{x})=f(g(\mathbf{x})), \) its derivative is: \(h^{\prime}(\mathbf{x})=f^{\prime}(g(\mathbf{x})) g^{\prime}(\mathbf{x})\)
Here, our loss depends on the final output,
and the final output \(A^L\) comes from a chain of composition of functions
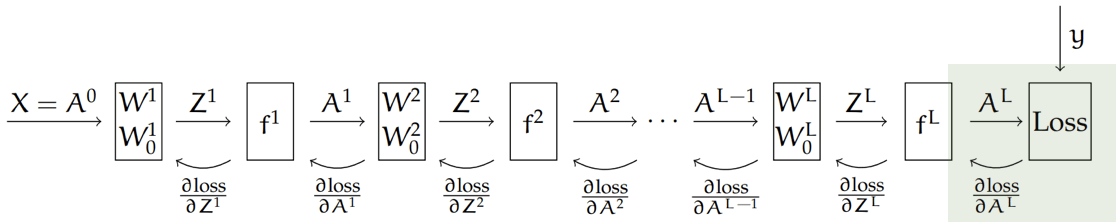
Backprop = gradient descent & the chain rule
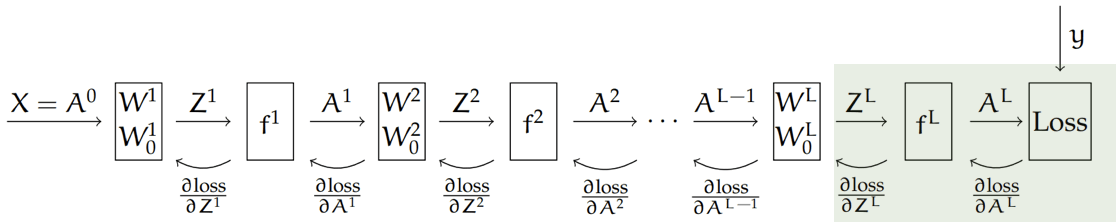
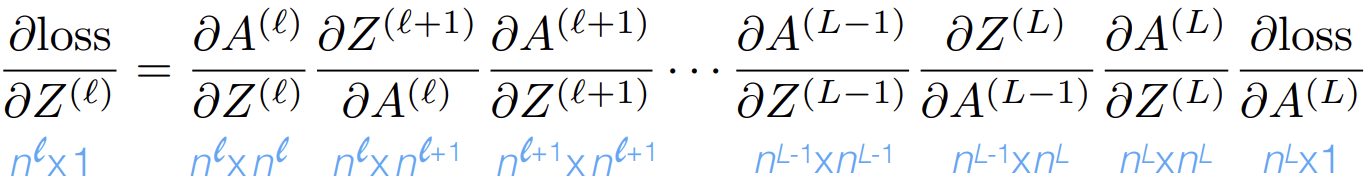
Backprop = gradient descent & the chain rule
(
(The demo won't embed in PDF. But the direct link below works.)
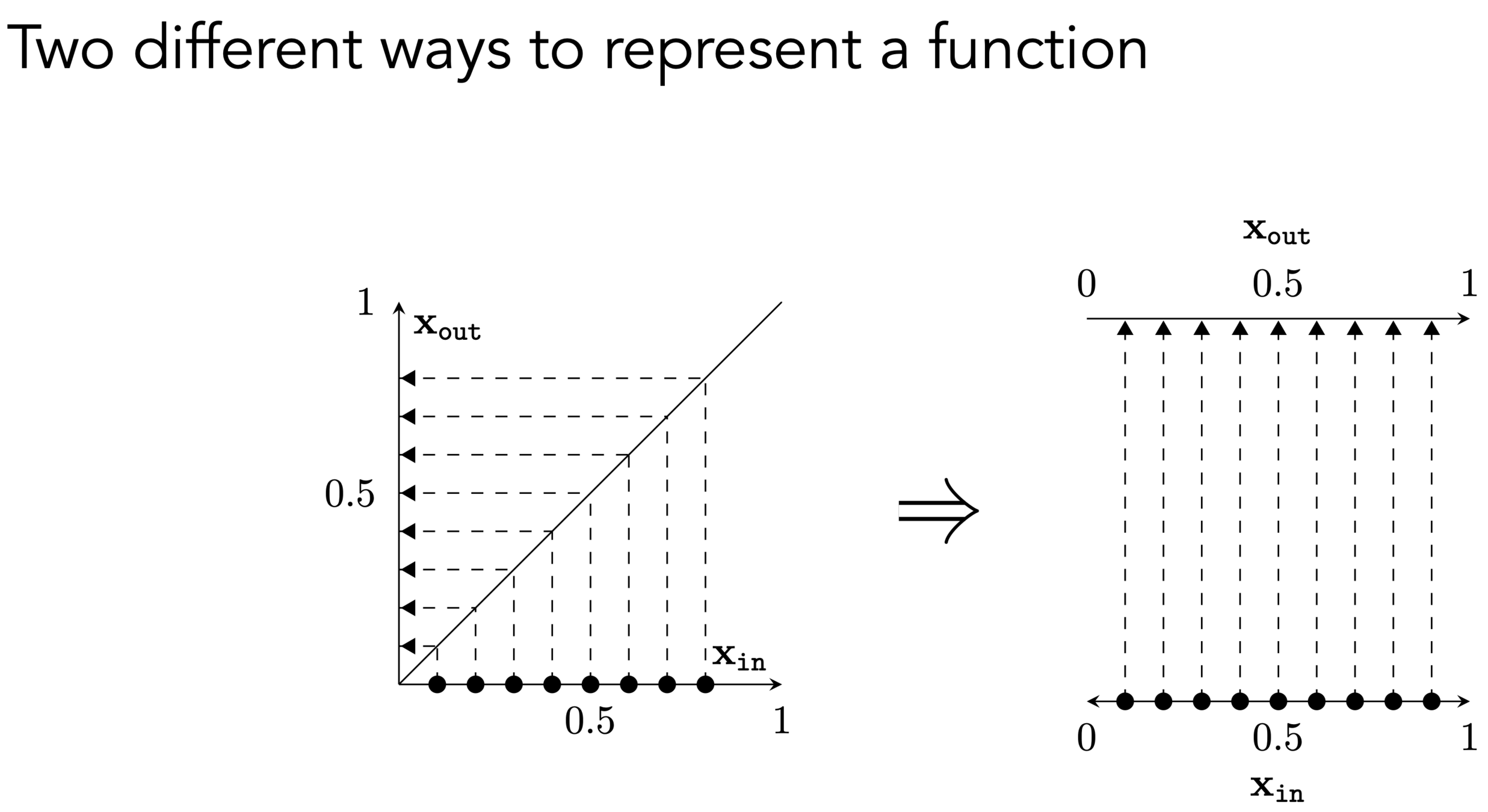
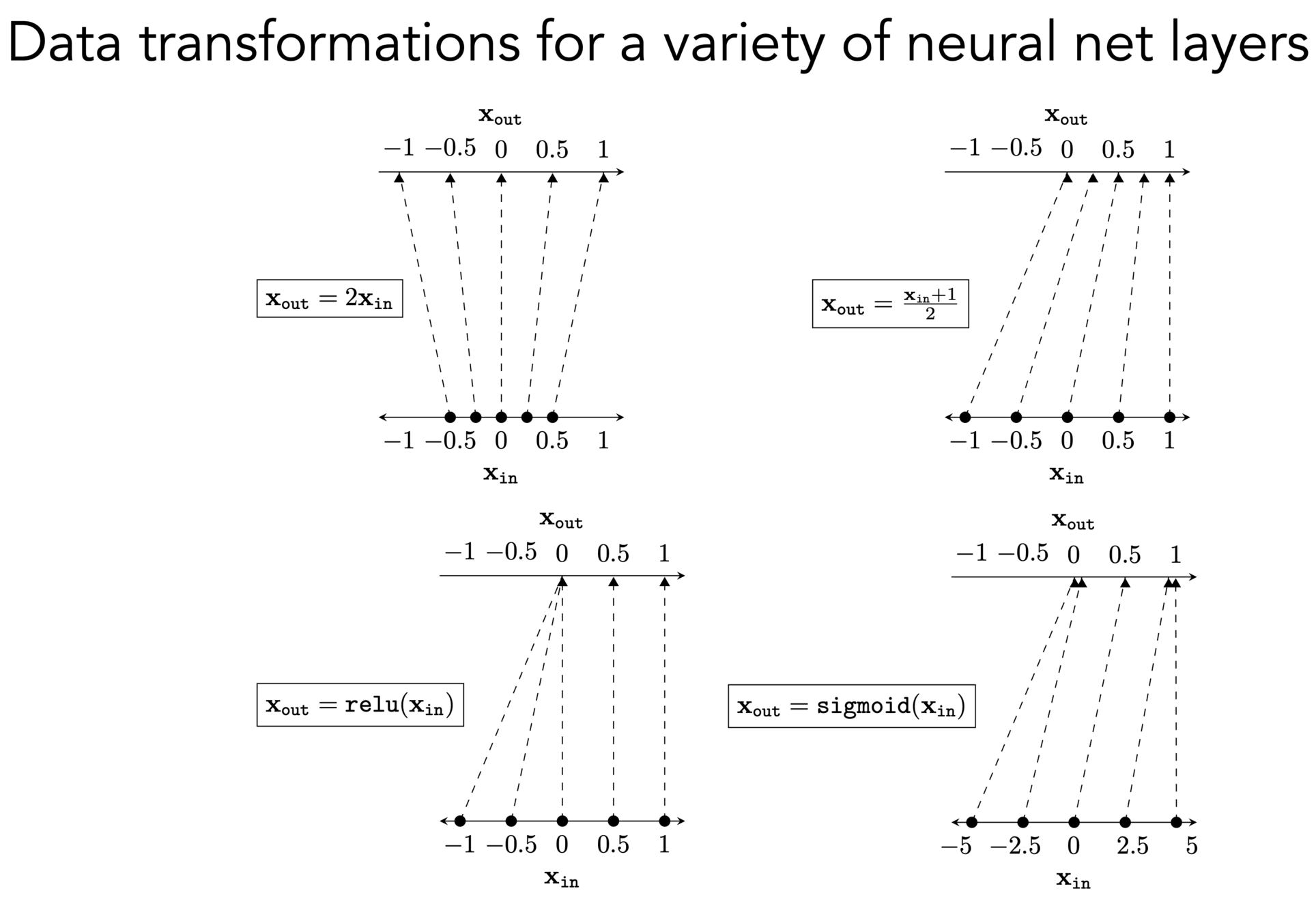
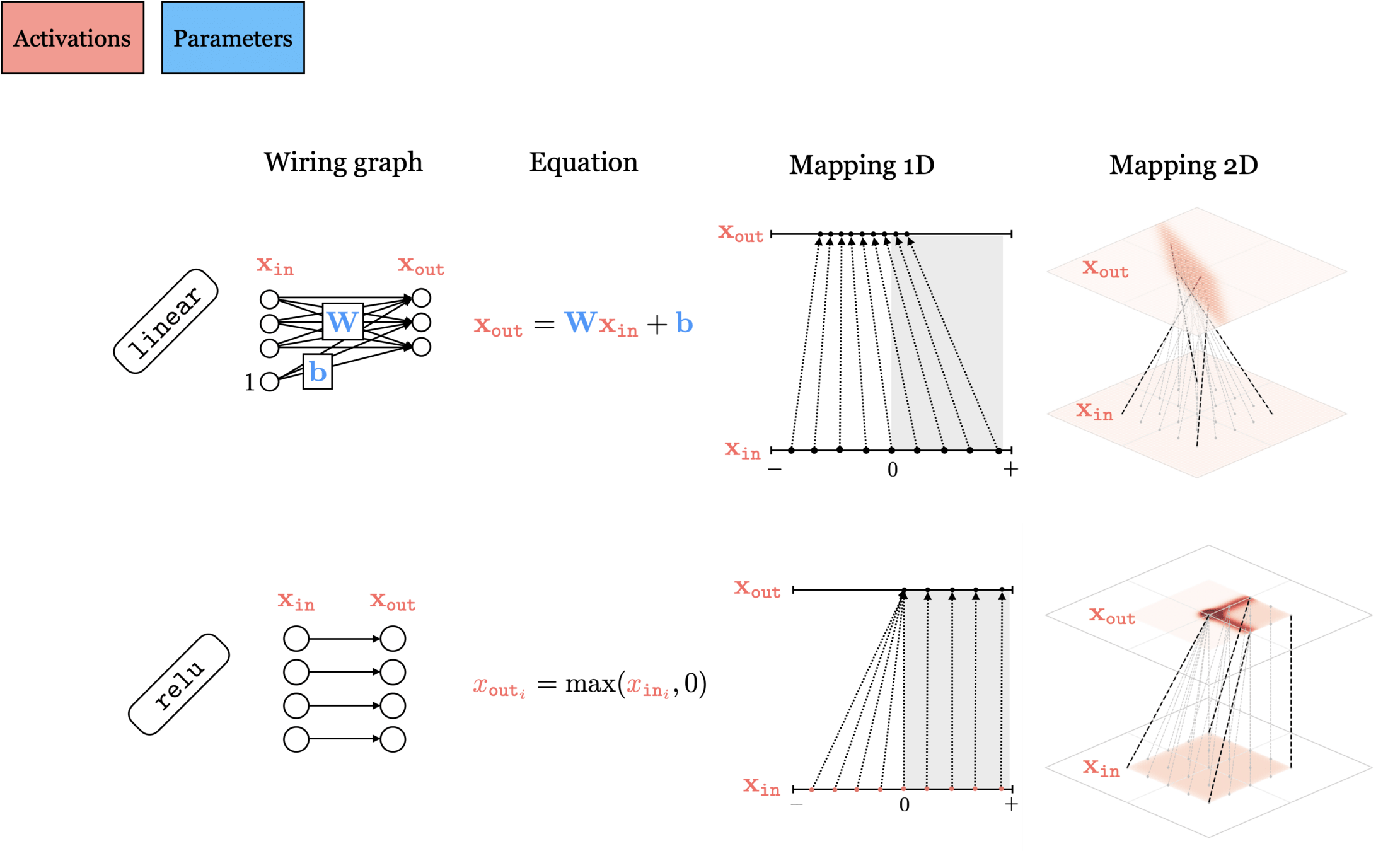
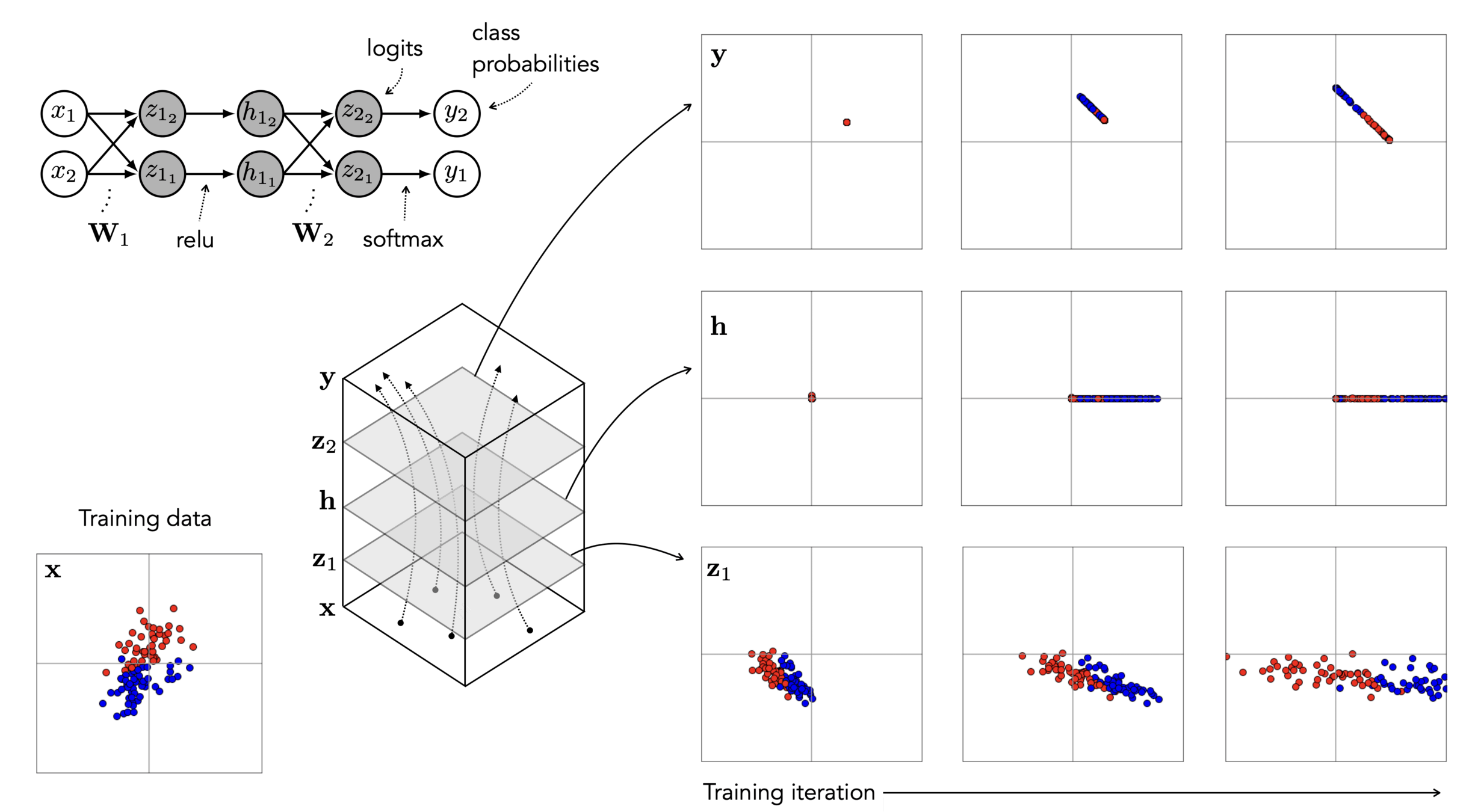
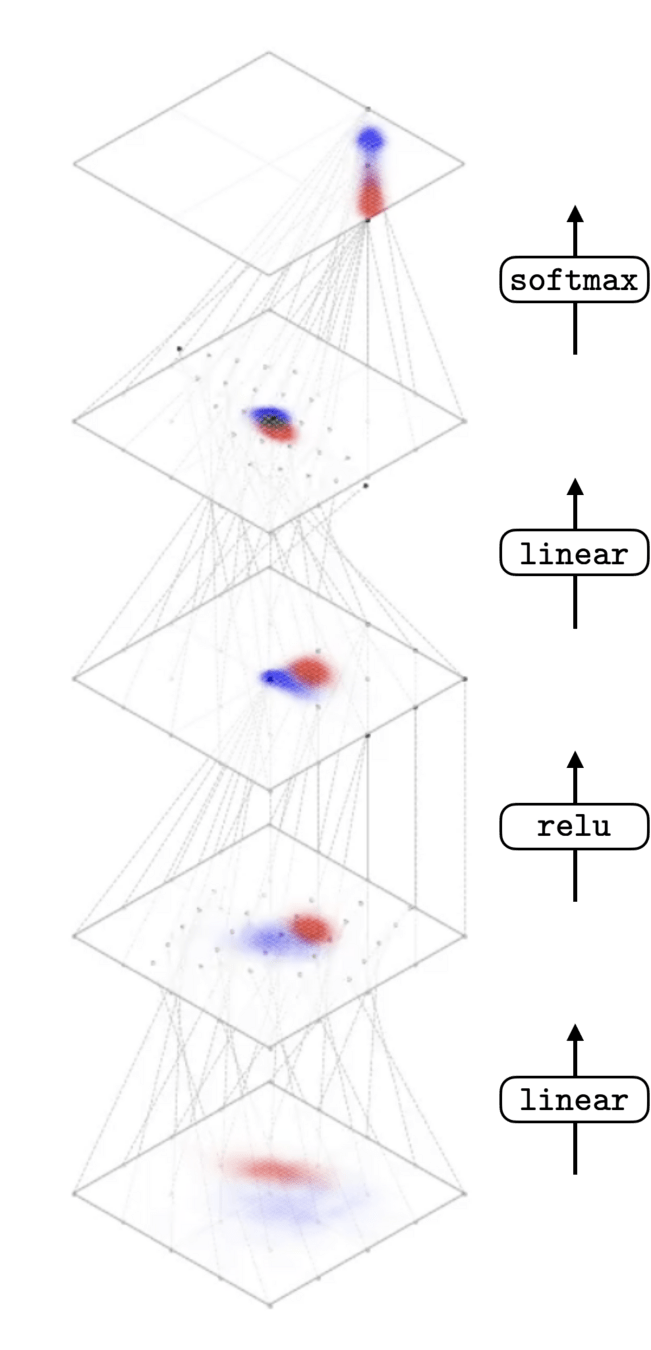
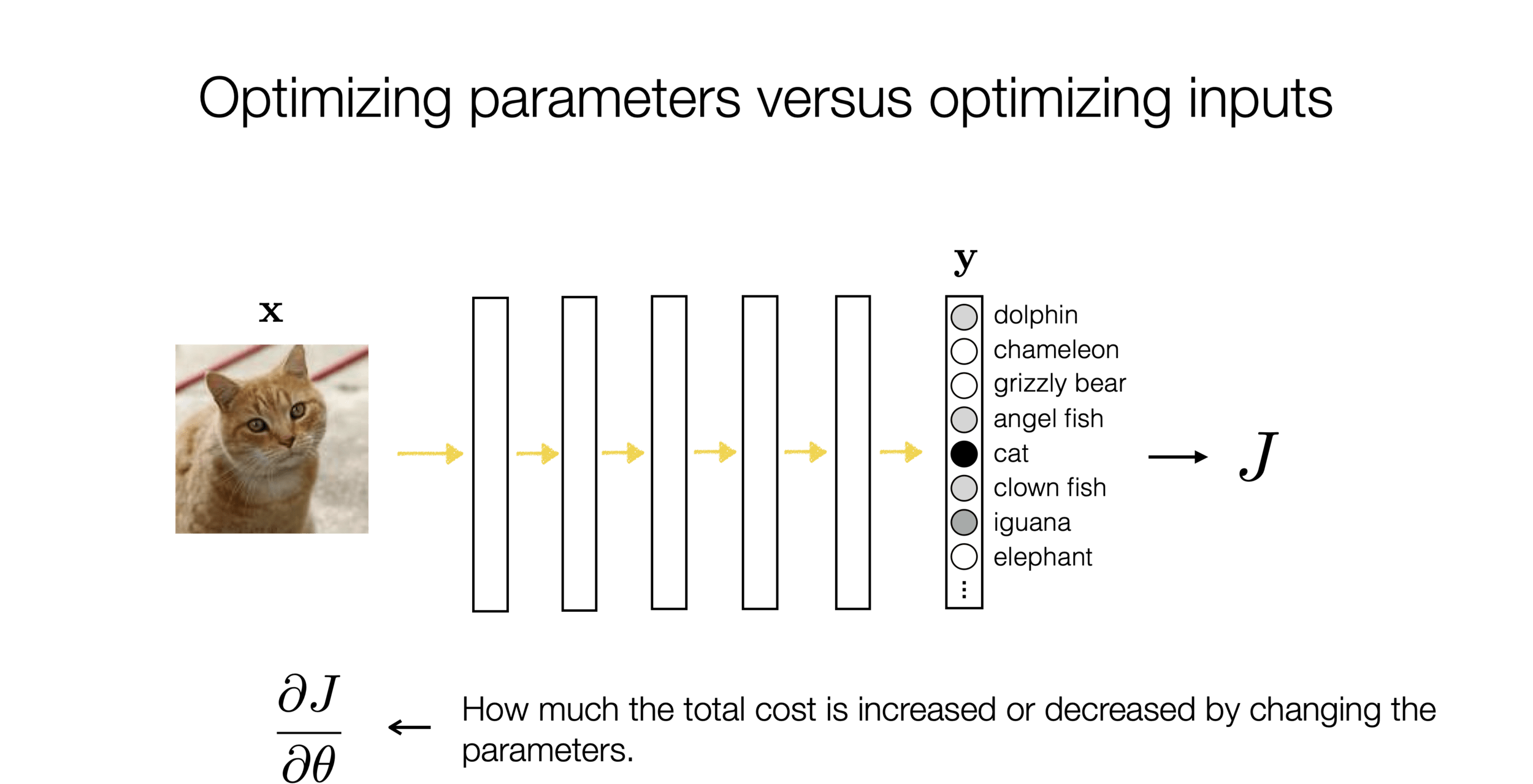
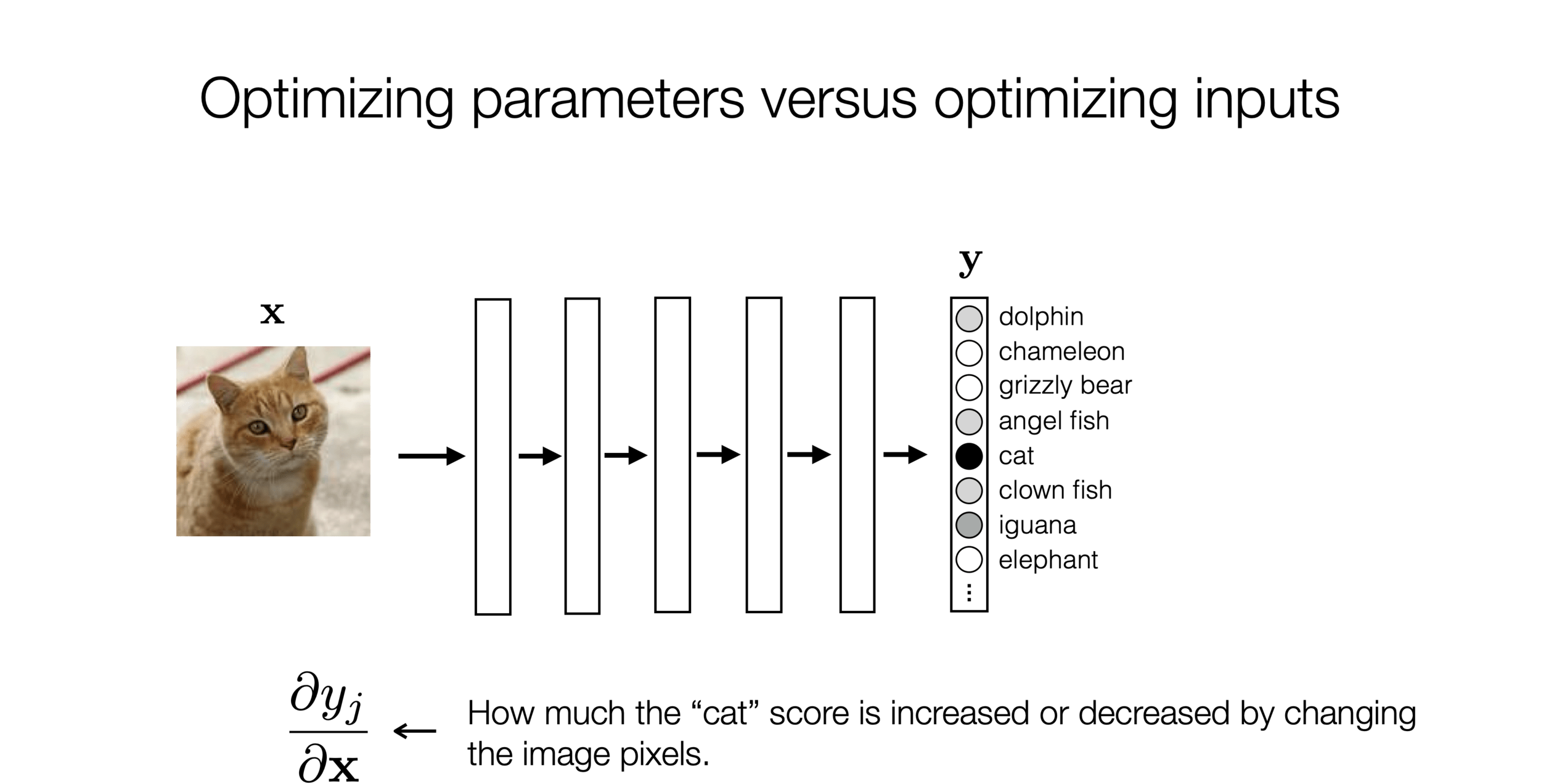
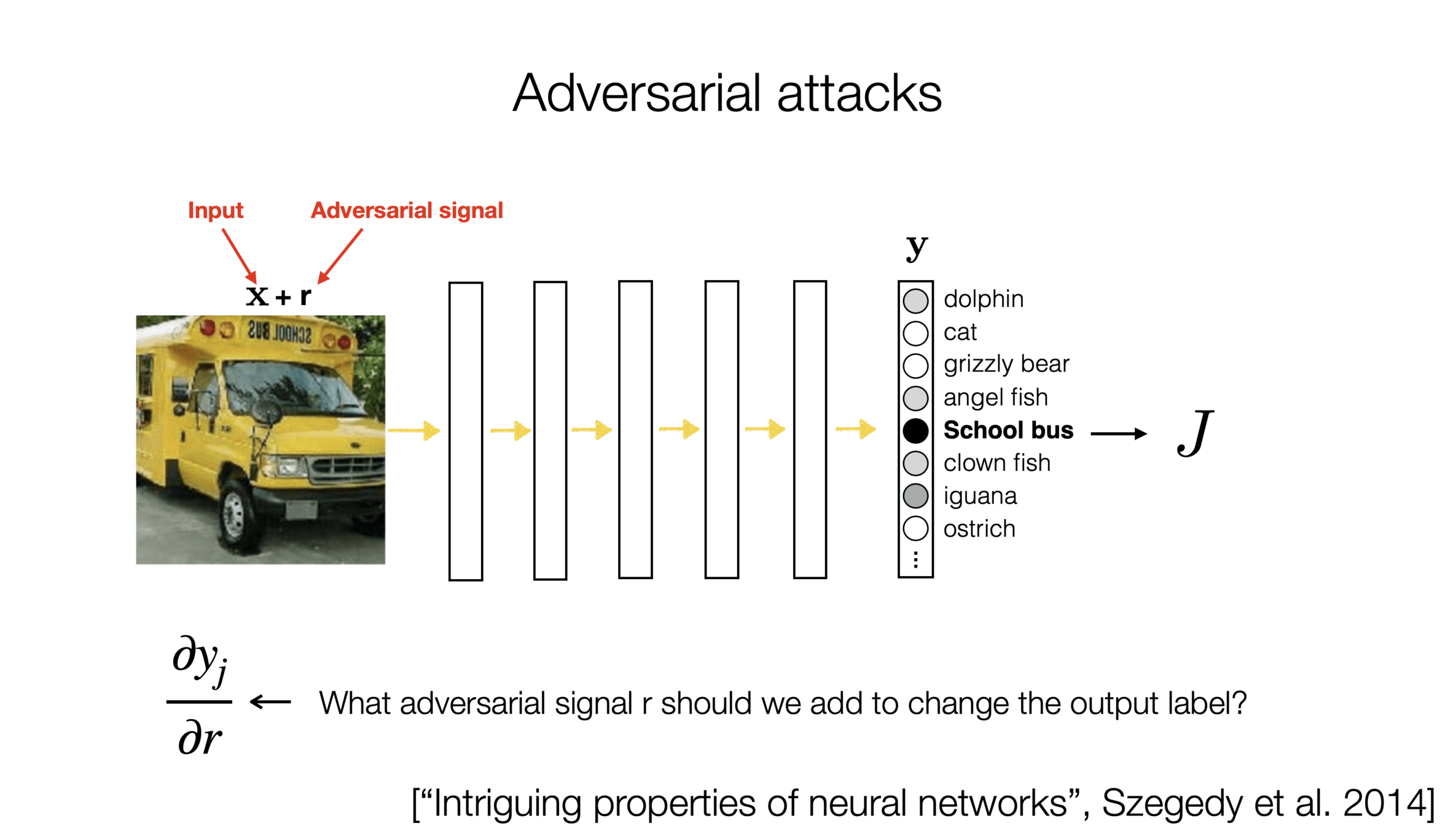
)
Summary
- We saw last week that introducing non-linear transformations of the inputs can substantially increase the power of linear regression and classification hypotheses.
- We also saw that it’s kind of difficult to select a good transformation by hand.
- Multi-layer neural networks are a way to make (S)GD find good transformations for us!
- Fundamental idea is easy: specify a hypothesis class and loss function so that d Loss / d theta is well behaved, then do gradient descent.
- Standard feed-forward NNs (sometimes called multi-layer perceptrons which is actually kind of wrong) are organized into layers that alternate between parametrized linear transformations and fixed non-linear transforms (but many other designs are possible!)
- Typical non-linearities include sigmoid, tanh, relu, but mostly people use relu
- Typical output transformations for classification are as we have seen: sigmoid and/or softmax
- There’s a systematic way to compute d Loss / d theta via backpropagation
Thanks!
We'd love it for you to share some lecture feedback.