Intro to Machine Learning

https://introml.mit.edu/

Lecture 6: Neural Networks

Shen Shen

March 8, 2024

(👉 the Live Slides)

(many slides adapted from Phillip Isola and Tamara Broderick)

Outline

  • Recap and neural networks motivation
  • Neural Networks
    • A single neuron
    • A single layer
    • Many layers
    • Design choices (activation functions, loss functions choices)
  • Forward pass
  • Backward pass (back-propogation)

e.g. linear regression represented as a computation graph

  • Each data point incurs a loss of \((w^Tx^{(i)} + w_0 - y^{(i)})^2  \)
  • Repeat for each data point, sum up the individual losses
  • Gradient of the total loss gives us the "signal" on how to optimize for \(w, w_0\)
\nabla \mathcal{L}_{\left(w, w_0\right)}

learnable parameters (weights)

y
\mathcal{L}(\cdot)
z
f(z)=z
g
\Sigma
f(\cdot)
= w^Tx + w_0
w_1
w_m
w_0
\dots
x_1
x_2
x_m
\dots
  • Each data point incurs a loss of \(- \left(y^{(i)} \log g^{(i)}+\left(1-y^{(i)}\right) \log \left(1-g^{(i)}\right)\right)\)
  • Repeat for each data point, sum up the individual losses
  • Gradient of the total loss gives us the "signal" on how to optimize for \(w, w_0\)
\nabla \mathcal{L}_{\left(w, w_0\right)}

learnable parameters (weights)

y
\mathcal{L}(\cdot)
z
f(z)=\sigma(z)
g
\Sigma
f(\cdot)
= \sigma(w^Tx + w_0)
w_1
w_m
w_0
\dots
x_1
x_2
x_m
\dots

e.g. linear logistic regression (linear classification)  represented as a computation graph

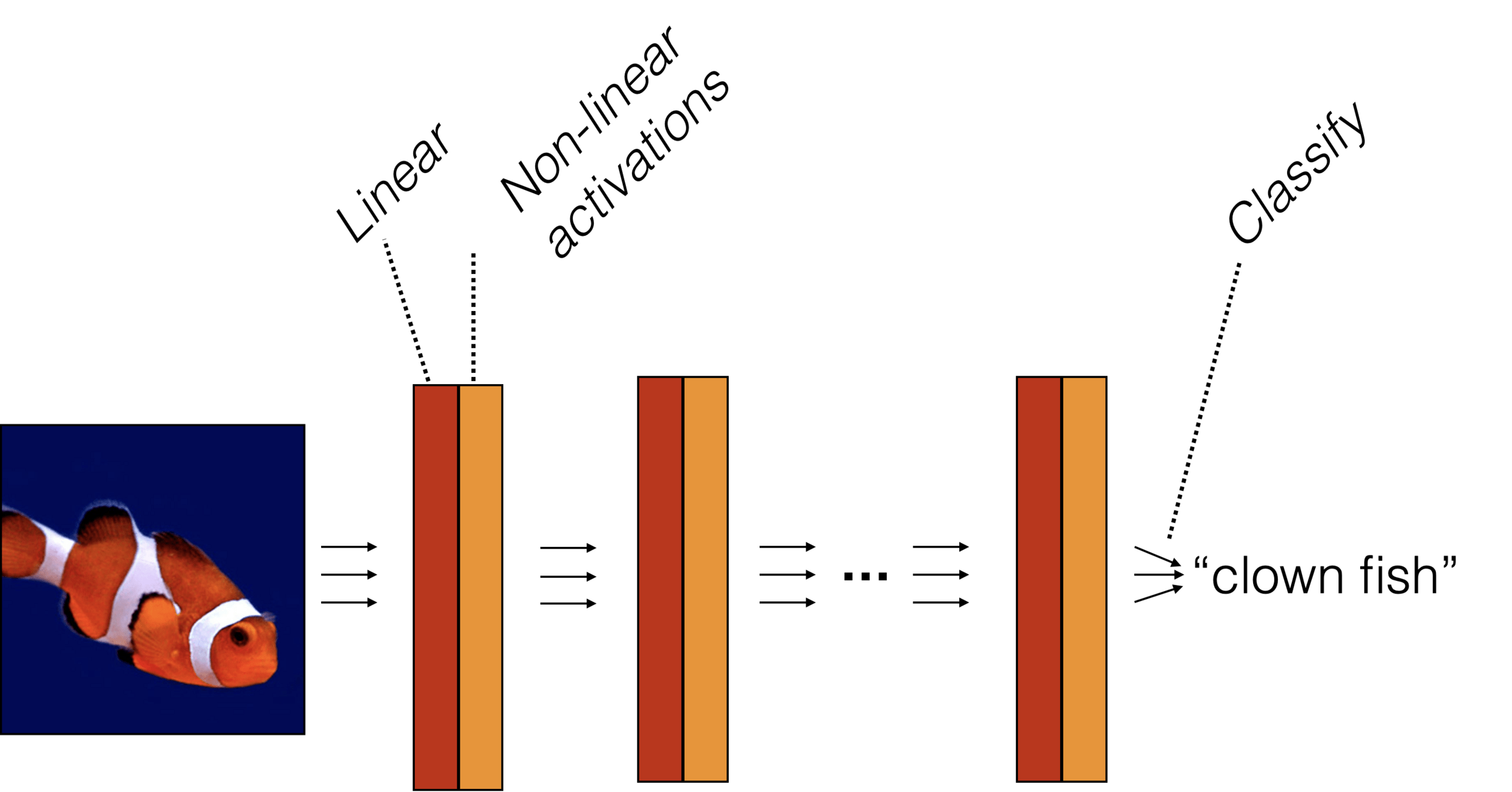
We saw that, one way of getting complex input-output behavior is

to leverage nonlinear transformations

\phi\left(\left[x_1, x_2\right]^{\top}\right)=\left[1, x_1, x_2, x_1^2, x_1 x_2, x_2^2\right]^{\top}
x_1
x_2

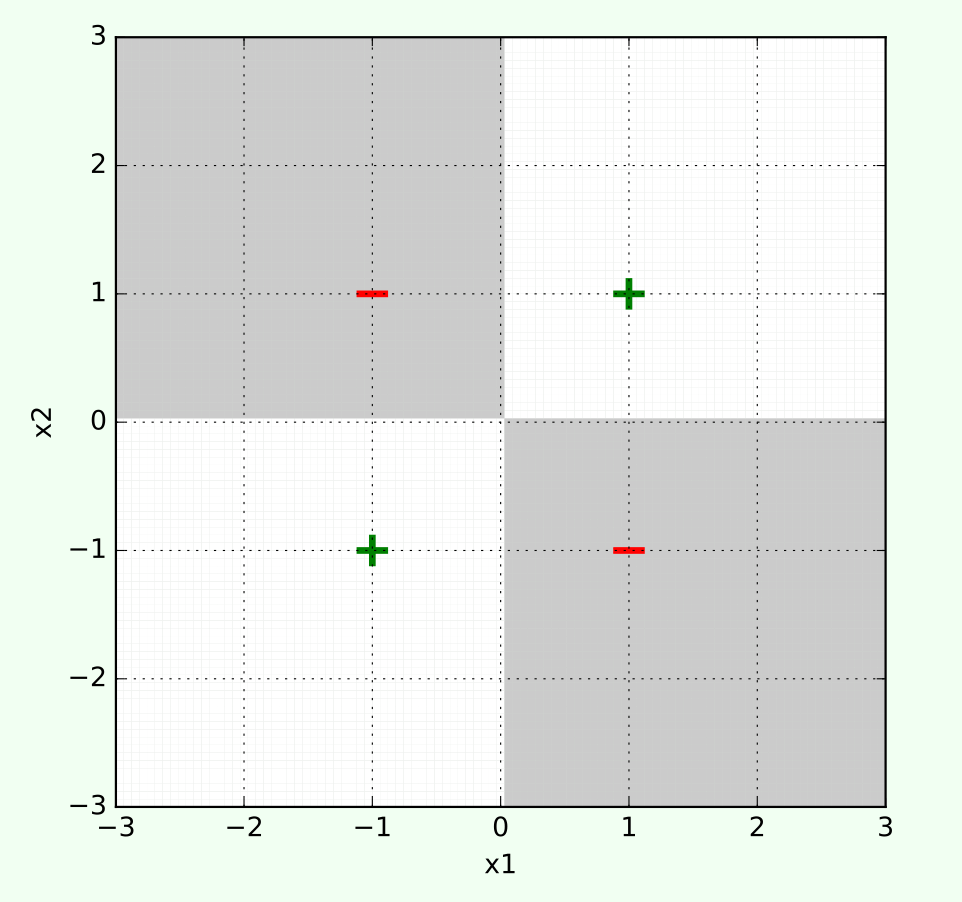
transform

\text{sign}(0+0 x_1+0 x_2+0 x_1^2+4 x_1 x_2+0 x_2^2+0)

e.g. use for decision boundary

👆 importantly, linear in \(\phi\), non-linear in \(x\)

Today (2nd cool idea): "stacking" helps too!

\begin{aligned} & z=w^T x \\ & y=\text{sign}(z) \end{aligned}
a_1
a_2
a_1
a_2
z_3
y
W_1
W_2
\begin{aligned} \mathbf{z} & = \mathbf{x}^T \mathbf{W}_1\\ \mathbf{a} & =\text{sign}(\mathbf{z}) \\ z_3 & = \mathbf{a}^T \mathbf{W}_2 \\ y & =\text{sign}\left(z_3\right) \end{aligned}

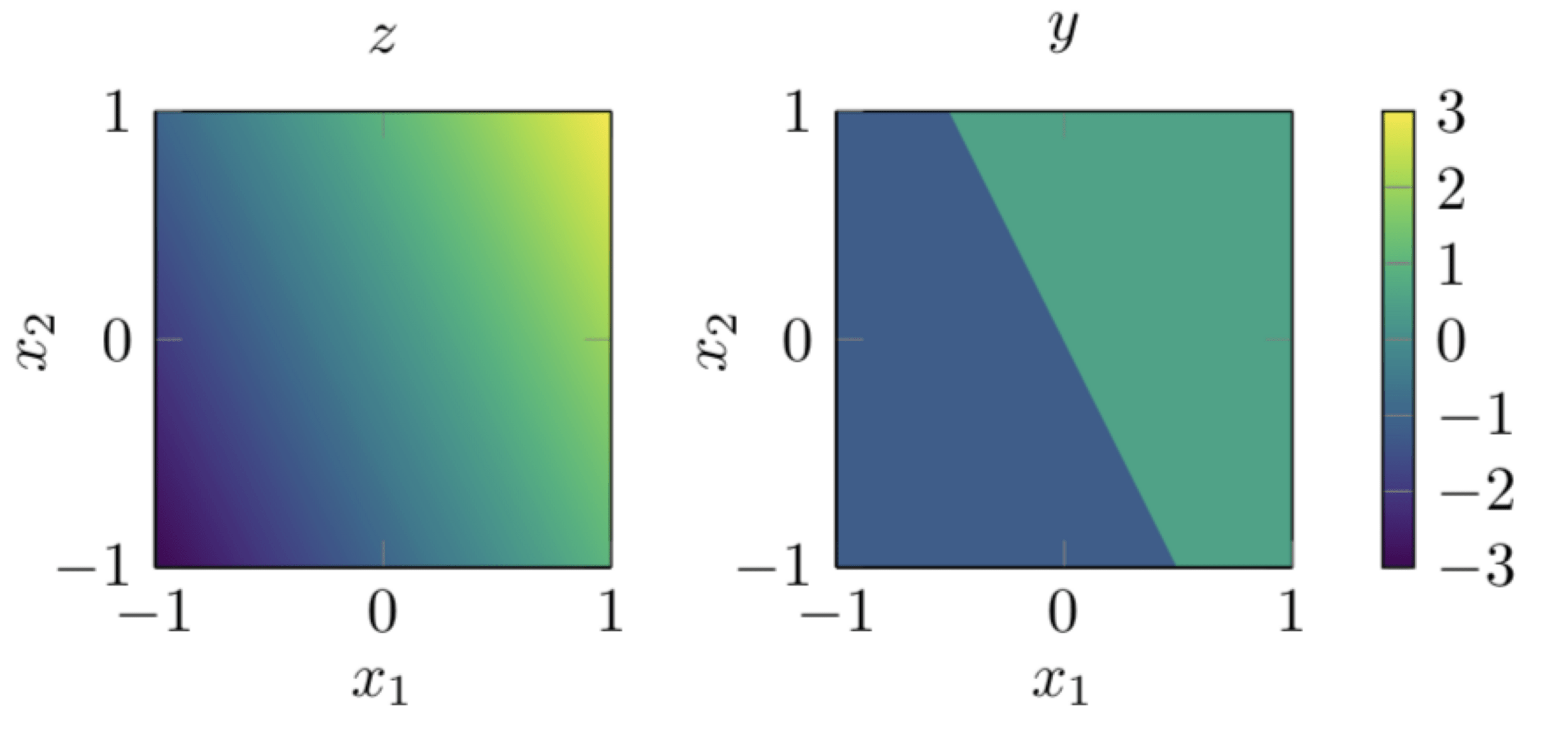
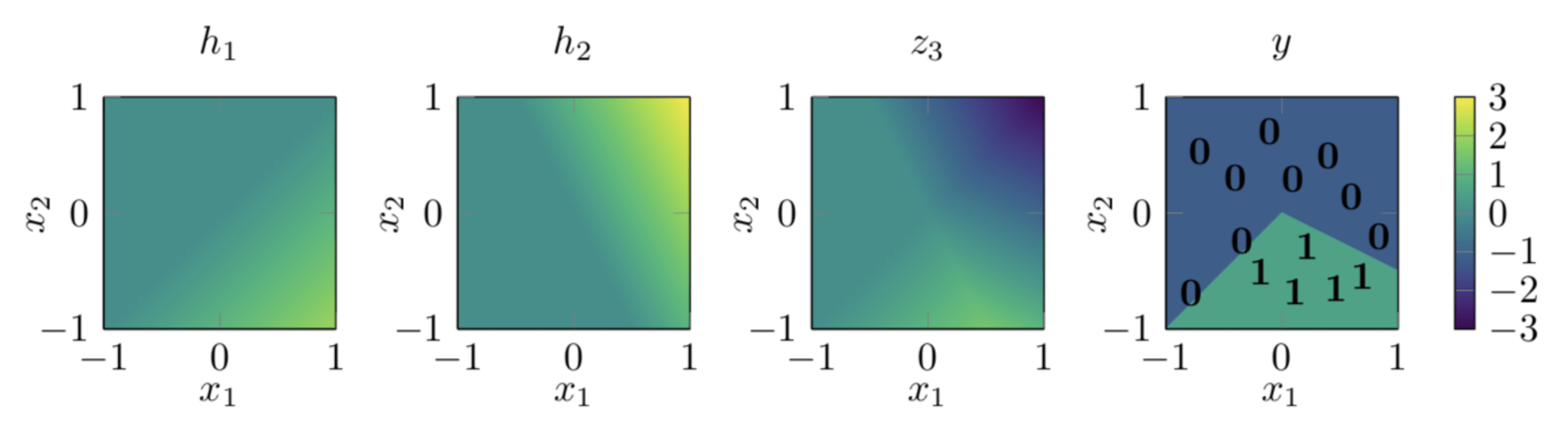
So, two epiphanies:  

  • nonlinearity empowers linear tools
  • stacking helps

 

(👋 heads-up:  all neural network graphs focus on a single data point for simple illustration.)

Outline

  • Recap and neural networks motivation
  • Neural Networks
    • A single neuron
    • A single layer
    • Many layers
    • Design choices (activation functions, loss functions choices)
  • Forward pass
  • Backward pass (back-propogation)

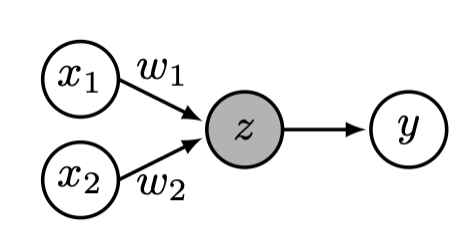
A single neuron is

  • the basic operating "unit" in a neural network. 
  • the basic "node" when a neural network is viewed as computational graph. 

 

 

 

 

 

 

 

  • neuron , a function, maps a vector input \(x \in \mathbb{R}^m\) to a scalar output 
  • inside the neuron, circles do function evaluation/computation
  • \(f\): we engineers choose
  • \(w\): learnable parameters
  • \(x\): \(m\)-dimensional input (a single data point)
  • \(w\): weights (i.e. parameters)
  • \(z\): pre-activation scalar output
  • \(f\): activation function
  • \(a\): post-activation scalar output
\dots
x_1
x_2
x_m
z
f(\cdot)
a
\Sigma
w_1
w_m
w_0

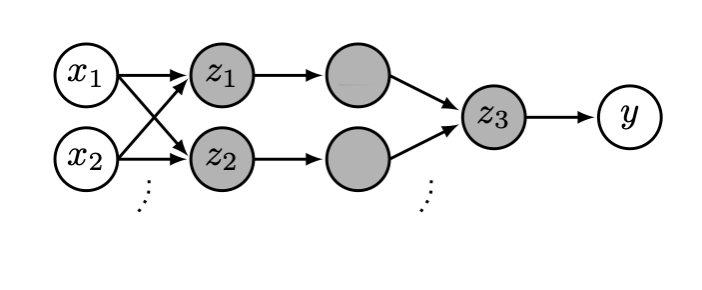
A single layer is

  • made of many individual neurons.
  • (# of neurons) = (layer output dimension).
  • typically, all neurons in one layer use the same activation \(f\) (if not; uglier/messier algebra)
  • typically, no "cross-wire" between neurons. e.g. \(z_1\) doesn't influence \(a_2\). in other words, a layer has the same activation applied element-wise. (softmax is an exception to this, details later.)
  • typically, fully connected. i.e. there's an edge connecting \(x_i\) to \(z_j,\) for all \(i \in \{1,2,3, \dots , m\}; j \in \{1,2,\dots, n\}\). in other words, all \(x_i\) influence all \(a_j.\)
z_1
z_2
z_3
z_n
W

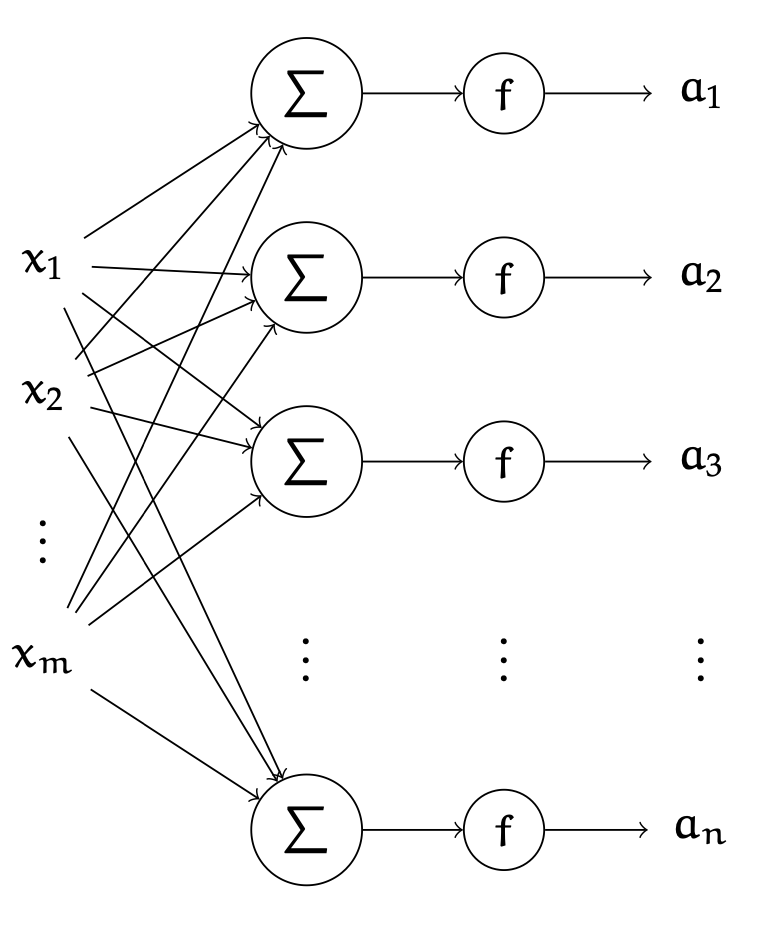
layer

learnable weights

f_1(\cdot)
\Sigma
\dots
x_1
x_2
x_m
f_1(\cdot)
\Sigma
f_1(\cdot)
\Sigma
f_1(\cdot)
\Sigma
\dots
f_2(\cdot)
\Sigma
f_2(\cdot)
\Sigma
\dots
f_2(\cdot)
\Sigma
\dots
W_1
W_2

learnable weights

layer

linear combo

activations

input

A (feed-forward) neural network is

Activation function \(f\) choices

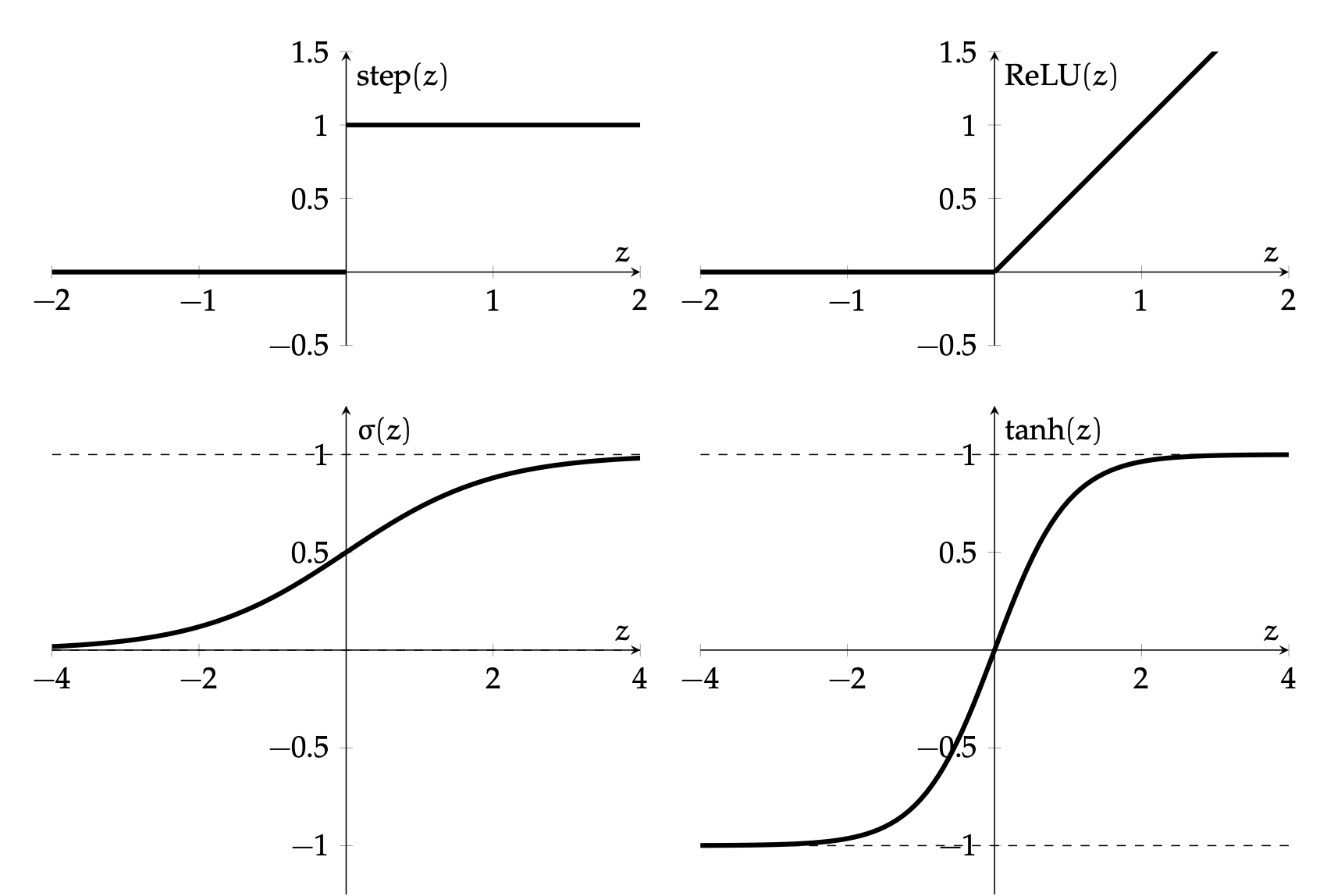
\(\sigma\) used to be popular

  • firing rate of neuron
  • \(\sigma^{\prime}(z)=\sigma(z) \cdot(1-\sigma(z))\)

ReLU is the de-facto activation choice nowadays

\frac{\partial \text{ReLU}(z)}{\partial z}:=\left\{\begin{array}{lll} 0, & \text { if } \quad z<0 \\ 1, & \text { if } \quad \text{otherwise} \end{array}\right.
  • Default choice in hidden layers.
  • Pro: very efficient to implement, choose to let the gradient be:

 

 

 

  • Drawback: if strongly in negative region, unit can be "dead" (no gradient).
  • Inspired variants like elu, leaky-relu.
\operatorname{ReLU}(z)=\left\{\begin{array}{ll} 0 & \text { if } z<0 \\ z & \text { otherwise } \end{array}\\ \\ \right.
=\max (0, z)

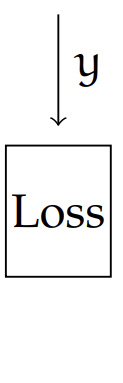
The last layer, the output layer, is special

 

  • activation and loss depends on problem at hand
  • we've seen e.g. regression (one unit in last layer, squared loss).

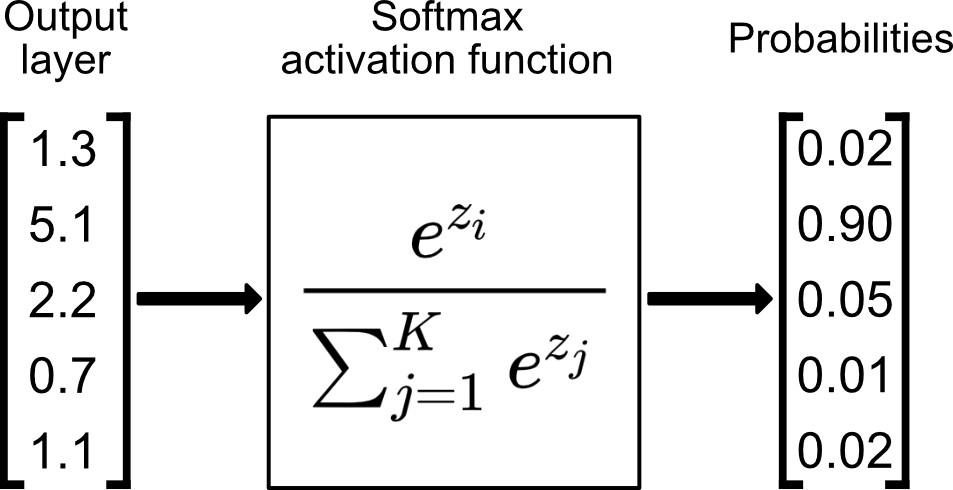
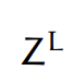
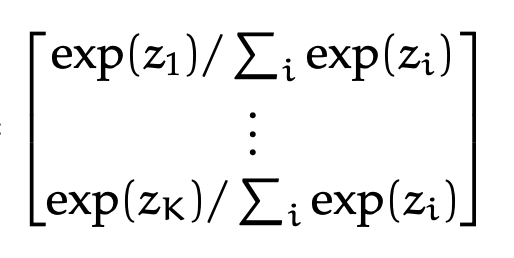
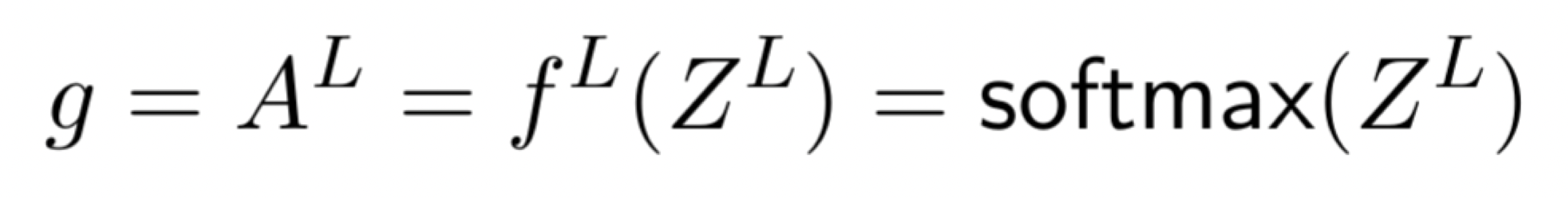
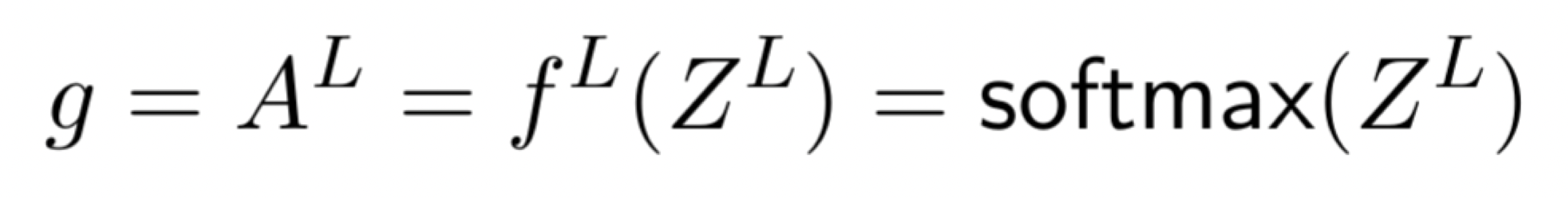
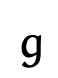
(output layer)

e.g., say \(K=5\) classes

More complicated example: predict one class out of \(K\) possibilities

then last layer: \(K\) nuerons, softmax activation 

 

=
\mathcal{L}_{\mathrm{nllm}}(\mathrm{g}, \mathrm{y})=-\sum_{\mathrm{k}=1}^{\mathrm{K}} \mathrm{y}_{\mathrm{k}} \cdot \log \left(\mathrm{g}_{\mathrm{k}}\right)

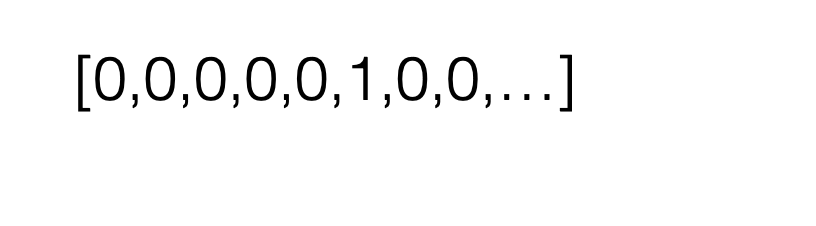
Outline

  • Recap and neural networks motivation
  • Neural Networks
    • A single neuron
    • A single layer
    • Many layers
    • Design choices (activation functions, loss functions choices)
  • Forward pass
  • Backward pass (back-propogation)
f_L\left(\ldots f_2\left(f_1\left(\mathbf{x}^{(i)}, \mathbf{W}_1\right), \mathbf{W}_2\right), \ldots \mathbf{W}_L\right)

How do we optimize

\(J(\mathbf{W})=\sum_{i=1} \mathcal{L}\left(f_L\left(\ldots f_2\left(f_1\left(\mathbf{x}^{(i)}, \mathbf{W}_1\right), \mathbf{W}_2\right), \ldots \mathbf{W}_L\right), \mathbf{y}^{(i)}\right)\) though?

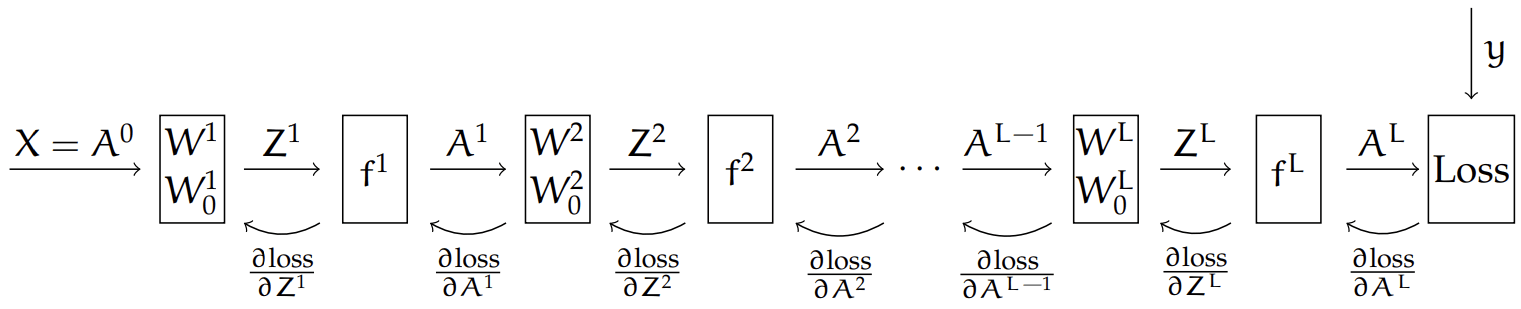
Backprop = gradient descent & the chain rule

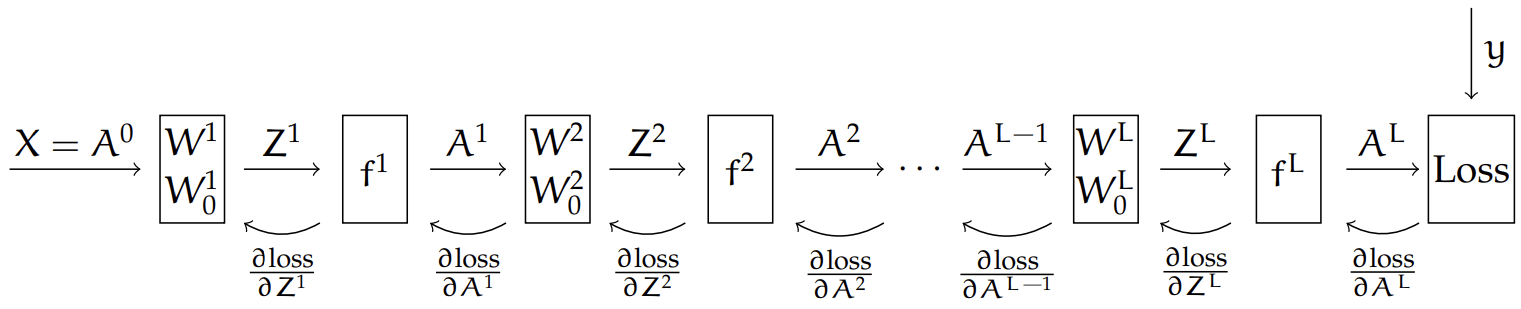
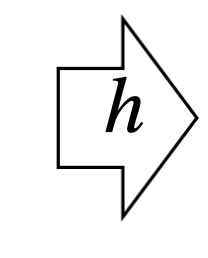
Recall that, the chain rule says:

For the composed function: \(h(\mathbf{x})=f(g(\mathbf{x})), \) its derivative is: \(h^{\prime}(\mathbf{x})=f^{\prime}(g(\mathbf{x})) g^{\prime}(\mathbf{x})\)

Here, our loss depends on the final output,

and the final output \(A^L\) comes from a chain of composition of functions

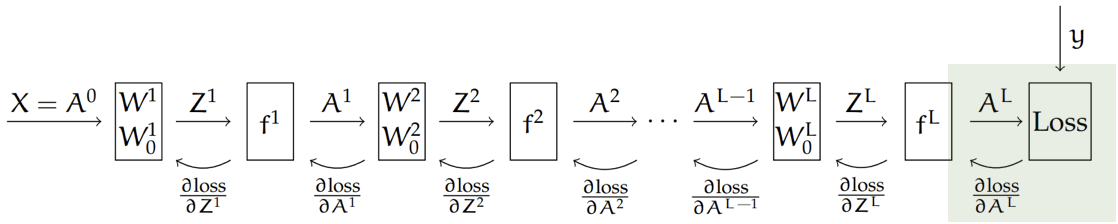
Backprop = gradient descent & the chain rule

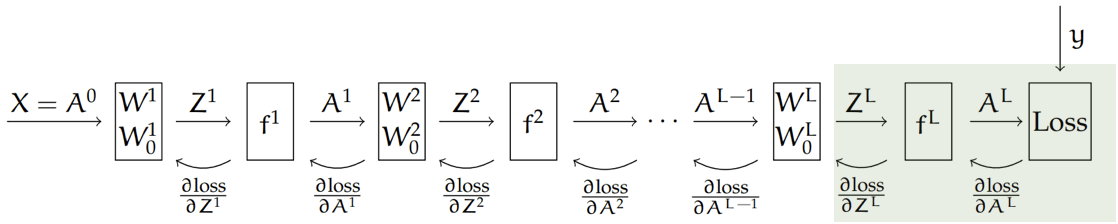
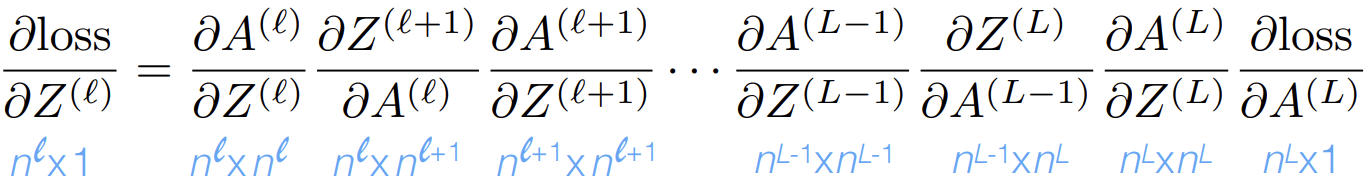
Backprop = gradient descent & the chain rule

(

(The demo won't embed in PDF. But the direct link below works.)

)

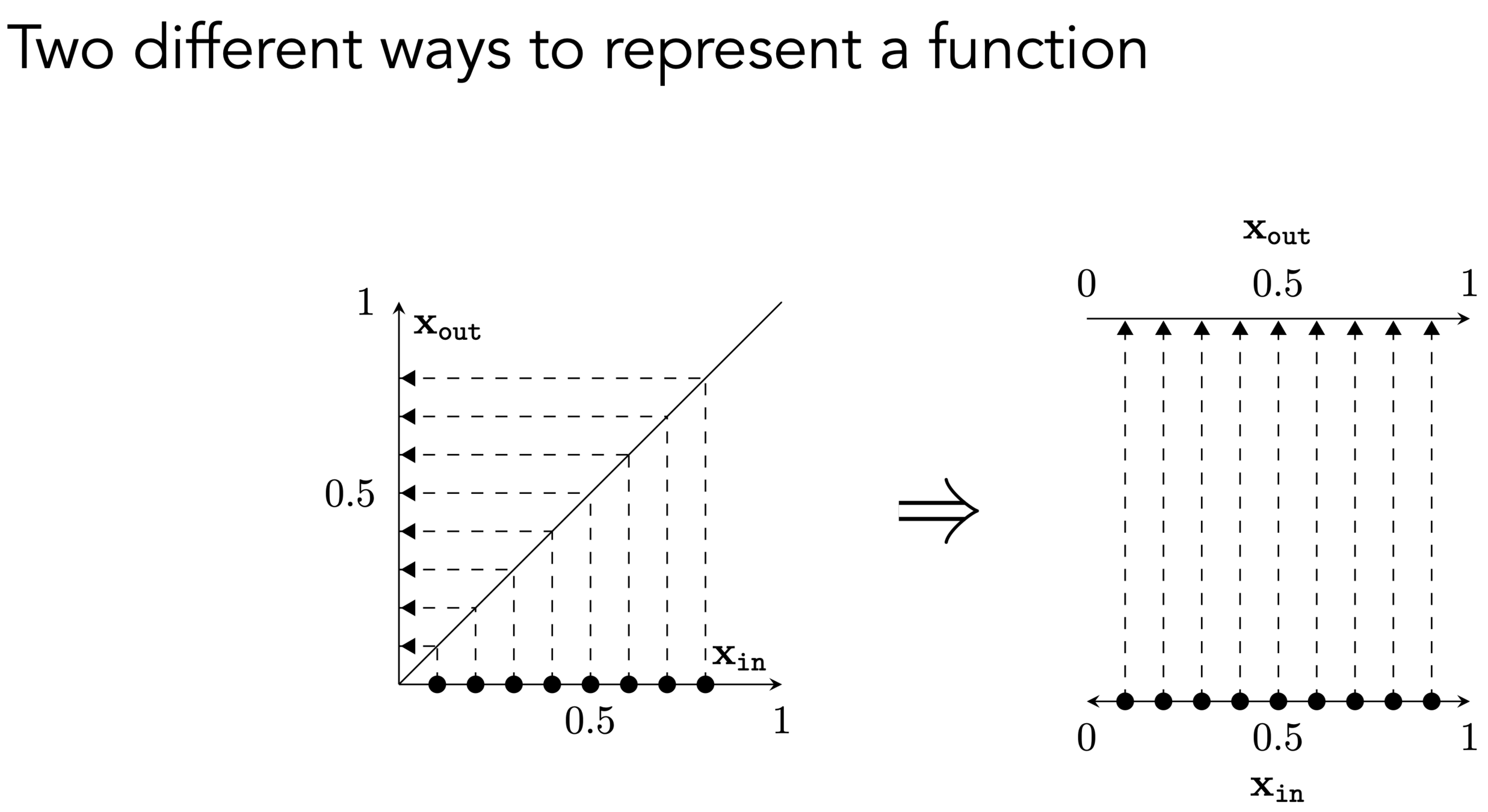
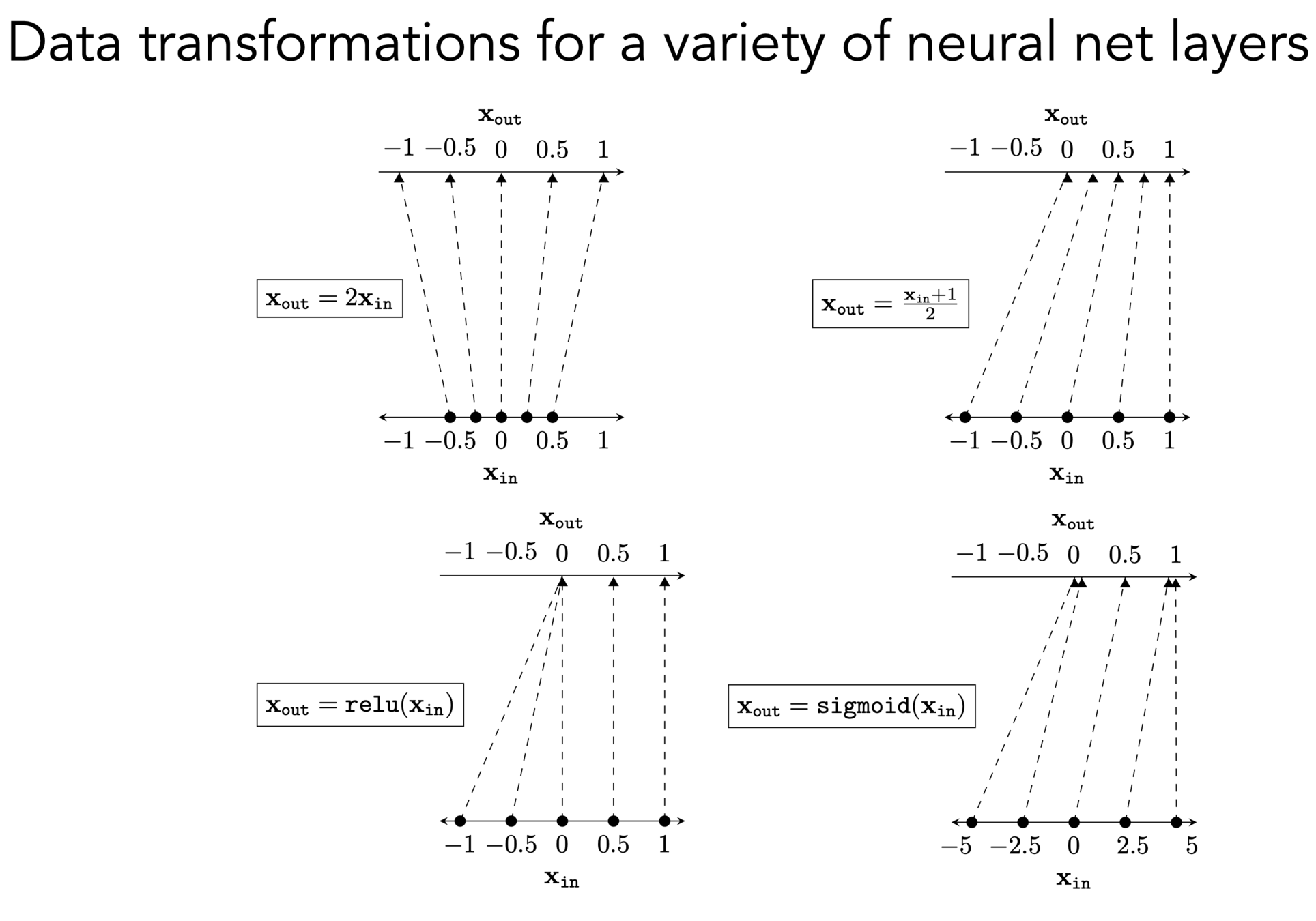
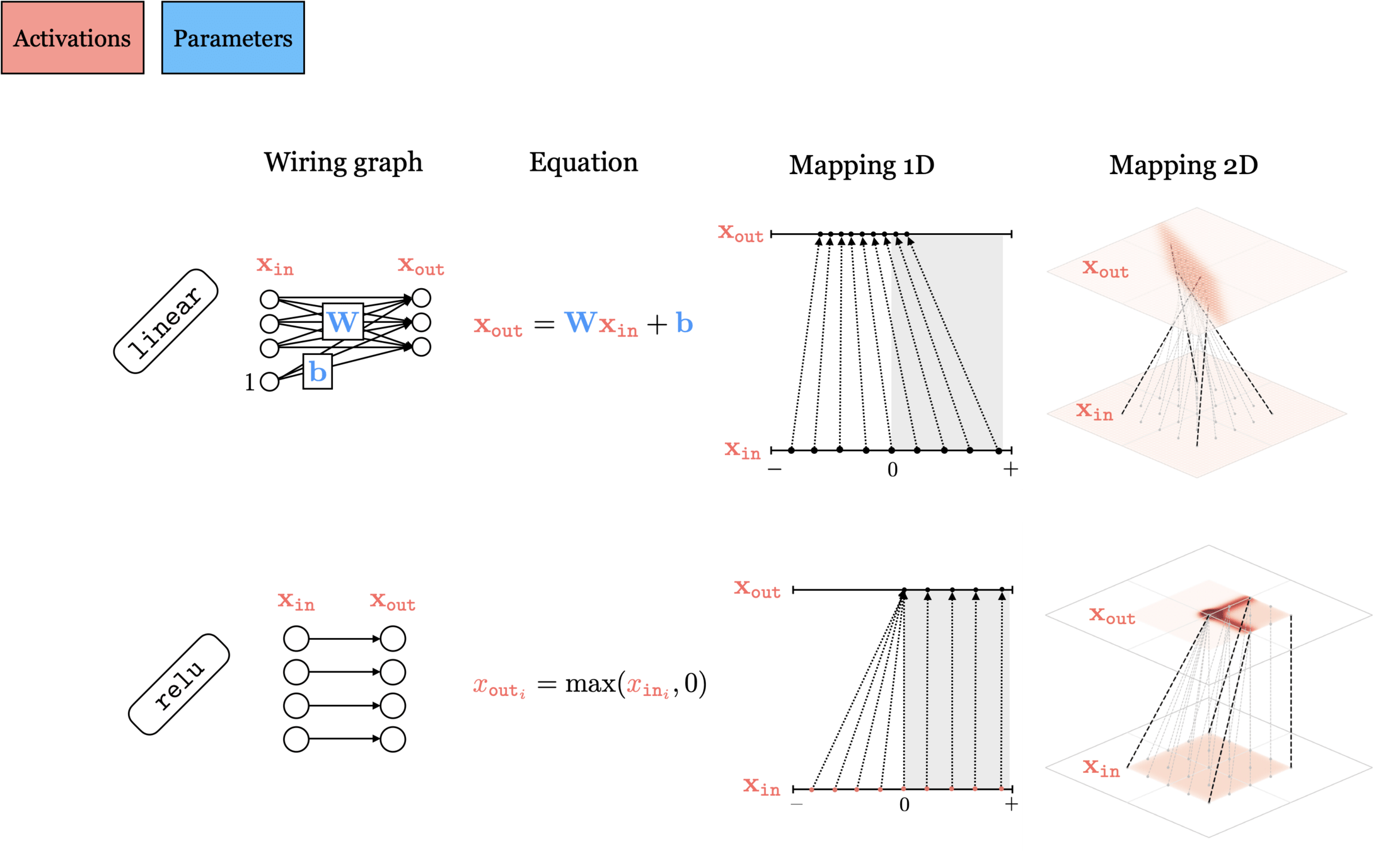
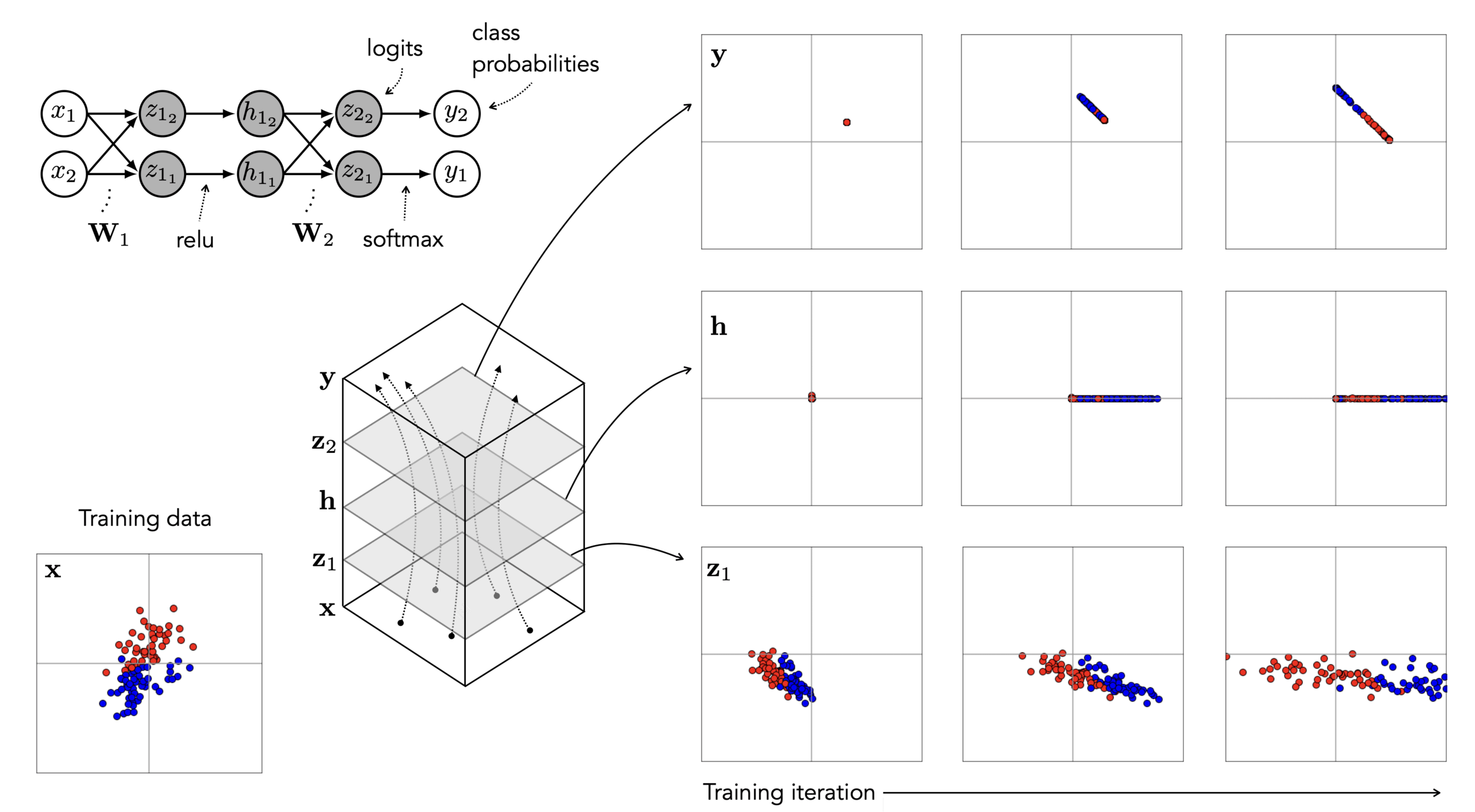
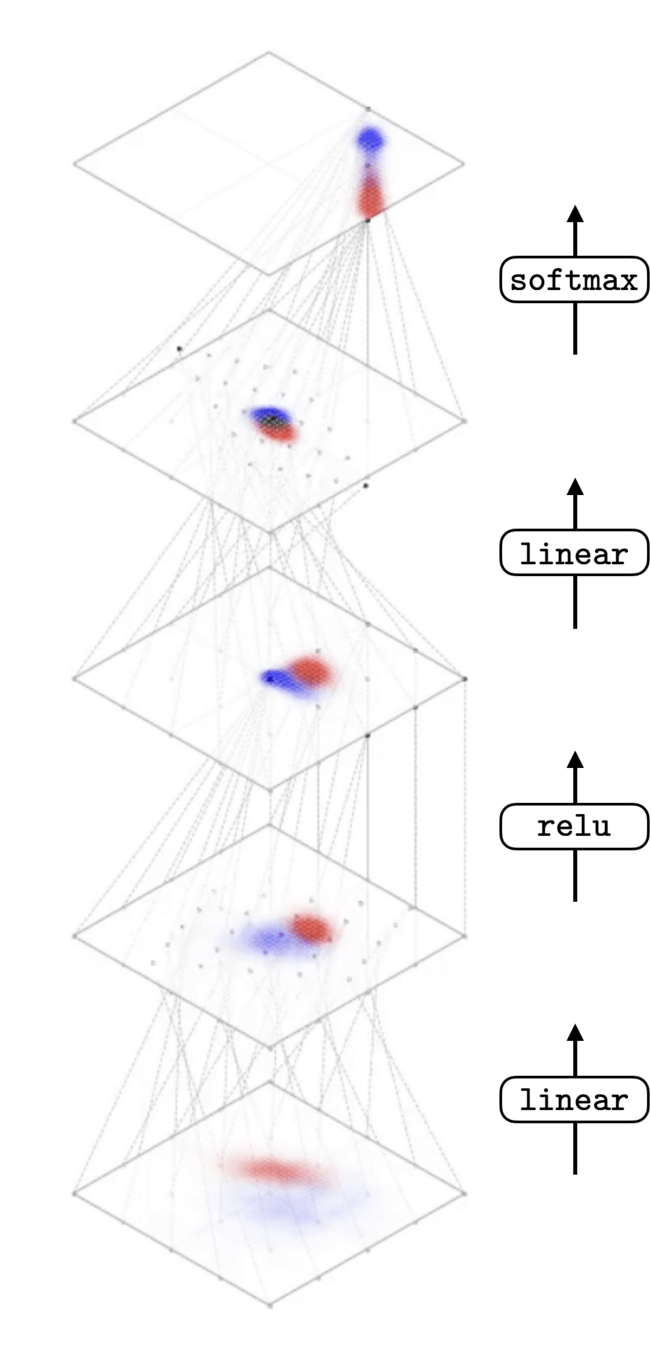
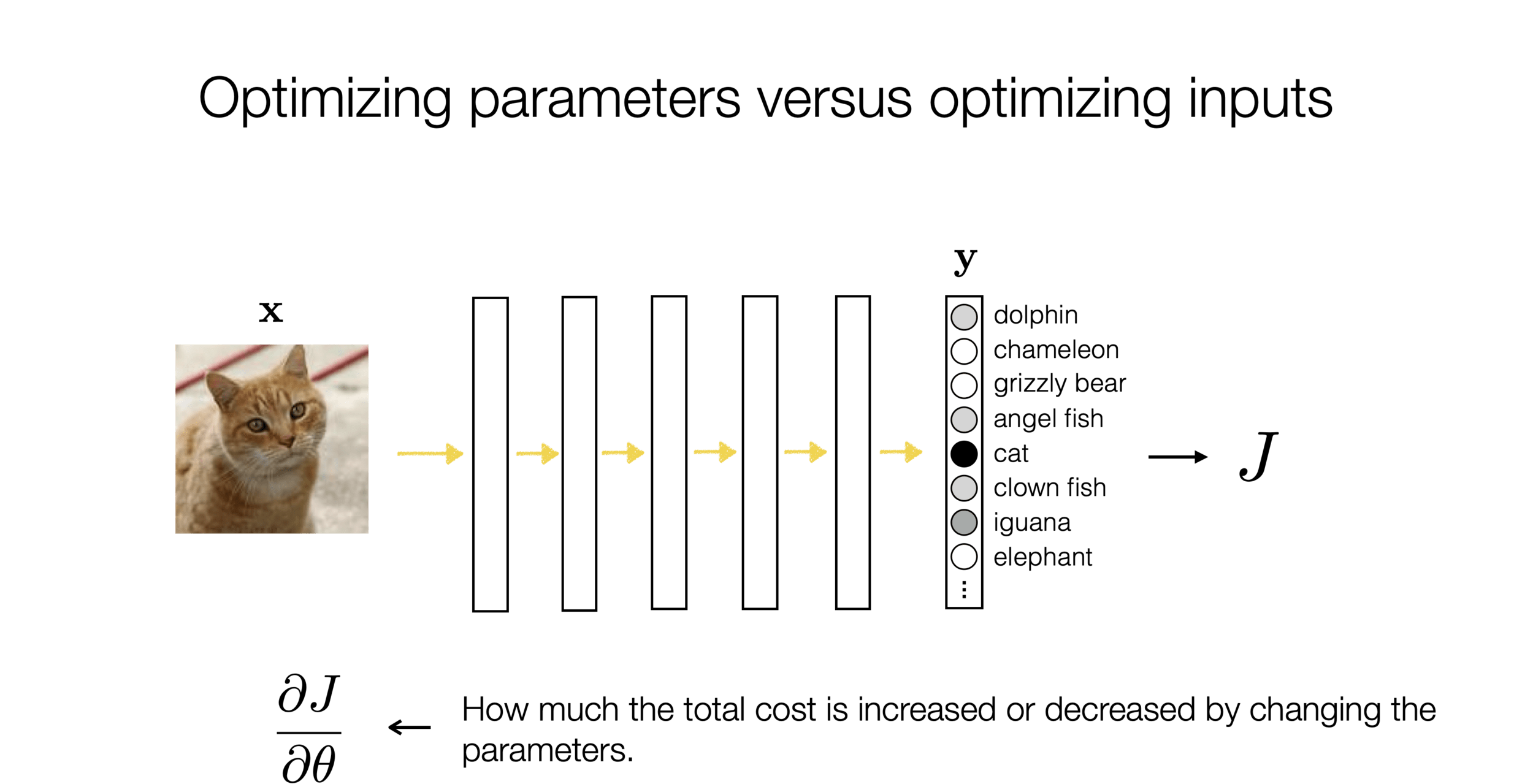
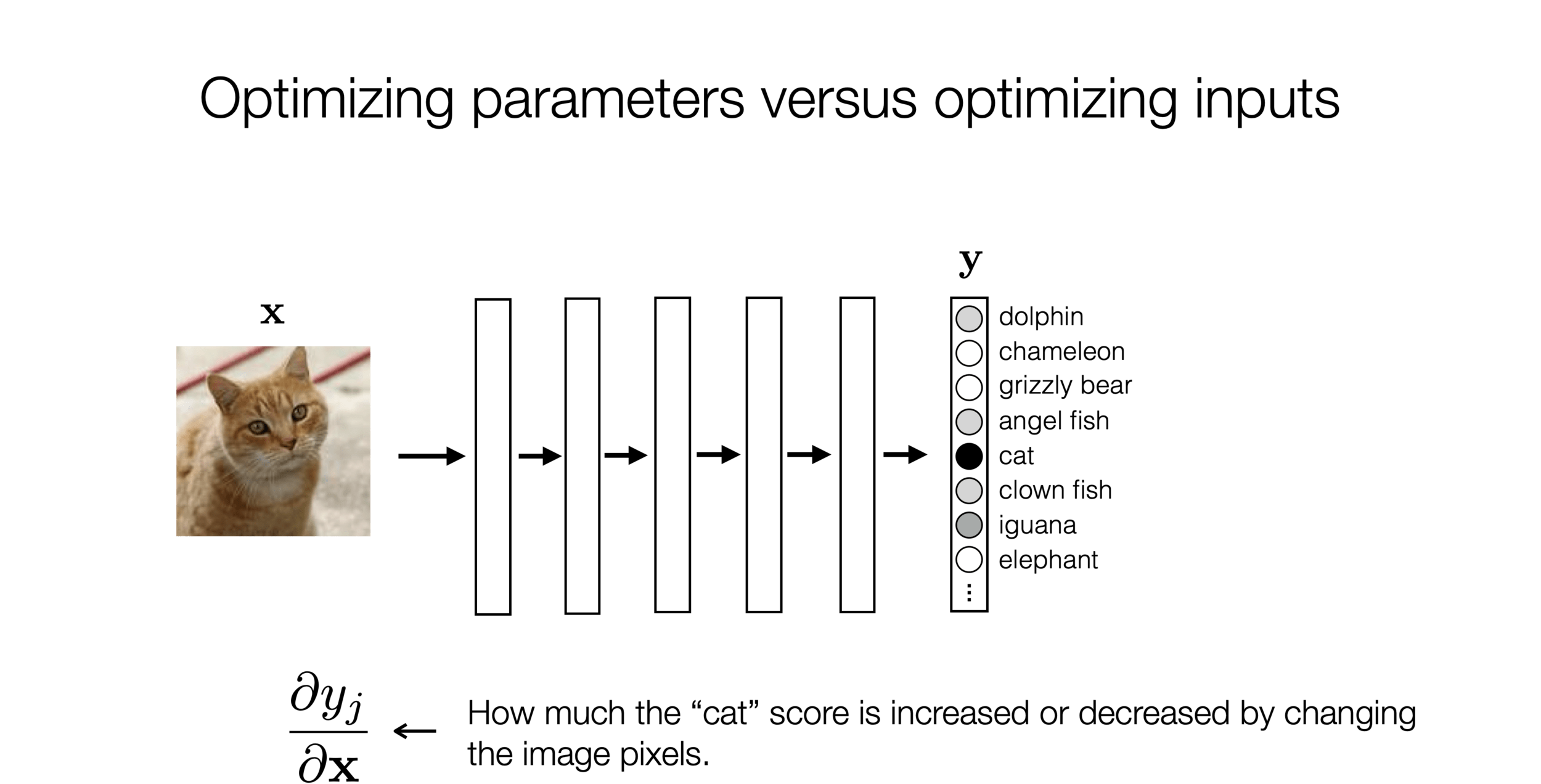
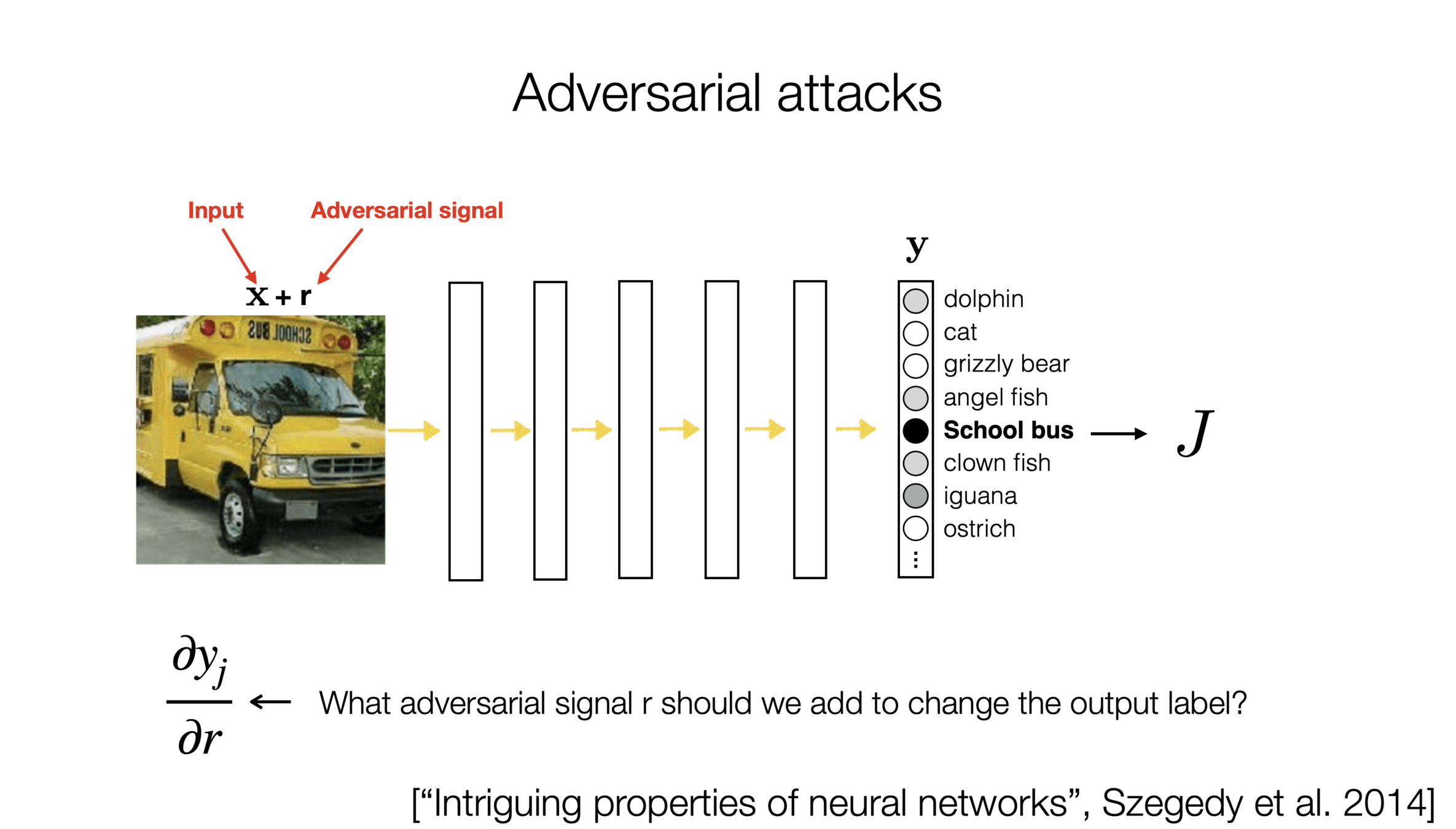
Summary

  • We saw last week that introducing non-linear transformations of the inputs can substantially increase the power of linear regression and classification hypotheses.
  • We also saw that it’s kind of difficult to select a good transformation by hand.
  • Multi-layer neural networks are a way to make (S)GD find good transformations for us!
  • Fundamental idea is easy:  specify a hypothesis class and loss function so that d Loss / d theta is well behaved, then do gradient descent.
  • Standard feed-forward NNs (sometimes called multi-layer perceptrons which is actually kind of wrong) are organized into layers that alternate between parametrized linear transformations and fixed non-linear transforms (but many other designs are possible!)
  • Typical non-linearities include sigmoid, tanh, relu, but mostly people use relu
  • Typical output transformations for classification are as we have seen: sigmoid and/or softmax
  • There’s a systematic way to compute d Loss / d theta via backpropagation

Thanks!

We'd love it for you to share some lecture feedback.

introml-sp24-lec6

By Shen Shen

introml-sp24-lec6

  • 82

More from Shen Shen