

Lecture 9: Transformers
Shen Shen
April 11, 2025
11am, Room 10-250
(interactive slides support animated walk-throughs of transformers and attention mechanisms.)
Intro to Machine Learning

Outline
- Recap, embedding and representation
- Transformers high-level intuition
- Transformers architecture overview
- (query, key, value) and self-attention
- matrix form
- Multi-head attention
- (Applications)
[video edited from 3b1b]
embedding
dict_en2fr = {
"apple" : "pomme",
"banana": "banane",
"lemon" : "citron"}Good embeddings enable vector arithmetic.
apple
pomme
banane
citron
banana
lemon
Key
Value
\(:\)
\(:\)
\(:\)
dict_en2fr = {
"apple" : "pomme",
"banana": "banane",
"lemon" : "citron"}
query = "lemon"
output = dict_en2fr[query]lemon
Query
Output
citron
A query comes:
apple
pomme
banane
citron
banana
lemon
Key
Value
\(:\)
\(:\)
\(:\)
Python would complain. 🤯
orange
Query
???
dict_en2fr = {
"apple" : "pomme",
"banana": "banane",
"lemon" : "citron"}
query = "orange"
output = dict_en2fr[query]What if:
Output
apple
pomme
banane
citron
banana
lemon
Key
Value
\(:\)
\(:\)
\(:\)
But we may agree with this intuition:
Query
Key
Value
Output
orange
apple
\(:\)
pomme
banana
\(:\)
banane
lemon
\(:\)
citron
0.1
pomme
0.1
banane
0.8
citron
+
+
0.1
pomme
0.1
banane
0.8
citron
+
+
dict_en2fr = {
"apple" : "pomme",
"banana": "banane",
"lemon" : "citron"}
query = "orange"
output = dict_en2fr[query]What if:
Now, if we are to formalize this idea, we need:
Query
Key
Value
Output
orange
apple
\(:\)
pomme
banana
\(:\)
banane
lemon
\(:\)
citron
0.1
pomme
0.1
banane
0.8
citron
+
+
0.1
pomme
0.1
banane
0.8
citron
+
+
2. calculate this sort of percentages
1. learn to get to these "good" (query, key, value) embeddings.
Query
Key
Value
Output
orange
apple
\(:\)
pomme
0.1
pomme
0.1
banane
0.8
citron
banana
\(:\)
banane
lemon
\(:\)
citron
+
+
orange
orange
0.1
pomme
0.1
banane
0.8
citron
+
+
apple
banana
lemon
orange
very roughly, with good embeddings, getting the percentages can be easy:
apple
banana
lemon
orange
orange
orange
Query
Key
Value
Output
orange
apple
\(:\)
pomme
banana
\(:\)
banane
lemon
\(:\)
citron
orange
orange
pomme
banane
citron
0.1
pomme
0.1
banane
0.8
citron
+
+
0.1
pomme
0.1
banane
0.8
citron
+
+
query compared with keys → dot-product similarity
very roughly, with good embeddings, getting the percentages can be easy:
what about percentages?
softmax
Query
Key
Value
Output
orange
apple
\(:\)
pomme
banana
\(:\)
banane
lemon
\(:\)
citron
orange
orange
pomme
banane
citron
0.1
pomme
0.1
banane
0.8
citron
+
+
pomme
banane
citron
+
+
0.1
0.1
0.8
- query compared with keys → percentages
apple
banana
lemon
orange
orange
orange
Query
Key
Value
Output
orange
apple
\(:\)
pomme
0.1
pomme
0.1
banane
0.8
citron
banana
\(:\)
banane
lemon
\(:\)
citron
+
+
orange
orange
0.8
pomme
0.1
banane
0.1
citron
+
+
0.1
0.1
0.8
pomme
banane
citron
+
+
(very roughly, the attention mechanism does just this "reasonable merging")
- query compared with keys → percentages
- combine values using these percentages as output
softmax
apple
banana
lemon
orange
orange
orange
Outline
- Recap, embedding and representation
- Transformers high-level intuition
- Transformers architecture overview
- (query, key, value) and self-attention
- matrix form
- Multi-head Attention
- (Applications)
Large Language Models (LLMs) are trained in a self-supervised way

- Scrape the internet for unlabeled plain texts.
- Cook up “labels” (prediction targets) from the unlabeled texts.
- Convert “unsupervised” problem into “supervised” setup.
"To date, the cleverest thinker of all time was Issac. "
feature
label
To date, the
cleverest
To date, the cleverest
thinker
To date, the cleverest thinker
was
To date, the cleverest thinker of all time was
Issac
e.g., train to predict the next-word
Auto-regressive
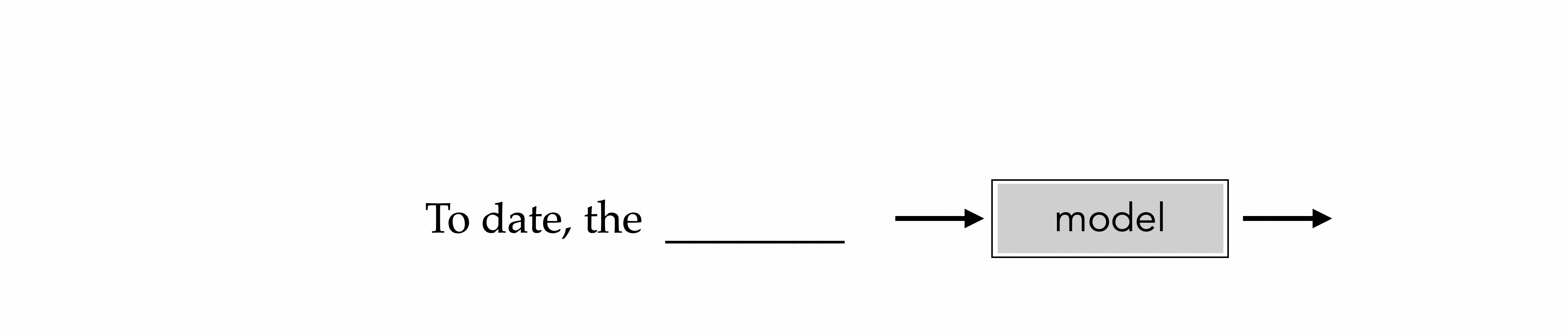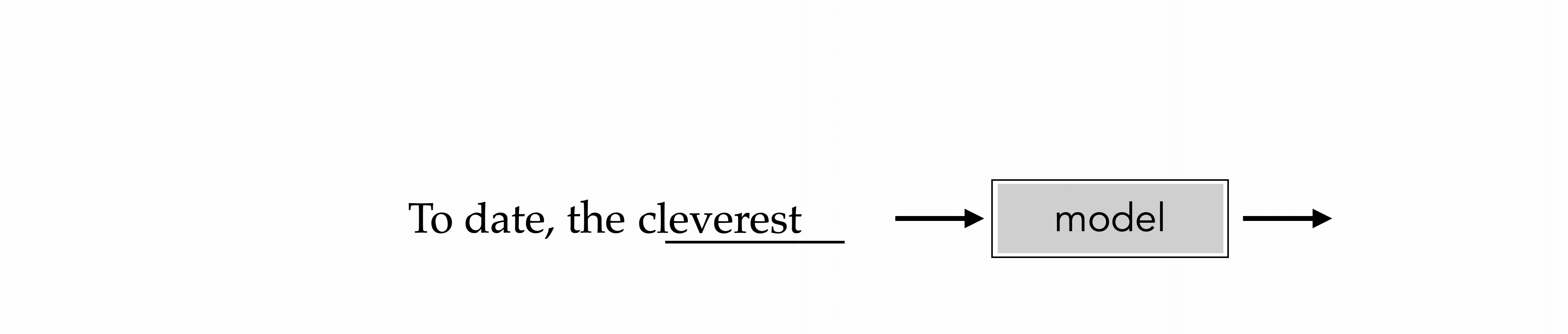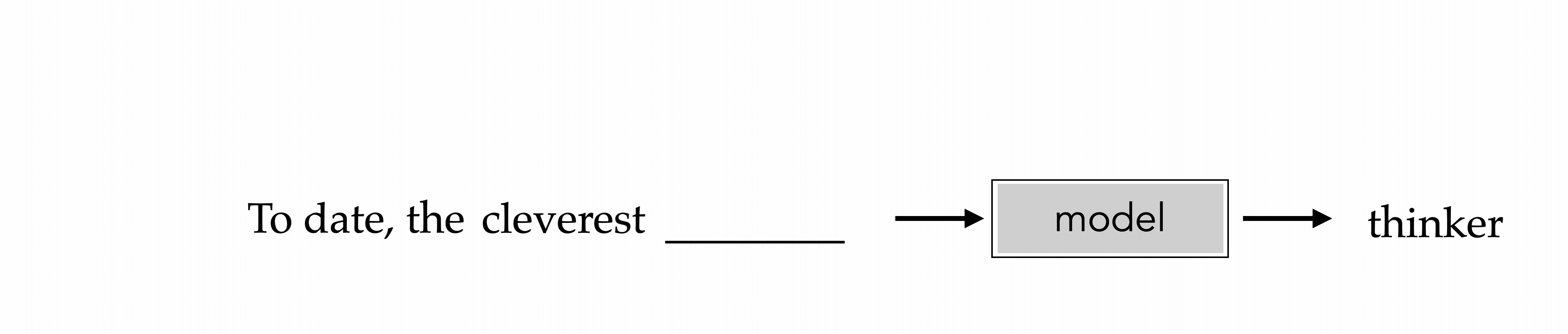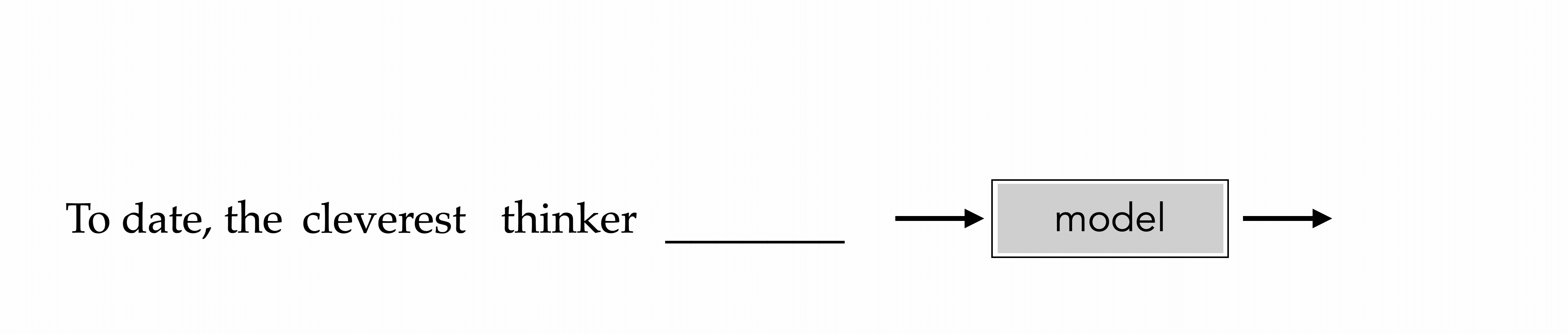
How to train? The same recipe:
- model has some learnable weights
- multi-class classification
[video edited from 3b1b]
[image edited from 3b1b]
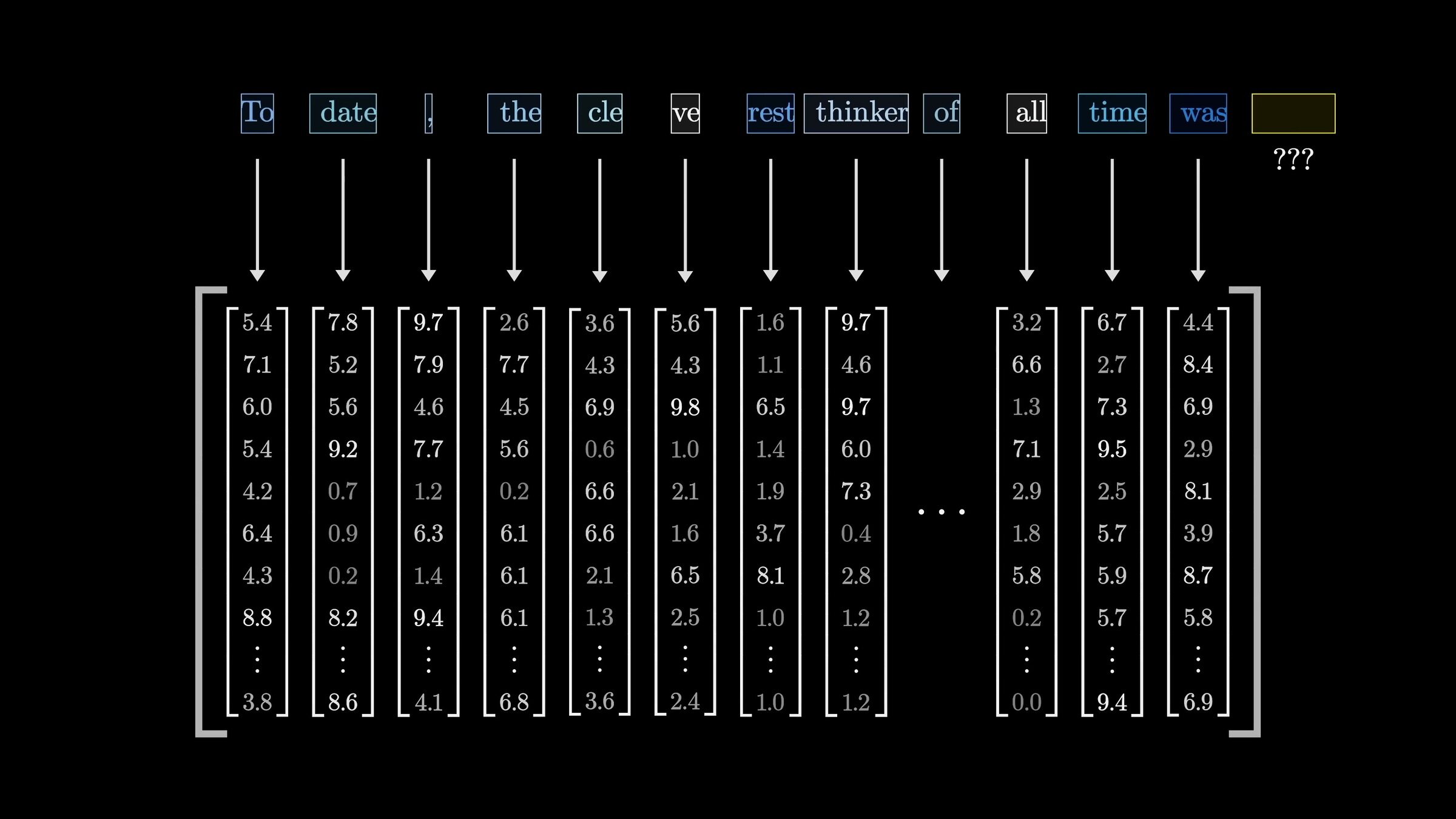
\(n\)
\(d\)
input embedding (e.g. via a fixed encoder)
[video edited from 3b1b]
[video edited from 3b1b]
[image edited from 3b1b]
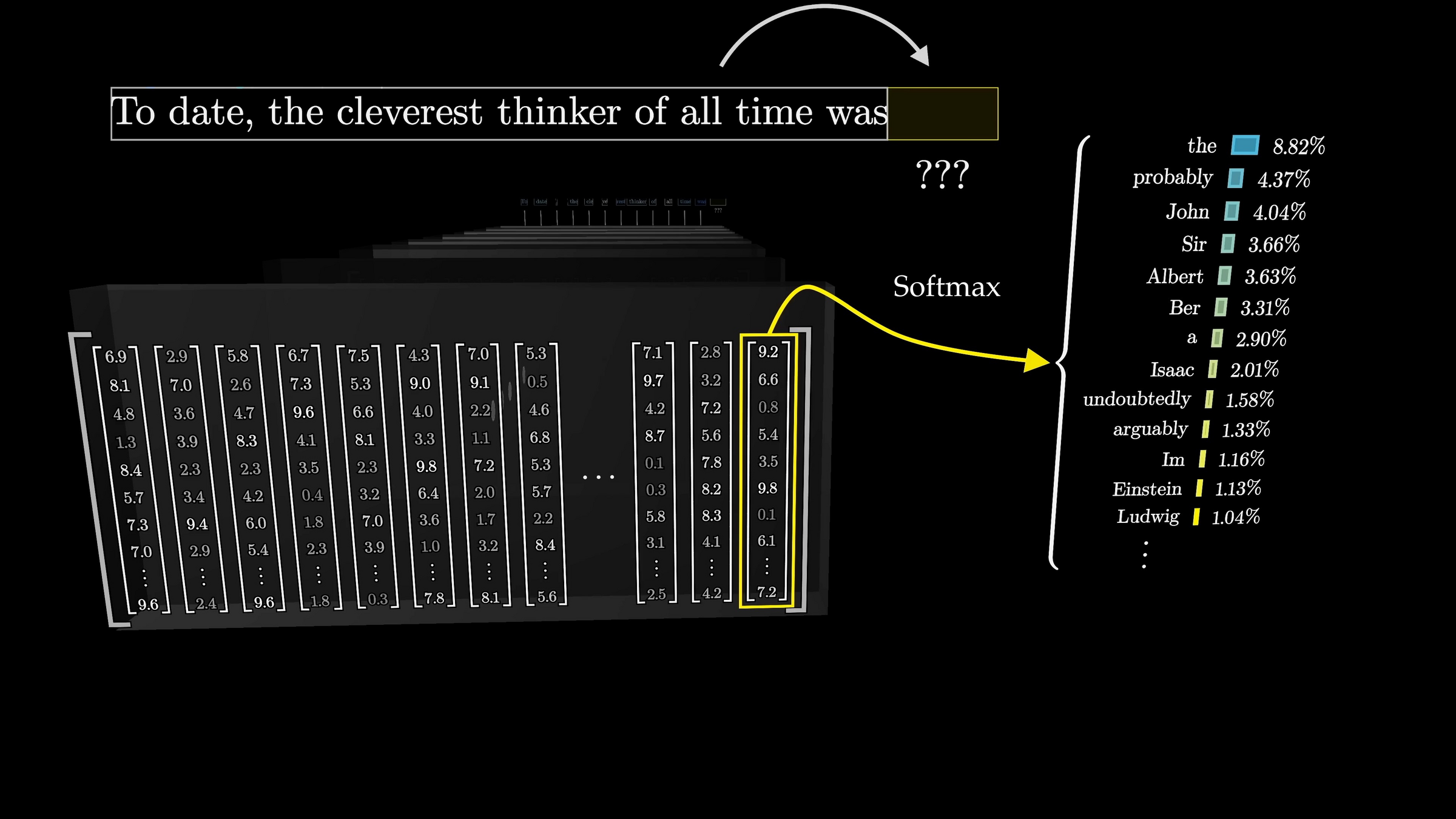
Cross-entropy loss encourages the internal weights update so as to make this probability higher
image credit: Nicholas Pfaff

Generative Boba by Boyuan Chen in Bldg 45
😉
😉
[video edited from 3b1b]
[video edited from 3b1b]
Outline
- Recap, embedding and representation
- Transformers high-level intuition
- Transformers architecture overview
- (query, key, value) and self-attention
- matrix form
- Multi-head Attention
- (Applications)
a
robot
must
obey
Transformer
"A robot must obey the orders given it by human beings ..."
push for Prob("robot") to be high
push for Prob("must") to be high
push for Prob("obey") to be high
push for Prob("the") to be high
distribution over the vocabulary
\(\dots\)
\(\dots\)
\(\dots\)
\(\dots\)
a
robot
must
obey
input embedding
output embedding
\(\dots\)
\(\dots\)
\(\dots\)
transformer block
transformer block
transformer block
\(L\) blocks
\(\dots\)
\(\dots\)
a
robot
must
obey
input embedding
output embedding
\(\dots\)
transformer block
transformer block
transformer block
A sequence of \(n\) tokens, each token in \(\mathbb{R}^{d}\)
\(\dots\)
\(\dots\)
\(\dots\)
\(\dots\)
a
robot
must
obey
input embedding
\(\dots\)
transformer block
output embedding
\(\dots\)
\(\dots\)
\(\dots\)
\(\dots\)
transformer block
transformer block
a
robot
must
obey
input embedding
output embedding
transformer block
self-attention layer
fully-connected network
\(\dots\)
\(\dots\)
\(\dots\)
\(\dots\)
learn
the usual weights
a
robot
must
obey
attention layer
attention mechanism
\((q,k,v)\)
embedding
attention mechanism
input
embedding
a
robot
must
obey
- sequence of \(d\)-dimensional input tokens \(x\)
- learnable weights, \(W_q, W_v, W_k\), all in \(\mathbb{R}^{d \times d_k}\)
- map the input sequence into \(d_k\)-dimensional (\(qkv\)) sequence, e.g., \(q_1 = W_q^Tx_1\)
- the weights are shared, across the sequence of tokens -- parallel processing
Outline
- Recap, embedding and representation
- Transformers high-level intuition
- Transformers architecture overview
-
(query, key, value) and self-attention
- matrix form
- Multi-head Attention
- (Applications)
attention mechanism
a
robot
must
obey
softmax
a
robot
must
obey
softmax
a
robot
must
obey
attention mechanism
softmax
softmax
attention mechanism
softmax
softmax
attention mechanism
softmax
softmax
Outline
- Recap, embedding and representation
- Transformers high-level intuition
- Transformers architecture overview
-
(query, key, value) and self-attention
- matrix form
- Multi-head Attention
- (Applications)
each row sums up to 1
softmax
softmax
softmax
softmax
attention matrix
attention mechanism
attention mechanism
attention mechanism
attention mechanism
attention mechanism
attention mechanism
attention mechanism
Outline
- Recap, embedding and representation
- Transformers high-level intuition
- Transformers architecture overview
- (query, key, value) and self-attention
- matrix form
- Multi-head Attention
- (Applications)
a
robot
must
obey
one attention head
attention mechanism
a
robot
must
obey
attention mechanism
a
robot
must
obey
attention mechanism
attention mechanism
a
robot
must
obey
attention mechanism
attention mechanism
attention mechanism
a
robot
must
obey
attention mechanism
attention mechanism
attention mechanism
a
robot
must
obey
attention mechanism
attention mechanism
attention mechanism
attention mechanism
Each attention head
- can be processed independently and in parallel with all other heads,
- learns its own set of \(W_q, W_k, W_v\),
- creates its own projected \((q,k,v)\) tokens,
- computes its own attention outputs independently,
- processes the sequence of \(n\) tokens simultaneously and in parallel
independent, parallel, and structurally identical processing across all heads and tokens.
a
robot
must
obey
attention mechanism
attention mechanism
attention mechanism
attention mechanism
multi-head attention
a
robot
must
obey
attention mechanism
attention mechanism
attention mechanism
attention mechanism
multi-head attention
a
robot
must
obey
attention mechanism
attention mechanism
attention mechanism
attention mechanism
multi-head attention
all in \(\mathbb{R}^{d}\)
Shape Example
| num tokens | 2 | |
| token dim | 4 | |
| dim | 3 | |
| num heads | 5 |
$$n$$
$$d$$
$$d_k$$
$$H$$
learned
| query proj | |||
| key proj | |||
| value proj | |||
| output proj | |||
| input | - | ||
| query | |||
| key | |||
| value | |||
| attn matrix | |||
| head out. | |||
| output | - |
$$W_q^h$$
$$W_k^h$$
$$W_v^h$$
$$W^o$$
$$Q^h$$
$$K^h$$
$$V^h$$
$$A^h$$
$$Z^h$$
$$d \times d_k$$
$$d\times Hd_k$$
$$n \times d$$
$$n \times d_k$$
$$n \times d_k$$
$$n \times d_k$$
$$n \times n$$
$$n \times d_k$$
$$n \times d$$
$$4 \times 3$$
$$4 \times 15$$
$$2 \times 4$$
$$2 \times 3$$
$$2 \times 3$$
$$2 \times 3$$
$$2 \times 2$$
$$2 \times 3$$
$$2 \times 4$$
$$d \times d_k$$
$$4 \times 3$$
$$d \times d_k$$
$$4 \times 3$$
$$(qkv)$$
Some practical techniques commonly needed when training auto-regressive transformers:

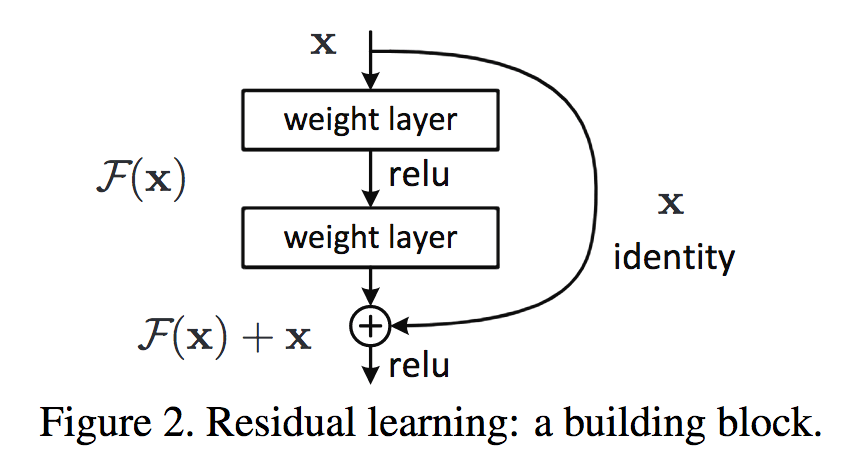

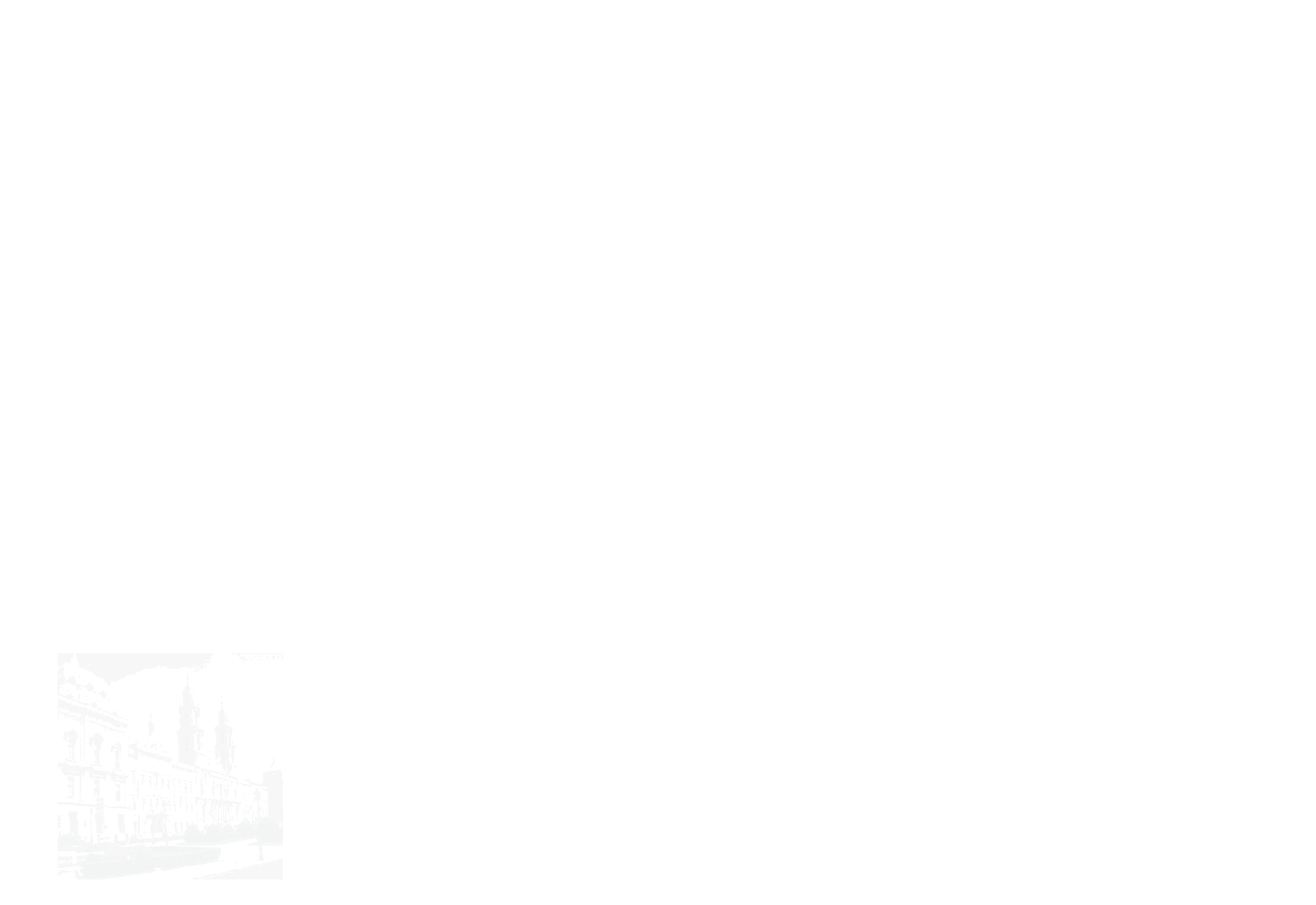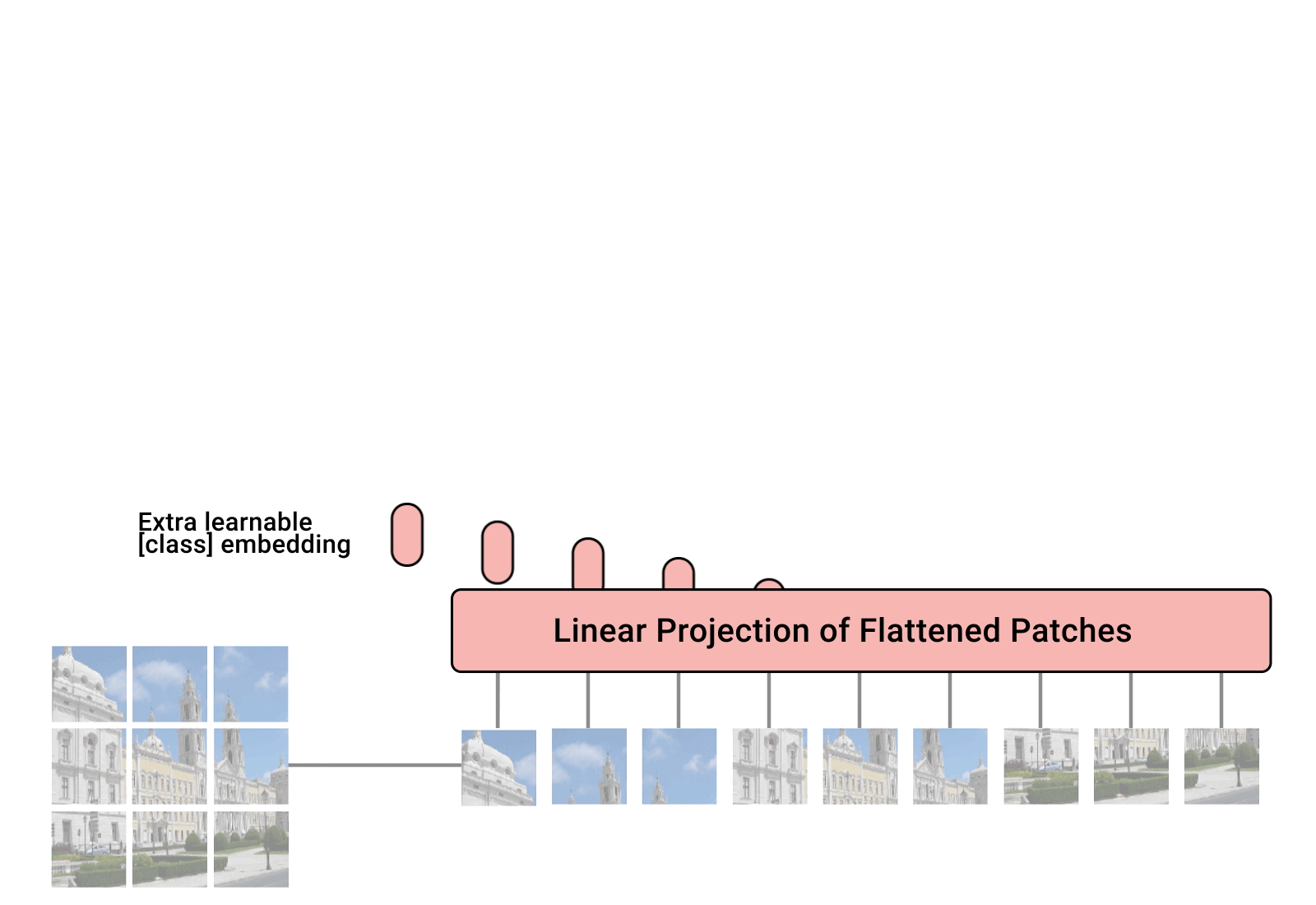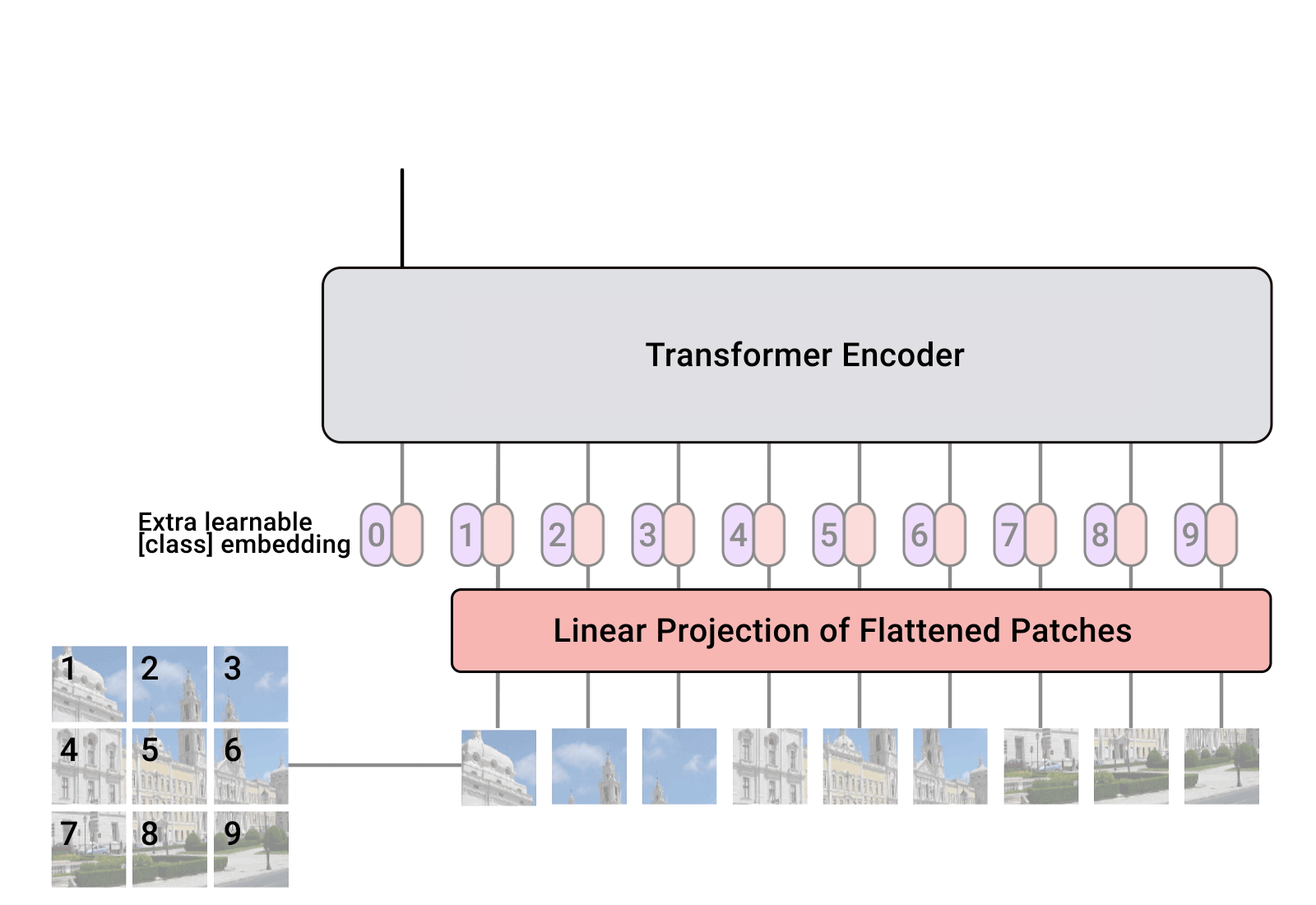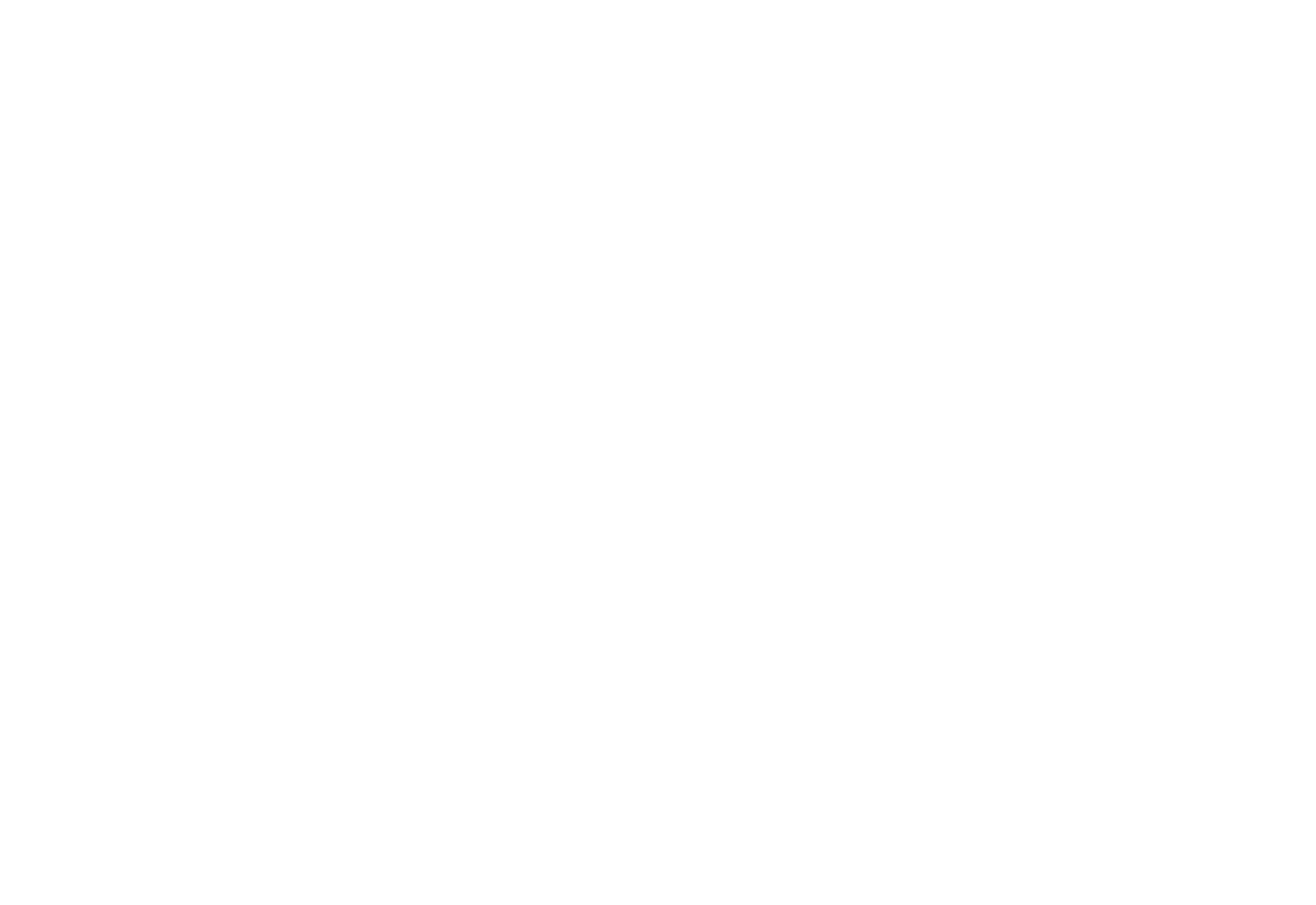
masking
Layer normlization
Residual connection
Positional encoding
applications/comments
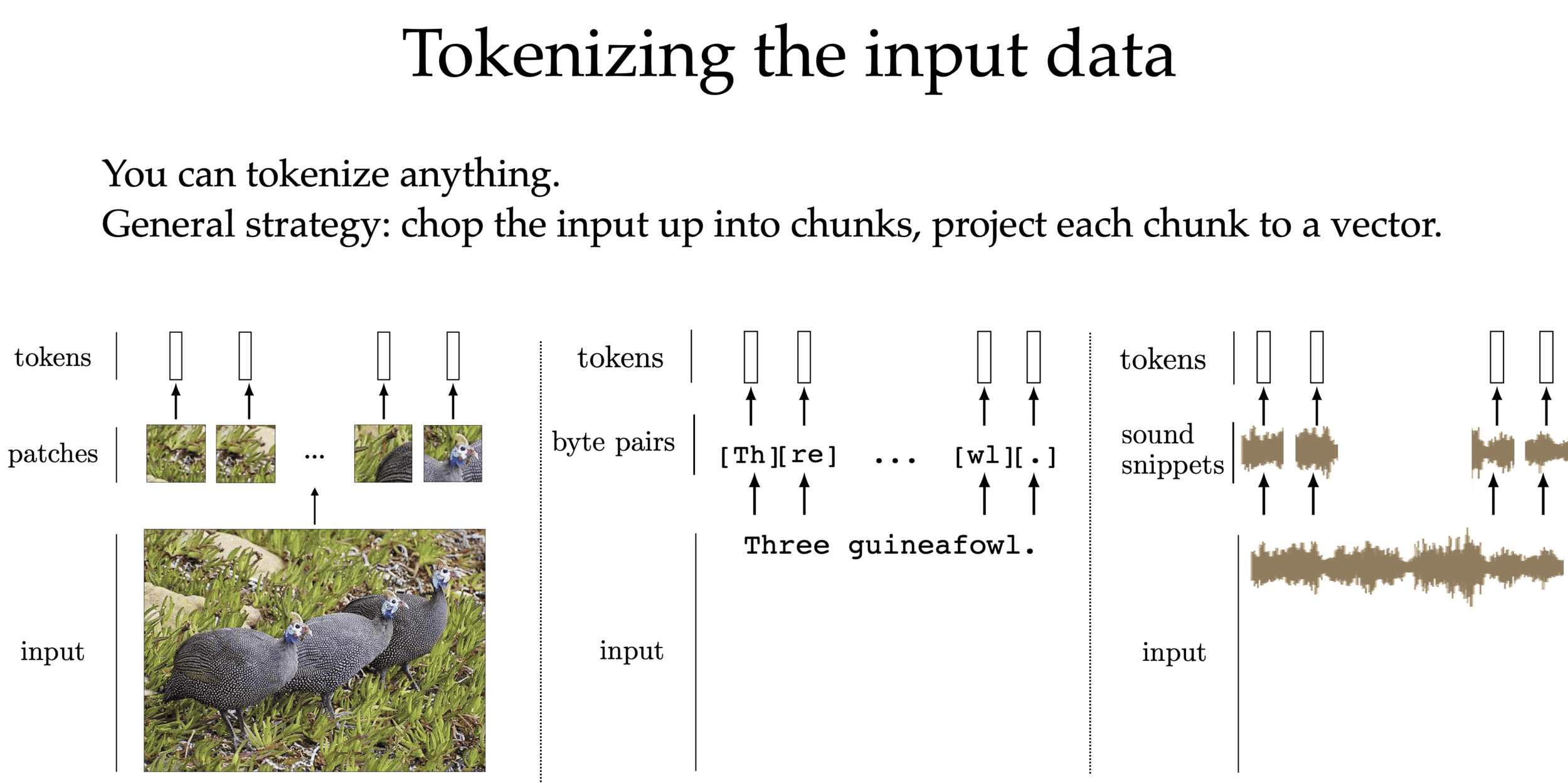
We can tokenize anything.
General strategy: chop the input up into chunks, project each chunk to an embedding
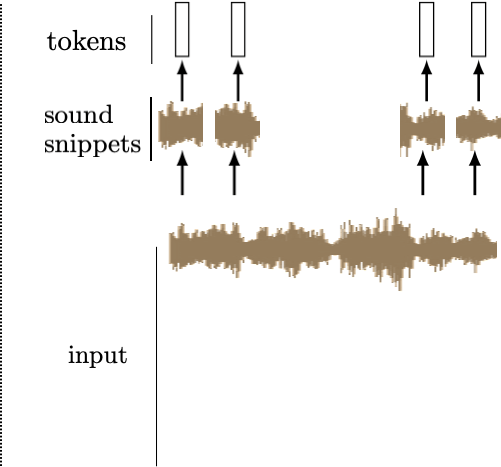
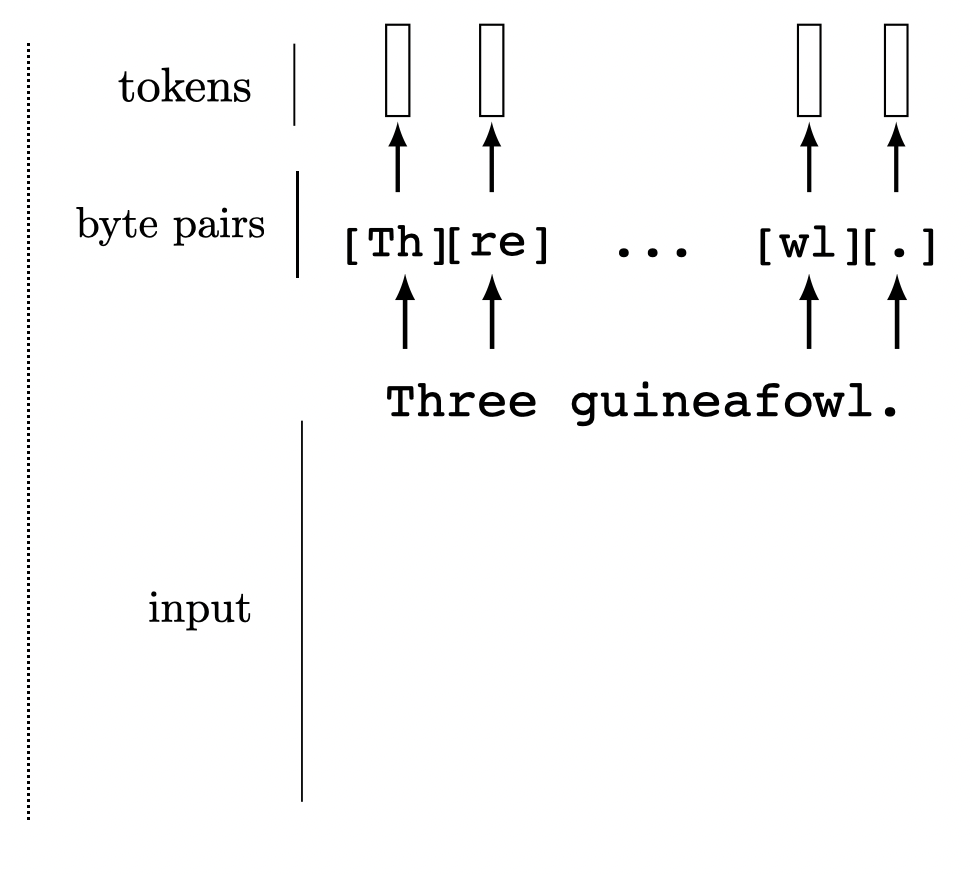
this projection can be fixed from a pre-trained model, or trained jointly with downstream task
[images credit: visionbook.mit.edu]

a sequence of \(n\) tokens
a projection, e.g. via a fixed, or learned linear transformation
each token \(\in \mathbb{R}^{d}\) embedding
[images credit: visionbook.mit.edu]
100-by-100

each token \(\in \mathbb{R}^{400}\)
20-by-20
a sequence of \(n=25\) tokens
suppose just flatten
[images credit: visionbook.mit.edu]
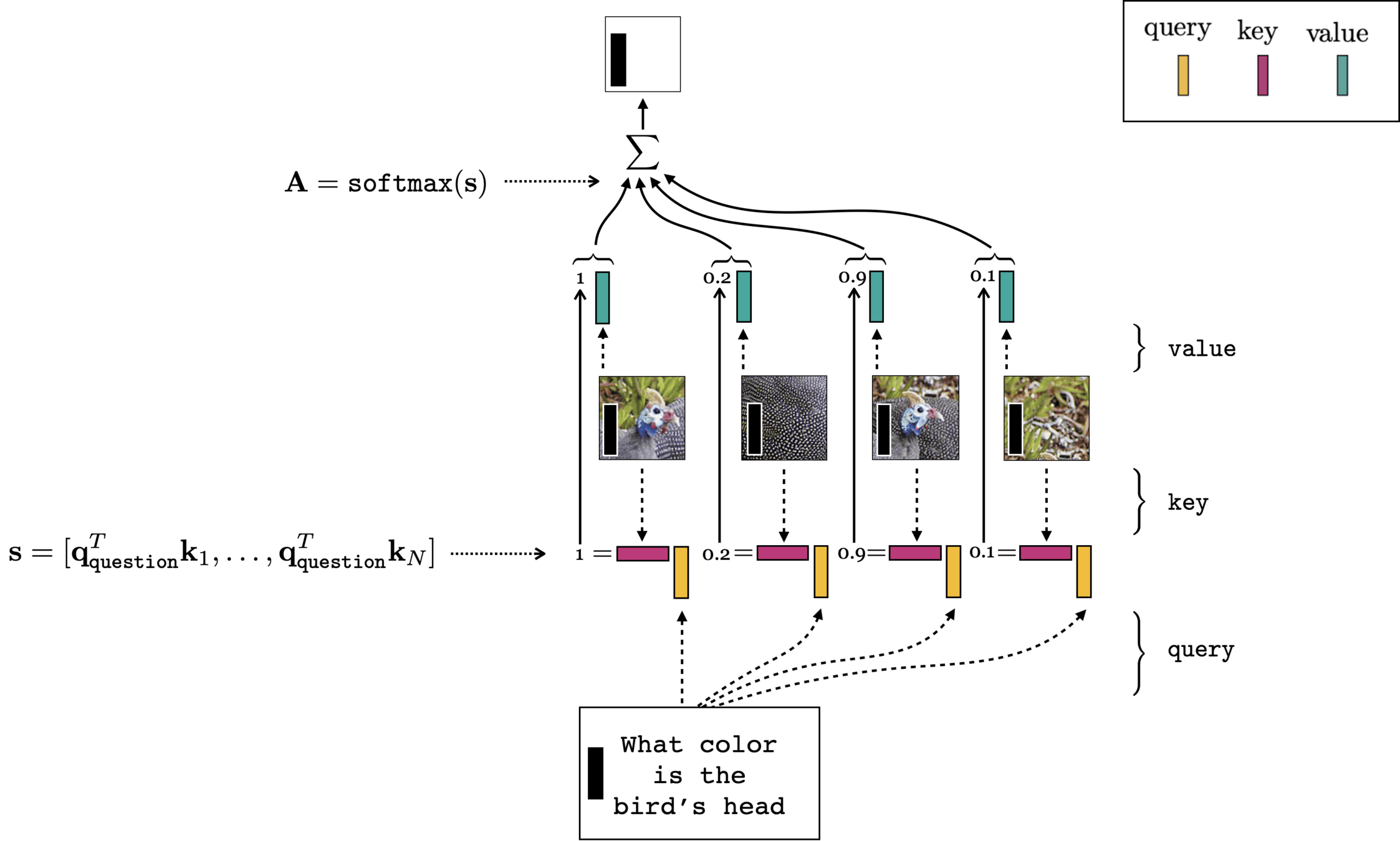
Multi-modality (text + image)
- (query, key, value) come from different input modality
- cross-attention
[images credit: visionbook.mit.edu]
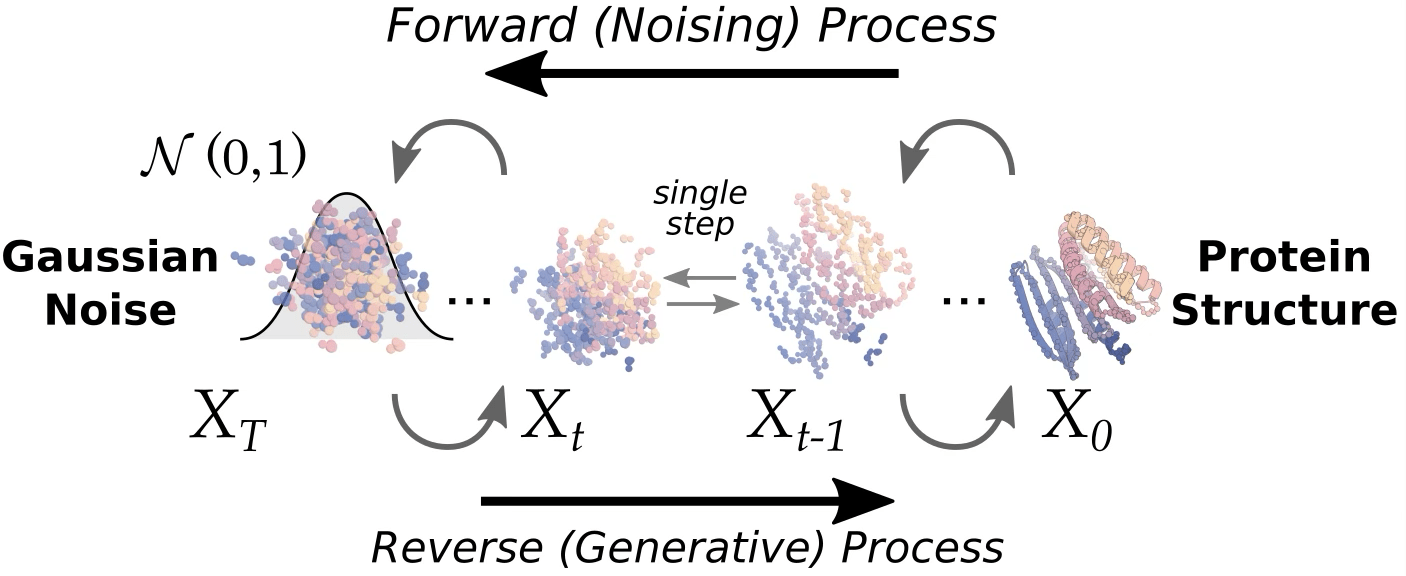
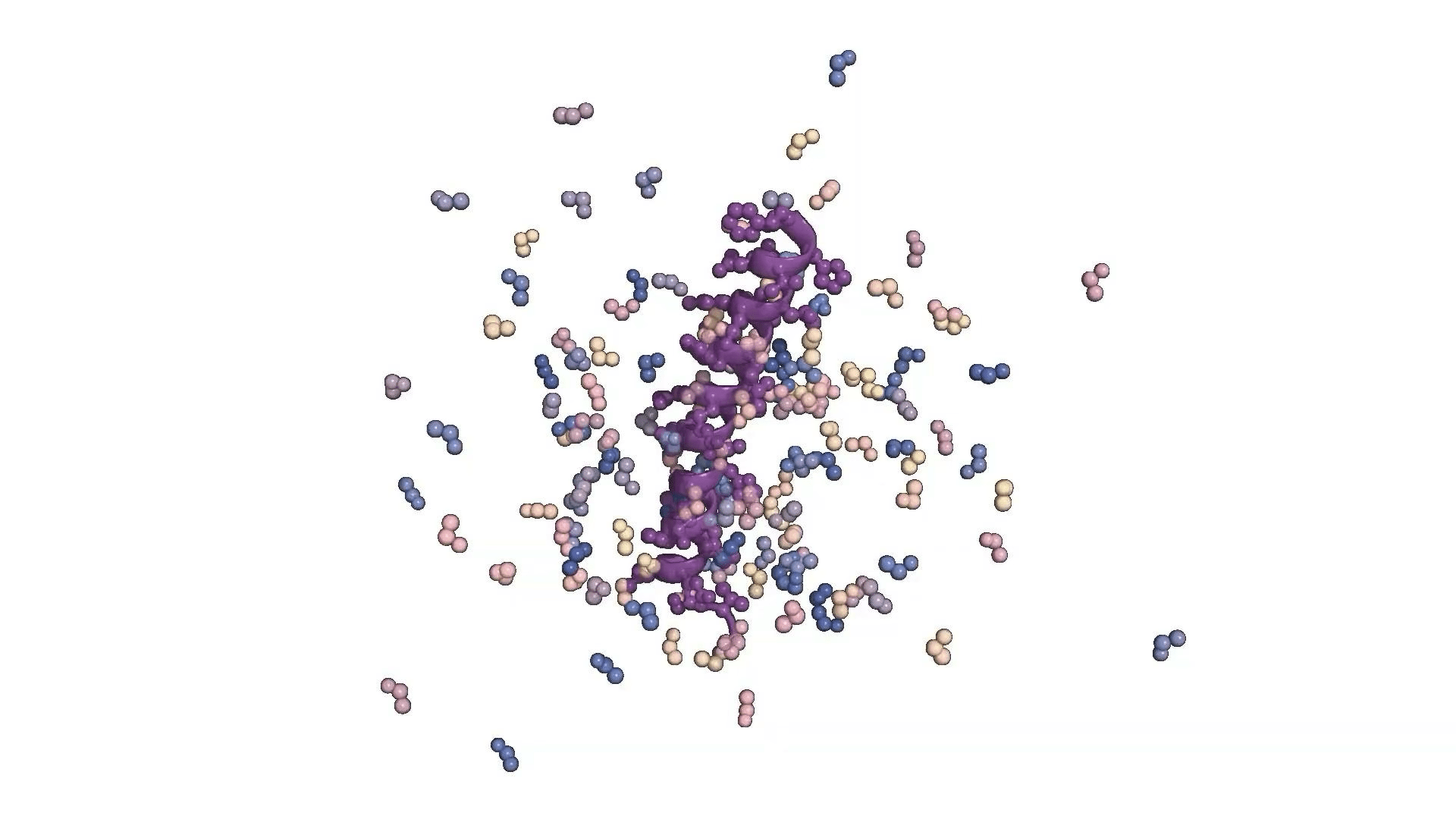
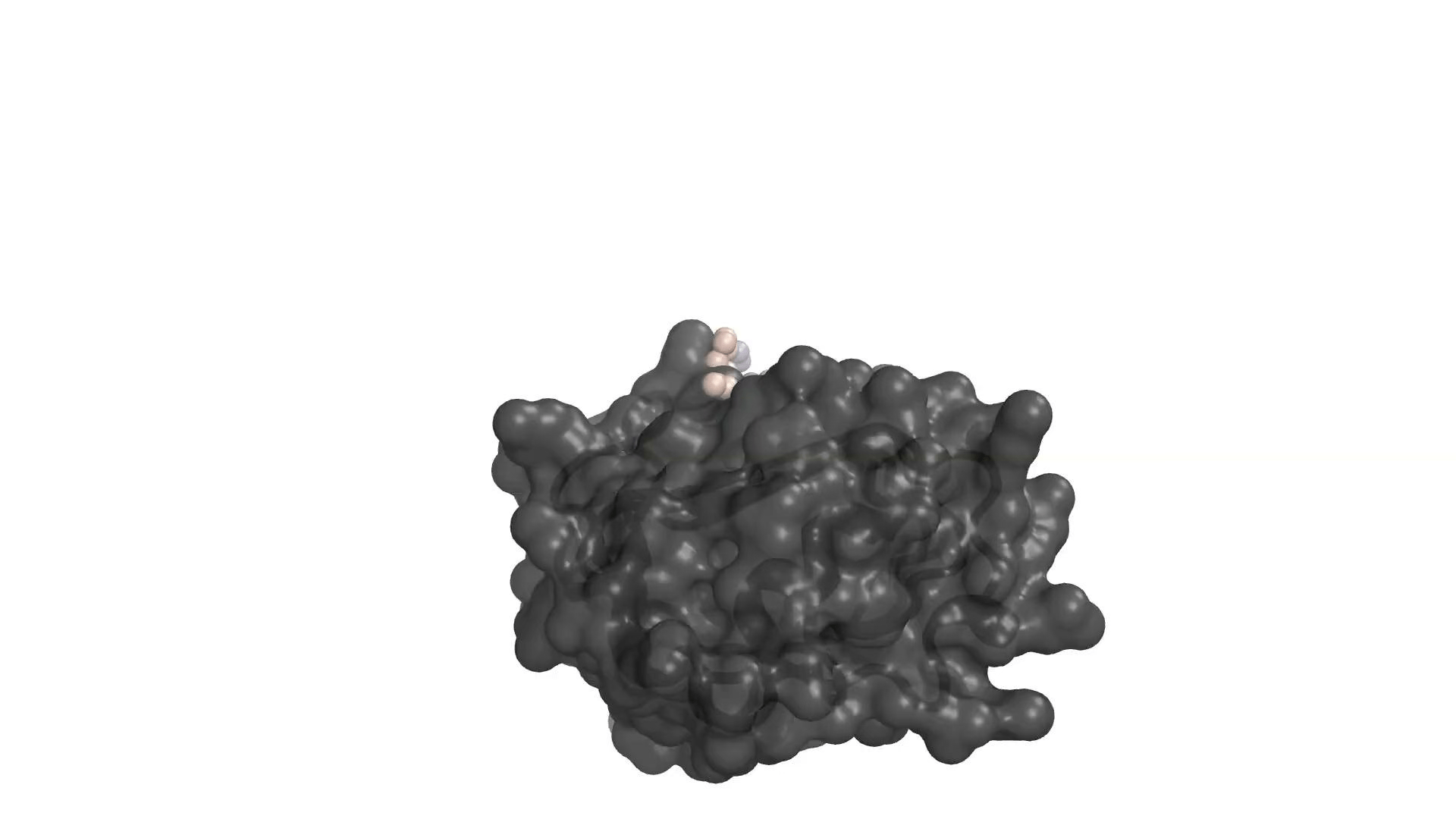
Image/video credit: RFDiffusion https://www.bakerlab.org
[“DINO”, Caron et all. 2021]
Success mode:
Success mode:
[Show, Attend and Tell: Neural Image Caption Generation with Visual Attention. Xu et al. CVPR (2016)]

Failure mode:

[Show, Attend and Tell: Neural Image Caption Generation with Visual Attention. Xu et al. CVPR (2016)]
Failure mode:
[Show, Attend and Tell: Neural Image Caption Generation with Visual Attention. Xu et al. CVPR (2016)]


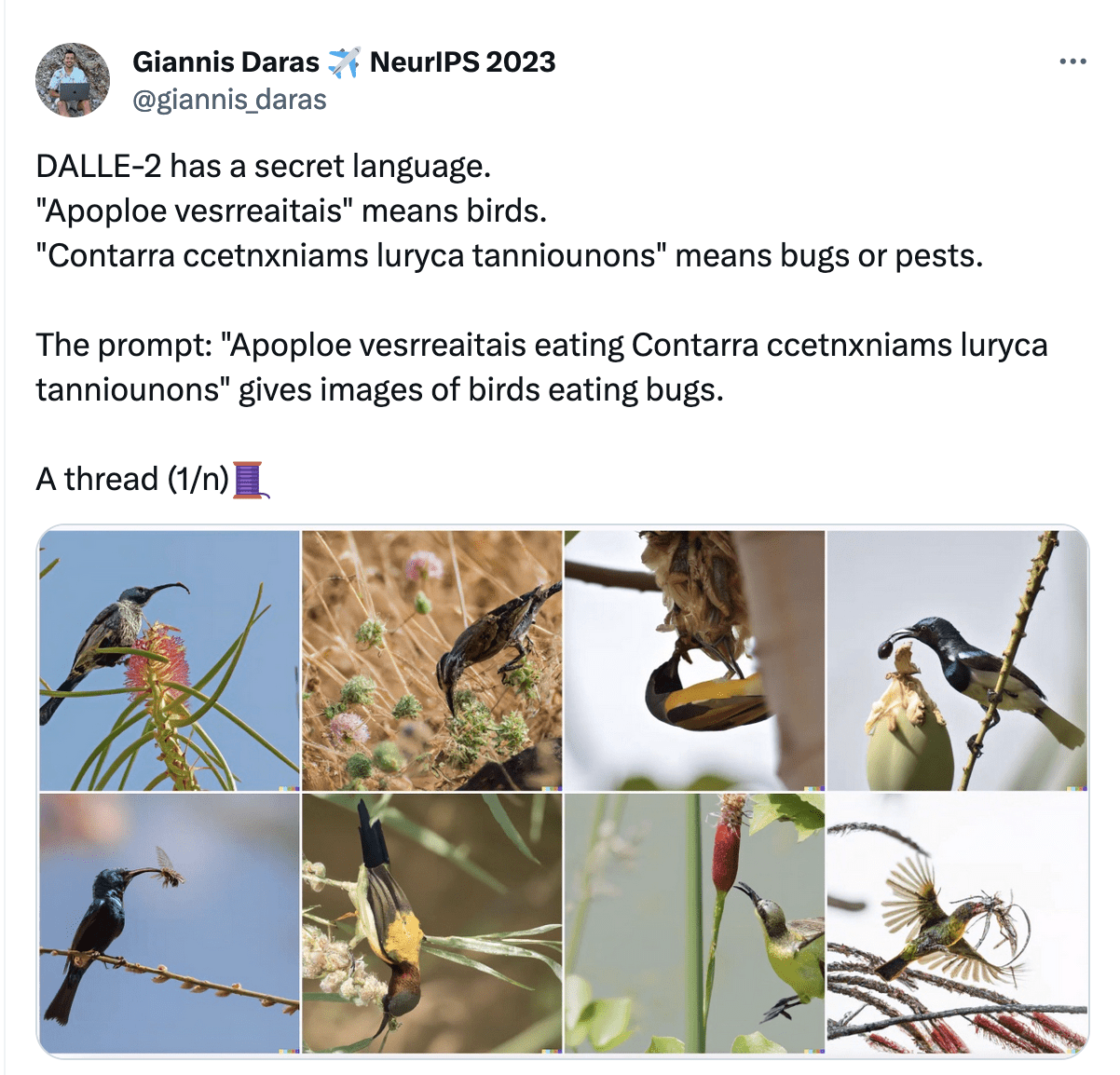
Failure mode:
Summary
- Transformers combine many of the best ideas from earlier architectures—convolutional patch-wise processing, relu nonlinearities, residual connections —with several new innovations, in particular, embedding and attention layers.
- Transformers start with some generic hard-coded embeddings, and layer-by-layer, creates better and better embeddings.
- Parallel processing everything in attention: each head is processed in parallel, and within each head, the \(q,k,v\) token sequence is created in parallel, the attention scores is computed in parallel, and the attention output is computed in parallel.
Thanks!
for your attention!
We'd love to hear your thoughts.