貪心法

greedy method

author: __Shioko

核心想法

貪心的想法

之前提到的枚舉法是透過考慮所有可能的解來獲得最佳解

而貪心法則是不斷做出看起來最好的選擇直接構造出一組解

也因此貪心演算法的時間複雜度通常會比枚舉還要好

硬幣交換問題

考慮以下問題

我們有無限個面額為{1, 5, 10, 50, 100, 500, 1000}的硬幣

請問最少需要用幾個硬幣才能湊出x元(x是任意正整數)

硬幣交換問題

考慮以下問題

我們有無限個面額為{1, 5, 10, 50, 100, 500, 1000}的硬幣

請問最少需要用幾個硬幣才能湊出x元(x是任意正整數)

通常最直覺的想法就是

不斷使用可以用的面額中最大的那個硬幣

硬幣交換問題

考慮以下問題

我們有無限個面額為{1, 5, 10, 50, 100, 500, 1000}的硬幣

請問最少需要用幾個硬幣才能湊出x元(x是任意正整數)

通常最直覺的想法就是

不斷使用可以用的面額中最大的那個硬幣

例如x = 67時會是50 + 10 + 5 + 1 + 1

最少需要5個硬幣

硬幣交換問題

那如果面額稍微改變一下

這個貪心演算法還會奏效嗎?

硬幣交換問題

那如果面額稍微改變一下

這個貪心演算法還會奏效嗎?

答案是不一定會!

我們可以舉出以下的反例

面額{1, 3, 4}, x = 6

剛才的貪心演算法會得出4 + 1 + 1, 需要3個硬幣

但實際上3 + 3, 兩個硬幣才是最佳解

硬幣交換問題

即使很多時候貪心演算法看起來很直覺

但也很有可能會是錯誤的

因此貪心演算法的證明是非常重要的!

證明貪心法的正確性

exchange argument

exchange arguments

在證明貪心演算法的時候

通常會使用叫做"exchange arguments"的一種證明手法

而這個東西的大致架構如下

exchange arguments

第一步: 給你的演算法產出的解和其他的解一個代號

這裡使用A代表貪心法所得出的解, O代表其他任意解

A = \{a_1, a_2, a_3, ..., a_n\}

O = \{o_1, o_2, o_3, ..., o_n\}

exchange arguments

第二步: 比較你的貪心解和其他的解

大致上會有以下兩種作法

如果你的解是要選擇一些元素:

考慮有一個元素不在A裡面但是在O裡面

以及有一個元素在A裡面但是不在O裡面

如果你的解是要考慮選擇的順序:

考慮在O當中有某兩個相鄰元素的順序和在A當中的順序不一樣

exchange arguments

第三步: 交換!

嘗試去證明, 考慮解O的時候,

把一個不在A當中的元素換成在A當中的元素時,

答案一定不會變得更差,

並且可以在不把答案變差的情況下,

從一個任意的解O不斷的交換一些元素得到解A

因此, 任何最佳解都可以透過這樣交換得到一個一樣好的解A

得證貪心演算法構造出的解A是最佳解

exchange arguments

第三步: 交換!

(如果答案是一些選擇的順序)

嘗試去證明, 考慮解O的時候,

有某兩個相鄰元素的順序是和在A的時候不一樣的

而把它們交換回來並不會使答案變差

並且透過一直交換相鄰元素可以得出解A

因此, 任何最佳解都可以透過這樣交換得到一個一樣好的解A

得證貪心演算法構造出的解A是最佳解

exchange arguments

總整:

第一步: 給貪心解及其他任意解一個編號

第二步: 比較兩個解不同的地方

第三步: 證明你能把任意解換成你的貪心解, 且不會使答案變差

聽起來可能會有一點抽象

接下來會再討論一些經典的貪心問題

並實際地使用這個證明手法讓你們更了解整個證明的方式

排程問題

給定n個活動的開始時間及結束時間

請找到一種排程的方法使得你可以參加盡量多的活動

(不能同時參加兩個以上的活動)

排程問題

給定n個活動的開始時間及結束時間

請找到一種排程的方法使得你可以參加盡量多的活動

(不能同時參加兩個以上的活動)

範例:

n = 4

活動A : [1, 3]

活動B : [2, 5]

活動C : [3, 9]

活動D : [6, 8]

一些"貪心"的想法

算法1:

在能挑的活動中從持續時間最短的活動開始挑

一些"貪心"的想法

反例:

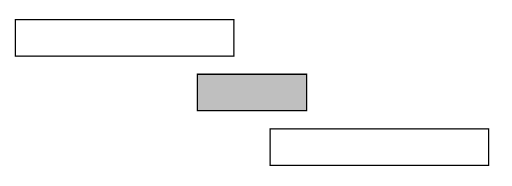
在這個例子中

從最短的活動開始選只能選到一個

但是最佳解是選擇旁邊兩個活動

一些"貪心"的想法

算法2:

在能挑的活動中從最早開始的活動開始挑

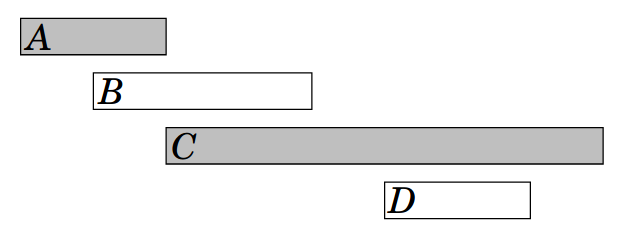
一些"貪心"的想法

反例:

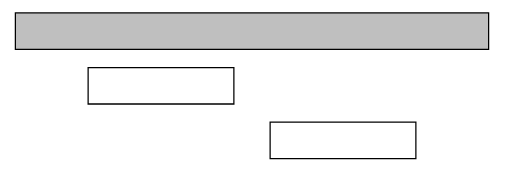
在這個例子中選擇先開始的活動明顯不是最佳解

一些"貪心"的想法

算法3:

在能挑的活動中從最早結束的活動開始挑

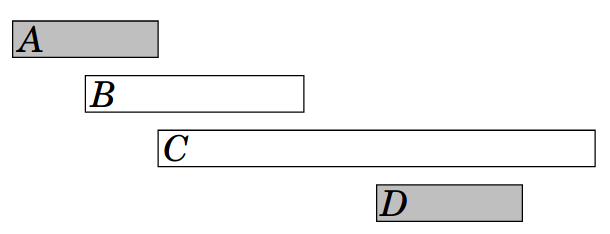
一些"貪心"的想法

雖然聽起來很不直覺

不過這個算法是正確的

至於要怎麼透過exchange argument證明呢?

我們先假設不斷選最早結束活動產出的最佳解是A

正確性的證明

證明:

考慮某個最佳解O選了x個活動(依照結束時間排序)

O = \{o_1, o_2, o_3, ..., o_x\}

並假設o_1不是第一個結束的活動(a_1)

那我們一定可以把它換成第一個結束的活動

(因為o_1的結束時間比a_1還要晚)

正確性的證明

證明:

考慮最佳解O選了x個活動(依照結束時間排序)

O = \{o_1, o_2, o_3, ..., o_x\}

同樣地, 假設o_2也不是第二個結束的活動(a_2)

我們也可以用相同的理由把它換成a_2

所以我們可以一直用同樣的手法把某個最佳解O

的元素換掉, 直到O長得和A一模一樣

正確性的證明

最後發現我們一定可以把任何最佳解換成算法產出的解A

且答案不會變差

因此, 我們就可以知道算法產出的解A一定是最佳解

正確性的證明

最後發現我們一定可以把任何最佳解換成算法產出的解A

且答案不會變差

因此, 我們就可以知道算法產出的解A一定是最佳解

想要自己實作看看的可以丟這題:

CSES - Movie Festival

https://cses.fi/problemset/task/1629

CF-1495A

Diamond Miner

CF-1495A Diamond Miner

有n個礦工在平面上的y座標軸上,

n個鑽石原礦在x座標軸上

並且每個礦工都要用鉤子挖一個鑽石原礦,

當位在(a, b)的礦工伸出鉤子挖位在(c, d)的鑽石原礦時,

會消耗的體力

\sqrt{(a - c)^2 + (b - d)^2}

請問若採取最好的策略,

所有礦工消耗的總體力和最少是多少?

n \le 10^5, -10^8 \le x, y \le 10^8

CF-1495A Diamond Miner

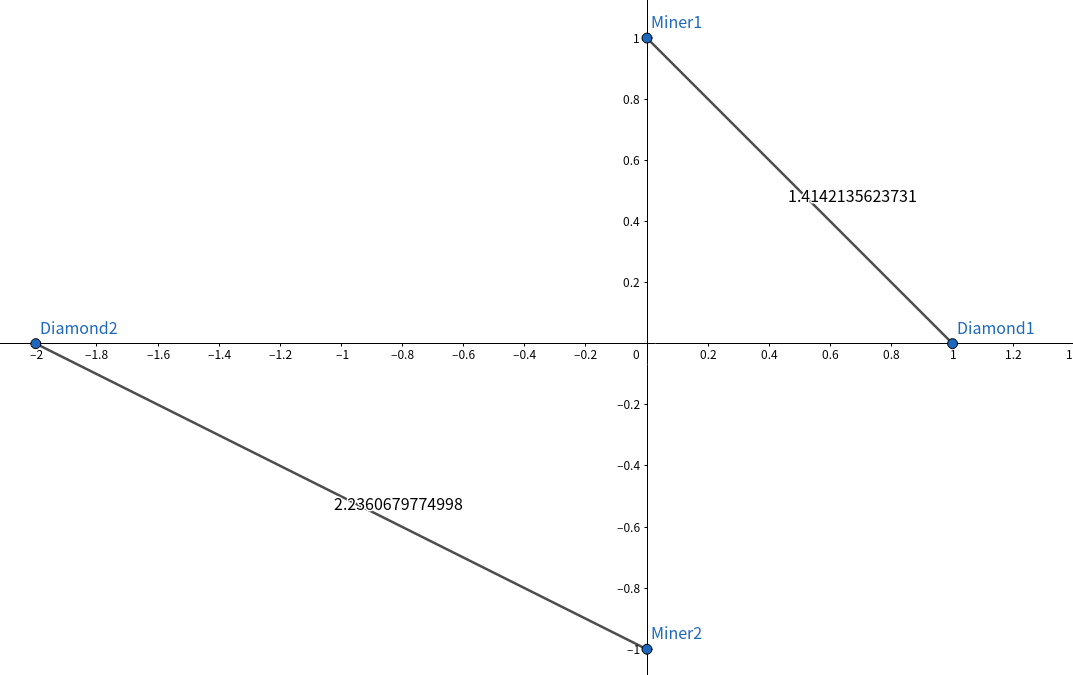
範例:

n = 2

礦工位置: (0, 1), (0, -1)

鑽石原礦位置: (-2, 0), (1, 0)

CF-1495A Diamond Miner

首先先觀察一下

可以發現其實座標軸的正負並不重要

因為當你把礦工從(0, -y)移到(0, y)時

他和所有鑽石原礦的距離都不會改變

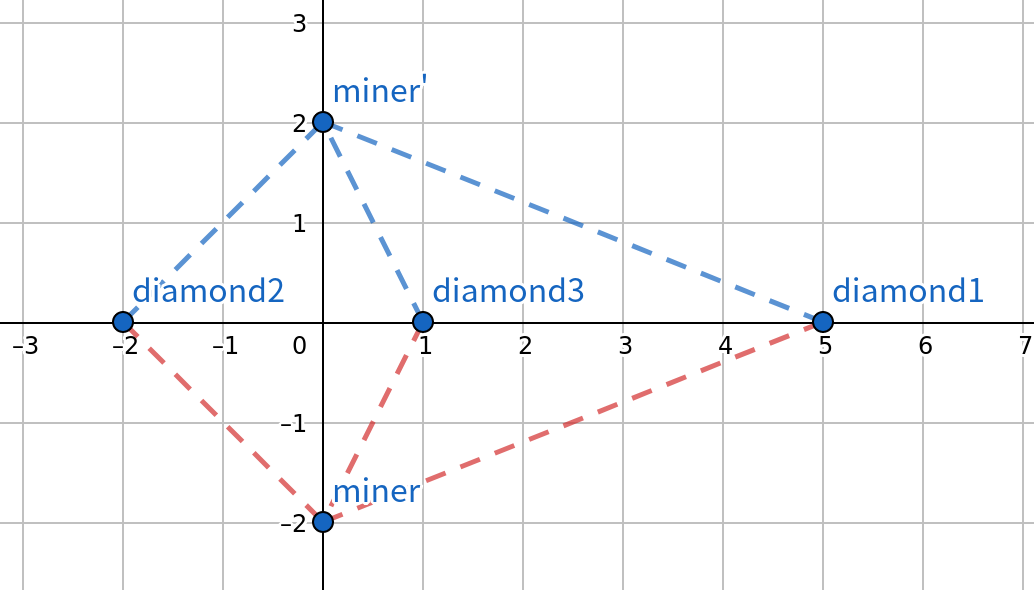
CF-1495A Diamond Miner

同理, 我們也可以把鑽石原礦從(-x, 0)搬到(x, 0)

所以我們就只需要考慮第一象限上的礦工和鑽石原礦了

CF-1495A Diamond Miner

再做一點觀察

可以發現如果有兩個礦工伸出的鉤子交叉了

則當你交換它們要挖的鑽石原礦之後

總體耗費的體力會減少

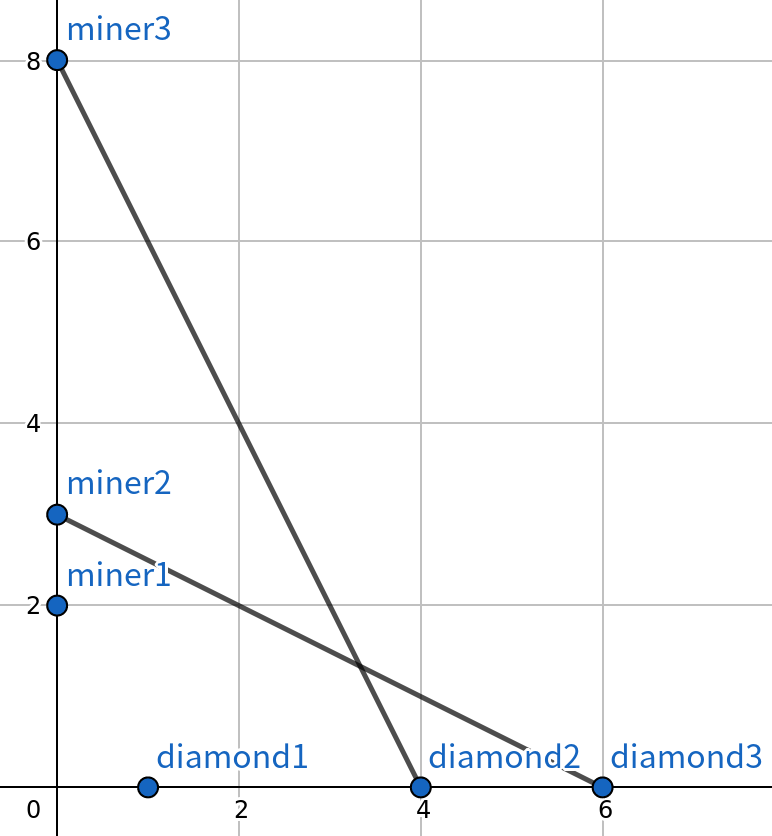
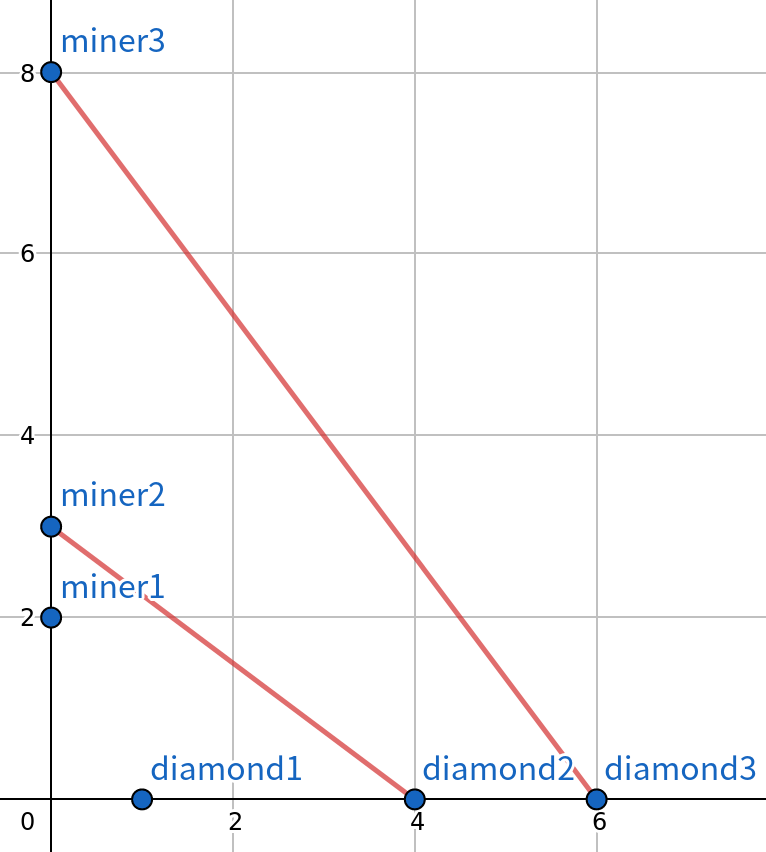
CF-1495A Diamond Miner

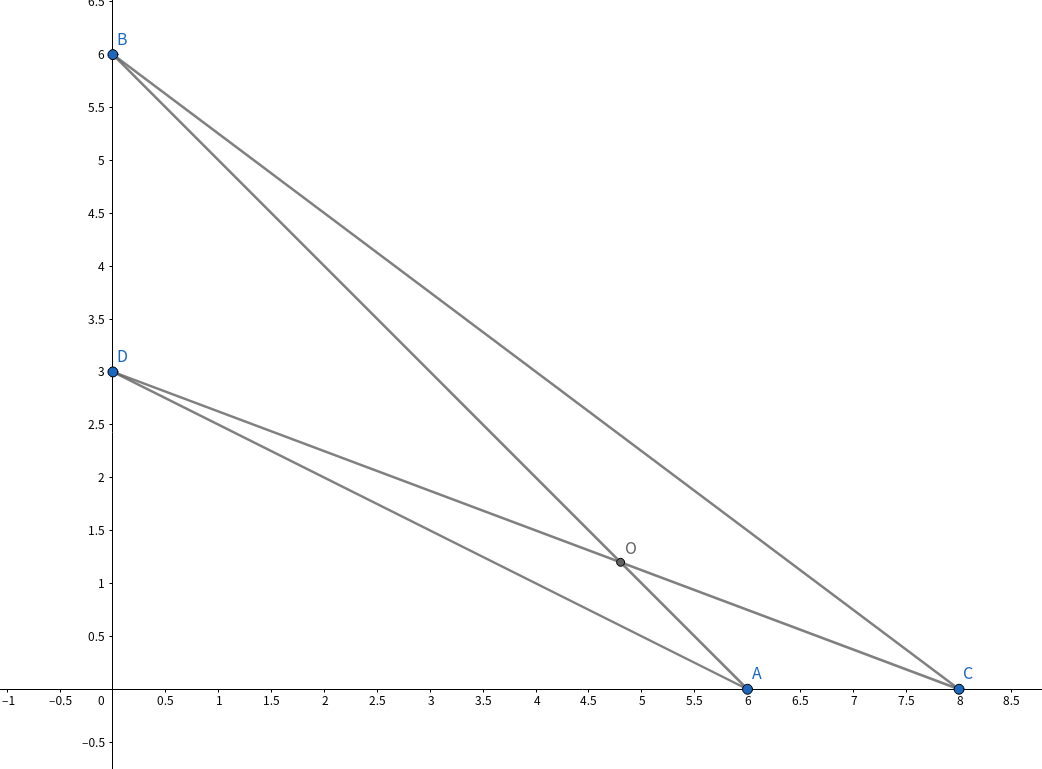
證明:

考慮三角不等式可知

OA + OD > AD, OB + OC > BC

因此可推出AB + CD > AD + BC

CF-1495A Diamond Miner

也就是說, 如果某種解有出現交叉的話,

把交叉的部份變成沒有交叉就可以使答案變小

CF-1495A Diamond Miner

也就是說, 如果某種解有出現交叉的話,

把交叉的部份變成沒有交叉就可以使答案變小

想到這裡, 你可能就會想出某種"貪心"的作法:

CF-1495A Diamond Miner

也就是說, 如果某種解有出現交叉的話,

把交叉的部份變成沒有交叉就可以使答案變小

想到這裡, 你可能就會想出某種"貪心"的作法:

"讓所有線段都不產生交叉"

CF-1495A Diamond Miner

也就是說, 如果某種解有出現交叉的話,

把交叉的部份變成沒有交叉就可以使答案變小

想到這裡, 你可能就會想出某種"貪心"的作法:

"讓所有線段都不產生交叉"

那該如何證明這樣的貪心是對的呢?

CF-1495A Diamond Miner

證明:

考慮任意一個有交叉出現的解O(不一定是最佳解)

O = \{o_1, o_2, o_3, ..., o_n\}

其中o_i代表第i個礦工所挖的鑽石原礦編號

CF-1495A Diamond Miner

證明:

考慮任意一個有交叉出現的解O(不一定是最佳解)

O = \{o_1, o_2, o_3, ..., o_n\}

其中o_i代表第i個礦工所挖的鑽石原礦編號

假設o_i和o_j是其中一個出現交叉的地方

那透過交換o_i和o_j, 我們可以得到一個更佳解

因此有交叉的解O不可能是最佳解

CF-1495A Diamond Miner

證明:

對於任意有出現交叉的解O, 都不可能是最佳解

因此最佳解不會有任何交叉出現,

而這樣的解只有一種:

x座標第一小的礦工挖y座標第一小的鑽石原礦

x座標第二小的礦工挖y座標第二小的鑽石原礦

...

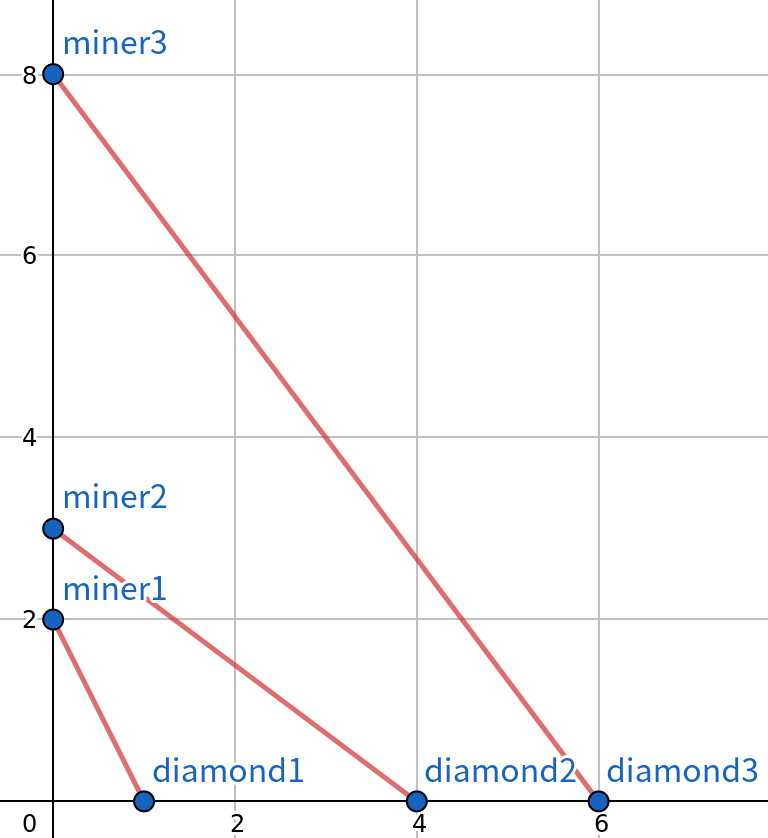
CF-1495A Diamond Miner

最後實作的部份

只需要把礦工跟鑽石原礦分別用x座標, y座標排序

並一個一個計算它們消耗的體力即可

總體時間複雜度O(nlgn)

Link: https://codeforces.com/problemset/problem/1495/A

結語

貪心演算法雖然通常很快

但是要想出並證明一個貪心演算法並不是一件簡單的事

想要學好如何使用貪心演算法的話

多證明自己想出來的貪心算法的正確性一定會有幫助的!

習題

CSES - Tower

https://cses.fi/problemset/task/1073

CSES - Tasks And Deadlines

https://cses.fi/problemset/task/1630

CSES - Movie Festival II

https://cses.fi/problemset/task/1632

classic

CodeForces Educational Round 17 pB - USB vs. PS/2

https://codeforces.com/contest/762/problem/B

CodeForces Round #773 (Div.1) pA - Great Sequence

https://codeforces.com/problemset/problem/1641/A

basic

如果覺得以上這些太簡單一下就秒掉的話

下一頁還有更有挑戰性的題目喔~

AtCoder ARC073 pE - Ball Coloring

https://atcoder.jp/contests/arc073/tasks/arc073_c

CodeForces Round #190 (Div.1) pB - Ciel and Duel

https://codeforces.com/contest/321/problem/B

advanced

參考資料

1. outline for greedy algorithm - exchange arguments

(http://www.cs.cornell.edu/courses/cs482/2007su/exchange.pdf)

2. competitive programmer's hand book

(https://usaco.guide/CPH.pdf#page=67)

延伸學習

USACO guide - greedy algorithm with sorting

https://usaco.guide/silver/greedy-sorting?lang=cpp

AP325 P.108 貪心演算法與掃描線演算法

https://drive.google.com/drive/folders/10hZCMHH0YgsfguVZCHU7EYiG8qJE5f-m