Network
Models
Minimal Spanning Tree
Spanning Tree:
A subgraph T of a undirected graph G = (V,E) is a spanning tree of G if it is a tree and contains every vertex of G.
MST:
Given a connected graph, find a spanning tree of minimum weight

Minimal Spanning Tree
The idea is to start with an empty graph and try to add edges one at a time, always making sure that what is built remains acyclic.
And if we are sure every time the resulting graph always is a subset of some minimum spanning tree, we are done.
MST: Algorithms
Greedy
Prim
Kruskal
MST: Prim
Start by picking any vertex to be the root of the tree.
While the tree does not contain all vertices in the graph find shortest edge leaving the tree and add it to the tree .
MST: Prim
Step 0: Choose any element r; set S = {r} and S = . .Take r as the root of our spanning tree.)
Step 1: Find a lightest edge such that one endpoint is in S and the other is in V \ S . Add this edge to A and its (other) endpoint to S.
Step 2: If V \ S = , then stop & output (minimum) spanning tree (S, A), otherwise go to Step 1


MST: Kruskal
-
Let G = (V, E) be the given graph, with | V| = n
-
Start with a graph T = (V,) consisting of only the vertices of G and no edges. This can be viewed as n connected components, each vertex being one connected component.
-
Arrange E in the order of increasing costs
-
for (i = 1, in - 1, i + +)
{ Select the next smallest cost edge;
if (the edge connects two different connected components)
add the edge to T;
}
MST: Example
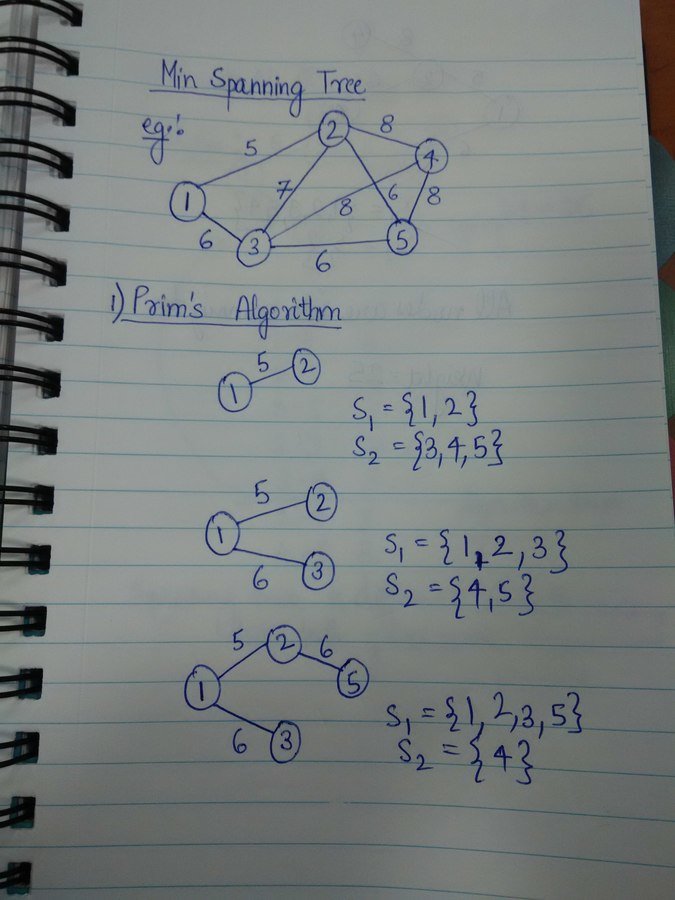
MST: Example
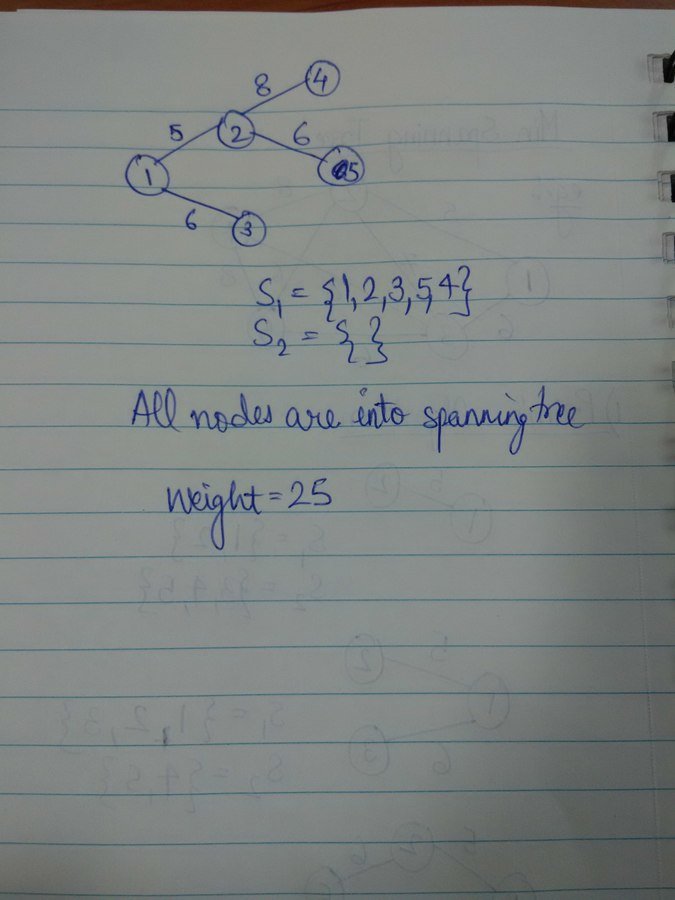
MST: Example

Maximal Flow Technique
Nodes
Arcs
Source
Sink
Capacity
Flow

Maximum Flow Problem
Find the maximum flow that can be sent through the arcs of the network from some specified node called the source, to a second specified node called the sink
Exhaustion of Paths Algorithm
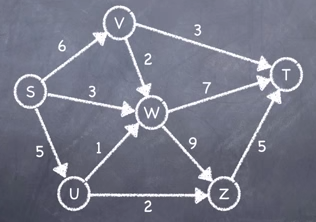
Step 1: Choose one possible route between S & T and identify the edge with the smallest capacity
Exhaustion of Paths Algorithm
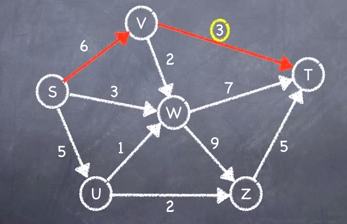
Record the smallest capacity.
Subtract this number from each capacity value on that path.
Exhaustion of Paths Algorithm
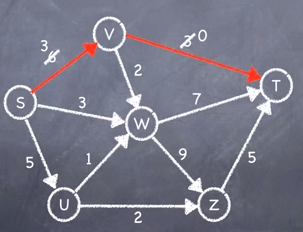
This is the updated capacity for each arc.
Exhaustion of Paths Algorithm
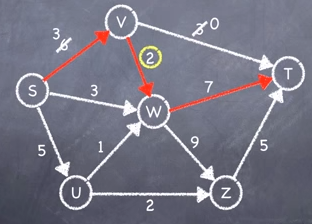
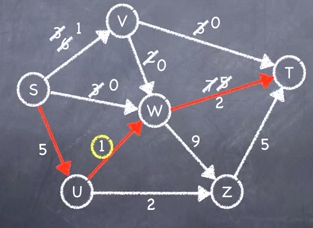
Step 2: Choose another route and repeat step 1, recording the smallest capacity again.
Exhaustion of Paths Algorithm
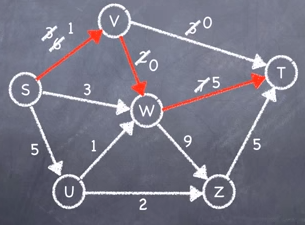
Subtracting and updating
Exhaustion of Paths Algorithm
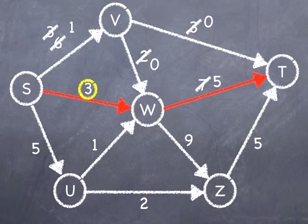
Step 3: Choose another route and repeat step 1 until all routes have been exhausted.
Exhaustion of Paths Algorithm
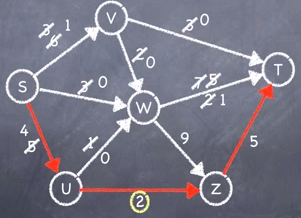
Exhaustion of Paths Algorithm
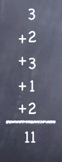
Step 4: Add all the capacities that were recorded in each step.
11 is the maximum flow of the network between S & T.
Labelling Algorithm
Node label:
( Pf , ± i) : {Pf = Potential ± flow at node i
{i= node
Arc label:
( f ,CAP) : {f = Actual flow through arc. {CAP=Capacity through arc
Labelling Algorithm
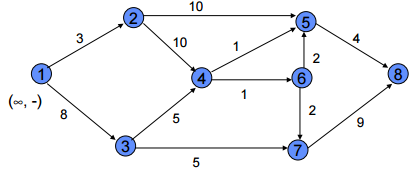
Labelling Algorithm

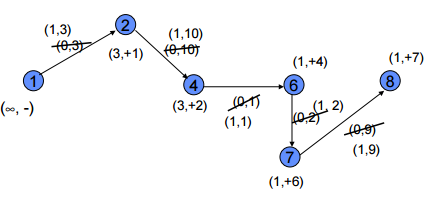
Labelling Algorithm

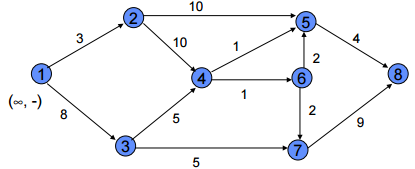
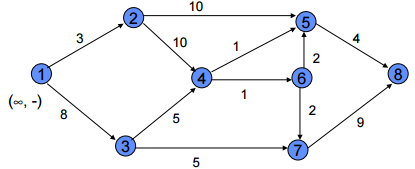
Labelling Algorithm
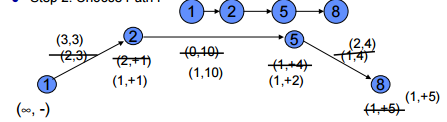

Labelling Algorithm
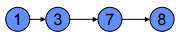
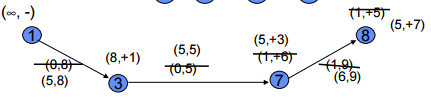

Labelling Algorithm

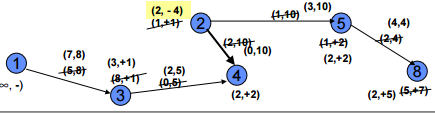

Labelling Algorithm
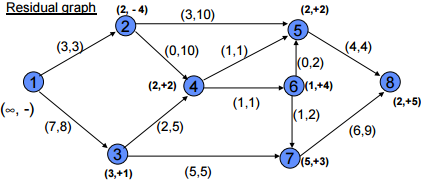
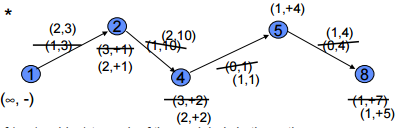
Problem Question
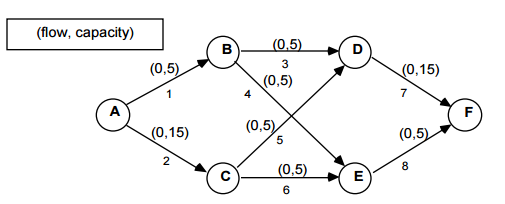
Max Flow-Min Cut
s-t Cut: is defined w.r.t. two distinguished nodes s and t and is a cut [S, Š] satisfying the property that s ∈ S and t ∈ Š.
A cut is a set of arcs which when deleted from the network, disconnects the source completely from the sink
Max Flow-Min Cut
Capacity of a cut
Min Cut
Theorem: The maximum value of the flow from a source node s to a sink node t in a capacitated network equals the minimum capacity among all the s-t cuts.
Operations Management Applications
Product Distribution System
Supply Chain Management
Maximum flow of orders through a job shop
References
https://www.youtube.com/watch?v=sxyCzzUuXLo
https://www.cse.ust.hk/~dekai/271/notes/L07/L07.pdf
http://www.cs.princeton.edu/courses/archive/spr04/cos226/lectures/maxflow.4up.pdf
http://www.me.utexas.edu/~jensen/methods/net.pdf/netmaxf.pdf
http://www.acsu.buffalo.edu/~nagi/courses/684/6.maxflow.pdf
Thank you!
Kamal
Karan
Natasha
Shreya
Tarun




