What we will be discussing today!

• Tail call optimization

• Memoization            

Using Fibonacci Sequence

Why Recursion!

• Looks elegant
• Mirroring the problem definition
• Needs to understand the problem

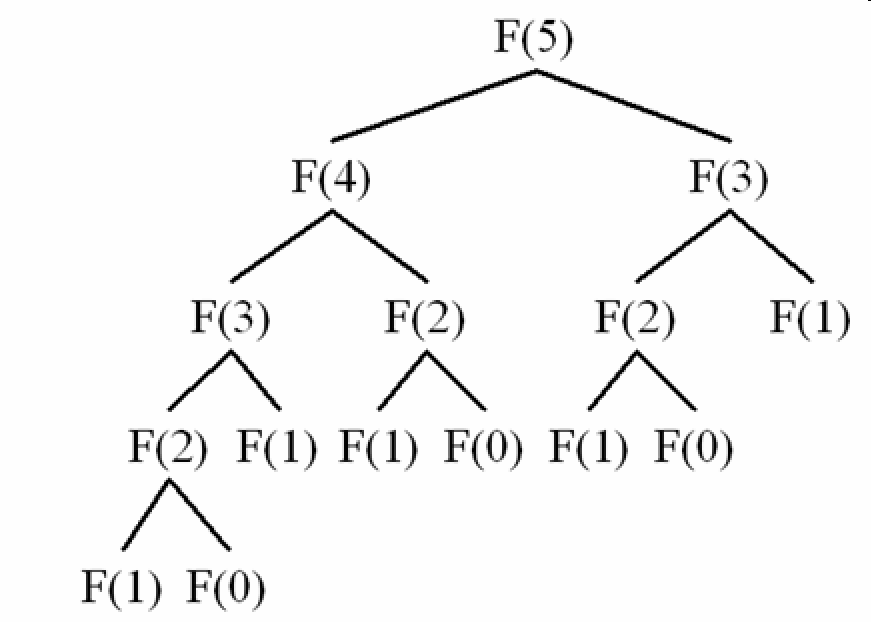
Why function is getting slower!

F(5) = 1

F(4) = 1

F(3) = 2

F(2) = 3

All these increases the time and space are taken by program exponentially.

Let's solve this using mathematical induction!

General rescue to tail recursion:

- tail call optimization

- tail call elimination

- Memoization            

Using Memoization !

f(5)

f(1)              f(0)

f(2)               f(1)

f(3)              f(2)                    

f(4)                  f(3)

Formation and calling of call stack

Algo :

def fib(n):
    if n <= 1
        return n
    if n is in memory:
        return F(n)
    else:
        F(n) <---F(n-1) + F(n-2)
        Save F(n) in memory
        return F(n)

Will reduces time complexity relatively

Using tail call optimization!

(Let's do some code)

What are Continuations!

- Representation of the control flow of your program at any point in       time, essentially the stack

- Allow you to literally "jump" to different places in your code

-They are a low-level primitive that gives you control over execution flow,            allowing you implement everything from resumable exceptions to coroutines.

fibonacci(5, 0, 1) => fibonacci(4, 1, 1) => fibonacci(3, 2, 1) => fibonacci(2, 3,2) => fibonacci(1, 5, 3)

 -Entire computation is done inline.                                                                                                      

-Recursion doesn't keep any state in the function - everything is carried forward in the arguments

Optimization using continuations