COMP2521

Data Structures & Algorithms

Week 5.2

Graph Implementations

Author: Hayden Smith 2021

In this lecture

Why?

Different graph implementations have different pros and cons, and we should try and understand the difference

What?

Array of edges graph
Adjacency Matrix graph
Adjacency List graph

Properties of Graphs

Terminology: |V| and |E| (cardinality) normally written just as V and E

A graph with V vertices has at most V(V - 1) / 2 edges

The ratio E:V can vary considerably:

If E is closer to V^2, the graph is dense
If E is closer to V, the graph is sparse

Thinking about these things may help us decide on an appropriate data structure

Graph Representations

There are many ways to represent the same graph. E.G. The same graph could be represented these ways:

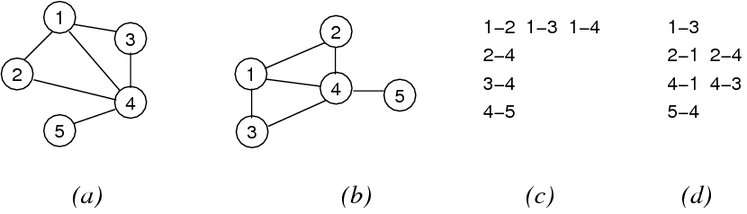
Graph Representations

There are 3 key different graph implementations we will discuss:

Array of Edges

Explicit representation as list of (v,w) vertex pairs

Adjacency Matrix

Edges defined by presence value in V*V matrix

Adjacency List

Edges defined by entries in array of V lists

Array-of-edges

Stored as an array of Edges (i.e. array of vertex pairs)

Space efficient
Adding/deleting: Mildly complex
Lookup: Mildly complex

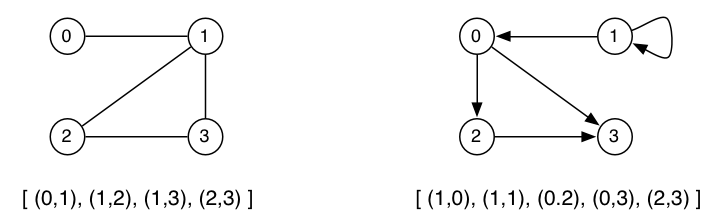
For directed graphs, the ordering of vertices within an edge pair denote direction

Array-of-edges Implementation

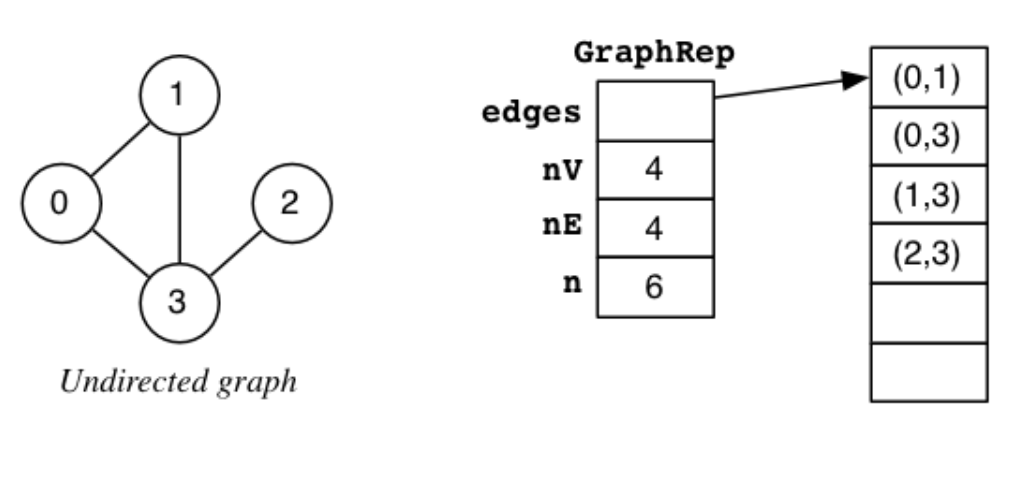
typedef struct GraphRep {
   Edge *edges; // array of edges
   int   nV;    // #vertices (numbered 0..nV-1)
   int   nE;    // #edges
   int   n;     // size of edge array
} GraphRep;

Array-of-edges Pseudocode

newGraph(V):
    g = new Graph with V verticies
    g.nV = V   // #vertices (numbered 0..V-1)
    g.nE = 0   // #edges
    allocate enough memory for g.edges[]
    return g

insertEdge(g,(v,w)):
  i=0
  while i < g.nE ∧ g.edges[i] ≠ (v,w):
     i = i + 1
  if i = g.nE: // (v,w) not found
     g.edges[i] = (v,w)
     g.nE = g.nE + 1

removeEdge(g,(v,w)):
  i = 0
  while i < g.nE ∧ g.edges[i] ≠ (v,w):
     i = i + 1
  if i < g.nE: // (v,w) found
     g.edges[i] = g.edges[g.nE-1]
     g.nE = g.nE - 1

showEdges(g):
  for all i=0 to g.nE-1:
    (v,w) = g.edges[i]
    print v"—"w

Array-of-edges Implementation

Full implementation in Graph-array-edges.c

Array-of-edges, Cost Analysis

Storage: O(E)
Operations:
- Initialisation: O(1)
- Insert edge: O(E)
- Delete edge: O(E)
- Search: O(E)
Other factors:
- If array is full on insert, realloc - still O(E) amortized
- Maintaining edges in order will allow for O(log(E)) binary search lookup

Adjacency Matrix

Stored as a 2D array (i.e. table) of edges. Easy to implement. Not memory efficient for sparse graphs.

For undirected graphs, the table is a mirror about the diagonal

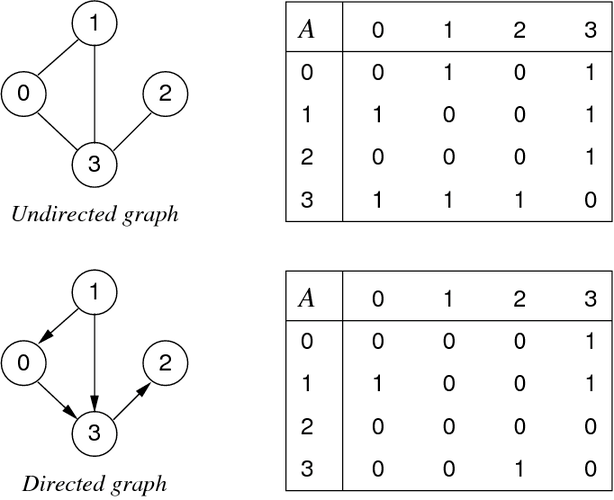
Adjacency Matrix Implementation

typedef struct GraphRep {
   int  **edges; // adjacency matrix
   int    nV;    // #vertices
   int    nE;    // #edges
} GraphRep;

Adjacency Matrix Pseudocode

newGraph(V):
  g.nV = V   // #vertices (numbered 0..V-1)
  g.nE = 0   // #edges
  allocate memory for g.edges[][]
  for all i,j=0..V-1:
     g.edges[i][j] = 0   // false
  return g

insertEdge(g,(v,w)):
  if g.edges[v][w] = 0: // (v,w) not in graph
    g.edges[v][w]=1    // set to true
    g.edges[w][v]=1
    g.nE=g.nE+1

removeEdge(g,(v,w)):
  if g.edges[v][w] ≠ 0:  // (v,w) in graph
    g.edges[v][w]=0       // set to false
    g.edges[w][v]=0
    g.nE=g.nE - 1

showEdges(g):
  for all i=0 to g.nV-1:
    for all j=i+1 to g.nV-1:
      if g.edges[i][j] ≠ 0 then
        print i"—"j

Adjacency Matrix Implementation

Full implementation in Graph-adj-matrix.c

Adjacency Matrix, Cost Analysis

Storage: O(V^2)
- If the graph is sparse, most space is wasted
Operations:
- Initialisation: O(V^2)
- Insert edge: O(1)
- Delete edge: O(1)
- Search: O(1)
Other factors:
- For undirected graphs, the matrix is repeated about a diagonal axis. We can have a coefficient improvement in time complexity if we only store on one half of the diagonal

Adjacency List

Stored as an array of linked lists. Each element of the array corresponds to a vertex, each node on that linked list is an edge connected to that vertex.

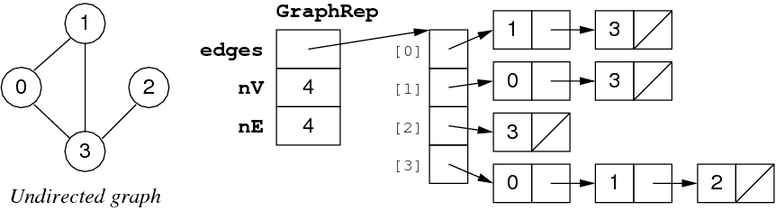
Adjacency List Implementation

typedef struct GraphRep {
   Node **edges;  // array of lists
   int    nV;     // #vertices
   int    nE;     // #edges
} GraphRep;

// Assumes we also have
typedef struct Node {
   Vertex v;
   struct Node *next;
} Node;
// with operations inLL, insertLL, deleteLL, freeLL

Adjacency List Pseudocode

newGraph(V):
  g.nV = V   // #vertices (numbered 0..V-1)
  g.nE = 0   // #edges
  allocate memory for g.edges[]
  for all i=0..V-1:
    g.edges[i]=newList()  // empty list
  return g

insertEdge(g,(v,w)):
  if not ListMember(g.edges[v],w):
    // (v,w) not in graph
    ListInsert(g.edges[v],w)
    ListInsert(g.edges[w],v)
    g.nE=g.nE+1

removeEdge(g,(v,w)):
  if ListMember(g.edges[v],w):
    // (v,w) in graph
    ListDelete(g.edges[v],w)
    ListDelete(g.edges[w],v)
    g.nE=g.nE-1

showEdges(g):
  for all i=0 to g.nV-1:
    for all v in g.edges[i]:
      if i < v:
        print i"—"v

Adjacency List Implementation

Full implementation in Graph-adj-list.c

Adjacency List, Cost Analysis

Storage: O(V + E)
Operations:
- Initialisation: O(V)
- Insert edge: O(V)
- Delete edge: O(V)
- Search: O(V)
Other factors:
- Sorting vertex lists has no benefit

Comparison of Graph Implementations

Terminology: |V| and |E| (cardinality) normally written just as V and E

A graph with V vertices has at most V(V - 1) / 2 edges

	Array of edges	Adjacency Matrix	Adjacency List
Space usage	E	V^2	V + E
Initialise	1	V^2	V
Insert edge	E	1	V
Remove edge	E	1	V
isPath(x,y)	E*log(V)	V^2	V + E
Copy graph	E	V^2	V + E
Destroy Graph	1	V	V + E
Search	E	1	V