COMP2521

Data Structures & Algorithms

Week 7.4

Shortest Path

Author: Hayden Smith 2021

In this lecture

Why?

Finding the shortest path through a graph is one of the most common use cases

What?

Shortest Path
Edge Relaxation
Dijkstra's Algorithm

Shortest Path

We're going to search for the shortest path between two vertices on a weighted graph with non-negative weights.

....Pretty much just a BFS with weighted edges....

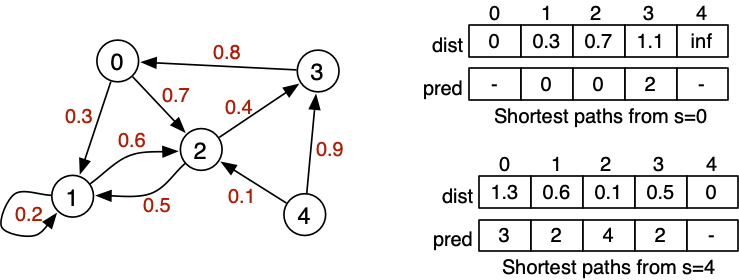
Shortest Path

Shortest paths from s to all other vertices:

dist[] V-indexed array of cost of shortest path from s
pred[] V-indexed array of predecessor in shortest path from s

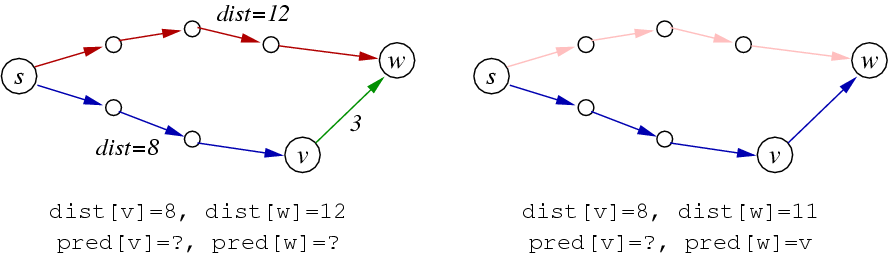
Edge Relaxation

Edge relaxation occurs whilst we are exploring a graph for the shortest path. This is because dist[] and pred[] show the shortest path so far.

If we have:

dist[v] is length of shortest known path from s to v
dist[w] is length of shortest known path from s to w
edge (v,w,weight)

Relaxation updates data for w if we find a shorter path from s to w :

if dist[v] + weight < dist[w] then
update dist[w]←dist[v]+weight and pred[w]←v

Edge Relaxation

Dijkstra's Algorithm

dijkstraSSSP(G,source):
  dist[]  // array of cost of shortest path from s
  pred[]  // array of predecessor in shortest path from s
  vSet    // vertices whose shortest path from s is unknown
  initialise all dist[] to ∞
  dist[source]=0
  initialise all pred[] to -1
  vSet = all vertices of G
  while vSet is not empty:
    find v in vSet with minimum dist[v]
    for each (v,w,weight) in edges(G):
      relax along (v,w,weight)
    vSet = vSet \ {v}

Dijkstra's Algorithm

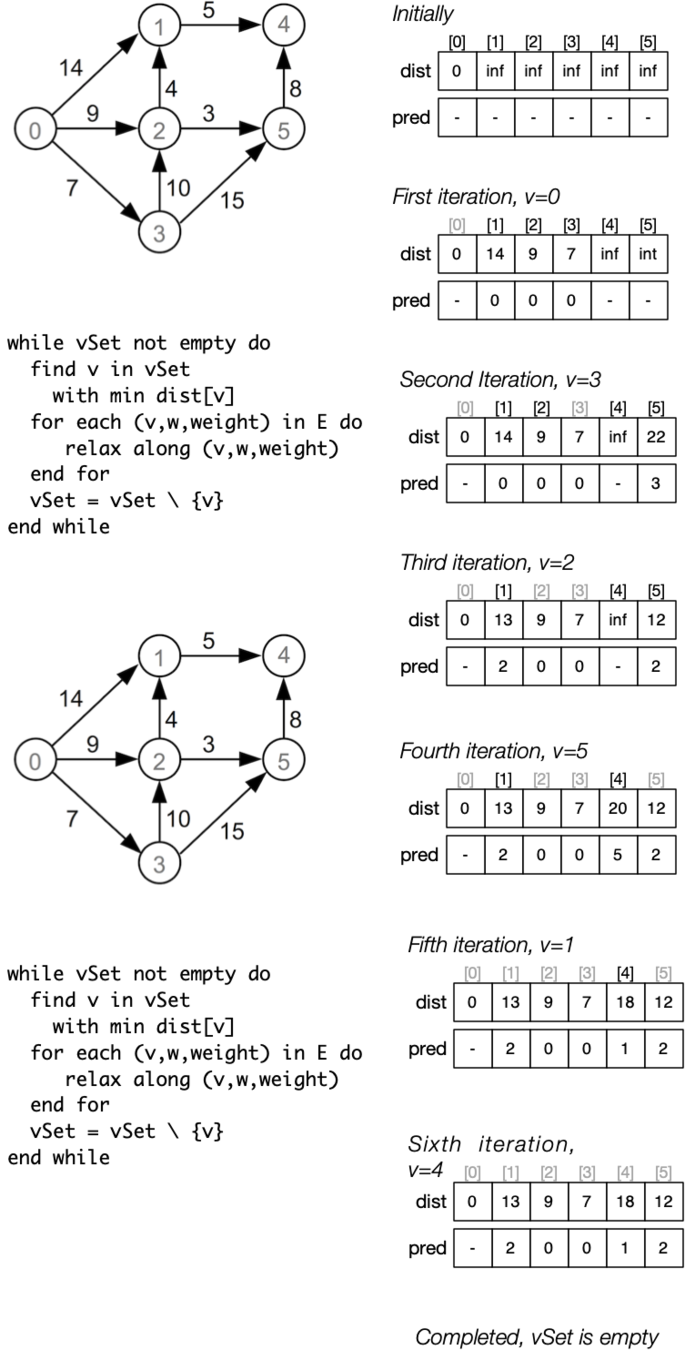
Dijkstra's Algorithm

Time Complexity

Each edge needs to be considered once ⇒ O(E).

Outer loop has O(V) iterations.

Implementing "find s ∈ vSet with minimum dist[s]"

try all s in vSet ⇒ cost = O(V) ⇒ overall cost = O(E + V^2) = O(V^2)
using a priority queue to implement extracting minimum... can improve overall cost to O(E + V·log V)