COMP2521

Data Structures & Algorithms

Week 9.1

Heaps & Priority Queues

Author: Hayden Smith 2021

In this lecture

Why?

Heap structures are tree-like structures used for things like priority queues - which are really common

What?

Heaps
Heap insert and delete
Priority Queues

Heaps

Heaps can be conceptualised as dense tree structures where:

Tree maintains a general order with higher elements up the top
New items are added in level order to the next available position on the bottom row. After added, they then "drift up" to appropriate level in tree
items are always deleted by removing root (top priority)
Since heaps are dense trees, depth = floor(log2N)+1

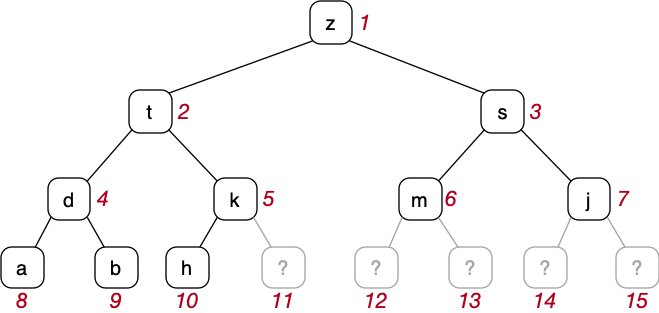
Heaps

BSTs are typically implemented as linked data structures.

Heaps are often implemented via arrays (assumes we know max size)

Simple index calculations allow navigation through the tree:

left child of Item at index i is located at 2i
right child of Item at index i is located at 2i+1
parent of Item at index i is located at i/2

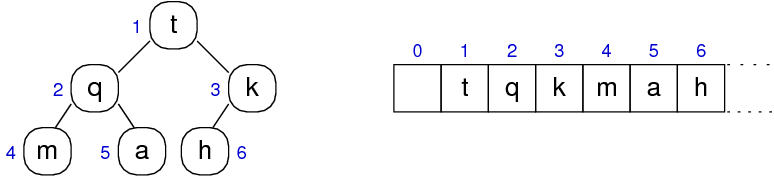
Heap Structure

typedef struct HeapRep {
   Item *items;  // array of Items
   int  nitems;  // #items in array
   int  nslots;  // #elements in array
} HeapRep;

typedef HeapRep *Heap;

Heap newHeap(int N)
{
   Heap new = malloc(sizeof(HeapRep));
   Item *a = malloc((N+1)*sizeof(Item));
   assert(new != NULL && a != NULL);
   new->items = a;   // no initialisation needed
   new->nitems = 0;  // counter and index
   new->nslots = N;  // index range 1..N
   return new;
}

Heap Inserting

Insertion is a two-step process

Add new element at next available position on bottom row
(but this might violate heap property; new value larger than parent)
Reorganise vales along path to root to restore heap property

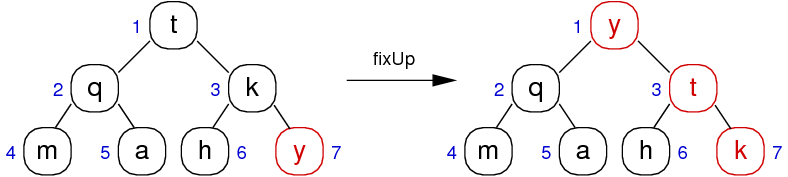
Heap Inserting

void HeapInsert(Heap h, Item it) {
   // is there space in the array?
   assert(h->nitems < h->nslots);
   h->nitems++;
   // add new item at end of array
   h->items[h->nitems] = it;
   // move new item to its correct place
   fixUp(h->items, h->nitems);
}

// force value at a[i] into correct position
void fixUp(Item a[], int i) {
   while (i > 1 && less(a[i/2], a[i])) {
      swap(a, i, i/2);
      i = i / 2;  // integer division
   }
}
void swap(Item a[], int i, int j) {
   Item tmp = a[i];
   a[i] = a[j];
   a[j] = tmp;
}

Heap Inserting

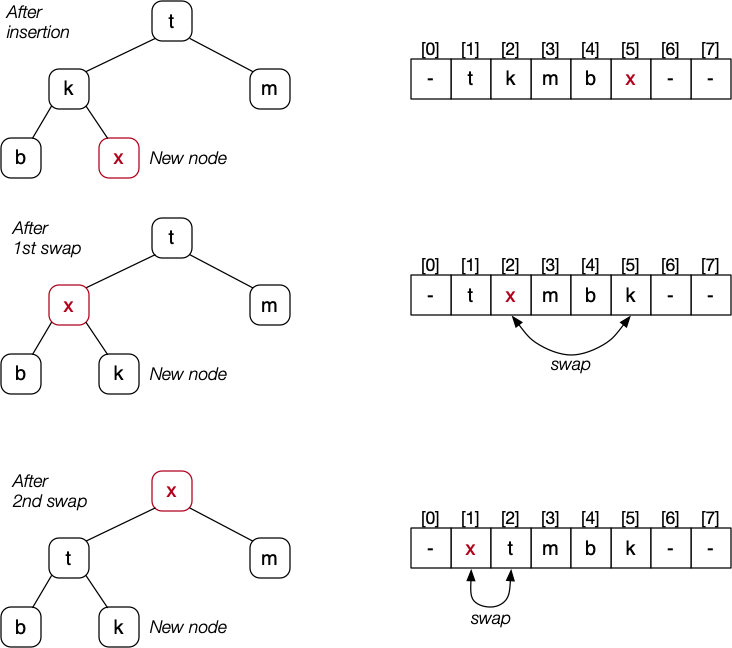
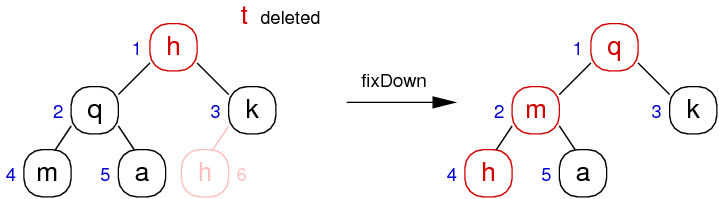
Heap Deletion

Deletion is a three-step process:

Replace root (always root) value by bottom-most, rightmost value
Remove bottom-most, rightmost value
Reorganise values along path from root to restore heap

Heap Deletion

Item HeapDelete(Heap h) {
   Item top = h->items[1];
   // overwrite first by last
   h->items[1] = h->items[h->nitems];
   h->nitems--;
   // move new root to correct position
   fixDown(h->items, 1, h->nitems);
   return top;
}


// force value at a[i] into correct position
// note that N gives max index *and* # items
void fixDown(Item a[], int i, int N) {
   while (2 * i <= N) {
      // compute address of left child
      int j = 2 * i;
      // choose larger of two children
      if (j < N && less(a[j], a[j+1])) j++;
      if (!less(a[i], a[j])) break;
      swap(a, i, j);
      // move one level down the heap
      i = j;
   }
}

Heap Complexity

For insertion:
- Add new item at end of array ⇒ O(1)
- Move item up into correct position ⇒ O(log2n)
- Summary: O(log(n))
For deletion:
- Replace root by item at end of array ⇒ O(1)
- Move new root down into correct position ⇒ O(log2n)
- Summary: O(log(n))

Priority Queue

Heap behaviour is exactly behaviour required for Priority Queue :

join(PQ,it): ensure highest priority item at front of queue
it = leave(PQ): take highest priority item from queue

typedef Heap PQueue;

void join(PQueue pq, Item it) { HeapInsert(pq,it); }

Item leave(PQueue pq) { return HeapDelete(pq); }

Priority Queue

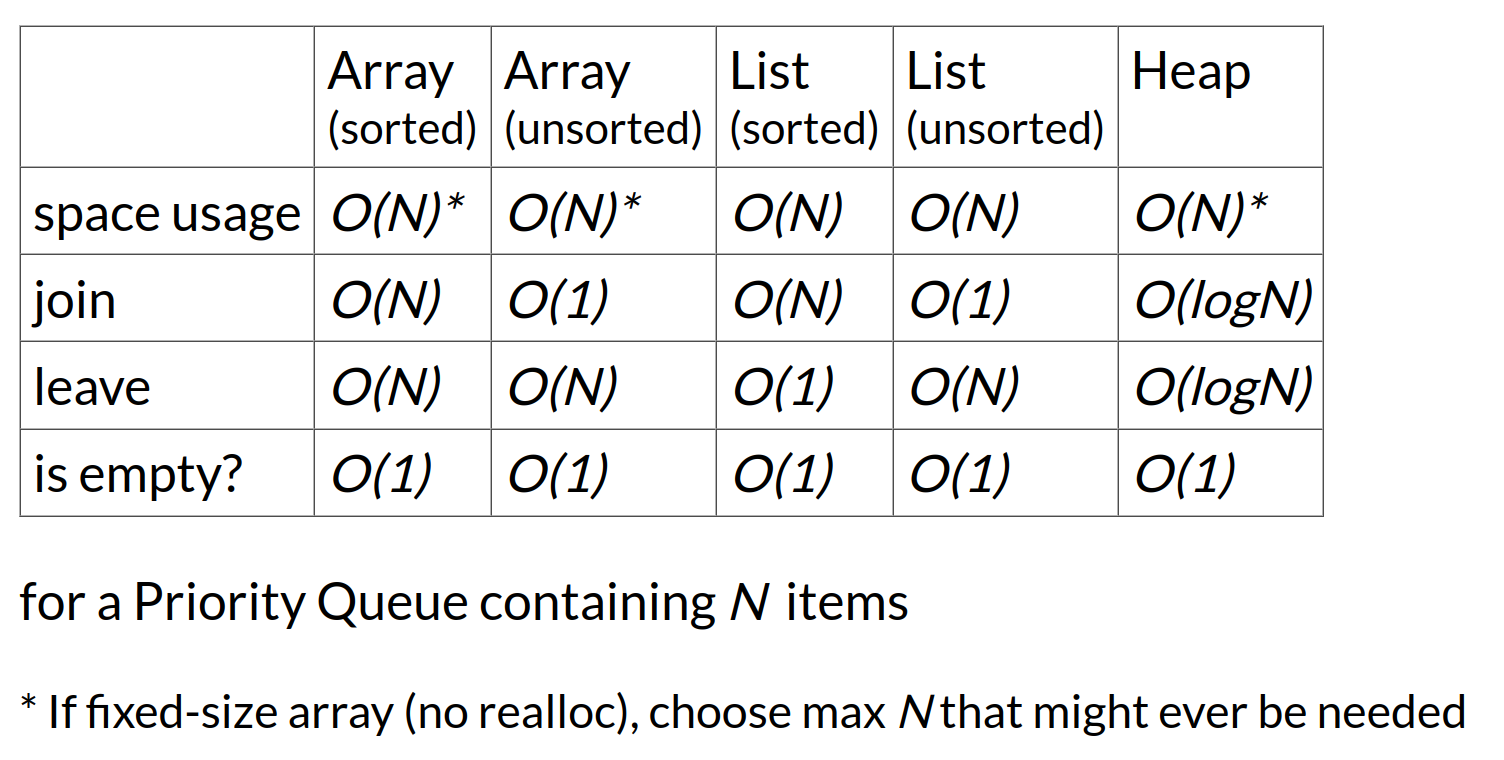
Implementation Comparison

Heap Sort

We can use a heap for sorting very easily:

Step 1: build a heap in the array
- iterates N times, each time doing fixUp()
- each fixUp() is O(logN), so overall O(NlogN)
Step 2: use heap to build sorted array
- iterates N times, each time doing swap() and fixDown()
- swap() is O(1), fixDown() is O(logN), so overall O(NlogN)

Cost of heapsort = O(NlogN)