Contact-Implicit Model-Predictive Control

Simon Le Cleac'h and Taylor Howell

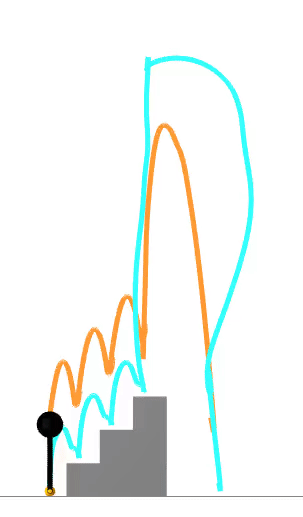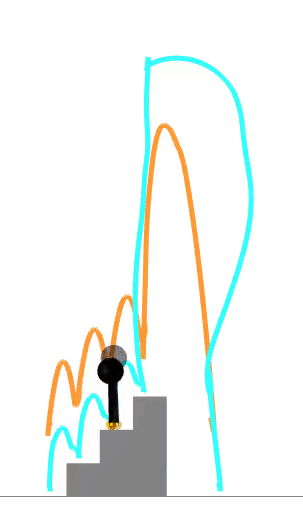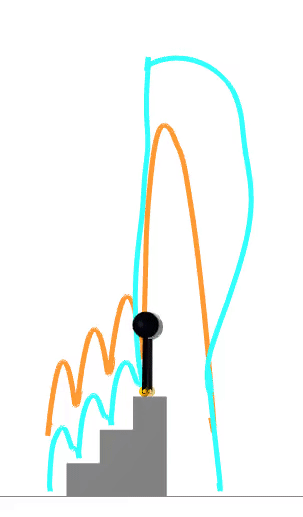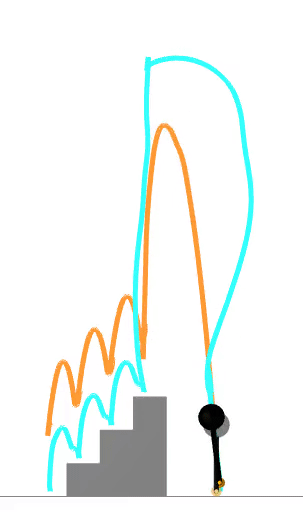
motivation: control through contact

motivation: linear MPC

linearization challenges

x(t)

reference trajectory

valid linearization domain

linearization challenges

x(t)

valid linearization domain

reference trajectory

\text{time}

\text{position}

\text{time}

\text{velocity}

strategic linearization

\underset{x_{t+1}}{\text{find}} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \\ \text{subject to} \quad \textbf{dynamics}(x_{t+1}, \gamma) = 0\\ % \quad \:\: \textbf{sdf}(x_{t+1}) = \phi \\ % \gamma \circ \phi = 0 \\ % \gamma, \phi \geq 0 \\

nonlinear complementarity problem (NCP)

impact force

strategic linearization

\underset{x_{t+1}}{\text{find}} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \\ \text{subject to} \quad \textbf{dynamics}(x_{t+1}, \gamma) = 0\\ \quad \:\: \textbf{sdf}(x_{t+1}) = \phi \\ % \gamma \circ \phi = 0 \\ % \gamma, \phi \geq 0 \\

nonlinear complementarity problem (NCP)

impact force

slack variable

strategic linearization

\underset{x_{t+1}}{\text{find}} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \\ \text{subject to} \quad \textbf{dynamics}(x_{t+1}, \gamma) = 0\\ \quad \:\: \textbf{sdf}(x_{t+1}) = \phi \\ \gamma \circ \phi = 0 \\ % \gamma, \phi \geq 0 \\

nonlinear complementarity problem (NCP)

impact force

slack variable

strategic linearization

\underset{x_{t+1}}{\text{find}} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \\ \text{subject to} \quad \textbf{dynamics}(x_{t+1}, \gamma) = 0\\ \quad \:\: \textbf{sdf}(x_{t+1}) = \phi \\ \gamma \circ \phi = 0 \\ \gamma, \phi \geq 0 \\

impact force

slack variable

nonlinear complementarity problem (NCP)

strategic linearization

\underset{x_{t+1}}{\text{find}} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \\ \text{subject to} \quad \textbf{linear dynamics}(x_{t+1}, \gamma) = 0\\ \quad \:\: \textbf{sdf}(x_{t+1}) = \phi \quad \quad \quad \\ \gamma \circ \phi = 0 \quad \quad \quad \quad \\ \gamma, \phi \geq 0 \quad \quad \quad \quad \\

strategic linearization

\underset{x_{t+1}}{\text{find}} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \\ \text{subject to} \quad \textbf{linear dynamics}(x_{t+1}, \gamma) = 0\\ \quad \quad \quad \quad \textbf{linear sdf}(x_{t+1}) = \phi \quad \quad \quad \\ \gamma \circ \phi = 0 \quad \quad \quad \quad \\ \gamma, \phi \geq 0 \quad \quad \quad \quad \\

linear complementarity problem (LCP)