Leveraging Differentiable Physics for Contact-rich Robotic Control

 

Simon Le Cleac'h

Summer 2022

contact is the primary mode of interaction in robotics

challenges

  • not differentiable
  • classical optimization methods fail
  • RL has shown impressive results but
    • gradient-free
    • ignores dynamics model

question

how can we leverage models and gradient information to solve contact-rich robotics tasks?

  • data generator for robotics optimization           

differentiable physics engine

  • robot's internal model of the world                   
  • simulate contact and provide gradients             

optimization problems

control parameters state parameters model parameters

decision variables

performance criteria

optimal control
 		 motion synthesis mechanism design
imitation learning state estimation system identification
movement costs
model-data mismatch
Emo Todorov, Optico: A Framework for Model-Based Optimization with MuJoCo Physics, NeurIPS 2019

optimization as an oracle

  • trajectory optimization with privileged information
  • can generate a lot of 'expert demonstrations' for a learning algorithm
  • useful gradient information

differentiable physics engine

  • stable and accurate simulation

contact physics

LCP

implicit complementarity

gradients

samples

subgradient

existing physics engines

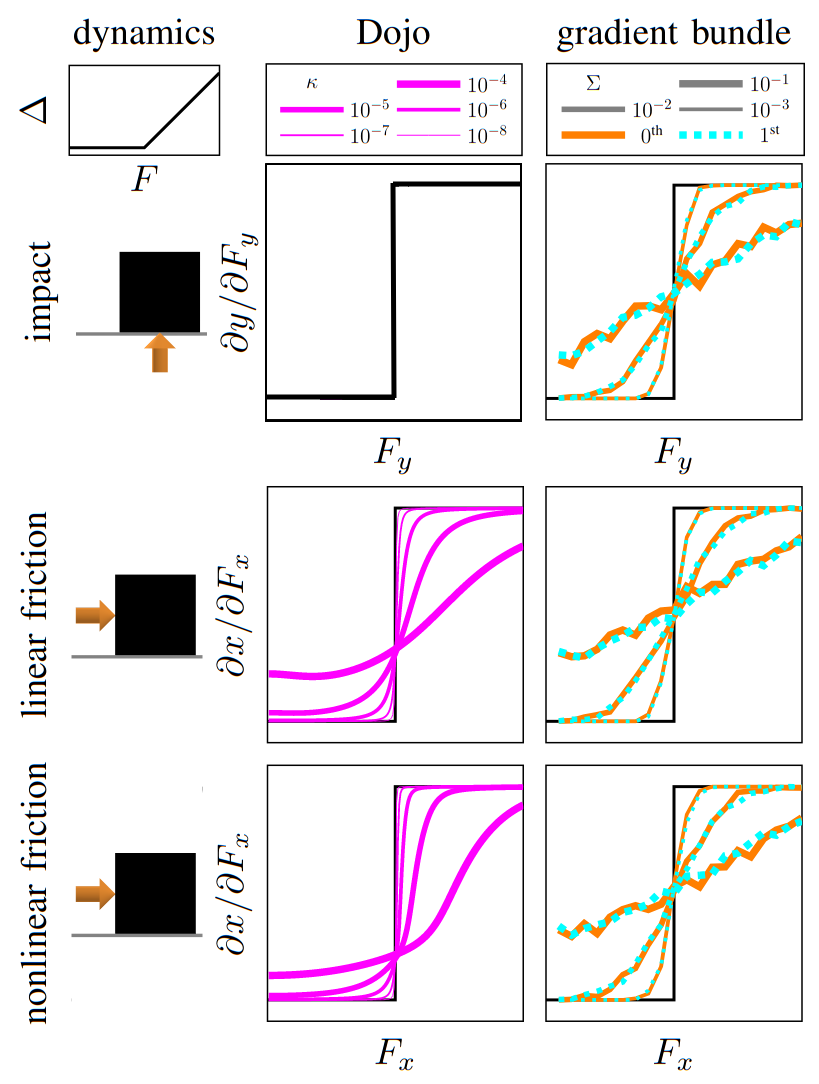
Dojo key ideas

stability at low rates

variational integrator

interior-point methods

accurate contact dynamics

implicit differentiation

smooth gradients

m(p_+ -2p +p_-)/h - hmg = 0
Discrete mechanics and variational integrators. J. E. Marsden and M. West.
S = \int_{t_1}^{t_2}{\mathcal{L} dt}

discretize

discretize

Euler-Lagrange

Euler-Lagrange

F = m a
p_+ = p + h (v + mg)
S_D = h \sum_{i=1}^{N} \mathcal{L}_i

variational integrator

variational integrator

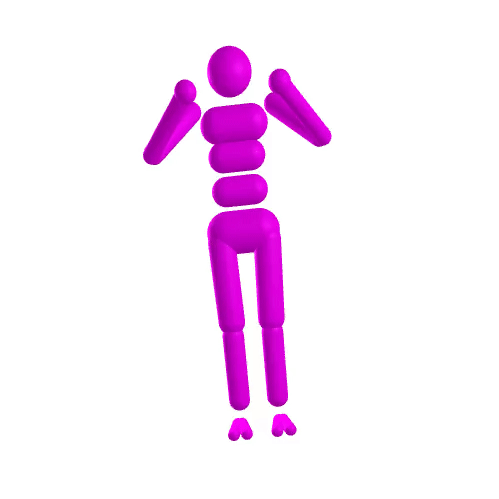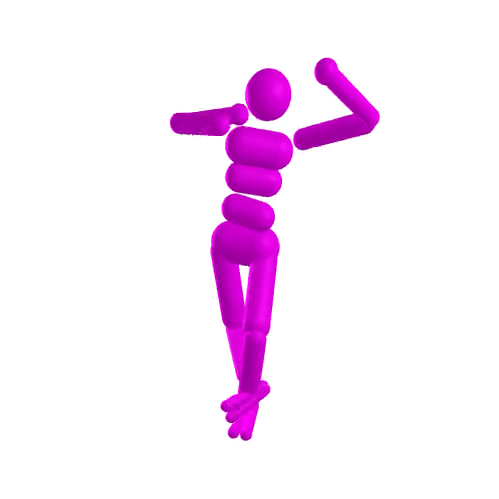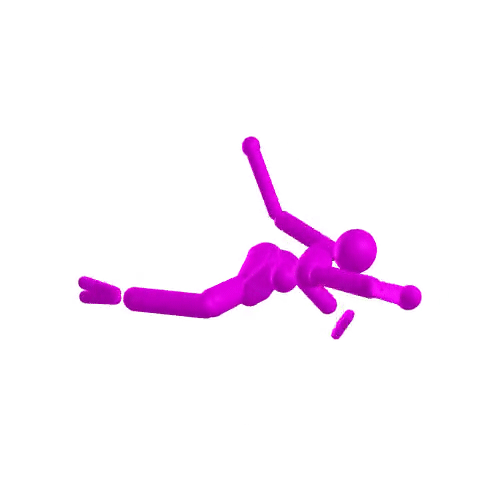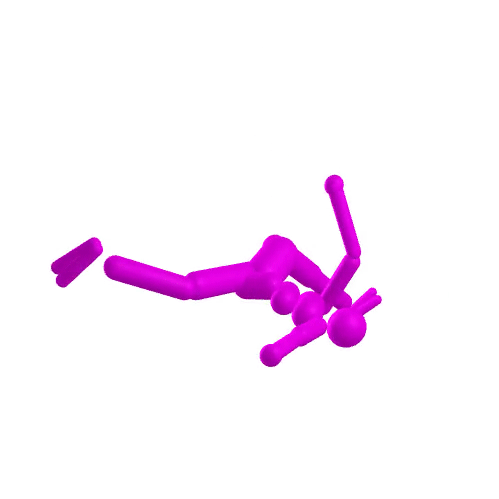
  • compare astronaut energy and momentum conservation to MuJoCo

  • Dojo performs orders of magnitude better
  • stability at low rates
t = 0s
t = 1s

accurate contact dynamics

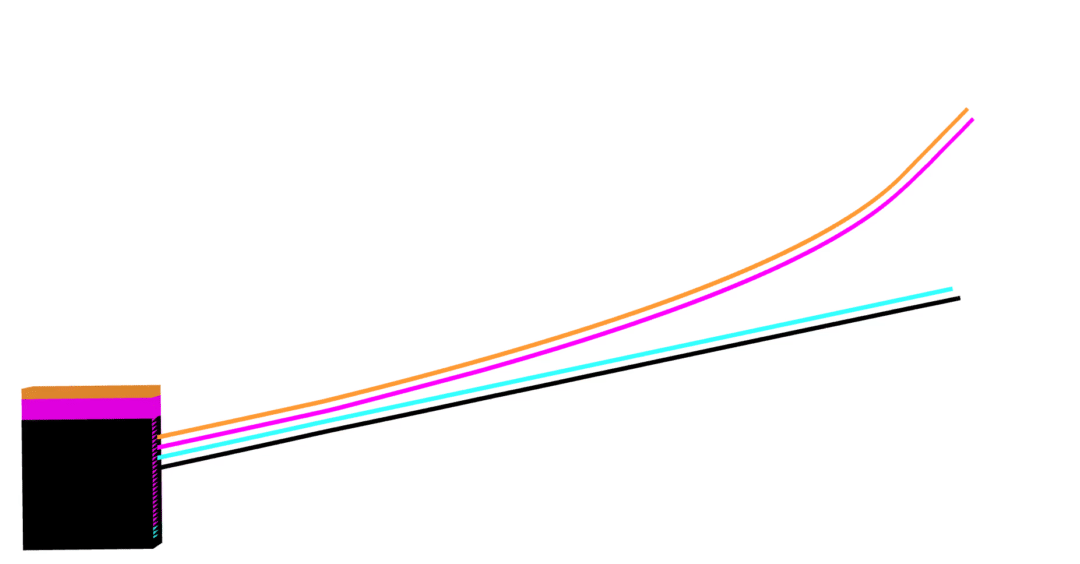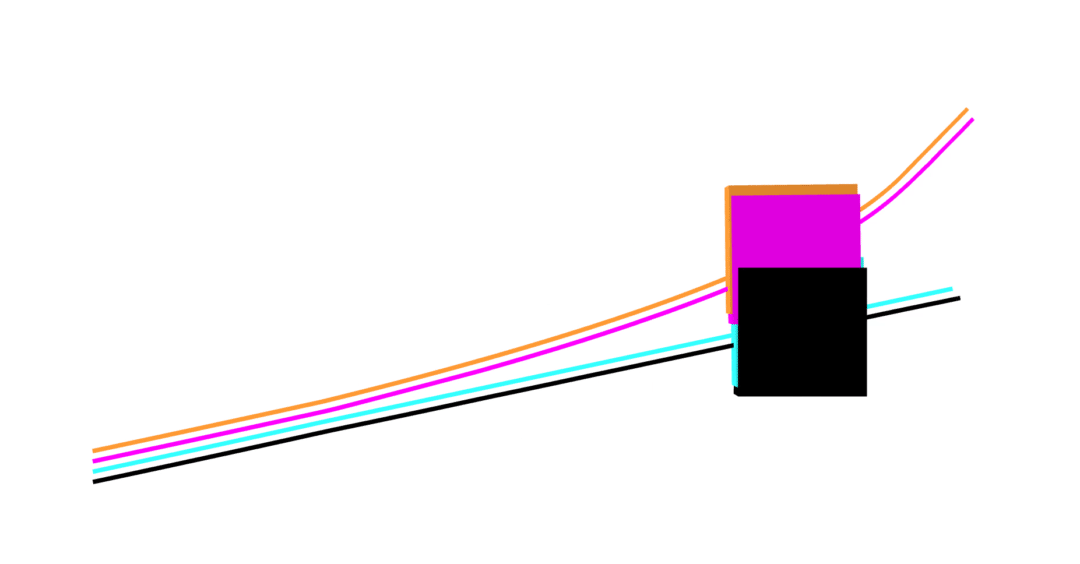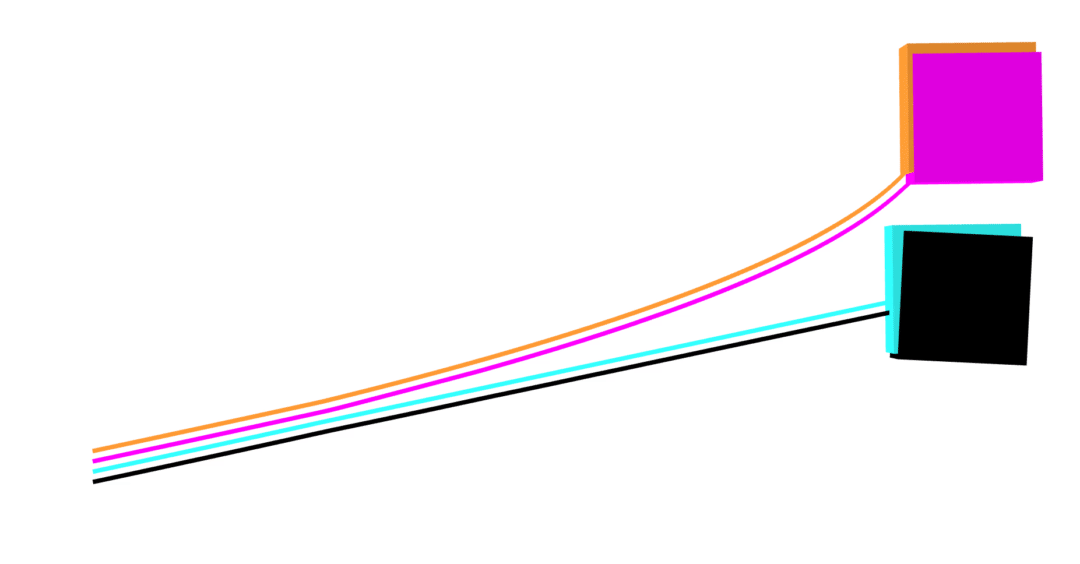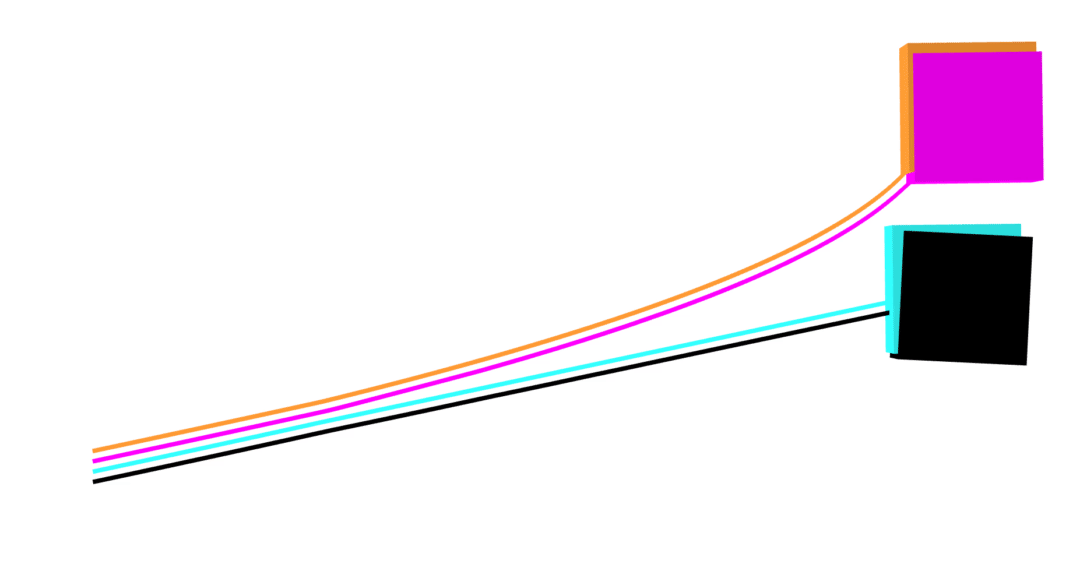
MuJoCo linear

Dojo linear

MuJoCo nonlinear

Dojo nonlinear

no collision violations

correct Coulomb friction

interior-point method

impact → inequalities

friction → second-order cone

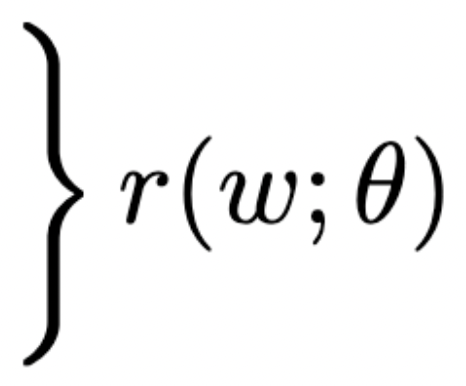
cone constraints

custom interior-point solver

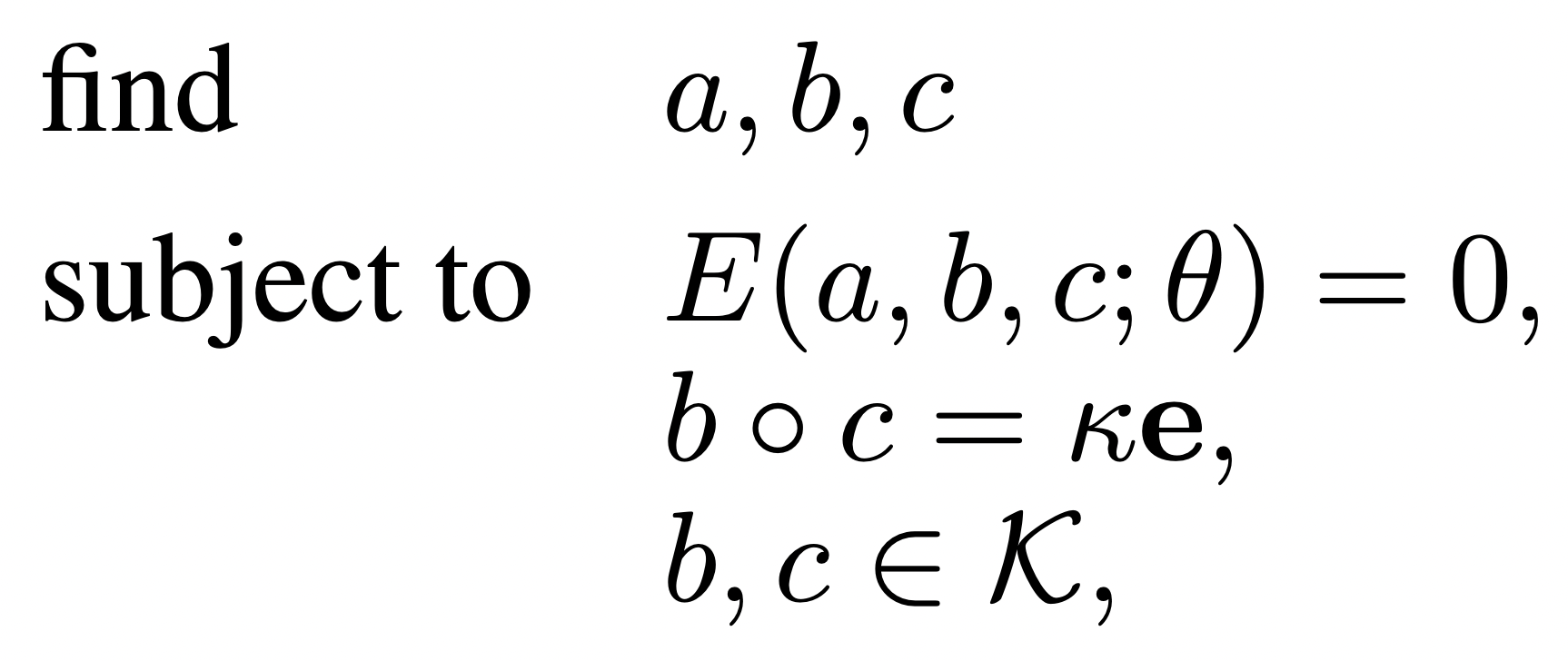
  • Mehrotra predictor-corrector algorithm
  • CVXOpt second-order cones
  • non-Euclidean support for quaternions

accurate contact dynamics

nonlinear complementarity problem

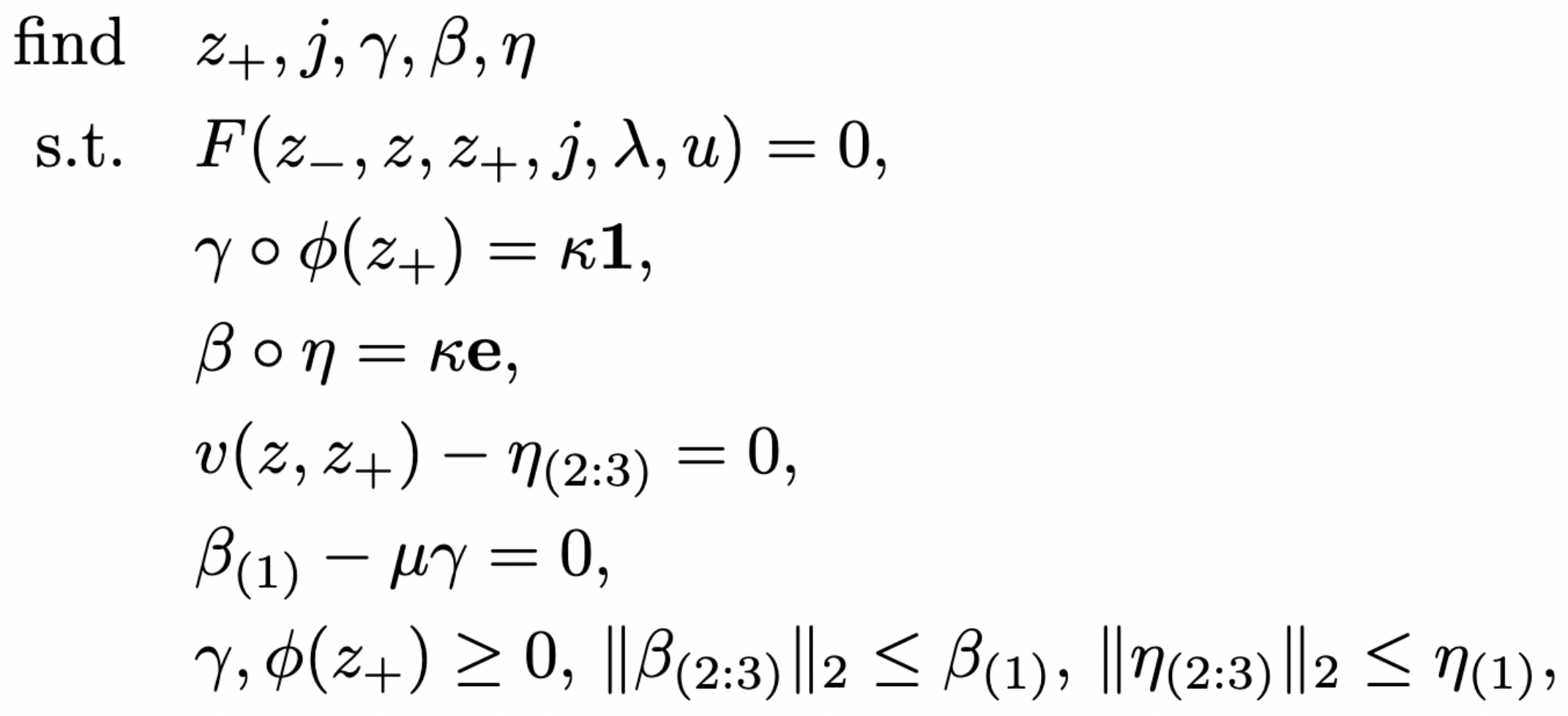
accurate contact dynamics

custom interior-point solver

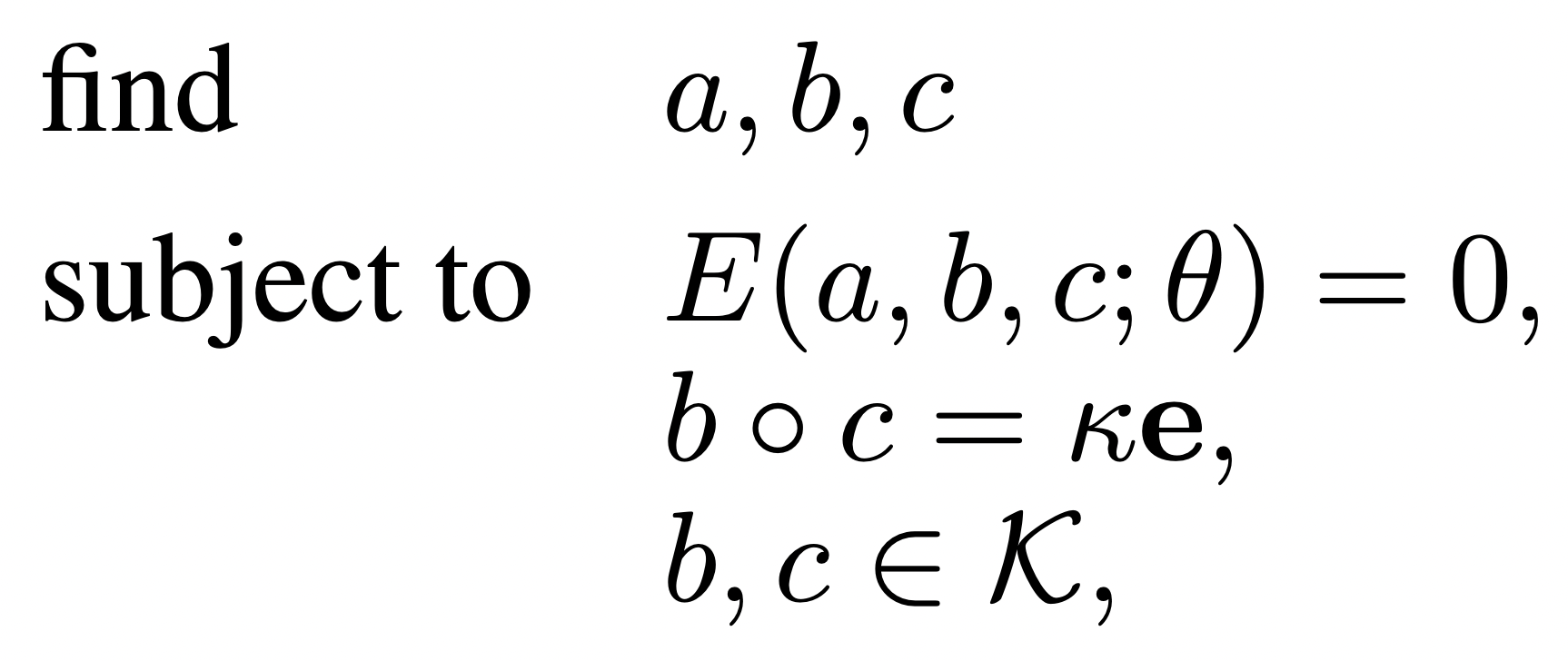
accurate contact dynamics

embedding learned models

f(x_{t+1}, x_t, u_t; \theta) = 0

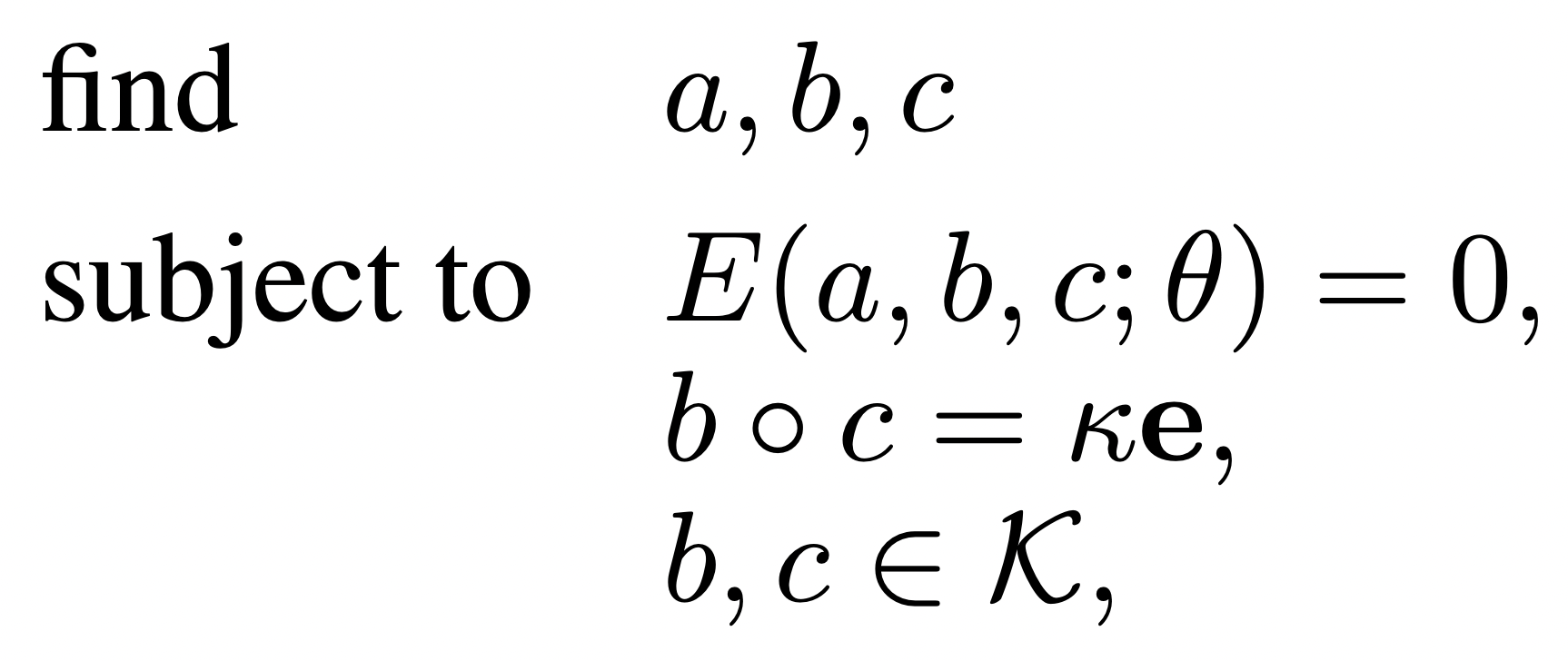
physics

physics

robot

environment

object

learned

r(w^*; \theta) = 0

→

smooth gradients

\big\{

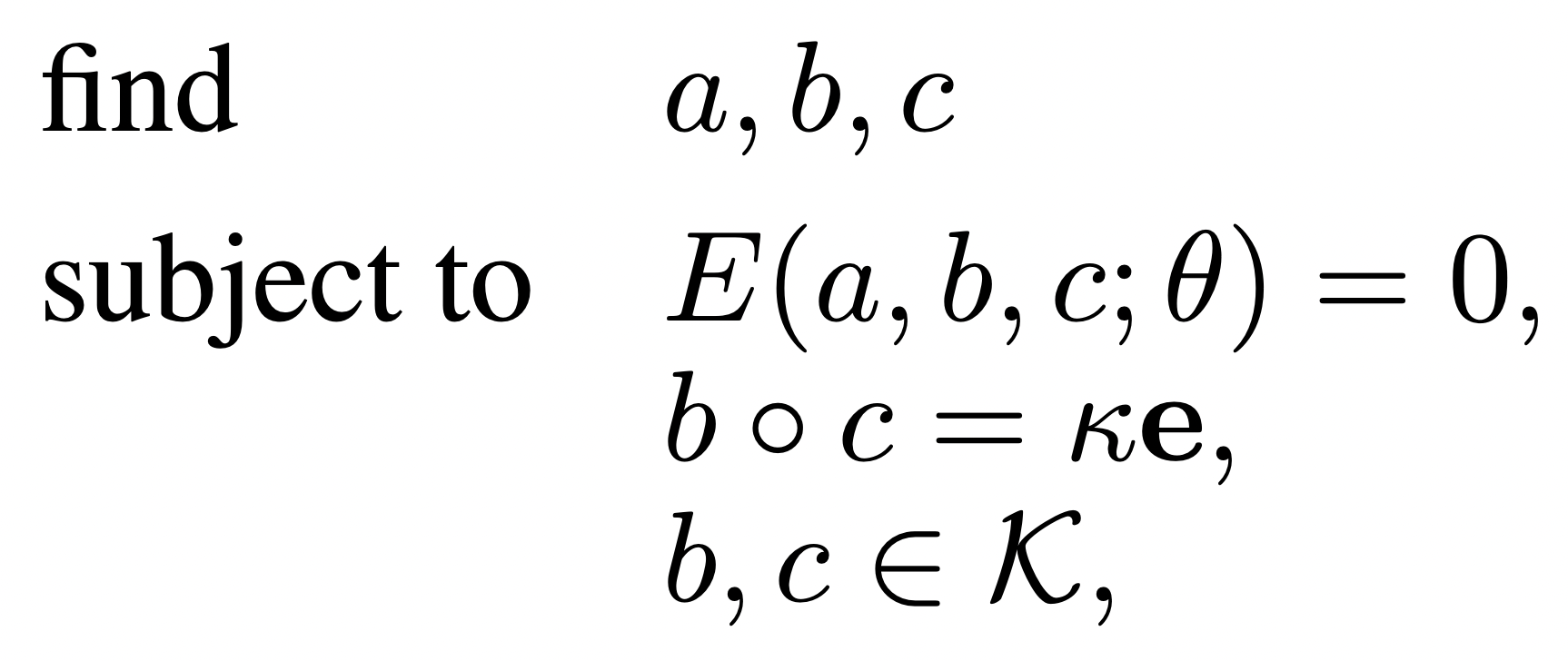
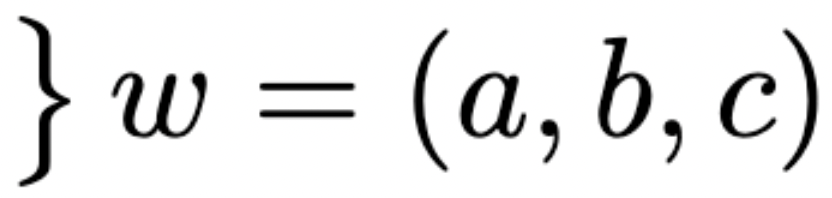
residual

solution

\big\{
\big\{

parameters

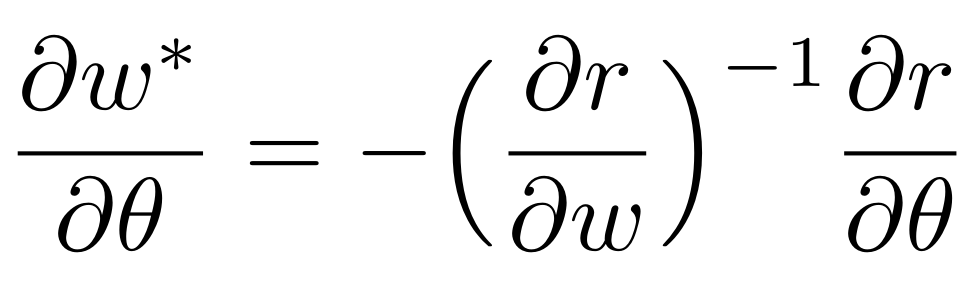
sensitivity of solution w.r.t problem data

computation cost of gradient is less than simulation step

smooth gradients

Lezioni di analisi infinitesimale. U. Dini.

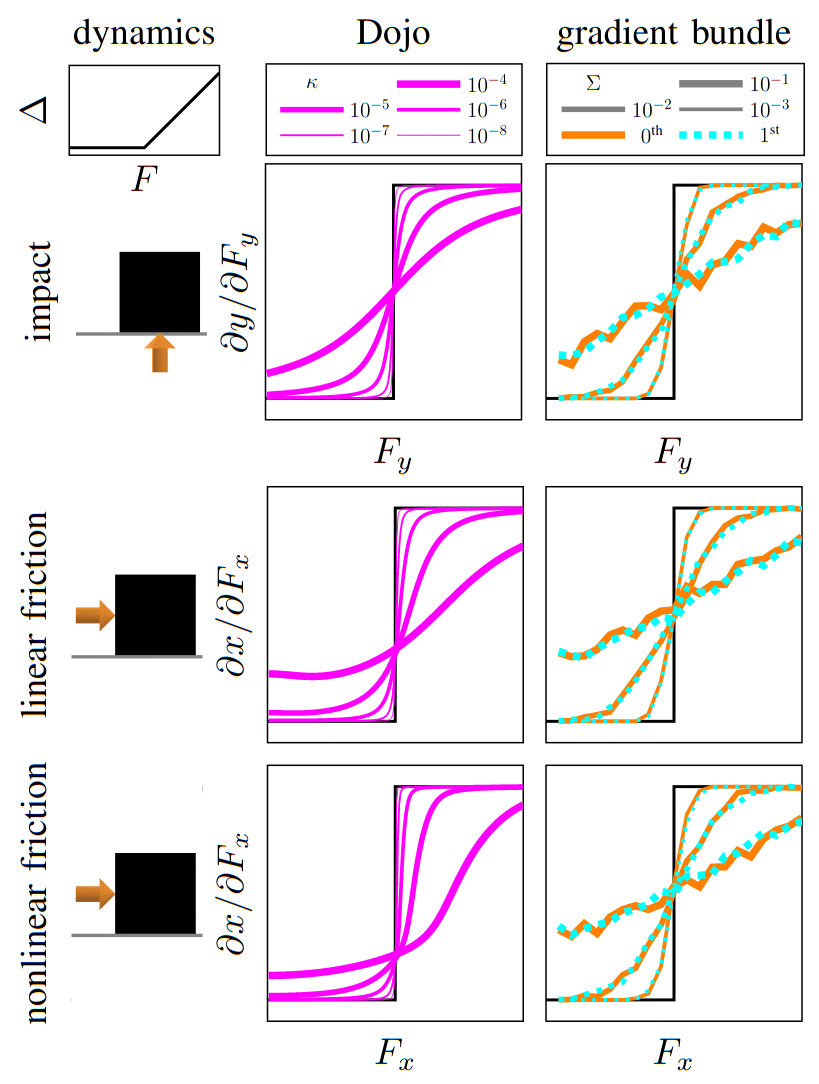
Dojo gradients vs sampling

less expensive to compute compared to finite-difference or stochastic sampling

randomized smoothing

finite difference

Dojo

matrix backward substitution

\mathcal{O}(n^2)

matrix factorization

\mathcal{O}(n^3)

matrix factorization

\mathcal{O}(n^3)

Dojo's gradient vs MuJoCo's finite difference

t = 0s
t = 1s

box push

non-smooth dynamics

gradient comparison

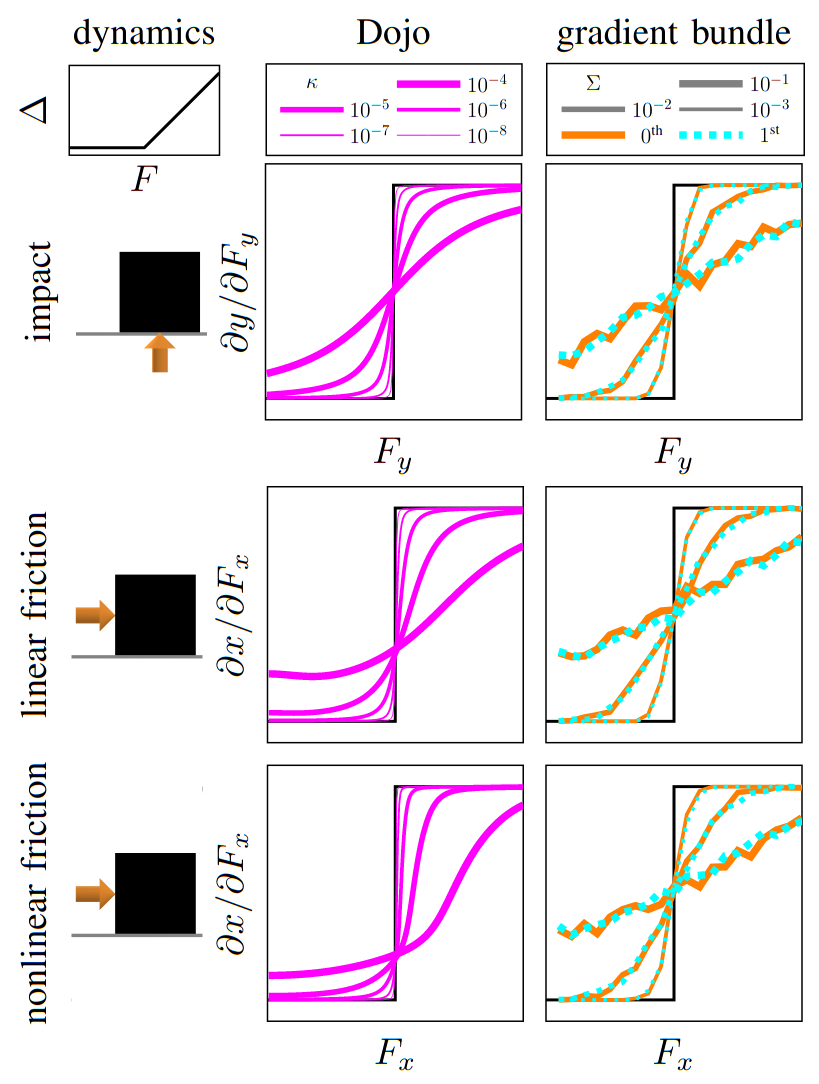
Dojo

randomized smoothing

differentiate intermediate barrier problems for smooth gradients

Dojo gradients vs sampling

examples

trajectory optimization

smooth-gradient-based optimization with iterative LQR

stability at low rates enables 2-5x sample-complexity improvement over MuJoCo

reinforcement learning

train static linear policies for locomotion

gradients enable 5-10x sample-complexity improvement over derivative-free method

stability at low rates enables 2-5x sample-complexity improvement over MuJoCo

system identification

ContactNets: Learning Discontinuous Contact Dynamics with Smooth, Implicit Representations. 
S. Pfrommer, M. Halm, and M. Posa.

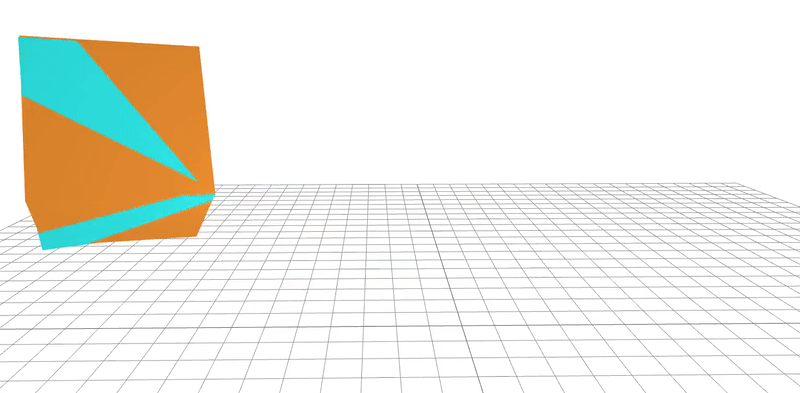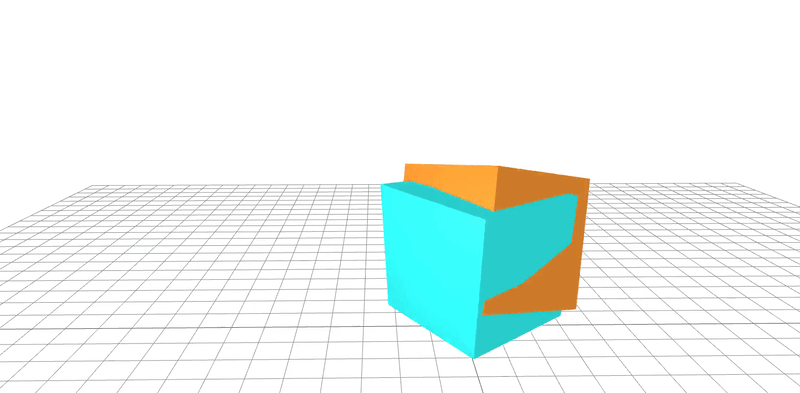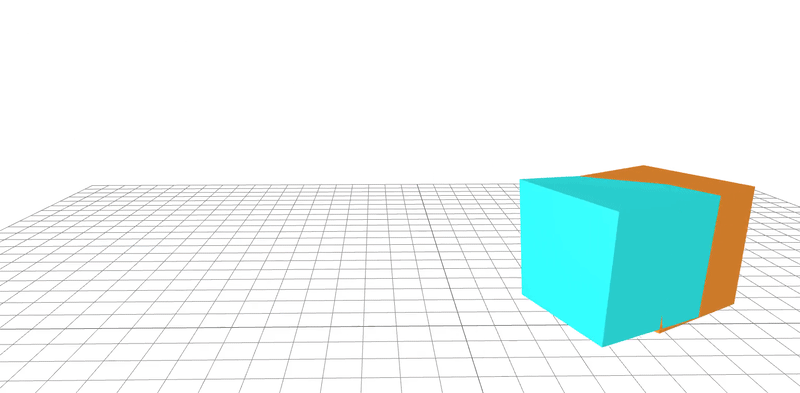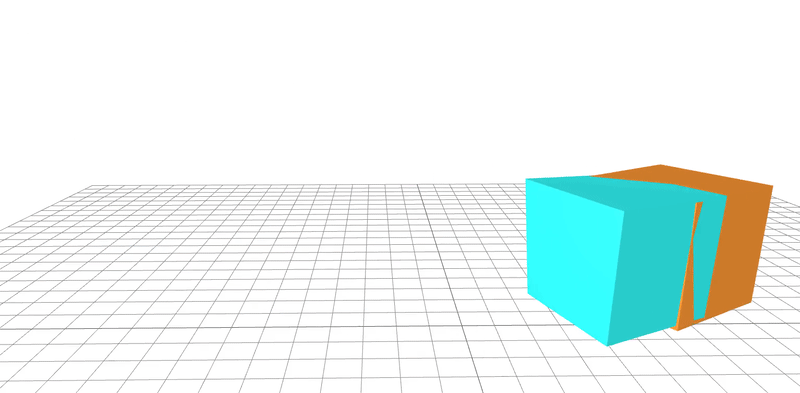
learned

 

ground-truth

real-word dataset

Dojo environment

system identification

geometry

friction coefficient

 

ground-truth

learned

Quasi-Newton method utilizes gradients to

learn parameters to 95% accuracy in 20 steps

model-predictive control

Fast Contact-Implicit Model-Predictive Control. 
S. Le Cleac'h & T. Howell, C. Lee, S. Yang, M. Schwager, Z. Manchester

simulation

push recovery

behavior generation

 running policy at 200-500Hz

related work

Global Planning for Contact-Rich Manipulation via Local Smoothing of Quasi-dynamic Contact Models, Tao Pang∗, H.J. Terry Suh∗, Lujie Yang and Russ Tedrake,

RRT using the same smoothed derivatives as Dojo

NeRF

Differentiable Physics Simulation of Dynamics-Augmented Neural Objects. 
S. Le Cleac'h, HX. Yu, M. Guo, T. Howell, R. Gao, J. Wu, Z. Manchester, M. Schwager

dynamics-augmented NeRF → complex collision geometries

optimization problems

control parameters state parameters model parameters

decision variables

performance criteria

optimal control
 		 motion synthesis mechanism design
imitation learning state estimation system identification
movement costs
model-data mismatch
Emo Todorov, Optico: A Framework for Model-Based Optimization with MuJoCo Physics, NeurIPS 2019

differentiable optimization modules

differentiable simulator

online optimization-based policy

(MPC, etc.)

control inputs

gradients

gradients

offline optimization

(RL, RRT, etc.)

motion plans

trajectories

optimization as a differentiable module

  • build fast robust and differentiable optimization tools:
    • sysID
    • motion generation
    • optimal control
    • state estimation
    • etc.
  • can act as layers or differentiable modules in a larger control struture
    • MPC autotuning
    • MPC with neural networks bits

Taylor Howell

Simon Le Cleac'h

Jan Brüdigam

Zico Kolter

Mac Schwager

Zachary Manchester

team

Shuo Yang

Chi Yen Lee

Made with Slides.com